Разложение вектора по двум неколлинеарным векторам / Метод координат / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Метод координат
- Разложение вектора по двум неколлинеарным векторам
Лемма
| Если векторы и коллинеарны и , то существует такое число , что . |
Доказательство
Дано: и коллинеарны, .
Доказать: существует такое число , что .
Доказательство:
Возможны два случая:
1) .
Пусть число . Так как , то векторы и сонаправлены.
При этом, их длины равны: . Следовательно, .
2) .
Пусть число . Так как , то векторы и сонаправлены.
При этом, их длины равны: . Следовательно, . Лемма доказана.
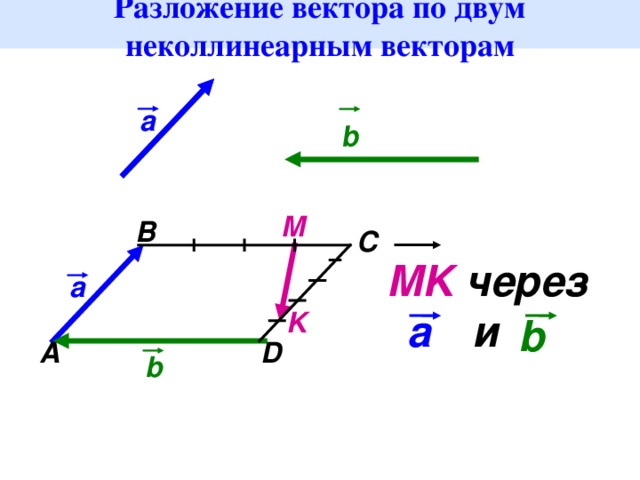
Пусть и два данных вектора. Если вектор представлен в виде , где и — некоторые числа, то говорят, что вектор разложен по векторам и . Числа и называются коэффициентами разложения.
Теорема
| На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом. |
Доказательство
Дано: и неколлинеарные.
Доказать: любой вектор можно разложить по векторам и , т.е. , и определяются единственным образом.
Доказательство:
1 случай
Вектор коллинеарен одному из векторов и , например, вектору .
Тогда по лемме о коллинеарных векторах вектор можно представить в виде , где — некоторое число, следовательно, , т.
2 случай
Вектор не коллинеарен ни вектору , ни вектору .
Отметим какую-нибудь точку О и отложим от нее векторы . Через точку Р проведем прямую, параллельную прямой ОВ, которая пересечет прямую ОА в точке А1.
По правилу треугольника сложения двух векторов , при этом векторы и коллинеарны векторам и , следовательно, по лемме о коллинеарных векторах существуют такие числа и такие, что и . Поэтому , т.е. вектор можно разложить по векторам и .
Докажем, что коэффициенты и определяются единственным образом.
Допустим, что вместе с разложением (1) существует и другое разложение . (2)
Вычтем из равенства 
(3)
Равенство (3) выполнимо только в том случае, когда и . Действительно, если предположить, что , то из равенства (3) получим, что , значит, векторы и коллинеарны, что противоречит условию теоремы. Следовательно, и , откуда и , а это говорит о том, что коэффициенты и разложения вектора определяются единственным образом. Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Координаты вектора
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Уравнение линии на плоскости
Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Метод координат
Правило встречается в следующих упражнениях:
7 класс
Задание 911, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 912, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 916, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 918, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 919, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 920, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 927, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 928, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Векторы.
Разложение вектора по направлениям. Координаты вектора. Скалярное произведение векторовПохожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Векторы Разложение вектора по направлениям Координаты вектора Скалярное произведение векторов
Вектор (направленный отрезок) отрезок, для которого указано, какая из его граничных точек считаетсяначалом, а какая – концом.
Обозначение:
или
Конец вектора
В
Длиной или модулем вектора
называется длина отрезка АВ:
АВ = АВ
А
Начало
вектора
a
Два
ненулевых вектора
называются
коллинеарными, если они лежат на одной прямой или на
параллельных прямых.
Коллинеарные, сонаправленные векторы
c
b
a
b
c
b
c
a
Коллинеарные,
противоположно направленные векторы
b
c
a
b
c
b
Векторы
называются
равными,
сонаправлены и их длины равны.
В
А
С
a
a
если
=
они
b
b
D
Векторы называются противоположными, если они
В
А
С
D
a b
a= b
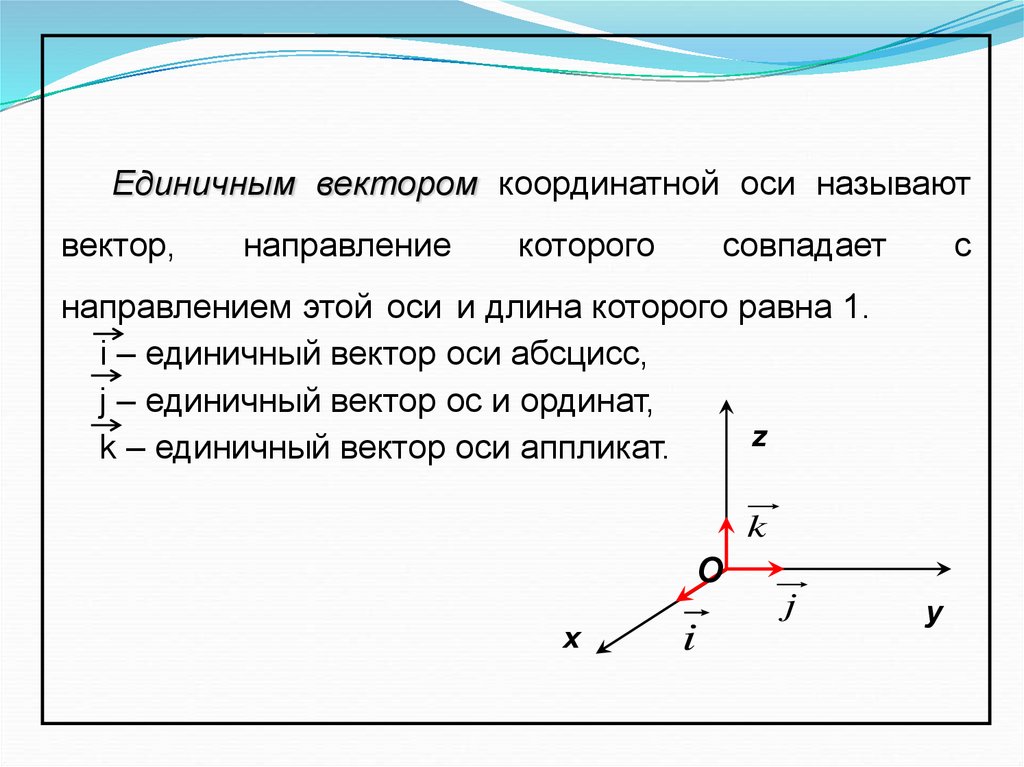
Рассмотрим
ПДСК. Единичным вектором коор-
динатной оси будем называть вектор, направление
которого совпадает с направлением этой оси и длина
которого равна 1.
i – единичный вектор оси абсцисс,
j – единичный вектор ос и ординат,
k – единичный вектор оси аппликат.
z
k
O
j
x
i
y
Любой вектор можно разложить
векторам, т.е. представить в виде:
по
координатным
Нулевой вектор также можно представить в таком виде:
Координаты равных векторов соответственно равны:
Сумма (разность) векторов:
Произведение вектора на число:
Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором
данной точки.
Координаты любой точки равны соответствующим координатам её радиус-вектора.Координаты середины отрезка
Длина вектора по его координатам:
Даны векторы:
Найти вектор, равный:
Найдите значения m и n, при которых векторы
коллинеарны.
А
Угол между векторами
а
О
Если
Если
Если
α
В
b
и
,то
и
, то.
, то
d c
= 180
0
a
f
d
c
f
a
30
d
0
b
d f
= 0
0
b
a b
a c
b c
= 30
0
= 120
= 90
0
0
Скалярным произведением двух векторов называется
произведение их длин на косинус угла между ними.
a
b
=
a
b cos( a b)
Скалярное произведение векторов – число (скаляр).
Если векторы перпендикулярны, то скалярное произведение
этих векторов равно нулю.
0
a b = 90
b
a
a b < 90
b
0
a
Если угол между векторами острый,
произведение этих векторов положительно.
b
a b > 90
то
скалярное
то
скалярное
0
a
Если угол между векторами тупой,
произведение этих векторов отрицательно.
a b
=
a
b сos (a b )
Пусть векторы заданы своими координатами a ( x1; y1; z1 )
и b ( x2; y2; z2 ). Тогда скалярное произведение этих векторов
равно
2
a · b = x1x2 + y1y2 + z1z2
2
a = |a|
cos
x1 x2 y1 y2 z1 z 2
x12 y12 z12 x22 y22 z 22
cos
a b
| a | | b |
English Русский Правила
векторов
вектороввекторов
Вектор — это величина, обладающая свойствами величины (размера) и направления. Чтобы представить это, мы рисуем векторы в виде стрелок, где величина вектора указывается длиной стрелки, а направление вектора указывается ориентацией стрелки. Общие векторы, возникающие при движении, — это силы (такие как тяга и сопротивление), скорость и ускорение.
Добавление вектора
Часто в проблеме участвуют несколько векторов, и нам нужно найти их «чистый» или «результирующий» эффект.
Чтобы найти результирующий вектор, мы должны использовать векторное сложение (суммирование). Сложение векторов отличается от сложения двух чисел, потому что мы должны учитывать как величину, так и направление векторов.
Типичным примером является суммирование сил, действующих на объект, для нахождения равнодействующей или «чистой» силы, действующей на объект. Это показано на рисунке ниже, где на блок действуют две силы. Одна сила имеет величину 30 Н в направлении x , а другая сила имеет величину 40 Н в направлении y . Поскольку эти силы имеют разные направления, мы не можем просто сложить их величины, чтобы получить результирующую силу.
Схема сил на блоке
Вместо этого мы можем сложить эти векторы графически, как показано на рисунке ниже. Графическое сложение векторов происходит путем выравнивания двух векторов «голова к хвосту». Тогда сумма векторов или результирующий вектор представляет собой вектор, проведенный из хвоста первого вектора в начало последнего вектора.
Общая проблема сложения векторов
Математически мы можем использовать теорему Пифагора, чтобы найти величину равнодействующей силы. Точно так же мы можем использовать тригонометрию, чтобы найти направление равнодействующей силы, выраженное как угол силы θ относительно горизонтали. Соответствующие расчеты приведены ниже.
Обозначение вектора: Иногда неудобно представлять векторы графически в виде стрелок. Вместо этого мы часто представляем векторы символически, используя векторную запись. Одним из распространенных методов является представление вектора как комбинации его компонентов в направлении x , или « i », и в направлении y , или « j ». Для приведенного выше случая чистый коэффициент силы выражается как
. где i и 9Символы 0015 j напоминают нам о направлении, связанном с величиной каждого компонента, а маленькая стрелка над F net указывает, что это вектор.
В качестве альтернативы, мы можем просто указать величину и направление вектора напрямую как
Обратите внимание, что величина вектора может быть представлена либо путем размещения вертикальных полос вокруг вектора, либо с помощью символа вектора, выделенного курсивом, без стрелки над ним.
Векторная декомпозиция
Векторная декомпозиция — это деконструкция вектора, который не лежит только в одном направлении, на несколько векторов в разных направлениях. По сути, разложение векторов — это сложение векторов в обратном порядке. Обычно мы разлагаем векторы на составные векторы, которые ортогональны. Это должно быть сделано таким образом, чтобы вектора компонентов суммировались с исходным вектором.
Для иллюстрации рассмотрим приведенный ниже вектор скорости, который равен 10 м/с при 53,1° относительно горизонтали. Мы хотели бы разложить этот вектор на его горизонтальную и вертикальную составляющие.
Общая задача векторной декомпозиции
Используя базовую тригонометрию, мы можем напрямую вычислить величину компонент векторов как в горизонтальном ( i ), так и в вертикальном ( j ) направлениях. Используя функцию синуса, можно определить величину вертикальной составляющей как
.Тогда, используя теорему Пифагора, можно определить оставшуюся сторону векторного треугольника следующим образом
В качестве альтернативы можно снова использовать тригонометрию для определения третьего катета треугольника, а именно
Часто бывает удобно разложить векторы на составляющие, когда для задачи важна только одна из составляющих. Кроме того, знание горизонтальной и вертикальной составляющих вектора позволяет нам представить вектор в векторной записи. Используя наши результаты, рассмотренный выше вектор скорости можно записать в векторной записи как
Относительное движение и векторы
Векторы также полезны для понимания концепции относительного движения.
Чтобы проиллюстрировать, как векторы используются для определения относительного движения, мы определим относительную скорость ветра, наблюдаемую с движущегося парусника.
Парусник, показанный ниже, плывет на северо-восток со скоростью 20 узлов, в то время как ветер дует с востока со скоростью 10 узлов. Каково направление и величина скорости ветра, которую ощущают (наблюдают) моряки на борту парусника?
Иллюстрация относительной скорости ветра
Чтобы определить наблюдаемую моряками скорость ветра, мы должны рассмотреть задачу с их точки зрения. В частности, они видят океан, движущийся мимо них со скоростью 20 узлов от носа лодки к корме, что означает, что они видят океан, движущийся в юго-западном направлении со скоростью 20 узлов. Добавление юго-западного движения, наблюдаемого моряками, к западному движению ветра со скоростью 10 узлов дает скорость ветра, наблюдаемую моряками. Графическое сложение векторов показано на рисунке ниже.
Поскольку скорость парусника находится под углом 45°, будет легче найти величину ( W ) и направление относительной скорости ветра, если мы сначала разложим вектор скорости парусника на его горизонтальную и вертикальную составляющие.
Векторы компонентов показаны на рисунке выше. Поскольку скорость парусной лодки находится под углом 45°, величины ее горизонтальной и вертикальной составляющих равны и легко определяются по теореме Пифагора как
После разложения скорости парусника на составляющие становится очевидным, что горизонтальная составляющая скорости относительного ветра является суммой двух горизонтальных составляющих (10 м/с и 14,1 м/с), а вертикальная составляющая равна как вертикальная составляющая скорости парусника. Итак, векторная запись у нас есть
Векторные вычисления
Обратите внимание, что знаки «-» используются для обозначения того, что вертикальная составляющая указывает на одну сторону, а горизонтальная составляющая указывает налево. Точно так же величина и направление Вт можно определить как
Расчеты величины и направления
Есть ли способ разложить вектор на ортогональные векторы с помощью регрессии?
Переформулировка задачи
Пусть каждый $Y_i$ является вектор-столбцом с $n$ компонентами, и пусть $Y$ будет матрицей, столбцы которой равны $Y_1, Y_2, \ldots, Y_k$ в любом порядке.
\prime$, для которых разности 92$$ любой матрицы $A$ есть сумма квадратов ее компонент. Поскольку ранг $U$, очевидно, не превышает числа его столбцов $p$, $UW$ является аппроксимацией $Y$ $Y$ по минимальной норме ранг-$p$ .
Анализ
Норма Фробениуса не меняется при умножении справа и слева на ортогональные матрицы (практически по определению ортогональных). Разложение по сингулярным числам, или SVD, любой матрицы, такой как $Y$, состоит из применения таких умножений, чтобы уменьшить матрицу до диагональ матрица $\Sigma$ (обязательно той же размерности, что и $Y$). («Диагональный» означает, что только ненулевые элементы $\Sigma$ должны иметь одинаковые индексы строк и столбцов.) Более того, поскольку перестановки строк и столбцов, а также отрицание целых строк или столбцов также являются ортогональными умножениями, можно устроить так, что ( 1) все элементы $\Sigma$ неотрицательны и (2) значения по диагонали убывают: $$\Sigma_{11} \ge \Sigma_{22} \ge \cdots \ge \Sigma_{\min( k,n),\min(k,n)} \ge 0.
$$ 9\prime$$
имеет не более чем $p$ ненулевых строк. Первые $p$ столбцов $U$ и $k$ векторов-столбцов $W$ (с остановкой в строке $p$) решают задачу: первые играют роль ортогональных регрессоров $A$ и $B $ в вопросе, а последние являются коэффициентами, полученными регрессией столбцов $Y$ на $A$ и $B$.
Конкретное решение
При $p=2$ возьмем $A$ за первый столбец таблицы $U$, а $B$ за второй столбец. По построению $A$ и $B$ будут ортогональны (и каждая будет иметь единичную длину). $\alpha_i$ и $\beta_i$ можно прочитать из столбцов $W$ ($\alpha_i$ находятся в первой строке, а $\beta_i$ — во второй строке).
Вот результат выполнения этого вычисления 5000 раз для набора случайных $12\times 6$ матриц ранга $2$, к которым были добавлены iid нормальные ошибки со стандартным отклонением $0.1$. Это стандартное отклонение можно оценить, разделив квадрат нормы Фробениуса остатков на степени свободы и извлекая квадратный корень. Степенями свободы будут количество данных в $Y$, $n\times k$, за вычетом числа оцениваемых параметров.
Количество параметров, необходимых для указания $p$ ортогональных векторов, равно $n + (n-1) + \cdots + (n-p+1) = (n+1)n/2 — (n+1-p)( п-п)/2$. Остальные параметры $pk$ оцениваются в $W$. Однако $p$ из них являются избыточными, поскольку все векторы $p$ нормированы на единицу длины. Таким образом, мы можем сравнить 92$ в качестве проверки того, насколько хорошо работает эта процедура. Их квадратные корни нанесены на гистограмму. Для справки: вертикальная красная линия указывает на значение самого $\sigma$.
Сравнение моделирования и теории превосходно. Он станет беднее, когда величина $\sigma$ станет большой по сравнению со средним размером компонентов $Y$, потому что тогда эта процедура не очень хорошо оценивает $\sigma$: может произойти существенное переоснащение. Но это не касается решения исходной проблемы.
Следующий код R создал цифру. Он содержит эффективную реализацию решения в четырех строках, следующих за комментарием «Найти приближение ранга p».