0 25 cos
0 25 cosВы искали 0 25 cos? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 0 5 cos, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «0 25 cos».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
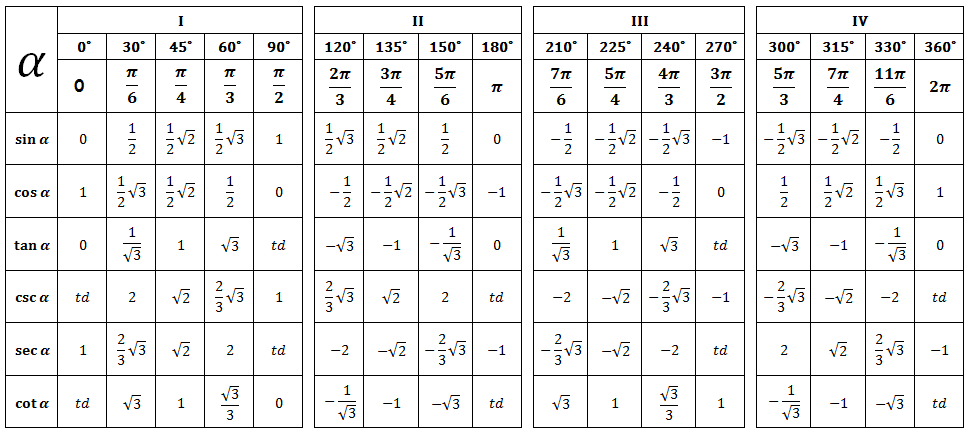
может решить задачи, такие, как 0 25 cos,0 5 cos,0 6 cos,0 7 cos,1 5 косинус,100 cos,100 косинус,11 cos,11 косинус,12 cos,2 косинус 0,2 косинус равен,22 cos,24 cos,270 градусов косинус,28 cos,3 cos 0,32 cos,39 cos,4 cos 0,5 cos,55 cos,7 cos,8 cos,cos 0,cos 0 2,cos 0 25,cos 0 3,cos 0 4,cos 0 5,cos 0 6,cos 0 6 сколько градусов,cos 0 7,cos 0 8,cos 0 cos п,cos 0 градусов,cos 0 равен,cos 1 2 в градусах,cos 1 90,cos 1 п,cos 1 равен,cos 10 градусов 10,cos 10 градусов равен,cos 11,cos 12,cos 13,cos 18,cos 180 градусов,cos 2 3 в градусах,cos 20 градусов,cos 20 градусов равен,cos 22,cos 25,cos 25 градусов,cos 25 градусов равен,cos 27,cos 270 градусов равен,cos 28,cos 3 4,cos 30 градусов равен таблица,cos 35,cos 35 градусов равен,cos 39,cos 4 3,cos 40 градусов,cos 40 градусов равен таблица,cos 45 градусов равен таблица,cos 48,cos 50,cos 50 градусов,cos 55,cos 55 45,cos 55 градусов равен,cos 56,cos 56 пи,cos 63,cos 65,cos 7,cos 70 градусов равен,cos 8,cos 80,cos 9,cos a 0,cos корень из 3 на 3,cos равен 0,cos таблица,cos таблица значений,cos0,cos1,cos12,cos22,cos24,cos25,cos45 значение,cos5,cos56,cos56 пи,градусы в косинус,значения косинусов,кос 0,кос 0 равен,кос 1 равен,кос 180 градусов равен,кос 45 градусов равен таблица,косинус 0,косинус 0 2,косинус 0 5,косинус 0 5 в градусах,косинус 0 5 равен,косинус 0 6 сколько градусов,косинус 0 8,косинус 0 9,косинус 0 в пи,косинус 0 градусов,косинус 1,косинус 1 2,косинус 1 2 в градусах,косинус 1 2 в пи,косинус 1 2 корень из 2,косинус 1 2 равен,косинус 1 2 чему равен,косинус 1 3,косинус 1 3 в градусах,косинус 1 4,косинус 1 6,косинус 1 в градусах,косинус 1 в пи,косинус 1 корень из 3,косинус 10,косинус 110,косинус 110 градусов,косинус 12,косинус 120 градусов таблица,косинус 13,косинус 135 градусов таблица,косинус 14,косинус 140,косинус 145,косинус 15,косинус 15 градусов,косинус 16,косинус 160,косинус 18,косинус 18 градусов,косинус 180 градусов,косинус 180 градусов равен,косинус 2 0,косинус 2 3,косинус 2 чему равен,косинус 20,косинус 20 градусов,косинус 20 градусов равен,косинус 21,косинус 22,косинус 225 градусов,косинус 24,косинус 25,косинус 25 градусов,косинус 25 градусов равен,косинус 27,косинус 27 градусов,косинус 270 градусов,косинус 28,косинус 3,косинус 3 2,косинус 3 4,косинус 3 5,косинус 3 градусов,косинус 3 корень из 3,косинус 30 градусов равен таблица,косинус 30 градусов таблица,косинус 30 таблица,косинус 31,косинус 32,косинус 34,косинус 35 градусов,косинус 35 градусов равен,косинус 36,косинус 36 градусов,косинус 360,косинус 37,косинус 37 градусов,косинус 38,косинус 39,косинус 3п 4,косинус 4,косинус 4 3,косинус 4 п,косинус 40,косинус 40 градусов,косинус 40 градусов равен,косинус 42,косинус 45 градусов 45 минут,косинус 45 градусов равен таблица,косинус 5,косинус 5 3,косинус 5 градусов,косинус 50,косинус 50 градусов,косинус 50 градусов равен,косинус 52,косинус 53,косинус 54,косинус 54 градусов,косинус 55 градусов 45 минут равен,косинус 56 пи,косинус 6,косинус 60 градусов равен таблица,косинус 60 градусов таблица,косинус 65,косинус 65 градусов,косинус 7,косинус 70,косинус 70 градусов,косинус 70 градусов равен,косинус 72,косинус 72 градусов,косинус 8,косинус 80,косинус 85,косинус 87,косинус 9,косинус 90 градусов таблица,косинус 95,косинус градусов,косинус корень из 3 на 3,косинус корень из 3 на 3 в градусах,косинус корень из 5 на 5,косинус корень из 6 на 6,косинус минус 1 2,косинус о,косинус одной второй,косинус п 8,косинус п на 2,косинус равен 0,косинус равен 0 5,косинус равен 0 угол равен,косинус равен 0 чему равен угол,косинус равен 1,косинус равен 1 чему равен угол,косинус равен чему равен угол,косинус таблица,косинус таблица значений,косинус угла 3,косинус угла равен,косинус угла таблица,косинусы,косинусы таблица,косинусы углов,косинусы углов таблица,не табличное значение косинуса,полная таблица косинусов,равен косинус 180 градусов,синус 0 косинус 0,таблица cos,таблица градусов cos 120 градусов,таблица градусов косинусов,таблица значений cos,таблица значений косинуса,таблица значений косинусов,таблица и косинусов,таблица кос,таблица косинус 120 градусов,таблица косинус 135 градусов,таблица косинус угла,таблица косинус углов,таблица косинуса,таблица косинусов,таблица косинусов в градусах,таблица косинусов в радианах,таблица косинусов градусов,таблица косинусов и,таблица косинусов и синусов от 0 до 360,таблица косинусов полная,таблица косинусов углов,таблица косинусов углов от 0 до 90,таблица косинусы,таблица полная косинусов,таблица синусов и косинусов от 0 до 360,таблица углов косинусов,таблицы косинусов,таблиця косинусів,табличные значения косинуса,угол по косинусу,чему равен 2 косинус,чему равен cos 30 градусов таблица,чему равен косинус 1 2,чему равен косинус 2,чему равен косинус 20 градусов,чему равен косинус 3,чему равен косинус 30 градусов таблица,чему равен косинус пи.
Решить задачу 0 25 cos вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. | |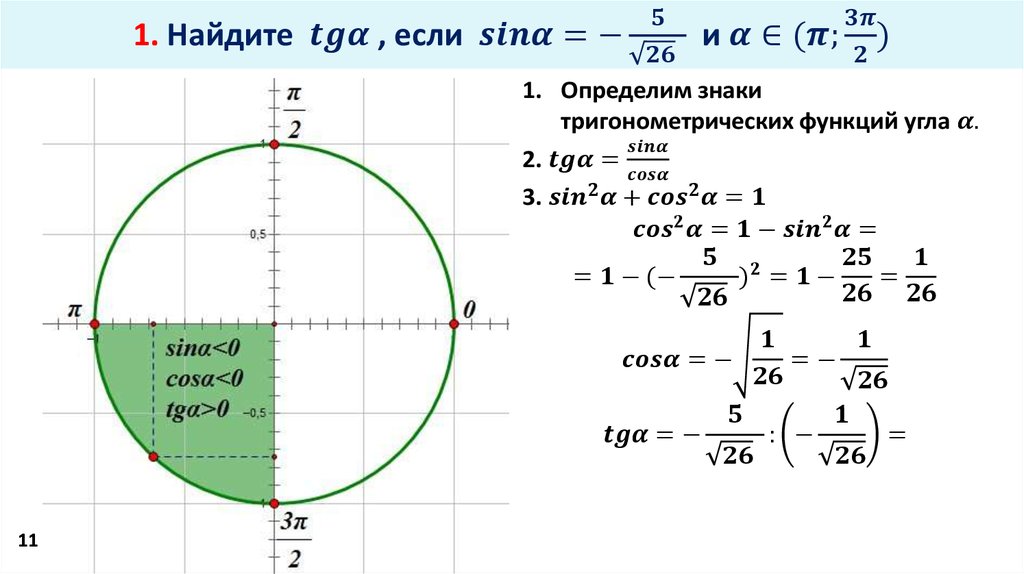
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | pi/3 | ||
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |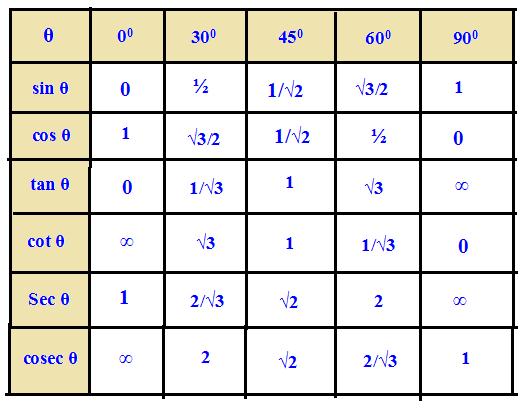
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |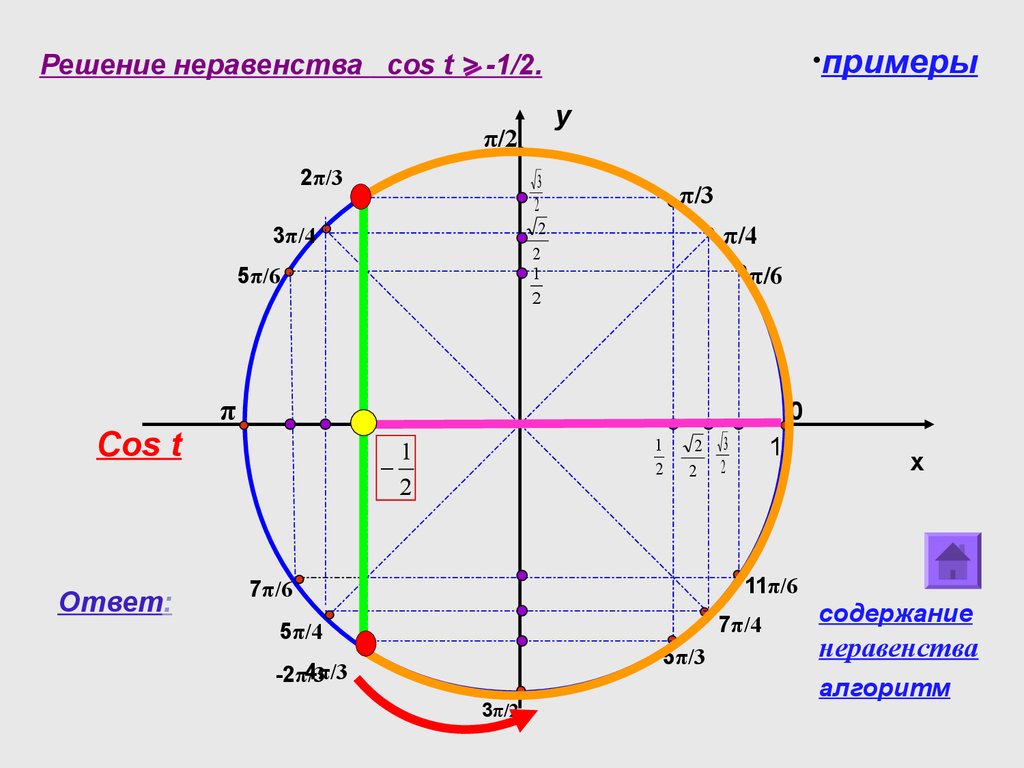
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |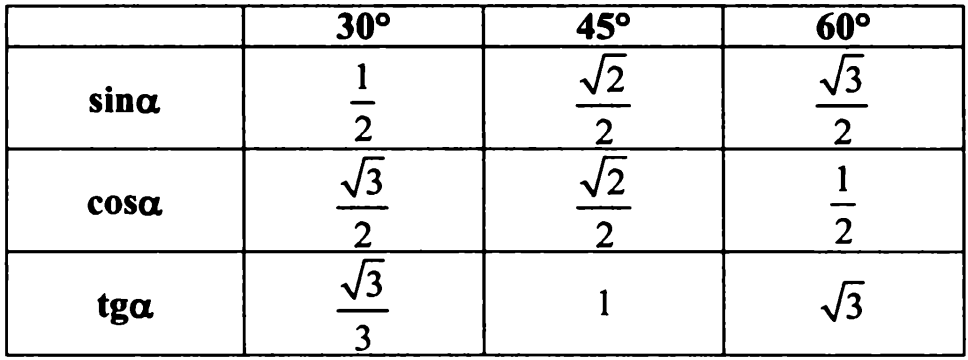
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Таблица определения реактивной мощности конденсаторной установки
Сертификаты
Новости 09.05.21 Уважаемые дамы и господа!
Поздравляем вас с днем Великой Победы! Мы желаем всем мирных побед и добра!
С уважением, ПК «СлавЭнерго» подробнее. 07.01.21 Уважаемые партнеры! Поздравляем вас с Новым годом и Рождеством! Желаем всем МНОГО: бумажных или электронных денег, ЖЕЛЕЗНОГО здоровья и ПРОСТОГО семейного счастья!
С уважением, коллектив ПК «СлавЭнерго»
подробнее… | Главная » Комплектные конденсаторные установки от 0,4 до 10 кВ » Конденсаторные установки 6,3 — 10,5 кВ » Таблица определения реактивной мощности конденсаторной установки — КРМ (кВАр) необходимой для достижения заданного cos(φ)
КРМ (кВАр) = Pa х (tg(φ1)-tg(φ2)) ПРИМЕР: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
..
18
00
10
62
90
45
03
08
07Функция COS Excel — voxt.ru
Функция COS Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения косинуса заданного числа или в терминах или тригонометрии значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент.
который является предоставленным входным номером.
который является предоставленным входным номером.Функция COS Excel
Это встроенная функция в MS Excel. Он относится к категории «Математические функции в MS Excel». Функция возвращает косинус угла в радианах. Параметр — это значение угла, для которого должен быть вычислен косинус. Угол можно рассчитать с помощью функции РАДИАНЫ или умножив его на PI () / 180.
Формула COS
Формула COS в Excel выглядит следующим образом:
Формула COS в Excel имеет один аргумент, который является обязательным параметром.
- количество = Это обязательный параметр. Он указывает угол, для которого должен быть вычислен косинус.
Как использовать функцию COS в Excel?
COS можно использовать в листе Excel как функцию листа (WS), а также в Excel VBA. Как функцию WS, ее можно ввести как часть формулы COS в ячейку рабочего листа. В качестве функции VBA ее можно ввести в код VBA.
Вы можете скачать этот шаблон Excel с функцией COS здесь — Шаблон Excel с функцией COS
Обратитесь к примерам, приведенным ниже, чтобы лучше понять.
Пример №1 — Вычислить значение cos (0)
В этом примере ячейка B2 содержит значение угла, для которого должен быть вычислен косинус. С ячейкой C2 связана формула COS — РАДИАНЫ. COS в Excel назначается ячейке D2. РАДИАНЫ (B2) равны 0. Далее, COS применяется к 0, то есть 1.
Следовательно, результирующая ячейка D2 имеет значение 1, поскольку COS (0) равно 1.
Пример №2 — Вычислить значение cos (30)
В этом примере ячейка B3 содержит значение угла, для которого должен быть вычислен косинус. С ячейкой C3 связана формула COS — РАДИАНЫ. COS в Excel назначается ячейке D3. РАДИАНЫ (B3) — 0,523598776. Далее, COS применяется к 0,523598776, что составляет 0,866025404.
Следовательно, результирующая ячейка D3 имеет значение 1, поскольку COS (0,523598776) равно 1.
Пример №3 — Вычислить значение cos (45)
В этом примере ячейка B4 содержит значение угла, для которого должен быть вычислен косинус.
С ячейкой C4 связана формула COS — РАДИАНЫ. COS назначается ячейке D4. РАДИАНЫ (B3) — 0,523598776. Далее, COS применяется к 0,785398163, что составляет 0,707106781.
Следовательно, результирующая ячейка D4 имеет значение 1, поскольку COS (0,707106781) равно 1.
Пример №4 — Вычислить значение cos (60)
В этом примере ячейка B5 содержит значение угла, для которого должен быть вычислен косинус. С ячейкой C5 связана формула COS — РАДИАНЫ. COS назначается ячейке D5. РАДИАНЫ (B5) — 1.047197551. Далее, COS применяется к 1.047197551, что составляет 0,5.
Следовательно, результирующая ячейка D5 имеет значение 0,5, поскольку COS (1,047197551) равно 0,5.
Пример # 5 — Вычислить значение cos (90)
В этом примере ячейка B6 содержит значение угла, для которого нужно вычислить косинус. С ячейкой C6 связана формула COS: B6 * PI () / 180. COS назначается ячейке D6. 90 * PI () / 180 равно 1,570796327. Значение PI () равно 3,14159.
Итак, это 90 * (3,14159 / 180) = 1,570796327. Далее, COS применяется к 1.570796327, то есть 6.12574E-17..
Следовательно, результирующая ячейка D6 имеет 6.12574E-17, поскольку COS (1.570796327) равен 6.12574E-17.
Что нужно помнить о COS Функция в Excel- COS в Excel всегда ожидает радиан в качестве параметра, для которого должен быть вычислен косинус.
- Если угол указывается в градусах, его необходимо вычислить с помощью функции РАДИАНЫ или умножить угол на PI () / 180.
COS в Excel можно использовать в Excel VBA следующим образом. Он служит той же цели, которая заключается в получении значения косинуса заданного угла.
| Синтаксис: COS (Число) |
Пример VBA # 1
Dim val1 As Double val1 = Cos ( 0 ) val1 : 1
Здесь val1 — переменная.
Он объявлен как Double, что означает, что он может хранить данные с типом данных double. Косинус 0 равен 1. Следовательно, val1 имеет значение 1.
Пример VBA # 2
Const pi = 3.1415 Dim val As Double ' Convert 45 degrees to radians by multiplying by pi/180. val = Cos (45 * pi / 180 ) ' The variable val is now equal to 0.7071067
Здесь угол 45 преобразуется в радианы с использованием той же формулы COS, которая используется в листе Excel.
Если для Cos в excel указано нечисловое значение, оно вернет Несоответствие типов ошибка в коде Excel VBA.
УЗНАТЬ БОЛЬШЕ >>
Post Views: 967
Похожие записи
Прокрутить вверхCos 0- значение, объяснение и часто задаваемые вопросы
Cos 0 равен 1 (Cos 0 = 1). Другими словами, значение Cos 0 равно 1. Теперь вопрос в том, как было получено значение Cos 0. Значение может быть определено с помощью квадрантов единичного круга.
Этот процесс обсуждается в следующем разделе.
Как вы уже знаете, тригонометрические функции относятся к угловым функциям, которые относятся к углам треугольника. Для изучения периодических явлений световых и звуковых волн использовались тригонометрические функции. Эти функции также имеют решающее значение для изучения гармонических колебаний и изменений средней температуры.
Формула для нахождения Cos
Функция косинуса угла подчиняется определенной формуле. Согласно этой формуле значение функции косинуса угла равно длине прилежащей стороны, деленной на длину стороны гипотенузы. Формула написана ниже.
Cos X = \[\frac{\text{Смежная сторона}}{\text{Сторона гипотенузы}}\]
Эта формула говорит о функции косинуса (cos) и о том, как определить ее значение. Возьмем пример прямоугольного треугольника, один из острых углов которого равен х. Тогда формула косинуса cos x = (прилежащая сторона) / (гипотенуза), где сторона, примыкающая к углу x, соответствует названию, а сторона гипотенузы самая длинная (та, что противоположна прямому углу в треугольнике ).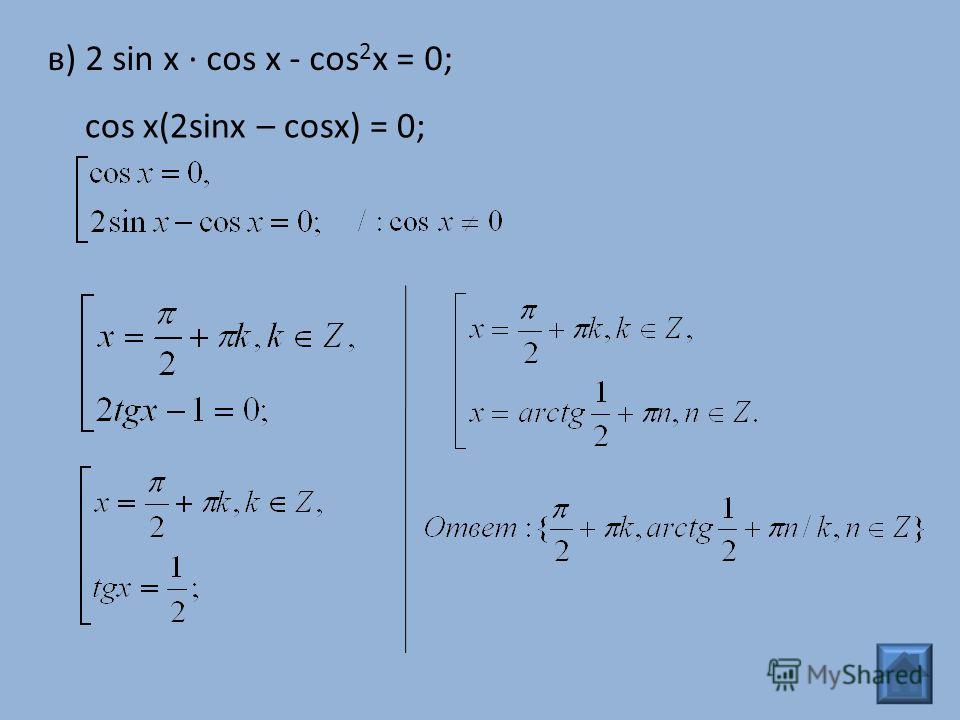
Помимо этой общей формулы, существуют и другие специальные формулы, но этой также достаточно, чтобы учащиеся хорошо поняли, как рассчитывается значение cos.
Почему важны тригонометрические функции?
В математике они необходимы для некоторых вещей, таких как комплексный анализ и анализ Фурье. Кроме того, они могут быть универсальными в виде решений, примеров, приемов и множества упражнений во всех областях математики, включая дифференциальные уравнения, геометрию, топологию, гильбертовы пространства и т. д.
Если говорить о физике и технике, то эти функции должны быть встречается повсюду. Всякий раз, когда что-то циклично, всякий раз, когда что-то повторяется во времени, вы можете ожидать, что в его описании будут указаны sin и cos. Сюда также входят звуковые волны, электромагнитные волны (включая свет), любые типы волн, поведение частиц и так далее.
Помимо использования в фундаментальной теории и теоретическом моделировании, эти функции предназначены для построения блоков и мотивации во вторичных целях, таких как помощь учащимся в расширении их знаний и помощь в развитии.
Их не только легко запомнить, но и очень весело решать и играть с учениками.
Как найти значение Cos 0?
Существует три основных тригнометрических соотношения: функция синуса, функция косинуса и функция тангенса. С помощью функций sin, cos и tan можно вычислить углы треугольника.
Чтобы понять функцию косинуса острого угла, вам нужно нарисовать прямоугольный треугольник на листе бумаги. Треугольник, очевидно, имеет три стороны, и эти стороны можно определить следующим образом: Выберите угол треугольника, и противоположная сторона выбранного угла будет называться «противоположная сторона». Сторона треугольника, расположенная напротив прямого угла, называется стороной гипотенузы. Примечательно, что это самая длинная сторона прямоугольного треугольника. Наконец, «прилежащая сторона» относится к оставшейся стороне треугольника. Определение значения Cos 0 с помощью единичного круга Используя единичный круг, можно получить значение «Cos 0».
Процесс начинается с принятия единичной окружности, центр которой совпадает с началом осей координат.
Почему значение Cos всегда меньше или равно 1?
Самый простой способ понять причину состоит в том, что измерение длины сторон прямоугольного треугольника всегда меньше, чем измерение длины угла гипотенузы. Итак, отношение любой стороны и гипотенузы также всегда меньше значения 1.
Что такое Cos 0?
Значение косинуса прямоугольного треугольника с углом 0° известно как косинус угла 0°. Косинус угла 0° — это величина, обозначающая остаток длины прилежащей стороны от длины гипотенузы, если угол прямоугольного треугольника равен 0°.
В шестидесятеричной системе косинус угла, равный нулю градусов, математически выражается как косинус 0°, а точное значение косинуса угла 0° = 1 . Таким образом, математически это записывается в следующей форме в тригонометрии, т.е. cos 0 ° = 1
. Мы также можем выразить косинус угла ноль градусов в двух других формах тригонометрической математики, т.
е. круговая система и сотенная система.
Cos 0 в круговой системе
В круговой системе косинус нуля градусов математически представляется как косинус нуля радиан. Это записывается в следующем виде в круговой системе cos (0) =1. Отмечается, что в методе единичного круга один полный оборот образует угол 2π радиан в самом центре единичного круга, поскольку все углы треугольника являются столь необходимыми кратными π/2, и это часто известно как квадрантные углы в академических кругах. Следовательно, координаты точек треугольника становятся (1, 0), (0, 1), (–1, 0) и (0, –1) соответственно. Поэтому, используя квадрантные углы, мы можем легко получить значения Cos.
99) =1. В этой системе один из прямых углов делится на 100 одинаковых частей, которые известны как градации. Она также известна как французская система измерения. Каждая ступень делится на 100 одинаковых частей, называемых минутами, а каждая минута делится на 100 одинаковых частей, называемых секундами.
Таким образом, 1 прямой угол равен 100 градусам (1009), 1 градус равен 100 минутам (100′), а 1 минута равна 100 секундам (100 дюймов).
Базовое понимание определения Cos 0 как 1
Значение Cos 0 градусов:
Чтобы лучше понять функцию косинуса острого угла, начните с рассмотрения прямоугольного треугольника с интересующего вас угла и сторон треугольника. Все стороны (три) треугольника определяются следующим образом:
Противоположная сторона известна как сторона, противоположная интересующему углу.
Сторона гипотенузы находится напротив прямого угла и является самой длинной стороной в треугольнике.
Оставшаяся сторона называется смежной стороной, и именно здесь она образует сторону угла интереса вместе с прямым углом.
Как помнить об этих ценностях?
Такая сложная задача по запоминанию множества значений или просто случайных чисел тригонометрических функций поначалу кажется полноценным наказанием, не имеющим академической цели или пользы. Кто-то использует таблицу для запоминания значений, кто-то круговую единицу делает до в 0 градусов, угол изучается по Единичной окружности в координатах (1,0). Эти координаты есть не что иное, как тригонометрические величины. Координата x — это значение, относящееся к cos, а координата y — это значение, относящееся к sin.
Но лучше всего понять, как действует формула. Это было то, что вы не будете грабить числа и забывать позже, а также иметь полное представление о значении Cos 0, почему оно равно 1 и многом другом.
Cos 0 градусов — Найдите значение Cos 0 градусов
LearnPracticeDownload
Значение cos 0 градусов равно 1 . Cos 0 градусов в радианах записывается как cos (0° × π/180°), т.
е. cos (0π) или cos (0). В этой статье мы обсудим методы определения значения cos 0 градусов на примерах.
- Кос 0°: 1
- Кос (-0 градусов): 1
- Cos 0° в радианах: cos (0π) или cos (0 . . .)
Каково значение Cos 0 градусов?
Значение cos 0 градусов равно 1. Cos 0 градусов также можно выразить с помощью эквивалента данного угла (0 градусов) в радианах (0 . . .)
Мы знаем, используя преобразование градусов в радианы, θ в радианы = θ в градусах × (pi/180°) 90 101
⇒ 0 градусов = 0° × (π/180°) рад = 0π или 0 . . .
∴ cos 0° = cos(0) = 1
Объяснение:
Для cos 0 градусов угол 0° лежит на положительной оси x. Таким образом, значение cos 0° = 1
Поскольку функция косинуса является периодической функцией, мы можем представить cos 0° как cos 0 градусов = cos(0° + n × 360°), n ∈ Z.
⇒ cos 0° = cos 360° = cos 720° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-0°) = cos(0°).
Методы определения значения Cos 0 градусов
Значение cos 0° равно 1. Мы можем найти значение cos 0 градусов с помощью:
- Используя тригонометрические функции
- Использование единичного круга
Cos 0° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить cos 0 градусов как:
- ± √(1-sin²(0°))
- ± 1/√(1 + tan²(0°))
- ± раскладушка 0°/√(1 + раскладушка²(0°))
- ±√(косек²(0°) — 1)/косек 0°
- 1/сек 0°
Примечание. Поскольку 0° лежит на положительной оси x, конечное значение cos 0° будет положительным.
Мы можем использовать тригонометрические тождества для представления cos 0° как
- -cos(180° — 0°) = -cos 180°
- -cos(180° + 0°) = -cos 180°
- sin(90° + 0°) = sin 90°
- sin(90° — 0°) = sin 90°
Cos 0 градусов с использованием единичной окружности
Чтобы найти значение cos 0 градусов с помощью единичной окружности:
- Нарисуйте радиус единичной окружности ‘r’, чтобы образовать угол 0° с положительной осью x.
- Cos 0 градусов равен x-координате(1) точки пересечения (1, 0) единичной окружности и r.
Отсюда значение cos 0° = x = 1
☛ Также проверьте:
- cos 300 градусов
- потому что 2 градуса
- потому что 53 градуса
- потому что 58 градусов
- cos 67 градусов
- соз 38 градусов
Примеры использования Cos 0 градусов
Пример 1: Используя значение cos 0°, решите: (1-sin²(0°)).
Решение:
Мы знаем, (1-sin²(0°)) = (cos²(0°)) = 1
⇒ (1-sin²(0°)) = 1Пример 2. Найдите значение cos 0°, если sec 0° равно 1.
Решение:
Так как cos 0° = 1/сек 0°
⇒ cos 0° = 1/1 = 1Пример 3. Найдите значение 2 cos(0°)/3 sin(90°).
Решение:
Используя тригонометрические тождества, мы знаем, что cos(0°) = sin(90° — 0°) = sin 90°.
⇒ cos(0°) = sin(90°)
⇒ Значение 2 cos(0°)/3 sin(90°) = 2/3
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Cos 0 градусов
Что такое Cos 0 градусов?
Cos 0 градусов — значение тригонометрической функции косинуса для угла, равного 0 градусов. Значение cos 0° равно 1
Каково значение Cos 0 градусов в терминах Tan 0°?
Мы знаем, что, используя триггерные тождества, мы можем записать cos 0° как 1/√(1 + tan²(0°)). Здесь значение tan 0° равно 0.
Как найти значение Cos 0 градусов?
Значение cos 0 градусов можно рассчитать, построив угол 0° с осью x и затем найдя координаты соответствующей точки (1, 0) на единичной окружности.
Значение cos 0° равно x-координате (1). ∴ cos 0° = 1.
Как найти Cos 0° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение cos 0° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-sin²(0°))
- ± 1/√(1 + tan²(0°))
- ± раскладушка 0°/√(1 + раскладушка²(0°))
- ± √(косек²(0°) — 1)/косек 0°
- 1/сек 0°
☛ Также проверьте: таблицу тригонометрии
Каково значение Cos 0° в пересчете на Sec 0°?
Поскольку функция секанса является обратной функцией косинуса, мы можем записать косинус 0° как 1/сек(0°). Значение sec 0° равно 1,
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
| 1 | Найдите точное значение | грех(30) | |
| 2 | Найдите точное значение | грех(45) | |
| 3 | Найдите точное значение | грех(30 градусов) | |
| 4 | Найдите точное значение | грех(60 градусов) | |
| 5 | Найдите точное значение | загар(30 градусов) | |
| 6 | Найдите точное значение | угловой синус(-1) | |
| 7 | Найдите точное значение | грех(пи/6) | |
| 8 | Найдите точное значение | cos(pi/4) | |
| 9 | Найдите точное значение | грех(45 градусов) | |
| 10 | Найдите точное значение | sin(pi/3) | |
| 11 | Найдите точное значение | арктан(-1) | |
| 12 | Найдите точное значение | cos(45 градусов) | |
| 13 | Найдите точное значение | cos(30 градусов) | |
| 14 | Найдите точное значение | желтовато-коричневый(60) | |
| 15 | Найдите точное значение | csc(45 градусов) | |
| 16 | Найдите точное значение | загар (60 градусов) | |
| 17 | Найдите точное значение | сек (30 градусов) | |
| 18 | Найдите точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найдите точное значение | грех(60) | |
| 21 | Найдите точное значение | cos(pi/2) | |
| 22 | Найдите точное значение | загар (45 градусов) | |
| 23 | Найдите точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найдите точное значение | csc(60 градусов) | |
| 25 | Найдите точное значение | сек (45 градусов) | |
| 26 | Найдите точное значение | csc(30 градусов) | |
| 27 | Найдите точное значение | грех(0) | |
| 28 | Найдите точное значение | грех(120) | |
| 29 | Найдите точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найдите точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найдите точное значение | соз(45) | |
| 34 | Упростить | 92||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найдите точное значение | детская кроватка(30 градусов) | |
| 37 | Найдите точное значение | арккос(-1) | |
| 38 | Найдите точное значение | арктический(0) | |
| 39 | Найдите точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найдите точное значение | sin((5pi)/3) | |
| 43 | Найдите точное значение | sin((3pi)/4) | |
| 44 | Найдите точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найдите точное значение | грех(300) | |
| 46 | Найдите точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найдите точное значение | соз(0) | |
| 49 | Найдите точное значение | соз(135) | |
| 50 | Найдите точное значение | cos((5pi)/3) | |
| 51 | Найдите точное значение | соз(210) | |
| 52 | Найдите точное значение | сек (60 градусов) | |
| 53 | Найдите точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найдите точное значение | грех(135 градусов) | |
| 61 | Найдите точное значение | грех(150) | |
| 62 | Найдите точное значение | грех(240 градусов) | |
| 63 | Найдите точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найдите точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найдите точное значение | cos(150 градусов) | |
| 68 | Найдите точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найдите точное значение | сек(0) | |
| 71 | Найдите точное значение | cos((5pi)/6) | |
| 72 | Найдите точное значение | КСК(30) | |
| 73 | Найдите точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найдите точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найдите точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найдите точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найдите точное значение | sin((7pi)/4) | |
| 80 | Найдите точное значение | угловой синус(-1/2) | |
| 81 | Найдите точное значение | sin((4pi)/3) | |
| 82 | Найдите точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найдите точное значение | грех(135) | |
| 85 | Найдите точное значение | грех(105) | |
| 86 | Найдите точное значение | грех(150 градусов) | |
| 87 | Найдите точное значение | sin((2pi)/3) | |
| 88 | Найдите точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найдите точное значение | sin(pi/2) | |
| 91 | Найдите точное значение | сек(45) | |
| 92 | Найдите точное значение | cos((5pi)/4) | |
| 93 | Найдите точное значение | cos((7pi)/6) | |
| 94 | Найдите точное значение | угловой синус(0) | |
| 95 | Найдите точное значение | грех(120 градусов) | |
| 96 | Найдите точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найдите точное значение | соз(270) | |
| 98 | Найдите точное значение | sin((7pi)/6) | |
| 99 | Найдите точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор — cos(0) — Solumaths
Cos, расчет онлайн
Резюме:
Тригонометрическая функция cos вычисляет cos угла в радианах,
градусов или градианов.
cos online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус , синус и касательная угла через одноименные функции.
Косинус тригонометрической функции отметил cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.
- Расчет косинуса
- Специальные значения косинуса
- Основные свойства
Расчет косинуса угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, вы должны сначала
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Для вычисления косинуса 90, введите cos(90), после расчета возвращает 0.
Вычисление косинуса угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 50, введите cos(50), после вычисления,
возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения косинуса :
| cos(`2*pi`) | `1` | |
| cos(`pi`) | `-1` | |
| cos(`pi/2`) | `0` | |
| cos(`pi/4`) | `sqrt(2)/2` 52 cos7(`pi/3`) | `1/2` |
| cos(`pi/6`) | `sqrt(3)/2` | |
| cos(`2*pi/3`) | `-1/2` | |
| cos(`3*pi/4`) | `-sqrt(2)/2` | |
| cos(`5*pi/6`) | ` -sqrt(3)/2` | |
| cos(`0`) | `1` | |
| cos(`-2*pi`) | `1` | |
| cos(`-pi`) | `-1` | |
| cos(`2/7 `296 cos(`2/7 `296 cos(`2/7`296) 0` | ||
| cos(`-pi/4`) | `sqrt(2)/2` | |
| cos(`-pi/3`) | `1/2` | |
| cos(`-pi/3`) (`-pi/6`) | `sqrt(3)/2` | |
| cos(`-2*pi/3`) | `-1/2` | |
| cos(`-3 *pi/4`) | `-sqrt(2)/2` | |
| cos(`-5*pi/6`) | `-sqrt(3)/2` |
`AA x в RR, k в ZZ`,
- `cos(-x)= cos(x)`
- `cos(x+2*k*pi)=cos(x)`
- `cos(pi-x)=-cos(x) `
- `cos(pi+x)=-cos(x)`
- `cos(pi/2-x)=sin(x)`
- `cos(pi/2+x)=-sin(x) )`
Производная косинуса равна -sin(x).
Первообразная косинуса равна sin(x).
Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с косинусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или же `2*cos(x)=sqrt(2)` с этапами расчета.
Синтаксис:
cos(x), где x — мера угла в градусах, радианах или градах.
Примеры:
cos(`0`), возвращает 1
Производная косинус :
Чтобы дифференцировать функцию косинуса онлайн,
можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса.
Первообразная косинуса :
Калькулятор первообразной позволяет вычислить первообразную функции косинуса.
Первопроизводная cos(x) является первообразной(`cos(x)`)=`sin(x)`
Предел косинуса :
Калькулятор предела позволяет вычислить пределы функции косинуса.
предел cos(x) is limit(`cos(x)`)
Обратная функция косинуса :
обратная функция косинуса — это функция арккосинуса, отмеченная как arccos.
Графический косинус:
Графический калькулятор может отображать функцию косинуса в заданном интервале.
Свойство функции косинуса:
Функция косинуса является четной функцией.
Расчет онлайн с косинусом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
- Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
- Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Касательная: рыжевато-коричневая. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Калькулятор позволяет получить тригонометрическое разложение выражения.Напоминания о курсах, калькуляторы, упражнения и игры: тригонометрические функции, вещественные функции
Математическая сцена — тригонометрические функции sin, cos и tan
Математическая сцена — тригонометрические функции sin, cos и tan — урок 2 2008 Расмус Эф | Печать |
Урок 2
Единица окружности Мы
Начнем с прямоугольного треугольника, в котором гипотенуза имеет длину
1 блок.
Противоположная сторона = sin v | |
Смежная сторона = cos v |
В прямоугольном треугольнике
sin v = напротив сторона/гипотенуза
и
cos v = смежных сторона / гипотенуза .
Если гипотенуза в треугольнике имеет длину 1, то
sin v = противоположная сторона и cos v = соседняя сторона.
Теперь рассмотрим круг, нарисованный в система координат.
Круг радиусом 1 единица и его центр в (0, 0) называется единичным кругом.
Единичный круг
Если мы нарисуем радиус, образующий угол v с положительным плечом оси x, и опустим перпендикуляр, как
на диаграмме показано, что мы правильно
треугольник со сторонами длины cosv и sin v. Это означает, что координаты точки, где радиус
пересекает круг должен быть (cos v,
грех в).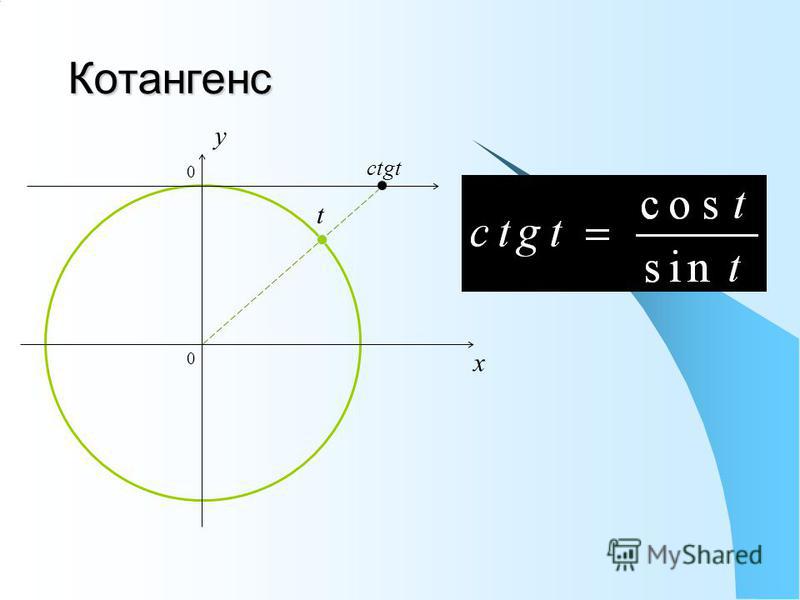
Теперь посмотрим на tan v таким же образом.
противоположная сторона = загар v | |
Смежная сторона = 1 |
На этот раз мы выбираем смежную сторону. длина 1 ед.
tan v = противоположная сторона / соседняя сторона .
Смежная сторона = 1, следовательно, тангенс v = противоположная сторона.
Мы можем добавить это к диаграмме единичного круга.
Чтобы увидеть связь между sin, cos и tan мы выполните следующие вычисления:
противоположная сторона
загар v =
соседняя сторона
противоположная сторона/гипотенуза | Деление числителя на
знаменатель через h y потенциал. |
Вычисления, которые мы показали до сих пор, применимы к
угол, проведенный в единичной окружности, отсчитываемый от оси x и лежащий в
первый квадрант системы координат. Если мы назовем точку, где радиус r пересекает
окружность P, и поверните радиус OP против часовой стрелки вокруг окружности от x
оси мы говорим, что угол v есть
положительное вращение. Если OP вращается по часовой стрелке от оси x, мы
говорят об отрицательном вращении. (это просто согласованное определение). Итак, если P движется по окружности вверх от оси x, мы
имеют положительное значение для поворота v. Если P движется по окружности и вниз
по оси x имеем отрицательное значение для v.
(см. схему).
Теперь обобщим определение синуса, косинуса и тангенс следующим образом:
cos v = x-координата P sin v = y-координата P |
Это
определение подразумевает, что триггерные функции могут быть положительными или отрицательными в зависимости от
от того, в каком квадранте системы координат находится точка P.
Поскольку точка P движется с положительным вращением по кругу он достигает одного и того же положения каждые 360 . Это означает, что значения синуса и косинуса повторяются каждые 360. Тангенс повторяет свое значение каждые 180, как мы увидим в примере 4.
Пример 1
Найти положительное вращение что приводит нас к тому же положению, что и −200
Для этого нам просто нужно добавить 360.
-200 + 360 = 160
Пример 2
Найдите угол на интервал 0 v < 360 эквивалент до 1100.
Нам нужно вычесть 360 несколько раз, пока не достигнем нужного интервала.
1 круг: 1∙ 360 = 360
2 круга: 2∙ 360 = 720
3 круга: 3∙ 360 = 1080
Этого достаточно.
1100 − 1080 = 20
Пример 3
Теперь мы увидим, как Пифагора можно использовать для
вычислить некоторые точные значения для триггерных функций.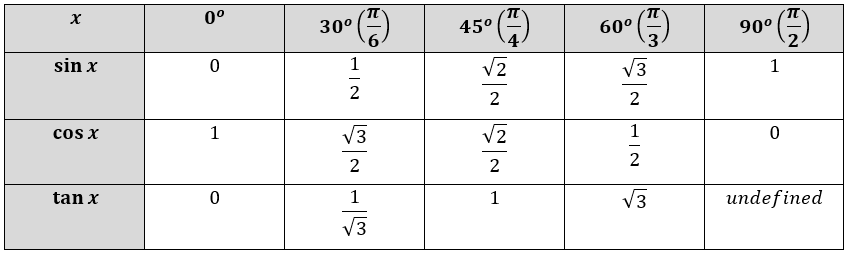
Сначала смотрим на 30. Треугольник на схеме — половина равностороннего треугольника и поэтому мы знаем, что противоположная сторона .
sin 30 = = 0,5 cos 2 30 + () 2 = 1 2 потому что 2 30= 1 — = ≈ 0,866 | Правило Пифагора |
≈ 0,577
Далее смотрим на угол 45. Треугольник равнобедренный, стороны назовем а.
2 + 2 = 1 2а 2 = 1 а 2 = | |
Теперь угол 60.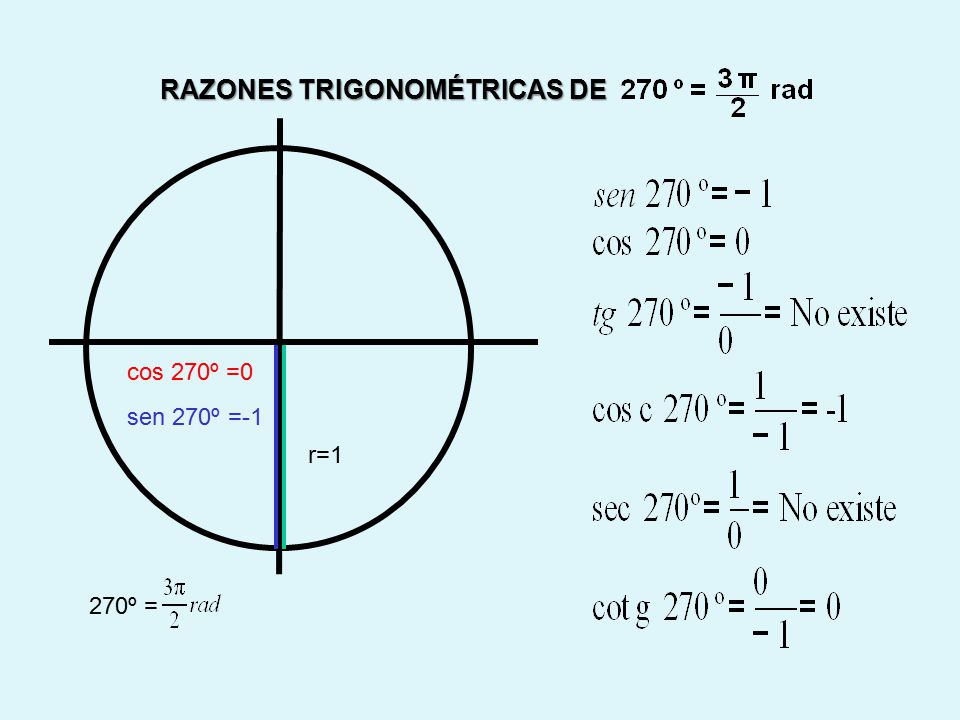
Снова у нас есть треугольник с 30, 60 и 90, поэтому мы можем использовать те же вычисления, что и для 30. Обратите внимание, что синус и косинус имеют обменялись ценностями. | |
Значения триггерных функций для числа 90 легко увидеть на единичном круге. OP, плечо угла лежит на оси y, поэтому координата x равна 0, а координата y равна 1,
потому что 90 = 0
sin 90 = 1
тан 90 = 1/0 не существует.
Можно найти углы, находящиеся в других квадрантах путем сравнения их с углами в первом квадранте.
120 лежит во втором квадранте (слева от положительной оси y), поэтому cos 120 отрицательно, а sin 120 положительно.. | |
Мы можем продолжать в том же духе.
135 (90+ 45) или ( 180− 45)
можно найти с 45, только
знаки меняются.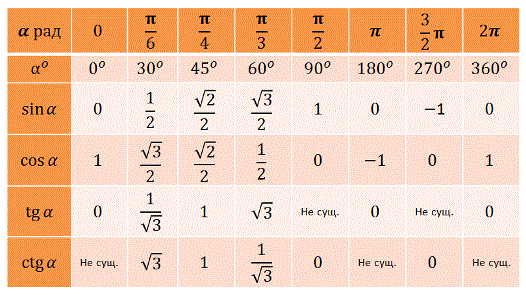
Пример 4
Найти значение синуса, косинус и тангенс для 225.
225 находится в третьем квадрант и может быть рассчитан от 45. (45 + 180 = 225). Начнем с рисования схемы.
Рассчитываем так же
как и в примере 3, и синус, и косинус отрицательны, а тангенс положителен | |
Обратите внимание, что загар 225 — это то же, что и tan 45. Другими словами, значение tan v повторяется каждые 180.
Пример 5
Найдите все решения уравнения tan x = 2, затем запишите, какие из этих решений находятся на интервале 0 х < 360,
Используйте функцию обратного тангенса, тангенс −1 , на вашем калькуляторе.
рыжевато-коричневый −1 (2) ≈ 63,44
Мы знаем, что значения tan повторяются
каждые 180, так что мы можем написать
формула для всех решений путем добавления k∙180, где k представляет собой любое целое число.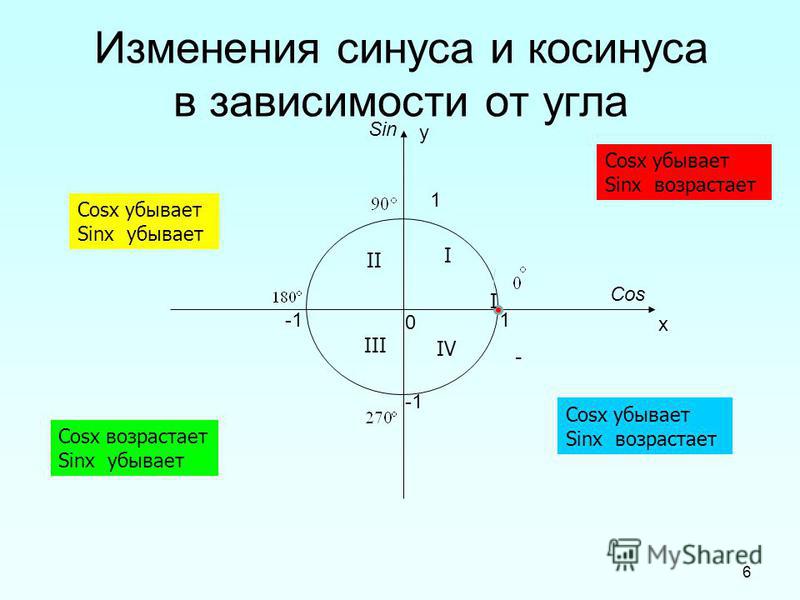
Полное решение
поэтому:
x ≈ 63,44 + k∙180 k — целое число.
Два из этих решений лежат на интервале 0 x < 360. Это x ≈ 63,44 и x ≈ 63,44 + 180 ≈ 243,44
Пример 6
Найдите углы, при которых синус принимает значение 0,5 .
Сначала решим уравнение sin v = 0,5 с помощью калькулятора и функция обратного синуса sin −1 . sin −1 (0,5) = 30. Теперь нарисуйте диаграмму единичного круга.
Нарисуйте угол v как
обычно начиная с положительной оси x и поворачивая против часовой стрелки. Они
координата точки на окружности (высота над осью x) равна sin v.
Нам дано это значение 0,5 (sin v = 0,5).
Если провести горизонтальную линию
через эту точку (пунктирная линия на диаграмме) мы видим, что есть
вторая точка на окружности, которая имеет ту же координату y и, следовательно,
одинаковое значение синуса.
Оба заштрихованных треугольника на диаграмме равны (
точно так же). Измерение вращения этого второго радиуса от
положительной оси x мы получаем второй ответ для v:
v = 180 — 30 = 150 .
Из этого примера получаем следующее правило:
| грех v = грех (180-в) |
Мы используем это правило, когда нужно решить уравнения типа
sin v = a
К сожалению калькуляторы
только одно решение, наименьший угол, который удовлетворяет уравнению
отсчитывается от положительной оси x. Находим второй ответ
вычитая этот ответ из 180. Чтобы найти все возможные решения, нам нужно
добавьте k∙360 к обоим решениям.
(k может быть любым целым числом).
Пример 7
Найдите все решения уравнения грех v = -0,6.
Нарисуйте схему агрегата круг, чтобы увидеть, что нам нужно сделать.
Калькулятор дает один
решение sin −1 (−0,6)
≈ −36,9.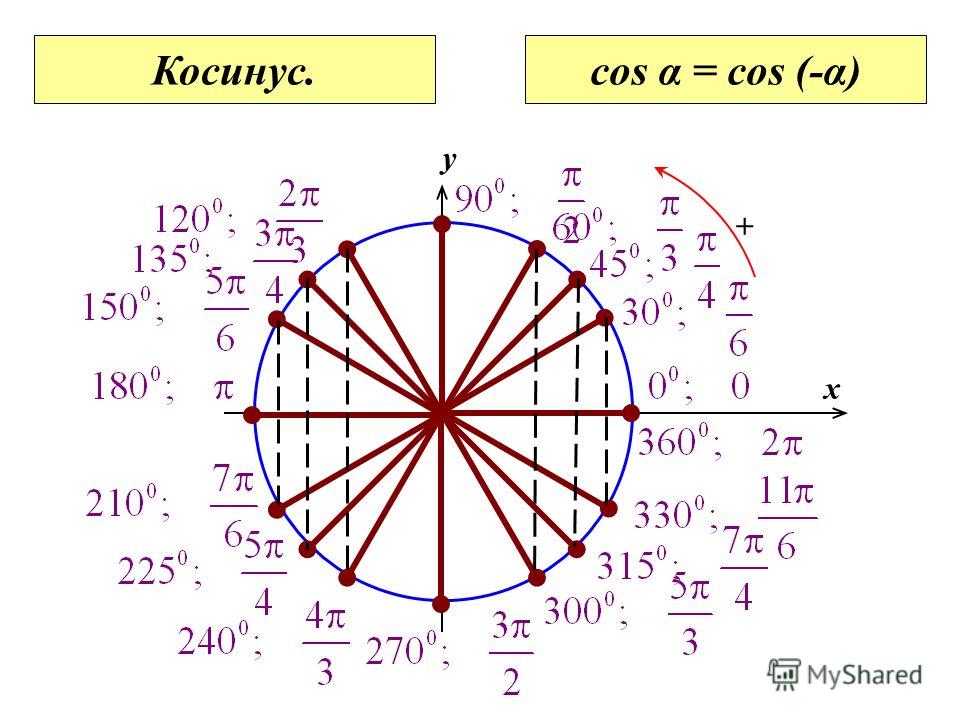
Второй ответ получаем вычитая из 180.
180 − (−36,9) ≈ 216,9
Добавьте 360 к −36,9, чтобы избавиться от отрицательного значения.
−36,9 + 360 ≈ 323,1
Полное решение: v 1 ≈ 216,9 + k∙360 og v 2 ≈ 323,1 + k∙360
(Хорошая идея использовать
калькуляторы для проверки ответов.
sin 216,9 ≈ −0,6 и
грех 323,1 ≈ −0,6 )
Пример 8
Решите уравнение cos v = 0,7.
Нарисуйте единичный круг, чтобы увидеть, что решения есть.
В этом примере нам дано координата x ( cos v = 0,7 ) точки на окружности, то есть расстояние от оси у. Перпендикулярная линия (пунктирная линия) через точку где радиус пересекает круг был нарисован. Эта перпендикулярная линия через 0,7 по оси абсцисс пересекает круг в двух точках, что говорит нам о двух углы, где cos v = 0,7.
С помощью калькулятора получаем
cos −1 (0,7) ≈
45.
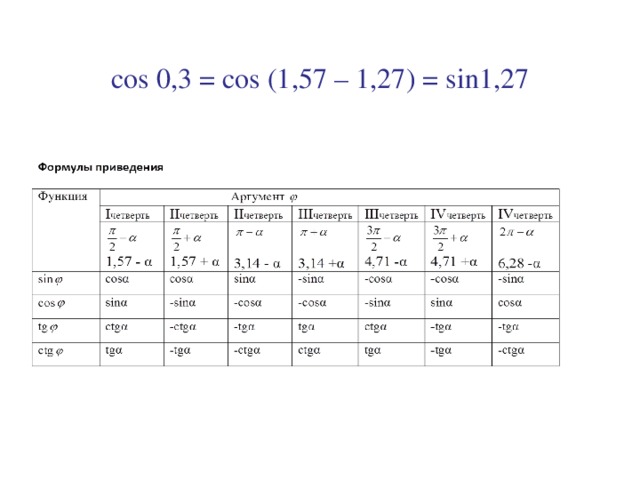57. Мы видим, что второй
угол равен −45,57 . Мы находим положительный угол, эквивалентный этому, добавляя 360,
Решения: v 1 ≈ 45,57 + k∙360
v 2 ≈ −45,57 + 360 + k∙360 ≈ 314,43 + k∙360
Из этого примера видно следующее правило.
| потому что v = кос(-в) |
Это правило мы используем для решить уравнения типа
потому что v = а
Калькулятор дает один ответ, второй ответ является отрицательным из первого ответа. Мы всегда можем преобразовать отрицательные ответы в положительные, добавив 360. Наконец, мы находим все решения добавлением k∙360 к каждый ответ.
Пример 9
Решите неравенство cos v < −0,7 на интервале 0 v < 360,
Сначала решим уравнение cos v = -0,7.
Калькулятор дает cos −1 (−0,7)
≈ 134,43.
Секунда
поэтому решение равно -134,43 или -134,43 + 360 ≈ 225,57. В настоящее время
нам нужно нарисовать единичный круг.
Мы видим, что cos v меньше -0,7, если v находится в заштрихованной области на диаграмме.
Следовательно, решение 134 < v< 226 .
Попробуйте Викторину 2
по триггерным функциям.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Как степенные определения sin и cos соотносятся с их геометрическими интерпретациями?
Я надеюсь, что большинство из вас либо задавали себе этот вопрос явно, либо, по крайней мере, испытывали смутное чувство беспокойства по поводу того, как определения, которые я давал в лекциях, а именно
и
соотносятся с вещами, подобными противоположным , смежная и гипотенуза. Используя определения степенных рядов, мы доказали несколько фактов о тригонометрических функциях, таких как формулы сложения, их производные и тот факт, что они периодические.
Но мы еще не дошли до доказательства того, что если и является углом, который линия от до образует с линией от до , то и . Так как же это установить? Как можно даже определить угол? В этом посте я дам один из возможных ответов на эти вопросы.
Пара возможных подходов, которые я не буду пытаться использовать
Обманом и не совсем удовлетворительным методом будет определение угла, который будет равен . Тогда это было бы тривиально, и мы могли бы использовать известные нам факты, чтобы доказать это. (Или могли бы? Разве мы не поняли бы, что это было? Тот факт, что многие ракурсы одинаковы, и создает для этого подхода досадные трудности, хотя такие, которые в принципе можно было бы обойти.) Но если бы мы это сделали, то как бы мы быть уверенным, что понятие угла, которое мы только что определили, совпадает с тем, каким, по нашему мнению, должен быть угол? Проблема полностью не решена.
Другой подход может состоять в том, чтобы определить тригонометрические функции геометрически, доказать, что они обладают основными свойствами, которые мы установили, используя определения степенных рядов, и доказать, что эти свойства характеризуют тригонометрические функции (имеется в виду, что любые две функции и, обладающие свойствами, должны быть а также ).
Однако это по-прежнему требует, чтобы мы каким-то образом понимали понятие угла, и мы могли бы также немного беспокоиться о том, действительно ли геометрические аргументы, которые мы использовали для обоснования формул сложения и тому подобного, были действительно строгими. (Я не говорю, что это не может быть сделано удовлетворительно — просто я не сразу вижу хороший способ сделать это, и у меня есть другой подход к представлению.)
Определение угла
Как определяются радианы? Вы берете прямую L, начинающуюся в начале координат, и она пересекает единичную окружность в некоторой точке P. Тогда угол, который эта линия образует с горизонтом (точнее, с горизонтом, направленным вправо), определяется как длина дуга окружности, которая проходит против часовой стрелки вокруг единичной окружности от до P. (Это определяет число от 0 до , но мы можем заняться числами за пределами этого диапазона позже.)
Вычисление длины дуги окружности
В этом определении нет ничего неправильного, за исключением того, что оно требует от нас строгого понимания длины дуги окружности.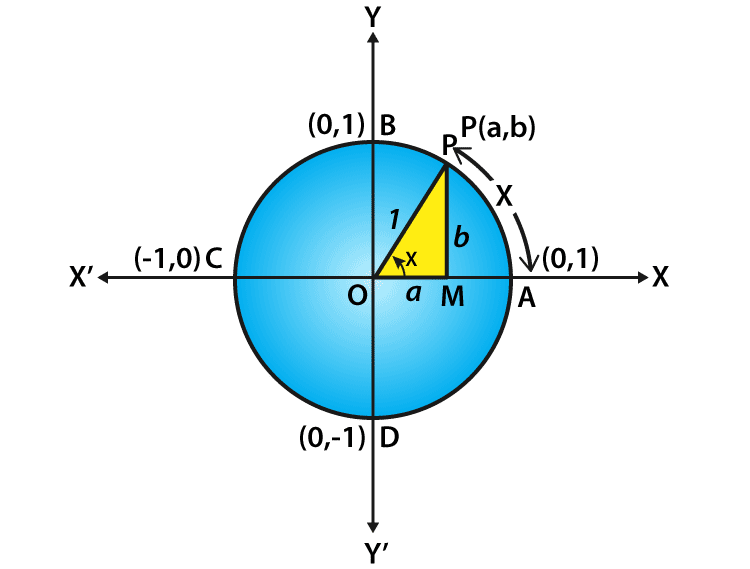
Как нам это сделать?
Для простоты предположим, что наша точка P есть и что обе точки и положительны. Таким образом, P находится в верхнем правом квадранте единичного круга. Как мы можем определить, а затем вычислить длину дуги от до или, что то же самое, от до?
Один нестрогий, но информативный способ думать об этом состоит в том, что для каждого между и мы должны взять интервал , определить длину части окружности по вертикали над этим интервалом и просуммировать все эти длины. Часть окружности, о которой идет речь, представляет собой прямую линию (поскольку бесконечно мала), и для подобных треугольников ее длина равна .
Как я это записал? Что ж, большой треугольник, о котором я думал, имел вершины и точку на окружности прямо над ней, что соответствует теореме Пифагора. Маленький треугольник имеет одну сторону длины, которая соответствует стороне большого треугольника длины. Итак, гипотенуза маленького треугольника равна , как я утверждал.
Складывая все эти длинны, получаем , так что осталось вычислить этот интеграл.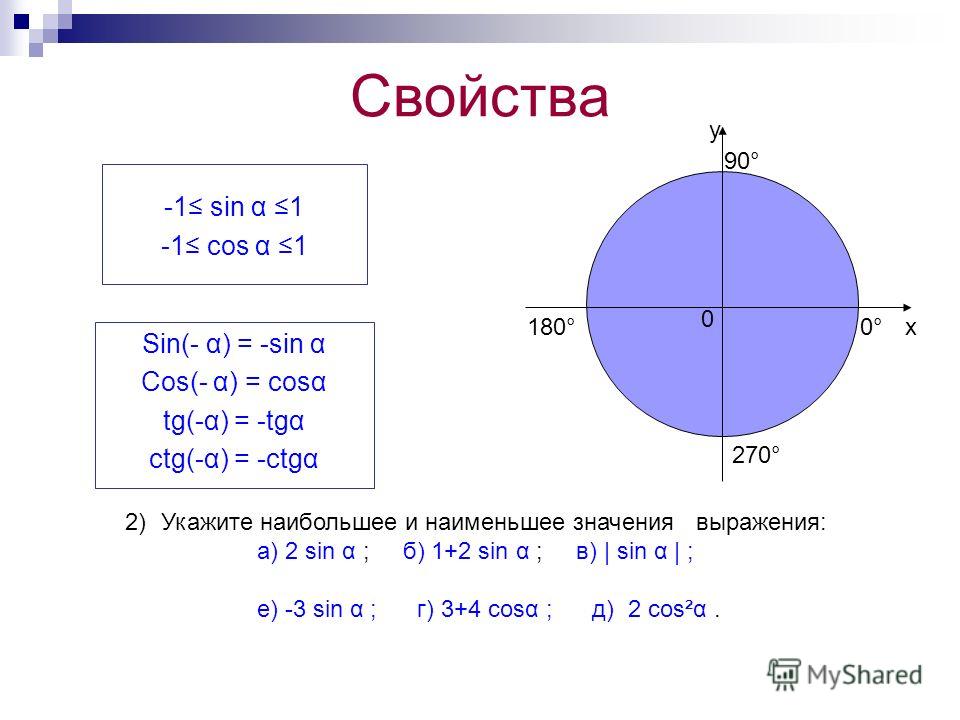
Это, конечно, очень стандартный интеграл, который обычно решается подстановкой или вместо . Если вы сделаете это, то обнаружите, что длина получается равной , на что мы и надеялись. Однако в этом курсе мы не обсуждали интегрирование путем подстановки, поэтому давайте рассмотрим его более элементарно (не то чтобы доказательство подходящей формы правила интегрирования путем подстановки особенно сложно).
Используя правила дифференцирования инверсий, мы находим, что
и поскольку , это дает нам . Таким образом, подынтегральная функция имеет в качестве первообразной и, следовательно, по основной теореме исчисления,
Таким образом, угол между горизонталью и линией, соединяющей начало координат с, является (по определению) длиной дуги от до , которую мы рассчитали быть . Следовательно, .
Насколько это было близко к строгости?
Процесс, через который я только что прошел, говоря: «Давайте сложим целую кучу бесконечно малых длин; это говорит о том, что мы должны записать следующий интеграл; вычисление интеграла дает нам L, поэтому длина равна L», — это процесс, который часто происходит при вычислении подобных величин.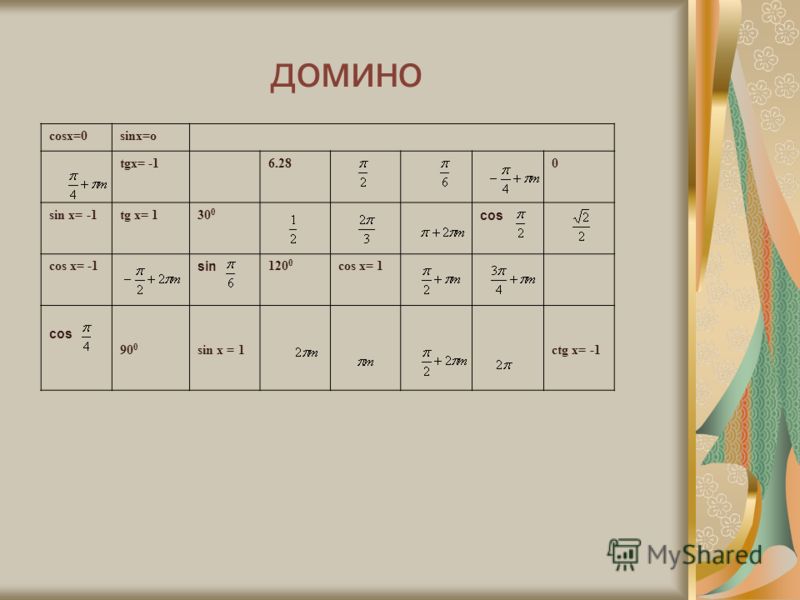
Почему мы так уверены, что это нормально?
Иногда с такими математическими вопросами я понимаю, что я много лет был математиком и никогда не беспокоился о них. Просто очевидно, что если функция достаточно хороша, то запись чего-то, что приблизительно соответствует истине с , а также превращение в и написание красивого знака впереди дает вам правильное выражение для рассматриваемой величины. Но давайте попробуем немного подумать о том, как мы можем строго определить длину.
Кривые
Прежде всего, мы должны сказать, что такое кривая. Существуют различные определения в зависимости от того, насколько хорошо мы хотим предположить, но позвольте мне взять основное определение: кривая — это непрерывная функция от интервала до . (Я не определял непрерывные функции для , но это просто означает, что если , то и обе являются непрерывными функциями от до .)
Это пример любопытной привычки математиков определять объекты как вещи, которыми они явно не являются. Конечно, кривая — это не функция — это особый вид подмножества плоскости.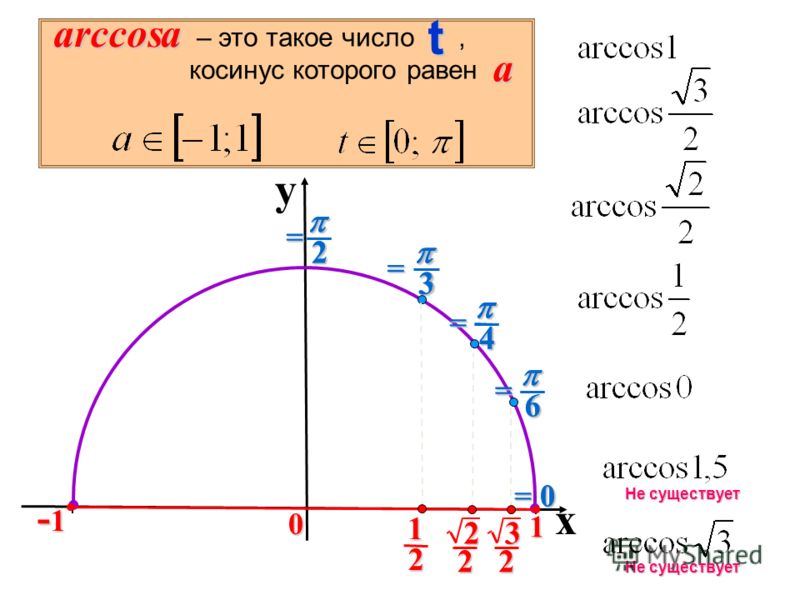
На самом деле, разве кривая не должна быть определена как образ непрерывной функции от до ? Это правда, что это больше соответствует тому, что мы думаем, когда используем слово «кривая», но определение, которое я только что дал, оказывается более удобным, хотя важно добавить, что две кривые (как я определили их) и составляют эквивалентно , если существует строго возрастающая непрерывная биекция такая, что для каждого . В этой ситуации мы думаем о и как о разных способах представления одной и той же кривой.
Между прочим, если вам нужна причина не отождествлять кривые с их изображениями, то достаточно хорошей причиной является существование объектов, называемых кривыми, заполняющими пространство . Это непрерывные функции от интервалов вещественных чисел до заполнения целых двумерных множеств. Вот фотография одного из них, взятая из Википедии.
Он показывает первые несколько итераций процесса, который дает вам последовательность функций, сходящихся к непрерывному пределу, который заполняет весь квадрат.
Длины кривых
Возвращаясь к длинам, давайте подумаем, как их можно определить. Единственное, что мы умеем определять, — это длину отрезка. (Строго говоря, мне нельзя так говорить, поскольку отрезок не является функцией, но давайте понимать его как особенно простую функцию от интервала до отрезка на плоскости.) Учитывая это, разумное определение длины, казалось бы, должно аппроксимировать данную кривую множеством маленьких отрезков. Это приводит к следующей идее по крайней мере аппроксимации длины кривой. Берем рассечение и складываем все маленькие расстояния. Здесь я определяю расстояние между двумя точками обычным способом по теореме Пифагора. Это дает нам выражение
для приблизительной длины, указанной вскрытием. Затем мы надеемся, что по мере того, как различия будут становиться все меньше и меньше, эти оценки будут стремиться к пределу. Нетрудно заметить, что если вы уточняете рассечение, то оценка увеличивается (вы заменяете длину отрезка, соединяющего две точки, на длину пути, состоящего из отрезков и соединяющего те же две точки).
.
На самом деле эта надежда не всегда сбывается: иногда оценки стремятся к бесконечности. Действительно, для кривых, заполняющих пространство, или фракталоподобных кривых, таких как снежинка Коха, оценки до стремятся к бесконечности. В этом случае говорят, что они имеют бесконечную длину. Но если оценки стремятся к пределу, когда максимум разностей стремится к нулю, мы называем это пределом длины кривой. Кривая, имеющая конечную длину, определенную таким образом, называется спрямляемой .
Теперь предположим, что у нас есть кривая, заданная и, что две функции и непрерывно дифференцируемы. Тогда оба и ограничены на , поэтому давайте предположим, что это верхняя граница для и . Тогда по теореме о среднем значении
Следовательно, для каждого рассечения, что означает, что кривая спрямляема. (Примечание: на самом деле я не использовал здесь непрерывность производных — только их ограниченность.)
Однако мы можем сказать немного больше.
Дифференцируемость говорит нам, что для некоторых . И аналогично для некоторых . Следовательно, оценка длины может быть записана как
Это очень похоже на то, что мы записываем при интегрировании по Риману, поэтому давайте посмотрим, сможем ли мы найти точную связь. Нас интересует функция . Если мы сейчас do используют непрерывность и , тогда она тоже непрерывна, поэтому ее можно интегрировать. Теперь, так как и принадлежат интервалу , и оба лежат между нижней и верхней суммами, заданными рассечением. Отсюда следует то же самое для
Поскольку интегрируема, предел как наибольшего (который часто называют сеткой рассечения) стремится к нулю .
Мы показали, что длина кривой определяется формулой
Теперь, наконец, давайте посмотрим, можем ли мы обосновать наш расчет длины дуги единичной окружности между и . Было бы неплохо параметризовать окружность как , но мы не можем этого сделать, так как мы определяем длину, поэтому в итоге мы получим круговое определение (более чем в одном смысле).
[На самом деле мы может сделать что-то очень близкое к этому. Подробнее см. в заключительном разделе поста.] Итак, давайте параметризуем его следующим образом. Определим на интервале и отправим в . Затем и , поэтому
Итак, длина равна , что в точности соответствует выражению, которое мы записали ранее.
Позвольте мне сделать два коротких замечания по этому поводу. Во-первых, вы можете возразить, что, хотя я показал, что окончательное выражение действительно верно, я не показал, что неформальное аргумент (по существу) правильный. Но у меня более или менее есть, так как я действительно вычислил длины гипотенуз маленьких треугольников немного другим способом. Раньше я пользовался тем, что одна сторона была и использовала подобные треугольники. Здесь я использовал тот факт, что одна сторона есть, а другая сторона есть, и использовал Пифагора.
Чуть более серьезное возражение состоит в том, что для этого вычисления я использовал общий результат, основанный на предположении, что оба и непрерывно дифференцируемы, но не проверял выполнение соответствующих условий, а это не так.
Проблема в том, что , так , что стремится к бесконечности как и не определено при .
Однако эту проблему легко обойти. Что мы делаем, так это интегрируем от до , и в этом случае аргумент действителен, а затем устремляем к нулю. Интеграл между и равен , и это стремится к .
И последнее замечание: это вычисление длины объясняет, почему обычная замена for в интеграле формы не является немотивированной магией. Это просто способ переключения от одной параметризации дуги окружности (с использованием координаты x) к другой (с использованием угла или, что то же самое, расстояния вдоль дуги окружности), который, как ожидается, будет проще.
Более простой аргумент
Благодаря приведенному ниже комментарию Джейсона Фордхэма я теперь понимаю, что мы все-таки можем параметризовать круг как . Однако это не то, что я пытаюсь вычислить, так что давайте назовем это . Я просто принимаю за обычное действительное число и даю определение и использую определение степенного ряда.