Cos 56 pi: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )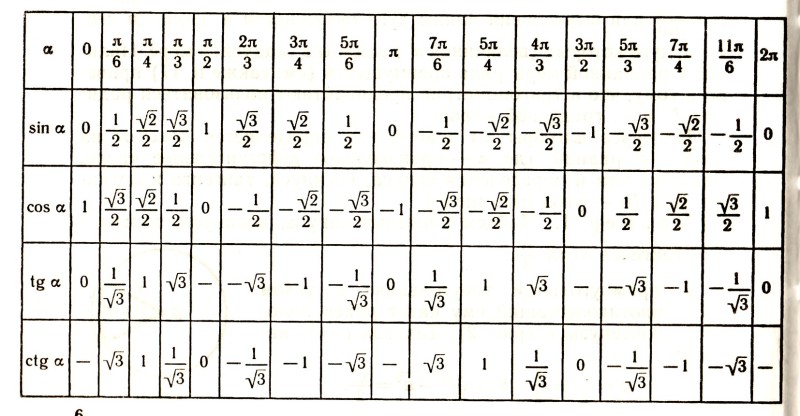
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )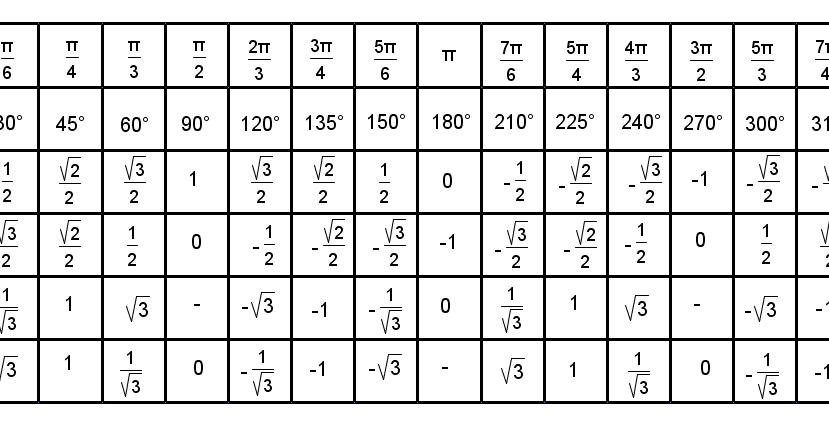
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81		Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы 88 град.

Мэтуэй | Популярные задачи

92
1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение угловой синус(-1)
7 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение cos(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан(квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

Математическая премия 2011 для девочек: №6–10

Вот комментарии и решения задач 6–10 на конкурсе Math Prize for Girls 2011, который проходил в Массачусетском технологическом институте 17 сентября 2011 года. Ранее я публиковал в блоге комментарии и решения задач 11–15 и 16–20.

Примечание. В задачах конкурса «Математическая премия для девочек 2011» нет необходимости предоставлять доказательства правильности ответа. Это делает задачи вроде №6 и №8 проще. После экзамена может быть целесообразно представить недостающие доказательства, и я укажу, как некоторые из этих доказательств могут быть здесь.

Задача № 6

a — мера указанного угла.

Чтобы минимизировать площадь квадрата, нам нужно, чтобы круги соприкасались, потому что, если круги не соприкасаются, можно представить, что квадрат уменьшается, а круги сжимаются до тех пор, пока они не соприкоснутся. Итак, нам нужно найти площадь наименьшего квадрата, который будет содержать две соприкасающиеся единичные окружности.

Стороны квадрата идут в двух перпендикулярных направлениях. Нам нужно измерить расстояние по двум окружностям в каждом из этих направлений. Большее расстояние соответствует наименьшей длине стороны содержащего квадрата, ориентированного в этом направлении.

Расстояния по двум окружностям задаются как и (см. рисунок). По симметрии нам нужно рассматривать только значения между 135 и 180 градусами. В этом диапазоне, . Минимальное значение в этом диапазоне возникает при значении 135 градусов, а значение при 135 градусах равно . Квадрат с такой длиной стороны имеет площадь .

Другой способ найти решение — зафиксировать квадрат и попытаться заполнить его парой самых больших конгруэнтных кругов, которые вы можете, а затем масштабировать результат так, чтобы круги имели единичные радиусы. (Или подумайте таким образом, чтобы найти оптимизирующую компоновку, а затем вычислить площадь квадрата, исходя из предположения, что круги, содержащиеся в нем, являются единичными кругами.) Один из вариантов такого подхода — утверждать, что любые два конгруэнтных круга, содержащиеся в квадрате, могут быть перемещены так, чтобы они плотно прилегали к противоположным углам квадрата, и что, следовательно, самыми большими такими кругами были бы те, которые не только плотно прилегали к противоположным углам, но и соприкасались в центре.

Если у вас возникли проблемы, вот несколько советов: сделайте хорошую иллюстрацию ситуации, используйте симметрию в задаче и убедитесь, что вы используете преимущества и соблюдаете различные характеристики задействованных геометрических фигур.

Задача №7

Прямой подход состоит в том, чтобы решить данное уравнение и подставить в нужное выражение.

Возможное изображение, которое можно было бы вообразить, которое могло бы сделать решения квадратного уравнения очевидными без каких-либо вычислений. Если это изображение не помогает, найдите решения любым удобным для вас способом, а затем нанесите их на комплексную плоскость. Сравните с этой цифрой.

Данное условие является квадратичным условием и может быть решено с помощью квадратичной формулы. Но операции с комплексными числами имеют красивые геометрические аналоги на комплексной плоскости, и часто стоит визуализировать ситуацию на комплексной плоскости, прежде чем заниматься алгеброй. Возможно, вы сможете увидеть решение или увидеть что-то, что значительно упростит алгебру и сэкономит ваше время. Здесь вам нужны два комплексных числа, которые являются обратными друг другу и сумма которых равна . Вы видите решения? Если не получается, не беспокойтесь… просто решите уравнение, как сможете. Затем, после решения, нанесите свои решения на комплексную плоскость и посмотрите, сможете ли вы увидеть, что они являются решениями. Делая это, в следующий раз, когда вы столкнетесь с уравнением, включающим комплексные числа, которое поддается такому «визуальному решению», вы с большей вероятностью увидите его.

В любом случае решения представляют собой два корня из единицы: , .

Поскольку желаемое выражение остается неизменным при замене и , не имеет значения, какой корень вы подставите вместо . Мы используем тот факт, что для вычисления:

.

Если вы не знакомы с комплексными числами, вы можете решить эту задачу чисто алгебраически путем рекурсивных вычислений. Например, обратите внимание, что . Также заметьте, что . Вычисляя различные значения , вы в конце концов увидите, что это значение зависит только от остатка, остающегося после деления на 12. (Или вы можете использовать подобные тождества для непосредственного вычисления желаемого выражения.)

Если у вас возникли проблемы, изучите комплексные числа и особенно корни из единицы. На контестах часто бывает, что когда видишь очень большой показатель, есть периодичность.

Задача #8

Мы можем представить себе собаку, прикрепленную к шесту (в точке A ) на поводке длиной 8 единиц. От B до C тянется непроницаемый забор. Куда может пойти собака? Область достижимости можно вывести, применив принцип, согласно которому на (евклидовой) плоскости кратчайшее расстояние между двумя точками представляет собой прямую линию.

Например, откуда мы знаем, что P недоступен? Любой путь от A до P должен пересекать либо луч от A до B (и дальше B ), либо луч от A через 6 C (и дальше ).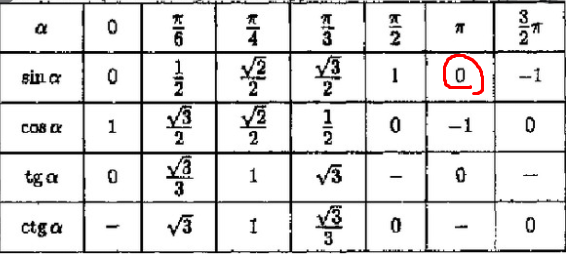 По симметрии можно считать, что путь пересекает луч от А до В в точке X . Поскольку кратчайшее расстояние между двумя точками — это прямая линия , длина пути не меньше длины кусочно-прямого пути от A до X и до P . Теперь XP не может превышать 8 — AX . Заметьте, что так. Таким образом, круг радиусом 8 – AX  с центром X полностью содержится внутри круга радиусом 2 с центром B . Таким образом, P недоступен.

Теперь, когда мы определили область, мы можем вычислить ее площадь. Область состоит из 3 круглых секторов и равностороннего треугольника. Серый круговой сектор имеет квадратные единицы площади. Каждый из двух розовых круглых секторов имеет общую площадь, равную квадратным единицам. А площадь равностороннего треугольника имеет квадратные единицы.

Таким образом, общая площадь достижимых точек равна квадратным единицам.

Задача № 9

В этой задаче много точек и линий, заданных отношением длин отрезков вдоль линии. Полезный метод решения таких задач использует тот факт, что аффинные преобразования сохраняют такие соотношения. Поскольку любой треугольник может быть отображен на любой другой треугольник с помощью аффинного преобразования, мы можем вычислить желаемое отношение для любого конкретного треугольника, чтобы получить ответ. (Сама постановка задачи подразумевает этот факт, поскольку в постановке не указаны конкретные размеры треугольника.)

Таким образом, мы можем указать любые неколлинеарные координаты для вершин A , B и C. Поскольку существует 3 процесса деления пополам и поскольку желаемое отношение относится к сегментам вдоль AB , я выберу вершины так, чтобы A и B лежали вдоль координатной оси, а все координаты были кратны . Итак, установите A = (0, 0), B = (0, 8) и C = (8, 0).

Тогда D = (4, 4), E = (2, 2) и F  = (1, 5). x -координата G равна 0, а ее y -координата y — точка пересечения линии, проходящей через C = (8, 0) и F = (1, 5). Уравнение этой прямой. Итак, G = (0, 40/7).

Таким образом, .

Используемый принцип весьма полезен. Например, вы можете использовать его, чтобы показать, что медианы треугольника пересекаются в общей точке. Поскольку середины определяют медианы, нужно только убедиться, что медианы пересекаются в одной точке для одного треугольника, чтобы получить результат для всех треугольников, и по симметрии 3 медианы равностороннего треугольника совпадают. (Другое доказательство совпадения медиан треугольника см. в томе 3, номере 2 бюллетеня Girls’ Angle Bulletin.)

Задача № 10

Эта задача проверяет ваши алгебраические навыки и способности с функцией арктангенса. Чем больше вы знаете об арктангенсе, тем меньше вам придется заниматься алгеброй. В частности, если вы знаете формулу суммы арктангенсов и соотношение между арктангенсами дополнительных углов, то мы можем получить решение, подобное этому:

Объединив второй и третий арктангенсы в один, используя формулу суммы арктангенсов арктангенсы дополнительных углов обратны друг другу, мы можем преобразовать данное тождество к

.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *