| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Вывод формул обратных тригонометрических функций
Основные формулы
Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций.
Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых. Свойства обратных функций можно разбить на две группы.
В первую группу входят формулы, справедливые на всей области определения обратных функций:
sin(arcsin x) = x
cos(arccos x) = x
tg(arctg x) = x (–∞ < x < +∞)
ctg(arcctg x) = x (–∞ < x < +∞)
Во вторую группу входят формулы, справедливые только на множестве значений обратных функций.
arcsin(sin x) = x при
arccos(cos x) = x при
arctg(tg x) = x при
arcctg(ctg x) = x при
Если переменная x не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n — целое):
sin x = sin(–x–π); sin x = sin(π–x); sin x = sin(x+2πn);
cos x = cos(–x); cos x = cos(2π–x); cos x = cos(x+2πn);
tg x = tg(x+πn); ctg x = ctg(x+πn)
Например, если известно, что то
arcsin(sin x) = arcsin(sin( π — x )) = π — x .
Легко убедиться, что при π – x попадает в нужный интервал. Для этого умножим на –1: и прибавим π: или Все правильно.
Обратные функции отрицательного аргумента
Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin x
Поскольку то умножив на –1, имеем: или
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.
Аналогично для остальных функций.
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) = π – arccos x
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg x
arcctg(–x) = arcctg(–ctg arcctg x) = arcctg(ctg(π–arcctg x)) = π – arcctg x
Выражение арксинуса через арккосинус и арктангенса через арккотангенс
Выразим арксинус через арккосинус.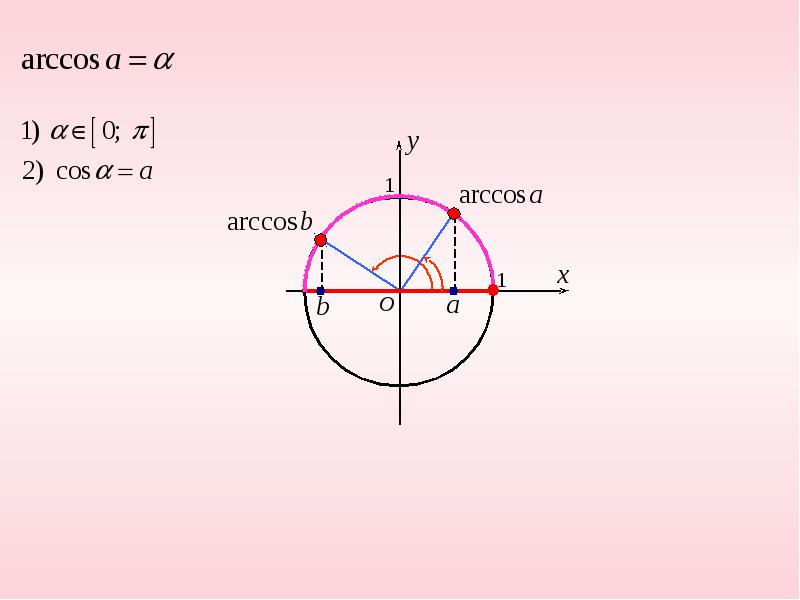
Формула справедлива при Эти неравенства выполняются, поскольку
Чтобы убедиться в этом, умножим неравенства на –1: и прибавим π/2: или Все правильно.
Итак,
Аналогично выражаем арктангенс через арккотангенс.
Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот
Поступаем аналогичным способом.
Формулы суммы и разности
Аналогичным способом, получим формулу суммы арксинусов.
Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin x, Y = arcsin y. Формула применима при
. Далее замечаем, что, поскольку arcsin(–x) = – arcsin x, arcsin(–y) = – arcsin y, то при разных знаках у x и y, X и Y также разного знака и поэтому неравенства выполняются. Условие различных знаков у x и y можно написать одним неравенством: . То есть при формула справедлива.
Теперь рассмотрим случай x > 0 и y > 0, или X > 0 и Y > 0.
Тогда условие применимости формулы заключается в выполнении неравенства: . Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0, до π, то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:
;
;
;
.
Поскольку и ; то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;
.
Подставляем sin X = sin arcsin x = x:
;
;
;
.
Итак, полученная формула справедлива при или .
Теперь рассмотрим случай x > 0, y > 0 и x2 + y2 > 1. Здесь аргумент синуса принимает значения: . Его нужно привести к интервалу области значения арксинуса :
.
Итак,
при и.
Заменив x и y на – x и – y, имеем
при и.
Выполняем преобразования:
при и.
Или
при и.
Итак, мы получили следующие выражения для суммы арксинусов:
при или ;
при и ;
при и .
Аналогичным способом получаются остальные формулы:
при или ;
при и ;
при и ;
при ;
при ;
при ;
при ;
при ;
при ;
при ;
при ;
при ;
при .
Автор: Олег Одинцов. Опубликовано:
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия
Предположим, что число a удовлетворяет неравенству . Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:
Предположим, что число a удовлетворяет неравенству . Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:
Рассмотрим произвольное число a .
Число x называют арктангенсом числа a и обозначают x = arctg a, если выполнены два условия:
Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают x = arcctg a, если выполнены два условия:
Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:
| arcsin (– a) = – arcsin a , |
| arccos (– a) = = π – arccos a , |
| arctg (– a) = – arctg a , |
| arcctg (– a) = = π – arcctg a . |
Обратными тригонометрическими функциями называют функции:
Графики этих функций изображены на рисунках 1, 2, 3, 4.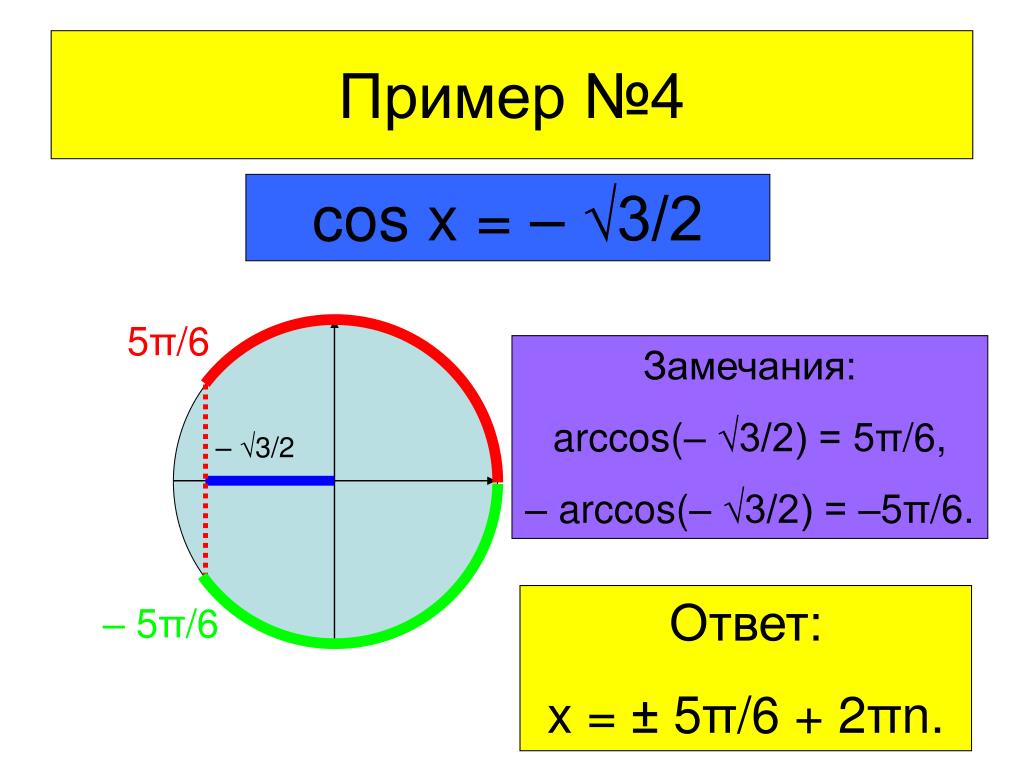
Рис. 1. График функции y = arcsin x
Таблица значений функции y = arcsin x
Рис. 2. График функции y = arccos x
Таблица значений функции y = arccos x
Рис. 3. График функции y = arctg x
Таблица значений функции y = arctg x
Рис. 4. График функции y = arcctg x
Таблица значений функции y = arcctg x
Пример. Решить уравнение
2 arcsin 2x = arccos 7x .
Решение. Возьмём косинус от обеих частей уравнения. Тогда в левой части уравнения получим:
cos ( 2 arcsin 2x ) = 1 – 2sin2( arcsin 2x ) = 1 – 2 ( 2x )2 = 1 – 8x2 .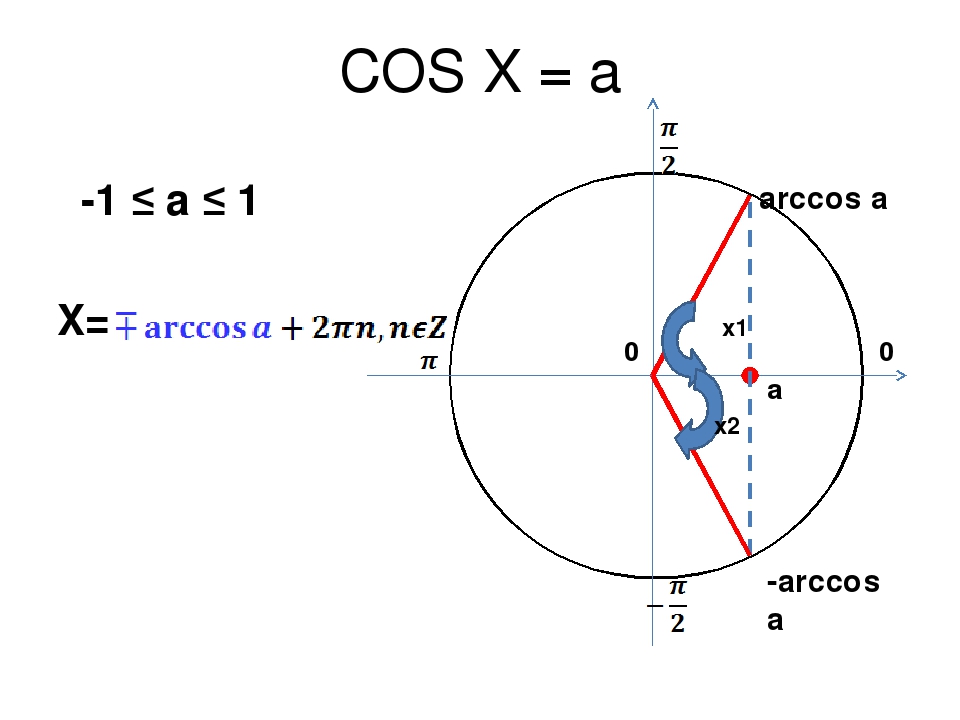
cos ( 2 arcsin 2x ) =
= 1 – 2sin2( arcsin 2x ) =
= 1 – 2 ( 2x )2 = 1 – 8x2 .
В правой части уравнения получим:
cos ( arccos 7x ) = 7x.
Следовательно, возникает квадратное уравнение:
В силу того, что область определения обратных тригонометрических функций y = arcsin x и y = arccos x имеет вид: , второй корень должен быть отброшен.
Ответ:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
для α∈-1, 1 sin(arccis α)=α, cos(arccos α)=α,для α∈(-∞, ∞) tg(arctg α)=α, ctg(arcctg α)=α
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
для -π2≤α≤π2 arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Определение 1Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
для α∈-1, 1 arccis (-α)=-arcsin α, arccos (-α)=π-arccos α,для α∈(-∞, ∞) arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
для α∈-1, 1 arccis α+arccos α=π2,для α∈(-∞, ∞) arctg α+arcctg α=π2
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
| -1≤α≤1,sin (arcsin α)=α | -1≤α≤1,sin (arccos α)=1-α2 | -∞≤α≤+∞,sin (arctg α)=α1+α2 | -∞≤α≤+∞, sin (arcctg α)=11+α2 |
| -1≤α≤1,cos (arcsin α)=1-α2 | -1≤α≤1,cos (arccos α)=α | -∞≤α≤+∞,cos (arctg α)=11+α2 | -∞≤α≤+∞, cos (arcctg α)=11+α2 |
| -1<α<1,tg (arcsin α) =α1-α2 | α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α | -∞≤α≤+∞,tg (arctg α)=α | α≠0 ,tg (arcctg α)=1α |
| α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α | -1<α<1,ctg (arccos α)=α1-α2 | α≠0,ctg (arctg α)=1α | -∞≤α≤+∞, ctg (arcctg α)=α |
Теперь разберем примеры, как они применяются в задачах.
Вычислите косинус арктангенса из 5.
Решение
У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2
Подставляем нужное значение: cos(arctg5)=11+(5)2=26
Пример 2Вычислить синус арккосинуса 12.
Решение
Для этого нам понадобится формула: sin (arccos α)=1-a2
Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеДля того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др.
Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin2α+cos2α=11+ctg2α=1sin2α
Вспомним, что tgα·ctgα=1. Из этого можно получить:
sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
- sinα=1-cos2α, 0≤α≤π
Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2
- sinα=tgα1+tgα, -π2<α<π2,
Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2
- sinα=11+ctg2α, 0<α<π
Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
- Из cosα=1-sin2α, -π2≤α≤π2 следует, что
cos(arcsin α)=1-sin2(arcsin α)=1-a2
- Из cosα=11+tg2α, -π2<α<π2 следует, что
- Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2
следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из tgα=sin α1-sin2α, -π2<α<π2. Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.
- Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем
tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).
- Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
ctgα=1tgα
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса.
Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции. Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0
А так мы выразим арккосинус через остальные обратные функции:
arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1
Формула выражения арктангенса:
arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0
Последняя часть – выражение арккотангенса через другие обратные функции:
arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.
Мы знаем, что arctgα1-α2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α
Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.
Вывод: arcsina=arctga1-a2, -1<a<1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Пример 3Условие Вычислить синус арккотангенса минус корня из 3.
Решение
Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0
Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π
В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2 sin(arcctg(-3))=11+(-3)2=12
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач.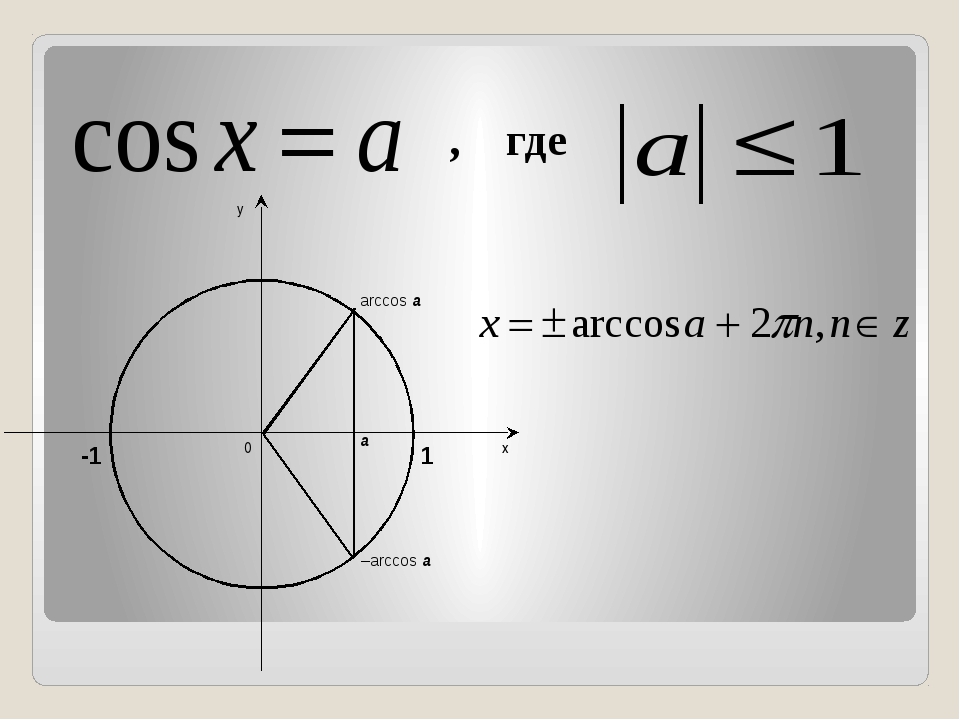
Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
sin2α2=1-cosα2
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
sinα2=1-cosα2
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
arccosα2=arcsin1-α2
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
определение и синонимы слова arccos в словаре английский языка
ARCCOS — определение и синонимы слова arccos в словаре английский языкаEducalingo использует cookies для персонализации рекламы и получения статистики по использованию веб-трафика. Мы также передаем информацию об использовании сайта в нашу социальную сеть, партнерам по рекламе и аналитике.
ПРОИЗНОШЕНИЕ СЛОВА ARCCOS
ЧТО ОЗНАЧАЕТ СЛОВО ARCCOS
Нажмите, чтобы посмотреть исходное определение слова «arccos» в словаре английский языка.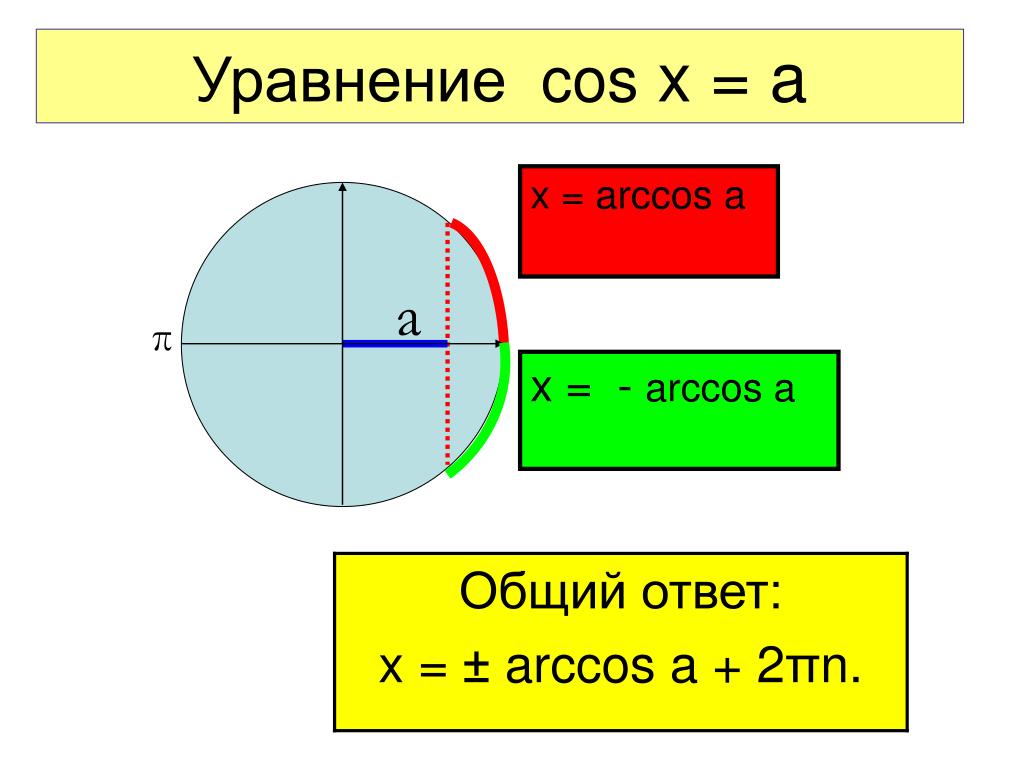
Нажмите, чтобы посмотреть автоматический перевод определения на русский языке.Значение слова arccos в словаре английский языка
Определение арккоса в словаре является дуговым косинусом: функция, значение которой для данного аргумента между -1 и 1 является углом в радианах, косинус которого является тем аргументом: обратным косинусоидальной функции.The definition of arccos in the dictionary is arc-cosine: the function the value of which for a given argument between –1 and 1 is the angle in radians, the cosine of which is that argument: the inverse of the cosine function.
Нажмите, чтобы посмотреть исходное определение слова «arccos» в словаре английский языка. Нажмите, чтобы посмотреть автоматический перевод определения на русский языке.
СЛОВА, РИФМУЮЩИЕСЯ СО СЛОВОМ ARCCOS
Синонимы и антонимы слова arccos в словаре английский языка
Перевод слова «arccos» на 25 языков
ПЕРЕВОД СЛОВА ARCCOS
Посмотрите перевод слова arccos на 25 языков с помощью нашего многоязыкового переводчика c английский языка. Переводы слова arccos с английский языка на другие языки, представленные в этом разделе, были выполнены с помощью автоматического перевода, в котором главным элементом перевода является слово «arccos» на английский языке.Переводчик с английский языка на
китайский язык ARCCOS1,325 миллионов дикторов
Переводчик с английский языка на
испанский язык arccos570 миллионов дикторов
английский arccos
510 миллионов дикторов
Переводчик с английский языка на
хинди язык ARccOS380 миллионов дикторов
Переводчик с английский языка на
арабский язык قوس جيب تمام الزاوية280 миллионов дикторов
Переводчик с английский языка на
русский язык агссоз278 миллионов дикторов
Переводчик с английский языка на
португальский язык arccos270 миллионов дикторов
Переводчик с английский языка на
бенгальский язык arccos260 миллионов дикторов
Переводчик с английский языка на
французский язык arccos220 миллионов дикторов
Переводчик с английский языка на
малайский язык Arccos190 миллионов дикторов
Переводчик с английский языка на
немецкий язык arccos180 миллионов дикторов
Переводчик с английский языка на
японский язык ARccOSコピー130 миллионов дикторов
Переводчик с английский языка на
корейский язык ARCCOS85 миллионов дикторов
Переводчик с английский языка на
яванский язык Arccos85 миллионов дикторов
Переводчик с английский языка на
вьетнамский язык arccos80 миллионов дикторов
Переводчик с английский языка на
тамильский язык arccos75 миллионов дикторов
Переводчик с английский языка на
маратхи язык आर्कको75 миллионов дикторов
Переводчик с английский языка на
турецкий язык arccos70 миллионов дикторов
Переводчик с английский языка на
итальянский язык arccos65 миллионов дикторов
Переводчик с английский языка на
польский язык arccos50 миллионов дикторов
Переводчик с английский языка на
украинский язык агссоз40 миллионов дикторов
Переводчик с английский языка на
румынский язык arccos30 миллионов дикторов
Переводчик с английский языка на
греческий язык arccos15 миллионов дикторов
Переводчик с английский языка на
африкаанс язык arccos14 миллионов дикторов
Переводчик с английский языка на
шведский язык arccos10 миллионов дикторов
Переводчик с английский языка на
норвежский язык arccos5 миллионов дикторов
Тенденции использования слова arccos
ТЕНДЕНЦИИ ИСПОЛЬЗОВАНИЯ ТЕРМИНА «ARCCOS»
ЧАСТОТНОСТЬ
Слово используется достаточно часто
На показанной выше карте показана частотность использования термина «arccos» в разных странах.
Тенденции основных поисковых запросов и примеры использования слова arccos Список основных поисковых запросов, которые пользователи ввели для доступа к нашему онлайн-словарю английский языка и наиболее часто используемые выражения со словом «arccos».
ЧАСТОТА ИСПОЛЬЗОВАНИЯ ТЕРМИНА «ARCCOS» С ТЕЧЕНИЕМ ВРЕМЕНИ
На графике показано годовое изменение частотности использования слова «arccos» за последние 500 лет. Формирование графика основано на анализе того, насколько часто термин «arccos» появляется в оцифрованных печатных источниках на английский языке, начиная с 1500 года до настоящего времени.
Примеры использования в литературе на английский языке, цитаты и новости о слове arccos
КНИГИ НА АНГЛИЙСКИЙ ЯЗЫКЕ, ИМЕЮЩЕЕ ОТНОШЕНИЕ К СЛОВУ
«ARCCOS» Поиск случаев использования слова arccos в следующих библиографических источниках.
Книги, относящиеся к слову arccos, и краткие выдержки из этих книг для получения представления о контексте использования этого слова в литературе на английский языке.1
Calculus of a Single Variable15. arcsec 1.269 arccos 0.8 14. 16. arctan 5 arcsin 0.39 In Exercises 17–20, evaluate each expression without using a calculator. (Hint: See Example 3.) 17. ( a) (b) sec arcsin sin arctan 4 5 19. (a) cot arcsin (b) csc arctan 3 4 18. (a) tan arccos 2 …
Ron Larson, Bruce Edwards, 2008
π 2 π 2 − −3 −2 123 9. arctan 3 3 11. arccsc 2 6. arcsin 0 8. arccos 1 10. arccot 3 12. arcsec 2 In Exercises 13–16, use a calculator to approximate the value. Round your answer to two decimal places. 13. 15. arcsec 1.269 arccos 0.8 14.
Ron Larson, Bruce Edwards, 2009
3
Handbook of Integral Equations: Second Edition [A arccos(Ax) + B arccos(Ai)] y{t) dt = f(x).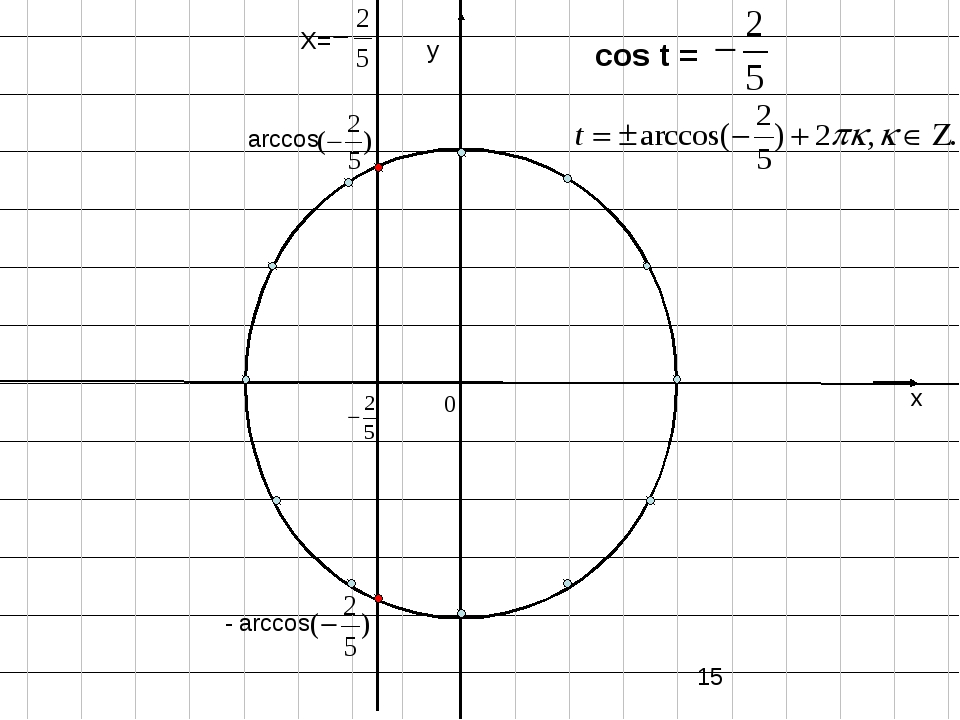
| [arccos(Ax)] f [arccos(At)] ft{t) dt J . pX 3. / [A arccos(Acc) + B arccos(/xt) + C] y(t)
…
Andrei D. Polyanin, Alexander V. Manzhirov, 2008
4
Calculus: Single VariableThe inverse cosine .v i-> Cos~'(jc) is also called the arccosine and denoted by arccos(.v). We reflect the graph of y = Cos(.v) across the line y = ,v to obtain the graph of y = Cos~'(.v), as is shown in Figure 6. Example 2 Calculate arccos(— …
Brian E. Blank, Steven George Krantz, 2006
5
Handbook of Mathematics for Engineers and Scientists 2.3.2-1. Simplest formulas. sin(arcsin x) = x, cos(arccos x) = x, tan(arctan a:) = x,
cot(arccot a;) = x. 2.3.2-2. Some properties. arcsin(-a:) = -arcsin x, arccos(-x) = ir — arccos x, arctan(-a;) = — arctan x, arccot(-x) = it — arccot x, arcsin(sin x) arccos(cos
.
..
Andrei D. Polyanin, Alexander V. Manzhirov, 2006
6
Handbook of First-Order Partial Differential Equations+ y +A(arccosx) y-a + aA(arccosx) = 0. ox dy Principal integral: 5 = + / e~2axEdx, E = exp A / (arccos i)n dx y+a J [ J dw , 2 dw 6. + y + Ax(arccos x)ny + A(arccos x) n = 0. ax dy Principal integral: — — + / x 2Edx, E = exp A / x(arccos x)n dx x(xy …
Andrei D. Polyanin, Valentin F. Zaitsev, Alain Moussiaux, 2001
The graph of y = arccos x is the reflection about the line y = x of the graph of the restricted cosine function, as shown in red in Figure 3(b). EXAMPLE 2 Evaluate each expression. a. cos [ arccos ( − 1 2 )] b. arccos ( cos π 3 ) c. arccos [ cos ( − π 4 ) …
J.
) > jod where 70 := 1 — >/2- V3.
Proof. Observe that the Balancing and Separation theorems still apply. Moreover
…
10
Table of Integrals, Series, and Products/arccos Ё (11 : 1 arccos Ё — (12 — 12 (1 (1 1 2 $ 2 $ 2. (arccos -) (11 1 $(arccos —) — 2 (12 — 12 arccos — — 2$. (1 (1 (1 1 3 1 3 1 2 $ 3. (arccos -) (11 1 $(arccos —) — 3 (12 — 12 (arccos -) — 6$ arccos — Jr 6\/ (12 — 12 (1 (1 (1 (1 2.82 The …
Alan Jeffrey, Daniel Zwillinger, 2000
НОВОСТИ, В КОТОРЫХ ВСТРЕЧАЕТСЯ ТЕРМИН «ARCCOS»
Здесь показано, как национальная и международная пресса использует термин arccos в контексте приведенных ниже новостных статей.Arccos Golf review: Club sensors and iOS app can pinpoint where …
If you play a lot of golf and want to get better, Arccos Golf is a reasonable investment for determining what areas of the game you should work .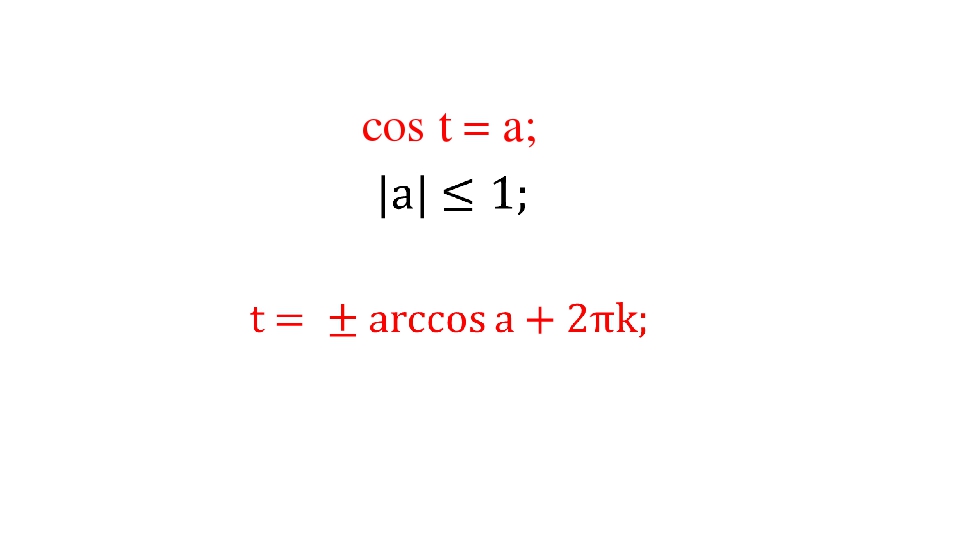
.. «Macworld, Июл 15»
Arccos Golf signs Jamie Sadlowski as brand ambassador
STAMFORD, Conn. — Arccos Golf — maker of the game’s only GPS + Live Shot Tracking + Tour Analytics platform — announces the signing of … «WorldGolf.com, Июн 15»
Still on the front nine, Arccos adds GPS
Arccos CEO Sal Syed on June 23, 2015, at the startup’s offices in Stamford, Conn. Arccos sells sensors in the Apple Store and other retailers … «Greenwich Time, Июн 15»
Arccos Golf GPS
That’s where Arccos Golf comes in with its newest hand-held device that includes advanced GPS capabilities, providing users with precise … «The Desert Sun, Июн 15»
Great golf for Father’s Day: Gadgets, gear and glorious courses
Arccos Golf: Launched last year, Arccos was initially created by clubmaker Callaway, but has captured a lot of attention given its ease of use.
«Globalnews.ca, Июн 15»
A Guide to Father’s Day in Harrisburg
For the serious golfer, Arccos Golf can show off dad’s accomplishments. His friends at the club might not believe he made that hole-in-one, but … «witf.org, Июн 15»
Game Tracker: Overcoming My Golf Game’s Vulnerabilities Through …
Enter the Arccos Golf game tracking system, which runs $400. It consists of a free smartphone (or Apple Watch) app plus 14 sensors that each … «Forbes, Июн 15»
How the Internet of Things is Poised to Shake Up Sports Marketing
One of our clients, Arccos, is addressing golfers’ desire for self-improvement with a set of connected golf club sensors paired to a mobile app, … «SocialTimes, Июн 15»
2015 Father’s Day: Gift ideas for the dad that loves golf
Arccos Golf performance tracking system ($299): If you’ve got a good budget for dad and he spends a lot of time on the course, then Arccos Golf .
.. «Golf News Net, Июн 15»
GPS trackers give golfers a fresh edge
Game Golf and Arccos Golf have produced impressive GPS tracking systems that give the average golfer a chance to see break down stats like … «U-T San Diego, Июн 15»
ССЫЛКИ
« EDUCALINGO. Arccos [онлайн]. Доступно на <https://educalingo.com/ru/dic-en/arccos>. Июн 2021 ».
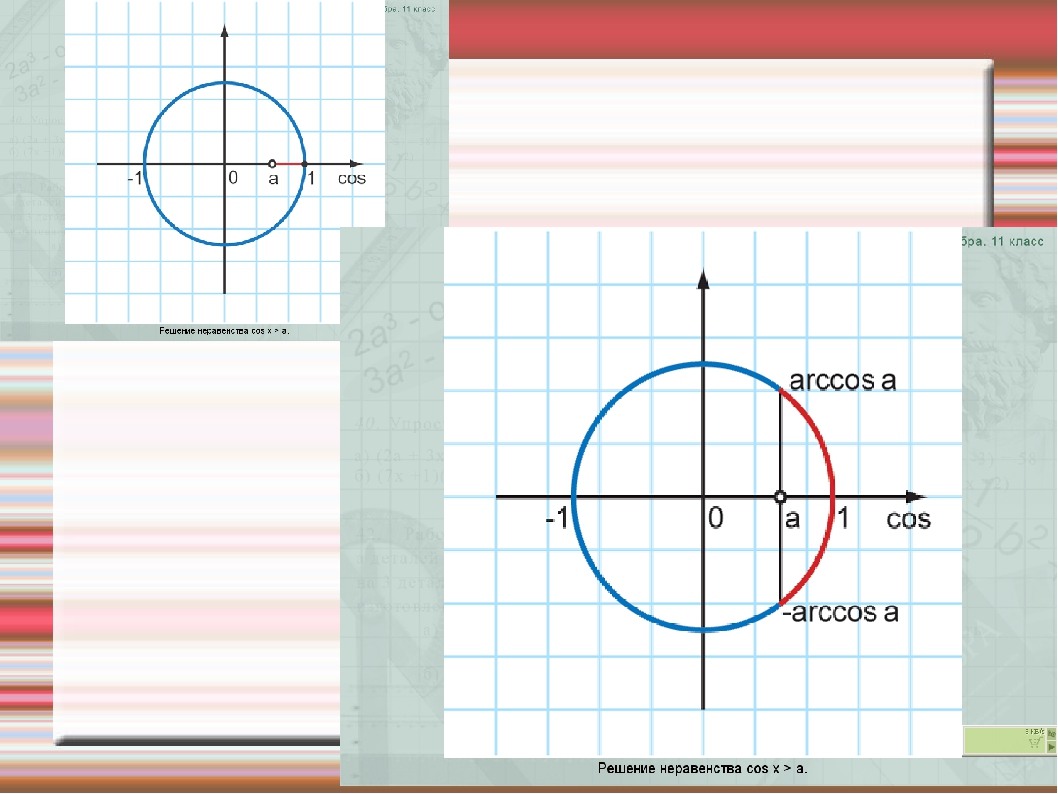
Урок 41. уравнение cos x = a — Алгебра и начала математического анализа — 10 класс
Урок Конспект Дополнительные материалыУравнение cos x = a
Сколько точек пересечения с тригонометрической окружностью имеет прямая x=m в зависимости от значения m:
ПодсказкаВспомните, какой радиус имеет тригонометрическая окружность
Ни одной | Одной | Две |
|---|---|---|
m=-1,2
m=3
m=1,000001
m=2,22
m=-5
m=-1,001001
m=1
m=-1
m=0
m=-0,9999999
m=0,45
m=0,91
Уравнение cos x = a
Выберите из списка решение уравнения
$cosx=\frac{1}{2}$
ПодсказкаВспомните, косинус какого аргумента равен $\frac{1}{2}$
Уравнение cos x = a
Поставьте в соответствие каждому уравнению его решение.
Вспомните формулы решения простейшего тригонометрического уравнения $cos x=а.$
Уравнение cos x = a
Подчеркните верное равенство
- $arccos (-\frac{1}{2})=-\frac{2\pi}{3}$
- $arccos (-\frac{1}{2})= \frac{2\pi}{3}$
- $arccos (-\frac{1}{2})= -\frac{\pi}{3}$
- $arccos (-\frac{1}{2})= \frac{\pi}{3}$
- $arccos (-\frac{1}{2})= \frac{\pi}{3}$
Уравнение cos x = a
Сколько точек на отрезке $ [-\pi; \pi] $имеет уравнение $2 cos (2x) = \sqrt{3}$
ПодсказкаВспомните формулу решения простейшего квадратного уравнения $cos x=a$, затем разделите результат на коэффициент при х
Уравнение cos x = a
Решите уравнение $cos \alpha =-\frac{1}{2}$.
Заполните пропуски в ответе
Ответ: $\alpha = \pm \frac{a \pi}{b}+c\pi k, k \epsilon Z$
ПодсказкаВспомните формулу решения простейшего квадратного уравнения $cos x=a$
Уравнение cos x = a
Расположите значения арккосинусов в порядке возрастания.
ПодсказкаПодумайте, как ведет себя арккосинус при увеличении значений его аргумента
$arccos (\frac{\sqrt{3}}{2})$
$arccos (-\frac{\sqrt{2}}{2})$
$arccos (-\frac{\sqrt{3}}{2})$
Уравнение cos x = a
Выделите цветом верные равенства
ПодсказкаВспомните тождества с арккосинусом
- cos(arccos(−0,4))=−0,4
- arccos(cos2)=2
- cos(arccos2)=2
- arccos(cos(−2))=−2
- cos(arccos(0,2))=0,2
Уравнение cos x = a
Найдите для каждого уравнения количество решений на отрезке $[0; 2π]$.
Вспомните решение простейшего уравнения cos x=a
Ни одного решения | Одно решение | Два решения | Больше двух решений |
|---|---|---|---|
$cosx=1,1$
$(cos x +1)(cos x -2)=0$
$(2cosx -1)(2cosx -3)=0$
$(2cosx +1)(3cos x -2)=0$
Уравнение cos x = a
Решите уравнение $cos (2-3x) = cos (4x -5)$
В ответ запишите наименьший положительный корень.
Вспомните условие равенства косинусов
Уравнение cos x = a
Решите уравнение $(4cos x +1)(2 cos x +3)$
Выберите верный ответ.
ПодсказкаВспомните условие равенства произведения нулю, затем решите простейшие тригонометрические уравнения $cos x=a$
Уравнение cos x = a
Решите уравнение $cos (x^2 -4x + \frac{\pi}{4}) = \frac{1}{2}$
Определите, сколько решений имеет это уравнение при:
ПодсказкаВспомните формулу решения простейшего тригонометрического уравнения, а затем зависимость числа корней квадратного уравнения от его дискриминанта
Уравнение cos x = a
Даны числа
1) $arccos(\frac{1}{4})$
2) $arccos(0,2)$
3) $arccos(\frac{\sqrt5}{12})$
4) $arccos(−0,14)$
5) $arccos(\frac{\sqrt3}{6})$
6) $arccos(−0,4)$
7) $arccos(−\frac{\sqrt2}{3})$
ПодсказкаВспомните, как ведет себя значение арккосинуса при увеличении значения аргумента
Уравнение cos x = a
Найдите для каждого уравнения его наименьшее решение на отрезке $[0;2π]$
ПодсказкаВспомните формулу решения простейшего тригонометрического уравнения $cos x=a$
numpy.
arccos — NumPy v1.20 ManualТригонометрический обратный косинус, поэлементно.
Обратная величина cos , так что если y = cos (x) , то x = arccos (y) .
- Параметры
- x array_like
x — координата на единичной окружности. Для реальных аргументов доменом является [-1, 1].
- из ndarray, None или кортеж из ndarray и None, необязательно
Местоположение, в котором сохраняется результат.Если предусмотрено, оно должно иметь форма, которой транслируются входы. Если не указано или Нет, возвращается только что выделенный массив. Кортеж (возможно только как аргумент ключевого слова) должен иметь длину, равную количеству выходов.
- , где array_like, необязательно
Это условие транслируется по входу. В местах, где Условие равно True, массив out будет установлен на результат ufunc.
В другом месте массив out сохранит свое исходное значение.Обратите внимание, что если неинициализированный массив out создается по умолчанию out = None, местоположения внутри него, где условие False будет оставаться неинициализированным.- ** kwargs
Другие аргументы, содержащие только ключевые слова, см. В ufunc docs.
- Возврат
- угол ndarray
Угол луча, пересекающего единичную окружность в данном x — координата в радианах [0, пи].Это скаляр, если x — скаляр.
В другом месте массив out сохранит свое исходное значение.Обратите внимание, что если неинициализированный массив out создается по умолчанию Банкноты
arccos — многозначная функция: на каждые x приходится бесконечно
много чисел z , таких что cos (z) = x . Соглашение состоит в том, чтобы вернуться
угол z , действительная часть которого лежит в [0, pi] .
Для типов входных данных с действительным знаком arccos всегда возвращает действительный вывод.
Для каждого значения, которое не может быть выражено действительным числом или бесконечностью,
он дает нан и устанавливает флаг ошибки с плавающей запятой недопустимый .-1.
Список литературы
М. Абрамовиц, И.А. Стегун, “Справочник по математическим функциям”, 10-е издание, 1964 г., с. 79. http://www.math.sfu.ca/~cbm/aands/
Примеры
Мы ожидаем, что arccos 1 будет 0, а -1 будет пи:
>>> np.arccos ([1, -1]) массив ([0., 3.14159265])
Площадь участка:
>>> импортировать matplotlib.pyplot как plt
>>> x = np.linspace (-1, 1, число = 100)
>>> plt.plot (x, np.arccos (x))
>>> plt.axis ('плотно')
>>> plt.show ()
математических слов: обратный косинус
обратный
Косинус
cos -1
Cos -1
arccos
Arccos
функция, обратная косинусу.
Основная идея : Найти cos -1 (½),
мы спрашиваем «что
угол имеет косинус, равный ½? »
ответ 60 °.
В результате мы говорим cos -1 (½)
= 60 °.
В радианах это cos -1 (½).
= π / 3.
Подробнее : На самом деле существует много углов, у которых косинус равен ½. Мы действительно спрашиваем, «какой самый простой, самый основной угол, который косинус равен ½? «Как и прежде, ответ 60 °. Таким образом, cos -1 (½) = 60 ° или cos -1 (½) = π / 3.
Подробности : Что такое cos -1 (–½)? Мы выбираем 120 °, –120 °, 240 °, или под другим углом? Ответ — 120 °.Обратным косинусом выбираем угол в верхней половине блока. круг. Таким образом, cos -1 (–½) = 120 ° или cos -1 (–½) = 2π / 3.
В другими словами, диапазон cos -1 равен ограничивается [0, 180 °] или [0, π].
Примечание: arccos означает «арккосинус»,
или радианная мера дуги на окружности, соответствующая
заданное значение косинуса.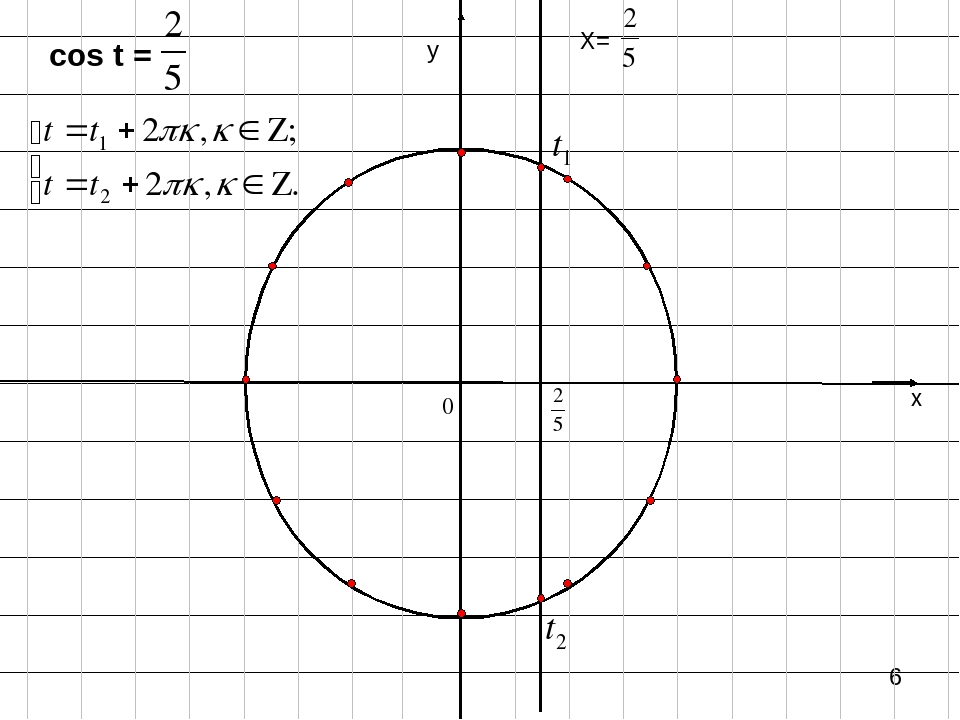
Техническое примечание : Поскольку ни одна из шести триггерных функций не синусоида, косинус, тангенс, косеканс, секанс и котангенс взаимно однозначны, их инверсии не являются функциями.Каждая триггерная функция может иметь свой домен ограничен, однако, чтобы сделать его инверсию функцией. Некоторые математики пишут эти ограниченные триггерные функции и их переворачивается с заглавной буквы (например, Cos или Cos -1 ). Однако большинство математиков не следуют этой практике. Этот веб-сайт не делает различий между заглавными и не заглавными буквами триггерные функции.
См. также
обратный тригонометрия, обратная триггерные функции, интервальное обозначение
7.
Обратные тригонометрические функцииМ. Борна
В разделе Тригонометрические функции любого угла мы решали вопросы типа
«Найдите 2 угла, косинус которых равен 0,7.»
В этом вопросе использовалась кнопка cos -1 на наших калькуляторах. Мы нашли cos -1 0,7, а затем рассмотрели квадранты, в которых косинус был положительным. Помните, что число, которое мы получаем при нахождении функции обратного косинуса, cos -1 , представляет собой угол .-1`, когда мы говорим об обратной косинусной функции.]
Давайте сначала вспомним график `y = cos \ x` (который мы встречали в Graph of y = a cos x), чтобы мы могли видеть, откуда берется график` y = arccos \ x`.
0.5ππ-0.5π0.511.522.5-0.5-1xyГрафик y = cos x .
Теперь мы выбираем часть этого графика от x = 0 до x = π , показанную здесь заштрихованной частью:
0.
5ππ-0.5π0.511.522.53-0.5-1xyГрафик y = cos x с заштрихованной частью `0
График , обратный косинуса x , находится путем отражения выбранной части графика cos x через линию y = x.
0.5ππ-0.5π0.511.522.53-0.5-1xyy = xГрафик y = cos x и линия `y = x`.
Теперь мы отразим каждую точку на этой части кривой cos x через линию y = x (я показал только несколько отражаемых типичных точек).
0,5ππ-0,5π123-1xy (π, −1) (- 1, π) 0,5πТочки отражения на кривой проходят через линию `y = x`.
Результатом является график `y = arccos x`:
См. Анимацию этого процесса здесь: Графические анимации обратной тригонометрической функции.
Вот и все, что касается графика — он не выходит за рамки того, что вы видите здесь. (Если бы это было так, было бы несколько значений y для каждого значения x , и тогда у нас больше не было бы функции.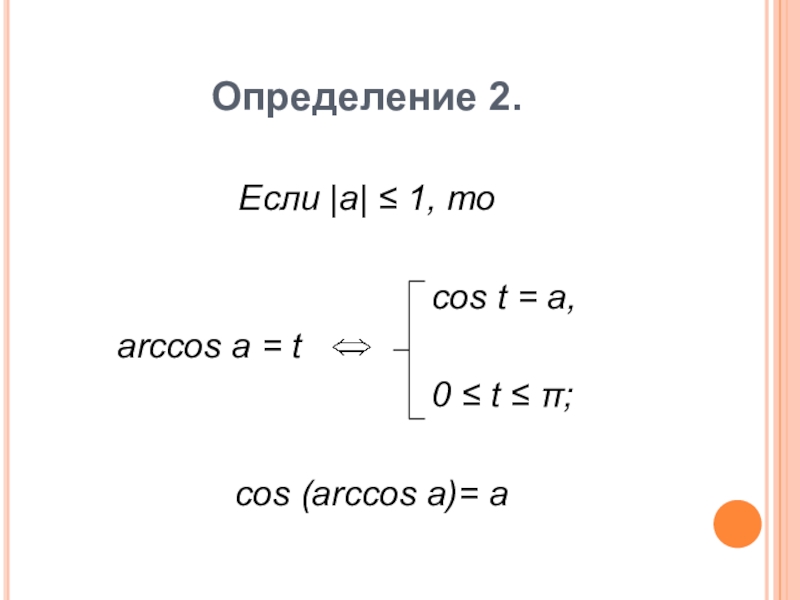
) Я указал «начальную» и «конечную» точки, `(-1 , pi) `и` (1,0) `с точками.
ПРИМЕЧАНИЕ 1: Метки осей также были отражены. То есть теперь есть обычные числа по оси x и кратные 0.5pi по оси y .
ПРИМЕЧАНИЕ 2: Вы также увидите «arccos», записанное как «« acos »« », особенно в компьютерном программировании.
Область (возможные значения x ) для arccos x — это
-1 ≤ x ≤ 1
Диапазон (из значений y для графика) для arccos x составляет
0 ≤ arccos x ≤ π
Функция обратной синусоиды (arcsin)
Мы определяем функцию обратного синуса как
`y = arcsin \ x` для` -pi / 2 <= y <= pi / 2`
, где y — угол, синус которого равен x .Это означает, что
`x = sin y`
График
y = arcsin x Давайте сначала посмотрим на график y = sin x , а затем построим кривую y = arcsin x .
График y = sin x , с выделенной частью от «-pi / 2» до «pi / 2».
Как мы делали ранее, если мы отразим указанную часть y = sin x (часть между `x = -pi / 2` и` x = pi / 2`) через линию y = x , получаем график y = arcsin x :
Еще раз, что вы видите, то и получаете.График не выходит за указанные границы x и y . Я обозначил точки «начало» и «конец».
Область (возможные значения x ) для arcsin x — это
-1 ≤ x ≤ 1
Диапазон (из значений y для графика) для arcsin x составляет
`-π / 2 ≤ arcsin \ x ≤ π / 2`
Посмотрите анимацию этого процесса здесь:
Обратные тригонометрические функции графической анимации.
Функция обратной касательной (arctan)
Напоминаем, что вот график y = tan x , который мы встречали ранее на графиках tan, cot, sec и csc.
Отражая заштрихованную часть графика (от `x = -pi / 2` до` pi / 2`) в строке y = x , получаем график y = arctan x :
График `y =» arctan «\ x`.
На этот раз график выходит за пределы того, что вы видите, как в отрицательном, так и в положительном направлениях x , и он не пересекает пунктирные линии (асимптоты в `y = -pi / 2` и` y = pi / 2`).
Область (возможные значения x ) для arctan x составляет
Все значения x
Диапазон (из значений y для графика) для arctan x составляет
`-π / 2
Числовые примеры arcsin, arccos и arctan
Используя калькулятор в режиме радиан, получаем:
arcsin 0,6294 = sin -1 (0.6294) = 0,6808
arcsin (-0,1568) = sin -1 (-0,1568) = -0,1574
arccos (-0,8026) = cos -1 (-0,8026) = 2,5024
арктан (-1,9268) = загар -1 (-1,9268) = -1,0921
Обратите внимание, что калькулятор выдаст значения
которые находятся в пределах определенного диапазона для каждой функции.
Ответы в каждом случае: углов (в радианах).
Функция обратной секущей (угл. Сек.)
График y = sec x , который мы встречали ранее на графиках tan, cot, sec и csc:
График y = arcsec x получен путем отражения заштрихованной части приведенной выше кривой в линии y = x :
:График `y =» arcsec «\ x`.
Кривая определяется вне участка между -1 и 1. Я обозначил «начальные» точки `(-1, pi)` и `(1,0)` точками.
Домен для «arc» sec \ x` равен
Все значения x , кроме -1 < x <1
Диапазон угловых секунд x составляет
0 ≤ arcsec x ≤ π , «arcsec» \ x ≠ π / 2`
Обратная функция косеканса (arccsc)
График y = csc x , который мы встречали ранее на графиках tan, cot, sec и csc, выглядит так:
Обратите внимание, что нет значений y между -1 и 1.
Теперь для графика y = arccsc x , который мы получаем путем отражения заштрихованной части кривой выше в линии y = x :
График `y =» arccsc «\ x`.
График не определен между -1 и 1, но простирается оттуда в отрицательном и положительном направлениях x .
Домен arccsc x равен
Все значения x , кроме -1 < x <1
Диапазон arccsc x равен
`-π / 2 ≤» arc «csc \ x ≤ π / 2,` arccsc x ≠ 0
Функция обратного котангенса (arccot)
График y = cot x , который мы встречали ранее на графиках tan, cot, sec и csc, выглядит следующим образом:
Взяв выделенную часть, как указано выше, и отразив ее в линии y = x , мы получим график y = arccot x :
График `y =» arccot »\ x`.
График простирается в отрицательном и положительном направлениях x (он не останавливается на -8 и 8, как показано на графике).
Итак, домен для arccot x :
Все значения x
Диапазон arccot x равен
0
x < π
Альтернативный вид
Некоторые учебники по математике (и некоторые уважаемые математические программы, например,грамм. Mathematica) рассматривают следующее как область y = детская кроватка x , которую следует использовать:
Это дало бы следующее при отражении в строке y = x :
График `y =» arccot »\ x`; альтернативный взгляд.
И снова график расширяется в отрицательном и положительном направлениях x .
Домен для arccot x также будет:
Все значения x
Используя эту версию, диапазон arccot x будет:
`-π / 2 арккота x ≠ 0)
См.
Обсуждение этого вопроса по адресу:
Какой правильный график arccot x ?.(-1) (- 1) = — pi / 4`
`cos (-pi / 4) = 1 / 2sqrt (2)`
Простой калькулятор Arccos | Калькулятор обратного косинуса Cos-1
Калькулятор Arccos:
Воспользуйтесь нашим онлайн-калькулятором Arccos и калькулятором обратного косинуса (калькулятор cos-1 ).
Рекламные объявленияЕсли вы хотите преобразовать результат в другого ангела, используйте наш онлайн-конвертер углов.
Cos
−1 ( x ), пример ArccosПример 1: найти точное значение cos [arccos (-0.5)]
Если косинус 120 ° равен -0,5, что дает нам cos (120 °) = — 0,5, тогда cos [arccos (-0,5)] = — 0,5.
, но мы можем избежать выполнения всех этих вычислений, просто используя свойства cos-1 (arccos), так как -1≤-0,5≤1, затем cos [arccos (-0,5)] = — 0,5.
Пример 2: найти точное значение для cos [arccos (2/3)]
, мы можем просто использовать наш калькулятор arccos, который даст нам arccos (2/3) = 0,841068671 рад, затем cos (0,841068671) = 2/3
, но мы можем избежать выполнения всех этих вычислений, просто используя свойства cos-1 (arccos), мы преобразуем, поскольку -1≤-2 / 3≤1, затем cos [arccos (2/3)] = 2/3.
Cos
−1 ( x ), Arccos Определение:Определение Arccos предоставлено википедией:
Калькулятор обратного cosarccos (тригонометрия), обратная тригонометрическая функция косинуса.
В математике обратные тригонометрические функции (иногда называемые циклометрическими функциями [1]) являются обратными функциями тригонометрических функций (с подходящими ограничениями). В частности, они являются обратными функциями синуса, косинуса, тангенса, котангенса, секанса и косеканса и используются для получения угла из любого из тригонометрических соотношений угла.Обратные тригонометрические функции широко используются в инженерии, навигации, физике и геометрии.
Арккосинус x определяется как обратная тригонометрическая функция косинуса, когда -1≤x≤1.
Когда:
cos y = x.
Тогда арккосинус x равен тригонометрической функции обратного косинуса x, которая равна y:
arccos x = cos -1 x = y.
Cos −1 ( x ), ArccosDefinition.Таблица Arccos (cos-1):
Таблица Arccos (cos-1).
x arccos (x) arccos (x) Угловые единицы рад), выраженные в пи (°) в градусах arccos -1 π 180 ° arccos -√3 / 2 5π / 6 150 ° arccos -√2 / 2 3π / 4 135 ° arccos -1/2 2π / 3 120 ° arccos 0 π / 2 908 ° arccos 1/2 π / 3 60 ° arccos √2 / 2 π / 4 45 ° arccos √3 / 2 30 ° 909 30 arccos 1 0 ′ 0 ° Подробнее Калькулятор
c ++ — Быстрый алгоритм Arc Cos?
У меня есть своя. Это довольно точно и быстро. Он основан на теореме, которую я построил вокруг сходимости четвертой степени. Это действительно интересно, и вы можете увидеть уравнение и то, как быстро оно может привести к сходимости моего естественного логарифмического приближения, здесь: https://www.desmos.com/calculator/yb04qt8jx4
Вот мой код arccos:
функция acos (x) локальный a = 1,43 + 0,59 * x a = (a + (2 + 2 * x) / a) / 2 местный b = 1.65-1,41 * х b = (b + (2-2 * x) / b) / 2 местный c = 0,88-0,77 * x c = (c + (2-a) / c) / 2 return (8 * (c + (2-a) / c) - (b + (2-2 * x) / b)) / 6 конецПо большей части это просто приближение квадратного корня. Он также работает очень хорошо, если только вы не подойдете слишком близко к извлечению квадратного корня из 0. Он имеет среднюю ошибку (исключая x = от 0,99 до 1), равную 0,0003.
Если вас не слишком заботит точность, вы можете просто сделать одну итерацию на квадратный корень, что по-прежнему должно держать вас где-то в диапазоне 0,0162 или что-то в том смысле, что касается точности:
функция acos (x) локальный a = 1,43 + 0,59 * x a = (a + (2 + 2 * x) / a) / 2 местный b = 1,65-1,41 * x b = (b + (2-2 * x) / b) / 2 местный c = 0,88-0,77 * x c = (c + (2-a) / c) / 2 возврат 8/3 * c-b / 3 конецЕсли вас это устраивает, вы можете использовать уже существующий код извлечения квадратного корня.Это избавит от уравнения, которое немного сумасшедшее при x = 1:
.функция acos (x) локальный a = math.Честно говоря, если у вас действительно мало времени, помните, что вы можете линеаризовать arccos в 3,14159-1,57079x и просто сделать:
функция acos (x) возврат 1.57079-1.57079 * x конецВ любом случае, если вы хотите увидеть список моих приближенных уравнений arccos, вы можете перейти на https: // www.desmos.com/calculator/tcaty2sv8l Я знаю, что мои приближения не самые лучшие для некоторых вещей, но если вы делаете что-то, где мои приближения были бы полезны, используйте их, но постарайтесь отдать мне должное.
КалькуляторArccos. Поиск обратного косинуса
Добро пожаловать в калькулятор arccos, также известный как калькулятор обратного косинуса. Благодаря нашему инструменту вы можете быстро найти arccos — что, как ни удивительно, является основным применением этого калькулятора.
Что является обратным к косинусу (arccos)?
Arccos — это функция, обратная тригонометрической функции, а именно обратная функция косинуса. Однако, поскольку тригонометрические функции являются периодическими, тогда, в строгом смысле, они не могут быть инвертированы .Мы можем решить эту проблему, выбрав интервал, в котором основная функция является монотонной. Вы можете выбрать много разных диапазонов, но для косинуса обычно выбирается [0, π] . Этот диапазон называется набором основных значений .
Сокращение Определение Домен arccos x
для реального результатаДиапазон обычных
основных значенийarccos (x)
cos -1 x,
acosх = соз (у) -1 ≤ х ≤ 1 0 ≤ y ≤ π
0 ° ≤ y ≤ 180 °Arccos (x) — наиболее часто используемое обозначение, поскольку cos -1 x может вводить в заблуждение — помните, что обратный косинус — это не то же самое, что обратная величина функции (другими словами, возведение в степень — 1):
cos -1 x ≠ 1 / cos (x)График обратного косинуса
Функция f имеет обратную функцию тогда и только тогда, когда f является взаимно однозначной функцией.
cos (x) = cos (x + 2πn), для каждого целогоnЧто же тогда делать?
Как указано в предыдущем абзаце, нам нужно ограничить область определения базовой периодической косинусной функции. Таким образом, поскольку косинус всегда находится в диапазоне [-1,1], и мы выбираем область, [0, π], свойства функции обратного косинуса будут обратными:
Область обратного косинуса x для реального результата: [-1,1]
Диапазон обратного косинуса обычного главного значения: [0, π]
В таблице ниже вы найдете график обратного косинуса, а также некоторые часто используемые значения arccos:
x arccos (x) График ° рад -1 180 ° π -√3 / 2 150 ° 5π / 6 -√2 / 2 135 ° 3π / 4 -1/2 120 ° 2π / 3 0 90 ° π / 2 1/2 60 ° π / 3 √2 / 2 45 ° π / 4 √3 / 2 30 ° π / 6 1 0 ° 0 Хотите знать, откуда взялся этот график обратного косинуса? Он просто создается путем отражения графика cos x через линию y = x (не забывайте о наших доменных ограничениях!):
Обратный косинус — какое мне дело? Некоторые малоизвестные приложения arccos
Вы можете подумать, что arccos — еще один бесполезный термин из тригонометрии, но мы хотим убедить вас, что это не так! Функция обратного косинуса действительно полезна для решения многих научных и реальных задач (круто, не правда ли?):
I Наука
Математика:
- 📐 Решаем треугольник по закону косинусов.
Физика:
Химия:
- 🧪 Arccos полезен для оценки оптимальных валентных углов многоатомных молекул, таких как, например, H 2 O или CH 4
II Примеры из реальной жизни
- 🏠 Расчет угла наклона крыши или угла наклона лестницы (хотя, в зависимости от того, какие размеры указаны, могут также пригодиться калькуляторы обратного синуса или тангенса)
- ♿ Проектирование пандуса для инвалидов или колясок.Обратный косинус будет чрезвычайно полезен, если вы знаете длину пандуса и доступное расстояние по горизонтали.
- 🖥️ Даже выбирая эргономичное положение на работе ! Если вы хотите правильно настроить свою рабочую станцию, вам необходимо знать оптимальную высоту стола или высоту стоячего стола, но, что касается расположения монитора, с помощью этого калькулятора arccos гораздо проще определить угол наклона или угол обзора.
Теперь вы уверены? Не ждите больше, воспользуйтесь нашим калькулятором обратного косинуса, чтобы решить (почти все) ваши проблемы!
Arcsin, Arccos, Arctan — Тригонометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
.
Калькулятор Arcos cos-1
Проблема, однако, в том, что при 0,99 он начинает срать, а при x = 1 разница в точности становится 0,05. Конечно, это можно решить, выполнив больше итераций с квадратными корнями (lol nope) или, что угодно, например, если x> 0.99 затем используют другой набор линеаризации квадратного корня, но это делает код длинным и некрасивым.
sqrt (2 + 2 * x)
локальный b = math.sqrt (2-2 * x)
локальный c = math.sqrt (2-a)
возврат 8/3 * d-b / 3
конец
Однако для тех из вас, кто хочет узнать больше, мы подготовили небольшую статью, объясняющую , что такое обратный косинус , сопровождаемую таблицей и графиком обратного косинуса .Кроме того, если вы немного неохотно или запутались, перейдите к разделу о приложениях arccos , чтобы узнать, что общего у обратного косинуса с физикой, химией или даже с эргономикой строительства и работы!
Вся функция косинуса не является взаимно однозначной, поскольку
Если вы знаете три стороны треугольника и хотите найти любой из углов треугольника, вам нужно использовать arccos.
org.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.