Знаки тригонометрических функций по четвертям — примеры определения
При решении задач определенного типа по математике необходимо знать знаки тригонометрических функций по четвертям. Этот прием нужен для правильного вычисления или упрощения какого-либо выражения и так далее. Существует универсальный способ, но перед тем, как им воспользоваться, следует изучить основные понятия и формулы.
Содержание
- Общая информация
- Виды углов
- Смысл функций
- Определение знака
- Дополнительные сведения
- Построение окружности
- Использование готового инструмента
- Примеры решения задач
- Положительное значение
- Свыше 2ПИ
Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.
Специалисты рекомендуют для понимания материала получить базовые знания об углах и основных тригонометрических функциях. Следует применять принцип «от простого к сложному», поскольку нужно учитывать физиологические особенности головного мозга.
Виды углов
Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов. Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.
Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:
Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:
Последний случай встречается очень часто в различных задачах, в которых следует вычислить определенное значение, упростить тригонометрическое выражение или использовать формулы приведения, а также найти разность между функциями.
Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%).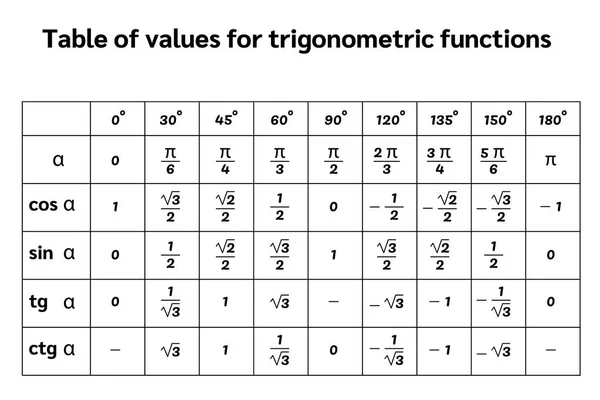 Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:
Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:
Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.
Смысл функций
Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.
С их помощью можно описывать законы изменения различных периодических величин.
Для определения функции необходимо представить прямоугольный треугольник. Его стороны называются катетами и гипотенузой. Угол между двумя катетами является прямым, то есть он равен 90 градусам.
Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.
Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.
Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.
Определение знака
Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.
Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.
Дополнительные сведения
Для определения знака применяется обыкновенная система координат с двумя осями. 2 (c, a и b — гипотенуза и два катета соответственно).
2 (c, a и b — гипотенуза и два катета соответственно).
Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180. Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).
Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).
Построение окружности
Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».
Рекомендуется чертить произвольную окружность.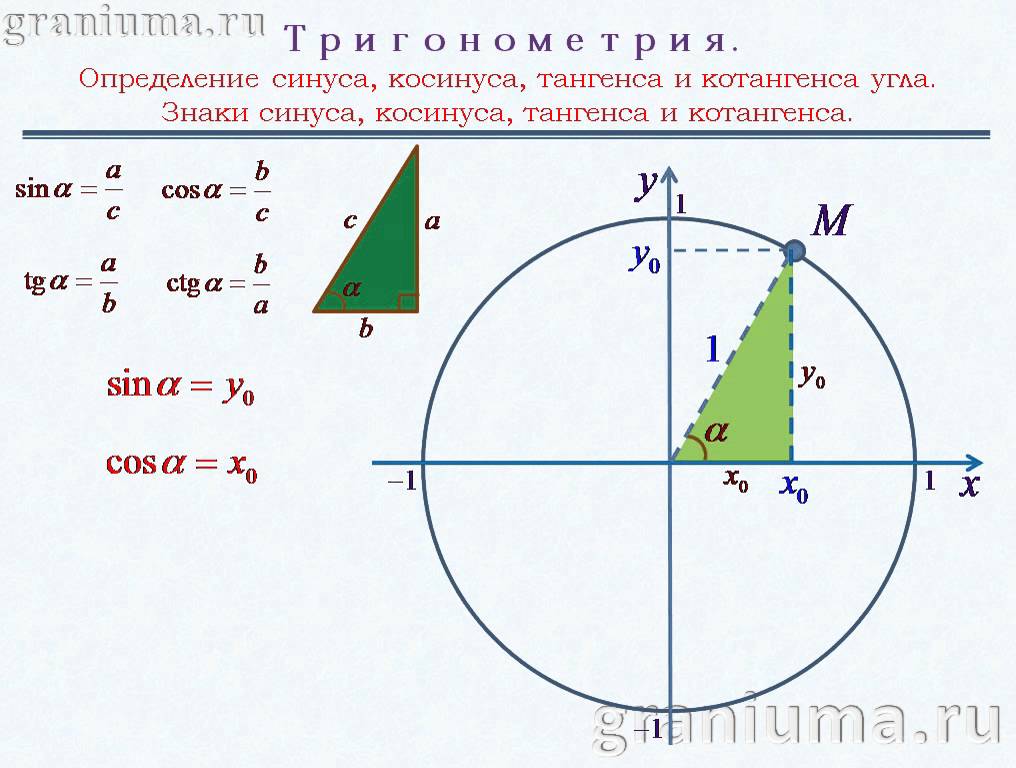 Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:

Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям. Рекомендуется отметить для удобства значения углов в радианах рядом с точками пересечения следующим образом:
Знаки других функций (tg и ctg) определяются из отношения sin к cos или наоборот. Можно также составить специальную табличку с уже готовыми значками функций. Этот прием еще больше оптимизирует работу.
Использование готового инструмента
Однако необязательно самостоятельно чертить единичную окружность для определения знаков. Можно воспользоваться уже готовыми вариантами (например, рис. 1).
Рисунок 1. Пример тригонометрического круга.
Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:
С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:
Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.
Примеры решения задач
Задачи на нахождение знака попадаются редко, поскольку они являются довольно простыми. Рекомендуется потренироваться в нахождении знака. Для этого можно придумать углы любой меры (радианной или градусной).
После решения следует проверить результат, подставив значения в тригонометрический калькулятор. Его можно найти в стандартных программах операционных систем Windows, Linux и Mac (расширенная версия инструмента). Кроме того, следует обратить внимание на то, что линия должна проходить по направлению, которое зависит от знака. Необходимо также учитывать четность или нечетность, а также периодичность каждой функции.
Положительное значение
Для изготовления детали следует рассчитать значение тригонометрических функций угла 225 градусов. В этой задаче ничего не сказано про знаки функций. Из-за этого и делают ошибки. Решение следует разбить на несколько шагов. Использование такого метода (дробление задачи на подзадачи) позволяет избежать неверных вычислений. Каждый из пунктов можно легко проверить. Алгоритм нахождения ответов имеет следующий вид:
Решение следует разбить на несколько шагов. Использование такого метода (дробление задачи на подзадачи) позволяет избежать неверных вычислений. Каждый из пунктов можно легко проверить. Алгоритм нахождения ответов имеет следующий вид:
После расчетов нужно выполнить проверку знаков. В III четверти больше нуля только тангенс и котангенс. Однако бывают случаи, когда значение градусной меры угла превышает 360.
Свыше 2ПИ
Существует определенный тип задач, в которых величина градусной меры угла свыше 360 градусов. Например, следует вычислить значения тригонометрических функций угла -26ПИ/6.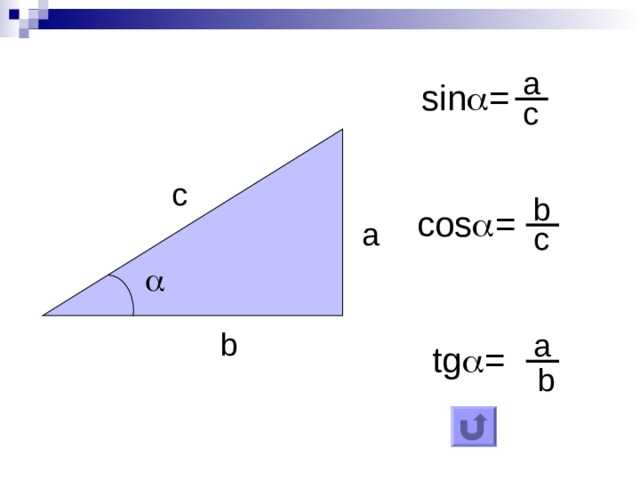 Решается она следующим образом:
Решается она следующим образом:
Во втором, четвертом и пятом пунктах функции являются нечетными. Если посмотреть на график, то движение осуществляется по часовой стрелке, поскольку угол является отрицательным числом. Функция косинуса является четной. Ее числовое значение — положительная величина. Последним этапом считается проверка знаков. Угол находится в IV четверти. Значения функций совпадают.
Таким образом, при решении задач по тригонометрии следует применять тригонометрическую окружность, с помощью которой можно безошибочно определять знак функции.
Предыдущая
МатематикаРациональные числа в математике
Следующая
МатематикаРешение кубических уравнений — методы и примеры вычислений
Формулы тригонометрии и простейшие уравнения
На этой странице вы узнаете- Как лошадь может помочь в тригонометрии?
- Какие знаки принимают функции в разных четвертях?
- Что за 6 секретов преобразования тригонометрических выражений помогут нам?
Любые формулы достаточно коварны. {2} \alpha}\)
{2} \alpha}\)
А что делать, если угол в тригонометрической функции отложен от вертикальной или горизонтальной оси, например, \(cos (x + \frac{\pi}{2})\) или sin(x + π)?
Для всех таких записей существуют специальные формулы, их называют формулами приведения. Но запомнить их все достаточно сложно. Поэтому рассмотрим правило, которое поможет вам упростить решение и избавиться от известного слагаемого в угле тригонометрической функции.
| Как лошадь может помочь в тригонометрии? Правило лошади |
Применив правило лошади, нужно обязательно определить знак новой функции от х. Её знак совпадает со знаком изначальной функции.
Нумерация четвертей на окружности идет по часовой стрелке.
Какие знаки принимают функции в разных четвертях?
Теперь давайте рассмотрим на примере применение данного правила:
\(tg(x + \frac{3 \pi}{2})\)
- Применим правило лошади и узнаем, меняется ли функция на противоположную.
\(\frac{3 \pi}{2}\) находится на горизонтальной оси, значит лошадь кивает, и функция tg меняется на кофункцию ctg.
- Разберемся со знаком.
Так как tg в 4-ой четверти отрицательный, значит перед ctg ставим минус и получим
\(tg(x + \frac{3 \pi}{2}) = -ctg\:x\)
| Что за 6 секретов преобразования тригонометрических выражений помогут нам? Также существуют и другие тригонометрические формулы: 1) Формулы отрицательных углов: 2) Синус, косинус, тангенс и котангенс двойного угла: 3) Формулы сложения и вычитания углов: 4) Формулы понижения степени: 5) Формулы суммы и разности синусов и косинусов: 6) Произведение синусов и косинусов: |
Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.
Чтобы решить такое тригонометрическое уравнение, нужно воспользоваться тригонометрической окружностью, найти значение тригонометрической функции на оси этой функции и записать значения точек с периодом, так как данные функции периодические.
Для этого, возможно, потребуется прочитать статью «Тригонометрическая окружность и графики функций».
Рассмотрим решение таких уравнений на примерах.
Пример 1:
\(cos\:x = -\frac{1}{2}\)
Найдём на тригонометрической окружности точки, для которых значение косинуса равно \(-\frac{1}{2}\)
На окружности есть две таких точки. При этом вторую точку можно отложить на отрицательном направлении, тогда решения можно записать следующим образом:
\(x = \pm \frac{2 \pi}{3} + 2 \pi k, k \in Z\)
Важно: обязательно нужно прописывать период, так как точки на данных местах, находящиеся на всех витках спирали, будут иметь такое значение косинуса.
Пример 2:
\(sin\:x = \frac{1}{2}\)
Проведем перпендикулярную к оси синусов линию через значение \(\frac{1}{2}\). Запишем эти две точки в виде совокупности.
Запишем эти две точки в виде совокупности.
Пример 3:
tg x = 1
Найдем нужное значение на оси тангенсов. Проведем линию и заметим, что в ответ должны идти две диаметрально противоположные точки. Следовательно, можно записать начальную точку, но с периодом в половину окружности, то есть πk, где k ∈ Z
\(x = \frac{\pi}{4} + \pi k, k \in Z\)
Пример 4:
\(ctg\:x = \sqrt{3}\)
Найдем \(\sqrt{3}\) на оси котангенсов и проведём прямую, найденные точки будут диаметрально противоположными. Поэтому запишем первую точку с периодом в половину окружности.
\(x = \frac{\pi}{6} + \pi k, k \in Z\)
| Алгоритм решения простейших тригонометрических уравнений: 1) Найти значение тригонометрической функции на оси этой функции на тригонометрической окружности. 2) Отметить точки. 3) Записать точки. |
- sin2x + cos2x = 1 — основное тригонометрическое тождество.

- Формулы приведения применяются, если угол в тригонометрической функции отложен от вертикальной или горизонтальной оси.
- Функция меняется на кофункцию в формулах приведения, если угол отложен от вертикальной оси.
- Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.
Задание 1.
Чему равно sin(x + π)?
- sin x
- -sin x
- 1
- cos x
Задание 2.
Чему равно \(ctg(x + \frac{\pi}{2})\)?
- tg x
- ctg x
- — ctg x
- — tg x
Задание 3.
Чему равно tg(-2x — π)?
- 2x
- 0
- -tg(2x)
- tg(2x)
Задание 4.
Решите уравнение \(sin(x + \frac{3 \pi}{2}) = 1\)
- x = π + 2πk, k ∈ Z
- x = π + πk, k ∈ Z
- x = 2πk, k ∈ Z
- x = -π + 2πk, k ∈ Z
Задание 5.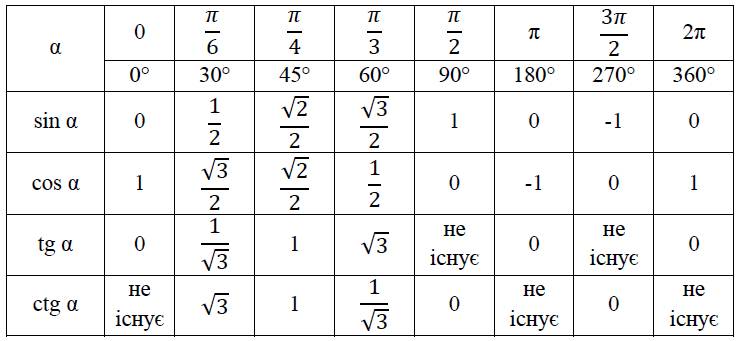
Решите уравнение cos (2x) = 1
- x = -π + πk, k ∈ Z
- x = 2πk, k ∈ Z
- x = πk, k ∈ Z
- x = -π + 2πk, k ∈ Z
Ответы: 1. — 2; 2. — 4; 3. — 3; 4. — 1; 5. — 3
Знаки тригонометрических функций — определение с помощью круга
Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.
Специалисты рекомендуют для понимания материала получить базовые знания об углах и основных тригонометрических функциях.
Следует применять принцип «от простого к сложному», поскольку нужно учитывать физиологические особенности головного мозга.
Виды углов
Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов. Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.
Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:
- При х < 90 угол считается острым.
- Если х = 90, то является прямым.
- В случае, когда выполняется неравенство, он считается тупым: 90 < x < 180.
- Развернутый: х = 180.

- Выпуклый: 180 < x < 360.
- Полный: х = 360.
- Свыше 360: x > 360.
Последний случай встречается очень часто в различных задачах, в которых следует вычислить определенное значение, упростить тригонометрическое выражение или использовать формулы приведения, а также найти разность между функциями.
Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:
- В радианы: P = (a * ПИ) / 180.

- В градусы: а = (P * 180) / ПИ.
Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.
Смысл функций
Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.
Для определения функции необходимо представить прямоугольный треугольник.
Его стороны называются катетами и гипотенузой. Угол между двумя катетами является прямым, то есть он равен 90 градусам.
Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.
Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.
Определение знака
Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.
Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.
Дополнительные сведения
Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». 2 (c, a и b — гипотенуза и два катета соответственно).
2 (c, a и b — гипотенуза и два катета соответственно).
Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180. Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).
Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).
Построение окружности
Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».
Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
- Координаты заключаются в круглые скобки и разделяются «;».
- На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).
Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:
- Значения по x и y больше 0 соответствуют первой четверти (I).
- II: x<0 и y>0.

- III: x<0 и y<0.
- IV: x>0 и y<0.
Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям.
- 0 и 2ПИ (0 и 360 градусов) — (1;0).
- ПИ/2 (90) — (0;1).
- 3ПИ/2 (270) — (1;0).
Знаки других функций (tg и ctg) определяются из отношения sin к cos или наоборот. Можно также составить специальную табличку с уже готовыми значками функций. Этот прием еще больше оптимизирует работу.
Использование готового инструмента
Однако необязательно самостоятельно чертить единичную окружность для определения знаков.
Рисунок 1. Пример тригонометрического круга.
Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:
- cos(-a) = cos(a).
- sin(-a) = -sin(a).
- tg(-a) = -tg(a).
- ctg(-a) = -ctg(a).
С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:
- Определить четверть, в которой находится угол: 240 = 4ПИ/3 соответствует III четверти.
- В III четверти величина функции принимает только отрицательные значения.

- Вычислить: cos(4ПИ/3) = — 1/2.
Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.
Примеры решения задач
Задачи на нахождение знака попадаются редко, поскольку они являются довольно простыми. Рекомендуется потренироваться в нахождении знака. Для этого можно придумать углы любой меры (радианной или градусной).
После решения следует проверить результат, подставив значения в тригонометрический калькулятор. Его можно найти в стандартных программах операционных систем Windows, Linux и Mac (расширенная версия инструмента). Кроме того, следует обратить внимание на то, что линия должна проходить по направлению, которое зависит от знака. Необходимо также учитывать четность или нечетность, а также периодичность каждой функции.
Положительное значение
Для изготовления детали следует рассчитать значение тригонометрических функций угла 225 градусов. В этой задаче ничего не сказано про знаки функций. Из-за этого и делают ошибки. Решение следует разбить на несколько шагов. Использование такого метода (дробление задачи на подзадачи) позволяет избежать неверных вычислений. Каждый из пунктов можно легко проверить. Алгоритм нахождения ответов имеет следующий вид:
- Перевод градусной меры в радианную: 5ПИ/4.
- Значение находится в III четверти, следовательно: sin<0, cos<0, tg>0 и ctg>0.
- -sin(ПИ + ПИ/4) = -sin(ПИ/4) = -cos(ПИ/4) = -sqrt(2)/2.
- tg(ПИ/4) = ctg(ПИ/4) = -sin(ПИ/4) / -cos(ПИ/4) = 1.
После расчетов нужно выполнить проверку знаков. В III четверти больше нуля только тангенс и котангенс. Однако бывают случаи, когда значение градусной меры угла превышает 360.
youtube.com/embed/DIIGMFHypN0″>Свыше 2ПИ
Существует определенный тип задач, в которых величина градусной меры угла свыше 360 градусов. Например, следует вычислить значения тригонометрических функций угла -26ПИ/6. Решается она следующим образом:
- Следует выделить целую часть из -26ПИ/6 и привести к удобному виду: 26/6 = 4 + 2/6 = 4 + 1/3. Угол находится в IV четверти (движение по часовой стрелке).
- -sin(4ПИ + ПИ/3) = -sin(ПИ/3) = — sqrt(3)/2.
- cos(ПИ/3) = 1/2.
- -tg(ПИ/3) = — sqrt(3).
- -сtg(ПИ/3) = — 1/sqrt(3).
Во втором, четвертом и пятом пунктах функции являются нечетными. Если посмотреть на график, то движение осуществляется по часовой стрелке, поскольку угол является отрицательным числом. Функция косинуса является четной. Ее числовое значение — положительная величина. Последним этапом считается проверка знаков. Угол находится в IV четверти. Значения функций совпадают.
Таким образом, при решении задач по тригонометрии следует применять тригонометрическую окружность, с помощью которой можно безошибочно определять знак функции.
Урок 7. Знаки тригонометрических функций
ВИДЕО УРОК
Длина радиуса-вектора
всегда число положительное. Проекции его на координатные оси – величины алгебраические и в зависимости от координатных четвертей имеют следующие знаки:
в I четверти ах > 0; ау > 0;
во II четверти ах < 0; ау > 0;
в III четверти ах < 0; ау < 0;
в IV четверти ах > 0; ау < 0.
Функция sin α.
В силу того, что для тригонометрической функции sin α число 2π (или 360°) является периодом, достаточно исследовать знаки этой функции на каком-нибудь промежутке изменения α длиной 2π, например для значений α от 0 до 2π;
0 ≤ α < 2π (0° ≤ α < 360°).
Если угол α заключён между 0 и π (0° и 180°), то ордината у конца М подвижного радиуса ОМ единичной окружности положительна, а следовательно, и синус угла α, составленного с осью Ох этим радиусом, положителен. На чертеже
показано несколько положений подвижного радиуса:
ОМ1, ОМ2, … , ОМ5.
Если же угол α заключён между π и 2π (180° и 360°), то ордината у конца М подвижного радиуса ОМ отрицательна,
а следовательно, и sin α на этом промежутке отрицательный.
Теперь, пользуясь равенством
sin (α + 2kπ) = sin α,
получаем заключение о знаке синуса для любых значений α:
1) если 2kπ < α < π + 2kπ, то
sin α ˃ 0,
2) если π + 2kπ < α < 2π + 2kπ, то
sin α < 0.
Соответственно тригонометрическая функция имеет знаки, указанные на рисунку.
ПРИМЕР:
Определите знак тригонометрической функции:
sin 3π/4.
РЕШЕНИЕ:
sin 3π/4. = sin (3 ∙ 180°/4) = sin 135°.
Поскольку
135° ∈ [90°, 180°],
это угол из II координатной четверти.Синус во II четверти положителен, поэтому
sin 3π/4 ˃ 0.
Функция cos α.
Исследуем знаки cos α также на промежутке изменения α от 0 до 2π (от 0° до 360°).
Если угол α заключён между 0 и π/2 (0° и 90°), то абсцисса х конца М подвижного радиуса ОМ единичной окружности положительна,
а следовательно, и косинус угла α, составленного
с осью Ох этим
радиусом ОМ, – положительный.
Если угол α заключён
между π/2 и 3π/2 (90° и 270°), то абсцисса
точки М отрицательна, а следовательно, и cos α – отрицательный.
Если же угол α заключён между 3π/2 и 2π (270° и 360°), то как видно из чертежа
cos α – положительный.
Пользуясь равенством
cos (α + 2kπ) = cos α,
получаем
1) если 2kπ ≤ α < π/2 + 2kπ, то
cos α ˃ 0,
2) если π/2 + 2kπ < α < 3π/2 + 2kπ, то
cos α < 0,
3) если 3π/2 + 2kπ < α < 2π + 2kπ, то
cos α ˃ 0.
Соответственно тригонометрическая функция имеет знаки, указанные на рисунку.
ПРИМЕР:
Определите знак тригонометрической функции:
cos 7π/6.
РЕШЕНИЕ:
cos 7π/6. = cos (7 ∙ 180°/6) = cos 210°.
Поскольку
210° ∈ [180°, 270°],
это угол из III координатной четверти.Косинус в III четверти отрицателен, поэтому
cos 7π/6 < 0.
Функция tg α.
Так как периодом
функций tg α и сtg α является π (или 180°), исследуем знаки tg α и сtg α при изменении α от 0 до π (от 0° до 180°).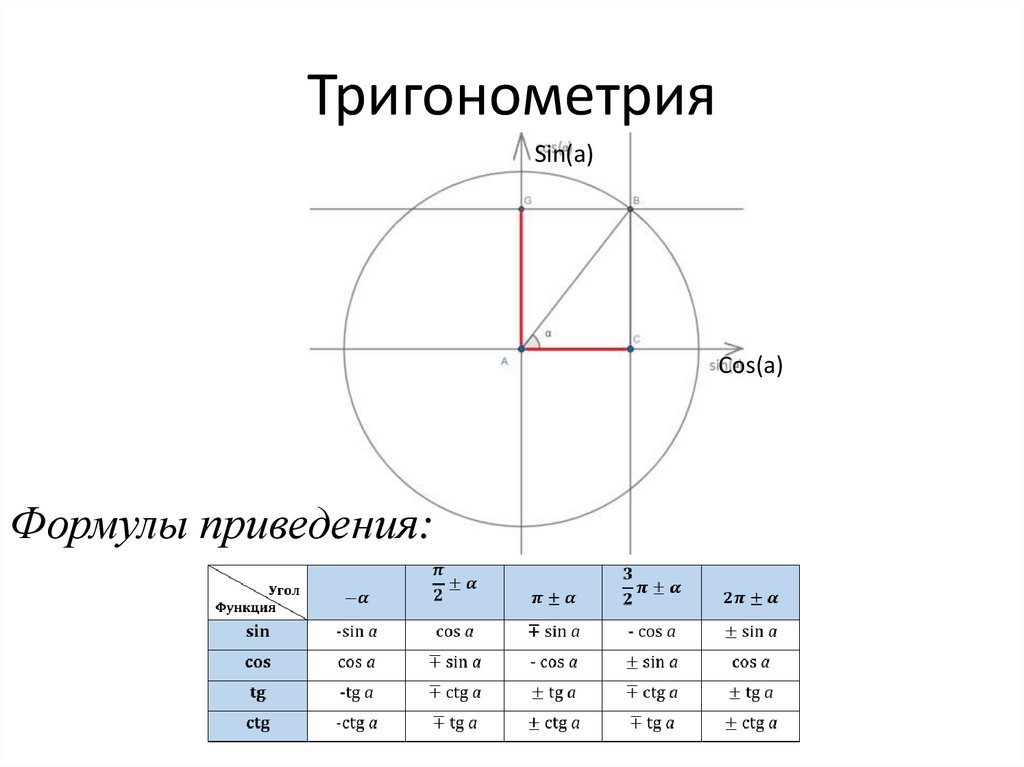 Если угол оканчивается
в I четверти
(0 < α < π/2 или 0° < α < 90°), то продолжение
подвижного радиуса ОМ единичной окружности, образующего с осью Ох
угол α, пересечёт ось тангенсов в точке Т,
Если угол оканчивается
в I четверти
(0 < α < π/2 или 0° < α < 90°), то продолжение
подвижного радиуса ОМ единичной окружности, образующего с осью Ох
угол α, пересечёт ось тангенсов в точке Т,
ордината которой положительна. Это означает, что тангенсы углов,
оканчивающихся в I четверти – положительны.
Если же угол α
оканчивается во II четверти (π/2 < α < π или 90° < α < 180°), то продолжение
подвижного радиуса ОМ единичной окружности, образующего с осью Ох
угол α, пересечёт ось тангенсов в точке Т,
ордината которой отрицательна. Следовательно, тангенсы углов, оканчивающиеся во II четверти, отрицательны.
В силу периодичности функции tg α имеем, что тангенсы углов, оканчивающихся
в III четверти, положительны, а в IV четверти –
отрицательны.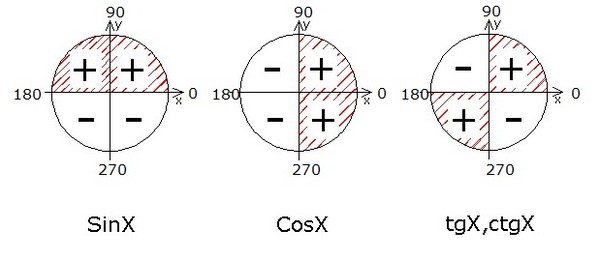
И вообще, так как
tg (α + kπ) = tg α,
имеем:
1) если kπ < α < kπ + π/2, то
tg α ˃ 0,
2) если kπ + π/2 < α < kπ + π, то
tg α < 0.
где k – любое целое число.
Соответственно тригонометрическая функция tg α имеет знаки, указанные на рисунку.
ПРИМЕР:
Определить, какой знак имеет выражение:
tg 2.
РЕШЕНИЕ:
Так как π/2 < 2 < π, то угол 2 рад будет углом II четверти, поэтому
tg 2 < 0.
ОТВЕТ: Знак –
Функция сtg α.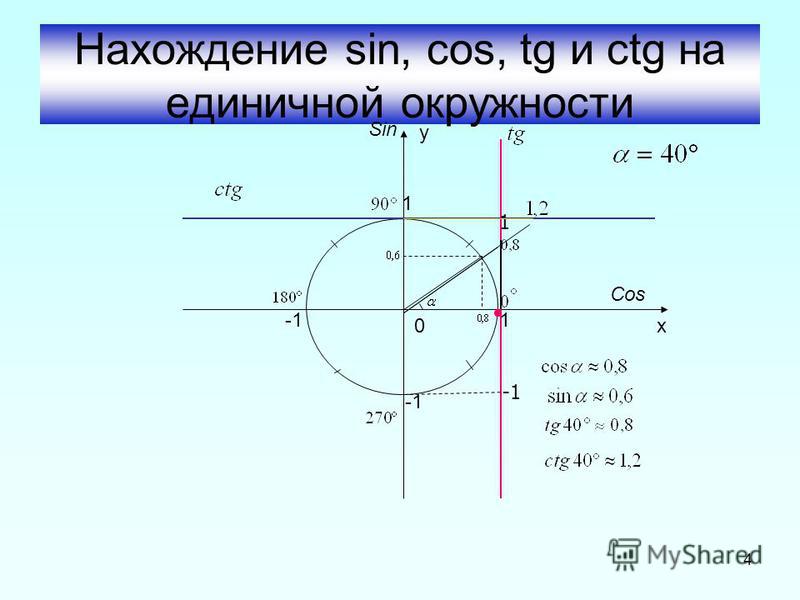
Аналогично приходим к выводу:
если 0 < α < π/2, то
сtg α ˃ 0,
если π/2 < α < π, то
сtg α < 0,
если π < α < 3π/2, то
сtg α ˃ 0,
если 3π/2 < α < 2π, то
сtg α < 0.
И вообще:
1) если kπ < α < π/2 + kπ, то
сtg α ˃ 0,
2) если kπ + π/2 < α < kπ + π, то
сtg α < 0.
где k – любое целое число.
Соответственно тригонометрическая функция сtg α имеет знаки, указанные на рисунку.
ПРИМЕР:
Определите знак тригонометрической функции:
сtg 5π/3.
РЕШЕНИЕ:
сtg 5π/3 = сtg (5 ∙ 180°/3) = сtg 300°.
Поскольку
300° ∈ [270°, 360°],
это угол из IV координатной четверти.Котангенс в IV четверти отрицателен, поэтому
сtg 5π/3 < 0.
ПРИМЕР:
Определите знак выражения:
sin 3π/4 ∙ cos 5π/6.
РЕШЕНИЕ:
sin 3π/4 ∙ cos 5π/6 =
sin (3 ∙ 180°/4) ∙ cos (5 ∙ 180°/6) =
sin 135° ∙ cos 150°.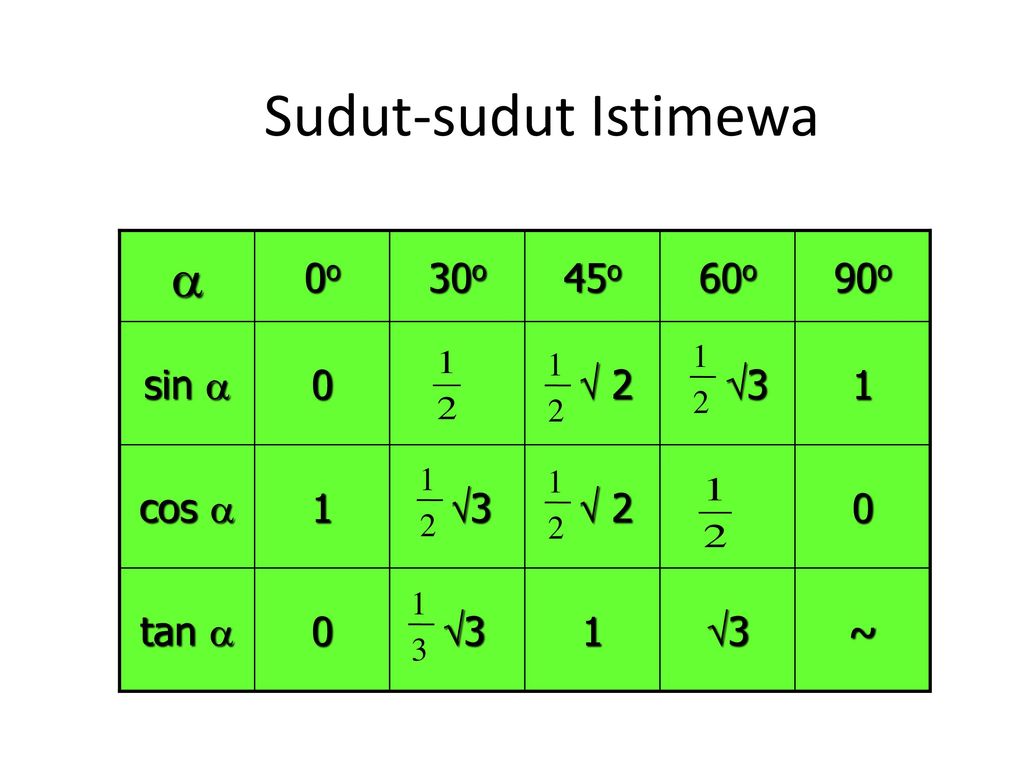
Разберёмся с синусом. Так как
135° ∈ [90°, 180°],
это угол из II координатной четверти.Синус во II четверти положителен, поэтому
sin 3π/4 ˃ 0.
Разберёмся с косинусом. Так как
150° ∈ [90°, 180°],
это угол из II координатной четверти.Косинус во II четверти отрицателен, поэтому
cos 5π/6 < 0.
Получили произведение, в котором множители разных знаков.
Пользуясь правилом
<<плюс на минус даёт знак минус>>,
получаем
sin 3π/4 ∙ cos 5π/6 < 0.
ПРИМЕР:
Определите знак выражения:
cos 2π/3 ∙ tg π/4.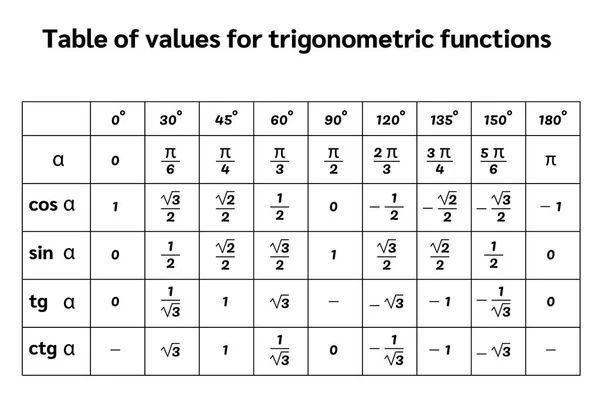
РЕШЕНИЕ:
cos 2π/3 ∙ tg π/4 =
cos (2 ∙ 180°/3) ∙ tg (180°/4) =
cos 120° ∙ tg 45°.
Разберёмся с косинусом. Так как
120° ∈ [90°, 180°],
это угол из II координатной четверти.Косинус во II четверти отрицателен, поэтому
cos 2π/3 < 0.
Разберёмся с тангенсом. Так как
45° ∈ [0°, 90°],
это угол из I координатной четверти.Тангенс в I четверти положителен, поэтому
tg π/4 ˃ 0.
Получили произведение, в котором множители разных знаков. Пользуясь правилом
<<минус на плюс даёт минус>>,
получаем
cos 2π/3 ∙ tg π/4 < 0.
ПРИМЕР:
Определите знак выражения:
sin 5π/6 ∙ cos 7π/4.
РЕШЕНИЕ:
sin 5π/6 ∙ cos 7π/4 =
sin (5 ∙ 180°/6) ∙ cos (7 ∙ 180°/4) =
sin 150° ∙ cos 315°.
Разберёмся с синусом. Так как
150° ∈ [90°, 180°],
это угол из II координатной четверти.Синус во II четверти положителен, поэтому
sin 5π/6 ˃ 0.
Разберёмся с косинусом. Так как
315° ∈ [270°, 360°],
это угол из IV координатной четверти.Косинус в IV четверти положителен, поэтому
cos 5π/6 < 0.
Получили произведение, в котором множители одного знака.
Пользуясь правилом
<<плюс на плюс даёт знак плюс>>,
получаем
sin 5π/6 ∙ cos 7π/4 ˃ 0.
ПРИМЕР:
Определите знак выражения:
tg 3π/4 ∙ cos 5π/3.
РЕШЕНИЕ:
tg 3π/4 ∙ cos 5π/3 =
tg (3 ∙ 180°/4) ∙ cos (5 ∙ 180°/3) =
tg 135° ∙ cos 300°.
Разберёмся с тангенсом. Так как
135° ∈ [90°, 180°],
это угол из II координатной четверти.Тангенс во II четверти отрицателен, поэтому
tg 3π/4 < 0.
Разберёмся с косинусом. Так как
Так как
300° ∈ [270°, 360°],
это угол из IV координатной четверти.Косинус в IV четверти положителен, поэтому
cos 5π/3 ˃ 0.
Получили произведение, в котором множители разных знаков. Пользуясь правилом
<<минус на плюс даёт минус>>,
получаем
tg 3π/4 ∙ cos 5π/3 < 0.
ПРИМЕР:
Определите знак выражения:
сtg 4π/3 ∙ tg π/6.
РЕШЕНИЕ:
сtg 4π/3 ∙ tg π/6 =
сtg (4 ∙ 180°/3) ∙ tg (180°/6) =
сtg 240° ∙ tg 30°.
Разберёмся с котангенсом. Так как
240° ∈ [180°, 270°],
это угол из III координатной четверти. Котангенс в III четверти положителен,
поэтому
Котангенс в III четверти положителен,
поэтому
сtg 4π/3 ˃ 0.
Разберёмся с тангенсом. Так как
30° ∈ [0°, 90°],
это угол из I координатной четверти.Тангенс в I четверти положителен, поэтому
tg π/6 ˃ 0.
Получили произведение, в котором множители одинаковых знаков. Пользуясь правилом
<<плюс на плюс даёт плюс>>,
получаем
сtg 4π/3 ∙ tg π/6 ˃ 0.
ПРИМЕР:
Определите знак выражения:
cos 123° × tg 231° × sin 312°.
РЕШЕНИЕ:
Так как
123° – угол II четверти,
231° – угол III четверти,
312° – угол IV четверти, то
cos 123° < 0, tg 231° ˃ 0, sin 312° < 0
и их произведение будет величиной положительной, то есть
cos 123° × tg 231° × sin 312° ˃ 0.
ОТВЕТ:
Знак +
Задания к уроку 7
В каких точках синус меняется на косинус. Формулы приведения: доказательство, примеры, мнемоническое правило
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
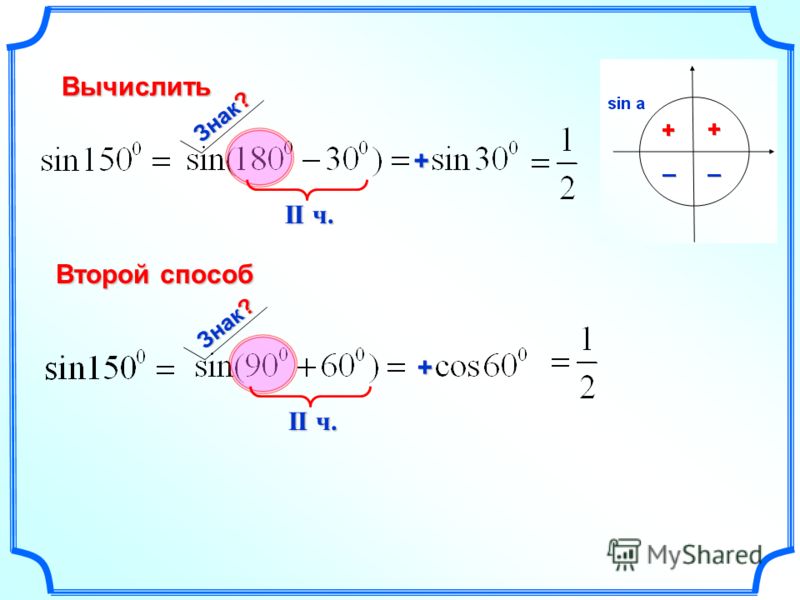
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.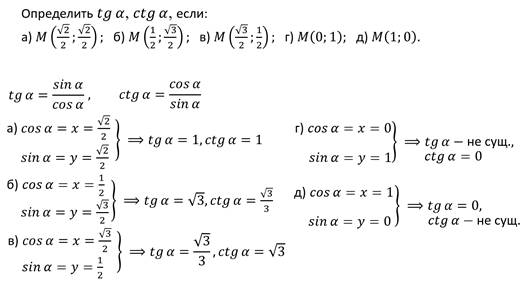
Тема урока
- Изменение синуса, косинуса и тангенса при возрастании угла.
Цели урока
- Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
- Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Проверить знания учащихся.
План урока
- Повторение ранее изученного материала.
- Задачи на повторение.
- Изменение синуса, косинуса и тангенса при возрастании угла.
- Практическое применение.
Повторение ранее изученного материала
Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Предмети > Математика > Математика 8 класс
Тригонометрия.Формулы приведения.
Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.
Разберем в каждой четверти функции sin(a) и cos(a).
Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.
В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).
Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.
А функция cos(a) , потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).
В третьей четверти видно, что функции sin(a) Третья четверть можно описать через градусную меру, как (180+α) или (270-α).
В четвертой четверти видно, что функция sin(a) , потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0 , потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).
Теперь рассмотрим сами формулы приведения.
Запомним простой алгоритм :
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется .
И так начнем разбирать по четвертям данный алгоритм.
Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
Будет cos(90-α) = sin(α)
Выясни чему будет равно выражение sin(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
Будет sin(90-α) = cos(α)
Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
Будет cos(360+α) = cos(α)
Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)
Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)
Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)
Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)
Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)
Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Формулы приведения — это соотношения, которые позволяют перейти от синус, косинус, тангенс и котангенс с углами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. \circ \pm \alpha`):
\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
Мнемоническое правило формул приведения или как их запомнить
Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.
Само привило содержит 3 этапа:
- Аргумент функции должен быть представлен в виде `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
- Для аргументов `\frac {\pi}2 \pm \alpha`, `\frac {3\pi}2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
- Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:
1. \circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac{\pi}2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac{\pi}2-\alpha)= — cos (\frac{\pi}2-\alpha)= — sin \alpha`.
Ответ: `cos(\frac {7\pi}2 — \alpha)=- sin \alpha`.
Лошадиное правило
Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?
Итак, мы имеем функции с аргументами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac {\pi}2`, `\pi`, `\frac {3\pi}2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac {\pi}2` и `\frac {3\pi}2` на вертикальной оси ординат.
Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка. \circ=-\frac{\sqrt 3}2`.
\circ=-\frac{\sqrt 3}2`.
Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac {9\pi}8` и `cos \frac {9\pi}8`; 2) `sin \frac {\pi}8` и `cos \frac {3\pi}10`.
Решение: 1)`sin \frac {9\pi}8=sin (\pi+\frac {\pi}8)=-sin \frac {\pi}8`
`cos \frac {9\pi}8=cos (\pi+\frac {\pi}8)=-cos \frac {\pi}8=-sin \frac {3\pi}8`
`-sin \frac {\pi}8> -sin \frac {3\pi}8`
`sin \frac {9\pi}8>cos \frac {9\pi}8`.
2) `cos \frac {3\pi}10=cos (\frac {\pi}2-\frac {\pi}5)=sin \frac {\pi}5`
`sin \frac {\pi}8
`sin \frac {\pi}8
Докажем сначала две формулы для синуса и косинуса аргумента `\frac {\pi}2 + \alpha`: ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha` и` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.
Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`.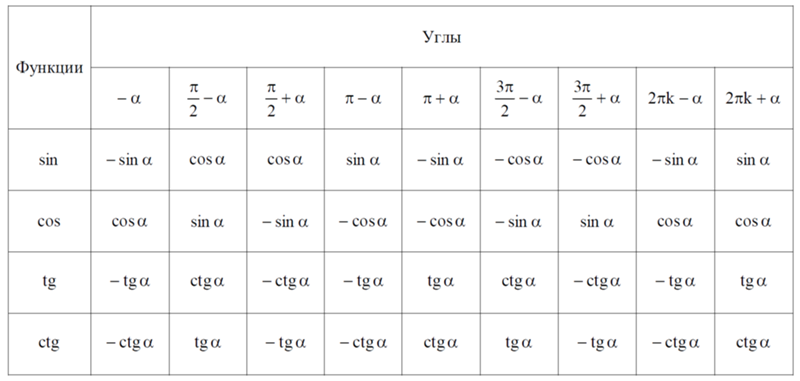 Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Выходя из определения тангенса и котангенса, получим ` tg(\frac {\pi}2 + \alpha)=\frac {sin(\frac {\pi}2 + \alpha)}{cos(\frac {\pi}2 + \alpha)}=\frac {cos \alpha}{-sin \alpha}=-ctg \alpha` и ` сtg(\frac {\pi}2 + \alpha)=\frac {cos(\frac {\pi}2 + \alpha)}{sin(\frac {\pi}2 + \alpha)}=\frac {-sin \alpha}{cos \alpha}=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac {\pi}2 + \alpha`.
Чтобы доказать формулы с аргументом `\frac {\pi}2 — \alpha`, достаточно представить его, как `\frac {\pi}2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac {\pi}2 +(\frac {\pi}2+\alpha)` и `\frac {\pi}2 +(\frac {\pi}2-\alpha)` соответственно.
А `\frac {3\pi}2 + \alpha` и `\frac {3\pi}2 — \alpha` как `\pi +(\frac {\pi}2+\alpha)` и `\pi +(\frac {\pi}2-\alpha)`.
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет.
2. Правило «каким ты был, таким ты и остался».
Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс».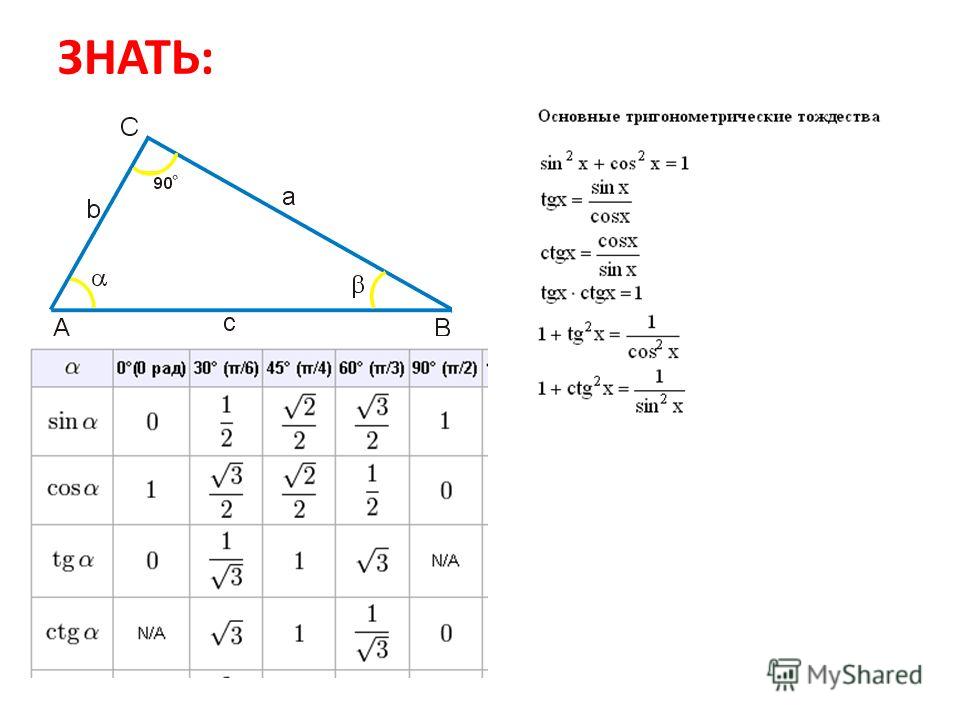 Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Вычислить Sin(150˚)
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен +. Значит у приведенной функции тоже будет знак «плюс». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
При желании все формулы приведения можно свести в одну таблицу. Но все же легче запомнить эти два правила и пользоваться ими.
Нужна помощь в учебе?
Предыдущая тема:
1
Первый слайд презентации: Определение и знаки тригонометрических функций
Изображение слайда
2
Слайд 2: Угол поворота
х у 1 -1 1 -1 II IV I III ОР 0 — неподвижный луч ОР — подвижный луч Р Р 0 Угол поворота соответствует длине пути, пройденного точкой Р от начального положения Р 0 Угол поворота можно измерить двумя мерами : градусной и радианной О
Изображение слайда
3
Слайд 3: Окружность с центром в начале системы координат Oxy и радиусом, равным единице, называется единичной, а ограниченный ей круг – тригонометрическим
Приняв точку пересечения окружности с положительной частью оси Ох за начало отсчета;
Выбрав положительное направление – против часовой стрелки, отрицательное – по часовой стрелке;
Отложив от начала отсчета дугу в 1 рад, мы получим, что тригонометрическая окружность в некотором смысле «эквивалентна» понятию «числовая прямая». x
y
0
1
1
0
«+»
« »
1
x
y
0
1
1
0
«+»
« »
1
Изображение слайда
4
Слайд 4: Тригонометрические функции
Определение. Тригонометрические функции — это неалгебраические функции, устанавливающие зависимость между сторонами и углами треугольника. Тригонометрические функции угла α определяются при помощи числовой окружности, а также из прямоугольного треугольника (для острых углов).
Изображение слайда
5
Слайд 5: Определение синуса
Синусом угла х называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол х (обозначается sin x ).
Изображение слайда
6
Слайд 6: Определение косинуса
Косинусом угла х называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол х (обозначается cos x ).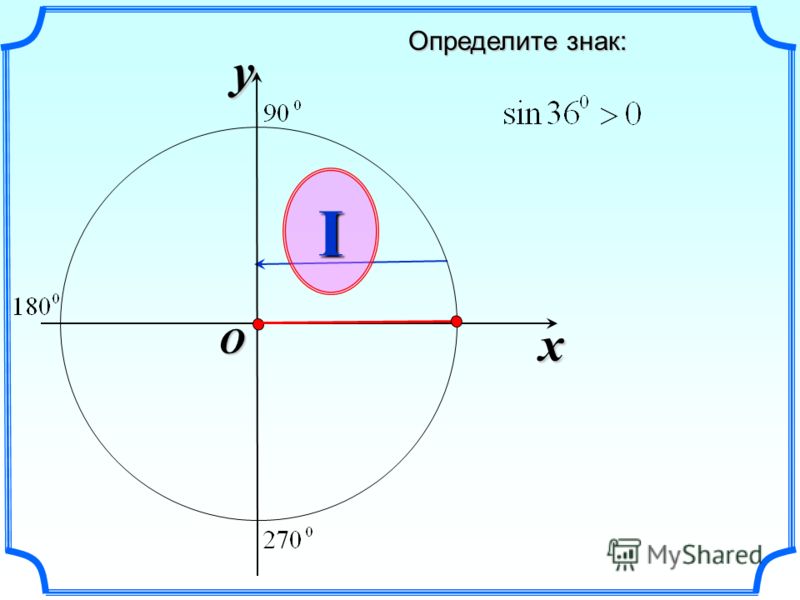
Изображение слайда
7
Слайд 7: Определение тангенса
Тангенсом угла х называется отношение синуса угла х к косинусу угла х.
Изображение слайда
8
Слайд 8: Определение котангенса
Котангенсом угла х называется отношение косинуса угла х к синусу угла х.
Изображение слайда
9
Слайд 9: Тригонометрическая окружность
Изображение слайда
10
Слайд 10
ЗНАКИ тригонометрических функций sin a cos a tg a ctg a – + + + + + + + + – – – – – – –
Изображение слайда
11
Слайд 11
Изображение слайда
12
Слайд 12
sin α cos α tg α ctg α Область опреде-ления Область значе — ний (- ∞;+ ∞) (- ∞;+ ∞) + n n -целое число n n -целое число (- ∞;+ ∞) (- ∞;+ ∞) ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЙ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА
Изображение слайда
13
Слайд 13
α 0° 30° 45° 60° 90° 180° 270° 360° 0 π 2 π sin α cos α tg α ctg α 0 0 0 1 0 — 0 0 0 0 0 0 1 — -1 -1 1 — — — 1 1 ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Изображение слайда
14
Слайд 14: Пример: Вычислить
Задание: Вычислить
Изображение слайда
15
Последний слайд презентации: Определение и знаки тригонометрических функций: Учебник «Алгебра и начала анализа» (10 кл.
 )
)
Стр.178 № 563(2,3,4) Стр.179 № 567 Стр.179 № 566
Изображение слайда
Где синус положительный, а где отрицательный. Свойства синуса, косинуса, тангенса и котангенса угла
Позволяет установить ряд характерных результатов — свойства синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. В первом из них указаны знаки синуса, косинуса, тангенса и котангенса угла α в зависимости от того, в какой координатной четверти угла находится α. Далее рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α при изменении этого угла на целое число оборотов. Третье свойство выражает связь между значениями синуса, косинуса, тангенса и котангенса противоположных углов α и −α.
Если вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи.
Навигация по страницам.
Знаки синуса, косинуса, тангенса и котангенса в четвертях
Ниже в этом абзаце встречается словосочетание «угол I, II, III и IV координатной четверти». Поясним, что это за углы.
Возьмем единичную окружность, отметим на ней начальную точку A(1, 0) и повернем ее вокруг точки O на угол α, при этом будем считать, что попали в точку A 1 (x, y) .
Говорят, что угол α есть угол I, II, III, IV координатной четверти , если точка А 1 лежит соответственно в I, II, III, IV четвертях; если угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.
Для наглядности приведем графическую иллюстрацию. На рисунках ниже показаны углы поворота 30, -210, 585 и -45 градусов, которые являются углами I, II, III и IV координатных четвертей соответственно.
углы 0, ±90, ±180, ±270, ±360, … градусов не принадлежат ни одной из координатных четвертей.
Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, какая четверть угла равна α.
Для синуса и косинуса это легко сделать.
По определению, синус угла α является ординатой точки A 1 . Очевидно, что в I и II координатных четвертях она положительна, а в III и IV четвертях отрицательна. Таким образом, синус угла α имеет знак плюс в I и II четвертях, а знак минус в III и VI четвертях.
В свою очередь, косинус угла α является абсциссой точки A 1 . В I и IV четвертях он положительный, а во II и III четвертях отрицательный. Следовательно, значения косинуса угла α в I и IV четвертях положительны, а во II и III четвертях отрицательны.
Для определения знаков по четвертям тангенса и котангенса нужно запомнить их определения: тангенс — отношение ординаты точки А 1 к абсциссе, а котангенс — отношение абсциссы точки А 1 к ординате. Тогда с правил деления числа с одинаковыми и разными знаками, следует, что тангенс и котангенс имеют знак плюс, когда знаки абсцисс и ординаты точки А 1 совпадают, и имеют знак минус, когда знаки абсцисс и ординаты точки А 1 разные. Следовательно, тангенс и котангенс угла имеют знак + в I и III координатных четвертях, а знак минус во II и IV четвертях.
Следовательно, тангенс и котангенс угла имеют знак + в I и III координатных четвертях, а знак минус во II и IV четвертях.
Действительно, например, в первой четверти и абсцисса x, и ордината y точки A 1 положительны, то и частное x/y, и частное y/x положительны, следовательно, тангенс и котангенс имеют + признаки. А во второй четверти абсцисса х отрицательна, а ордината у положительна, поэтому и х/у, и у/х отрицательны, откуда тангенс и котангенс имеют знак минус.
Перейдем к следующему свойству синуса, косинуса, тангенса и котангенса.
Свойство периодичности
Теперь разберем, пожалуй, самое очевидное свойство синуса, косинуса, тангенса и котангенса угла. Он заключается в следующем: при изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.
Это и понятно: при изменении угла на целое число оборотов мы всегда попадем из начальной точки А в точку А 1 на единичной окружности, поэтому значения синуса, косинуса, тангенса и котангенса остаются без изменений, так как координаты точки A 1 неизменны.
Используя формулы, рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать следующим образом: sin(α+2 π z)=sinα , cos(α+2 π z)=cosα , tg(α+2 π z)=tgα , ctg(α+2 π z)=ctgα , где α — угол поворота в радианах, z — любое , абсолютное значение которого указывает на число полных оборотов, на которое изменяется угол α, а Знак числа z указывает направление поворота.
Если угол поворота α задан в градусах, то эти формулы перепишутся как sin(α+360° z)=sinα , cos(α+360° z)=cosα , tg(α+360° z)= tgα , ctg(α+360° z)=ctgα .
Приведем примеры использования этого свойства. Например, как , а . Вот еще пример: или .
Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.
Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Пусть А 1 — точка, полученная в результате поворота начальной точки А(1, 0) вокруг точки О на угол α, а точка А 2 — результат поворота точки А на угол −α, противоположный углу α.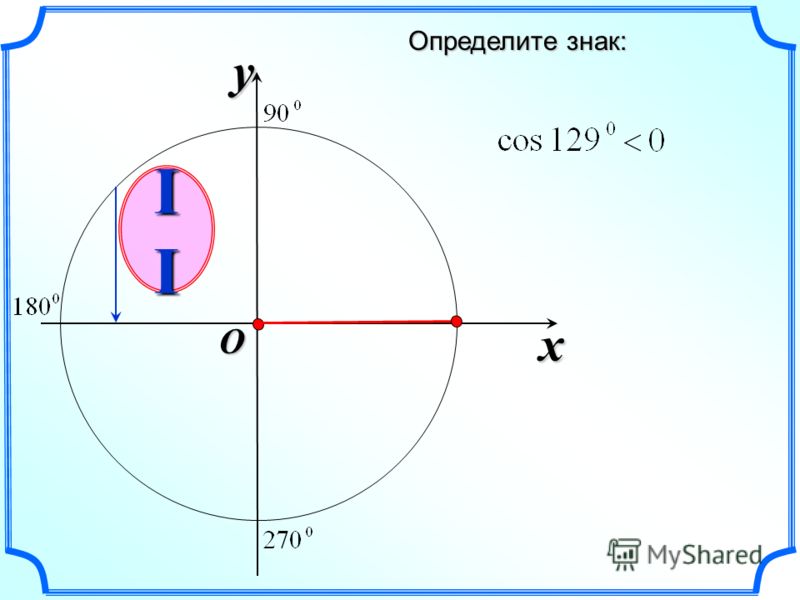
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов основано на достаточно очевидном факте: упомянутые выше точки А 1 и А 2 либо совпадают (при), либо расположены симметрично относительно оси Ох. То есть, если точка A 1 имеет координаты (x, y), то точка A 2 будет иметь координаты (x, −y). Отсюда по определениям синуса, косинуса, тангенса и котангенса запишем равенства и .
Сравнивая их, приходим к соотношениям синусов, косинусов, тангенсов и котангенсов противоположных углов α и −α вида .
Это рассматриваемое свойство в виде формул.
Приведем примеры использования этого свойства. Например, равенства и .
Остается только отметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Библиография.
- Алгебра: Учеб. на 9 кл.
 среднее школа / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Эд. С. А. Теляковский.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
среднее школа / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Эд. С. А. Теляковский.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7 - Алгебра и начало анализа: Учеб. на 10-11 кл. общеобразовательные учреждения / А.Н. Колмогоров, А.М. Абрамов, Ю.В. П. Дудницын и др.; Эд. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Башмаков М.И. Алгебра и начало анализа: Учеб. на 10-11 кл. среднее школа — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для абитуриентов техникумов): Учеб. пособие.- М.; Высшая школа, 1984.-351 с., ил.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были разработаны астрономами для создания точного календаря и ориентирования по звездам. Эти расчеты относятся к сферической тригонометрии, а в школьном курсе изучают отношения сторон и углов плоского треугольника.
Тригонометрия — это раздел математики, изучающий свойства тригонометрических функций и отношения между сторонами и углами треугольников.
В период расцвета культуры и науки в I тысячелетии нашей эры знания распространились с Древнего Востока в Грецию. Но главные открытия тригонометрии — заслуга мужчин Арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений синусов, тангенсов и котангенсов. Понятие синуса и косинуса ввели индийские ученые. Много внимания уделено тригонометрии в трудах таких великих деятелей древности, как Евклид, Архимед и Эратосфен.
Основные тригонометрические величины
Основными тригонометрическими функциями числового аргумента являются синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синус, косинус, тангенс и котангенс.
Формулы для расчета значений этих величин основаны на теореме Пифагора.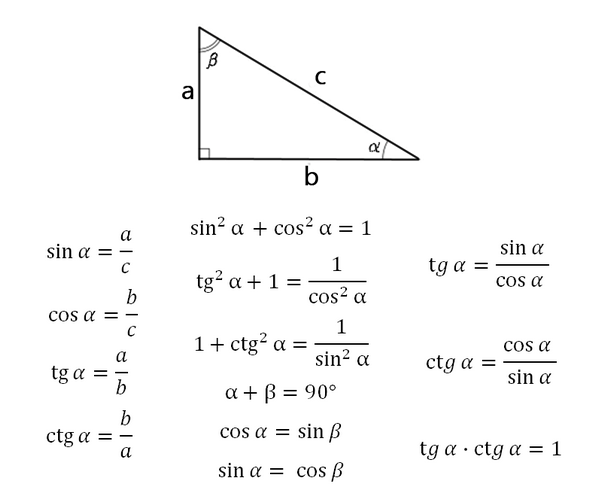 Школьникам оно более известно в формулировке: «Пифагорейские штаны, равные во всех направлениях», так как доказательство приведено на примере равнобедренного прямоугольного треугольника.
Школьникам оно более известно в формулировке: «Пифагорейские штаны, равные во всех направлениях», так как доказательство приведено на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы расчета этих величин для угла А и проследим связь тригонометрических функций:
Как видите, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы c, а катет b как cos A*c, то получим следующие формулы для тангенса и котангенса:
тригонометрическая окружность
Графически соотношение указанных величин можно представить следующим образом:
Окружность в данном случае представляет все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от угла. Например, sin α будет со знаком «+», если α принадлежит I и II четвертям окружности, то есть находится в диапазоне от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательной величиной.
При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательной величиной.
Попробуем построить тригонометрические таблицы для конкретных углов и выяснить значение величин.
Значения α, равные 30°, 45°, 60°, 90°, 180° и так далее, называются частными случаями. Значения тригонометрических функций для них рассчитываются и представляются в виде специальных таблиц.
Эти ракурсы выбраны не случайно. Обозначение π в таблицах относится к радианам. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Это значение было введено для того, чтобы установить универсальное отношение; при расчете в радианах фактическая длина радиуса в см значения не имеет.
Углы в таблицах для тригонометрических функций соответствуют значениям в радианах:
Итак, нетрудно догадаться, что 2π — это полный круг или 360°.
Свойства тригонометрических функций: синус и косинус
Для того чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо нарисовать их функции.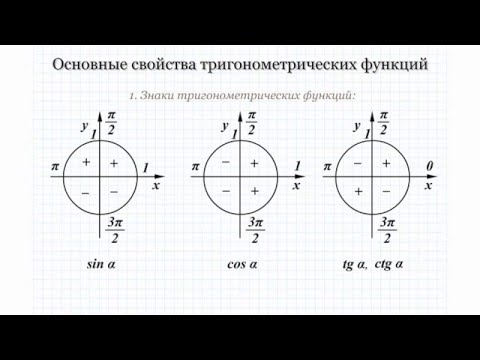 Это можно сделать в виде кривой, расположенной в двумерной системе координат.
Это можно сделать в виде кривой, расположенной в двумерной системе координат.
Рассмотрим сравнительную таблицу свойств синусоиды и косинуса:
| синусоида | косинусоид |
|---|---|
| у = sin x | y = cos x |
| ОДЗ[-1; один] | ОДЗ [-1; один] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, для x = π/2 + 2πk, где k ϵ Z | cos x = 1, для x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. нечетная функция | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период 2π | |
| sin x › 0, где x принадлежит четвертям I и II или от 0° до 180° (2πk, π + 2πk) | cos x › 0, где x принадлежит четвертям I и IV или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, где x принадлежит четвертям III и IV или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, где x принадлежит четвертям II и III или из 90 ° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на интервале [- π/2 + 2πk, π/2 + 2πk] | возрастает на интервале [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить, является функция четной или нет, очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси ОХ. Если знаки одинаковые, функция четная; в противном случае это странно.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси ОХ. Если знаки одинаковые, функция четная; в противном случае это странно.
Введение радиан и перечисление основных свойств синусоиды и косинуса позволяют вывести следующую закономерность:
Проверить правильность формулы очень легко. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверка может быть выполнена путем просмотра таблиц или отслеживания кривых функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса существенно отличаются от синусоиды и косинуса. Значения tg и ctg обратны друг другу.
- Y = tgx.
- Тангенс стремится к значениям y при x = π/2 + πk, но никогда их не достигает.
- Наименьший положительный период тангеноида равен π.
- Tg(-x)=-tgx, т. е. функция нечетная.
- Tg x = 0, для x = πk.

- Функция увеличивается.
- Tg x › 0, для x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, для x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое представление котангенсоида ниже по тексту.
Основные свойства котангенсоида:
- Y = ctgx.
- В отличие от функций синуса и косинуса, в тангеноиде Y может принимать значения множества всех действительных чисел.
- Котангенсоид стремится к значениям y при x = πk, но никогда их не достигает.
- Наименьший положительный период котангенсоида равен π.
- Ctg(- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, для x = π/2 + πk.
- Функция уменьшается.
- Ctg x › 0, для x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, для x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Fix
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию.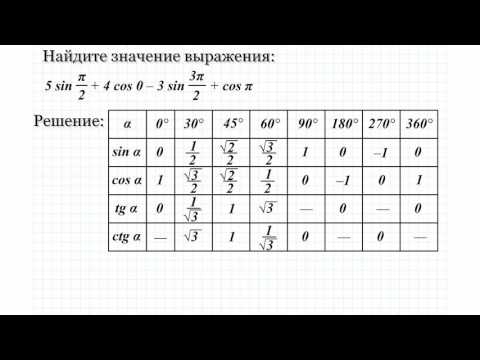 Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы подаете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и информировать вас об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки вам важных уведомлений и сообщений.

- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном поощрении, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, судебным приказом, в порядке судопроизводства и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть свои Персональные данные. Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.

- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему правопреемнику третьей стороны.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Обеспечение конфиденциальности на уровне компании
Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам о правилах конфиденциальности и безопасности и строго следим за соблюдением правил конфиденциальности.
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синус, косинус, тангенс и котангенс.
Первым свойством является знак функции, зависящий от того, какой четверти единичной окружности принадлежит угол α. Второе свойство – периодичность. Согласно этому свойству тигонометрическая функция не меняет своего значения при изменении угла на целое число оборотов. Третье свойство определяет, как изменяются значения функций sin, cos, tg, ctg при противоположных углах α и – α.
Согласно этому свойству тигонометрическая функция не меняет своего значения при изменении угла на целое число оборотов. Третье свойство определяет, как изменяются значения функций sin, cos, tg, ctg при противоположных углах α и – α.
Яндекс.РТБ R-A-339285-1
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это?
Давайте посмотрим на единичный круг. Он разделен на четыре квартала. Отмечаем на окружности начальную точку A 0 (1, 0) и, повернув ее вокруг точки O на угол α, попадаем в точку A 1 (x, y) . В зависимости от того, в какой четверти будет лежать точка A 1 (x, y), угол α будем называть соответственно углом первого, второго, третьего и четвертого квадрантов.
Для наглядности приведем иллюстрацию.
Угол α = 30° лежит в первой четверти. Угол — 210° это вторая четверть угла. Угол 585° — это угол третьей четверти. Угол — 45° это угол четвертой четверти.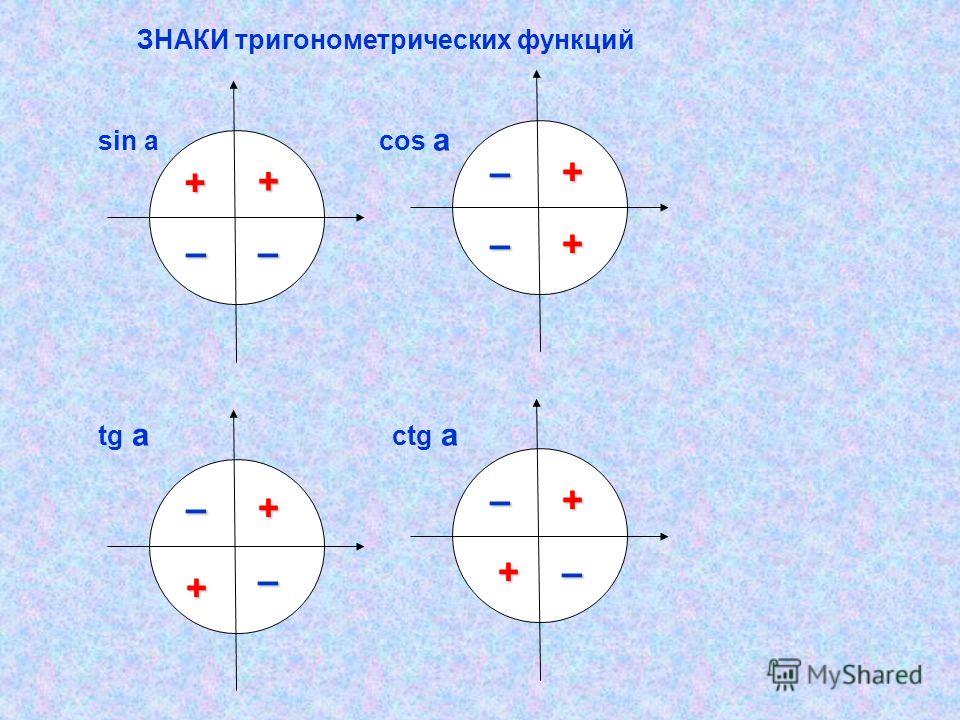
При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на осях координат.
Теперь рассмотрим знаки синуса, косинуса, тангенса и котангенса в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса в четвертях, вспомним определение. Синус – это ордината точки A 1 (x , y) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус – это абсцисса точки A 1 (x, y) . В соответствии с этим определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях и отрицателен во второй и третьей четвертях.
Для определения знаков тангенса и котангенса по четвертям напомним также определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Это означает, что по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак касательной на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки, он будет отрицательным .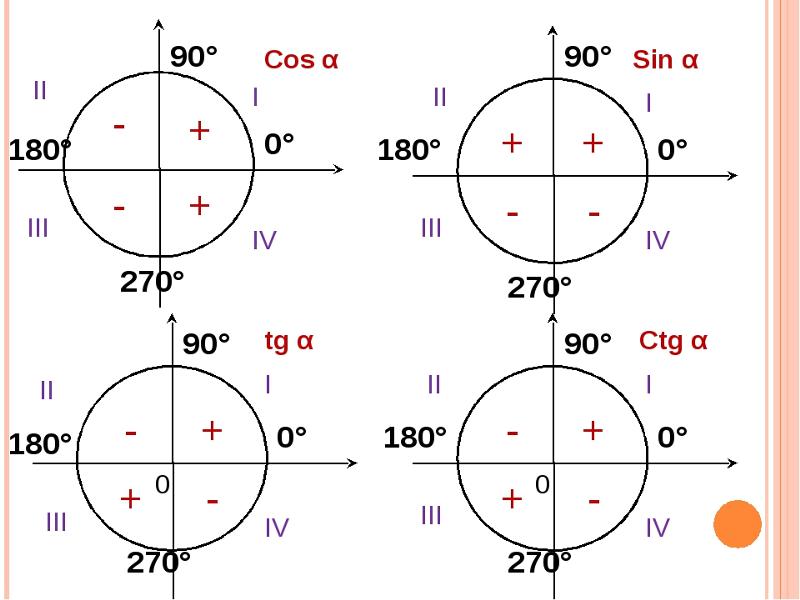 Аналогично определяются знаки котангенса в четвертях.
Аналогично определяются знаки котангенса в четвертях.
Важно помнить!
- Синус угла α имеет знак плюс в 1-й и 2-й четвертях, знак минус в 3-й и 4-й четвертях.
- Косинус угла α имеет знак плюс в 1-й и 4-й четвертях, знак минус во 2-й и 3-й четвертях.
- Тангенс угла α имеет знак плюс в 1-й и 3-й четвертях, знак минус во 2-й и 4-й четвертях.
- Котангенс угла α имеет знак плюс в 1-й и 3-й четвертях, знак минус во 2-й и 4-й четвертях.
Свойство периодичности
Свойство периодичности является одним из наиболее очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда попадем из начальной точки А на единичной окружности в точку А 1 с теми же координатами. Соответственно значения синуса, косинуса, тангенса и котангенса не изменятся.
Математически это свойство записывается следующим образом:
sin α + 2 π z = sin α cos α + 2 π z = cos α t g α + 2 π z = t g α c t g α + 2 π z = c t g α
Каково практическое применение этого свойства? Свойство периодичности, как и формулы приведения, часто используют для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g (- 689°) = t g (31° + 360° (- 2)) = t g 31° t g (- 689°) = t g (- 329° + 360° (- 1)) = t g (- 329°)
Посмотрим снова на единичном круге.
Точка A 1 (x, y) является результатом поворота начальной точки A 0 (1, 0) вокруг центра окружности на угол α. Точка A 2 (x, — y) является результатом поворота начальной точки на угол — α.
Точки A 1 и A 2 симметричны относительно оси x. В случае, когда α = 0°, ±180°, ±360° точки А1 и А2 совпадают. Пусть одна точка имеет координаты (x, y), а вторая — (x, — y). Вспомните определения синуса, косинуса, тангенса, котангенса и запишите:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α равенства
sin — 48° = — sin 48°, c t g π 9= — c t g — π 9 , cos 18° = cos — 18°
Рассматриваемое свойство часто используется при решении практических задач в тех случаях, когда необходимо избавиться от отрицательных знаков углов в аргументах тригонометрических функций.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter
Heroes of Might & Magic III– HD Edition (Heroes of Might and Magic III) v1
Настольная игра «Уно»: увлекательно и интересно !
Математические символы LaTeX — глоссарий
Обзор часто используемых математических символов в LaTeX Поскольку LaTeX предлагает большое количество функций, трудно запомнить все команды. Несмотря на то, что команды следуют логической схеме именования, в какой-то момент вам, вероятно, понадобится таблица для наиболее распространенных математических символов.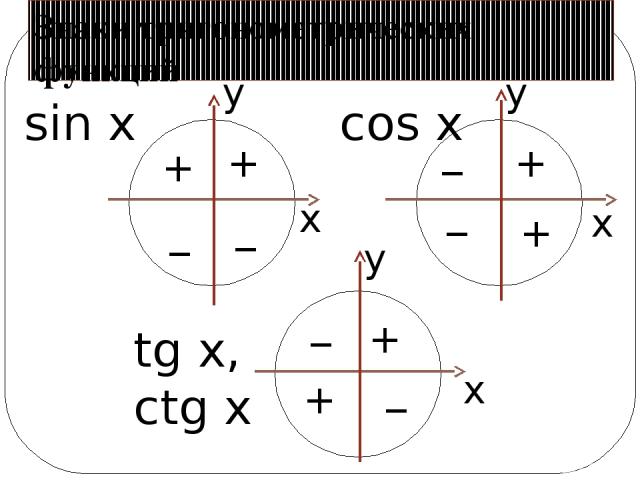 Я не хочу предоставлять полный список символов LaTeX на этом сайте. ctan уже предоставляет огромный список с 5913 символами, который вы можете скачать здесь. Вместо этого я пытаюсь ограничить этот список наиболее распространенными математическими символами и командами. Если вы думаете, что я забыл здесь какую-то очень важную функцию или символ, сообщите мне об этом.
Я не хочу предоставлять полный список символов LaTeX на этом сайте. ctan уже предоставляет огромный список с 5913 символами, который вы можете скачать здесь. Вместо этого я пытаюсь ограничить этот список наиболее распространенными математическими символами и командами. Если вы думаете, что я забыл здесь какую-то очень важную функцию или символ, сообщите мне об этом.
Список общих \(\LaTeX\) математических символов
- Тригонометрические функции
- Интегралы
- Матрицы
- точек
- Прочие функции
Тригонометрические функции
Символы тригонометрических функций имеют очень простую схему именования. Просто перед общими сокращениями поставьте обратную косую черту \ и поместите свои переменные в фигурные скобки.
| Имя | Символ | Команда |
|---|---|---|
| Синус | \(\грех х\) | \sin х |
| Косинус | \(\cos х\) | \cos х |
| Касательная | \(\загар х \) | \загар х |
| Котангенс | \(\кроватка х\) | х |
| Секущая | \(\сек х\) | мс x |
| Интеграл области | \(\int_D f(x) dx\) | \int_D f(x) dx |
| Двойной цельный | \(\iint f(x,y) dx dy\) | \iint f(x,y) dx dy |
| Тройной интеграл | \(\iiint f(x,y,z) dx dy dz\) | \iiint f(x,y,z) dx dy dz |
| Интеграл с замкнутой кривой | \(\oint_C F дс\) | \oint_C F дс |
Матрицы
Конечно, LaTeX также может набирать матрицы. Для этого LaTeX предлагает следующие среды. Столбцы разделяются амперсандом &, а строки — двойной обратной косой чертой \\ (команда переноса строки). Убедитесь, что количество амперсандов одинаково для каждой строки.
Для этого LaTeX предлагает следующие среды. Столбцы разделяются амперсандом &, а строки — двойной обратной косой чертой \\ (команда переноса строки). Убедитесь, что количество амперсандов одинаково для каждой строки.
| Имя | Символ | Команда |
|---|---|---|
| Матрица | \(\начало{матрица}1&0\\1&0\конец{матрица}\) | \начало{матрица}1&0\\ 1&0\конец{матрица} |
| bMatrix | \(\begin{bmatrix}1&0\\1&0\end{bmatrix}\) | \begin{bmatrix}1&0\\ 1&0\конец{bmatrix} |
| pMatrix | \(\begin{pmatrix}1&0\\1&0\end{pmatrix}\) | \begin{pmatrix}1&0\\ 1&0\конец{pmatrix} |
| вМатрикс | \(\начало{vmatrix}1&0\\1&0\конец{vmatrix}\) | \begin{vmatrix}1&0\\ 1&0\конец{vmatrix} |
| Определитель | \(\det{\begin{vmatrix}1&0\\1&0\конец{vmatrix}}\) | \det{\begin{vmatrix}1&0\\ 1&0\конец{vmatrix}} |
Если вы хотите печатать очень большие матрицы, вам также могут пригодиться следующие команды.
Точки
Наиболее распространенные точечные символы, используемые в математической записи, также доступны в LaTeX.
| Имя | Символ | Команда |
|---|---|---|
| Средняя точка / Точка по центру | \(\кдот\) | \cdot |
| Горизонтальные точки / Центрированные точки | \(\cdots\) | \cdots |
| Вертикальные точки | \(\вдоц\) | \vточки |
Диагональные точки | \(\ddots\) | \дточки |
Нижние точки | \(\ldots\) | \ldots |
Пример: \(\begin{bmatrix}1 & 0 & \cdots & 0\\1 & 0 & \cdots & 0\\\vdots & \vdots & \ddots & \vdots \\1 & 0 & 0 & 0 \end{bmatrix}\) | \begin{bmatrix} 1 и 0 & \cdots & 0\\ 1 и 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 1 и 0 и 0 и 0 \end{bmatrix} | |
Прочие функции
Вот еще несколько основных функций, не подпадающих под указанные выше категории.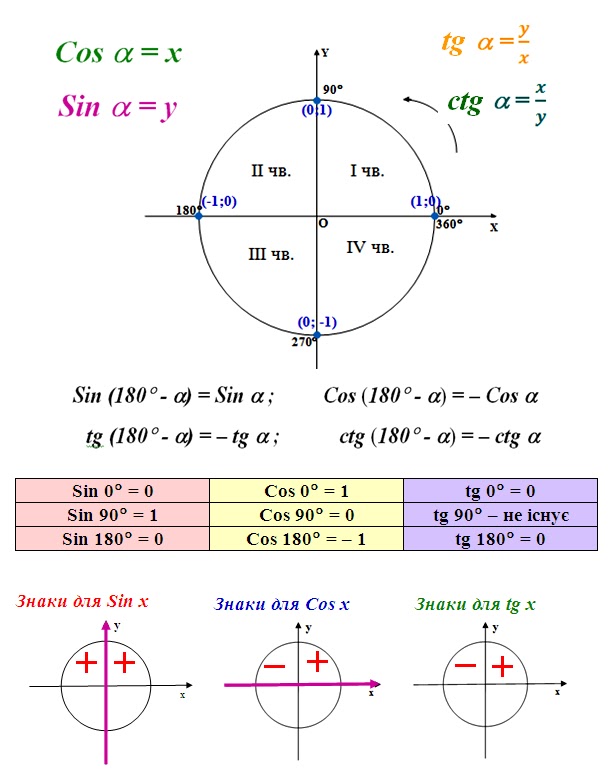
| Имя | Символ | Команда |
|---|---|---|
| Логарифмическая функция/логарифм | \(\лог{х}\) | \лог{х} |
| Логарифм (основание а) | \(\log_a{b}\) | \log_a{b} |
| Функция квадратного корня / квадратный корень | \(\квт{х}\) | \sqrtx} |
| n-я корневая функция / n-й корень | \(\sqrt[n]{x}\) | \sqrt[n]{x} |
| Рациональная функция / Дробь | \(\ гидроразрыва {и (х)} {v (х)} \) | \ гидроразрыва {и (х)} {v (х)} |
S1-Рекомендации по использованию КТГ во время беременности и родов
1. Agrawal S K, Doucette F, Gratton R. et al. Интранатальные компьютеризированные параметры сердечного ритма плода и метаболический ацидоз при рождении.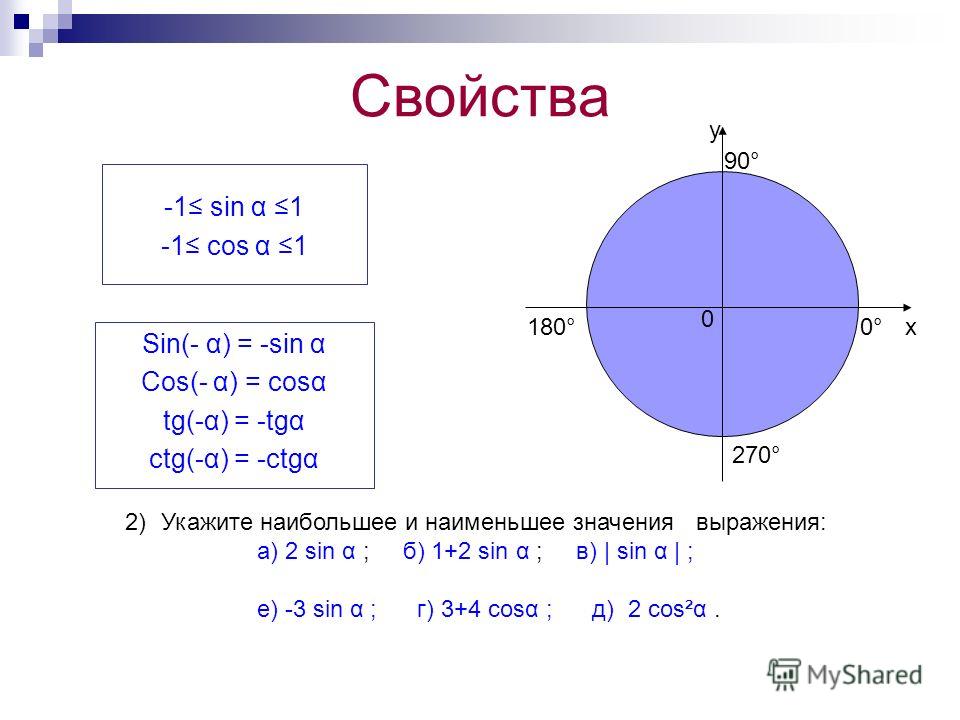 Акушерство Гинекол. 2003; 102: 731–738. [PubMed] [Google Scholar]
Акушерство Гинекол. 2003; 102: 731–738. [PubMed] [Google Scholar]
2. Alfirevic Z Neilson JP Биофизический профиль для оценки плода при беременности с высоким риском Cochrane Database Syst Rev 20081CD000038 [бесплатная статья PMC] [PubMed] [Google Scholar]
3. Alfirevic Z Devane D Gyte G M Непрерывная кардиотокография (КТГ) как форма электронного мониторинга плода (EFM) для оценки плода во время родов Cochrane Database Syst Rev 20063CD006066 [PubMed] [Google Scholar]
4. Практический бюллетень ACOG № . 106: Интранатальный мониторинг сердечного ритма плода. номенклатура, интерпретация и общие принципы управления. Акушерство Гинекол. 2009; 114:192–202. [PubMed] [Google Scholar]
5. Практический бюллетень ACOG № 116: Ведение интранатальной записи сердечного ритма плода. Акушерство Гинекол. 2010;116:1232–1240. [PubMed] [Академия Google]
6. Ашкенази С., Мецкер А., Мерлоб П. и соавт. Изменения скальпа после мониторинга плода. Арч Дис Чайлд. 1985; 60: 267–269.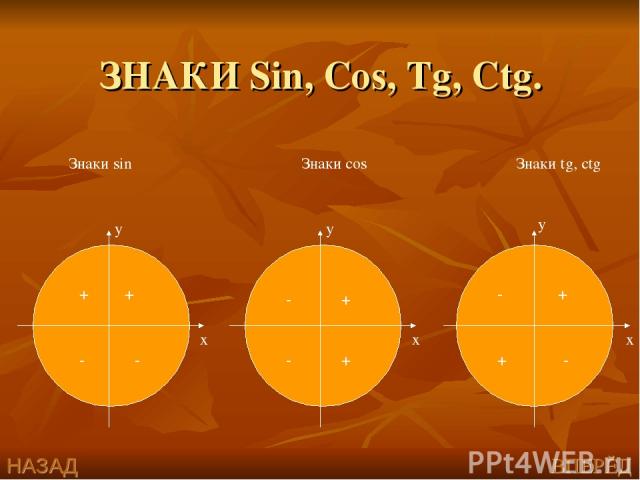 [Бесплатная статья PMC] [PubMed] [Google Scholar]
[Бесплатная статья PMC] [PubMed] [Google Scholar]
7. Бекли С., Стенхаус Э., Грин К. Разработка и оценка компьютерной обучающей программы для интранатального мониторинга плода. БЖОГ. 2000;107:1138–1144. [PubMed] [Google Scholar]
8. Berger R, Bender S, Sefkow S. et al. Пери/внутрижелудочковое кровоизлияние: краниальное ультразвуковое исследование 5286 новорожденных. Eur J Obstet Gynecol Reprod Biol. 1997;75:191–203. [PubMed] [Google Scholar]
9. Bernardes J, Costa Pereira A, Ayres de Campos D. et al. Оценка межнаблюдательного согласования кардиотокограмм. Int J Gynaecol Obstet. 1997; 57: 33–37. [PubMed] [Google Scholar]
10. Bloom S L, Spong C Y, Thom E. et al. Пульсоксиметрия плода и кесарево сечение. New Engl J Med. 2006; 355:195–202. [PubMed] [Google Scholar]
11. Brown VA, Sawers R S, Parsons R J. et al. Значение антенатальной кардиотокографии при ведении беременности с высоким риском: рандомизированное контролируемое исследование. Br J Obstet Gynaecol. 1982;89:716–722. [PubMed] [Google Scholar]
1982;89:716–722. [PubMed] [Google Scholar]
12. Butterwegge M, Gonser M, Roemer V M. Stellungnahme zu einem Gutachten der BQS über geburtshilfliche Qualitätsindikatoren. З Гебурц Неонатол. 2005; 209: 69–75. [PubMed] [Google Scholar]
13. Carbonne B, Langer B, Goffinet F. et al. Клиническое значение пульсоксиметрии плода. II. Сравнительные прогностические значения оксиметрии и pH кожи головы. Многоцентровое исследование. J Gynecol Obstet Biol Reprod (Париж) 1999;28:137–144. [PubMed] [Академия Google]
14. Цибилис Л.А. Об интранатальном мониторинге плода. Am J Obstet Gynecol. 1996; 174: 1382–1389. [PubMed] [Google Scholar]
15. Chow O Larbig A Kabartas B et al. Подводные камни внешнего мониторинга ЧСС во втором периоде родов J Mat Fet Neonat Med 201023(Suppl.)236 [Google Scholar]
16. Dawes GS, Moulden M, Redman C WG. Краткосрочные колебания частоты сердечных сокращений плода, замедления и кривые скорости пуповины перед родами. Акушерство Гинекол. 1992; 80: 673–678. [PubMed] [Академия Google]
[PubMed] [Академия Google]
17. Daumer M, Scholz M, Boulesteix A L. et al. Исследование нормального сердечного ритма плода: план анализа. Труды о природе. 2007 г.: 10.1038/npre.980.1. [CrossRef] [Google Scholar]
18. Devoe L D, Ross M, Wilde C. et al. Многоцентровое клиническое исследование использования электронной системы мониторинга плода STAN 21 в США. Am J Obstet Gynecol. 2006; 195:729–734. [PubMed] [Google Scholar]
19. DKG Leitfaden: Aufbewahrungsverpflichtungen und -fristen von Dokumenten im Krankenhaus. НКГ Миттейлунг. 2006:394. [Google Scholar]
20. Дрогтроп А.П., Убелс Р., Нейхуис Дж.Г. Связь между движениями тела плода, движениями глаз и частотой сердечных сокращений при беременности между 25 и 30 неделями беременности. Ранний Хам Дев. 1990; 23: 67–73. [PubMed] [Google Scholar]
21. Dudenhausen JW, Luhr C, Dimer JS. Газы крови пупочной артерии у здоровых доношенных новорожденных. Int J Gynaecol Obstet. 1997; 57: 251–258. [PubMed] [Google Scholar]
22. East C E Colditz P B Пульсоксиметрия плода для оценки плода в родах Cochrane Database Syst Rev 20072CD004075 [PubMed] [Google Scholar]
East C E Colditz P B Пульсоксиметрия плода для оценки плода в родах Cochrane Database Syst Rev 20072CD004075 [PubMed] [Google Scholar]
23. Elliott C, Warrick PA, Graham E. et al. Поэтапная классификация записей сердечного ритма плода: связь с неонатальным метаболическим ацидозом и неврологической заболеваемостью. Am J Obstet Gynecol. 2010;202:2580–2.58E10. [Google Scholar]
24. Федорков Д.М., Стюарт Т.Дж., Парбоосингх Дж. Изменения частоты сердечных сокращений плода, связанные с общей анестезией. Ам Дж. Перинат. 1989; 6: 287–288. [PubMed] [Google Scholar]
25. Ferrazzi E, Rigano S, Bozzo M. et al. Кровоток в пупочной вене у плода с задержкой роста. УЗИ Акушерство Гинекол. 2000; 16: 432–438. [PubMed] [Академия Google]
26. Письмо FDA «Уважаемый медицинский работник» Мэнсфилд Х. и др. Рандомизированное контролируемое исследование нестрессовой дородовой кардиотокографии. Br J Obstet Gynaecol. 1982; 89: 427–433. [PubMed] [Google Scholar]
28. Gaffney G, Flavell V, Johnson A. et al. Детский церебральный паралич и неонатальная энцефалопатия. Arch Dis Child Fetal Neonat Ed. 1994; 70: F195–F200. [Бесплатная статья PMC] [PubMed] [Google Scholar]
et al. Детский церебральный паралич и неонатальная энцефалопатия. Arch Dis Child Fetal Neonat Ed. 1994; 70: F195–F200. [Бесплатная статья PMC] [PubMed] [Google Scholar]
29. Gaffney G, Sellers S, Flavell V. et al. Исследование случай-контроль интранатальной помощи, церебрального паралича и перинатальной смерти. Бр Мед Дж. 1994; 308:743–750. [Бесплатная статья PMC] [PubMed] [Google Scholar]
30. Garcia J, Corry M, MacDonald D. et al. Взгляд матерей на непрерывный электронный мониторинг сердца плода и периодическую аускультацию в рандомизированном контролируемом исследовании. Рождение. 1985; 12: 79–86. [PubMed] [Google Scholar]
31. Garite T J, Dildy G A, McNamara H. et al. Многоцентровое контролируемое исследование пульсоксиметрии плода при интранатальном лечении неудовлетворительных паттернов сердечного ритма плода. Am J Obstet Gynecol. 2000;183:1049–1058. [PubMed] [Google Scholar]
32. Garnier Y, Coumans A, Berger R. et al. Эндотоксемия серьезно влияет на кровообращение при нормоксии и асфиксии у неполовозрелых эмбрионов овец. J Soc Gynecol Invest. 2001; 8: 134–142. [PubMed] [Google Scholar]
J Soc Gynecol Invest. 2001; 8: 134–142. [PubMed] [Google Scholar]
33. Gnirs J, Schelling M, Kolben M. et al. Referenzkurven für das fetale Bewegungsprofil. Гебуртш Фрауэнгейлк. 1998; 58: 355–362. [Google Scholar]
34. Gonser M, König M, Marzusch K. Schema zur CTG-Interpretation nach den FIGO-Richtlinien. Гинеколь Пракс. 1995;19:649–659. [Google Scholar]
35. Graatsma EM, Jacod BC, van Egmond L AJ. и другие. Электрокардиотокография плода: возможность долгосрочной регистрации сердечного ритма плода. БЖОГ. 2009; 116: 334–337. [PubMed] [Google Scholar]
36. Grant A, OʼBrien N, Joy M T. et al. Детский церебральный паралич у детей, родившихся во время Дублинского рандомизированного исследования интранатального мониторинга. Ланцет. 1989; 8674: 1233–1236. [PubMed] [Google Scholar]
37. Grivel R M Alfirevic Z Gyte G M et al. Антенатальная кардиотокография для оценки состояния плода Cochrane Database Syst Rev 20101CD007863 [PubMed] [Google Scholar]
38. Хансен П.К., Смит С.Ф., Ним Дж. и соавт. Отношение матери к наблюдению за плодом. Eur J Obstet Gynecol Reprod Biol. 1985; 20:43–51. [PubMed] [Google Scholar]
Хансен П.К., Смит С.Ф., Ним Дж. и соавт. Отношение матери к наблюдению за плодом. Eur J Obstet Gynecol Reprod Biol. 1985; 20:43–51. [PubMed] [Google Scholar]
39. Haverkamp A D, Thompson H E, McFee J G. et al. Оценка непрерывного мониторинга сердечного ритма плода при беременности высокого риска. Am J Obstet Gynecol. 1976; 125: 310–317. [PubMed] [Google Scholar]
40. Haverkamp A D, Orleans M, Langendoerfer S. et al. Контролируемое исследование дифференциальных эффектов интранатального мониторинга плода. Am J Obstet Gynecol. 1979;134:399–412. [PubMed] [Google Scholar]
41. Хербст А., Ингемарссон И. Прерывистый и непрерывный электронный мониторинг плода в родах: рандомизированное исследование. Br J Obstet Gynaecol. 1994; 101: 663–668. [PubMed] [Google Scholar]
42. Ход М., Кернер Р. Телемедицина для антенатального наблюдения за беременностями высокого риска с амбулаторным и домашним мониторингом сердца плода — обновление. J Перинат Мед. 2003; 31: 195–200. [PubMed] [Google Scholar]
43. Impey L, Reynolds M, MacQuillan K. et al. Кардиотокография при поступлении: рандомизированное контролируемое исследование. Ланцет. 2003; 361: 465–470. [PubMed] [Академия Google]
Impey L, Reynolds M, MacQuillan K. et al. Кардиотокография при поступлении: рандомизированное контролируемое исследование. Ланцет. 2003; 361: 465–470. [PubMed] [Академия Google]
44. Йенсен А., Мартиус Г. Штутгарт: Тиме; 1991. Überwachung und Leitung der Entbindung; стр. 386–442. [Google Scholar]
45. Дженсен А., Роман С., Рудольф А. М. Влияние снижения распределения маточного кровотока и доставки кислорода. Дж Дев Физиол. 1991; 15: 309–323. [PubMed] [Google Scholar]
46. Keith RD, Beckley S, Garibaldi JM. et al. Многоцентровое сравнительное исследование 17 специалистов и интеллектуальной компьютерной системы ведения родов с использованием кардиотокограммы. Br J Obstet Gynaecol. 1995;102:688–700. [PubMed] [Google Scholar]
47. Kelso A M, Parsons R J, Lawrence G F. et al. Оценка непрерывного мониторинга сердечного ритма плода в родах. Am J Obstet Gynecol. 1978; 131: 526–532. [PubMed] [Google Scholar]
48. Кидд Л., Патель Н., Смит Р. Нестрессовая антенатальная кардиотокография – проспективное рандомизированное клиническое исследование. Br J Obstet Gynaecol. 1985; 92: 1156–1159. [PubMed] [Google Scholar]
Br J Obstet Gynaecol. 1985; 92: 1156–1159. [PubMed] [Google Scholar]
49. Killien MG, Shy K. Рандомизированное исследование электронного мониторинга плода при преждевременных родах: взгляды матери. Рождение. 1989;16:7–12. [PubMed] [Google Scholar]
50. Kühnert M, Schmidt S. Интранатальное управление неутешительными моделями сердечного ритма плода: рандомизированное контролируемое исследование пульсоксиметрии плода. Am J Obstet Gynecol. 2004; 191:1989–1995. [PubMed] [Google Scholar]
51. Kühnert M, Hellmeyer L, Stein W. et al. Суточный КТГ-мониторинг: сравнение нормальных беременностей на сроке 25-30 недель и сроке беременности 36-42 недели. Arch Gynecol Obstet. 2007; 275:451–460. [PubMed] [Академия Google]
52. Langendoerfer S, Haverkamp A D, Murphy J. et al. Педиатрическое наблюдение за результатами рандомизированного контролируемого исследования интранатальных методов наблюдения за плодом. J Пед. 1980; 97: 103–107. [PubMed] [Google Scholar]
53. Leveno KJ, Cunningham FG, Nelson S. et al. Проспективное сравнение селективного и универсального электронного мониторинга плода при 34 995 беременностях. N Engl J Med. 1986; 315: 615–619. [PubMed] [Google Scholar]
Leveno KJ, Cunningham FG, Nelson S. et al. Проспективное сравнение селективного и универсального электронного мониторинга плода при 34 995 беременностях. N Engl J Med. 1986; 315: 615–619. [PubMed] [Google Scholar]
54. Листон Р., Савчук Д., Янг Д. Наблюдение за здоровьем плода: консенсусное руководство до и во время родов. J Obstet Gynecol Канада. 2007;2904:3–56. [PubMed] [Google Scholar]
55. Лотгеринг Ф.К., Валленбург Х.С., Схоутен Х.Дж. Межнаблюдательские и внутринаблюдательные вариации в оценке дородовых кардиотокограмм. Am J Obstet Gynecol. 1982; 144: 701–705. [PubMed] [Google Scholar]
56. Lumley J, Lester A, Anderson I. et al. Рандомизированное исследование еженедельной кардиотокографии у акушерских пациенток высокого риска. Br J Obstet Gynaecol. 1983; 90: 1018–1026. [PubMed] [Google Scholar]
57. Люти Д.А., Шай К.К., ван Белль Г. Рандомизированное исследование электронного мониторинга сердца плода при преждевременных родах. Акушерство Гинекол. 1987;69:687–695. [PubMed] [Google Scholar]
[PubMed] [Google Scholar]
58. Макдональд Д., Грант А., Шеридан-Перрейра М. Дублинское рандомизированное контролируемое исследование интранатального мониторинга сердечного ритма плода. Am J Obstet Gynecol. 1985; 152: 524–539. [PubMed] [Google Scholar]
59. Маэда К. Новости FIGO: отчет Исследовательской группы FIGO по оценке новых технологий. Оценка и стандартизация мониторинга плода. Int J Gynaecol Obstet. 1997; 59: 169–173. [PubMed] [Google Scholar]
60. Mahomed K, Nyoni R, Mulambo T. et al. Рандомизированное контролируемое исследование интранатального мониторинга сердечного ритма плода. Бр Мед Дж. 1994;308:497–500. [Бесплатная статья PMC] [PubMed] [Google Scholar]
61. Macones G A, Hankins G D, Spong C Y. et al. Отчет семинара Национального института детского здоровья и развития человека 2008 г. об электронном мониторинге плода: обновление определений, интерпретации и руководящих принципов исследований. Акушерство Гинекол. 2008; 112: 661–666. [PubMed] [Google Scholar]
62. Mardirosoff C, Dumont L, Boulvain M. et al. Брадикардия плода из-за интратекального введения опиоидов для обезболивания родов: систематический обзор. БЖОГ. 2002;109: 274–281. [PubMed] [Google Scholar]
Mardirosoff C, Dumont L, Boulvain M. et al. Брадикардия плода из-за интратекального введения опиоидов для обезболивания родов: систематический обзор. БЖОГ. 2002;109: 274–281. [PubMed] [Google Scholar]
63. Миллер Д.А., Рабелло Ю.А., Пол Р.Х. Модифицированный биофизический профиль: дородовое тестирование в 1990-х годах. Am J Obstet Gynecol. 1996; 174: 812–817. [PubMed] [Google Scholar]
64. Morgenstern J, Abels T., Somville T. et al. Точность мониторинга сердечного ритма плода. Гинеколог. 1994; 27: 123–129. [PubMed] [Google Scholar]
65. Мюррей М.Л., Хиггинс П. Компьютер против лекции: стратегии обучения мониторингу плода. Дж. Перинатол. 1996; 16:15–19. [PubMed] [Google Scholar]
66. Национальный совет по здравоохранению и медицинским исследованиям . Канберра: Биотекст; 1999. Как рассматривать доказательства: систематическая идентификация и обзор научной литературы. [Google Scholar]
67. Neilson J P Электрокардиограмма плода (ЭКГ) для мониторинга плода во время родов Cochrane Database Syst Rev 20124CD000116 [PubMed] [Google Scholar]
68. Neilson D R jr., Freeman R K, Mangan S. Результат неоднозначности сигнала при неожиданном исходе при внешнем мониторинге сердечного ритма плода. Am J Obstet Gynecol. 2008;199: 717–724. [PubMed] [Google Scholar]
Neilson D R jr., Freeman R K, Mangan S. Результат неоднозначности сигнала при неожиданном исходе при внешнем мониторинге сердечного ритма плода. Am J Obstet Gynecol. 2008;199: 717–724. [PubMed] [Google Scholar]
69. Neldam S, Osler M, Hansen P K. et al. Мониторинг родов с кардиотокографией и стетоскопическим исследованием при нормальных родах и родах с риском. Угескр Лаегер. 1985; 147: 2901–2907. [PubMed] [Google Scholar]
70. Нелдам С., Ослер М., Хансен П.К. и соавт. Интранатальный мониторинг сердечного ритма плода в комбинированной популяции низкого и высокого риска: контролируемое клиническое исследование. Eur J Obstet Gynecol Reprod Biol. 1986; 23:1–11. [PubMed] [Академия Google]
71. Нельсон К.Б., Дамброзия Дж.М., Тинг Т.Ю. и соавт. Неопределенная ценность электронного мониторинга плода в прогнозировании детского церебрального паралича. N Engl J Med. 1996; 334: 613–618. [PubMed] [Google Scholar]
72. NICHD (Национальный институт детского здоровья и развития человека). Электронный мониторинг сердечного ритма плода: руководство по интерпретации исследований. Семинар по планированию исследований. Am J Obstet Gynecol. 1997; 177:1385–1390. [PubMed] [Google Scholar]
Электронный мониторинг сердечного ритма плода: руководство по интерпретации исследований. Семинар по планированию исследований. Am J Obstet Gynecol. 1997; 177:1385–1390. [PubMed] [Google Scholar]
73. Нейхуис Дж. Г., ван де Пас М. Поведенческие состояния и их онтогенез: исследования человека. Семин Перинатол. 1992;16:206–210. [PubMed] [Google Scholar]
74. Noren H, Blad S, Carlsson A. et al. STAN в клинической практике – результат 2 лет регулярного использования в городе Гётеборг. Am J Obstet Gynecol. 2006; 195:7–15. [PubMed] [Google Scholar]
75. OLG Oldenburg 15.5.90 5 U 114/89; ОЛГ Карлсруэ 28.11.97 U 28/79; ОЛГ Гамбург 30.03.79 1 У 115/77; BGH NJW 1992, 1560=VersR 1992: 745
76. Парер Дж. Т., Кинг Т. Л. Мониторинг сердечного ритма плода: следующий шаг? Am J Obstet Gynecol. 2010; 202: 520–521. [PubMed] [Академия Google]
77. Pattison N McCowan L Кардиотокография для дородовой оценки плода (Кокрановский обзор) Cochrane Database Syst Rev 20101CD001068 [PubMed] [Google Scholar]
78. Petrie R H, Yeh S Y, Murata Y. et al. Влияние лекарственных препаратов на вариабельность сердечного ритма плода. Am J Obstet Gynecol. 1987; 130: 294–299. [PubMed] [Google Scholar]
Petrie R H, Yeh S Y, Murata Y. et al. Влияние лекарственных препаратов на вариабельность сердечного ритма плода. Am J Obstet Gynecol. 1987; 130: 294–299. [PubMed] [Google Scholar]
79. Renou P, Chang A, Anderson I. Контролируемое исследование интенсивной терапии плода. Am J Obstet Gynecol. 1976; 126: 470–476. [PubMed] [Академия Google]
80. Roemer V M. Количественный CTG-Bewertung sub partu mit einem neuen CTG-Score: Wie gut sind die Korrelationen mit den Parametern des fetalen Säure-Basen-Haushaltes im Nabelschnurblut? Z Geburtshilfe Неонатол. 2003; 207: 121–126. [PubMed] [Google Scholar]
81. Рут Г. Лунд: Студенческая литература; 1988. Перинатальный кислотно-щелочной баланс. [Google Scholar]
82. Rooth G, Huch A, Huch R. Новости FIGO: рекомендации по использованию мониторинга плода. Int J Gynaecol Obstet. 1987; 25: 159–167. [Академия Google]
83. Розен К.Г. Анализ формы волны электрокардиограммы плода в родах. Curr Opin Obstet Gynecol. 2005; 17: 147–150. [PubMed] [Google Scholar]
[PubMed] [Google Scholar]
84. Королевский колледж акушеров и гинекологов . Интранатальный уход. Лондон/Великобритания, сентябрь 2007 г.
85. Rüttgers H. Kardiotokography. Стандарты перинатальной медицины. Перинат Мед. 1989; 1: 9–14. [Google Scholar]
86. Samueloff A, Langer O, Berkus M. et al. Является ли вариабельность сердечного ритма плода хорошим предиктором исхода плода? Acta Obstet Gynecol Scand. 1994;73:39–44. [PubMed] [Google Scholar]
87. Saling E. Stuttgart: Thieme; 1966. Das Kind im Bereich der Geburtshilfe. [Google Scholar]
88. Schiermeier S, Westhof G, Daumer M. et al. Die Kurzzeitvariation der fetalen Herzfrequenz und der FIGO-CTG-Score. Erste Erfahrungen в der Kombination dieser Überwachungsparameter. Гебуртш Фрауэнгейлк. 2006; 66: 752–755. [Google Scholar]
89. Schindler T. Aachen: Verlag Mainz; 2002. Алгоритм скользящего окна с задержкой для онлайн-анализа кардиотокограммы: сравнение компьютеризированного анализа КТГ. 1-е изд. [Академия Google]
[Академия Google]
90. Шнайдер К ТМ. Die Überwachung der Geburt aus forensischer Sicht. Гинеколог. 1994; 27: 212–221. [PubMed] [Google Scholar]
91. Schneider K TM, Bung P, Weber S. et al. Ортостатический маточно-сосудистый синдром – проспективное лонгитюдное исследование. Am J Obstet Gynecol. 1993; 169: 183–189. [PubMed] [Google Scholar]
92. Shy K K, Luthy D A, Bennett F C. et al. Влияние электронного мониторинга сердечного ритма плода по сравнению с периодической аускультацией на неврологическое развитие недоношенных детей. N Engl J Med. 1990;322:588–593. [PubMed] [Google Scholar]
93. Spencer J A, Badawi N, Burton P. et al. Интранатальная КТГ до неонатальной энцефалопатии в срок: исследование случай-контроль. Br J Obstet Gynaecol. 1997; 104: 25–28. [PubMed] [Google Scholar]
94. Стайш К. Дж., Вестлейк Дж. Р., Башор Р. А. Слепой тест с окситоциновой нагрузкой и перинатальный исход. Am J Obstet Gynecol. 1980; 138: 399–403. [PubMed] [Google Scholar]
95. Street P, Dawes GS, Moulden M. et al. Краткосрочные изменения в аномальных антенатальных записях сердечного ритма плода. Am J Obstet Gynecol. 1991;165:515–523. [PubMed] [Google Scholar]
Street P, Dawes GS, Moulden M. et al. Краткосрочные изменения в аномальных антенатальных записях сердечного ритма плода. Am J Obstet Gynecol. 1991;165:515–523. [PubMed] [Google Scholar]
96. Tan K H Smyth R Виброакустическая стимуляция плода для облегчения тестов на состояние плода (Кокрановский обзор) Cochrane Database Syst Rev 201312CD002963 [PubMed] [Google Scholar]
97. Thacker S B, Berkelman R L. Оценка диагностической точности и эффективности выбранных методов дородового наблюдения за плодом. Акушерство Gynecol Surv. 1986; 41: 121–141. [PubMed] [Google Scholar]
98. Thacker S B Stroup D Chang M Непрерывный электронный мониторинг сердечного ритма для оценки состояния плода во время родов (Кокрановский обзор) Cochrane Database Syst Rev 20135CD006066 [Google Scholar]
99. Trimbos J B, Keirse M J. Изменчивость наблюдателя в оценке дородовых кардиотокограмм. Br J Obstet Gynaecol. 1978; 85: 900–906. [PubMed] [Google Scholar]
100. Van Geijn H P, Jongsma H W, Doesburg WH et al. Влияние введения диазепама во время беременности или родов на вариабельность сердечного ритма новорожденного. Eur J Obstet Gynecol Reprod Biol. 1980; 10: 187–201. [PubMed] [Google Scholar]
Влияние введения диазепама во время беременности или родов на вариабельность сердечного ритма новорожденного. Eur J Obstet Gynecol Reprod Biol. 1980; 10: 187–201. [PubMed] [Google Scholar]
101. Van Woerden E E, van Geijn H P. Amsterdam: Excerpta Medica; 1994. Факторы, влияющие на ЧСС плода; стр. 211–220. [Google Scholar]
102. Vintzileos A M, Antsaklis A, Varvarigos I. et al. Рандомизированное исследование интранатального электронного мониторинга сердечного ритма плода по сравнению с прерывистой аускультацией. Акушерство Гинекол. 1993; 81: 899–907. [PubMed] [Google Scholar]
103. Vintzileos A M, Nochimson D J, Antsaklis A. et al. Сравнение интранатального электронного мониторинга сердечного ритма плода с периодической аускультацией при выявлении ацидемии плода при рождении. Am J Obstet Gynecol. 1995;173:1021–1024. [PubMed] [Google Scholar]
104. Vintzileos A M, Nochimson D J, Guzman E R. et al. Интранатальный электронный мониторинг сердечного ритма плода по сравнению с прерывистой аускультацией: метаанализ. Акушерство Гинекол. 1995; 85: 149–155. [PubMed] [Google Scholar]
Акушерство Гинекол. 1995; 85: 149–155. [PubMed] [Google Scholar]
105. Visser GH, Dawes GS, Redman CW. Численный анализ нормального антенатального сердечного ритма плода человека. Br J Obstet Gynaecol. 1981; 88: 792–802. [PubMed] [Google Scholar]
106. Voigt M, Schneider K T, Jahrig K. Analyze des Geburtengutes des Jahrgangs 1992 Федеральной Республики Германии. Часть 1: Neue Perzentilwerte für die Körpermaße von Neugeborenen. Гебуртш Фрауэнгейлк. 1996; 56: 550–558. [PubMed] [Google Scholar]
107. Westergaard H B, Langhoff-Roos J, Lingman G. et al. Критическая оценка беременности с высоким риском: использование метаанализа в доказательном акушерстве. УЗИ Акушерство Гинекол. 2001; 17: 466–476. [PubMed] [Google Scholar]
108. Westerhuis M E, Moons K G, van Beek E. et al. Рандомизированное клиническое исследование кардиотокографии плюс забор крови плода по сравнению с кардиотокографией плюс ST-анализ электрокардиограммы плода (STAN®) для интранатального мониторинга. BMC Беременность Роды. 2007;26:13. [Бесплатная статья PMC] [PubMed] [Google Scholar]
BMC Беременность Роды. 2007;26:13. [Бесплатная статья PMC] [PubMed] [Google Scholar]
109. Вуд С., Реноу П., Оутс Дж. и соавт. Контролируемое исследование мониторинга частоты сердечных сокращений плода в акушерской популяции низкого риска. Am J Obstet Gynecol. 1981; 141: 527–534. [PubMed] [Google Scholar]
110. Общество акушеров-гинекологов Канады. Клиническое практическое руководство по наблюдению за здоровьем плода: согласованное руководство до и во время родов № 197 (заменяет № 90 и № 112), Оттава/Канада: SOGC; Сентябрь 2007 г.
111. Young D C, Gray J H, Luther E R. et al. Забор крови из кожи головы плода: его ценность в действующем акушерском отделении. Am J Obstet Gynecol. 1980;136:276–281. [PubMed] [Google Scholar]
112. Zalar R W Jr., Quilligan E J. Влияние взятия проб кожи головы на частоту кесарева сечения при дистрессе плода. Am J Obstet Gynecol. 1979; 135: 239–246. [PubMed] [Google Scholar]
| gif»> |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Математические функции Y=sin X, Y=cos X, Y=tg X, Y=ctg X Клипарт Изображения Клипарт =ctg X Изображения
Этот сайт использует файлы cookie. Продолжая просмотр, вы соглашаетесь на использование нами файлов cookie и других технологий отслеживания. Узнайте больше здесь. Понятно!
- Скачать исходный файл
- Просматривать
Описание
Получите это изображение tangent, Curve, sine в нужном вам формате. Найдите больше похожих векторов Контур, Чертеж, сумма.
Найдите больше похожих векторов Контур, Чертеж, сумма.
Скачать исходный файл
Теги
- Тангенс
- Кривая
- Синус
- Контур
- Составление
- Сумма
- Исследования
- Технология
- Старшая школа
- Котангенс
- Коллекция
- Координация
- Богатство
- Наука
- Математический символ
- Обучение
- Старшая школа
- Заказ
- Косинус
- Вектор
- Придаточные пазухи носа
- Встреча
- Тригонометрия
- Сетка
kotlin.
 math — Язык программирования Котлин
math — Язык программирования КотлинМатематические функции и константы.
Функции включают тригонометрическую, гиперболическую, возведение в степень и степень, логарифмическую, округление, знак и абсолютное значение.
Свойства
Common
JVM
JS
Native
1.2
absoluteValue
Возвращает абсолютное значение этого значения.
val Double.absoluteValue: Double
val Float.absoluteValue: Float
val Int.absoluteValue: Int
val Long.absoluteValue: Long
Common
JVM
JS
Native
1.2
E
Основание натуральных логарифмов примерно 2,71828.
const val E: Double
Common
JVM
JS
Native
1. 2
2
PI
Отношение длины окружности к ее диаметру, примерно 3,14159.
const val PI: Double
Common
JVM
JS
Native
1.2
sign
Returns the sign of this value:
val Double.sign: Double
val Float.sign: Float
val Int.sign: Int
val Long.sign: Int
ulp
Common
JVM
JS
Native
1.2
Возвращает ulp (единица измерения на последнем месте) этого значения.
val Double.ulp: Double
JVM
Native
1.2
Возвращает ulp этого значения.
val Float.ulp: Float
Функции
Common
JVM
JS
Native
1. 2
2
abs
Возвращает абсолютное значение заданного значения x.
fun abs(x: Double): Double
fun abs(x: Float): Float
Возвращает абсолютное значение заданного значения n.
Веселый ABS (N: Int): INT
FIN ABS (N: LONG): LONG
Common
JVM
JS
Compate
1,2
ACOS
Comporte
1,2
ACOS
. значения х;
возвращаемое значение представляет собой угол в диапазоне от 0,0 до PI радиан.
FUN ACOS (x: Double): Double
Fun ACOS (x: Float): Float
Common
JVM
JS
Native
1.2
ACOSH
. косинус значения х.
Fun Acosh (x: Double): Double
Fun Acosh (x: Float): Float
Common
JVM
JS
Натив
1.2
JS
0005
asin
Вычисляет арксинус значения x;
возвращаемое значение представляет собой угол в диапазоне от -PI/2 до PI/2 радиан.
Fun Asin (x: Double): Double
Fun Asin (x: Float): Float
Common
JVM
JS
Native
1.2
ASINH
Native
1.2
ASINH
1.2
7
1.2
7
1.2
синус значения х.
весело asinh(x: Double): Double
Fun Asinh (x: Float): Float
Common
JVM
JS
Натив
1,2
ATAN
Вычисляет дуговую тангенс значения x;
возвращаемое значение представляет собой угол в диапазоне от -PI/2 до PI/2 радиан.
fun atan(x: Double): Double
fun atan(x: Float): Float
Common
JVM
JS
Native0005
1.2
atan2
Возвращает угол тета полярных координат (r, тета) , которые соответствуют
к прямоугольным координатам (x,y) путем вычисления арктангенса значения y/x;
возвращаемое значение представляет собой угол в диапазоне от -PI до PI радиан.
fun atan2(y: Double, x: Double): Double
fun atan2(y: Float, x: Float): Float
Common
JVM
JS
Собственный
1.2
atanh
Вычисляет аркгиперболический тангенс значения x.
Fun Atanh (x: Double): Double
Fun Atanh (x: Float): Float
Common
JVM
JS
Native
1,7
CBRT
7777Native
1,7
CBRT
77777777. х. Для любого
х. Для любого x , cbrt(-x) == -cbrt(x) ;
то есть кубический корень отрицательного значения является отрицательным значением кубического корня
величины этого значения. Особые случаи:
FUN CBRT (x: Double): Double
Fun CBRT (x: Float): Float
Common
JVM
JS
Native
1.2
7Native
1.2
70002. x до целого числа в сторону положительной бесконечности.
FUN CEIL (X: Double): Double
FUN CEIL (X: Float): Float
Common
JVM
JS
СТИНА
1,2
COS
2027
Вычисляет косинус угла x, заданного в радианах.
Fun Cos (x: Double): Double
Fun Cos (x: Float): Float
Common
JVM
JS
Compate
1,2
COSH
COSCEIN значения х.
fun cosh(x: Double): Double
fun cosh(x: Float): Float
Common
JVM
JS
Исходный
1.2
exp
Вычисляет число Эйлера e , возведенное в степень значения x.
Fun Exp (x: Double): Double
Fun Exp (x: Float): Float
Common
JVM
JS
Compity
1,2
Expm11
Computes
1,2
Expm11
. х) — 1 .
fun expm1(x: Double): Double
fun expm1(x: Float): Float 92) без промежуточного переполнения или недолива.
Fun Hypot (x: Double, Y: Double): Double
Fun Hypot (x: Float, Y: Float): Float
JVM
Натив
1,2
IEEEREM
. остаток от деления этого значения на значение делителя согласно стандарту IEEE 754.
остаток от деления этого значения на значение делителя согласно стандарту IEEE 754.
fun Double.IEEErem(divisor: Double): Double
fun Float.IEEErem(divisor: Float): Float
Common
JVM
JS
Native
1.2
ln
Вычисляет натуральный логарифм (по основанию E ) значения.
FUN LN (x: Double): Double
Fun LN (X: Float): Float
Common
JVM
JS
Computes
1,2
LN1PLE
77771,2
LN1PA
77777799000 21,2
LN1P
777777 х + 1) . fun ln1p(x: Double): Double
Компьютеры In(a + 1) .
FUN LN1P (x: Float): Float
Common
JVM
JS
Натив
1,2
Log
Вычисляет логарифм значения x до данной базы.
Fun Log (x: Double, Base: Double): Double
Fun Log (x: Float, Base: Float): Float
Common
JVM
JS
Tapis
10009
JS
0005
log10
Вычисляет десятичный логарифм (по основанию 10) значения x.
FUN LOG10 (x: Double): Double
Fun Log10 (x: Float): Float
Common
JVM
JS
Computes
1.2
Log2
CompureDite
1,2
9
. (основание 2) значения x.
fun log2(x: Double): Double
fun log2(x: Float): Float
Common
JVM
JS
Собственный
1.2
макс.

Возвращает большее из двух значений.
max(a: Double, b: Double): Double
max(a: Float, b: Float): Float
max(a: Int, b: Int): Int
FUN MAX (A: Long, B: Long): Long
Common
JVM
JS
Native
1,2
мин
Возвращает меньшее из двух значений.
мин. веселья(a: Double, b: Double): Double
Fun Min Min (a: long, b: long): long
Nextdown
Common
JVM
JS
Native
1,2
Возвращает двойное значение для этого. бесконечность.
весело Double.nextDown(): Double
JVM
Собственный
1.2
Возвращает значение с плавающей запятой, ближайшее к этому значению в направлении отрицательной бесконечности.
Fun Float.nextdown (): Float
NextTowards
Common
JVM
JS
Натив
1,2
Возвращает двойное значение ближе к этому значению в направлении от этого значения.
fun Double.nextTowards(to: Double): Double
JVM
Собственный
1.2
Возвращает значение с плавающей запятой, ближайшее к этому значению в направлении от этого значения к значению до.
Fun Float.NextTowards (TO: FLOAT): FLOAT
NEXTUP
Common
JVM
JS
Натив
1,2
Возвращает двойное значение ближе к этому значению в направлении положительной непрерывной.
забава Double.nextUp(): Double
JVM
Собственный
1.2
Возвращает значение с плавающей запятой, ближайшее к этому значению в положительном направлении бесконечности.
fun Float.nextUp(): Float
Common
JVM
JS
Native
1.2
Увеличить это значение до степени x 920 920
fun Double.pow(x: Double): Double
fun Float.pow(x: Float): Float
Возводит это значение в степень целого числа n.
fun Double.pow(n: Int): Double
fun Float.pow(n: Int): Float
Common
JVM
JS
Native
1.2
round
Округляет заданное значение x в сторону ближайшего целого числа с округлением до четного целого числа.
fun round(x: Double): Double
fun round(x: Float): Float
Common
JVM
JS
2 Native0005
1. 2
2
roundToInt
Округляет это значение Double до ближайшего целого числа и преобразует результат в Int. Галстуки округлены в сторону положительной бесконечности.
fun Double.roundToInt(): Int
Округляет это значение Float до ближайшего целого числа и преобразует результат в Int. Галстуки округлены в сторону положительной бесконечности.
fun Float.roundToInt(): Int
Общий
JVM
JS
Родной
1.2
roundToLong
Округляет это значение Double до ближайшего целого числа и преобразует результат в Long. Галстуки округлены в сторону положительной бесконечности.
fun Double.roundToLong(): Long
Округляет это значение Float до ближайшего целого числа и преобразует результат в Long. Галстуки округлены в сторону положительной бесконечности.
fun Float. roundToLong(): Long
roundToLong(): Long
Common
JVM
JS
Native
1,2
Знак
Возврат знака заданного значения x:
Веселый знак (x: двойной): двойной
Веселый знак (x: float): Float
Common
JVM
12 JS
Native
1.2
sin
Вычисляет синус угла x, заданного в радианах.
fun sin(x: Double): Double
fun sin(x: Float): Float
Common
JVM
JS
Собственный
1.2
sinh
Вычисляет гиперболический синус значения x.
Fun Sinh (x: Double): Double
Fun Sinh (x: Float): Float
Common
JVM
JS
Computes
1. 2
2
SQRT
7777. корень значения х.
fun sqrt(x: Double): Double
fun sqrt(x: Float): Float
Обычный
JVM
JS
Собственный
1.2
tan
Вычисляет тангенс угла x, заданный в радианах.
Fun Tan (x: Double): Double
Fun Tan (x: Float): Float
Common
JVM
JS
Compity
1,2
TANH
COMPORTER
1,2
TANH
. значения х.
fun tanh(x: Double): Double
Fun Tanh (x: Float): Float
Common
JVM
JS
Натив
1,2
Truncate
Раунд.
Веселый усечение (x: Double): Double
Веселый усек бит знака такой же, как и у значения знака.



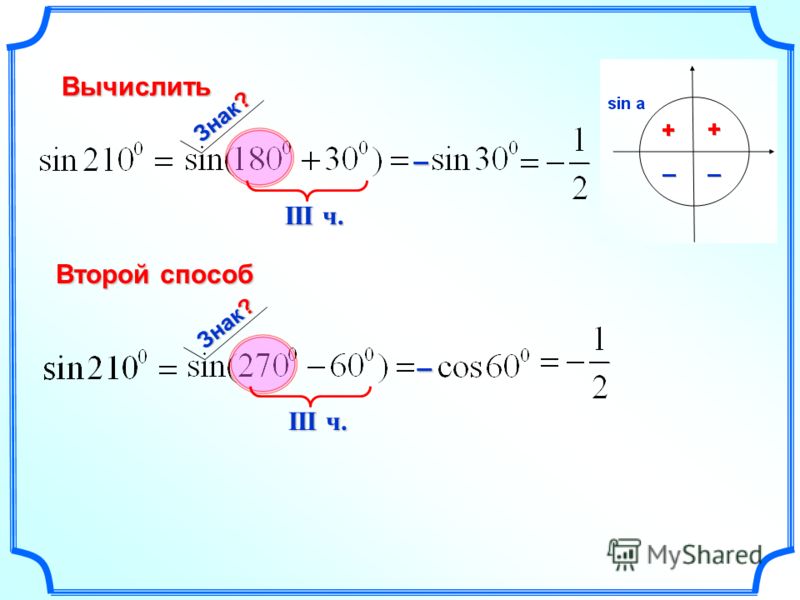 Следует применять принцип «от простого к сложному», поскольку нужно учитывать физиологические особенности головного мозга.
Следует применять принцип «от простого к сложному», поскольку нужно учитывать физиологические особенности головного мозга.
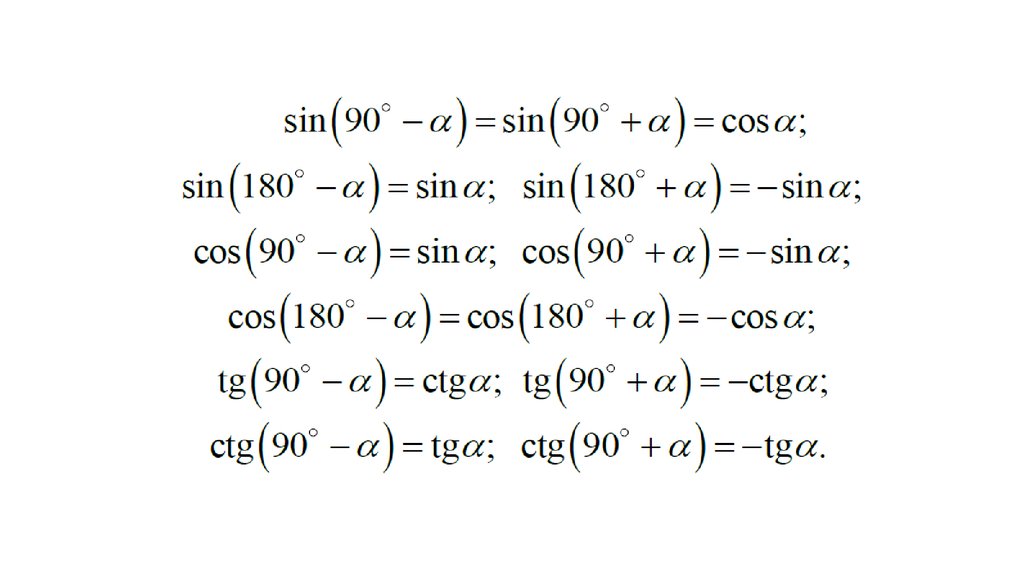
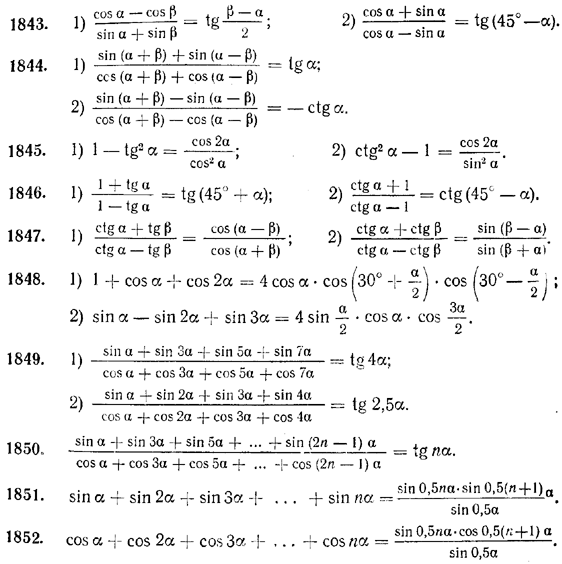
 Его стороны называются катетами и гипотенузой. Угол между двумя катетами является прямым, то есть он равен 90 градусам.
Его стороны называются катетами и гипотенузой. Угол между двумя катетами является прямым, то есть он равен 90 градусам.


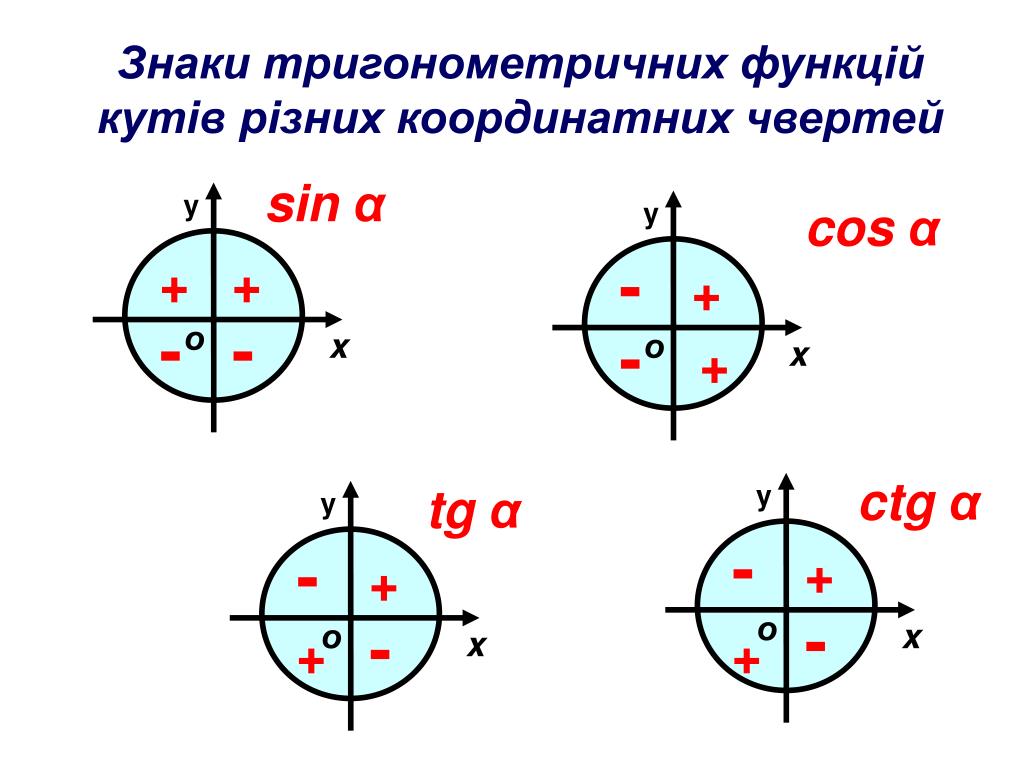 среднее школа / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Эд. С. А. Теляковский.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
среднее школа / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Эд. С. А. Теляковский.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7