Cosa cosb cosc: Решить cosa+cosb-cosc | Microsoft Math Solver

Докажите, что в треугольнике ABC (cosB-cosC)/(cosA+1) =(c-b)/a

• Курс
  • NCERT
    • Класс 12
    • Класс 11
    • Класс 10
    • Класс 9
    • Класс 8
    • Класс 7
    • Класс 6
  • IIT JEE

• Экзамен
  • JEE MAINS
  • JEE ADVANCED
  • X BOARDS
  • XII BOARDS
  • NEET
    • Neet Предыдущий год (по годам) )
    • Физика Предыдущий год
    • Химия Предыдущий год
    • Биология Предыдущий год
    • Нет Все образцы работ
    • Образцы работ Биология
    • Образцы работ Физика
    • Образцы работ Химия 900 08

• Скачать PDF-файлы
  • Класс 12
  • Класс 11
  • Класс 10
  • Класс 9
  • Класс 8
  • Класс 7
  • Класс 6

• Экзаменационный уголок

• Онлайн-класс

• Викторина

• Задать вопрос в Whatsapp

• Поиск Doubtnut

• Английский словарь

• Toppers Talk

• Блог

• Скачать

• Получить приложение

Вопрос

Обновлено: 26. 04.2023

Рекомендуемые вопросы

9 видео

РЕКЛАМА

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

---

Видео по теме

Если A, B и C углы треугольника, то определитель
∣∣ ∣∣−1cosCcosBcosC−1cosAcosBcosA−1∣∣ ∣∣ равно

642508075

03:32

यदि A,B और C एक त्रिभुज के कोण है तो सारणिक ∣∣ ∣∣−1cosCcosBcosC−1cosAcosBcosA−1∣∣ ∣∣ बराबर है

642733930

04:03

यदि A,B और C एक त्र िभुज के कोण है तो सारणिक ∣∣ ∣∣−1cosCcosBcosC−1cosAcosBcosA−1∣∣ ∣∣ बराबर है

642741084

05:09

Если в треугольнике ABC cosAa=cosBb=cosCc, то треугольник равен

642975984

03:18 901 23

В ΔABC докажите, что
b+ca=cosB+cosC1−cosA

643160604

10:11

В ΔABC докажите, что
(b+c)cosA + (c+a)cosB + (a+b)cosC = a+b+c

643160606 9 0123

03:05

Если A,B,C — углы треугольника, то докажите, что ,∣∣ ∣∣−1cosCcosBcosC−1cosAcosBcosA−1∣∣ ∣∣=0

644175832

08:52

РЕКЛАМА

• Рекомендуемые вопросы

• Докажите, что в треугольнике ABC (cosB-cosC)/(co sA+1) =(c-b)/a

  03:27

• Если A,B и C углы треугольника, то определитель |(-1,cosC. ..

  04:10

• Дельта ABC में सिद्ध क ीजिए कि — (b+c)cosA+(c +a)cosB+(a+b)cosC=a+b+c

  03:02

• Если A,B,C — углы треугольника, то докажите, что |{:(-1,cosC, cosB),(…

  08:09

• Если в треугольнике ABC (cosA)/a=(cosB)/b=(cosC)/c, то треугольник равен

  01:58

• यदि А, Б और C एक त्रिभुज के कोण हैं तो सारणिक |(1,cosC,cosB),(cosC,1…

  Text Решение

• Если A,B,C углы треугольника, то Delta=|( -1,cosC, cosB),(co…

  04:05

• В треугольнике ABC (cosB+cosC)/(1-cosA)=

  02:54

• Если А ,B и C углы треугольника, то определитель : |(-1,c…

  02:18

1. Ask Unlimited Doubts
2. Видеорешения на нескольких языках (включая хинди)
3. Видеолекции экспертов
4. Бесплатные PDF-файлы (документы за предыдущий год, книжное решение) s и многое другое)
5. Посетить специальное предложение Консультационные семинары для IIT-JEE, NEET и экзаменов Совета

Doubtnut хочет отправлять вам уведомления. Разрешите получать регулярные обновления!

Listening…

[Решено] Рассмотрим треугольник ABC, в котором cos A + cos B + cos C = &

Рассмотрим треугольник ABC, в котором cos A + cos B + cos C = √3 sin (π/3)

Каково значение \(\;{\rm{sin}}\frac{{\rm{A}}}{2}{\rm{sin}}\frac{{\rm{B}}}{2 }{\rm{sin}}\frac{{\rm{C}}}{2}\)?

1. \(\frac{1}{2}\)
2. \(\frac{1}{4}\)
3. \(\frac{1}{8}\)
4. \(\ frac{1}{{16}}\)

Вариант 3: \(\frac{1}{8}\)

Концепция:

1. \({\rm{cos\;A \;}} + {\rm {\;cos\;B\;}} = {\rm{\;}}2{\rm{cos}}\left({\frac{{{\rm{A}} } + {\rm{B}}}}{2}} \right)\cos \left( {\frac{{{\rm{A}} — {\rm{B}}}}{2}} \ справа)\) 92}\frac{{\rm{\theta}}}{2}\)
2. \({\rm{cos}}\left( {\frac{{\rm{\pi}}}{2} — \frac{{\rm{\theta}}}{2}} \right) = \sin \left( {\frac{{\rm{\theta}}}{2}} \right)\) и \({\rm{sin}}\left( {\frac{{\rm{\pi }}}{2} — \frac{{\rm{\theta}}}{2}} \right) = \cos \left( {\frac{{\rm{\theta}}}{2}} \ справа)\)

Расчет:

Дано: cos A + cos B + cos C = √3 sin (π/3)

Чтобы найти: \({\rm{sin}}\frac{{\rm {A}}}{2}{\rm{sin}}\frac{{\rm{B}}}{2}{\rm{sin}}\frac{{\rm{C}}}{2} \) 92}\frac{{\rm{C}}}{2}\;\;\;\;\; \ ldots .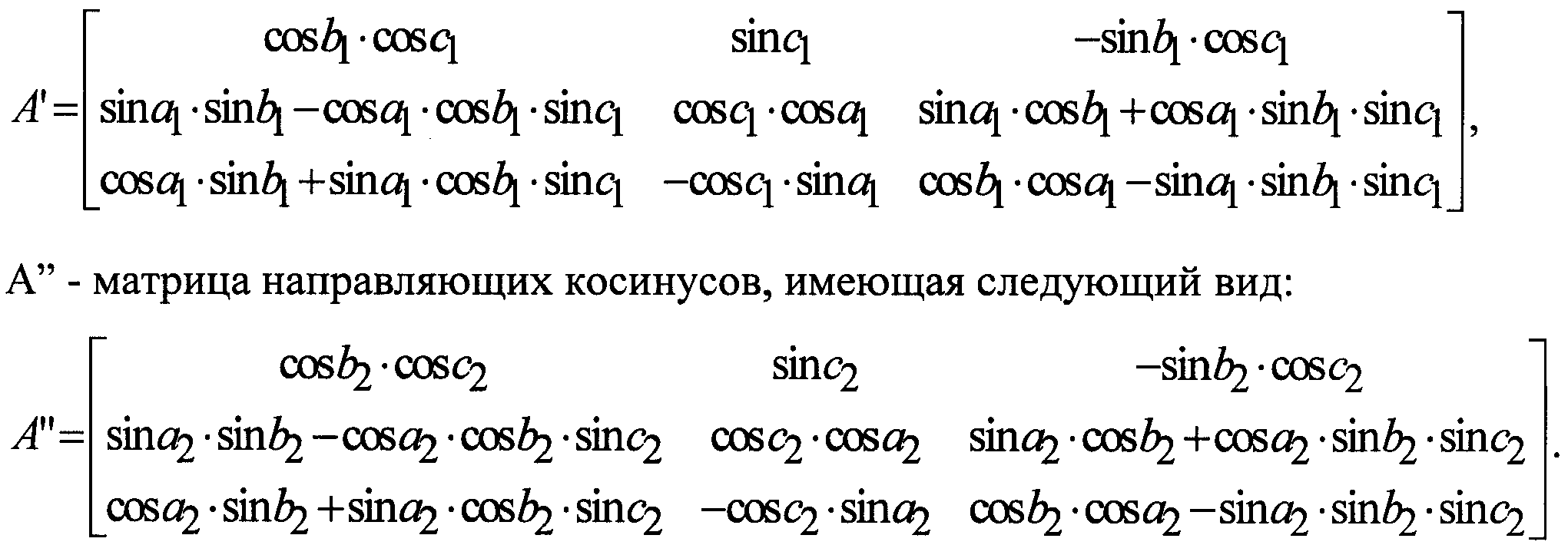 . \ влево ( {{\ rm {cos}} \ влево ( {\ frac {{\ rm {\ pi}}} {2} — \ frac {{\ rm {\ theta}}} {2} } \right) = \sin \left( {\frac{{\rm{\theta}}}{2}} \right)} \right)\)

\(\Rightarrow {\rm{cos}}\ влево ( {\ frac {{{\ rm {\ pi}} — {\ rm {C}}}} {2}} \ right) = {\ rm {sin}} \ left ( {\ frac {{\ rm {C}}}{2}} \right)\)   …. (1)

\(= 1 + 2{\rm{sin}}\left( {\frac{{\rm{C}}}{2}} \right)\left({\cos \left({ \frac{{{\rm{A}} — {\rm{B}}}}{2}} \right) — \sin \frac{{\rm{C}}}{2}} \right)\ )               (принимая 2sin (C/2))

\ (= 1 + 2 {\ rm {sin}} \ left ( {\ frac {{\ rm {C}}} {2}} \ right) \ left ( {\ cos \ left ( {\ frac { {{\rm{A}} — {\rm{B}}}}{2}} \right) — \cos \left( {\frac{{{\rm{A}} + {\rm{B} }}}{2}} \right)} \right)\)         (C = π – (A + B))

\(= 1 + 2{\rm{sin}}\left( {\frac{{ \rm{C}}}{2}} \right)2\left( {\sin\left( {\frac{{\frac{{{\rm{A}} — {\rm{B}}}} {2}\; + \;\frac{{{\rm{A}} + {\rm{B}}}}{2}}}{2}} \right)\sin \left( {\frac{ {\ frac {{{\ rm {A}} + {\ rm {B}}}} {2} \; — \; \; \ frac {{{\ rm {A}} — {\ rm {B} }}}{2}}}{2}} \right)} \right)\)            \({\rm{Using\;}}\cos {\rm{A}} — \cos {\rm{B} } = 2 \ sin \ left ( {\ frac {{{\ rm {A}} + {\ rm {B}}}} {2}} \ right) \ sin \ left ( {\ frac {{{\ rm {B}} — {\rm{A}}}}{2}} \справа)\)

\( = 1 + 4\sin \left( {\frac{{\rm{C}}}{2}} \right)\sin \left({\frac{{\rm{A}}}}{ 2}} \right)\sin \left( {\frac{{\rm{B}}}{2}} \right)\)

= RHS

\(\Стрелка вправо 1 + 4\sin \left( {\frac{{\rm{C}}}{2}} \right)\sin \left( {\frac{{\rm{A}}} {2}} \right)\sin \left( {\frac{{\rm{B}}}{2}} \right) = \surd 3{\rm{\;sin\;}}\left( { {\rm{\pi }}/3} \right)\)

\(\Rightarrow \sin \left( {\frac{{\rm{C}}}{2}} \right)\sin \left ( {\ frac {{\ rm {A}}} {2}} \right) \ sin \ left ( {\ frac {{\ rm {B}}} {2}} \ right) = \ frac {{\ sqrt 3 {\rm{sin\;}}\left( {\frac{{\rm{\pi }}}{3}} \right) — 1}}{4}\)

\(= \frac{{\frac{{\sqrt 3 \sqrt 3}}{2} — 1}}{4}\)               \(\ldots (\sin \left( {\frac {{\rm {\pi}}}{3}} \right) = \frac{{\sqrt 3}}{2}\}}

\(= \frac{{3\; — \;2}}{{2 \; \times \;4}}\)

\(= \frac{1}{8}\)

Следовательно, вариант 3 правильный.