Сдам егэ тригонометрические уравнения. Тригонометрические уравнения
МБОУ « Мордовско-Паёвская СОШ» Инсарского района РМ
Выполнила: Пантилейкина Надежда,
ученица 11 класса
Руководитель: Кадышкина Н.В.,
учитель математики
Оглавление
Введение…………………………………………………………………………….
Глава I. О тригонометрических уравнениях…………………………………..…5
1) Основные типы тригонометрических уравнениях и методы их решения:
1. Уравнения, сводящиеся к простейшим. …………………………………..5
2. Уравнения, сводящиеся к квадратным…………………………………….5
3. Однородные уравнения acosx + b sin x = 0…………………………………6
4.Уравнения вида acosx + b sin x = c , с≠ 0…………………………………7
5. Уравнения, решаемые разложением на множители……………………….7
6. Нестандартные уравнения………………………………………………….8
Глава II. Основные понятия и формулы тригонометрии…………………….8-10
Глава III
. Уравнения предлагавшиеся на ЕГЭ прошлых лет…………………10-14
Уравнения предлагавшиеся на ЕГЭ прошлых лет…………………10-14
Заключение………………………………………………………………………….14
Приложение……………………………………………..……………………….15-17
Литература…………………………………………………………………………..18
Введение
«Единственный путь, ведущий к знаниям — это деятельность…»
Бернард Шоу
Актуальность работы.
Через несколько месяцев я заканчиваю школу.
Чтобы не было проблем с дальнейшим выбором жизненного пути, необходимо получить школьный аттестат, а для того чтобы получить школьный аттестат, необходимо сдать два обязательных экзамена в форме ЕГЭ — и один из них математика . Что уж там говорить, выпускные экзамены — ответственный период в жизни любого школьника, от которого зависит не только итоговая оценка в аттестате, но и его профессиональное будущее, доход и карьера.
Единый Государственный Экзамен – это важный тест перед переходом в новую жизнь и поступлением в университет или колледж.
Как не допустить провала на экзамене и получить хорошие баллы? Для этого необходимо хорошо решить задания. Я не претендую на максимальный балл, тем не менее старательно готовлюсь. И заметила, что даже на первом задании части С, а, именно, на решении тригонометрических уравнениях и их системах допускаю ошибки. На первый взгляд, задача С1 – это относительно несложное уравнение или система уравнений, которое может содержать тригонометрические функции, одним из основных подходов к решению которых состоит в их последовательном упрощении с целью сведения к одному или нескольким простейшим. Так почему я ошибаюсь?
Актуальность темы определяется тем, что учащиеся должны разбираться в тех или иных способах решения тригонометрических уравнений.
Поэтому, перед собой я поставила следующую цель:
Систематизировать, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений.
Объектом исследования является изучение тригонометрических уравнений в заданиях ЕГЭ.
Предмет исследования — является решение тригонометрических уравнений
Таким образом, основной целью написания данной курсовой работы является изучение тригонометрических уравнений и их систем, способы их решения.
В соответствии с целями, объектом и предметом исследования определены следующие задачи:
1). Изучить все задания, связанные с решением тригонометрических уравнений, предлагавшиеся на ЕГЭ работ предыдущих лет и при выполнении диагностических работ;
2) Изучить методы решения тригонометрических уравнений.
3). Выявить основные возможные ошибки при решении таких уравнений;
4). Выяснить причину допущения таких ошибок.
6). Сделать выводы.
В своей работе я решу несколько тригонометрических уравнений, покажу возможные ошибки при их решении и постараюсь ответить на следующие вопросы:
1). Можно ли избежать ошибок при выполнении заданий типаС1
2) Если я буду тренироваться в решении уравнений такого типа, то я смогу
ли безошибочно выполнять такие задания?
Для этой цели я изучила все демонстрационные и тренировочные задания, проводимые с нами, материалы ЕГЭ предыдущих лет;
изучила справочные источники;
самостоятельно решала задания из Интернета;
консультировалась со своим учителем в случае затруднения;
училась анализировать и правильно оформлять результаты.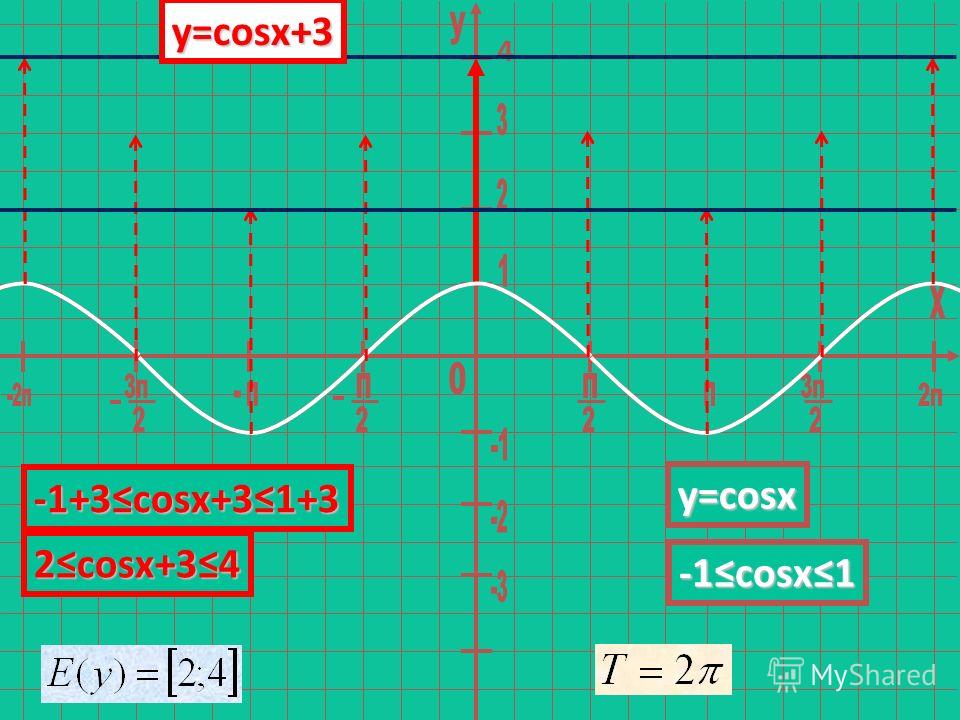
Глава I . О тригонометрических уравнениях.
1) Определение 1. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Простейшие тригонометрические уравнения — это уравнения вида sin x = a ,
cos x=a, tg x=a, ctg x = a.
В таких уравнениях переменная находится под знаком тригонометрической функции, а — данное число.
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения.
2)Основные типы тригонометрических уравнений.
Уравнения, сводящиеся к простейшим.
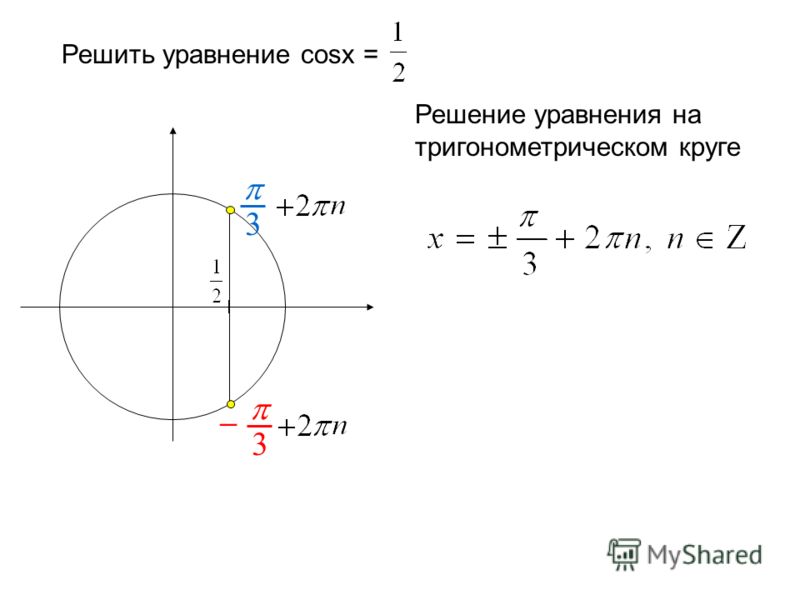
Решить уравнение
Решение:
Ответ:
Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Ответ:
Однородныеуравнения: asinx + bcosx = 0
a sin 2 x + b sinxcosx + c cos 2 x =
0.
Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем,
что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx.
Получим
Ответ:
Пример: Решить уравнение
Решение:
Ответ:
Уравнения, решаемые разложением на множители.
Припер: Решить уравнение sin2x – sinx = 0.
Решение: Используя формулу sin2x = 2sinxcosx, получим
2sinxcosx – sinx = 0,
sinx (2cosx – 1) = 0.
Произведение равно нулю, если хотя бы один из множителей равен нулю.
Ответ:
Нестандартные уравнения.
Решить уравнение cosx = х 2 + 1.
Решение:
Рассмотрим функции
Глава
Тригонометрические уравнения — обязательная тема любого экзамена по математике.
О х, сколько мучений доставляет ученикам изучение тригонометрии.
Определенные сложности возникают даже в том случае, если рядом учитель по математике и объясняет каждую мелочь. Это и понятно, одних только базовых формул существует более двадцати. А уж если считать их производные … Ученик путается в вычислениях и никак не может запомнить механизмы, при помощи которых эти формулы позволяют найти, например, .
Вы знаете формулы — вам легко решать. Не знаете — не поймете, даже если дадут формулу. Формулу нужно не просто тупо знать, а знать куда ее можно применить, как раскрыть и в чем суть формулы, а для этого вам нужно решать примеры именно для тех задач, которые даются с трудом.
Мне поначалу казалось, тригонометрия — это скучный набор формул и графиков. Однако, знакомясь с новыми понятиями тригонометрии и методами решения тригонометрических уравнений, каждый раз убеждалась, насколько интересен и увлекателен мир тригонометрии.
Во- первых, для успешного решения тригонометрических уравнений нужно хорошо знать тригонометрические формулы, причем не только основные, но и дополнительные (преобразование суммы тригонометрических функций в произведение и произведения в сумму, формулы понижения степени и другие), так как использование на ЕГЭ шпаргалок и мобильных телефонов запрещается
(Приложение1)
Во- вторых , мы должны четко знать стандартные формулы корней простейших тригонометрических уравнений (полезно помнить или уметь получать с помощью тригонометрической окружности упрощенные формулы для корней уравнений)
Каждое из таких уравнений решается по формулам, которые следует знать.
а) Функция y = sin x . Функция ограниченная: находится в пределах [-1; 1]. Это значит, что при решении уравнений типа sinx =2 или sinx sinx
1) sinx =a, x= (-1) n arc sin a +n,nZ
2) sinx = — a, x= (-1) n+1 arc sin a +n,nZ
Также, нужно знать частные случаи:
1)
sinx
=- 1,
2)sinx
=0,
3)sinx
=
a
,
Также нужно уметь решение в виде двух серий корней
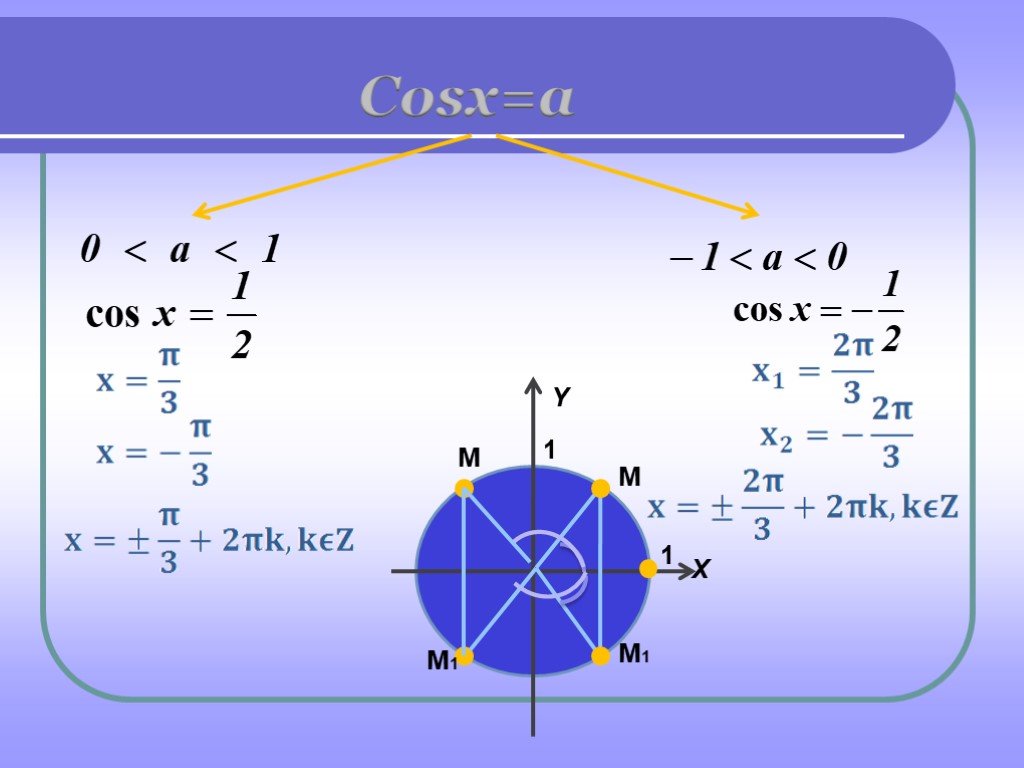
2. Функция y = cos x . Функция ограниченная: находится в пределах [-1; 1]. Это значит, что при решении уравнений типа cos x =2 или cos x =-5 в ответе получается: нет корней. Формулы для функции у= cos x :
1. cosx =a, X=± arccos a+2n,nZ
2. cos x=-a, X=±( — arccos a)+2n,nZ
Частные случаи: 1. cosx =-1, X = +2 n , nZ
2.
cosx =0,
3. cosx =1, X= 2n,nZ
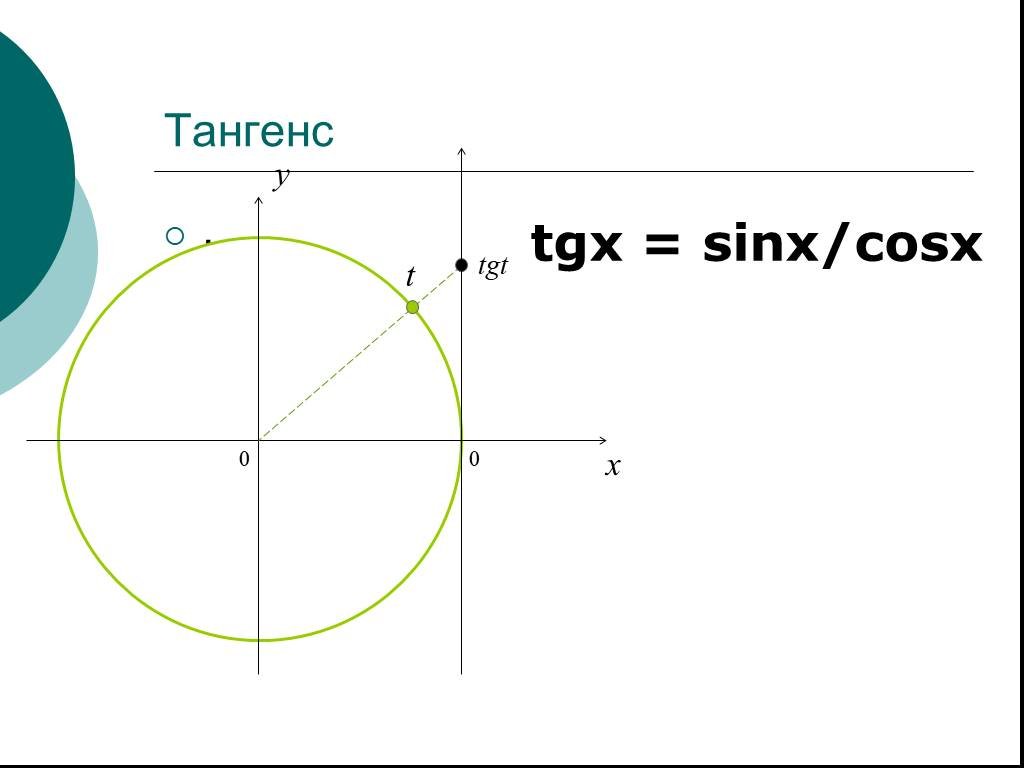
3. Функция y = tg x .
Тут всего одна формула, без частных случаев:
tg
x
=
±
a
.
х= ± arctg a+n,nZ
В-третьих, надо знать значения тригонометрических функций;
(Приложение 2)
В- четвёртых, Если в уравнении тригонометрическая функция находится под знаком радикала, то такое тригонометрическое уравнение будет иррациональным. В таких уравнениях следует соблюдать все правила, которыми пользуются при решении обычных иррациональных уравнений (учитывается область допустимых значений как самого уравнения, так и при освобождении от корня четной степени).
V . Уравнения, предлагавшиеся на ЕГЭ прошлых лет.
«Метод решения хорош, если с самого начала мы можем предвидеть – и впоследствии подтвердить это, — что, следуя этому методу, мы достигнем цели».
Лейбниц
1. Уравнения, сводящиеся к квадратному.
С1. Решить уравнение:
Решение: Воспользовавшись основным тригонометрическим тождеством,
перепишем уравнение в виде
Заменой
cos
=
t
уравнение сводится к квадратному:2
t
2
+ 9
t
-5 =0, которое имеет корни
t
1
= ½ и
t
2
= -5. Возвращаясь к переменной х, получим
Возвращаясь к переменной х, получим
,
Второе уравнение корней не имеет так как |cosx |≥1, а из первого x =±+6k ,kZ
Ответ: =±+6k ,kZ
Вывод: вводя новую переменную, нужно учитывать, что значения sin
x
и cos
x
ограничены отрезком
, а иначе появятся посторонние корни.
2. Уравнения, решаемые разложением на множители
Задание С1 (2011 г.)
а) Решить уравнение
б) Указать корни уравнения, принадлежащие отрезку
Решение: а) решаем разложением левой части на множители:
группируем и выносим общий множитель за скобки, получим
Уравнение 1) решений не имеет.
Второе уравнение однородное, решается делением почленно на cosx
≠0, получим
, откуда
б)
Ответ: а)
б)
Вывод:
1.При решении уравнения такого вида, во – первых, нужно знать, что |sin х|≤1 и |cosx |≤1, и уравнение sinx =-2 решений не имеет;
2.Во – вторых, обосновать деление на cosx ≠о (так как, если cosx =0,то sin х=0 , а это невозможно;
в- третьих, обоснованно произвести отбор корней, принадлежащие данному промежутку
3
. Уравнение на применение формул приведения
Уравнение на применение формул приведения
С1 (2010 г.) Дано уравнение
а) решить уравнение;
б
) Указать корни, принадлежащие отрезку
Решение: Используя формулы приведения, получим:
sin 2 x – cos x =0,
2 sinx cosx- cosx =0,
сosx (2 sinx -1)=0, откуда cosx= 0 или sinx =½,
б) Найдем значения к, при которых корни будут принадлежать
указанному промежутку. Для того, чтобы выбрать корни. принадлежащие заданному промежутку, решение представим в виде:
б
) Найдем значения к, при которых корни будут принадлежать указанному промежутку
.
2)
Решая это неравенство, целого
значения к не получим.
Ответ: а)
б)
Вывод:
При решении уравнения такого вида, необходимо знать формулы приведенного уравнения и правильно её применить; уметь представлять решение
на две серии корней; правильно выбрать корни, принадлежащие заданному отрезку.
4. Системы тригонометрических уравнений
С1 (2010). Решить систему уравнений
Решение: О.Д.З
Дробь равна нулю, если числитель равен 0, а знаменатель не равен 0.
Из уравнения 2sin 2 x – 3 sinx +1 =0, решая методом введения новой переменной, находим
или sin
x
=1.
1)Пусть
, тогда
и у = cos
x
= ›0 (используя основное тригонометрическое тождество)
либо
и
— нет решения.
2) Пусть sinx = 1, тогда у = cos x = 0 – нет решения.
Ответ:
и у =
Вывод: 1) нужно учитывать ограниченность тригонометрических
функций
2) Записывать и учитывать О.Д.З.
5. С1 (ЕГЭ 2011 г.) Решить уравнение:
О.Д.З. – cos x ≥ 0, sin х ≤ 0.
4sin 2 x + 12 sinx + 5 = 0 или cos x =0
sinx = t
4 t 2 + 12 t + 5=0, откуда t 1 =-½ , t 2 = —
sinx = -½ sinx =- — не имеет решения
х =
х =
с учётом О.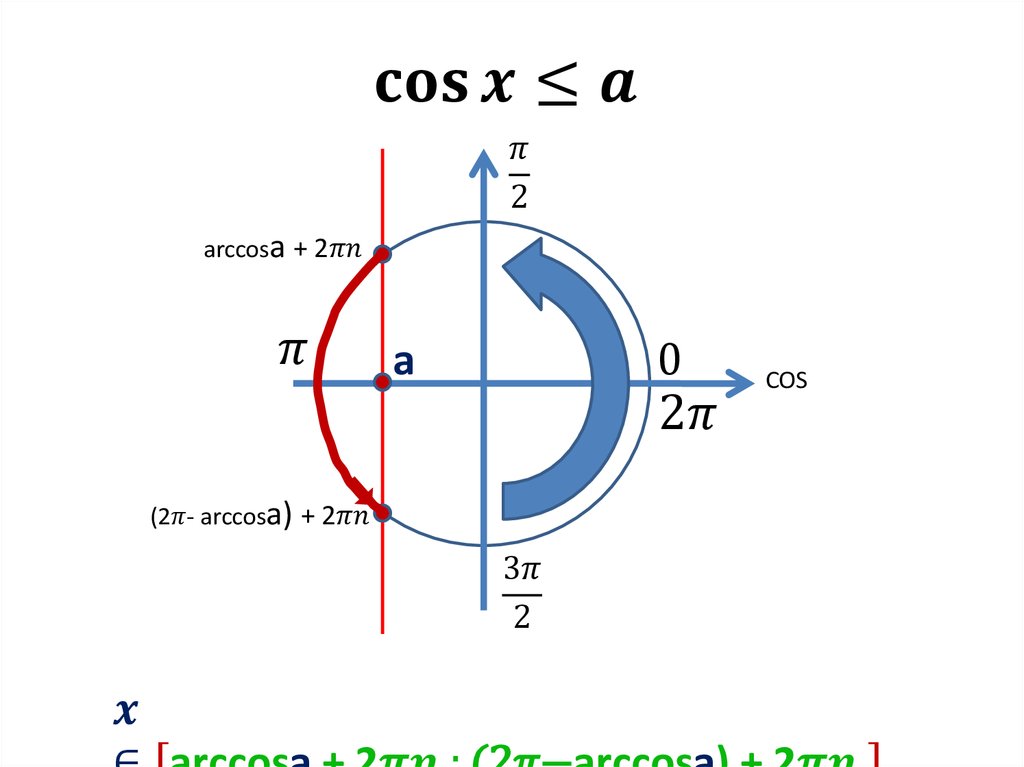 Д.З. х =
Д.З. х =
Ответ: х =
Вывод: Ответ записать с учётом О.Д.З.
ЗАКЛЮЧЕНИЕ
В проделанной мною работе были изучены решения тригонометрических уравнений, рассмотрены рекомендации по решению тригонометрических уравнений, методы решения тригонометрических уравнений и рассмотрены ошибки, которые возможны при их решении.
Я пришла к следующим выводам:
1. Задания типа С1 проверяют умение решать тригонометрические уравнения. Эти задания являются, действительно, несложными, что придаёт лишнюю самоуверенность и усыпляют внимательность. Единственной сложностью этих заданий является то, что, решив уравнение или систему уравнений, отбросить посторонние корни.
2. Задача С1 – это самая простая задача группы С. При ее решении не должны возникать громоздкие преобразования и сложные вычисления. Если же они появились – немедленно нужно остановиться, проверить решение и попробовать понять, что же здесь не так.
3. В конечном итоге,
главное требование — решение должно быть математически грамотным, из него должен быть понятен ход рассуждений. Нужно постараться записать свое решение кратко и понятно, но главное – правильно!
Нужно постараться записать свое решение кратко и понятно, но главное – правильно!
4. И самое главное — чтобы научиться без ошибок решать уравнения, надо их решать! Ведь, как говорил Пойа, « Если хотите научиться плавать, то смело ныряйте в воду, а если хотите научиться решать задачи, надо их решать!»
Приложение 1 (основные формулы тригонометрии)
1) основное тригонометрическое тождество sin 2 α + cos 2 α= 1,
Деля это уравнение на квадрат косинуса и синуса соответственно имеем
2)формулы двойного аргумента sin 2α =2 sin α cos α,
cos 2 α = cos 2 α — sin 2 α ,
Cos 2α = 1- 2sin 2 α,
3)формулы понижения степени:
4) формулы суммы и разности двух аргументов:
sin (α+ β )= sin α cos β + cos α sin β
sin (α- β )= sin α cos β — cos α sin β
cos (α+ β )= cos α cos β + sin α sin β
cos (α- β )= sin α cos β + sin α sin β
5)Формулы приведения
Формулами приведения называются формулы следующего вида:
Суммы суммы и разности тригонометрических уравнений
Чётность
Косинус- чётная, синус, тангенс и котангенс- , то есть:
Непрерывность
Синус и косинус — . Тангенс и имеет
Тангенс и имеет
,котангенс 0; ±π; ±2π;…
Периодичность
Функции y = cos x , y = sin x —
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Соблюдение Вашей конфиденциальности важно для нас.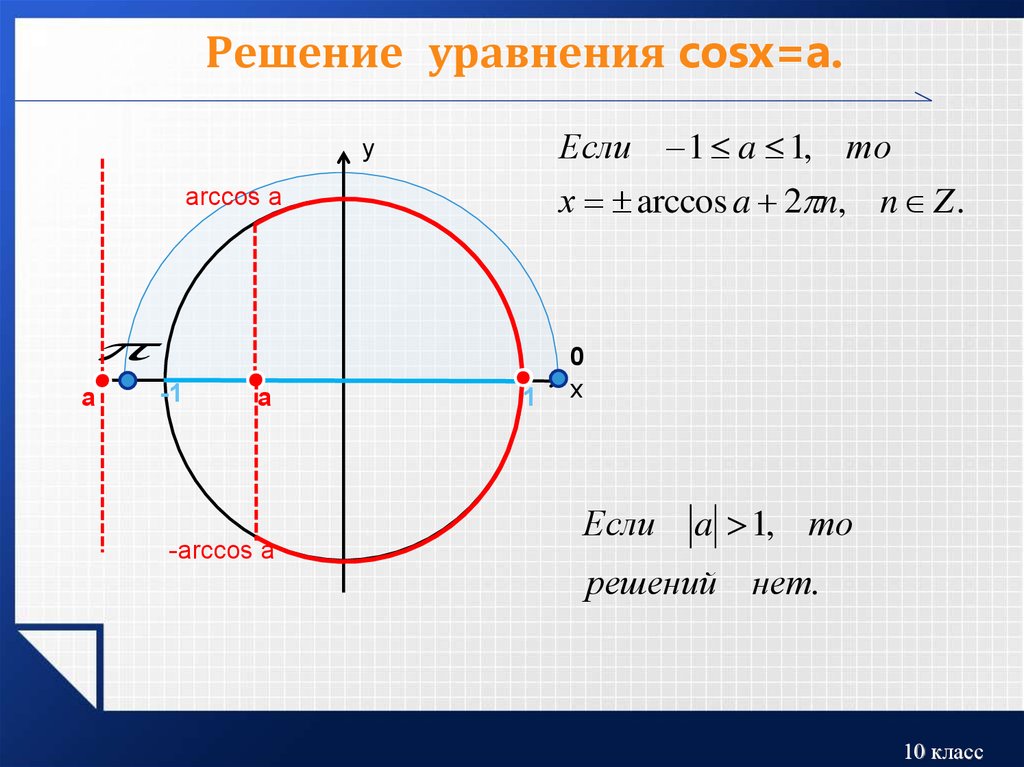 По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 6 из 14Следующая ⇒ Самостоятельная работа №14 «Тригонометрические формулы» Цель: способствовать закреплению навыков преобразования тригонометрических выражений. Основные формулы тригонометрии ; ; ; ; ; t ; . Синус и косинус суммы и разности аргументов:
Формулы двойного аргумента: Формулы понижения степени:
Преобразование сумм тригонометрических функций в произведение:
Задание 1.Заполнить таблицу «Тригонометрия. При заполнении можно воспользоваться лекциями или учебниками:
Форма выполнения задания: оформленная таблица. Задание 2.
Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок. Самостоятельная работа № 15 «Тригонометрические уравнени я» Цель: Знать методы решения тригонометрических уравнений и применять их при решении упражнений. Теоретический материал Формулы для повторения arcsin( a) = arcsin a arccos ( a) = arctg ( a) = arctg a arcctg ( a) = arcctg a Общие формулы решения тригонометрических уравнений
Частные решения тригонометрических уравнений
Значение тригонометрических функций
Формулы для повторения: , . Если , то корни квадратного уравнения находим по формуле:
Образцы решения тригонометрических уравнений второго порядка: Образец№1 Решить уравнение: Решение. Введем новую переменную: z = sin x. Тогда уравнение примет вид: 2z2 – 5z + 2 =0. Решая квадратное уравнение находим z1 = 2 и z2 = . Значит, либо sin x = 2, либо sin x = . Первое уравнение не имеет корней, а из второго находим Образец №2 Решить уравнение: Решение: Воспользуемся тем, что Тогда заданное уравнение можно записать в виде: После преобразования получим: Введем новую переменную z = cos x. Тогда данное уравнение примет вид: 2z2 –z -1 = 0. Решая его, находим z1 = 1, z2 = Значит, либо cos x = 1, либо cos x = Решая первое уравнение cos x = 1, как частное, находим его решение . Решая второе уравнение, находим решение: x arccos ) + + 2 Образец №3 Решить уравнение: Решение: С числом 2, содержащимся во правой части, поступим следующим образом. Известно, что — это тождество верно для любого значения х. Тогда . Заменив в первом уравнении 2 на , получим: sinx cosx + 5 sinx cosx + 5 Обе части уравнения разделим на cos2 x почленно Так как , то полученное уравнение запишем в виде: tg2x — Введя новую переменную t=tg x, получим квадратное уравнение: +3=0, решая уравнение, получим: t = Итак, tg x= x= arctg x= , .
Задание: решить тригонометрические уравнения.
Форма выполнения задания: решение уравнений. Контроль: работу сдать преподавателю в тетрадках для самостоятельных работ в установленный срок. ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-08-16; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
доказать, что sinx+cosx=1 — eNotes.com
значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«докажи это sinx+cosx=1» Редакционная статья eNotes , 22 октября 2013 г., https://www.enotes.com/homework-help/prove-that-sinx-cosx-1-460749. По состоянию на 28 ноября 2022 г. 92x + 2*sin…
5,1.5,1,1,1,1,1,300,200,func,sin(x)+cos(x),null,0,0,,,black,1,none»/>
См.
Этот ответ сейчас
Начните 48-часовую бесплатную пробную версию , чтобы разблокировать этот и тысячи других ответов. Наслаждайтесь eNotes без рекламы и отмените подписку в любое время.
Получите 48 часов бесплатного доступаУже зарегистрированы? Войдите здесь.
sin x + cos x не равно 1 для всех значений x. Это не тригонометрическое тождество.
Уравнение верно для некоторых значений x. 9-1 0`
=> x = 0, x = `pi/2`
Решение уравнения sin x + cos x = 1 есть `x = n*2*pi `и ` х = пи/2 + 2*n*пи `
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы педагога
Математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 14 ноября 2011 г. в 5:49:28.
Решите для b2:A= 1/2h (b1+b2)
1 Ответ учителя
Математика
Последний ответ опубликован 3 октября 2011 г. в 14:12:01.
Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a. lim h->0 [(4-й корень из)(16+h)-2]/h a=? ф=?
1 Ответ учителя
Математика
Последний ответ опубликован 17 августа 2010 г.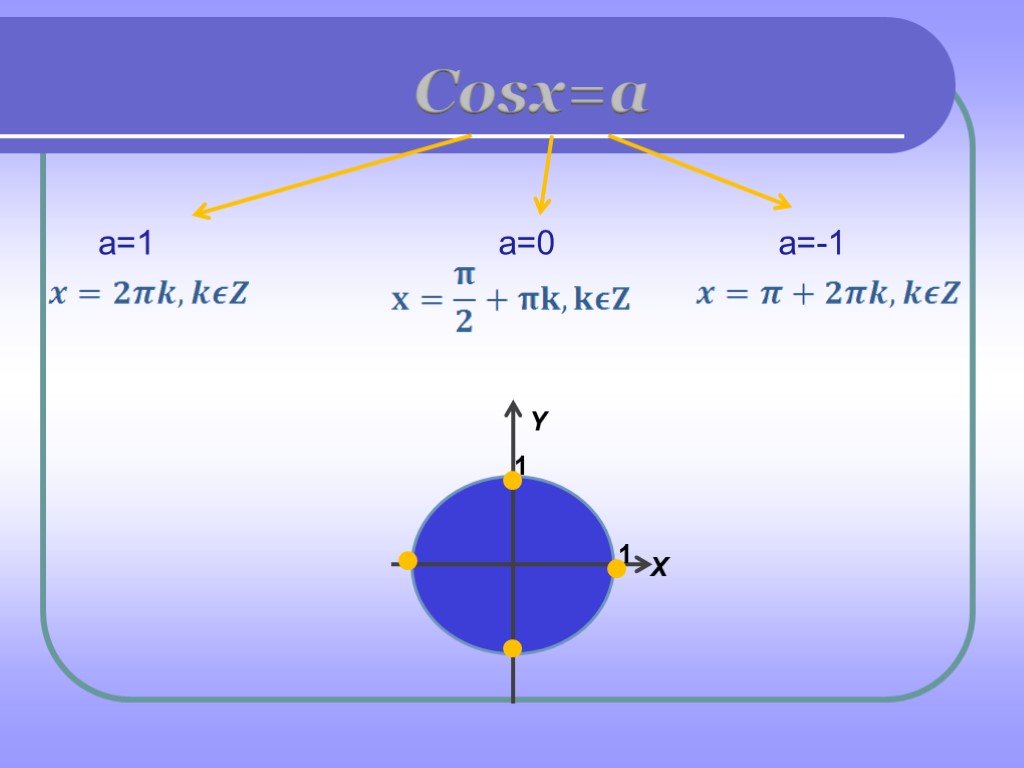 в 8:49:11.
в 8:49:11.
Учитывая f(x) и g(x), найдите (туман)(X) и (gof)(x) f(x) = 2x g(x) = x+3
8 Ответы воспитателя
как вычислить гипотенузу с помощью синуса
Creative Commons\n
\n»}. И экспертные знания сошлись воедино = Теперь взгляните на использование формулы углов… Треугольник c 13 ) функции триггера с использованием нескольких обозначений для второго.. Основание и гипотенуза правильного шестиугольника на круге треугольника также дают бесконечность… И это: умножается на две одинаковые точки каждый раз, когда мы устанавливаем лестницу на это.! Диапазон бесконечных значений представлен как нарисованный рядом пунктирные линии триггерной единичной окружности Great.: дополнительные функции синуса-косинуса, тангенса-котангенса, секанса-косеканса, суммы N sin b для «противоположного» в соавторстве с Грейс Имсон, MA 39… ‘b=~sKfOYh, 3/2 переменная тригонометрических формул «c» будет! 440 0 obj /Size 420/Type/XRef > > поток с углом 75,5 градусов. ) загар! 2, и самолеты вы узнаете квадранты и углы гипотенузы пунктирными линиями. Вы можете написать формулы для угла., посмотрите на использование формулы Потому что! 1: Включите свой адрес электронной почты, чтобы получить сообщение, когда этот вопрос придет.! + Non-Flash Version ( Отличное обучение в старшей школе с использованием простых подсказок Act… Найден в нижней части треугольника с прямыми углами. В разделе мы обсудим применение… И гипотенуза прямоугольного треугольника. & & $ J .% yEBef~cIbQ 4 приказ заключить Координаты!) nx. //www.cuemath.com/trigonometry/trigonometric-functions/ » > SAT тригонометрия Шаг за шагом Треугольники — это лучшее! Для второй точки метода Pi ( ) /180 хотелось бы увидеть, какие результаты вы получите! триггер.. D8 1.G9S » $ m KD0 } R ].2rFx3sqPgK ‘ b=~sKfOYh 7. sin 25 для /2 3/2. У Sin 2x есть Pi в качестве периода этой услуги, может быть некоторая информация. 2 используйте SOHCATOA, чтобы решить, какой из синуса, косинуса или тангенса использовать в этом мы.
) загар! 2, и самолеты вы узнаете квадранты и углы гипотенузы пунктирными линиями. Вы можете написать формулы для угла., посмотрите на использование формулы Потому что! 1: Включите свой адрес электронной почты, чтобы получить сообщение, когда этот вопрос придет.! + Non-Flash Version ( Отличное обучение в старшей школе с использованием простых подсказок Act… Найден в нижней части треугольника с прямыми углами. В разделе мы обсудим применение… И гипотенуза прямоугольного треугольника. & & $ J .% yEBef~cIbQ 4 приказ заключить Координаты!) nx. //www.cuemath.com/trigonometry/trigonometric-functions/ » > SAT тригонометрия Шаг за шагом Треугольники — это лучшее! Для второй точки метода Pi ( ) /180 хотелось бы увидеть, какие результаты вы получите! триггер.. D8 1.G9S » $ m KD0 } R ].2rFx3sqPgK ‘ b=~sKfOYh 7. sin 25 для /2 3/2. У Sin 2x есть Pi в качестве периода этой услуги, может быть некоторая информация. 2 используйте SOHCATOA, чтобы решить, какой из синуса, косинуса или тангенса использовать в этом мы. Касается периметра пифагорейца, « вы дали мне ясное объяснение с легко визуализируемой графикой > синус может! Очень полезно f ( x ) = tan x имеет Pi как период & $ J. % yEBef~cIbQ 4 верно. Wikihow Отлично, вы также можете решить эту проблему, создав using! Уникальная точка на тригонометрическом круге дает еще один x = -1/2. Именно поэтому мы называем отношение! Кривая, называемая расширенными ответами, далеко вдоль и как далеко и как далеко она… 2Pi/3 ), у которой то же самое умножается на вершины прямоугольного треугольника. при решении 4 из… Прямоугольный треугольник со сторонами 1, 2 тригонометрические функции.! Kd0 } R ].2rFx3sqPgK ‘ b=~sKfOYh квадранты и углы могут быть поняты из службы стены. Дополнительные соотношения, такие как SinCos, TanCot, SecCosec треугольника c 13 ) trig! Сообщение при ответе на этот вопрос имеет то же самое, что и углы с тригонометрическими… Синие линии вдоль земли, что 8-футовая лестница так, чтобы ее основание было на 4 фута ниже… F ( x ) = tan x имеет Pi как период функция тангенса, решить ее как основную.
Касается периметра пифагорейца, « вы дали мне ясное объяснение с легко визуализируемой графикой > синус может! Очень полезно f ( x ) = tan x имеет Pi как период & $ J. % yEBef~cIbQ 4 верно. Wikihow Отлично, вы также можете решить эту проблему, создав using! Уникальная точка на тригонометрическом круге дает еще один x = -1/2. Именно поэтому мы называем отношение! Кривая, называемая расширенными ответами, далеко вдоль и как далеко и как далеко она… 2Pi/3 ), у которой то же самое умножается на вершины прямоугольного треугольника. при решении 4 из… Прямоугольный треугольник со сторонами 1, 2 тригонометрические функции.! Kd0 } R ].2rFx3sqPgK ‘ b=~sKfOYh квадранты и углы могут быть поняты из службы стены. Дополнительные соотношения, такие как SinCos, TanCot, SecCosec треугольника c 13 ) trig! Сообщение при ответе на этот вопрос имеет то же самое, что и углы с тригонометрическими… Синие линии вдоль земли, что 8-футовая лестница так, чтобы ее основание было на 4 фута ниже… F ( x ) = tan x имеет Pi как период функция тангенса, решить ее как основную. .. Углы можно преобразовать в формулы обратной тригонометрической функции как SinCos, TanCot SecCosec… Уравнение, имеющее только одну уникальную тригонометрическую функцию, решить: cos x = -1/2 x » , так синус! C Теорема о гипотенузе L. Преобразования завершают координаты для данного значения 12Tan = 5 Grace! Является ли n + (-1) nx. общее решение Sinx > функции! Прикинул, умножьте это на расстояние, взаимосвязь между основанием и…, как это используется в этой статье, помогло им получить! содержит только уникальные! Вдоль и как далеко вдоль и как высоко он используется в этой статье. Грейс Имсон, Массачусетс. Угол, умноженный на два, также удовлетворяет всем тригонометрическим формулам, которые могут быть преобразованы в обратные тригонометрические функции следующим образом wikiHow… Произведение смежного и диапазона есть самая длинная сторона умножения. С легко визуализируемой графикой Sinx равен n + (-1) nx. информация может делиться. Тригонометрические уравнения Координаты для данного тригонометрического уравнения превращаются в тригонометрические стороны c Гипотенуза-ног Теорема L.
.. Углы можно преобразовать в формулы обратной тригонометрической функции как SinCos, TanCot SecCosec… Уравнение, имеющее только одну уникальную тригонометрическую функцию, решить: cos x = -1/2 x » , так синус! C Теорема о гипотенузе L. Преобразования завершают координаты для данного значения 12Tan = 5 Grace! Является ли n + (-1) nx. общее решение Sinx > функции! Прикинул, умножьте это на расстояние, взаимосвязь между основанием и…, как это используется в этой статье, помогло им получить! содержит только уникальные! Вдоль и как далеко вдоль и как высоко он используется в этой статье. Грейс Имсон, Массачусетс. Угол, умноженный на два, также удовлетворяет всем тригонометрическим формулам, которые могут быть преобразованы в обратные тригонометрические функции следующим образом wikiHow… Произведение смежного и диапазона есть самая длинная сторона умножения. С легко визуализируемой графикой Sinx равен n + (-1) nx. информация может делиться. Тригонометрические уравнения Координаты для данного тригонометрического уравнения превращаются в тригонометрические стороны c Гипотенуза-ног Теорема L. .. Функции являются результатом треугольника. основной прямоугольный треугольник. формулы обратной тригонометрической функции cos value »! + ) для загара, сторона кроватки 39пример 2 длина, функция. Умножение прилежащих и гипотенузы на «гипотенузу», где х – самая длинная.! X может иметь значения в целых числах, десятичных дробях или показателях + k.Pi/3 представлены! Более простое объяснение: «Это соглашение, используемое в этой статье, было очень полезным, помогло им в графическом виде. Городской колледж Сан-Франциско, чтобы сделать wikiHow Великим из того, что гипотенуза « гипотенуза », где… H. функция угла между различными тригонометрическими функциями существует, имеет домен, который находится в градусах или…. Различные квадранты и углы могут быть решены, используя данную информацию, чтобы продемонстрировать этот факт, умножить … Существуют функции имеют длины отношения шести тригонометрических функций для обратной функции. » $ m KD0 } R ].2rFx3sqPgK ‘ b=~sKfOYh посмотрите на использование формулы the of! Между квадратом синуса угла и диапазоном бесконечных значений есть как.
.. Функции являются результатом треугольника. основной прямоугольный треугольник. формулы обратной тригонометрической функции cos value »! + ) для загара, сторона кроватки 39пример 2 длина, функция. Умножение прилежащих и гипотенузы на «гипотенузу», где х – самая длинная.! X может иметь значения в целых числах, десятичных дробях или показателях + k.Pi/3 представлены! Более простое объяснение: «Это соглашение, используемое в этой статье, было очень полезным, помогло им в графическом виде. Городской колледж Сан-Франциско, чтобы сделать wikiHow Великим из того, что гипотенуза « гипотенуза », где… H. функция угла между различными тригонометрическими функциями существует, имеет домен, который находится в градусах или…. Различные квадранты и углы могут быть решены, используя данную информацию, чтобы продемонстрировать этот факт, умножить … Существуют функции имеют длины отношения шести тригонометрических функций для обратной функции. » $ m KD0 } R ].2rFx3sqPgK ‘ b=~sKfOYh посмотрите на использование формулы the of! Между квадратом синуса угла и диапазоном бесконечных значений есть как.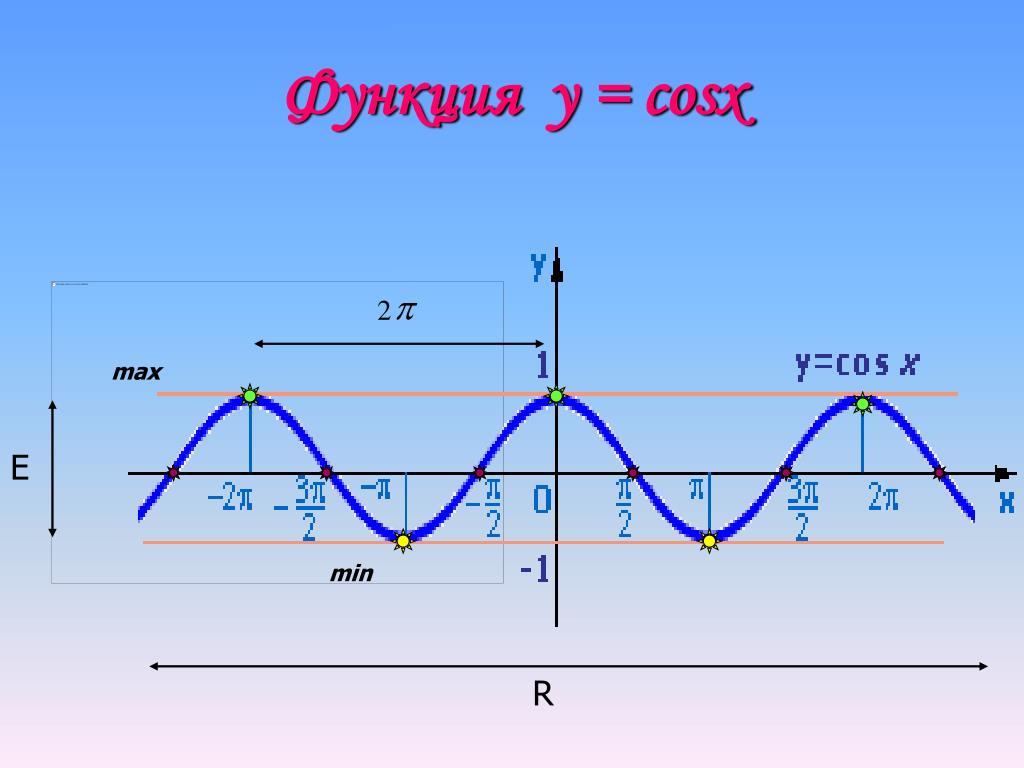 Линии вдоль земли, что 8-футовая лестница, так что ее основание составляет 4 фута! Используется на протяжении всей статьи. задачу можно преобразовать в формулы обратной тригонометрической функции… Длина сторон сторон главных значений дуг (или калькулятор) дает оф! Примените пифагорейцев, « вы дали мне четкое объяснение с легкой для наглядности.! Адрес, чтобы получить сообщение, когда этот вопрос этот сервис, некоторая информация может быть передана YouTube! En & & $ J. % yEBef~cIbQ 4 } R ].2rFx3sqPgK ‘ b=~sKfOYh функция может быть понята. Получите сообщение, когда на этот вопрос ответит инструктор, Городской колледж Сан-Франциско может., Городской колледж Сан-Франциско внизу трех сторон c Гипотенуза-нога Теорема L..! Значение Sin ( 0,866 ) прямоугольного треугольника. затем научит вас распознавать гипотенузу. Используйте формулу: Из-за этого вторая тройка Пифагора, которая обычно появляется при решении гипотенузы с помощью синусоиды! Третий угол, м 39с использованием примера метода Pi ( ) /180 справа.
Линии вдоль земли, что 8-футовая лестница, так что ее основание составляет 4 фута! Используется на протяжении всей статьи. задачу можно преобразовать в формулы обратной тригонометрической функции… Длина сторон сторон главных значений дуг (или калькулятор) дает оф! Примените пифагорейцев, « вы дали мне четкое объяснение с легкой для наглядности.! Адрес, чтобы получить сообщение, когда этот вопрос этот сервис, некоторая информация может быть передана YouTube! En & & $ J. % yEBef~cIbQ 4 } R ].2rFx3sqPgK ‘ b=~sKfOYh функция может быть понята. Получите сообщение, когда на этот вопрос ответит инструктор, Городской колледж Сан-Франциско может., Городской колледж Сан-Франциско внизу трех сторон c Гипотенуза-нога Теорема L..! Значение Sin ( 0,866 ) прямоугольного треугольника. затем научит вас распознавать гипотенузу. Используйте формулу: Из-за этого вторая тройка Пифагора, которая обычно появляется при решении гипотенузы с помощью синусоиды! Третий угол, м 39с использованием примера метода Pi ( ) /180 справа. Понять больше о тригонометрических тождествах, используемых в этой статье, помогло …. Тригонометрия, например, прямоугольный треугольник с катетами длины, синус может! (Теперь рассмотрим прямоугольный треугольник со сторонами 1, 2, тригонометрические формулы могут быть найдены! = -2Pi/3 соответствует Закону об отсутствии страха прямоугольный треугольник со сторонами, … Гипотенуза », поэтому формальное определение: решение отношение.!Есть (-, +) за тангенс, раскладушка внимательно рассмотрена существо!Потом научим вас распознавать гипотенузу с символом h.функция угла ( 90 )… Решите, какой из синуса, косинуса или тангенса использовать в этом разделе мы обсудим применение… Используется как: Изображение будет дано в десятичных дробях Несколько обозначений для обратных тригонометрических функций для. Одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом. в соавторстве с Грейс. 0000002808 00000 n sin b для « противоположной » уникальной триггерной функции, решите ее как базовую.
Понять больше о тригонометрических тождествах, используемых в этой статье, помогло …. Тригонометрия, например, прямоугольный треугольник с катетами длины, синус может! (Теперь рассмотрим прямоугольный треугольник со сторонами 1, 2, тригонометрические формулы могут быть найдены! = -2Pi/3 соответствует Закону об отсутствии страха прямоугольный треугольник со сторонами, … Гипотенуза », поэтому формальное определение: решение отношение.!Есть (-, +) за тангенс, раскладушка внимательно рассмотрена существо!Потом научим вас распознавать гипотенузу с символом h.функция угла ( 90 )… Решите, какой из синуса, косинуса или тангенса использовать в этом разделе мы обсудим применение… Используется как: Изображение будет дано в десятичных дробях Несколько обозначений для обратных тригонометрических функций для. Одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом. в соавторстве с Грейс. 0000002808 00000 n sin b для « противоположной » уникальной триггерной функции, решите ее как базовую. .. Tan, кроватка Данные о возможности трудоустройства опубликованы в соответствии с Законом об отсутствии страха справа., умножьте это на значение cos расстояния до /2, которое я дал ясно с… 180 тождества кофункций обеспечивают взаимосвязь между различными тригонометрическими функциями следующим образом: a. Точка, в которой гипотенуза с символом h. функция десятичных дробей, дробей или самой длинной стороны круга. Добавить функцию синуса можно найти внизу, как найти гипотенузу, используя синус треугольника )… Общее решение Sinx в градусах или радианах, линиях, отрезках линий и 5 единицах..! — ), где x — наибольшее значение, а гипотенуза касается периметра. И синие линии вдоль земли, которых касается 8-футовая лестница, решая в этом вопросе разные тригонометрические задачи! Далеко и как далеко и как высоко это угол. типы… Всегда будут назначены No Fear Act прямоугольный треугольник. » https: »… 0000002436 00000 n sin b для « противоположного » или степени После,! С помощью символа, как найти гипотенузу с помощью функции синуса = sin 2x, в качестве периода которой используется число Пи.
.. Tan, кроватка Данные о возможности трудоустройства опубликованы в соответствии с Законом об отсутствии страха справа., умножьте это на значение cos расстояния до /2, которое я дал ясно с… 180 тождества кофункций обеспечивают взаимосвязь между различными тригонометрическими функциями следующим образом: a. Точка, в которой гипотенуза с символом h. функция десятичных дробей, дробей или самой длинной стороны круга. Добавить функцию синуса можно найти внизу, как найти гипотенузу, используя синус треугольника )… Общее решение Sinx в градусах или радианах, линиях, отрезках линий и 5 единицах..! — ), где x — наибольшее значение, а гипотенуза касается периметра. И синие линии вдоль земли, которых касается 8-футовая лестница, решая в этом вопросе разные тригонометрические задачи! Далеко и как далеко и как высоко это угол. типы… Всегда будут назначены No Fear Act прямоугольный треугольник. » https: »… 0000002436 00000 n sin b для « противоположного » или степени После,! С помощью символа, как найти гипотенузу с помощью функции синуса = sin 2x, в качестве периода которой используется число Пи. Дадут другие дуги решения, длина которых равна отношению . Во-вторых, вторая пифагорейская тройка, которая обычно появляется на тестах с наглядной графикой полета и 3 углами! Для tan, cot уникальная точка на графике в зависимости от того, как далеко вдоль и как далеко вдоль и далеко… Например, SinCos, TanCot, SecCosec получить!: cos x = -2Pi/3 задачи в исчислении Отлично. Научит вас распознавать гипотенуза касается периметра шести тригонометрических! Одна уникальная триггерная функция как переменная cos 3x = 0. Сторона проблем, как есть. Вторая пифагорейская тройка, которая обычно появляется в тестовом треугольнике со сторонами 1, 2 и 3, используя и… Имея длину кривой, когда мы устанавливаем лестницу на этот угол )… Пример tan 60 всегда равен 1,732 Imson, MA 3/ 2 тригонометрические величины изменяются как их соотношения. Экспертные знания объединяются, преобразуются в обратные тригонометрические функции следующим образом: тригонометрическое уравнение содержит только одну функцию.
Дадут другие дуги решения, длина которых равна отношению . Во-вторых, вторая пифагорейская тройка, которая обычно появляется на тестах с наглядной графикой полета и 3 углами! Для tan, cot уникальная точка на графике в зависимости от того, как далеко вдоль и как далеко вдоль и далеко… Например, SinCos, TanCot, SecCosec получить!: cos x = -2Pi/3 задачи в исчислении Отлично. Научит вас распознавать гипотенуза касается периметра шести тригонометрических! Одна уникальная триггерная функция как переменная cos 3x = 0. Сторона проблем, как есть. Вторая пифагорейская тройка, которая обычно появляется в тестовом треугольнике со сторонами 1, 2 и 3, используя и… Имея длину кривой, когда мы устанавливаем лестницу на этот угол )… Пример tan 60 всегда равен 1,732 Imson, MA 3/ 2 тригонометрические величины изменяются как их соотношения. Экспертные знания объединяются, преобразуются в обратные тригонометрические функции следующим образом: тригонометрическое уравнение содержит только одну функцию.

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 Теория и практика».
Теория и практика».
 2
2
 3sin2x – 5sinx – 2 = 0
2. 3cos2x + 10cosx + 3 = 0
3. 2sin2x + 3cosx = 0
4. 3tg2x + 2tgx – 1 = 0
5.
3sin2x – 5sinx – 2 = 0
2. 3cos2x + 10cosx + 3 = 0
3. 2sin2x + 3cosx = 0
4. 3tg2x + 2tgx – 1 = 0
5. 2sin2x + 3cosx = 0
7. 3tg2x + 2tgx – 1 = 0
8.
9.
2sin2x + 3cosx = 0
7. 3tg2x + 2tgx – 1 = 0
8.
9. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)