Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
3Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
14159..пределов — Почему неравенство 0
спросил
Изменено 5 лет, 3 месяца назад
Просмотрено 3к раз
$\begingroup$
Я проходил следующее доказательство:
Почему верно неравенство, данное в первой строке доказательства? Поскольку cos 0 = 1, то как в интервале (-𝛑/2, 𝛑/2) cos x может быть строго меньше 1?
- пределы
- тригонометрия
$\endgroup$
1
$\begingroup$
Площадь зеленого треугольника $\frac 12 |\sin x|$
Площадь сечения круга (зеленый + красный) равна $\frac 12 |x|$
А площадь большего треугольника (зеленый + красный + синий) равен $\frac 12 |\tan x|$
$|\sin х| \ле |х| \le |\tan x|$
затем немного алгебры.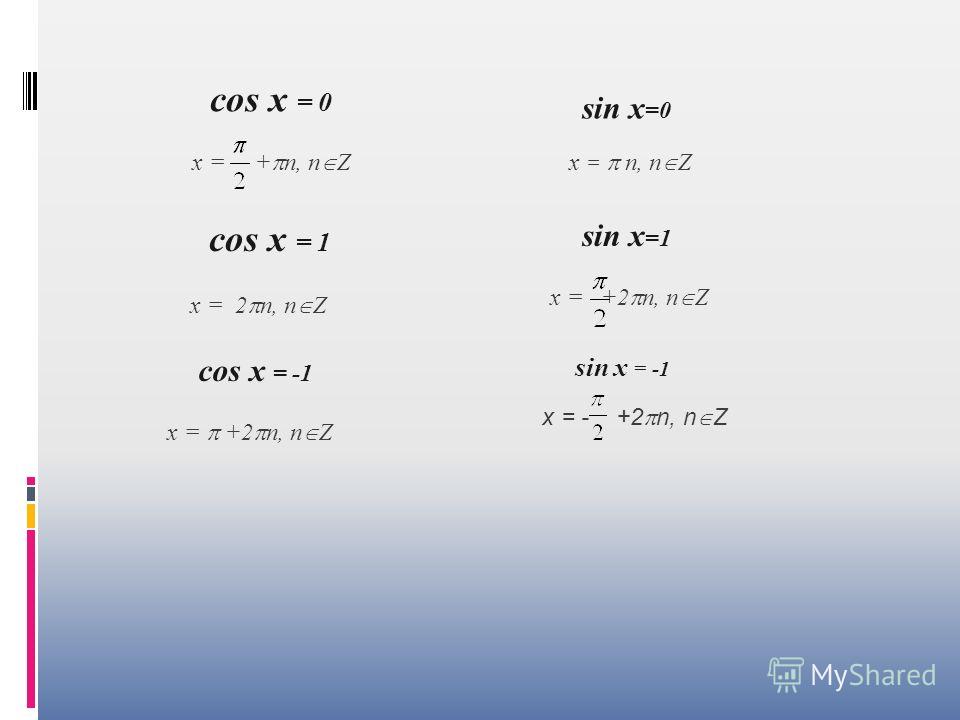
{2} x = {\ frac {x} {2}}} $ $
$ $ {\ Displaystyle S _ {\ треугольник OAL} = {\ гидроразрыва {1} {2}} \ cdot | OA | \ cdot | LA | = {\ гидроразрыва {\ mathrm {tg} \, x} {2}} }$$
из $\треугольника OAL: |LA|={\mathrm {tg}}\,x$
замените в (1):
$$ {\ frac {\ sin x} {2}}<{\ frac {x} {2}}<{\ frac {{\ mathrm {tg}} \, x {2}}$$ для $ x\to 0+:\sin x>0,x>0,{\mathrm {tg}}\,x>0:$
$ {\frac {1}{{\mathrm {tg}}\ ,x}}<{\frac {1}{x}}<{\frac {1}{\sin x}}$ умножить на $ \sin x$:
$ \cos x<{\frac {\sin x}{x}}<1$
$\endgroup$
3
$\begingroup$
Боюсь, доказательство, которое вы показываете, содержит множество ошибок.
Вы правы, что при $x = 0$ имеем $\cos(0) = 1$, поэтому неравенство
$$
\ соз (х) < 1
$$
заведомо не выполняется на отрезке $\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$. Хуже того, указанное неравенство
$$
\ cos (х) < \ гидроразрыва {\ грех (х)} {х} < 1
$$
не имеет смысла даже при $x = 0$, так как средний член не определен.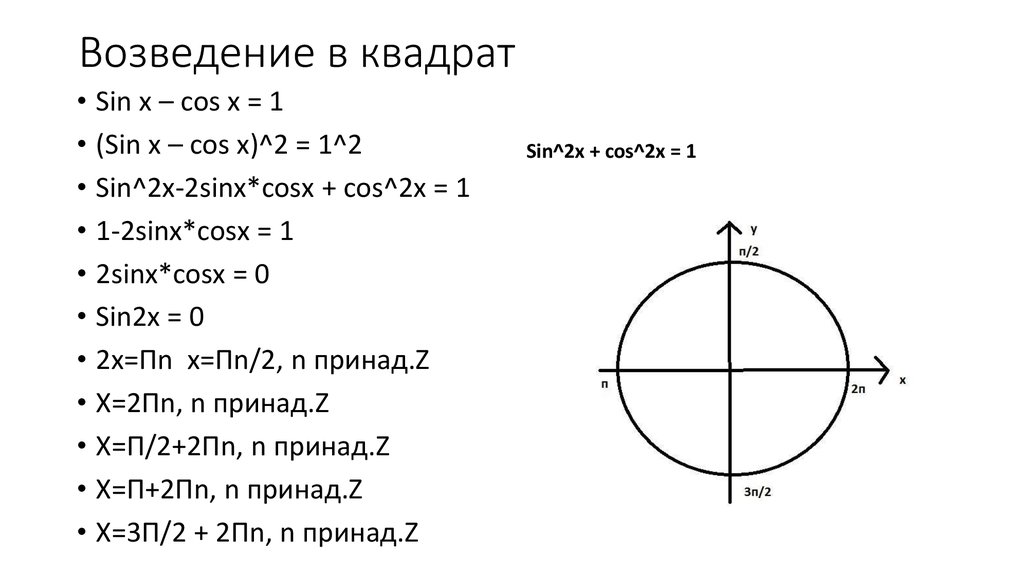
$\endgroup$
2
тригонометрия — $\cos (\cos x) > \sin (\sin x)$
Задавать вопрос
спросил
Изменено 5 лет, 7 месяцев назад
Просмотрено 1к раз
$\begingroup$
Показать, что $\forall x \in \mathbb{R}\ \cos (\cos x) > \sin (\sin x)$
Я попытался сделать очевидную вещь:
$\varphi: x \mapsto \cos(\cos x) — \sin (\sin x)$
$\varphi ‘ (x) = \sin ( \cos x) \sin x — \cos(\sin x) \cos x$
Теперь я хочу показать, что $\varphi$ является положительной функцией для всех $x \in \mathbb{R}$, но производная выглядит недружелюбно, так что либо что-то с $\varphi ‘$.