| В доме трое детей |
И облапошить тебя будет не просто. У меня эта схема работала почти всегда. Вы можете либо выучить несколько цифр, либо выписать их себе на листочек. Либо просто почитать.| Добрый день | мехрабА |
| Добрый вечер | сабАк эльхрИр |
| До свидания | мЭа ас салЯма |
| Как дела? | кОли тамАм |
| Хорошо, слава Богу | тамАм, хамдюлЯ |
| Как тебя зовут? | эсмАк/эсмИк э? |
| Меня зовут Елена | Ана эсмИк Елена |
| Спасибо/Пожалуйста | шукрАн/афуАн |
| Что ты хочешь? | айз/Айза э? |
| Я хочу воды | Ана айз/айза майя |
| Я не хочу | миш айз/айза |
| Я не понимаю | Ана миш Фахма |
| Чуть-чуть (немного) | швАя-швАя |
| Окей | меш |
| Да | Айва |
| Нет | ля |
| Нет, спасибо | ля, шукрАн |
| Сколько это стоит? | бикЕм (бикЕм ди) |
| Что это такое? | Эда? |
| Давай!/Скорее!/Поехали! | Ялла |
| Остановите (автобус)! | алЕ гам |
В арабском языке, как и в русском, различается женский и мужской род.
Например, обращение на ты/вы к мужчине будет «Энта», а к женщине – «Энти».
Прожив какое-то время в Египте, я поймала себя на мысли, что зачастую, даже если я не могу многое сказать, то прекрасно понимаю, о чем идет разговор. Как бы «страшно» не звучали арабские слова на первый взгляд, на деле язык запоминается довольно легко.
Шукран, дорогие читатели, что уделили внимание этой статье. Удачных путешествий!
Источник
Онлайн школа изучения арабского языка
Елены Клевцовой
РАЗ, ДВА, ТРИ, ЧЕТЫРЕ, ПЯТЬ или «я хочу стырить» Часть №4. КАЛЬЯН-МАЛЬЯН ИЛИ ЭТОТ ВЕСЕЛЫЙ АРАБСКИЙ
Теги: кальян-мальян,Арабский разговорник
Пособие по практическому изучению АРАБСКОГО ЯЗЫКА для лежащих на пляже
Сегодня, друзья мои, мы научимся считать до двенадцати. Почему именно до двенадцати? Да потому что в году двенадцать месяцев J И названия всех месяцев мы с вами изучим ровно за полторы минуты. Не верите? Включайте секундомер и – поехали!
Яна́ир, фебра́ир, ма́рес, абри́л, ма́йо, ю́ньо, ю́льо, агху́стос, себте́мбр, окто́бр, нофе́мбр, десе́мбр
Вам это ничего не напоминает? 🙂 Да, именно так по-арабски звучат названия месяцев.
Однако есть и более упрощенная система называния месяцев по номерам:
Месяц первый, месяц второй и так далее до бесконечности 🙂
Месяц по-арабски «шахр»
Цифры по-арабски
Давайте теперь с цифрами разберемся!
1 – уахид
2 – иснан (этнин)
3 – саласа (талэта)
4 – арбаа
5 – хамса
6 – ситта
7 – сабаа
8 – самания (таманья)
9 – тэсаа
10 – ашара
11 – хадашар
12 – итнашар
Названия месяцев по-арабски
Итак, шагхр уахид – это янаир,
шагхр этнин – это фебраир,
шагхр талета – это марес,
шагхр арбаа – это абрил,
шагхр хамса – это майо,
шагхр сетта – юньо,
шагхр сабаа – юльо,
шагхр таманья – агхустос,
шагхр тесаа – себтембр,
шагхр ашара – октобр,
шагхр хедашар – нофембр,
шагхр этнашар – десембр
Итак, мы учим не только названия месяцев, но и цифры до двенадцати.
Ноль по-арабски
Да, вот еще важное число:
сыфр – значит ноль. Кстати отсюда русское слова «цифра».
Считаем деньги
Но коль уж мы с вами дошли до цифр, давайте деньги посчитаем.
Египетский фунт называется гиней масри. Или просто гиней. Итак, мы имеем следующие денежные знаки:
Ашара гиней – 10 фунтов
Ашрин гиней – 20 фунтов
Хамсин гиней – 50 фунтов
Мит гиней – 100 фунтов
Денежные единицы в других популярных арабских странах
В ОАЭ денежная единица – дирхам.
В Саудовской Аравии и Катаре – риал.
Слово «купить» по-арабски звучит очень просто – иштыри. Можно – шари. Ну типа: пошарил и стырил:))) Кстати, древнерусский глагол «тырить» имел весьма позитивное значение «преумножать». Так что смело можно тыри… ой, в смысле иштыри.
Ана айз иштыри – я хочу купить.
Автор: Елена Клевцова
Последние публикации блога:
Учим названия цветов по-арабски за 1 минуту.
Белый, черный, красный, оранжевый..Так как же всё-таки пишется русское имя Алла по-арабски? Нет сходства с Именем Всевышнего!
Так как же всё-таки пишется русское имя Алла по-арабски? Нет сходства с Именем Всевышнего!
Полная версия. Сура Аль-Фатиха с нуля для начинающих. Учимся читать, не зная арабский алфавит
Полная версия. Сура Аль-Фатиха с нуля для начинающих. Учимся читать, не зная арабский алфавит
Шрифты арабской письменности. Почерки Насх, Рыка (рука). Куфический, Османский стиль. Шрифты в Word
Шрифты арабской письменности. Почерки Насх, Рыка (рука). Куфический, Османский стиль. Шрифты в Word
Источник
Количественные числительные
Содержание
От 1 до 10 [ править | править код ]
| Число | Мужской род | Произношение | Женский род | Произношение |
|---|---|---|---|---|
| один | وَاحِدٌ | [wa:hidun] | وَاحِدَةٌ | [wa:hidatun] |
| два | إِثْنَانِ | [ithna:ni] | إِثْنَتَانِ | [ithnata:ni] |
| три | ثَلاَثٌ | [thala:thun] | ثَلَاثَةٌ | [thala:thatun] |
| четыре | أَرْبَعٌ | [‘arba3un] | أَرْبَعَةٌ | [‘arba3atun] |
| пять | خَمْسٌ | [hamsun] | خَمْسَةٌ | [hamsatun] |
| шесть | سِتٌّ | [sittun] | سِتَّةٌ | [sittatun] |
| семь | سَبْعٌ | [sab3un] | سَبْعَةٌ | [sab3atun] |
| восемь | ثَمَانٍ | [thama:nin] | ثَمَانِيَةٌ | [thama:niyatun] |
| девять | تِسْعٌ | [tis3un] | تِسْعَةٌ | [tis3atun] |
| десять | عَشَرٌ | [3asharun] | عَشَرَة | [3asharatun] |
От 11 до 19 [ править | править код ]
| Число | С исчисляемыми мужского рода | Произношение | С исчисляемыми женского рода | Произношение |
|---|---|---|---|---|
| одиннадцать | أَحِدَ عَشَرَ | [‘ahida3ashara] | إِحْدَى عَشَرَةَ | [‘ihda:3asharata] |
| двенадцать | إِثْنَا عَشَرَ | [‘ithna3ashara] | إِثْنَتَا عَشَرَةَ | [‘ithnata:3asharata] |
| тринадцать | ثَلاَثَةَ عَشَرَ | [thala:thata3ashara] | ثَلَاثَ عَشَرَةَ | [thala:tha3asharata] |
| четырнадцать | أَرْبَعَةَ عَشَرَ | [‘arba3ata3ashara] | أَرْبَعَ عَشَرَةَ | [‘arba3a3asharata] |
| пятнадцать | خَمْسَةَ عَشَرَ | [hamsata3ashara] | خَمْسَ عَشَرَةَ | [hamsa3asharata] |
| шестнадцать | سِتَّةَ عَشَرَ | [sittata3ashara] | سِتَّ عَشَرَةَ | [sitta3asharata] |
| семнадцать | سَبْعَةَ عَشَرَ | [sab3ata3ashara] | سَبْعَ عَشَرَةَ | [sab3a3asharata] |
| восемнадцать | ثَمَانِيَةَ عَشَرَ | [thama:niyata3ashara] | ثَمَانِيَ عَشَرَةَ | [thama:niya3asharata] |
| девятнадцать | تِسْعَةَ عَشَرَ | [tis3ata3ashara] | تِسْعَ عَشَرَةَ | [tis3a3asharata] |
Имя исчисляемое после количественных числительных от 11 до 19 следует в форме единственного числа неопределенного состояния винительного падежа.
Младший разряд от 13 и выше ставятся в противоположном к исчисляемому роде. Старший от 11 до 19 согласуется в роде.
От 20 до 99 [ править | править код ]
Количественные числительные от 20 до 99 образуются из двух частей: десятков и единиц.
Десятки образуются от корня соответствующего числительного, кроме 20ти.
| единицы | на арабском | десятки | на арабском |
|---|---|---|---|
| 2 | إِثْنَانِ | 20 | عِشْرُونَ |
| 3 | ثَلاَثٌ | 30 | ثَلاَثُونَ |
| 4 | أَرْبَعٌ | 40 | أَرْبَعُونَ |
| 5 | خَمْسٌ | 50 | خَمْسُونَ |
| 6 | سِتٌّ | 60 | سِتُّونَ |
| 7 | سَبْعٌ | 70 | سَبْعُونَ |
| 8 | ثَمَانٍ | 80 | ثَمَانُونَ |
| 9 | تِسْعٌ | 90 | تِسْعُونَ |
Числительные, обозначающие круглые десятки, имеют единую форму для обоих родов и склоняются по третьему типу склонения.
Единицы в сложных числительных от 23 до 29 и 33 до 39 и т.д ставятся в роде противоположном исчесляемому.
Исчесляемое всегда в форме единственного числа винительного падежа неопределенного состояния.
Источник
Видео
Урок № 10: Арабские цифры
Арабские цифры от 1 до 19-ти. Учимся считать по-арабски!
Числа от 1 до 100 — Арабский язык — Русский язык
Числа от 1 до 10 — Арабский язык — Русский язык
Арабский язык. Урок 30. Счет и цифры в арабском языке
Арабские цифры или цифры по-арабски? Учим, пишем, играем!
Арабский язык с носителем — 16 — Цифры на арабском الأعداد
Учим аят и цифры на арабском. #коран #АрабиЯ #намаз
Песенка Арабские Цифры
Арабские цифры от 1 до 10
Поделиться или сохранить к себе:
Арабские цифры от 1 до 10. Как пишутся арабские цифры
Автор Historian Просмотров 131 Опубликовано
Числа имеют признаки букв арамейского, греческого и финикийского алфавитов. В основном, цифры начали появляться во II веке до нашей эры. В то время существовали индейские племенные царства.
Содержание
- Арабские цифры — Arabic numerals
- Содержание
- Происхождение
- Происхождение символов арабских цифр
- Откуда взялись современные числовые знаки от 1 до 10
- Особенности арабской цифры 0 (ноль)
- Использование нуля в расчетах
- арабские цифры
- Содержание
- Истоки править
- Происхождение символов арабских цифр править
- Перевод арабского числа в римское (и наоборот)
- Особенности арабской цифры 0 (ноль)
- Откуда взялись современные числовые знаки от 1 до 10
Арабские цифры — Arabic numerals
Арабские цифры состоят из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Этот термин часто относится к десятичным числам, описываемым этими цифрами (в отличие, в частности, от латинских).
Однако этот термин может относиться и к самим числам. С утверждением «число 80 написано по-арабски».
Индусская числовая система1 2 (т.е. десятичные цифры) была разработана индийскими математиками примерно в 500 году нашей эры, но первоначально использовались три совершенно разные формы числовых цифр. В Северной Африке они были преобразованы в арабские цифры. В алжирском городе Беджая итальянский ученый Фибоначчи первым познакомился с цифрами. Его работа имела решающее значение для продвижения по всей Европе. Европейская торговля, книги и колониализм способствовали распространению арабских номеров по всему миру. Числа широко используются во всем мире, далеко за пределами современного распространения латинского алфавита, и вторглись в системы письма в тех областях, где используются другие варианты индуистских чисел, например, китайская и японская письменность.
Период, термин арабские цифры может относиться к цифрам, используемым в арабской графике, например, восточно-арабские цифры.
В Оксфордском словаре английского языка для западных чисел используются строчные арабские цифры, а для восточных — прописные. 4
Другие альтернативные названия: западные арабские цифры, западные цифры, индусские арабские цифры, и Unicode просто используют безошибочные термины цифр. 5
Содержание
Происхождение
Индусская арабская система цифр сложилась в Индии около 700 года.8 Эволюция происходила постепенно и продолжалась в течение нескольких столетий, но важным шагом, вероятно, стала формулировка нуля как числа, сделанная Брагуптой в 628 году.
Числовая система была написана такими математиками, как перс аль-Хваризими (араб. الجمعوالتريقبالحسابالهندي аль-джам валь-хинди) в его книге об индусских числовых вычислениях. 825 лет. Араб, арабский математик аль-Чиди написал четыре тома по использованию индийских чисел (арабск: كك любовь: كك любовь: كك любовь: كك любовь: كك любовь: كك любовь: ك. Ответственный за популяризацию индийской системы счисления на Ближнем Востоке и Западе.
9
Математики на Ближнем Востоке расширили систему дробных чисел, включив в нее десятичные, как это зафиксировано в работе сирийского математика Абу Хасана аль-Укридиси в 952 — 953 годах. Когда была написана десятичная точка? Синд ибн Али также написал первую работу об арабских числах.
Происхождение символов арабских цифр
Согласно аль-Берни, в Индии использовались различные формы чисел, и «арабы выбрали те, которые показались им более полезными». Ан-Насави писал, что в начале 11 века математики не пришли к согласию относительно формы чисел, но большинство из них согласились учить эти формы. ? (Западный) арабский. 11
Первоначально расчеты велись с помощью пылевых досок (ТАХТ, лат. tabla). Аль-Уклидиси изобрел Би-Гайр Тахт Ва-ЛаМаḥvБал-Дават Ва-Киршас). Использование 12 пылевых панелей также, по-видимому, привело к различиям в терминологии. Индусское измерение на востоке называлось Шизаб аль-Хинди, а на западе — Шизаб аль-Габаль (буквально «расчет пыли»). 13 Само число было названо на Западе Ашкал аль-Габаль (пыльное число по Ибн аль-Ясамину) или Карам аль-Габаль (пыльное письмо).
14
Западноарабская вариация символа начала использоваться в Магрибе и Аль-Андалузии, являясь прямыми предками современных «арабских цифр», используемых во всем мире. Ученые, которые повелись на терминологию 15, стали предполагать, что западноарабские цифры имеют иное происхождение, чем «губарские цифры», но имеющиеся данные не указывают на другое происхождение. 16 Вёпеке также предположил, что западноарабские цифры уже использовались в Испании, вероятно, до прибытия мавританцев через Александрию, но эта теория не принимается учеными. 17 18 19
Леонардо Фибоначчи (Леонардо из Пизы), математик, родившийся в Пизанской республике и учившийся в Беджае (Алжир), популяризировал индийские записи в Европе в книге Либерта Абейси «1202».
Откуда взялись современные числовые знаки от 1 до 10
Происхождение арабских цифр относят к древней Южной Индии. Во многих древних странах до появления письменности для счета использовались палочки. Одна палочка представляет одну, две палочки — две и т.
д. Эта система письма была вдохновлена зарубками. Отсюда идут латинские цифры (для 1, 2, 3). Индийские цифры заимствовали определенные буквы из разных стран того времени.
Числа имеют признаки букв арамейского, греческого и финикийского алфавитов. В основном, цифры начали появляться во II веке до нашей эры. В то время существовали индейские племенные царства.
В отличие от российской системы нумерации, где единица (1), двойка (2), тройка (3) и арабские цифры имеют собственные названия.
- 1 (один) — 1 Уахид;
- 2 (два) — 2 Итнан;
- 3 (три) — 3 Талата;
- 4 (четыре) — 4 Арба-а;
- 5 (пять) — 5 Хамиза;
- 6 (шесть) — 6 Ситта;
- 7 (семь) — 7 Саба-а;
- 8 (восемь) — 8 Таманиа;
- 9 (девять) — 9 Тизза;
- 10 (десять) — 10 Ашара.
Особенности арабской цифры 0 (ноль)
Ноль означает отсутствие числа или цифр. Ноль — очень полезное число. Просто потому, что это позволяет вести колонны. Другие системы счисления этого не позволяют.
Чтобы убедиться в этом, попробуйте создать колонку, используя латиницу. Ноль также был изобретен индийцами и назывался Сунья. В Индии оно означает «пустой». В древних арабских странах его также называли CIFRA.
Российского математика и педагога Магнитского также называют Zero — число или ничто. Часто его имя использовалось на первой странице книг. Есть и другие источники, где можно найти старое название 0 — номер. Чаще всего он встречается в рукописях русских и европейских ученых XVII и XVIII веков.
Использование нуля в расчетах
Школьников учат начинать считать с единицы. Однако большинство разработчиков используют расчеты. Здесь нумерация всегда начинается с нуля. Этот способ записи всех десяти чисел удобен тем, что в представлении используется только одна буква. И экономика планирования является ее неотъемлемой частью. Если вы начинаете с нуля, нет необходимости писать число 10.
У нуля есть и другие интересные свойства при взаимодействии с числами. Например, если вы попытаетесь прибавить к нулю или отнять ноль от числа, оно не изменится.
При умножении числа во всех случаях получается ноль. Умножьте каждое число на ноль и получите единицу. Также нельзя делить другое целое или дробное число на ноль (0).
Закон Бенфорда доступен. Не описывая подробно типы или таблицы, он утверждает, что в реальной жизни вы с гораздо большей вероятностью встретите числа от 1 до 4, чем от 5 до 9. Закон также имеет практическое применение. Он может использоваться для проверки счетов, результатов голосования и счетов расходов.
В некоторых штатах США судебные дела свидетельствуют об оценке несоответствий в Законе Бенфорда. Все расчеты по данному закону производятся по десятичной системе. Поэтому арабские цифры в области 1-10 являются самыми распространенными в мире.
Другие альтернативные названия: западные арабские цифры, западные цифры, индусские арабские цифры, и Unicode просто используют безошибочные термины цифр. 5
арабские цифры
Арабские цифры состоят из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Этот термин относится к десятичным числам, описываемым этими цифрами (особенно по сравнению с латинскими). Однако этот термин может относиться и к самому числу. С утверждением «число 80 написано по-арабски».
Индусская система счисления1 2 (т.е. десятичные дроби) была разработана примерно в 500 году н.э. индийскими математиками, которые первоначально использовали несколько различных форм числовых знаков. Позже они обратились к арабским цифрам Северной Африки. Там, в городе Безио в Алжире, итальянский ученый Фибоначчи впервые столкнулся с числами — его работа сыграла решающую роль в их популяризации по всей Европе. Европейская торговля, книги и колониализм способствовали распространению арабских номеров по всему миру. Числа широко используются во всем мире, далеко за пределами современного распространения латинского алфавита, и вторглись в системы письма в тех областях, где используются другие варианты индуистских чисел, например, китайская и японская письменность.
Термин «арабские цифры» может относиться к цифрам, используемым в арабской графике, например, к восточноарабским цифрам.
В Оксфордском словаре английского языка для западных чисел используются строчные арабские цифры, а для восточных — прописные. 4
Другими псевдонимами являются западные арабские цифры, западные арабские цифры и индусские арабские цифры, где Unicode просто использует простые числовые термины. 5
Содержание
Истоки править
Индусско-арабская система счисления была разработана в Индии около 700 года.8 Эволюция происходила постепенно и длилась несколько веков, но, возможно, важный шаг был сделан, когда Брахмагупта в 628 году сформулировал ноль как число.
Арифметические системы написал книгу по исчислению, используя цифры хинди (арабские цифры: الجمعوالتفريقبالحسابالهندي Al-Jam`wal-TafrīqBil-Hisābal-Hind около 825 года арабскими цифрами, затем четыре тома по использованию индийских цифр Арабский математик Аль-Кинди (арабские цифры: كتابفياستعمالالالأعدادالهندية Kitab¯FiIsti`mālal-‘A`dadal-Hindī). Их работа в первую очередь способствовала распространению индийской системы счисления на Ближнем Востоке и Западе.
9
Математики на Ближнем Востоке расширили десятичную систему счисления, включив в нее дроби, что зафиксировано в работе сирийского математика Абуль-Хасана аль-Уклидиси в 952-953 годах. Когда была введена десятичная система счисления? По словам СиндибнАли, который также написал первую работу об арабских цифрах.
Происхождение символов арабских цифр править
Согласно Бьелни, в Индии использовались различные формы арифметики, и «арабы выбирали между собой те, которые казались им наиболее полезными». Ан-Насави пишет, что в начале 11 века математики не пришли к согласию относительно формы чисел, но большинство согласилось изучать эти формы, известные сегодня как арабские цифры. 10 Ранние примеры чисел, написанных в Египте в 873-874 годах, показывают три формы числа «2» и две формы числа «3». Эти варианты позже стали называться восточными арабскими цифрами и (западными) арабскими цифрами. 11
Первоначально расчеты проводились с использованием пылевых таблиц (TAHTS, лат.
Tabula), в которых символы писались стилусом, и они удалялись в процессе расчета. Затем аль-Укридиси разработал систему расчетов с использованием чернил и бумаги «без таблиц и стирания» (bi-gairtakhtwa-lamaḥvbalbi-dawatwa-kirshas). Использование 12 таблиц пыли также, по-видимому, привело к расхождениям в терминологии. Индуистские измерения назывались ḥisābal-hindī на Востоке, но isābal-ghubār на Западе (буквально «расчеты пыли»).. 13 Само число Запад называл ashkalal-ghubār (пыльное письмо Ибн аль-Ясама) или kālamal-ghubār (пыльное письмо). 14
Западноарабский вариант символа начал использоваться в Магрибе и Андалузии, став прямым предком современных «арабских цифр», используемых во всем мире. 15 Из-за терминологических расхождений некоторые ученые предполагают, что западные арабские цифры имеют иное происхождение, чем так называемый «арифметический губар», но имеющиеся данные не указывают на иное происхождение. 16 Вёпеке также предположил, что западные арабские цифры уже использовались в Испании, вероятно, до прибытия мавров через Александрию, но эта теория не принимается учеными.
17 18 19
Что вы видите? Основание финикийской буквы исчезает, а карниз смещается влево. Следовательно, их не семь? Вывод: число семь — это семитская (финикийская, еврейская и арабская) буква Зайн (Заи). Число восемь соответствует восьмой букве алфавита Хет (HA).
Перевод арабского числа в римское (и наоборот)
Конечно, ручной перевод (тысячи, десятки и десятки) арабских цифр с латыни — это большой труд (и вряд ли кто-то этим занимается, кроме, пожалуй, математиков и историков).
Поэтому гораздо удобнее использовать программу, которая может рассчитать и перевести вас. К счастью, для расчета не требуется ничего сложнее Excel или word (если их нет, можно воспользоваться соответствующими, в том числе онлайн-версиями).
Особенности арабской цифры 0 (ноль)
Ноль означает отсутствие числа или цифр. Ноль — очень полезное число. Просто потому, что это позволяет вести колонны. Другие системы счисления этого не позволяют. Чтобы убедиться в этом, попробуйте создать колонку, используя латиницу.
Ноль также был изобретен индийцами и назывался Сунья. В Индии оно означает «пустой». В древних арабских странах его также называли CIFRA.
Каталог.
Российского математика и педагога Магнитского также называют Zero — число или ничто. Часто его имя использовалось на первой странице книг. Есть и другие источники, где можно найти старое название 0 — номер. Чаще всего он встречается в рукописях русских и европейских ученых XVII и XVIII веков.
Откуда взялись современные числовые знаки от 1 до 10
Происхождение арабских цифр относят к древней Южной Индии. Во многих древних странах до появления письменности для счета использовались палочки. Одна палочка представляет одну, две палочки — две и т.д. Эта система письма была вдохновлена зарубками. Отсюда идут латинские цифры (для 1, 2, 3). Индийские цифры заимствовали определенные буквы из разных стран того времени.
Числа имеют признаки букв арамейского, греческого и финикийского алфавитов. В основном, цифры начали появляться во II веке до нашей эры.
В то время существовали индейские племенные царства.
В отличие от российской системы нумерации, где единица (1), двойка (2), тройка (3) и арабские цифры имеют собственные названия.
- 1 (один) — 1 Уахид;
- 2 (два) — 2 Итнан;
- 3 (три) — 3 Талата;
- 4 (четыре) — 4 Арба-а;
- 5 (пять) — 5 Хамиза;
- 6 (шесть) — 6 Ситта;
- 7 (семь) — 7 Саба-а;
- 8 (восемь) — 8 Таманиа;
- 9 (девять) — 9 Тизза;
- 10 (десять) — 10 Ашара.
Панель.
Арабские цифры от 1 до 10
Цифры и буквы являются народным достоянием и имеют большую историю во всех народах мира. Самые распространенные на сегодняшний день числовые знаки — это арабские и римские. И те, и другие используют для создания списков в русском языке, для счета предметов и для математических вычислений. Из этой статьи вы узнаете все об арабских цифрах в диапазоне от 1 до 10.
Содержание статьи:
- История появления арабских цифр
- Откуда взялись современные числовые знаки от 1 до 10
- Особенности арабской цифры 0 (ноль)
- Использование нуля в расчетах
История появления арабских цифр
Арабские числовые знаки были выдуманы и записаны в Индии, произошло это около 5 века.
В это время был определен отсчет чисел при перечислении. Отправной точкой был ноль (оригинальное название шунья). Это число позволило сформировать нынешний порядок чисел при счете. Популяризацией арабских цифр занимался индийский ученый того времени Абу Аль-Хорезми, который создал несколько книг на эту тему. От одной из них произошло сегодняшнее название школьного предмета — алгебра. Предоставленный ученым способ записи числовых значений использовал десятичную систему.Археологи находили разные работы древних математиков и археологов, которые использовали арабские цифры для своих работ. Эти работы были созданы предположительно в 8-9 веке. Сегодня большинство арабских стран используют отличительную от привычной всем записи чисел в европейских и других регионах. Более того, на Востоке принято писать порядок чисел с права налево.
Существует множество мнений, что в формировании цифр арабского происхождения, которыми пользуемся сегодня мы — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, были использованы не только арабские цифры древней Индии.
Посмотрев на таблицу арабских цифр в диапазоне от 1 до 10 старого и нового представления, можно найти множество сходств. Например, 1, 2, 3, 4 в начальном представлении — это те же знаки, только повернутые на 90 градусов.
Читайте также: Рандомайзер чисел онлайн.
Откуда взялись современные числовые знаки от 1 до 10
Зарождение арабских цифр относят к древней южной Индии. Во многих древних странах, когда еще не было письма, использовались для счета палочки. Одна палочка обозначала 1, две — 2 и так далее. Такой способ записи навеян зарубками. Именно отсюда и происходят числа в римском представлении (для цифр 1, 2, 3). Индийские цифры позаимствовали некоторые элементы буквы из разных стран того времени.
Скриншот арабских цифр от 1 до 100В цифрах встречаются признаки букв арамейского, греческого и финикийского алфавитов. Предположительно числовые знаки начали зарождаться во 2 веке до нашей эры, в то время, когда существовало Индо-греческое царство.
В отличие от счета в русском языке — один (1), два (2), три (3), арабские цифры имеют свое название:
- 1 (один) — 1 Уахид;
- 2 (два) — 2 Итнан;
- 3 (три) — 3 Талата;
- 4 (четыре) — 4 Арба-а;
- 5 (пять) — 5 Хамиза;
- 6 (шесть) — 6 Ситта;
- 7 (семь) — 7 Саба-а;
- 8 (восемь) — 8 Таманиа;
- 9 (девять) — 9 Тизза;
- 10 (десять) — 10 Ашара.
Таблица
Особенности арабской цифры 0 (ноль)
Ноль понимается как отсутствие числового значения или разряда. Ноль — очень полезная цифра хотя бы тем, что позволяет производить вычисления в столбик. Ни в одной другой числовой системе нет возможности это сделать. Чтобы убедиться в этом, попробуйте сделать расчет в столбик, используя римские цифры. Ноль придумали тоже индийцы и названа была эта цифра «сунья». На индийском значит — «пустой». В древних арабских странах этот знак еще называли cifra.
Российский математик и педагог Магницкий называет ноль также — цифра или ничто.
Часто её название использовали для первой страницы книг. Есть и другие источники, в которых можно найти старое название 0 — цифра. Чаще всего оно встречается в рукописях русских и европейских ученых 17-18 века.
Это может быть полезным: Лучшие генераторы случайных чисел для конкурса.
Использование нуля в расчетах
Детей в школе учат начинать отсчет с единицы. Но большинство программистов используют вычисления, где отсчет всегда начинается с нуля. Такая запись всех 10 чисел удобна тем, что для их представления используется только 1 символ. А экономия в программировании является неотъемлемой его частью. Если мы начнем отсчет с нуля, записывать цифру 10 нам не нужно. Её место занимает девятка.
Ноль обладает другими интересными свойствами при взаимодействии с числами. Так, если вы попытаетесь прибавить к нулю или отнять ноль от какого-нибудь числа — оно не изменится. Когда производится умножение на это число — вы получите 0 во всех случаях.
При возведении каждого числа в ноль, получится единица. А также на ноль (0) нельзя разделить другое целое или дробное число.
Существует Закон Бенфорда. Если не вдаваться в подробности с рассмотрением формул и таблиц, он гласит, что в реальной жизни цифры от 1 до 4 встретить гораздо вероятнее, чем цифры от 5 до 9. Сюда можно отнести номера домов улиц, различную статистику и тому подобное. Есть у этого закона и практическое применение. Используя его, можно проверять бухгалтерские отчетности, результаты голосований, подсчет расходов.
В некоторых американских штатах несоответствие каких-либо расчетов по Закону Бенфорда является уликой, имеющей вес в судебном процессе. Все расчеты по этому закону производятся в десятичной системе. Таким образом, арабские цифры в диапазоне от 1 до 10 являются самыми распространенными во всем мире.
Leave a comment
23 урок.
Числительные от 1 до 10В этом уроке мы с вами пройдем числительные от 1 до 10, в согласовании с исчисляемыми именами существительными.
Фраза, в котором есть число (الْعَدَدُ) и исчисляемое слово (الْمَعْدُودُ) называется числовой фразой (الْمُرَكَّبُ الْعَدَدِيُ), либо числовым словосочетанием.
Посмотрите для начала таблицу:
| перевод | фраза | перевод | число |
| Одна книга | كِتَابٌ وَاحِدٌ | один | وَاحِدٌ |
| Два карандаша | قَلَمَانِ اثْنَانِ | два | اثْنَانِ |
| Три книги | ثَلاثَةُ كُتُبٍ | три | ثَلاثَةٌ |
| Четыре человека | أَرْبَعَةُ رِجَالٍ | четыре | أَرْبَعَةٌ |
| Пять детей | خَمْسَةُ أَوْلادٍ | пять | خَمْسَةٌ |
| Шесть риалов | سِتَّةُ رِيَالاتٍ | шесть | سِتَّةٌ |
| Семь дверей | سَبْعَةُ أَبْوَابٍ | семь | سَبْعَةٌ |
| Восемь тетрадей | ثَمَانِيَةُ دَفَاتِرٍ | восемь | ثَمَانِيَةٌ |
| Девять братьев | تِسْعَةُ إِخْوَةٍ | девять | تِسْعَةٌ |
| Десять пиастров | عَشَرَةُ قُرُوْشٍ | десять | عَشَرَةٌ |
Числа один и два в арабском языке формируются так же как существительное и ее прилагательное, где прилагательное полностью согласуется с существительным в числе, роде и падеже.
В случае с цифрой два числительное формируется в двойственной форме.
Например:
| Одна книга | كِتَابٌ وَاحِدٌ | |
| Две тетради | كُرْسِيَّانِ اثْنَانِ |
Следует также знать, что в арабском языке для выражения единичности или двух предметов достаточно сказать их в единственном числе и в двойственном числе соответственно. Однако числа произносятся для акцентирования внимания.
Для закрепления данного правила давайте внимательно посмотрим примеры:
| На моем столе один карандаш | عَلَى مَكْتَبِي قَلَمٌ وَاحِدٌ. | ||
| Я видел одного солдата | رَأَيْتُ جُنْدِيًّا وَاحِدًا. | ||
| Али сел на один стул | جَلَسَ عَلِيٌّ عَلَى كُرْسِيٍّ وَاحِدٍ. | ||
| Это два брата | هَذَانِ أَخَوَانِ اثْنَانِ. | ||
| Я навестил двух друзей | زُرْتُ صَدِيْقَيْنِ اثْنَيْنِ. | ||
| Я остановился возле двух столов | وَقَفْتَ عَلَى مَكْتَبَيْنِ اثْنَيْنِ. |
Внимание, двойственное число от слова ( أَخٌ ) будет ( أَخَوَانِ ) , не ( أَخَانِ ).
Для чисел от 3 до 10 применяются следующие правила:
- Число всегда предшествует исчисляемому существительному,
например: ثَلاثَةُ أَقْلامٍ означает «три карандаша». - Исчисляемое имя существительное всегда должно быть во множественном числе, тогда как число всегда появляется в единственном числе, например: أَرْبَعَةُ جُنُودٍ означает «четыре солдата».
- Число может быть любого падежа, в зависимости от ситуации, но исчисляемое всегда будет принимать родительный падеж, например: سَبْعَةُ أيَّامٍ «семь дней».
- Исчисляемое имя в основном следует в неопределенном состоянии, عَشَرَةُ أَشْخَاصٍ «десять человек».
- Когда имя исчисляемое мужского рода, то числительное должно быть женского рода, например: خَمْسَةُ رِجَالٍ «5 человек».
Для лучшего закрепления правила рассмотрим примеры:
| В доме трое детей | فِي الْبَيْتِ ثَلاثَةُ أَوْلادٍ. | ||
| Ахмад сел рядом с шестерыми учителями | جَلَسَ أَحْمَدُ مَعَ سِتَّةِ مُدَرِّسِينَ. | ||
| Ваджид съел девять виноградин | أَكَلَ وَاجِدٌ تِسْعَةَ أَعْنَابٍ. | ||
| Халида посетила восемь стран | زَارَتْ خَالِدَةُ ثَمَانِيَةَ بِلاَدٍ. | ||
| Насер открыл четыре двери | فَتَحَ نَاصِرٌ أَرْبَعَةَ أَبْوَابٍ. | ||
| В моем портфеле пять фильмов | فِي حَقِيبَتِي خَمْسَةُ أَقْلامٍ. |
Упражнения
1. Формируйте из ниже приведенных слов фразы с числом один и два. Используйте аудио для подсказки:
| كِتَابٌ ….. | كِتَابٌ ….. | ||
| قَلَمٌ ….  . | قَلَمٌ ….. | ||
| تَاجِرٌ ….. | تَاجِرٌ ….. | ||
| طَالِبٌ ….. | طَالِبٌ ….. | ||
| أَخٌ ….. | أَخٌ ….. | ||
| ابْنٌ ….. | ابْنٌ ….. |
2. Ответьте на вопросы, используя цифру, указанную в скобках. Аудио для подсказки.
Сколько у тебя дядей? | كَمْ عَمًّا عِنْدَكَ؟ (٣) …. | Сколько у тебя братьев? | كَمْ أَخًا عِنْدَكَ؟ (٤) …. |
Сколько уроков в этой книге? | كَمْ دَرْسًا فِي هَذَا الْكِتَابِ؟ (٩) …. | Сколько у тебя сыновей? | كَمْ ابْنًا عِنْدَكَ؟ (٢) …. |
Сколько риалов в твоем кармане? | كَمْ رِيَالا فِي جَيْبِكَ؟ (٦) …. | Сколько пассажиров в автобусе? | كَمْ رَاكِبًا فِي الْحَافِلَةِ؟ (٨) ….  |
Сколько яблок у тебя? | كَمْ تُفَّاحَةً مَعَكَ؟ (٧) …. | Сколько дверей в этом доме? | كَمْ بَابًا فِي هَذَا الْبَيْتِ؟ (٥) …. |
Новые слова
| Числительное | الْعَدَدُ | Цифровая фраза | الْمُرَكَّبُ الْعَدَدِيُ |
| Один | وَاحِدٌ | Исчисляемое | الْمَعْدُودُ |
| Три | ثَلاثَةٌ | Два | اثْنَانِ |
| Пять | خَمْسَةٌ | Четыре | أَرْبَعَةٌ |
| Семь | سَبْعَةٌ | Шесть | سِتَّةٌ |
| Девять | تِسْعَةٌ | Восемь | ثَمَانِيَةٌ |
| Солдат | جُنْدِيٌّ | Десять | عَشَرَةٌ |
| Виноград | عِنَبٌ \ أَعْنَابٌ | Страна / Страны | بَلَدٌ \ بِلادٌ |
| Карман / Карманы | جَيْبٌ \ جُيُوبٌ | Пассажир / Пассажиры | رَاكِبٌ \ رُكَّابٌ |
| Автобус | الْحَافِلَةُ | Пиастр / Пиастры (1/10 риала) | قَرْشٌ \ قُرُوشٌ |
Числительные в арабском языке
Путешествуем к переменам
БЛОГ ПУТЕШЕСТВУЮЩЕГО ВИДЕОМОНТАЖЕРА
↓ СОДЕРЖАНИЕ СТАТЬИ: ↓
- Цифры от 1 до 10 на арабском языке
- Количественные числительные от 11 до 19
- Числительные круглых десятков
- Числительные круглых сотен
- Числительные круглых тысяч
- Числительные круглых десятков тысяч
- Числительные круглых сотен тысяч
- Египетский фунт — названия бумажных денег и монет
Слова в арабском языке пишутся справа налево, а вот числа — как и привычно нам — слева направо.
Цифры от 1 до 10 на арабском языке
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
один | وَاحِد | ١ | уахид |
два | اثْنَان | ٢ | итнин |
три | ثَلاثَة | ٣ | талята |
четыре | أَرْبَعَة | ٤ | эрба |
пять | خَمْسَة | ٥ | хэмса |
шесть | سِتَّة | ٦ | ситта |
семь | سَبْعة | ٧ | сааба |
восемь | ثَمانِيَة | ٨ | самания |
девять | تِسْعَة | ٩ | тыса |
десять | عَشَرَة | ١٠ | ашара |
Количественные числительные от 11 до 19
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
одиннадцать | أَحَدَ عَشَرَ | ١١ | ахда ашер |
двенадцать | اِثْنا عَشَرَ | ١٢ | итнин ашер |
тринадцать | ثَلاثَ عَشْرَة | ١٣ | талята ашер |
четырнадцать | أَرْبَعَ عَشْرَة | ١٤ | эрба ашер |
пятнадцать | خ َمْسَ عَشْرَة | ١٥ | хэмса ашер |
шестнадцать | سِتَّ عَشْرَة | ١٦ | ситта ашер |
семнадцать | سَبْع عَشْرَة | ١٧ | сааба ашер |
восемнадцать | ثَمانِيَ عَشْرَة | ١٨ | самания ашер |
девятнадцать | تِسْعَ عَشْرَة | ١٩ | тыса ашер |
Числительные круглых десятков
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
десять | عَشَرَة | ١٠ | ашара |
двадцать | اعِشْرُون | ٢٠ | ашрин |
тридцать | ثلاثون | ٣٠ | талятин |
сорок | أَرْبَعُون | ٤٠ | арбаин |
пятьдесят | خَمْسُون | ٥٠ | хамсин |
шестьдесят | ستون | ٦٠ | ситтин |
семьдесят | سَبْعُونَ | ٧٠ | сабаин |
восемьдесят | ثَمَانُونَ | ٨٠ | саманин |
девяносто | تِسْعُونَ | ٩٠ | тысин |
Числительные круглых сотен
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
сто | مِائَة | ١٠٠ | ми’а |
двести | مِائَتَيْنْ | ٢٠٠ | ми’атейн |
триста (три сотни) | ثَلاثْ مِائَة | ٣٠٠ | саляс ми’а |
четыреста (четыре сотни) | ﺁﺭﺒﻤﻴﺔ | ٤٠٠ | эрба ми’а |
пятьсот (пять сотен) | ﺨﻤﺴﻤﻴﺔ | ٥٠٠ | хэмса ми’а |
шестьсот (шесть сотен) | ﺴﺘﻤﻴﺔ | ٦٠٠ | ситта ми’а |
семьсот (семь сотен) | ﺴﺒﻌﻤﻴﺔ | ٧٠٠ | сабаа ми’а |
восемьсот (восемь сотен) | ﺘﻤﻨﻤﻴﺔ | ٨٠٠ | томму ми’а |
девятьсот (девять сотен) | ﺘﺴﻌﻤﻴﺔ | ٩٠٠ | тыс’а ми’а |
Числительные круглых тысяч
| Число | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
1 000 | ﺁﻟﻒ | ١٠٠٠ | альф |
2 000 | ﺁﻟﻓﻴﻦ | ٢٠٠٠ | альфейн |
3 000 | ﺘﻟﺘﻼﻒ | ٣٠٠٠ | талет талеф |
4 000 | ﺁﺮﺒﻌﺘﻼﻒ | ٤٠٠٠ | арбаа талеф |
5 000 | ﺨﻤﺴﺘﻼﻒ | ٥٠٠٠ | хамса талеф |
6 000 | ﺴﺘﻼﻒ | ٦٠٠٠ | сит талеф |
7 000 | ﺴﺒﻌﻼﻒ | ٧٠٠٠ | сабаа талеф |
8 000 | ﺘﻤﻨﺘﻼﻒ | ٨٠٠٠ | таман талеф |
9 000 | ﺘﺴﻌﺘﻼﻒ | ٩٠٠٠ | тысса талеф |
Числительные круглых десятков тысяч
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
10 000 | ﻋﺸﺮﺘﻼﻒ | ١٠٠٠٠ | ашр талеф |
11 000 | ﺤﺪﺍﺸﺭﺁﻠﻑ | ١١٠٠٠ | хэдашр альф |
12 000 | ﺍﺘﻨﺎﺸﺭﺁﻠﻑ | ١٢٠٠٠ | итнашр альф |
13 000 | ﺘﻠﺘﺎﺸﺭﺁﻠﻑ | ١٣٠٠٠ | таляташр альф |
14 000 | ﺁﺭﺒﻌﺘﺎﺸﺭﺁﻠﻑ | ١٤٠٠٠ | арбаташр альф |
15 000 | ﺤﻤﺴﺘﺎﺸﺭﺁﻠﻑ | ١٥٠٠٠ | хамасташр альф |
16 000 | ﺴﺘﺎﺸﺭﺁﻠﻑ | ١٦٠٠٠ | ситташр альф |
17 000 | ﺴﺒﻌﺘﺎﺸﺭﺁﻠﻑ | ١٧٠٠٠ | сабаташр альф |
18 000 | ﺘﻤﻨﺘﺎﺸﺭﺁﻠﻑ | ١٨٠٠٠ | таманташр альф |
19 000 | ﺘﺴﻌﺘﺎﺸﺭﺁﻠﻑ | ١٩٠٠٠ | тыссаташр альф |
20 000 | ﻋﺸﺭﻴﻦﺁﻠﻑ | ٢٠٠٠٠ | ашриин альф |
30 000 | ﺘﻼﺘﻴﻦﺁﻠﻑ | ٣٠٠٠٠ | талятин альф |
40 000 | ﺁﺭﺒﻌﻴﻦﺁﻠﻑ | ٤٠٠٠٠ | арбаин альф |
50 000 | ﺤﻤﺴﻴﻦﺁﻠﻑ | ٥٠٠٠٠ | хамсин альф |
60 000 | ﺴﺘﻴﻦ ﺁﻠﻑ | ٦٠٠٠٠ | ситтин альф |
70 000 | ﺴﺒﻴﻦﺁﻠﻑ | ٧٠٠٠٠ | сабаин альф |
80 000 | ﺘﻤﻨﻴﻦ ﺁﻠﻑ | ٨٠٠٠٠ | таманин альф |
90 000 | ﺘﺴﻌﻴﻦ ﺁﻠﻑ | ٩٠٠٠٠ | тыссаин альф |
Числительные круглых сотен тысяч
| Русский | Арабский (прописью) | Арабский (число) | Как произносить |
|---|---|---|---|
100 000 | ﻤﻴﺖ ﺁﻠﻑ | ١٠٠٠٠٠ | мит альф |
200 000 | ﻤﺘﻴﻦ ﺁﻠﻑ | ٢٠٠٠٠٠ | митейн альф |
300 000 | ﺘﻟﺘﻤﻴﺖ ﺁﻠﻑ | ٣٠٠٠٠٠ | тульту мит альф |
400 000 | ﺭﺒﻌﻤﻴﺖ ﺁﻠﻑ | ٤٠٠٠٠٠ | робу мит альф |
500 000 | ﺤﻤﺴﻤﻴﺖ ﺁﻠﻑ | ٥٠٠٠٠٠ | хомсу мит альф |
600 000 | ﺴﺘﻤﻴﺖ ﺁﻠﻑ | ٦٠٠٠٠٠ | ситу мит альф |
700 000 | ﺴﺒﻤﻴﺖ ﺁﻠﻑ | ٧٠٠٠٠٠ | собу мит альф |
800 000 | ﺘﻤﻭﻤﻴﺖ ﺁﻠﻑ | ٨٠٠٠٠٠ | тому мит альф |
900 000 | ﺘﺴﻌﻤﻴﺖ ﺁﻠﻑ | ٩٠٠٠٠٠ | тысса мит альф |
Египетский фунт — названия бумажных денег и монет
Подробная статья про египетские деньги с фотографиями здесь: Деньги Египта.
| Русский | Арабский (число) | Как произносить (масри) |
|---|---|---|
200 фунтов | ٢٠٠ | ми’атейн гине |
100 фунтов | ١٠٠ | ми’а гине |
50 фунтов | ٥٠ | хамсин гине |
20 фунтов | ٢٠ | ашрин гине |
10 фунтов | ١٠ | ашер гине |
5 фунтов | ٥ | хэмса гине |
1 фунт | ١ | уахид гине |
50 пиастров | ٥٠ | нысф гине (хамсин эрш) |
25 пиастров | ٢٥ | хэмс-ашрин эрш |
75 пиастров | ٧٥ | хэмс-саабаин эрш |
1 фунт 25 пиастров | гине уа хэмс-ашрин эрш |
История цифр для детей (с видео)
Все мы знаем, что используем при счете арабские цифры.
Однако как они появились и дошли до нас? Процесс возникновения арабских чисел очень интересен и занимателен.
Как они зародились?
Десятичная система арабского счета включает в себя 10 основных чисел от 0 до 9. С их помощью можно записать цифру любой величины.
До происхождения цифр люди пользовались пальцами для счета, но однажды им понадобилось посчитать такое большое количество предметов, что пальцев уже не хватало. Так возникла запись чисел.
Основные методы исчисления в древности.История цифр началась 5 тысячелетий назад в Египте и Месопотамии. И хотя эти два культурных пласта мало пересекались друг с другом, их системы исчисления очень похожи. Первоначально для записей использовали камень или выполняли засечки на дереве. Впоследствии в Месопотамии стали пользоваться глиняными табличками, а в Египте писали на папирусе. Внешний вид цифр в этих культурах отличается, однако одно можно сказать точно: найденные археологами артефакты подтверждают, что это были не просто записи чисел, а именно математические действия.
История происхождения арабских цифр в том виде, в каком мы их знаем сегодня, довольно запутана. Точное время их возникновения неизвестно, однако ученые знают наверняка, что впервые числами стали пользоваться астрономы. Между 2 и 6 веками н.э. астрономы Индии узнали о греческой шестидесятеричной системе исчисления и переняли у греков ноль. Затем основы греческого исчисления были совмещены в Индии с десятичной системой, заимствованной из Китая.
Именно в Индии стали обозначать цифры одним символом. Популяризатором индийской записи стал ученый по имени Аль-Хорезми, который написал труд под названием «Об индийском счете». Впоследствии книга об исчислении была переведена на латинский язык, что привело к распространению десятичной системы в Европе.
Именно Индии мы сегодня обязаны возникновению арабских чисел, что произошло около 5 века н. э. Уже в 10-12 веках арабские цифры стали известны Европе. Это произошло благодаря захвату Испании маврами, принесшими с собой мусульманскую культуру и арабские книги.
Ученый по имени Сильвестр, прибывая в мусульманской Кордове, мог получить доступ к такой литературе, которую Европа еще не знала. Поскольку часть Испании по-прежнему оставалась христианской, перевод индийской книги на латынь позволил популяризировать ее в христианской Европе.
На Руси почти до времен Петра для обозначения чисел использовали старославянские буквы. С приходом европейской культуры стала внедряться арабская система записи. Поскольку старославянская азбука с древних времен существенно изменилась, арабские цифры глубоко вошли в нашу жизнь.
Арабские цифры были намного удобнее римских и быстро завоевали популярность. Сегодня мы пользуемся ими во всех областях нашей деятельности. Присмотритесь внимательно: мы используем числами, чтобы просматривать телевизионные передачи, разговаривать по телефону, получать деньги с банковского счета, измерять время, покупать продукты и многое другое. Без чисел наша современная жизнь просто невозможна.
Так почему же цифры, придуманные в Индии, стали называть арабскими?
В 7 веке нашей эры образовалось новое государство – Арабский халифат, который захватил в свое господство северо-запад Индии.
Арабы насаждали на этих землях свою культуру, но в результате именно достижения индийских астрономов дали миру десятичное исчисление, а арабский ученый Аль-Хорезми только популяризировал ее. Так что получилось, что европейцы знали о цифрах уже от арабов.
История чисел (слайды презентации)
Как они выглядят?
У детей часто возникает вопрос: почему цифры выглядят именно так, какими мы их знаем? Какова история появления цифр именно в таком виде, как мы знаем их сейчас?
Письмо на бумаге существенно изменило первоначальный облик арабских цифр. Поскольку древние люди вынуждены были писать числа на глине, дереве или папирусе, движения руки были затруднены. Легче было рисовать не скругленные формы, а линии и углы. Именно поэтому первоначальные цифры составлялись из черт. Их комбинации не случайны: каждая цифра содержала столько углов в написании, сколько обозначало само число. Например, в единице мы видим один угол, в двойке – два угла и т.
д. Частично восстановить древнее начертание арабских цифр помогут электронные часы, где обозначения существенно отличаются от прописных и тоже состоят из линий и углов.
Видео-материал по теме
Итак, история цифр очень интересна и насчитывает сотни лет. Обойти стороной эту информацию в детских садах и начальных классах школы просто невозможно. История появления арабских чисел может стать плодотворной почвой для организации тематического утренника или КВН. Подготовьте викторину, попросите детей самим подобрать интересную информацию об истории чисел. Они наверняка с увлечением отнесутся к подготовке и участию в мероприятии.
Арабский Числа от 1 до 10 на диалектах
Считается одним из самых сложных языков для изучения, некоторые могут задаться вопросом, что делает арабский язык таким. Что ж, одним из аспектов сложности является различие между стандартной формой الفُصْحَى (официальная, образовательная форма) и диалектной, разговорной, разговорной формой العَامِّيَّة .
Что касается чисел, то, как и в случае с большинством вариаций, разница морфо-фонологическая. То есть некоторые слова смешаны (в случае 11-19), а звуки произносятся по-разному.
Изображение Бабака Фахамзаде на flickr.com
MSA الفُصْحَى:
В MSA количественные числа имеют мужские и женские формы. Женщина получена из мужского, добавляя женский маркер «Таа Марбута» ة / ـة к концу, следовательно, ثَلَاث становится ثَلاثَة и أَرْبَع становится أ Щеты и أَرْبَع .
| وَاحِد | waaHid (м) | 1 |
| وَاحِدَة | вааХида (ф) | |
| اِثْنَيْن | итнайн (м) | 2 |
| اِثْنَتَيْن | итнатайн (ф) | |
| ثَلَاثَة | талаата (ф) | 3 |
| ثَلَاث | талаат (м) | |
| أَرْبَعَة | арбаа (ф) | 4 |
| أَرْبَع | арба (м) | |
| خَمْسَة | хамса (ж) | 5 |
| خَمْس | хамс (м) | |
| سِتَّة | ситта (ж) | 6 |
| سِتّ | сидя (м) | |
| سَبْعَةَ | сабъах (ф) | 7 |
| سَبْع | саб’ (м) | |
| ثَمَانِيَة | тамаания (ф) | 8 |
| ثَمَان | тамаан (м) | |
| تِسْعَة | тиса (ф) | 9 |
| تِسْع | тис (м) | |
| عَشْرَة | ашра (ф) | 10 |
| عَشْر | ‘ашр (м) | |
| NB: ‘ = ع ’ = أ | ||
Levantine الشَّامِيَّة:
За исключением чисел 1 и 2, числа от 3 до 10 имеют одинаковую форму как мужской, так и женский تِسْعَه وِلَاد tis’a wilaad «девять мальчиков».
Египетский المِصْرِيَّة:
Этот диалект напоминает левантийский, за исключением группы согласных.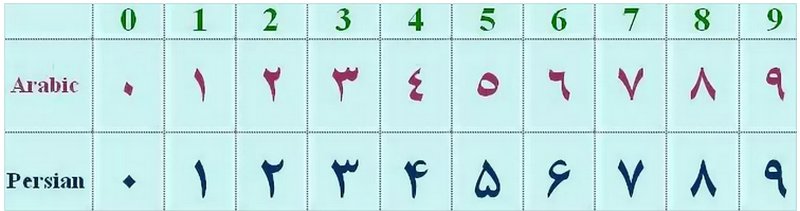
В египетском языке последовательность из двух согласных прерывается вставкой гласной перед или после согласной, поэтому tniin , tlaate и tmaanye в левантийском языке становятся itniin , talaata 9 07 3 , и talaata 6 , и 9003 соответственно. . Разрыв групп согласных путем вставки гласных является обычным явлением в египетском арабском языке.
| وَاحِد | waaHid (м) | 1 |
| وَحْدَة | Вахда (ж) | |
| اِتْنِيْن | итниин | 2 |
| تَلاتَة | талаата | 3 |
| أرْبَعة | арба | 4 |
| خَمْسْة | хамса | 5 |
| سِتّة | ситта | 6 |
| سَبْعْة | сабъа | 7 |
| تَمَنيْه | таманья | 8 |
| تِسْعْة | тиса | 9 |
| عَشَرة | ашара | 10 |
| Примечание: ‘ = ع | ||
Полуостров الج®
Арабский язык, в состав которого входят йеменский арабский, арабский и арабский арабский язык.
Различия в произношении действительно скудны, как видно из списка.
| وَاحِد | waaHid (м) | 1 |
| وَاحِدِة | вааХидих (ф) | |
| اِثْنَيْن | итнайн (м) | 2 |
| ثِنْتَيْن | тхинтайн (ж) | |
| ثَلاثَة | талаата (ф) | 3 |
| ثَلاث | талаат (м) | |
| أَرْبَعَة | арбаа (ф) | 4 |
| أَرْبَع | арба‘ (м) | |
| خَمْسَة | хамса (ж) | 5 |
| خَمْس | хамс (м) | |
| سِتَّة | ситта (ж) | 6 |
| سِتّ | сидя (м) | |
| سَبْعَة | сабъах (ф) | 7 |
| سَبْع | саб’ (м) | |
| ثَمَانِيَة | тамаания (ф) | 8 |
| ثَمَان | тамаан / тимаан (ф) | |
| تِسْعَة | тиса (ф) | 9 |
| تِسْع | тис (м) | |
| عَشَرَة | ашара / ашра (ф) | 10 |
| عَشْر، عَشَر | ашр / ашар (м) |
Марокканский المَغْرِبِيَّة :
Отличительной чертой марокканского арабского языка является чрезмерная кластеризация.
То есть короткие гласные MSA часто опускаются и заменяются последовательностью из сукунов , то есть группой из двух или более согласных. Именно это явление делает эту разновидность арабского языка трудной для восприятия/понимания. Возьмем случай khmsa, stta, sb’a, и thmnya , в каждом слове есть группа из трех согласных. Это затрудняет воспроизведение и понимание диалекта другими носителями арабского языка.
| وَاحِد | waaHid (м) | 1 |
| وَاحِدة | ваахида (ф) | |
| جُوْج | иууж | 2 |
| تِلاتة | Тилаата | 3 |
| رْبْعَة | рба | 4 |
| خْمْسَة | хмса | 5 |
| سْتَّة | стта | 6 |
| سْبْعَة | сб’а | 7 |
| ثْمْنيَة | тмня | 8 |
| تْسْعُود | цууд | 9 |
| عْشْرَة | шра | 10 |
Что касается juuj , которое иногда произносится как juuz , оно взято из слова MSA zawj «пара».
Это слово также распространено в йеменском арабском языке и используется почти так же, как и марокканцами. ts‘uud — интересный случай.
Цифры на арабском языке — Rocket Languages
Этот бесплатный аудиоурок по цифрам на арабском языке — незаменимая вещь в вашем наборе для выживания на арабском языке! Собираетесь ли вы на рынок за продуктами, хотите ли вы сообщить кому-то свой возраст или хотите передать свой номер телефона, знание своих арабских чисел и умение считать на арабском языке необходимы во всех культурах.
Примечание. В этом уроке все слова и предложения, относящиеся к определенному полу, имеют форму мужского рода.
Ресурсы для дальнейшего чтения:
- Сколько времени нужно, чтобы разговаривать на арабском языке?
- Лучшие советы по изучению арабского языка онлайн
От 1 до 10 на арабском языке
Давайте поговорим о цифрах на арабском языке! Мы начинаем с основных чисел от 1 до 10 (١,٢,٣,٤,٥,٦,٧,٨,٩ и ١٠).
. Просто послушайте звук носителя языка, а затем используйте значок микрофона, чтобы записать себя. Как только вы закончите, вы получите 100 баллов за свое произношение и сможете прослушать собственное аудиовоспроизведение. (Для достижения наилучших результатов используйте микрофон гарнитуры.) Проблемы? Кликните сюда!
وَاحِد
اِتْنِين
itnein
تَلَاتَه
talātah
اَرْبَعَه
arba’ah
خَمْسَه
khamsah
سِتَّه
sittah
سَبْعَه
sab’ah
تَمَانْيَه
tamanyah
تِسْعَه
тисах
عَشَرَه
‘ашара
от 11 до 20 на арабском языке
Счет на арабском довольно прост. Однако есть правила, которым необходимо следовать, особенно с более высокими числами, такими как те, которые мы сейчас рассмотрим! Мы начнем с меньших чисел, а затем перейдем к кратным большим числам.
حِدَاشَر
ḥidāshar
eleven
اِتْنَاشَر
itnāshar
twelve
تَلَتَّاشَر
talattāshar
thirteen
اَرْبَعْتَاشَرْ
arba’tāshar
fourteen
خَمَسْتَاشَر
khamastāshar
fifteen
سِتَّاشَر
ситташар
шестнадцать
سَبَعْتَاشَر
саба’ташар
семнадцать
تََْمْ0007tamantāshar
eighteen
تِسِعْتَاشَر
tisa’tāshar
nineteen
عِشْرِين
‘ishrīn
twenty
Multiples of 10
Now for multiples of 10 in Arabic:
عَشَرَه
‘ashara
عِشْرِين
‘Ishrīn
двадцать
تَلَاتِين
Talatīn
Thirty
اَرْبَعِين
Arba’yn
اَرْبسِين
Arba’īn
اَرْينтей
0002 khamsīnسِتِّين
sittīn
سَبْعِين
sab’īn
seventy
تَمَانِين
tamanīn
eighty
تِسْعِين
tis’īn
ninety
مِيَّه
miyyah
one hundred
Используя эти числа и базовый шаблон, можете ли вы построить что-то свое? Попробуйте попрактиковаться с этими:
خَمْسَهْ وِعِشْرِين
хамса в ‘ишрин
двадцать пять
تَمَانْيَهْ وِعِشْرِين
tamanyah w ‘ishrīn
twenty eight
وَاحِدْ وِتَلَاتِين
wāḥid w talatīn
thirty one
تِسْعَهْ وِتَلَاتِين
tis’a w talatīn
thirty nine
اَرْبَعَهْ وِاَرْبَعِينْ
arba’a w Arba’īn
сорок четыре
خَمْسَهْ وِاَرْبَعِين
KHAMSA W Arba’īn
сорок пять
خَمْسَهْ وِ®
KHAMSA wittīn 9 0007
KHAMSA Wittīn
KHAMSA Wittīn
KHAMSA wittīn
0007sixty five
خَمْسَهْ وِسَبْعِين
khamsa w sab’īn
seventy five
وَاحِدْ وِسَبْعِين
wāḥid w sab’īn
seventy one
تِسْعَهْ وِسَبْعِين
tis’a w sab’īn
seventy nine
Как дела? Как только вы освоите эту схему, вы сможете составить любое число меньше 100.
Числа больше 100
مِيَّهْ وِوَاحِدْ
miyyah w wāḥid
сто один0007
مِيَّهْ وِاِتْنِينْ
miyya w itnein
one hundred and two
مِيَّهْ وِعِشْرِينْ
miyya w ‘ishrīn
one hundred and twenty
مِيَّهْ اِتْنِينْ وِعِشْرِينْ
miyya itnein w ‘ishrīn
one hundred and twenty two
Говоря о числах от 100 до 999, всегда начинайте с числа, кратного 100, а затем читайте последние две цифры, начиная справа, например:
ميه خمسة و تلاتين
Meyah 7aamsa wa talatin
135 (100+5+30)
متن سبعة و اربعين
Metyn Sab3a wa arb3in
247 (200+70,407
htámet. wa sab3in
379 (300+9+70)
Now for some multiples of 100 and 1000:
مِيتِينْ
meitein
two hundred
تُلْتُمِيَّهْ
toltomiyya
three hundred
رُبْعُمِيَّهْ
riob’ омия
four hundred
خُمْسُمِيَّهْ
khomsomiyya
five hundred
سُتُّمِيَّهْ
sottomiyya
six hundred
سُبْعُمِيَّهْ
sob’omiyya
seven hundred
تُمْنُمِيَّهْ
tomnomiyya
eight hundred
تُسْعُمِيَّهْ
тосомийя
девятьсот
одна тысяча
اَلْفِينْ
альфейн
две тысячи
تَلَتَّلَافْ
talattalāf
three thousand
اَرْبَعْتَلَافْ
arba’talāf
four thousand
خَمَسْتَلَافْ
khamastalāf
five thousand
سِتَّلَافْ
sittalāf
six thousand
سَبَعْتَلَافْ
saba’talāf
семь тысяч
تَمَنْتَلَافْ
таманталаф
восемь тысяч
تِسَعْتَلَ7
таманталаф0002 тиса’талаф
девять тысяч
مِلْيُونْ
милйон
один миллион
Ух ты! Это очень много цифр, которые нужно принять за один раз! Не забывайте практиковаться в счете в повседневной жизни, например, при подсчете сдачи или чтении уличных адресов.
Удачи!
Вот несколько рекомендуемых уроков арабского языка, которые стоит попробовать в следующий раз!
!مع السلامة (Ma3a essalama!) До свидания!
Амира Заки: Ракетный арабский
Закрепите свои знания на этом уроке с помощью заданий «Ракетное усиление»!
Грамматика использования арабских чисел – Арабские страницы
عَدَد
корень: ع-د-د / существительное / множественное число: أَعْداد / определение: число
для изучения арабской грамматики в университете . Это казалось довольно простым, так как по сути было три набора правил: один для чисел от 3 до 10, один для чисел от 11 до 99 и еще один для целых сотен, тысяч и т. д.
Но когда я посмотрел немного глубже, я понял, что было несколько маленьких исключений и особых случаев! Что ж, сейчас как никогда хорошее время, чтобы вникнуть в детали…
Вот несколько вещей, которые нужно знать, прежде чем мы перейдем к правилам:
- исчисляемое существительное — это существительное, которое — да — считается или определяется числом; поэтому, если мы скажем «8 планет», планета — это исчисляемое существительное
- составное число — это число, состоящее из единиц, десятков, тысяч и т. д., например: 34, 108, 7020 и 97592
д., например: 34, 108, 7020 и 97592- в этом посте я больше сосредоточусь на грамматических отношениях между числом и исчисляемым существительным, а не столько на том, как произносится каждое число — я думаю, нам понадобится целый другой пост на эту тему!
- есть удобный инструмент под названием تفقيط , который отлично подходит, когда вам нужно увидеть число, написанное словами, и вам не хочется сверяться со своими грамматическими примечаниями (!) — узнайте, как его лучше всего использовать, здесь
Как я упоминал в начале, есть три основных набора правил… хотя, как видите, есть и подмножества:
- 3–10
- 11–99
- целые десятки
- Составные номера, заканчивающиеся 1 или 2
- Составные номера, заканчивающиеся 3-9
-
- WHOLE, сотни, тысячи 9999999999999999999999999999999999999999999999999999999999999999999999999999999999999.
- пишется прописью (не цифрами)
- род противоположен роду (форма единственного числа) исчисляемого существительного
причина, по которой мы начинаем с 3, заключается в том, что для чисел 1 и 2 исчисляемое существительное принимает форму единственного или двойного числа!)Начнем!
3-10
Для чисел от 3 до 10 номер :
as the number and counted noun are in an إضافة)
- единственное число
- منصوب (в винительном падеже)
- Тот же пол, как и у подсчета существительного
- неизменно для пола
- того же рода, что и исчисляемое существительное
- the opposite gender to that of the counted noun
- singular
- مجرور (because it forms an إضافة with the number)
- 1 История
- 1.1 Происхождение
- 1.1.1 Происхождение символов арабских цифр
- 1.2 Принятие в Европе
- 1.2.1 Усыновление в России
- 1.3 Принятие в Китае
- 1.1 Происхождение
- 2 Эволюция символов
- 2. 1 Кодировка
- 2.
- 3 См. также
- 4 Примечания
- 6 источников
- 7 Дополнительная литература
- Широко распространенные западно-арабские цифры, используемые с латинским шрифтом, в таблице ниже обозначенные как European , произошли от западно-арабских цифр, разработанных в Аль-Андалусе (Андалусия, Испания) и Магрибе. Испанские ученые из-за географической близости, торговли и постоянных войн с мусульманскими королевствами Южной Испании увидели потенциал в простоте арабских чисел и решили принять эти символы, а позже их примеру последовали и другие европейцы. Существует два типографских стиля для отображения европейских цифр, известных как выравнивающие фигуры и текстовые фигуры.
- Арабско-индийские или восточно-арабские цифры, используемые с арабским письмом, появились в основном на территории современного Ирака. Вариант восточно-арабских цифр, используемых в персидском языке и языках урду, показан ниже как восточно-арабско-индийский.
- Числа деванагари, используемые с деванагари и родственными вариантами, сгруппированы как индийские цифры.
- Цифры текста
- Абджад цифры
- Китайские цифры
- Счетные стержни – десятичная позиционная система счисления с нулем
- Десятичный
- Греческие цифры
- японские цифры
- Цифры майя
- Региональные вариации современных рукописных арабских цифр
- Гений средневековой науки: от медицины до механических часов
8 11–99 8 11–99 Examples:
سَبعَةُ كُتُبٍ
7 books
أَربَعُ نِساءٍ
4 women
عَشَرُ مَرّاتٍ
10 раз
11-99
Для чисел 11-99 мы пишем числа цифрами, а не словами. Однако я распишу их в примерах, чтобы грамматика была понятна.
С этой категорией чисел исчисляемое существительное всегда:
. Давайте посмотрим на разные подгруппы…
11-19
для 11, 12 и все числа «подростка», № :
Примеры:
اِثنَتا формативный РАТ
12 (female) novelists
أَحَدَ عَشَرَ عاماً
11 years
ثَمانِيَةَ عَشَرَ بَيتاً
18 houses
سِتَّ عَشرَةَ صَفحةً
16 страниц
Обратите внимание, что для чисел 13-19 два компонента числа (десятки и единицы) противоположны по роду.
Пол десяти определяет пол числа.Т.е. خَمسَةَ عَشَرَ — мужской род, а خَمسَ عَشرَةَ — женский.
целые десятки
Для целых десятков, т.е. 20, 30, 40 и т. д. — число равно:
Примеры:
عِشرونَ ساعةً
20 часов
تِسعونَ يَوماً
90 дней
ثَلاثونَ شَخصاً
. (как в примерах выше) или ـينَ.
составные числа, оканчивающиеся на 1 или 2
Для составных чисел, оканчивающихся на 1 или 2, число :
Examples:
واحِدٌ وَعِشرونَ قَلَماً
21 pens
اِثنَتانِ وَسَبعونَ مَدينةً
72 cities
واحِدَةٌ وَسِتّونَ مِتراً
61 metres
اِثنانِ وَخَمسونَ أُسبوعاً
52 недели
составные числа, оканчивающиеся на 3-9
Для составных чисел, оканчивающихся на единицу от 3 до 9, номер равен:
Examples:
ثَلاثَةٌ وَثَلاثونَ شارِعاً
33 roads
أَربَعٌ وَعِشرونَ ساعَةً
24 hours
سَبعٌ وَتِسعونَ مِنطَقَةً
97 areas
خَمسтили وَسِتّونَ زَعيماً
65 Лидеров
100+
Числа 100 (которые могут быть записаны مِئة или مائة), а также выше на рисунке.
Более крупные и сложные числа часто сочетают разные наборы правил. Например, 3000 полков — это ثَلاثَةُ آلافِ رَفٍّ — где أَلف ( Aundle ) — это существительное ثلاثة (и, следовательно, множественное число и مجرور), а رَ является исчисленным существительным 3000 (и, следовательно я упомяну ниже).
целые сотни, тысячи и т. д.
Для целых сотен, тысяч, миллионов (в основном все, что заканчивается не менее чем двумя нулями), counted noun is:
Examples:
خَمسُمِئةِ (/خَمسُ مِئةِ) طِفلٍ
500 children
ثَمانِيَةُ آلافِ شَجَرَةٍ
8000 деревьев
ثَمانِيَةُ آلافٍ وَخَمسُمِئَةِ صورةٍ
8500 Pictures
اِثنِ Chy etringف трите
9000 29292 9000 292.192.9007 9000 292.192.192.192.192.192.192.192.192.192.192.192.192.192. 9.67 29292. 9000 2 9000 29000 2
9000 2
9000 2
9000 2
9000 2
9000 2
9000 2
9000 2
9000 2
9000 2
9000 2
.0037
مِليونا مِرآةٍ
2 000 000 зеркал
составные числа
Последняя категория! (Ну, на самом деле это скорее примечание…)
Когда у нас есть число больше 100, которое включает десятки или единицы, мы используем последние две цифры , чтобы определить, какой набор правил использовать.
Например, для числа 28,0 61 мы будем использовать те же правила, что и для числа 61: число того же рода, что и исчисляемое существительное, а исчисляемое существительное стоит в единственном числе и منصوب.
А если бы у нас было число 5,000,0 05 , мы бы использовали набор правил для числа 5: число противоположно роду исчисляемого существительного, а исчисляемое существительное имеет форму множественного числа и مجرور.
…и, выдох ! Вот и все, вы дошли до конца правил!
(После этого мне нужно полежать.)
Какой пост вы хотели бы видеть следующим? Вы можете сообщить мне об этом в комментариях ниже или в социальных сетях!
!مع السلامة
Подпишитесь на The Arabic Pages в Instagram и Twitter и узнайте, как вы можете поддержать этот блог!
Если вы хотите получать уведомления по электронной почте всякий раз, когда на The Arabic Pages публикуется новая публикация, введите свой адрес электронной почты ниже и нажмите «Подписаться»:
Адрес электронной почты:
Нравится:
Нравится Загрузка…
Почему арабы отказались от арабских цифр?
(7-минутное чтение)
Имея опыт работы в области инженерии и геодезии, я работаю с большим количеством чисел. Поскольку я тоже живу в Египте, мне пришлось погрузиться в мир арабского языка, и поэтому я использую числа, написанные на арабском языке.
Раньше мое западное образование заставляло меня почти всегда работать с европейскими/английскими номерами.Чтобы подготовить сцену для этой статьи, английские числа, как правило, называются «арабскими цифрами», в то время как цифры, которые мы используем в арабском языке, называются цифрами «хинди» (проверьте это в настройках чисел Microsoft, в разделе «Параметры», Передовой). Еще больше усложняет ситуацию то, что арабы давным-давно называли арабские цифры хинди, в то время как европейцы называли те же цифры арабскими (посмотрите Википедию). На протяжении всей этой статьи и во избежание путаницы я имею в виду следующее:
Эта запутанная классификация заинтриговала меня, и после нескольких быстрых поисков я узнал, что арабские цифры были теми, кто изобрел арабские цифры, которые мы используем сегодня в английском языке, и что они были экспортированы в Европу через североафриканскую торговлю на материковую часть Европы примерно с 1000 до н.э. 1200 лет назад. Когда я еще немного поискал информацию о происхождении чисел, я обнаружил (на неофициальном веб-сайте: messages.
snopes.com — незащищенный веб-сайт) логику чисел, основанную на количестве углов, образованных ребрами цифр, кульминацией которых является все важные нули «0»).Приведенная выше логика не может быть проверена и, возможно, действительно является мифом, хотя, должен признать, она довольно интересна. Чтобы подвергнуть критике эту логику, вы можете просто возразить, что если бы ноль был написан тем же шрифтом, что и цифры от 1 до 9 выше (то есть в виде прямоугольника), идея «без углов» не сработала бы.
Не желая углубляться в историю числительных и огромные усилия математиков, таких как Эль Хаваризми (чье имя связано с современным термином Алгоритм , благодаря историческим итальянским исследователям), я просто изучаю, почему (на что, вероятно, никогда не будет ответа) арабы решили отказаться от своего собственного изобретения. Поскольку я ежедневно работаю с числами и совсем недавно начал использовать числа на арабском языке для составления счетов за объемы работ в своей сфере деятельности, я столкнулся с рядом проблем при использовании хинди-числительных в современном деловом мире.
Ниже я излагаю эти практические неудачи и приглашаю всех вас, коллеги-билингвы, прокомментировать свой собственный опыт, а также сравнить и сопоставить использование двух разных систем счисления.Направление письма
Английский язык пишется слева направо, а арабский язык пишется справа налево. Однако, когда дело доходит до чисел на арабском языке, вам внезапно требуется изменить направление чтения вашего мозга: числа на арабском языке (независимо от того, используются ли цифры на арабском языке или на хинди) всегда пишутся слева направо. Эта путаница очевидна при использовании текстового процессора, поскольку курсор внезапно меняет направление (попробуйте стереть числа, которые вы напечатали в середине арабского текста, и вы поймете, что я имею в виду).
Я уверен, что мы все были в такой ситуации, когда нас просили назвать длинный серийный номер, например, наш национальный идентификационный номер, и первое, что было сказано, это «слева…»
Эта путаница также очевидна при написании даты на арабском языке в краткой форме: гггг/мм/дд.
Много раз мне звонил смеющийся банковский служащий, чтобы указать, что я неправильно написал дату на чеке, возможно, шепча себе под нос: «Что за хавага!» — действительно стыдно!Хинди Ноль
Прорывное изобретение знаменитого ноль означало, что люди теперь могут считать больше девяти. В нашем современном мире нам нужно считать не только миллионы, но даже миллиарды, а иногда и триллионы. Ноль в системе счисления хинди — это просто точка — да, маленькая точка! (плохо отфотокопированный документ с цифрами на нем может заставить вас почесать затылок, было ли это случайное пятно на бумаге, которое случайно появилось в неудачном месте, или кто-то действительно хотел напечатать ноль!).
Десятичная точка
В арабской системе счисления мы используем десятичные точки (.) для обозначения частей целого числа. Однако в числительных на хинди мы используем запятую (,). По понятным причинам арабы, использующие формат хинди, не могли использовать десятичную точку, как их англоязычные собратья, поскольку ее можно было бы спутать с цифрой ноль, также обозначаемой точкой.
Я думаю, что некоторые европейцы (например, итальянцы) могут использовать ту же систему, что и арабы. Друзья-итальянцы, пожалуйста, прокомментируйте это.Разделение сотен и тысяч
В английском языке мы используем запятые (,) для разделения сотен и тысяч, ставя запятую через каждые три цифры. Это облегчает чтение больших чисел. А вот в арабском такого разделения нет: надо сидеть и считать точки! См. приведенный ниже пример числа 30 миллионов:
Я думаю, практическое решение этой проблемы при использовании хинди-числительных состоит в том, чтобы оставлять пробел между каждым набором из трех цифр.
Наконец, рукописные «2» и «3» можно перепутать
Для тех, кто не знаком с арабским языком, цифры 2 и 3 иногда можно перепутать. Каждая из этих цифр имеет несколько вертикальных штрихов в верхней части знака: 2 штриха для числа 2 и 3 для числа 3.
Однако в повседневном письме число 3 иногда сокращается до двух штрихов. чтобы он напоминал цифру 2 — сбивает с толку, не так ли?
Так почему же
арабы отказались от арабских цифр?Возможно, это риторический вопрос, но я также читал в Интернете, что цифры хинди были импортированы с Востока в современный Ирак через языки наших восточных соседей, урду и персидский.
Арабы того времени, вероятно, сочли эти числа на хинди более интересными или, может быть, более удобными в использовании, но я думаю, мы никогда не узнаем….Что касается меня, то я задавался вопросом: почему арабы не возвращаются к своему собственному изобретению и не возвращают обратно то, что было их собственным? Если они этого не сделают (что, я думаю, произойдет нескоро), как они смогут внести практические улучшения в то, как арабы выражают числа? Будь то формат десятичной точки или запятой, или использование трехзначных разделителей для сотен/тысяч, или, что еще более радикально, изменение направления письма в соответствии с направлением арабского текста, я чувствую, что что-то нужно изменить…
Были ли у вас подобные ситуации? разочарования? Или, может быть, вы видите пользу или ценность числительных на хинди, которых не вижу я? Пожалуйста, не стесняйтесь комментировать ниже и дайте мне знать ваши мысли….
Примечание: данная статья отражает личную точку зрения автора и никоим образом не является научной, технической или исследовательской статьей — просто личным стенанием.
Цитаты все из интернета и собственные знания автора. Арабские цифры — Математика
Чтобы узнать о других значениях, см. Арабские цифры (значения) .
арабские цифры , также называемые индийско-арабские цифры , [1] [2] — это десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Этот термин часто подразумевает десятичное число, записанное с использованием этих цифр, что является наиболее распространенной системой символического представления чисел в современном мире. Однако этот термин может означать сами цифры, например, в утверждении «восьмеричные числа записываются с использованием арабских цифр».
Индо-арабская система счисления (т.е. десятичная) была разработана индийскими математиками около 500 г. н.э. Арабские цифры появились в Северной Африке. Именно в североафриканском городе Беджая итальянский ученый Фибоначчи впервые столкнулся с цифрами; его работа сыграла решающую роль в том, чтобы сделать их известными по всей Европе.
Европейская торговля, книги и колониализм помогли популяризировать использование арабских цифр во всем мире.Термин арабские цифры неоднозначен, он также может означать цифры, используемые арабами, и в этом случае он обычно относится к восточным арабским цифрам. Хотя фраза «арабская цифра» часто пишется с заглавной буквы, иногда она пишется строчными буквами: например, в ее статье Оксфордского словаря английского языка , [4] , которая помогает отличить ее от «арабских цифр» как восточных Арабские цифры.
Другие альтернативные имена Западные арабские цифры , Западные цифры , Индийские цифры , а Unicode называет их цифрами . [5]
Содержание
История
Происхождение
Основная статья: История индийско-арабской системы счисления
Десятичная индийско-арабская система счисления с нулем была разработана в Индии примерно к 700 г. н.э. [8] Развитие было постепенным, охватывая несколько столетий, но решающим шагом, вероятно, стала формулировка Брахмагуптой нуля как числа в 628 году нашей эры. До Брахмагупты ноль использовался в различных формах, но считался «белым пятном» (9).1887 sunya sthana ) в позиционном номере. Его использовали только математики ( ганаков — люди, занимающиеся вычислениями), в то время как население в целом использовало традиционные числа Брахми. После 700 г. н.э. десятичные числа с нулем заменили числа Брахми. Система была революционной, поскольку ограничивала количество отдельных цифр десятью.
Это считается важной вехой в развитии математики.Система счисления стала известна при дворе Багдада, где работали такие математики, как персидский Аль-Хорезми, чья книга г. «О вычислениях с индийскими цифрами » было написано о 825 г. на арабском языке, а арабский математик Аль-Кинди, написавший четыре тома, г. «Об использовании индийских цифр » ( г. хинди ) около 830 г., распространил его в арабском мире. Их работа в основном способствовала распространению индийской системы счисления на Ближнем Востоке и на Западе. [9]
В 10 веке математики Ближнего Востока расширили десятичную систему счисления, включив в нее дроби, как записано в трактате сирийского математика Абу’л-Хасана аль-Уклидиси в 952–953. Обозначение десятичной точки было введено Синдом ибн Али, который также написал самый ранний трактат об арабских цифрах.
Происхождение символов арабских цифр
По словам Аль-Беруни, в Индии использовалось несколько форм цифр, и «арабы выбирали среди них то, что казалось им наиболее полезным».
[10] Ан-Насави писал в начале одиннадцатого века, что математики не договорились о форме чисел, но большинство из них согласились тренироваться с формами, теперь известными как восточно-арабские цифры. [11] Самые старые образцы письменных цифр, доступные из Египта в 260 г. хиджры (873–874 гг. Н. Э.), показывают три формы числительного «2» и две формы числительного «3», и эти вариации указывают на расхождение между то, что позже стало известно как восточные арабские цифры и (западные) арабские цифры. [12] Расчеты первоначально выполнялись с использованием пылевой доски ( тахт , латиница : tabula ), которая включала написание символов пером и их стирание в ходе вычислений. Аль-Уклидиси тогда изобрел систему расчетов чернилами и бумагой «без доски и стирания» (9).1887 би-гайр тахт ва-ла махв бал би-дават ва-киртас ). [13] Использование пылевой доски, по-видимому, также внесло расхождение в терминологию: в то время как индуистское исчисление называлось ḥisab al-hindī на востоке, оно называлось ḥisab al-ghubar на западе.
(буквально «расчет с пылью»). [14] Сами числительные назывались на западе как ашкал аль-губар (пылевые фигуры, у Ибн аль-Ясамина) или калам аль-губар г. (пыль писем). [15] Западно-арабские варианты символов стали использоваться в Магрибе и Аль-Андалусе, которые являются прямыми предками современных «арабских цифр», используемых во всем мире. [16] Расхождение в терминологии побудило некоторых ученых предположить, что западные арабские цифры имели отдельное происхождение от так называемых «числительных ghubār », но имеющиеся данные указывают на отсутствие отдельного происхождения. [17] Вопеке также предположил, что западные арабские цифры уже использовались в Испании до прибытия мавров, якобы полученных через Александрию, но эта теория не принимается учеными. [18] [19] [20]
Некоторые популярные мифы утверждали, что первоначальные формы этих символов указывали на их числовое значение через количество содержащихся в них углов, но никаких доказательств такого происхождения не существует.
[21] Принятие в Европе
В 825 году Аль-Хорезми написал трактат на арабском языке «О расчетах с помощью индуистских цифр» , [22] , который сохранился только как латинский перевод XII века8 Algoritmi, 918 de numero Индорум . [23] [24] Algoritmi , перевод имени автора, дал начало слову алгоритм . [25]
Первые упоминания о числительных на Западе встречаются в Codex Vigilanus от 976 года. [26]
положение для распространения знаний о числительных в Европе. В юности Герберт учился в Барселоне. Известно, что он запросил математические трактаты об астролябии у Люпита Барселонского после того, как вернулся во Францию.
Леонардо Фибоначчи (Леонардо Пизанский), математик, родившийся в Пизанской Республике, который учился в Беджайе (Бужи), Алжир, продвигал индийскую систему счисления в Европе своей книгой 1202 года Liber Abaci :
Когда мой отец, назначенный своей страной нотариусом на таможне в Бугии, действовавшим от имени пизанских купцов, направлявшихся туда, был ответственным лицом, он призвал меня к себе, когда я был еще ребенком и имел к полезности и удобству в будущем, пожелал, чтобы я остался там и получил образование в школе бухгалтерского учета.
Там, когда я познакомился с искусством девяти символов индейцев благодаря замечательному обучению, знание этого искусства очень скоро понравилось мне больше всего на свете, и я пришел к его пониманию.Числительные упорядочиваются так, чтобы их наименьшее значение было справа, а старшие значения добавлялись слева. Это расположение одинаково как в арабском, так и в индоевропейских языках.
Причина, по которой цифры более известны как «арабские цифры» в Европе и Америке, заключается в том, что они были введены в Европу в 10 веке арабоязычными жителями Северной Африки, которые тогда использовали цифры от Ливии до Марокко. Арабы, с другой стороны, называют систему с основанием 10 (не только эти цифры) «индуистскими цифрами», [27] [28] ссылаясь на их происхождение в Индии. Это не следует путать с тем, что арабы называют «числительными хинди», а именно с восточно-арабскими цифрами (٠ — ١ — ٢ — ٣ -٤ — ٥ — ٦ — ٧ — ٨ — ٩), используемое на Ближнем Востоке, или любое из числительных, используемых в настоящее время в индийских языках (например, деванагари: ०.
१.२.३.४.५.६.७.८.९). [21] Принятие числительных в Европе было ускорено изобретением печатного станка, и они стали широко известны в 15 веке. Ранние свидетельства их использования в Британии включают: равночасовой хорарный квадрант от 1396, [29] в Англии, надпись 1445 года на башне церкви Хитфилд, Суссекс; надпись 1448 года на деревянных воротах церкви Брей, Беркшир; и надпись 1487 года на двери колокольни церкви Пиддлетрентхайд, Дорсет; а в Шотландии — надпись 1470 года на могиле первого графа Хантли в соборе Элгина. (Дополнительные примеры см. GF Hill, The Development of Arabic Numerals in Europe .) В Центральной Европе король Венгрии Ладислав Посмертный начал использовать арабские цифры, которые впервые появляются в королевском документе 1456 года. [30] К середине 16 века они широко использовались в большинстве стран Европы. [31] Римские цифры по-прежнему использовались в основном для обозначения лет anno Domini и для чисел на циферблатах.
Сегодня римские цифры по-прежнему используются для нумерации списков (в качестве альтернативы алфавитной нумерации), для последовательных томов, для различения монархов или членов семьи с одинаковыми именами и (в нижнем регистре) для нумерации страниц в вводных материалах. в книгах.
г. Принятие в России
Кириллические цифры были системой нумерации, производной от кириллицы, используемой южно- и восточнославянскими народами. Эта система использовалась в России еще в начале 18 века, когда Петр Великий заменил ее арабскими цифрами.
Принятие в Китае
Арабские цифры были введены в Китай во времена династии Юань (1271–1368) мусульманами Хуэй. В начале 17 века арабские цифры в европейском стиле были введены испанскими и португальскими иезуитами. [32] [33] [34]
Эволюция символов
Основная статья: Алгоризм
Используемая система счисления, известная как алгоритмизм, представляет собой позиционную десятичную запись.
Различные наборы символов используются для представления чисел в индийско-арабской системе счисления, потенциально включая как символы, которые произошли от цифр брахманов, так и символы, которые развились независимо. Символы, используемые для представления системы, со времен средневековья разделились на различные типографские варианты:Эволюция числительных в ранней Европе показана здесь в таблице, составленной французским ученым Жаном-Этьеном Монтукла в его Histoire de la Mathematique , опубликованный в 1757 году:
Кодировка
Арабские цифры 0–9 кодируются в ASCII в позициях от 0x30 до 0x39. Маскирование младшими 4 двоичными битами (или взятие последней шестнадцатеричной цифры) дает значение цифры, что очень помогает при преобразовании текста в числа на первых компьютерах. Эти позиции были унаследованы в Unicode [35] и практически во всех других кодировках, так или иначе основанных на ASCII. EBCDIC использовал разные значения, но также имел младшие 4 бита, равные цифровому значению.
Двоичный Окталь Десятичный Шестнадцатеричный Глиф Юникод 0011 0000 060 48 30 0 U+0030 ЦИФРА НОЛЬ 0011 0001 061 49 31 1 U+0031 ЦИФРА ОДИН 0011 0010 062 50 32 2 U+0032 ЦИФРА ДВА 0011 0011 063 51 33 3 U+0033 ЦИФРА ТРИ 0011 0100 064 52 34 4 U+0034 ЦИФРА ЧЕТЫРЕ 0011 0101 065 53 35 5 U+0035 ЦИФРА ПЯТЬ 0011 0110 066 54 36 6 U+0036 ЦИФРА ШЕСТЬ 0011 0111 067 55 37 7 U+0037 ЦИФРА СЕДЬМАЯ 0011 1000 070 56 38 8 U+0038 ЦИФРА ВОСЕМЬ 0011 1001 071 57 39 9 U+0039 ЦИФРА ДЕВЯТЬ См.
такжеВ этой статье используется материал из статьи в Википедии. «Арабские цифры», которая выпущена под Лицензия Creative Commons Attribution-Share-Alike 3.0. есть список всех авторы в Википедии
Индийско-арабские цифры: история и как они произвели революцию в математике
Попробуйте добавить LIX к VII, и вы быстро поймете, почему математика не продвинулась далеко вперед с римской системой счисления
До той эпохи , когда европейцам нужно было решить математическую задачу, они обычно использовали римские цифры, которые были сложными и громоздкими.
Представьте, что вы пытаетесь прибавить LIX (59) к VII (7), и вы быстро поймете, почему математика не развилась далеко как дисциплина с этой древней системой счисления. Гениальность индийско-арабской системы заключается в использовании в ней позиционной записи, также известной как позиционная запись. Каждая цифра может быть помещена в столбцы единиц, в то время как десятичную точку (введенную в 16 веке) можно перемещать влево или вправо по столбцам, чтобы увеличить или уменьшить значение числа в степени 10 — система, которая сделала возможным для выражения дробей с гораздо большей точностью.Эта простая, но гениальная идея означает, что любое число может быть записано с использованием тех же девяти символов и нуля, что позволяет выполнять безграничные вычисления и перестановки. Тем не менее, несмотря на эту очевидную силу, только через столетия после того, как эти цифры и система позиционного обозначения были разработаны, они стали широко использоваться.
Радость шестерых
Ранние цивилизации разработали сложные математические теории, используя свои собственные системы.
Вавилоняне, вышедшие из 19 в.до н.э. в долине Евфрата была разработана шестидесятеричная система счисления (основанная на числе 60), наследие которой сохранилось до наших дней в делении часов на 60 минут и секунд. Древние греки использовали аспекты этой шестидесятеричной системы счисления, но записывали числа с помощью букв, а не специальных символов, а также, в отличие от вавилонян, использовали символ для обозначения нуля. Древнегреческие математики в основном занимались геометрией — длинами, формами и углами, которые обозначались буквами, а не числами, — и их идеи оказали огромное влияние на развитие этой дисциплины.Больше похоже на это
Однако в первые века нашей эры в Индии начала процветать другая традиция математики, вероятно, основанная на идеях, заимствованных из китайской цивилизации. Ученые начали использовать девять специальных цифр для обозначения первых девяти чисел, а примерно в 600 году нашей эры они начали писать эти символы по порядку в соответствии с их значением.
Последним кусочком головоломки был ноль, который жизненно важен для системы позиционной записи, основанной на числе 10. Первоначально он был записан как точка для обозначения пустого значения в последовательности чисел. Важно отметить, что эта система была описана примерно в 625 году нашей эры индийским математиком по имени Брахмагупта в сложном астрономическом трактате, написанном на санскрите и названном Сиддханта .
Ученые, стекавшиеся в Багдад, правильно рассчитали окружность Земли с точностью до пары сотен миль Халиф аль-Мансур на излучине реки Тигр в качестве столицы своей растущей мусульманской империи. Один из них предполагает, что он был привезен непосредственно из Индии в 773 году приезжим ученым, но возможно, что к тому моменту индийско-арабские цифры уже были известны в Багдаде. Конечно, они достигли этой части света несколько раньше: в 662 году сирийский священник по имени Северус Себохт с восхищением писал о «девяти знаках» индейцев.
К началу девятого века нашей эры Багдад был крупным центром научных знаний, которым руководил неудержимо любопытный и умный халиф аль-Мамун. Это был также самый большой и самый важный город на Земле, столица огромной мусульманской империи, которая простиралась от атлантического побережья Африки до реки Инд, занимая поразительные пять миллионов квадратных миль. Люди приезжали со всей империи в поисках счастья, и город стал ярким центром обучения и культуры.
Следуя примеру нескольких просвещенных халифов, элита вложила свои значительные средства в создание библиотек и финансирование обучения. Ученые стекались, чтобы принять участие в интеллектуальных усилиях, и рукописи были привезены со всего Ближнего Востока и из-за его пределов для перевода и использования знаний, которые они хранили.
Ученые используют астрономические инструменты в Константинополе, следуя традиции, заложенной в первые века в Багдаде, месте первой обсерватории в мусульманском мире. (Изображение Universal Images Group/Getty Images)
Астрономия и математика были двумя наиболее важными предметами, и достижения ученых, изучавших их, были поистине поразительны.
Они правильно рассчитали окружность Земли с точностью до нескольких сотен миль. Они построили первую обсерваторию в мусульманском мире, где получали данные, изменившие человеческое представление о Вселенной. Они переводили, исправляли и улучшали древнегреческие научные теории, сочетая их с индийскими и своими собственными идеями, продвигая знания вперед.Сила чисел
Во время интеллектуального расцвета при аль-Мамуне в Багдаде было несколько выдающихся математиков, но самым талантливым был Мухаммад ибн Муса аль-Хорезми. Его имя говорит о том, что его происхождение лежало в провинции Хорезм, далеко на северо-востоке на берегу Аральского моря. Если это так, то он, как и многие звезды багдадской интеллектуальной сцены, был не арабом, а персом, хотя всегда писал по-арабски.
Аль-Хорезми читал Брахмагупту Siddhanta и понял, что индийско-арабские цифры и система позиционных значений имеют гораздо больший потенциал, чем системы, используемые в настоящее время в мусульманской империи, которые использовали счет по пальцам и аспекты шестидесятеричной системы и выражали дроби словами вместо чисел.
. Книга Аль-Хорезми о сложении и вычитании по методу индейцев была первой книгой на арабском языке, объясняющей индийско-арабскую систему, с главой о каждой из девяти цифр и демонстрацией того, как писать числа с использованием разряда. система.Аль-Хорезми был дальновидным математиком. В самом деле, мы бы сейчас описали его как исключение. За исключением нескольких коллег-ученых, никто, похоже, не интересовался новой системой чисел, которую он восхвалял, а глубинный сдвиг парадигмы, необходимый для ее принятия, не происходил в течение нескольких столетий. Тем не менее, когда этот сдвиг, наконец, наступил, его книге суждено было сыграть ключевую роль: она была переведена на латынь в XII веке и стала важной частью европейской интеллектуальной традиции.
Статуя математика девятого века аль-Хорезми в Хиве, Узбекистан, возможно, регион его рождения (Konstik/Getty Images)
Имя Аль-Хорезми сегодня мало известно в Европе, но оно сохранилось в мире алгоритм, полученный из латинизированной версии его имени «Algorismus».
Он также дал нам слово алгебра, производное от al-jabr , часть арабского названия его Compendious Book on Calculation by Compendious and Balancing , практического руководства по вычислениям, написанного по просьбе халифа аль-Ма’. мун. В нем аль-Хорезми впервые дал определение этой дисциплине, описав различные виды квадратных уравнений. Интересно, что он сделал это словами, а не системой обозначений, используемой сегодня в алгебре, которая была разработана в эпоху Возрождения.Копии обеих книг аль-Хорезми были вывезены из Багдада в другие места, где они были изучены и переведены. К десятому веку они достигли Испании, большая часть которой в то время находилась под властью мусульман. В XI и XII веках христианские силы на севере Пиренейского полуострова начали завоевывать великие города Аль-Андалуса. Толедо пал в 1085 году, и в последующие десятилетия европейские ученые приезжали в город в поисках арабских книг, в том числе текстов аль-Хорезми, которые они перевели на латынь.
Это был медленный процесс, отчасти из-за сопротивления христиан, которые считали числительные злыми и опасными – просто потому, что они пришли из мусульманского мира
Эти ученые, возможно, уже были знакомы с формами самих цифр, которые присутствовали на абаке (счетной доске) определенного типа, который, как считается, был введен монахом десятого века по имени Герберт (впоследствии Папа Сильвестр II), чей талант и страсть к математике привели его в Испанию в поисках знания. Таким образом, индо-арабские цифры и система позиционных значений были постепенно введены в Европу. Это был медленный процесс, отчасти из-за сопротивления христиан, которые считали числительные злыми и опасными просто потому, что они пришли из мусульманского мира.
Фибоначчи и вычислительная революция числительные не в Испании, а в Африке: Леонардо Пизанский, известный сегодня как Фибоначчи (хотя это имя применялось к нему только с XIX века).
Родившийся около 1170 года, он был сыном успешного пизанского купца, назначенного в торговую палату в Бужи (теперь называемом Беджайя в Алжире) в эпоху, когда Пиза была одной из четырех основных итальянских торговых держав — другие Амальфи, Венеция. и Генуя — с торговыми связями и поселениями по всему Средиземноморью.В Бужи арабские математики научили юного пизанца индо-арабским цифрам, вероятно, используя труды аль-Хорезми, и показали ему великолепие разрядной системы наряду с другими чудесами своей математической традиции.
Будучи подростком, Фибоначчи путешествовал со своим отцом по восточному Средиземноморью, тем самым получив возможность сравнить несколько систем исчисления, использовавшихся в то время. Он быстро осознал огромный потенциал индийско-арабской системы для преобразования обучения на Западе. В 1202 году он написал книгу под названием Liber abbaci (Книга расчетов). В этой книге, первой оригинальной работе на латыни по этому вопросу, он объяснил работу каждого из числительных и метод записи чисел в порядке их значения.
К 1220-м годам Фибоначчи вернулся в Пизу и провел некоторое время при дворе Фридриха II, императора Священной Римской империи, человека, по-видимому, настолько умного и великолепного, что его прозвали Stupor Mundi — «Чудо света». Фибоначчи процветал под покровительством Фридриха, и в 1228 году он выпустил исправленное издание 9-го числа.0036 Liber abbaci с большим акцентом на практическое применение в торговле. В нем подробно описывалось, как проводить транзакции в разных валютах и как использовать различные системы мер и весов — методы, которые становились все более важными по мере того, как процветала Европа, а торговый мир расширялся и развивался. Торговцы должны были иметь возможность выполнять сложные вычисления и эффективно регистрировать свои счета — это стало возможным благодаря индо-арабской системе чисел, изложенной Фибоначчи.
Первоначальным влиянием Фибоначчи было введение индо-арабских цифр и системы позиционных значений людям, которым математика была нужна для практических целей: торговцам, геодезистам и архитекторам, которые использовали их для выполнения вычислений, необходимых в их трудовой жизни.
Более сложные аспекты его работ были рассмотрены позже и помогли добиться прогресса в теоретической математике. В 15-м и 16-м веках ученые начали использовать цифры в своих исследованиях алгебры, особенно после 1585 года, когда фламандский математик Саймон Стевин опубликовал новаторскую брошюру о десятичных дробях.Введение десятичной точки заставило людей задуматься о математике по-новому, проложив путь к альтернативным понятиям, таким как логарифмы, отрицательные и комплексные числа. Как обычно, было и много практических применений: измерения в инженерии и геодезии, расчеты в астрономии и коммерции. На этом этапе алгебраические задачи и уравнения записывались с использованием цифр, символов и букв, а не слов, что позволяло ученым выражать и вычислять чрезвычайно сложные задачи.
Введение десятичной точки заставило людей задуматься о математике по-новому, проложив путь к альтернативным концепциям
немецкий мастер Иоганн Гутенберг около 1440 г.
– изменил мир знаний. Поскольку количество доступных книг росло в геометрической прогрессии, их цена упала, что сделало их доступными для гораздо большего числа людей. Подсчитано, что к 1500 году, всего через полвека после начала книгопечатания в Европе, было выпущено около 20 миллионов книг. Печать также сделала тексты более стандартизированными, помогла зафиксировать форму индийско-арабских цифр и сделала их широко узнаваемыми и известными. В то же время ученые начали переводить математические тексты на местные языки (итальянский, немецкий, английский), вводя содержащиеся в них математические понятия в повседневную жизнь европейцев.Подробнее: История Библии: кто и когда ее написал?
К 1550 году очень немногие люди в Европе все еще использовали старую римскую систему счисления для ведения счетов. Простота и элегантное великолепие индийско-арабской системы, наконец, победили, открыв удивительные новые пути в областях математики и естественных наук, создав мир, в котором мы живем сегодня, — мир, основанный на бесконечных последовательностях чисел.
причина, по которой мы начинаем с 3, заключается в том, что для чисел 1 и 2 исчисляемое существительное принимает форму единственного или двойного числа!)
Пол десяти определяет пол числа.
9.67 29292. 9000 2 9000 2
Раньше мое западное образование заставляло меня почти всегда работать с европейскими/английскими номерами.
snopes.com — незащищенный веб-сайт) логику чисел, основанную на количестве углов, образованных ребрами цифр, кульминацией которых является все важные нули «0»).
Ниже я излагаю эти практические неудачи и приглашаю всех вас, коллеги-билингвы, прокомментировать свой собственный опыт, а также сравнить и сопоставить использование двух разных систем счисления.
Много раз мне звонил смеющийся банковский служащий, чтобы указать, что я неправильно написал дату на чеке, возможно, шепча себе под нос: «Что за хавага!» — действительно стыдно!
Я думаю, что некоторые европейцы (например, итальянцы) могут использовать ту же систему, что и арабы. Друзья-итальянцы, пожалуйста, прокомментируйте это.
Арабы того времени, вероятно, сочли эти числа на хинди более интересными или, может быть, более удобными в использовании, но я думаю, мы никогда не узнаем….