Д от ф это область определения: Функции. Область определения и область значений. 9-й класс

2

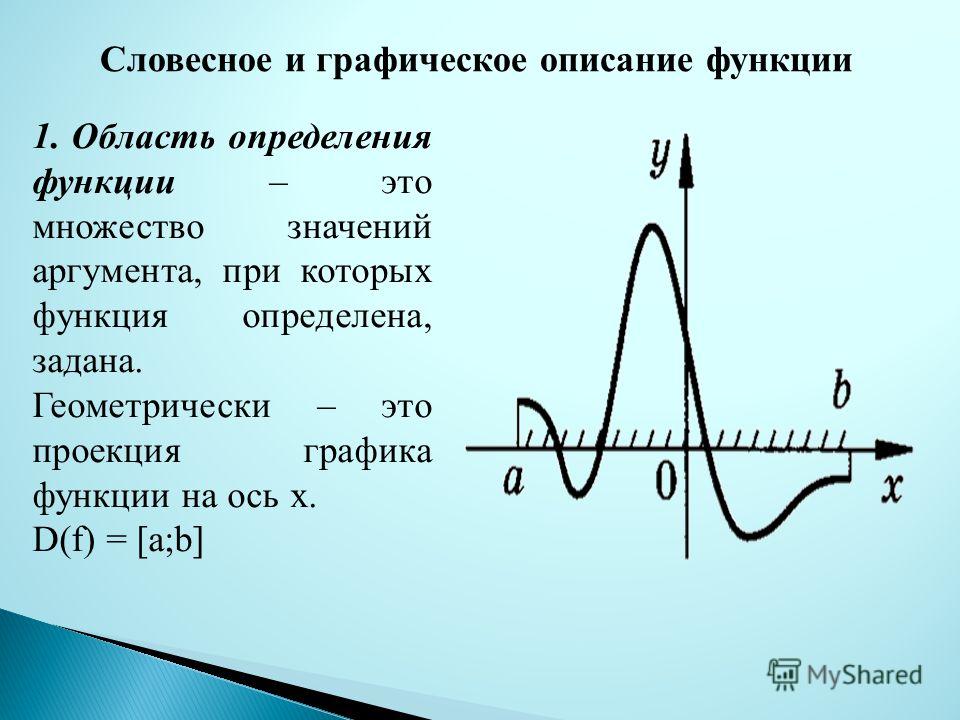
Область определения функции | это… Что такое Область определения функции?

Область определения функции — множество, на котором задаётся функция.

Содержание 1 Определение 2 Примеры 2.1 Числовые функции 2.1.1 Тождественное отображение 2.1.2 Гармоническая функция 2.1.3 Дробно-рациональные функции 2.1.4 Мера 2.1.5 Функционал 3 См. также 4 Литература

Определение

Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения.

Более формально, пусть задано отображение , которое отображает множество в , то есть: ; тогда

• множество называется областью определения функции
• и обозначается , или (от англ. domain «область»).

Обычно предполагается, что , из-за чего понятие области определения выглядит тавтологией: «область определения функции — это область, где определена функция». Для того, чтобы придать чёткий смысл данному понятию, рассматривается некоторое более широкое множество, которое называется

областью отправления, и тогда область определения функции  — это такое подмножество множества (которое и есть область отправления функции), где для каждого элемента определено значение функции .

Этот факт коротко записывают в виде: .

Примеры

Наиболее наглядные примеры областей определения доставляют числовые функции. Мера и функционал также доставляют важные в приложениях виды областей определения.

Числовые функции

Числовые функции — это функции, относящиеся к следующим двум классам:

• вещественнозначные функции вещественного переменного — это функции вида ;
• а, также, комплекснозначные функции комплексного переменного это функции вида ,

где и  — множества вещественных и комплексных чисел соответственно.

Тождественное отображение

Область определения функции совпадает с областью отправления ( или ).

Гармоническая функция

Область определения функции : представляет собой комплексную плоскость без нуля

и не совпадает с областью отправления (вся комплексная плоскость).

Дробно-рациональные функции

Область определения дробно-рациональной функции вида

представляет собой вещественную прямую или комплексную плоскость за исключением конечного числа точек, которые являются решениями уравнения

.

Эти точки называются полюсами функции .

Мера

Если каждая точка области определения функции — это некоторое множество, например, подмножество заданного множества, то говорят, задана функция множества.

Мера — пример такой функции, где в качестве области определения функции (меры) выступает некоторая совокупность подмножеств заданного множества, являющееся, например, кольцом или полукольцом множеств.

Например, определённый интеграл представляет собой функцию ориентированного промежутка.

Функционал

Пусть  — семейство отображений из множества в множество . Тогда можно определить отображение вида . Такое отображение называется функционалом.

Если, например, фиксировать некоторую точку , то можно определить функцию , которая принимает в «точке» то же значение, что и сама функция в точке .

См. также

• Область значений функции

Литература

• Функция. Математический энциклопедический словарь. — Гл. ред. Ю. В. Прохоров. — М.: «Большая российская энциклопедия», 1995.
• Клейн Ф. Общее понятие функции. В кн.: Элементарная математика с точки зрения высшей. Т.1. М.-Л., 1933
• ISBN 5-02-014844-X
• А. Н. Колмогоров, С. В. Фомин. Глава 1.. Элементы теории множеств // Элементы теории функций и функционального анализа. — 3-е изд.. — М.: Наука, 1972. — С. 14 — 18. — 256 с.
• А. Н. Колмогоров «Что такое функция» // «Квант». — М.: «Наука», 1970. — В. 1. — С. 27-36. — ISSN 0130-2221.

Исчисление

— Область определения $\frac{x}{\sin(x)}$.

спросил 9 лет, 9 месяцев назад

Изменено 9 лет, 9 месяцев назад

Просмотрено 241 раз

$\begingroup$

Будет ли область определения $\displaystyle\frac{x}{\sin(x)}$ равна $0$? Функция графического калькулятора выглядит так, будто у нее много бесконечных пределов, так что я не уверен.

• исчисление
• алгебра-предварительное исчисление
• функции
• тригонометрия

$\endgroup$

$\begingroup$

Пусть $f$ и $g$ — две вещественнозначные функции с областями определения $\mathcal{D}(f)$ и $\mathcal{D}(g)$ соответственно. Фактор-функция $\frac{f}{g}$ имеет область определения

$$\mathcal{D}\left(\frac{f}{g}\right) = \{x\in \mathcal{D}( f)\cap\mathcal{D}(g)\ |\ g(x) \neq 0\}.$$

В этом случае $f(x) = x$, $g(x) = \sin x $ и $\mathcal{D}(f) = \mathcal{D}(g) = \mathbb{R}$, поэтому $\mathcal{D}(f)\cap\mathcal{D}(g) = \mathbb{R}$. Так как $\sin x = 0$ именно тогда, когда $x = k\pi$ для $k \in \mathbb{Z}$, нам нужно исключить эти точки из области определения. Следовательно, областью определения $\displaystyle\frac{x}{\sin x}$ является $\mathbb{R}\setminus\{k\pi\ |\ k \in \mathbb{Z}\}$. 9{k = +\infty}\{\pi k\}$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Домены как регионы в плоскости xy

Домены как регионы в плоскости xy

Часть 2:

Домены как регионы в плоскости xy

В частности, функция двух переменных — это функция, входами которой являются точки ( x,y ) на плоскости xy , а выходами — действительные числа.

Определение 1.1: Функция двух переменных f ( x,y ) представляет собой отношение, которое отображает каждую точку ( x,y ) в наборе D на плоскости xy не более чем одному действительному числу z .

Множество D называется областью определения функции, которую часто обозначают dom ( f ). Домены часто записываются в заданной нотации, где {} представляет собой фразу «является набором» и вертикальной чертой | представляет фразу «такой, что». Например,

A = {( x , y )     | х > у }

означает, что A — это набор точек ( x , y ), таких, что x больше, чем y .

ПРИМЕР 4    Определите домен f ( x , y ) = ln( y -2 х )

Решение: Поскольку аргумент ln( ^. ) должен быть положительным, домен числа f — множество точек ( x , y ), для которых знаменатель не равно 0. Однако

y -2 x > 0        означает    , что         y > 2 x

В системе обозначений это записывается как dom ( f ) = {( x , y )     | y > 2 x } .

В этом тексте большинство наборов в плоскости xy , с которыми мы столкнемся, будут ограничен замкнутой кривой. Множество всех точек внутри , но не включая , замкнутая кривая называется открытая область , а множество всех точек внутри и включая замкнутую кривую говорят, что это закрытый регион. Аналогичные определения справедливы для конечного объединения замкнутые кривые.

В более общем смысле точка (

p , q ) называется границей . точка набора R , если любой круг с центром в ( p , q ) содержит как точки внутри, так и точки за пределами Р.

Набор R является открытым , если он не содержит ни одной своей границы точек и является закрытым , если содержит все своих граничных точек (если он содержит некоторые, но не все свои граничные точки, то он не является ни открытым или закрыт).