Даны вершины треугольника найти высоту: Даны вершины треугольника ABC. решение задачи Аналитическая геометрия с ответом

Даны вершины треугольника вычислить длину его высоты — Dudom

Даны координаты вершин треугольника

.

1) Вычислить длину стороны

.

2) Составить уравнение линии

.

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

А

1. Длина стороны ВС равна модулю вектора

.

; .

2. Уравнение прямой ВС:

; ; .

3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку

перпендикулярно вектору :

. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

4. Найдем координаты точки N – середины стороны ВС:

; ; .

Точка пересечения медиан О делит каждую медиану на отрезки в отношении

.

Используем формулы деления отрезка в данном отношении

:

.

5. Косинус угла при вершине В найдем как косинус угла между векторами

и ;

.

6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы

Систему решим по формулам Крамера:

.

Точка К является серединой отрезка АМ.

.

Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	.	10.	.
11.	.	12.	.
13.	.	14.	.
15.	.	16.	.
17.	.	18.	.
19.	.	20.	.
21.	.	22.	.
23.	.	24.	.
25.	.	26.	.
27.	.	28.	.
29.	.	30.	.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10578 —

| 7333 — или читать все.

УСЛОВИЕ:

Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение линии ВС;
3) составить уравнение высоты, проведенной из вершины А;
4) вычислить длину высоты, проведенной из вершины А;
5) найти точку пересечения медиан;
6) вычислить внутренний угол при вершине В;
7) найти координаты точки М, расположенной симметрично точке А относи-тельно прямой ВС.

РЕШЕНИЕ ОТ sova ✪ ЛУЧШЕЕ РЕШЕНИЕ

7)Точка М, симметричная точке А, относительно прямой ВС лежит на прямой, перпендикулярной ВС. Уравнение перпендикулярной прямой — это уравнение высоты из точки А

см. в)
3x-4y+107=0
и расстояния от точки М до прямой ВС и от точки А до прямой ВС

4x_(M)+3y_(M)-33=9 или 4x_(M)+3y_(M)-3=-9

найдем координаты точки М или точки А ( А нам не надо).

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC.

A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

1) длину ребра AB; 2) угол между ребрами AB и AD; 3) угол между ребром AD и гранью ABC; 4) площадь грани ABC; 5) объем пирамиды; 6) уравнения прямой AB; 7) уравнение плоскости ABC; 8) уравнения высоты, опущенной из вершины D на грань ABC. Сделать чертеж. №61. Найти собственные значения и собственные столбцы матрицы А. №71. Привести уравнение 2-го порядка к каноническому виду и построить кривые — Контрольная работа #1201514 — Высшая математика

№1. 3
№11. 5
№25. 7
№31. 8
№41. 9
№51. 12
№61. 13
№71. 15

Решить задачи: №1. Даны координаты вершин треугольника ABC. Найти: 1) уравнение стороны АВ; 2) уравнение высоты CD, опущенной из вершины С на сторону АВ; 3) уравнение медианы АЕ; 4) уравнение окружности, для которой медиана АЕ служит диаметром
№11. Решить систему уравнений с тремя неизвестными двумя способами:
1) при помощи определителей по формулам Крамера,

2) с помощью обратной матрицы
№25. Решить систему уравнений методом Гаусса
№41.
Даны координаты вершин пирамиды ABCD.
Найти:
1) длину ребра AB;
2) угол между ребрами AB и AD;
3) угол между ребром AD и гранью ABC;
4) площадь грани ABC;
5) объем пирамиды;
6) уравнения прямой AB;
7) уравнение плоскости ABC;
8) уравнения высоты, опущенной из вершины D на грань ABC.
Сделать чертеж.
№61.
Найти собственные значения и собственные столбцы матрицы А.
№71.
Привести уравнение 2-го порядка к каноническому виду и построить кривые

1. Высшая математика для экономистов : учебник /под ред. Н.Ш. Кремера. – 3-е изд. –М. : ЮНИТИ-ДАНА, 2007.
2. Математика: учеб. пособие / Ю.М. Данилов, Л.Н. Журбенко, Г.А. Никонова, Н.В. Никонова, С.Н. Нуриева; под. ред. Л.Н. Журбенко, Г.А. Никоновой. – М. : ИФРА-М, 2009.

3. Журбенко Л.Н, Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дектярева О.М. Математика в примерах и задачах : учеб. пособие. – М. : ИНФРА-М, 2009.

Тема:	Решить задачи: №1. Даны координаты вершин треугольника ABC. Найти: 1) уравнение стороны АВ; 2) уравнение высоты CD, опущенной из вершины С на сторону АВ; 3) уравнение медианы АЕ; 4) уравнение окружности, для которой медиана АЕ служит диаметром №11. Решить систему уравнений с тремя неизвестными двумя способами: 1) при помощи определителей по формулам Крамера, 2) с помощью обратной матрицы №25. Решить систему уравнений методом Гаусса №41. Даны координаты вершин пирамиды ABCD. Найти: 1) длину ребра AB; 2) угол между ребрами AB и AD; 3) угол между ребром AD и гранью ABC; 4) площадь грани ABC; 5) объем пирамиды; 6) уравнения прямой AB; 7) уравнение плоскости ABC; 8) уравнения высоты, опущенной из вершины D на грань ABC. Сделать чертеж. №61. Найти собственные значения и собственные столбцы матрицы А. №71. Привести уравнение 2-го порядка к каноническому виду и построить кривые
Артикул:	1201514
Дата написания:	10.01.2013
Тип работы:	Контрольная работа
Предмет:	Высшая математика
Оригинальность:	Антиплагиат.ВУЗ — 71%
Количество страниц:	17

геометрия — Найдите площадь треугольника по координатам его вершин

Вопрос задан 6 лет, 11 месяцев назад

Изменено 6 лет, 11 месяцев назад

Просмотрено 2к раз

$\begingroup$

Ниже приведен вопрос пробного теста GRE, который я не понимаю.

В соответствии с этим общим рассуждением получается, что любая произвольная точка $(x, 7)$ будет иметь «высоту», равную 10, но тогда, если у нас $x = 1000000$, например, окажется, что площадь треугольник был бы значительно больше, чем всего 30 единиц.

Или я неправильно понимаю аргумент, приведенный в этом объяснении?

• геометрия
• тригонометрия
• треугольники
• площадь
• gre-exam

$\endgroup$

5

$\begingroup$

В соответствии с этим общим аргументом представляется, что любое произвольное точка $(x,7)$ будет иметь «высоту» равную 10, но тогда, если у нас есть $x=1000000$ например может показаться, что площадь треугольник был бы значительно больше, чем всего 30 единиц.

Или я неправильно понимаю аргумент, приведенный в этом объяснении?

Как правильно указали другие, высота треугольника — это измерение, перпендикулярное основанию, в данном случае измерение строго в направлении оси Y, в частности, $7 — (-3) = 7 + 3 = 10$. В самом деле, сделав верхней точкой любое значение $(x, 7)$, мы сохранили бы ту же высоту и, следовательно, ту же площадь, равную 30. больше, если это было скорректировано. В то время как треугольник, безусловно, получил бы длиннее , он одновременно стал бы тоньше и, таким образом, площадь сбалансировалась бы до того же значения. Например, вот график с верхней точкой $(1000, 7)$ от Wolfram Alpha:

Дополнительное примечание: если вы войдете в точку с $x = 1000000$, тогда Wolfram Alpha захлебнется и ошибочно скажет: «невозможный треугольник»! Видимо ей очень не нравится такой ничтожно тощий треугольник.

$\endgroup$

$\begingroup$

Представьте себе стопку монет. Вы можете сдвинуть монетки так, чтобы получился наклонный цилиндр |>/ При этом преобразовании общий объем монет не изменился. Тот же принцип, только в 2D. Надеюсь, это помогло!

$\endgroup$

$\begingroup$

Площадь треугольника равна половине длины основания, умноженной на высоту/высоту.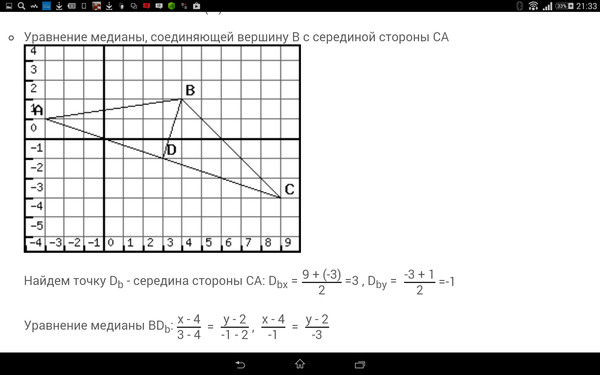 Можно также утверждать, что площадь одинакова для всех вытянутых треугольников между двумя параллелями с одинаковой длиной основания (на одной параллельной линии) и вершиной (на другой параллельной линии) ) и все они имеют одну и ту же высоту… независимо от того, где находится вершина на линии, параллельной основанию.

В зависимости от того, какую точку вы выберете для вызова вершины, и перпендикулярной длины/высоты, опущенной из нее на противоположную сторону, есть три пары вариантов (база, высота) для одной и той же области продукта.

$\endgroup$

$\begingroup$

Высота треугольника — это минимальное расстояние между основанием и противоположной вершиной (минимальное, потому что в прямоугольном треугольнике перпендикуляр — самая короткая сторона). Вы можете сравнить это с измерением высоты горы. Вы измеряете высоту наискось? Проведите прямую, параллельную основанию, через $(28,7)$. Итак, все точки на этой прямой равноудалены от основания. Это основной принцип.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

геометрия — Как найти координаты, где высота треугольника пересекает основание в 3 измерениях?

Пусть $\vec{p}_0$ и $\vec{p}_1$ — вершины в основании треугольника, а $\vec{p}_2$ — вершина.

Определить $\hat{b}$ как базовый единичный вектор, $$\шляпа{b} = \frac{\vec{p}_1 — \vec{p}_0}{\left\lVert\vec{p}_1 — \vec{p}_0\right\rVert}$$ где $\lVert\vec{p}_1 — \vec{p}_0\rVert = \sqrt{(\vec{p}_1-\vec{p}_0)\cdot(\vec{p}_1-\vec {p}_0)}$.

Если мы спроецируем вектор из первой базовой вершины в вершину вершины, $(\vec{p}_2 — \vec{p}_0)$, в базовый единичный вектор $\hat{b}$ (используя векторное скалярное произведение ), мы получаем (со знаком) расстояние от основания до точки непосредственно под вершиной вершины. Расстояние между этой точкой и вершиной равно высоте $h$ треугольника: $$h = \left\lVert (\vec{p}_2 — \vec{p}_0) — \hat{b} ( \hat{b} \cdot (\vec{p}_2 — \vec{p} _0) \право\rВерт$$ Подставляя $\hat{b}$, получаем $$h = \left\lVert \vec{p}_2 — \vec{p}_0 — \frac{\left(\vec{p}_1 — \vec{p}_0\right)\left(\left( \vec{p}_1 — \vec{p}_0 \right)\cdot\left(\vec{p}_2 — \vec{p}_0 \right)\right)}{\left(\vec{p} _1 — \vec{p}_0\right)\cdot\left(\vec{p}_1 — \vec{p}_0\right)} \right\rVert$$

В псевдокоде функция, вычисляющая высоту по координатам базовой вершины x0,y0,z0 и x1,y1,z1 и координатам вершины x2,y2,z2 , представляет собой

 function Triangle_height( х0, у0, z0, х1, у1, z1, х2, у2, z2):
    # x0,y0,z0 Первая базовая вершина
    # x1,y1,z1 Вторая базовая вершина
    # x2,y2,z2 вершина вершины
    tmp0 = х1 - х0
    tmp1 = у1 - у0
    tmp2 = z1 - z0
    tmp3 = х2 - х0
    tmp4 = у2 - у0
    tmp5 = z2 - z0
    tmp6 = tmp0*tmp0 + tmp1*tmp1 + tmp2*tmp2
    если (tmp6 <= 0), то
        # Вырожденный треугольник; (x0,y0,z0) = (x1,y1,z1). 
        # Это не треугольник, а линия (или точка).
        # Это возвращает длину строки,
        # или 0, если (x0,y0,z0) = (x1,y1,z1) = (x2,y2,z2).
        чч = tmp3*tmp3 + tmp4*tmp4 + tmp5*tmp5
    еще
        tmp7 = (tmp0*tmp3 + tmp1*tmp4 + tmp2*tmp5) / tmp6
        # tmpx,tmpy,tmpz — вектор вершины, перпендикулярный основанию
        tmpx = tmp3 - tmp7 * tmp0
        tmpy = tmp4 - tmp7 * tmp1
        tmpz = tmp5 - tmp7 * tmp2
        чч = tmpx*tmpx + tmpy*tmpy + tmpz*tmpz
    конец, если
    возврат кврт (чч)
 

Приведенный выше псевдокод настроен вручную из выходных данных модуля Maple codegen из векторной формулы с добавлением проверки. Хотя математика говорит, что tmp6 не может быть отрицательным, лучше практиковать вместо этого проверять, является ли оно неположительным. Видите ли, любое сравнение с плавающей запятой с точным значением всегда подозрительно, даже если целевое значение равно нулю.

---

В статье Wolfram Mathworld о трехмерном расстоянии точка-линия мимоходом упоминается еще более простая формула:

$$h = \frac{\left\lVert\left(\vec{p}_1 — \vec{p}_0\right)\times\left(\vec{p}_0 — \vec{p}_2 \right)\right\rVert}{\left\lVert\vec{p}_1 — \vec{p}_0\right\rVert}$$

(Обратите внимание на другую нумерацию здесь, $2\получает 0$, $0\ получает 1$, $1\получает 2$, по сравнению со страницей Mathworld).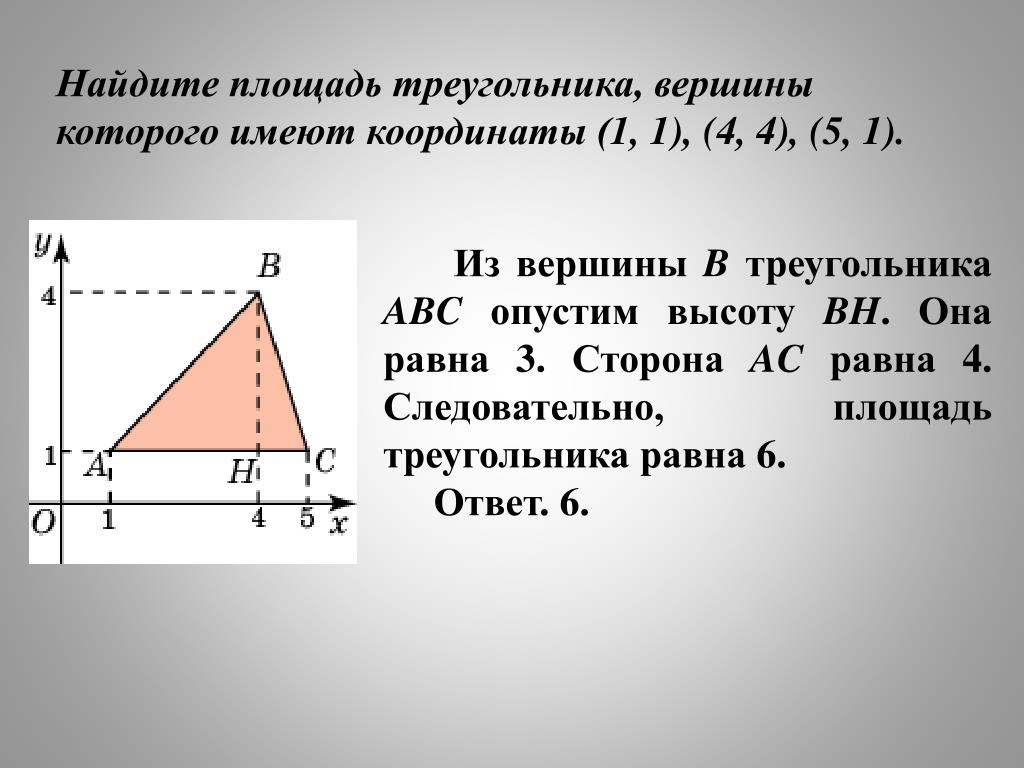 # x0,y0,z0 Первая базовая вершина # x1,y1,z1 Вторая базовая вершина # x2,y2,z2 вершина вершины tmp0 = х1 — х0 tmp1 = у1 — у0 tmp2 = z1 — z0 tmp3 = х0 — х2 tmp4 = у0 — у2 tmp5 = z0 — z2 tmp6 = tmp0*tmp0 + tmp1*tmp1 + tmp2*tmp2 если (tmp6 <= 0), то чч = tmp3*tmp3 + tmp4*tmp4 + tmp5*tmp5 еще tmp7 = tmp5*tmp1 - tmp2*tmp4 tmp8 = tmp2*tmp3 - tmp5*tmp0 tmp9= tmp4*tmp0 - tmp1*tmp3 чч = (tmp7*tmp7 + tmp8*tmp8 + tmp9*tmp9) / tmp6 конец, если возврат кврт (чч)

Обе функции математически одинаковы (но при использовании чисел с плавающей запятой ошибки округления могут различаться, поэтому не ожидайте, что результаты будут в точности одинаковыми при использовании математических вычислений с плавающей запятой). Я не вижу существенной разницы между ними. В частности, обеим требуется двенадцать умножений и одно деление. Последнее требует меньшего количества сложений/вычитаний в случаях невырожденного треугольника, поэтому может быть немного быстрее.