Действия со степенями при сложении: Свойства степеней, действия со степенями

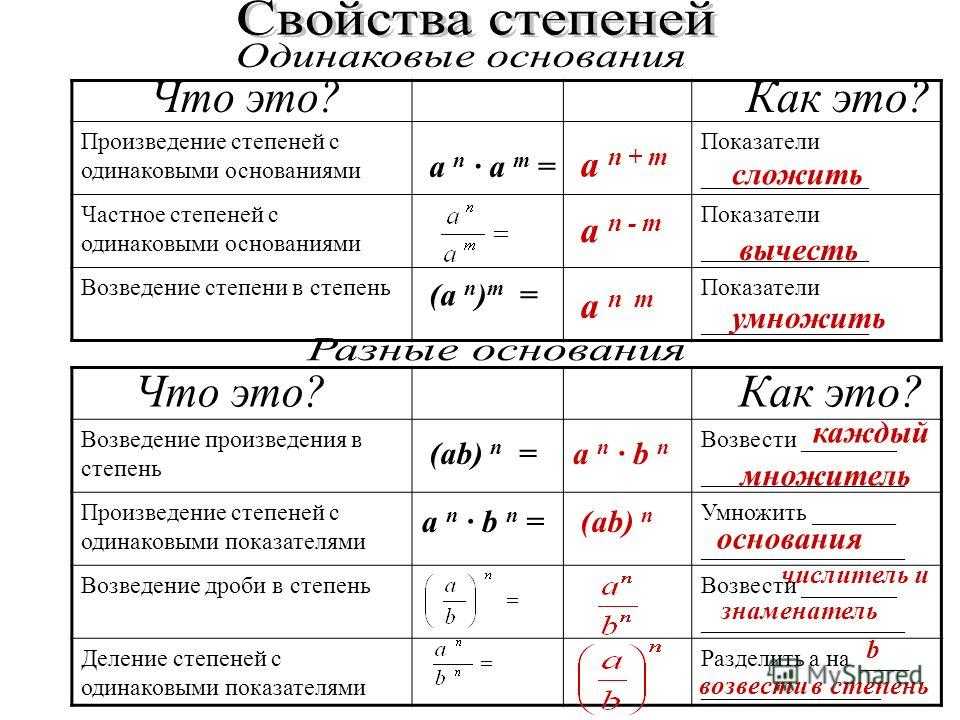
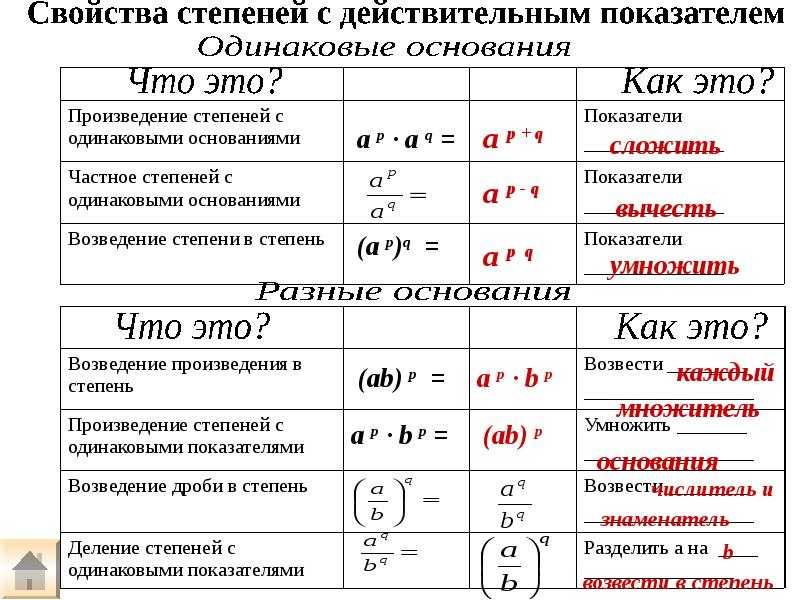
Свойства степеней с натуральным показателем: формулы, умножение и деление степеней, действия со степенями

Степень целого положительного числа с натуральным показателем

Изучая натуральные числа, мы анализировали понятие степени натурального числа (подробнее здесь: Степень числа. Возведение в степень. Таблица степеней натуральных чисел). На этом уроке мы рассмотрим основное свойство степени, формулы и действия со степенями.

Что такое степень числа с натуральным показателем?

Степенью числа а с натуральным показателем n больше единицы называют произведение множителей, каждый из которых равен а:

Основное свойство степени

Для любого целого числа a и натуральных показателей m и n выполняется равенство, характеризующее основное свойство степеней:

Исходя из основного свойства степеней, при умножении степеней одного и того же целого числа показатели степеней нужно сложить, а основу оставить без изменений.

Например:

Объяснение: при умножении степени складываются – основу степени (число 3) оставляем без изменений, а показатели степеней суммируем: 2 + 5 = 7. Получим в произведении число 3 в седьмой степени.

Возведение степени в степень

Для любого целого числа a и натуральных показателей m и n выполняется равенство:

Правило возведения степени в степень звучит так:

Чтобы возвести степень в степень, нужно показатели степеней перемножить, а основу оставить ту же.

Пример

Объяснение: основу степени (число 2) оставляем без изменений, показатели степеней перемножаем: 3 ⋅ 4 = 12

Степень произведения чисел

Для любых целых чисел a и b и натурального показателя степеней n выполняется равенство:

Чтобы найти n-ую степень произведения чисел, нужно перемножить n-ые степени множителей.

Пример

Возведение отрицательного числа в степень

Степень целого отрицательного числа с натуральным показателем: правило возведения

Чтобы возвести в степень отрицательное число, нужно возвести в такую же степень модуль этого числа и перед результатом поставить знак плюс, если показатель степени является четным числом, или минус, если показатель степени – нечетное число

Рассмотрим примеры, когда основой степени является целое отрицательное число -2:

В первом примере мы возвели число -2 к третьей степени. Показатель степени, число 3, нечетный, поэтому перед результатом ставим знак минус.

Если поднести к четвертой степени число -2, то получим в результате положительное число (ведь показатель степени число 4 является четным).

Действия со степенями. Примеры

Выше мы рассмотрели основные свойства степеней с натуральным показателем, если основа целое положительное число или целое отрицательное число. Теперь рассмотрим конкретные примеры, где нужно выполнить действия со степенями – сложение и вычитание, умножение и деление.

Сложение и вычитание степеней с одинаковыми основаниями

Складывая или вычитая выражения со степенями, мы пользуемся теми же правилами, что и для алгебраических выражений.

Например:

То есть, если выражение содержит степени с одинаковыми основами и показателями, действия сложения и вычитания выполняют как для целых чисел.

Умножение степеней с разными основами

Правило умножения степеней звучит так:

Чтобы умножить степень с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить таким же.

Формула умножения чисел с одинаковыми степенями:

где a и b – любые целые числа, n – натуральное число

Решим несколько примеров на умножение степеней, используя формулу и правило:

Деление степеней

Правило деления степеней с одинаковыми основами звучит так:

При делении степеней с одинаковыми основаниями от показателя степени делимого вычитается показатель степени делителя, а основа остается без изменений.

Формула: как делить степени

где а – целое число, которое не равно нулю, а m – и натуральные числа

Примеры

умножение, сложение и вычитание степеней

В предыдущей статье мы рассказали, что из себя представляют одночлены. В этом материале разберем, как решать примеры и задачи, в которых они применяются. Здесь будут рассмотрены такие действия, как вычитание, сложение, умножение, деление одночленов и возведение их в степень с натуральным показателем. Мы покажем, как определяются такие операции, обозначим основные правила их выполнения и то, что должно получится в результате. Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.

Удобнее всего работать со стандартной записью одночленов, поэтому все выражения, которые будут использованы в статье, мы приводим в стандартном виде. Если изначально они заданы иначе, рекомендуется сначала привести их к общепринятой форме.

Правила сложения и вычитания одночленов

Наиболее простые действия, которые можно проводить с одночленами – это вычитание и сложение. В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).

Когда мы складываем или вычитаем одночлены, сначала записываем в общепринятой форме соответствующую сумму и разность, после чего упрощаем получившееся выражение. Если есть подобные слагаемые, их нужно привести, скобки – раскрыть. Поясним на примере.

Пример 1

Условие: выполните сложение одночленов −3·x  и 2,72·x3·y5·z.

Решение

Запишем сумму исходных выражений. Добавим скобки и поставим между ними плюс. У нас получится следующее:

(−3·x)+(2,72·x3·y5·z)

Когда мы выполним раскрытие скобок, получится -3·x+2,72·x3·y5·z. Это многочлен, записанный в стандартной форме, который и будет результатом сложения данных одночленов.

Ответ: (−3·x)+(2,72·x3·y5·z)=−3·x+2,72·x3·y5·z.

Если у нас задано три, четыре и больше слагаемых, мы осуществляем это действие точно так же.

Пример 2

Условие: проведите в правильном порядке указанные действия с многочленами

3·a2-(-4·a·c)+a2-7·a2+49-223·a·c

Решение

Начнем с раскрытия скобок.

3·a2+4·a·c+a2-7·a2+49-223·a·c

Мы видим, что полученное выражение можно упростить путем приведения подобных слагаемых:

3·a2+4·a·c+a2-7·a2+49-223·a·c==(3·a2+a2-7·a2)+4·a·c-223·a·c+49==-3·a2+113·a·c+49

У нас получился многочлен, который и будет результатом данного действия.

Ответ: 3·a2-(-4·a·c)+a2-7·a2+49-223·a·c=-3·a2+113·a·c+49

В принципе, мы можем выполнить сложение и вычитание двух одночленов с некоторыми ограничениями так, чтобы получить в итоге одночлен. Для этого нужно соблюсти некоторые условия, касающиеся слагаемых и вычитаемых одночленов. О том, как это делается, мы расскажем в отдельной статье.

Правила умножения одночленов

Действие умножения не налагает никаких ограничений на множители. Умножаемые одночлены не должны соответствовать никаким дополнительным условиям, чтобы в результате получится одночлен.

Чтобы выполнить умножение одночленов, нужно выполнить следующие шаги:

1. Правильно записать произведение.
2. Раскрыть скобки в полученном выражении.
3. Сгруппировать по возможности множители с одинаковыми переменными и числовые множители отдельно.
4. Выполнить необходимые действия с числами и применить к оставшимся множителям свойство умножения степеней с одинаковыми основаниями.

Посмотрим, как это делается на практике.

Пример 3

Условие: выполните умножение одночленов 2·x4·y·z  и -716·t2·x2·z11 .

Решение

Начнем с составления произведения.

2·x4·y·z·-716·t2·x2·z11

Раскрываем в нем скобки и получаем следующее:

2·x4·y·z·-716·t2·x2·z11

Далее нам нужно объединить числовые множители в одну группу, а потом сгруппировать множители с одинаковыми переменными:

2·-716·t2·x4·x2·y·z3·z11

Все, что нам осталось сделать – это умножить числа в первых скобках и применить свойство степеней для вторых. В итоге получим следующее:

2·-716·t2·x4·x2·y·z3·z11=-78·t2·x4+2·y·z3+11==-78·t2·x6·y·z14

Ответ: 2·x4·y·z·-716·t2·x2·z11=-78·t2·x6·y·z14 .

Если у нас в условии стоят три многочлена и больше, мы умножаем их по точно такому же алгоритму. Более подробно вопрос умножения одночленов мы рассмотрим в рамках отдельного материала.

Правила возведения одночлена в степень

Мы знаем, что степенью с натуральным показателем называют произведение некоторого числа одинаковых множителей. На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.

Пример 4

Условие: выполните возведение одночлена −2·a·b4  в степень 3.

Решение

Мы можем заменить возведение в степень на умножение 3-х одночленов −2·a·b4. Запишем и получим нужный ответ:

 (−2·a·b4)3=(−2·a·b4)·(−2·a·b4)·(−2·a·b4)==((−2)·(−2)·(−2))·(a· a· a)·(b4·b4·b4)=−8·a3·b12

Ответ: (−2·a·b4)3=−8·a3·b12.

А как быть в том случае, когда степень имеет большой показатель? Записывать большое количество множителей неудобно. Тогда для решения такой задачи нам надо применить свойства степени, а именно свойство степени произведения и свойство степени в степени.

Решим задачу, которую мы привели выше, указанным способом.

Пример 5

Условие: выполните возведение −2·a·b4 в третью степень.

Решение

Зная свойство степени в степени, мы можем перейти к выражению следующего вида:

(−2·a·b4)3=(−2)3·a3·(b4)3.

После этого мы возводим в степень -2 и применяем свойство степени в степени:

(−2)3·(a)3·(b4)3=−8·a3·b4·3=−8·a3·b12.

Ответ: −2·a·b4=−8·a3·b12.

Возведению одночлена в степень мы также посвятили отдельную статью.

Правила деления одночленов

Последнее действие с одночленами, которое мы разберем в данном материале, – деление одночлена на одночлен. В результате мы должны получить рациональную (алгебраическую) дробь (в некоторых случаях возможно получение одночлена).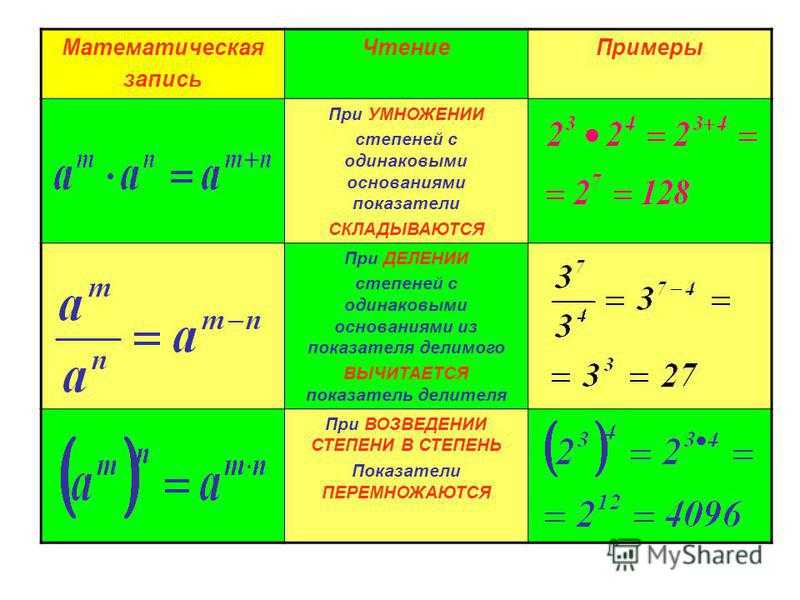

Сразу уточним, что деление на нулевой одночлен не определяется, поскольку не определяется деление на 0.

Для выполнения деления нам нужно записать указанные одночлены в форме дроби и сократить ее, если есть такая возможность.

Пример 6

Условие: выполните деление одночлена −9·x4·y3·z7  на −6·p3·t5·x2·y2.

Решение

Начнем с записи одночленов в форме дроби.

-9·x4·y3·z7-6·p3·t5·x2·y2

Эту дробь можно сократить. После выполнения этого действия получим:

3·x2·y·z72·p3·t5

Ответ: -9·x4·y3·z7-6·p3·t5·x2·y2=3·x2·y·z72·p3·t5.

Условия, при которых в результате деления одночленов мы получим одночлен, приводятся в отдельной статье.

Экспоненты: основные правила — сложение, вычитание, деление и умножение

Обновлено 14 декабря 2020 г.

Автор Lee Johnson

Выполнение вычислений и работа с экспонентами являются важной частью математики высокого уровня. Хотя выражения, включающие несколько степеней, отрицательные степени и т. д., могут показаться очень запутанными, все, что вам нужно сделать для работы с ними, можно суммировать с помощью нескольких простых правил. Узнайте, как складывать, вычитать, умножать и делить числа с показателями степени и как упростить любые выражения, в которых они используются, и вы почувствуете себя намного более комфортно, решая задачи с показателями степени.

TL;DR (слишком длинный; не читал)

Умножьте два числа с показателями степени путем сложения показателей степени: 0011 х ^м ​ ^{+ ​ n ​}

Разделите два числа с показателями степени, вычитая один показатель степени из другого: ​ x ^m ​ ÷ ​ x 900 12 н ​ = ​ х ^м ​ ^{− ​ п ​}

Когда показатель степени возведен в степень, умножьте показатели степени вместе: (​ x ^y ​)​ ^z ​ = ​ x ^y 90 014 ^{× z} ​

Любое число, возведенное в нулевую степень, равно единице: ​ x ​ ⁰ = 1

Что такое экспонента?

Показатель степени относится к числу, в степень которого что-то возводится. Например, 94 = x × x × x × x

Показатели также могут быть переменными; например, 4 ^x равно четырем, умноженным на себя x раз.

Правила для показателей степени

Выполнение вычислений с показателями степени требует понимания основных правил, регулирующих их использование. Вам нужно подумать о четырех основных вещах: сложении, вычитании, умножении и делении.

Сложение и вычитание степеней

Сложение показателей степени и вычитание показателей степени на самом деле не требует правила. Если число возведено в степень, добавьте его к другому числу, возведенному в степень (либо с другим основанием, либо с другим показателем степени), вычислив результат члена степени, а затем напрямую добавив его к другому. Когда вы вычитаете степени, применяется тот же вывод: просто вычислите результат, если можете, а затем выполните вычитание как обычно. Если и показатели степени, и основания совпадают, вы можете складывать и вычитать их, как любые другие совпадающие символы в алгебре. Например: 9{10} \end{aligned}

4 простых способа умножения показателей [+ Действия] | Блог Prodigy Math

Что общего между землетрясениями, фондовым рынком, информатикой и ядерной физикой?

Все они включают умножающих показателей степени .

Экспоненты являются неотъемлемой частью алгебры, полиномиальных уравнений и курсов математики более высокого уровня, но многие студенты с трудом понимают, как с ними работать. Вы прошли через правила экспоненты с вашим классом, и теперь пришло время применить их в действии. 95 = 243

Первое число называется основанием . Представляет собой число, которое умножается.

Второе, меньшее число — это показатель степени . Он представляет собой количество раз, когда основание умножается само на себя.

Существует семь правил экспоненты :

1. Правило произведения степеней : Сложение степеней при умножении одинаковых оснований
2. Правило отношения степеней : Вычитание степеней при делении одинаковых оснований
3. Правило степени степеней : Умножение степеней вместе при возведении степени в другую степень
4. Степень произведения правило e: Распределение мощности по каждому основанию при возведении нескольких переменных в степень
5. Степень правила частного : Распределить степень на все значения в частном
6. Правило нулевой степени : Любое основание, возведенное в нулевую степень, становится единицей
7. Правило отрицательного показателя взаимный

Понял? Тогда продолжим.

Как умножать экспоненты 4 способами

Помните, что все эти стратегии — всего лишь ярлыки, помогающие упростить более сложные уравнения. Чтобы найти фактическое значение показателя степени, учащиеся должны сначала понять, что это значит: повторное умножение .

Познакомьте учащихся с основами, такими как выражение показателей степени в виде произведений, прежде чем переходить к умножению показателей степени.

Когда они освоятся с концепцией, пора начинать. 92 не имеют ничего общего, что можно было бы объединить, ответ не может быть упрощен до одного показателя степени и должен быть выражен в виде обычного числа.

4. Умножение отрицательных показателей степени

Это может показаться сложным, но умножение показателей степени с отрицательными числами точно такое же, как умножение показателей степени с неотрицательными числами.

Начните с изучения свойств отрицательных чисел. В частности, просмотрите, как складывать и умножать их. Ваши ученики должны чувствовать себя комфортно, работая с отрицательными числами, прежде чем они перейдут к отрицательным показателям. 92

Сначала преобразуйте отрицательные показатели в обратные, затем вычислите.

Когда вы умножаете степени, напомните учащимся:

• Сложите степени  , если основания одинаковые
• Умножьте основания  если степени одинаковы
• Если ничего не изменилось , просто решите это

Упражнения для практики умножения показателей степени

1. Prodigy

Развитие беглости математики является важной частью того, чтобы учащиеся чувствовали себя уверенно на математических курсах средней школы и колледжа. Учащиеся могут практиковаться в умножении показателей и других математических понятиях с Prodigy, а вы задаете индивидуальные вопросы в игре, основанные на содержании урока.

Ваш класс будет исследовать мир, наполненный увлекательными квестами, экзотическими домашними животными и изучением математики. Вы сможете выбирать, на какие вопросы они будут отвечать, и получать в режиме реального времени данные о том, что они освоили, над чем работают и где им может понадобиться дополнительная помощь.

Имея 1400 навыков и подсчет, вы сможете предоставить материалов, соответствующих учебной программе  , по любой теме, которую вы изучаете, включая умножение показателей.

2. Экспонентная война

Education.com

Классическая карточная игра, но с экспоненциально интересным поворотом!

Учащиеся работают в командах по два человека и противостоят другой паре. Дайте каждой команде по колоде карт (с вынутыми дамами, валетами и королями) и попросите каждого игрока вытащить по две карты. Первая карта является основанием, а вторая карта является показателем степени.

Каждая пара должна решить свое уравнение и найти произведение. Побеждает команда с наибольшим ответом. Установите таймер для класса и посмотрите, кто наберет больше всего очков.

Пока ученики играют, пройдитесь по классу и убедитесь, что они не пропустили ни одного шага. Если вы видите много ошибок или неуспевающих учеников, воспринимайте это как знак того, что вам, возможно, нужно что-то пересмотреть.

3. Экспонентная охота за мусором

Дайте своим ученикам возможность найти сокровища и исследовать класс с экспонентной охотой за мусором.

Разделите свой класс на группы по три или четыре человека. В зависимости от количества групп, которые у вас есть, сделайте несколько разных наборов карточек. Начинайте каждый набор с карты, на которой есть проблема. Напишите ответ на задачу на следующей карточке, а на обороте поставьте еще одну задачу. Продолжайте, пока у вас не будет трех или четырех наборов задач (или больше).

Начиная с первой карточки, каждая группа должна решить задачу и найти правильный ответ в другом месте класса . Когда они находят карточку с правильным ответом, они могут перевернуть ее и решить следующую задачу. Дайте учащимся листочки для решения и позвольте им начать искать свои ответы. Какая команда финиширует первой, та и победительница!

4. Exponent Jeopardy

Каждый ученик любит классическую игру Jeopardy. Используя настраиваемый шаблон, замените викторины вопросами, которые дают учащимся возможность попрактиковаться в умножении показателей, и разделите класс на две команды.

Вот несколько советов, как обеспечить бесперебойную работу игры:

• Если у вас большой класс, подумайте о том, чтобы разделить класс на несколько игр, чтобы у каждого ученика была возможность принять участие.
• предложить учащимся самим сделать игру. Дайте им шаблон (или пусть более продвинутые ученики начнут с нуля) и попросите их сделать короткую игру.
• Используйте его в качестве проверки в конце модуля перед тестом и комбинируйте более важные вопросы с более сложными ответами

5. Рабочие листы для умножения показателей степени

Рабочие листы — это проверенный метод для развития беглости математики в определенном наборе навыков. Они также могут быть индикатором понимания учащимися, если используются как часть стратегии формативного оценивания. Вот некоторые из наших любимых:

• Папины рабочие листы
• Education.com
• Math Drills

).

Чтобы получить что-то более уникальное, попробуйте умножение многочленов. Как и в обычном рабочем листе, в нем есть вопросы, на которые должны ответить учащиеся, но он также содержит «банк ответов» для учащихся. Вырежьте соответствующие полоски и перемешайте их. Предложите учащимся сопоставить ответы с правильным разделом на своем рабочем листе после решения уравнения и показа своей работы.

Умножение показателей: Давайте повторим

Если ваши ученики помнят только три вещи, убедитесь, что это следующие понятия:

• Сложение степеней при умножении подобных оснований
• Умножение оснований при умножении как показателей степени
• Показатель степени — результат многократного умножения

Если они запомнят эти три правила, у них будет прочный фундамент, построенный еще до их первого максимума школьный урок алгебры.