Деление и умножение отрицательных и положительных чисел правило – Умножения и деление отрицательных чисел. Решение примеров.

Умножение положительных и отрицательных чисел. Видеоурок. Математика 6 Класс

На этом уроке мы повторим правила сложения положительных и отрицательных чисел. Также научимся умножать числа с разными знаками и узнаем правила знаков для умножения. Рассмотрим примеры умножения положительных и отрицательных чисел.

1. У каждого положительного числа существует противоположное отрицательное число. Сумма противоположных чисел равна нулю:

 

Выразив одно из слагаемых, это выражение можно записать иначе:

 

 

То есть, вычитая из нуля любое число, получаем противоположное.

2. Для сложения чисел с одинаковыми знаками отбрасываем знаки чисел и берем их модули. Далее складываем модули и перед суммой поставим знак, который был общим у данных чисел.

 

 

3. Для сложения чисел с разными знаками отбрасываем знаки перед числами, из большего модуля вычитаем меньший, перед разностью ставим тот знак, который был у числа с бОльшим модулем.

 

  

При умножении на единицу ничего не меняется, то есть любое число можно представить в виде произведения его же на единицу.

 

При умножении на (–1) число меняется на противоположное, то есть любое отрицательное число можно представить в виде произведения положительного числа и (–1).

 

Любое положительное число можно представить как произведение отрицательного числа на (–1).

 

Если число умножить один раз на (–1), то оно изменит знак. Если два раза, то оно изменит знак два раза, то есть вернется в исходное положение.

 

 

 

Рассмотрим примеры произведения чисел с разными знаками:

1.  

Каждое отрицательное число представим в виде произведения (–1) и положительного числа.

 

Произведение (–1) на (–1) – это будет единица, следовательно:

2.

Представляем (–5) в виде произведения 5 на (–1):

 

3.

Каждое отрицательное число представим в виде произведения (–1) и положительного числа.

1. При четном числе отрицательных множителей (четное число минусов) результат будет положительным.

2. При нечетном числе отрицательных множителей результат будет отрицательным.

Примеры

1.  

В данном выражении один отрицательный множитель, поэтому результат будет отрицательным.

 

2.

В данном выражении четное количество отрицательных множителей, поэтому результат будет положительным.

 

Рис. 1. Правила знаков для умножения (Источник)

Свойство умножения на ноль остается верным и в случае отрицательных чисел. Ноль умножить на любое число – будет ноль.

 

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

 

Домашнее задание

1. Вопросы в конце раздела 35 (§7), задание 1121 (стр. 192) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 (Источник)
2. Температура воздуха понижается каждый час на 2 градуса. Сейчас термометр показывает нуль градусов. Какую температуру он покажет через 3 часа?
3. Найдите значение выражений:
   
   

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Mnemonica.ru (Источник).
2. Интернет-портал Youtube.com (Источник).
3. Интернет-портал School-assistant.ru (Источник).
4. Интернет-портал Bymath.net (Источник).

interneturok.ru

Умножение и деление положительных и отрицательных чисел

Ученики: увеличение любой величины можно выразить положительным числом, а уменьшение – отрицательным.

Учитель: Для начала разберем задачи 1 и 2 в учебнике на стр. 190.

Задача 1. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход ткани на один костюм изменился на 0,4 м ². На сколько изменился расход ткани на костюмы за один день?

Решение.

Расход ткани на каждый костюм увеличился на 0,4 м². Поэтому, чтобы решить задачу, надо умножить 0,4 на 200. Получим 0,4 · 200 = 80. Значит, расход ткани на костюм за день увеличился на 80 м², иными словами, изменился на 80 м².

Задача 2. Фабрика выпускает в день 200 мужских костюмов. Когда стали выпускать костюмы нового фасона, расход ткани на один костюм изменился на ˗ 0,4 м ². На сколько изменился расход ткани на костюмы за один день?

Решение.

Расход ткани на каждый костюм уменьшился на 0,4 м². Поэтому, расход ткани на костюм за день уменьшился на 80 м²(0,4 · 200 = 80). Это значит, что расход ткани на костюмы за день изменился на ˗80м².

Таким образом, произведение ˗0,4 и 200 равно ˗80, т.е.

˗0,4 · 200 = ˗ (0,4 · 200) = ˗80.

Считают, что и 200 · (˗0,4) = ˗(200 · 0,4) = ˗80.

Учитель: Сформулируйте правило умножения чисел с разными знаками.

Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак « – »

Например:

-11 · 2 = -(11·2) = -22;

4 · (-5) = -(4·5) = -20;

· = — ( · ) = — = — ;

· = — ( · ) = —

Учитель: обратите внимание

3,35 · 0 = 0 (!)

Вывод: при изменении знака любого множителя знак произведения меняется, а его модуль останется тем же.

Учитель: сравним эти произведения

0,5 · 7 = 3,5 и 0,5 · (7) = 3,5.

В данном произведении знаки меняются у обоих множителей, следовательно, и произведение дважды меняет знак. В результате знак произведения не меняется. Можно сделать такой вывод:

Чтобы перемножить два отрицательных числа, надо перемножить их модули и поставить перед полученным числом знак « + ».

Например:

-7 · (-2) = 7 · 2 = 14;

-3 · (-2) = 3 · 2 = 6;

;

Учитель: при умножение отрицательных чисел принято первый множитель писать без скобок, так как (–1,5) 3 = – (1,5 3) = 4,5.

Запись решения выражения:

–1,5 · (–3) = |–1,5| · |–3| = 1,5 · 3 = 4,5.

Можно писать короче:

–1,5 · (–3) = 1,5 · 3 = 4,5; –2,3 · (–2) = 4,6; –0,3 · (–7) = 2,1.

Сформулируем правила умножения и деления чисел с разными знаками.

Учитель: итак запишем определение и таблицу общего правила умножения и деления.

При умножении или делении двух чисел одинакового знака (оба положительные или оба отрицательные) получается положительное число.

При умножении двух чисел разного знака (одно положительное, а другое отрицательное) получается отрицательное число.

Выводы:

– произведение двух отрицательных чисел есть число положительное;

– произведение двух чисел разных знаков есть число отрицательное.

Закрепление знаний на примерах.

Учитель: выполним устно:

(учитель записывает задачи на доске, ученики отвечают проговоривая правило)

Учитель: решим задачи из учебника у доски: №1121, 1122.

(учащиеся вызываются к доске по желанию)

Решение:

93. а) -5 · 6 = — (5 · 6) = — 30;

94. б) 9 · (-3) = -(9 ·3) = 27;

95. в) -8 · (-7) = + (8 · 7) =56;

96. г) ˗ 10 · 11 = ˗(10 · 11) = ˗110;

97. д) ˗11 · ( ˗12) = +(11 · 12) =132;

98. е) ˗1,45 ·0 = 0;

99. ж) 0,7 · ( ˗ 8) = ˗(0,7 · 8) = -5,6;

100. з) – 0,5 · 6 = -(0,5 · 6) = — 3;

101. и) 12 · (- 0,2) = — (12 · 0,2) = — 2,4;

102. к) – 0,6 · (- 0,9)= +(0,6 · 0,9)= 0, 54;

103. л) – 2,5 · 0,4= -(2,5 · 0,4)= — 1;

104. м) 0 · (-1,1)= 0.

109. Решение:

110. -42y, если y = 0, то –(42 · 0) = 0;

111. -42y, если y = 1, то –(42 · 1) = -42;

112. -42y, если y = -1, то 42 · 1 = 42;

113. -42y, если y = 3, то –(42 · 3) = -126;

114. -42y, если y = 5, то –(42 · 5) = -210;

115. -42y, если y = -30, то 42 · 30 = 1260.

118. Домашнее задание.

119. Запись на доске и в дневниках: пункт 35 (читать, выучить правила), письменно № 1143, 1146.

infourok.ru

Открытый урок по математике на тему «Умножение и деление положительных и отрицательных чисел»

Молодцы, вы справились и с этим заданием! Вы узнали имена греческого математика Диофанта и индийского математика Бхаскары, о которых нам коротко поведают историки. А те из вас, кто самостоятельно узнал имена математиков, не забывают в маршрутном листе поставить себе 1 балл.

6. Проектная работа

(Слайд 9) Первые сведения об отрицательных числах встречаются у китайских математиков во втором веке до н.э. Положительные количества в китайской математике называли “чжен”, отрицательные “фу”. Их изображали разными цветами: “чжен” – красным, “фу” – черным. Положительные числа тогда толковались как имущество, а отрицательные как долг.

(Слайд 10) Правила умножения и деления положительных и отрицательных чисел были предложены в 3 веке греческим математиком Диофантом Александрийским. Эти правила звучали так: (Слайд 11)

Вычитаемое, умноженное на прибавляемое, дает вычитаемое.

Вычитаемое, умноженное на вычитаемое, дает прибавляемое.

(Слайд 12) А позже индийский математик Бхаскара в 12 веке выразил те же правила в понятиях “имущества” и “долга”.

(Слайд 13)
Произведение двух имуществ или двух долгов есть имущество.
Произведение имущества и долга есть долг.

Те же правила верны и при делении.

(Слайд 14) Признанию отрицательных чисел способствовали работы французского математика Рене Декарта. Он предложил геометрическое истолкование положительных и отрицательных чисел, ввел координатную прямую.

7. Физминутка.

Зал бальный.

Следующий зал дворца “Бальный”. Король Нуль предлагает нам отдохнуть (Слайд 15)

Мы считали, мы решали

И на редкость все устали

Дружно встали, потянулись,

Наклонились, улыбнулись,

Разминаем кисти рук,

Посмотрим вдаль,

Потом вокруг,

Наклоняемся слегка,

Чтоб размять свои бока,

Упражняться нам не лень,

Будем добрыми весь день.

-А теперь продолжим.

8. Работа в тетрадях.

Мы продолжим наше путешествие. (слайд 16)

Попасть в следующий зал возможно только по лестнице. От времени некоторые ступеньки испортились. Давайте восстановим ее.

Реши наиболее удобным способом

-2* 12 * (-50) *6 =

*0,56 — 1,56 * = 

9. Самостоятельная работа

Тайная комната. (Слайд 17)

В тайной комнате спрятались корни уравнений. Решив эти уравнения, найдем их корни. (Слайд 18). Каждый в тетради работает самостоятельно, а на доски…..

Каждый работающий у доски не забывает отмечать себе в маршрутном листе по 1 баллу.

10. Тест (взаимопроверка)

(Слайд 19)

Итак, последнее задание короля Нуля – это зал размышлений, решение теста. (слайд20) И те, кто успешно справится с ним, будут почетными гостями во дворце. Приступайте к работе.

Тест.

(Слайд 21) А теперь взаимопроверка. Проверьте друг друга по готовым ответам и оцените работу своего одноклассника по критерию:

удовлетворительно – 3 балла;
хорошо – 4 баллов;
отлично – 5 баллов.

Эти баллы поставьте себе в маршрутный лист.

11. Итог урока

Мы совершили путешествие, вернулись домой. Посчитайте, пожалуйста, количество баллов, набранное вами за путешествие. (Слайд 22)

Если вы набрали 10-12баллов – «5»

7-9 баллов – «4»

4-6 баллов – «3»

Понравилось вам путешествовать? Как вы думаете, какие знания и умения помогли нам в пути? (Умножение и деление отрицательных чисел и чисел с разными знаками, определение модуля числа, сложение отрицательных чисел и чисел с разными знаками и вычитание чисел.)

Очень хорошо работали на уроке!

12. Домашнее задание (Слайд 23)

Решите задачу

Я задумала число. Это задуманное число я умножила на -5, затем к произведению прибавила , и в результате получила число -5,25. Какое число я задумала ?

Наряду с положительными и отрицательными числами есть понятие положительных и отрицательных качеств человека. Если качество положительное, то показываете “+”, если отрицательное, то “–”.

— Доброта, лень, предательство, трудолюбие, жестокость, целеустремленность, усидчивость.

Мне очень хотелось бы, чтобы положительных качеств было как можно больше. Прощаясь с вами, мне хочется узнать ваше мнение об уроке.

(Слайд 24)

Выберите одну из карточек и покажите мне “+”, если урок вам понравился, “-” , если не понравился.

Спасибо всем за урок. До свидания.

infourok.ru

Умножение положительных и отрицательных чисел

Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?

Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:

1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм., выражающее расстояние движущейся точки от A через 5 секунд. По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:

(+ 4) ∙ (+ 5) = + 20.

Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?

Ответ ясен: точка находилась влево от A на расстоянии 20 дм.

Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:

(+ 4) ∙ (– 5) = – 20.

Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?

Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:

(– 4) ∙ (+ 5) = – 20.

Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась движущаяся точка 5 секунд тому назад?

Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:

(– 4) ∙ (– 5) = + 20.

Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:

1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.

Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки (1-й и 4-й случаи) и знак –, когда у множителей разные знаки

(случаи 2-й и 3-й).

Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.

Упражнения.

Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.

Чтобы не спутать порядка действий, обратим внимание на формулу

ab + cd.

Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить. Также в формуле

a – bc

надо сперва число b умножить на c и затем полученное произведение вычесть из a.

Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).

Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).

Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.

Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:

Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:

Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:

Теперь останется выполнить умножение и вычитание:

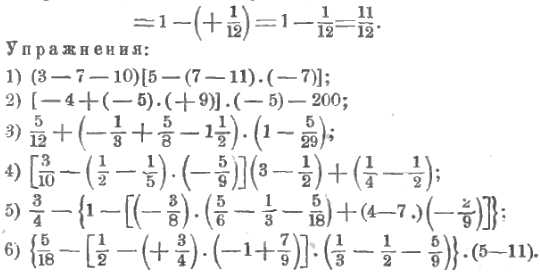
16. Произведение нескольких множителей. Пусть требуется найти

(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).

Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.

Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен

напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),

то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.

Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.

Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:

Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.

Итак, теперь мы легко узнаем, что

(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.

Также

(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.

Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.

Удобно, когда имеем дело с дробными числами, находить произведение сразу:

Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.

Пример на вычисление:

maths-public.ru

Умножение и деление положительных и отрицательных чисел

Умножение и деление положительных и отрицательных чисел 6 класс

Выполнили: Медведева Е.В.

Поладова М.Г.

Урок 1

ПЛАН-КОНСПЕКТ УРОКА

Цели:

• — обучающие: (формирование познавательных УУД) научить в процессе реальной ситуации использовать определения следующих понятий: «умножение положительных чисел», «умножение отрицательных чисел»;
• -развивающие: (формирование регулятивных УУД): развивать умение ставить перед собой цель – целеполагание, как постановку учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно; и планировать свою работу – планирование, как – определение последовательности промежуточных целей с учетом конечного результата;
• воспитательные: ( формирование коммуникативных и личностных УУД) учить планированию учебного сотрудничества с учителем и сверстниками; учить умению слушать и вступать в диалог участвовать в коллективном обсуждении проблемы.

Задача : сформировать умения для выполнения упражнений с умножением положительных и отрицательных чисел.

• Тип урока : Актуализация знаний и усвоение новых знаний.

Необходимое техническое оборудование : компьютер, проектор, экран. ЦОР http://math-prosto.ru/ .

• 1.Организационный момент
• 2. Актуализация знаний с использованием http://math-prosto.ru/
• 3. Освоение новых знаний с использованием http://math-prosto.ru/
• 4. Первичное закрепление
• 5. Самостоятельная работа с взаимопроверкой по эталону.
• 6. Рефлексия
• 7. Домашнее задание.

Актуализация знаний с использованием

http://math-prosto.ru/

Задача : актуализировать прежние знания по теме «Модуль числа», умение изображать координатную прямую и находить точки на ней; подготовка учащихся к работе на уроке

Умножения положительных и отрицательных чисел

Используя понятие модуля числа , сформулируем правила умножения положительных и отрицательных чисел .

Обозначим на координатной прямой две точки, которые соответствуют числам -4 и 2.

Учащиеся садятся за ПК, заходят по ссылке http://math-prosto.ru/ , и вместе с учителем пошагово актуализируют знания.

Учитель комментирует и параллельно проводит фронтальный опрос.

Точка A, соответствующая числу -4, находится на расстоянии 4 единичных отрезков от точки 0 (начала отсчёта), то есть длина отрезка OA равна 4 единицам.

Число 4 (длина отрезка OA) называют модулем числа -4.

Обозначают модуль числа так: |-4| = 4

Читают символы выше следующим образом: «модуль числа минус четыре равен четырём».

Точка B, соответствующая числу +2, находится на расстоянии двух единичных отрезков от начала отсчёта, то есть длина отрезка OB равна двум единицам.

Число 2 называют модулем числа +2 и записывают: |+2| = 2 или |2| = 2.

Если взять некоторое число «a» и изобразить его точкой A на координатной прямой, то расстояние от точки A до начала отсчёта (другими словами длина отрезка OA) и будет называться модулем числа «a».

|a| = OA

Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Освоение новых знаний с

использованием http://math-prosto.ru/

Задачи:

-научить добывать знания по умножению и делению положительных и отрицательных чисел; находить ответы на вопросы;

-научить формулировать правила по умножению и делению положительных и отрицательных чисел, повышать наглядность восприятия;

-сформировать умение осуществлять поиск информации.

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с

одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо :

• перемножить модули чисел;
• перед полученным произведением поставить знак « + »
• (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

• (- 3) • (- 6) = + 18 = 18
• 2 • 3 = 6

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо :

• перемножить модули чисел;
• перед полученным произведением поставить знак «-».

Примеры умножения отрицательных и положительных чисел.

(- 0,3) • 0,5 = — 1,5

1,2 • (- 7) = — 8,4

Правила знаков для умножения

Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Минус на минус даёт плюс,   Плюс на минус даёт минус.

• + • (+) = +
• + • (-) = —
• — • (-) = +
• — • (+) = —

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.

Пример.

(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

6 • 3 • 4 • 2 • 12 • 1 = 1728

Конечный результат умножения исходных чисел будет:

(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = — 1728

Умножение на ноль и единицу

Пример умножения отрицательных и положительных чисел.

Правила деления отрицательных чисел

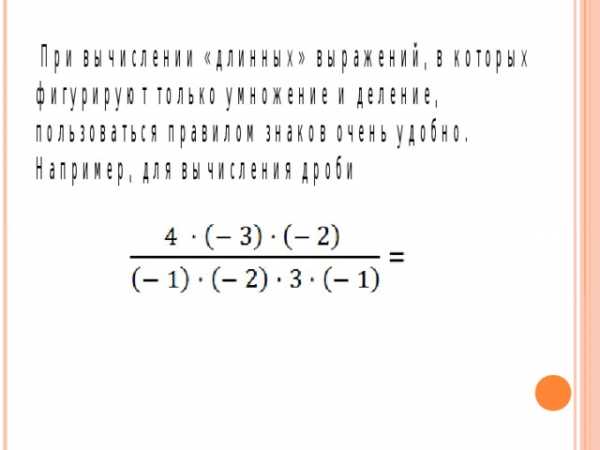
Урок 2

ПЛАН-КОНСПЕКТ УРОКА

Цели:

1) дидактические – отработать умение решать упражнения на умножение и деление положительных и отрицательных чисел;

— закрепить правил умножения и деления положительных и отрицательных чисел .

2) развивающие – развивать умение сравнивать, сопоставлять, обобщать, анализировать;

— развивать внимание, память, речь, самостоятельность

3) воспитывающие – воспитывать интерес учащихся к предмету математики через личный опыт.

Развивать навыки решения заданий на умножение и деление положительных и отрицательных чисел .

Задачи : Научить применять правила умножения и деления положительных и отрицательных чисел при выполнении упражнений.

Тип урока : Урок применения знаний, навыков и умений.

Необходимое техническое оборудование : компьютер, проектор, экран. ЦОР ООО «Дрофа 5-11»

• 1.Организационный момент
• 3. Проверка домашнего задания
• 2. Актуализация знаний
• 4. Закрепление с использованием ЦОР ООО «Дрофа 5-11»
• 5. Самостоятельная работа с взаимопроверкой по эталону.
• 6. Рефлексия
• 7. Домашнее задание.

2.6.15

Закрепление с использованием ЦОР ООО «Дрофа 5-11»

Задачи:

• Закрепить знания по правилам умножения и деления положительных и отрицательных чисел обучающихся , повысить уровень осмысления учащимися изученного материала;
• Развить у учащихся вычислительные навыки, внимание, мышление, память;

1. ЦОР ООО «Дрофа 5-11» 2. Раздел № 6 «Рациональные числа» 3. Пункт №6.3 «Умножение и деление рациональных чисел» 4. Номер заданий: 1,2,3,6,7.

Учащиеся садятся за ПК. По указанному пути работают в ЦОР.

multiurok.ru

Умножение положительных и отрицательных чисел

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо:

1) перемножить модули чисел;

2) перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

(−3) · (−6) = + 18 = 18

2 · 5= 10

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо:

1) перемножить модули чисел;

2) перед полученным произведением поставить знак «−».

Примеры умножения отрицательных и положительных чисел.

– 11 • 3 = – (11 • 3) = – 33;

4 • ( – 5) = – ( 4 • 5) = – 20;

Но, обратите внимание:

– 3,3 • 0 = 0 ( ! ) .

Правила знаков для умножения

Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Минус на минус даёт плюс,

Плюс на минус даёт минус.

+ · (+) = +

+ · (−) = −

− · (−) = +

− · (+) = −

Если умножается три или четыре числа, то  знак произведения можно определять по количеству отрицательных множителей. При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.

Пример.

(−6) · (−3) · (−4) · (−22) · 12 · (−1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

6 · 3 · 4 · 22 · 12 · 1 = 19008

Конечный результат умножения исходных чисел будет:

(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −19008

Здесь нужно быть очень внимательным

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

0 · a = 0

a · 0 = 0

a · 1 = a

a · (−1) = (−1) · a = −a

Примеры:

0 · (−5) = 0

8 · 1 = 8

spishy-u-antoshki.ru

Подскажите правило умножения, деления отрицательных и положительных чисел

Произведение, результат деления двух положительных чисел будет положительным. Произведение, результат деления двух отрицательных чисел будет положительным. Произведение, результат деления положительного, отрицательного х чисел будет отрицательным. Деление на 0 запрещено. 0 поделить на любое ненулевое число равно 0. Произведение любого числа и 0 равно 0.

Правило умножения положительных — это таблица умножения. Правило умножения отрицательных : -2*2=-4, -2* (-2) = 4 А вот тут про деление — <a rel=»nofollow» href=»http://www.coolmath.ru/lessons/6/316-delenie-polozhitelnyx-i-otriczatelnyx-chisel.html» target=»_blank»>http://www.coolmath.ru/lessons/6/316-delenie-polozhitelnyx-i-otriczatelnyx-chisel.html</a>

Гуру не знает правило

touch.otvet.mail.ru