Примеры на деление. Математика 4 класс.
Примеры на деление. Математика 4 класс. Задачи по математике 4 класс
MAT-ZADACHI.RU
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Математика 4 класс ->> Примеры
Чтобы увидеть решение, наведите на пример курсор мыши.
| 9520 : 8 = 1190 | 21000 : 210 = 100 | 5500 : 11 = 500 | 22000 : 20 = 1100 | 6860 : 7 = 980 |
| 78400 : 56 = 1400 | 228000 : 38 = 6000 | 905000 : 50 = 18100 | 844000 : 20 = 42200 | 18000 : 450 = 40 |
| 2610 : 9 = 290 | 29600 : 740 = 40 | 2400 : 48 = 50 | 80000 : 80 = 1000 | 66300 : 30 = 2210 |
| 50400 : 63 = 800 | 94500 : 35 = 2700 | 264000 : 300 = 880 | 84600 : 600 = 141 | 68000 : 680 = 100 |
| 8720 : 4 = 2180 | 32000 : 400 = 80 | 51700 : 47 = 1100 | 102000 : 600 = 170 | 10000 : 200 = 50 |
| 98800 : 260 = 380 | 9880 : 26 = 380 | 282000 : 60 = 4700 | 692000 : 40 = 17300 | 426000 : 71 = 6000 |
| 76300 : 700 = 109 | 81600 : 510 = 160 | 8400 : 70 = 120 | 60900 : 70 = 870 | 136000 : 80 = 1700 |
| 777000 : 37 = 21000 | 84800 : 800 = 106 | 450000 : 900 = 500 | 72000 : 200 = 360 | |
| 83200 : 400 = 208 | 6120 : 9 = 680 | 41800 : 380 = 110 | 68400 : 6 = 11400 | 252000 : 900 = 280 |
| 69000 : 50 = 1380 | 660000 : 550 = 1200 | 48000 : 96 = 500 | 43400 : 700 = 62 | 108000 : 300 = 360 |
| 671000 : 61 = 11000 | 8520 : 2 = 4260 | 89000 : 89 = 1000 | 79200 : 880 = 90 | 312000 : 80 = 3900 |
| 390000 : 300 = 1300 | 7700 : 77 = 100 | 188000 : 940 = 200 | 405000 : 500 = 810 | 436000 : 400 = 1090 |
| 600000 : 24 = 25000 | 7400 : 200 = 37 | 884000 : 17 = 52000 | 498000 : 30 = 16600 | 74200 : 200 = 371 |
| 7200 : 72 = 100 | 940 : 94 = 10 | 83200 : 800 = 104 | 3200 : 8 = 400 | 66300 : 17 = 3900 |
| 5820 : 6 = 970 | 630000 : 900 = 700 | 910000 : 70 = 13000 | 98000 : 50 = 1960 | 1280 : 8 = 160 |
| 83000 : 830 = 100 | 15000 : 75 = 200 | 540000 : 900 = 600 | 310000 : 500 = 620 | 120000 : 10 = 12000 |
| 80000 : 80 = 1000 | 52800 : 44 = 1200 | 636000 : 40 = 15900 | 2790 : 9 = 310 | |
| 297000 : 270 = 1100 | 969000 : 300 = 3230 | 67000 : 67 = 1000 | 86000 : 40 = 2150 | 894000 : 30 = 29800 |
| 332000 : 20 = 16600 | 583000 : 530 = 1100 | 882000 : 980 = 900 | 148000 : 20 = 7400 | 9325 : 25 = 373 |
| 7790 : 41 = 190 | 350000 : 250 = 1400 | 12600 : 60 = 210 | 48000 : 600 = 80 | 2100 : 70 = 30 |
| 432000 : 540 = 800 | 90300 : 300 = 301 | 26500 : 500 = 53 | 390 : 39 = 10 | 52600 : 200 = 263 |
| 64400 : 23 = 2800 | 19200 : 960 = 20 | 78000 : 200 = 390 | 552000 : 200 = 2760 | 65000 : 95 = 67000 |
| 61000 : 610 = 100 | 3180 : 6 = 530 | 696000 : 400 = 1740 | 7100 : 71 = 100 | 738000 : 60 = 12300 |
| 98000 : 70 = 1400 | 385000 : 11 = 35000 | 1120 : 7 = 160 | 89100 : 90 = 990 | 36400 : 91 = 400 |
| 4000 : 200 = 20 | 8900 : 89 = 100 | 98000 : 50 = 1960 | 6650 : 95 = 70 | 1500 : 2 = 750 |
| 546000 : 91 = 6000 | 55300 : 7 = 7900 | 10000 : 20 = 500 | 328000 : 40 = 8200 | 192000 : 960 = 200 |
| 33000 : 110 = 300 | 540000 : 600 = 900 | 952000 : 400 = 2380 | 39600 : 44 = 900 | 860 : 2 = 430 |
| 18000 : 150 = 120 | 18200 : 26 = 700 | 4500 : 5 = 900 | 6060 : 2 = 3030 | 408000 : 51 = 8000 |
| 53700 : 30 = 1790 | 54900 : 900 = 61 | 666000 : 370 = 1800 | 71200 : 400 = 178 | 4950 : 55 = 90 |
| 48800 : 61 = 800 | 203000 : 70 = 2900 | 450 : 9 = 50 | 170000 : 17 = 10000 | 81900 : 90 = 910 |
| ____________________ | ____________________ | ____________________ | ____________________ | ____________________ |
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Деление в столбик ➗ примеры и правила, как научиться
Деление с остатком
Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:
Если кратко, это такое деление, в результате которого получается остаток меньше делителя:
Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.
Деление трехзначного числа на однозначное
Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить;
- 7 — делитель или то, на что нужно поделить:
- частное — результат действия.

Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Для этого рассмотрим первую цифру делимого. Она меньше делимого: 3 < 7 — не подходит. Рассмотрим теперь две первые цифры делимого: 32 ﹥7. Подходит!
Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.
Важно
Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз.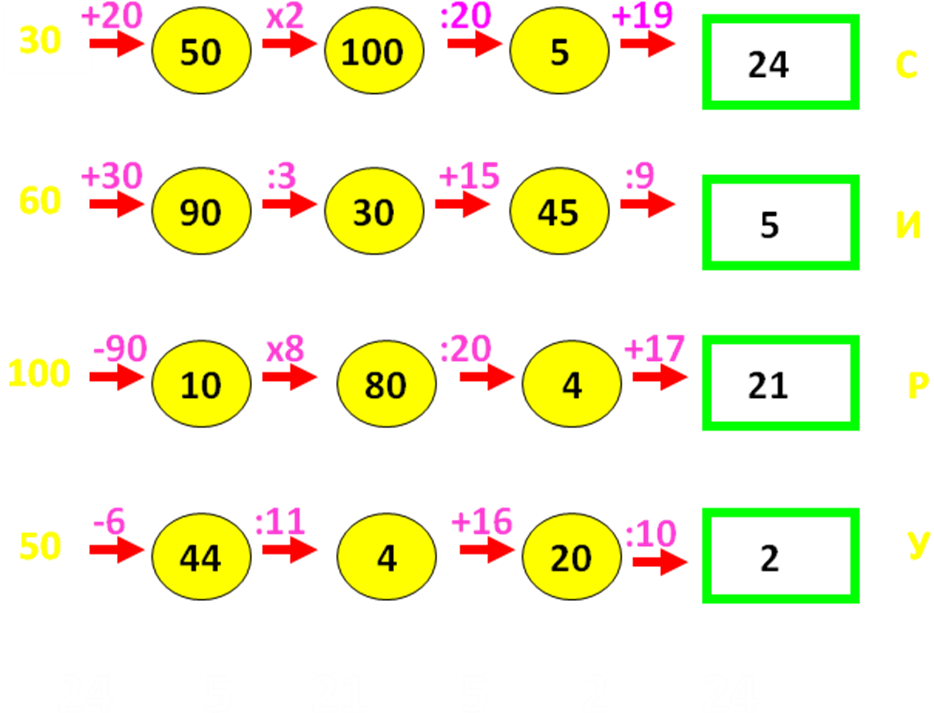 Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Деление трехзначного числа на двузначное с примерами
Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.
Пример №1.
Разделим трехзначное число 324 на двузначное 81.
Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.
Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4.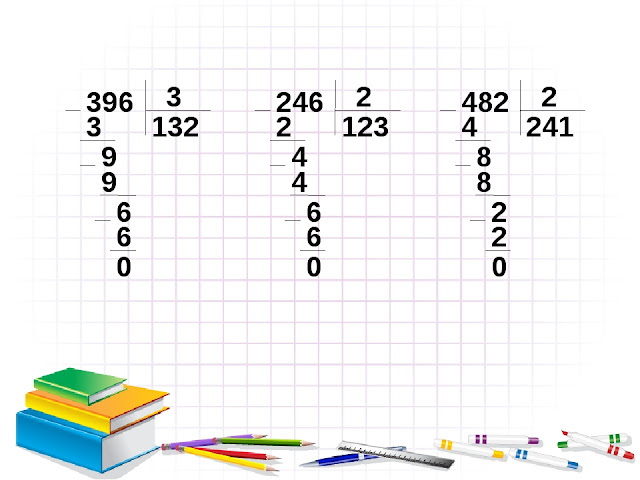 81*4=324. Подходит!
81*4=324. Подходит!
Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.
Ответ: 324:81=4.
Пример №2.
Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.
Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.
Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.
Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.
Ответ: 368:92=4.
Как делить однозначные и многозначные числа в столбик с остатком
Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.
Теперь разберем те же примеры, только поделим в столбик.
Пример №1
Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.
Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.
Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.
Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.
Ответ: 19:5=3
Пример №2.
Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.
Шаг 1. Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.
Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.
Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.
Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.
Ответ: 29:9=4(5)
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Примеры на деление в столбик для 3 класса
Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье. Это задание со звездочкой.
Легкий уровень | Средний уровень | Сложный уровень |
27:3= 48:4= 56:8= 72:9= 95:5= | 270:15= 504:14= 315:5= 728:8= 855:9= | 1749:11= 1080:45= 3888:72= 5248:64= 4818:66= |
Ответы:
- легкий уровень: 9; 12; 7; 8; 19;
- средний уровень: 18; 36; 63; 91; 95;
- сложный уровень: 159; 24; 54; 82; 73.

Если вам интересно, как еще можно научить ребенка делить двузначные и трехзначные числа, приглашаем на вводный урок в Skysmart! На на онлайн-курсах по математике для детей можно закрепить тему «Деление в столбик» и разобраться в других разделах из школьной программы.
«Деление на 4». 2-й класс
- Худолий Наталья Александровна, учитель начальных классов
Разделы: Математика, Начальная школа
Класс: 2
Ключевые слова: математика, УМК «Перспектива», Деление на 4
Цель: сформировать представления учащихся о делении чисел на 4.
Задачи:
Образовательная:
- совершенствовать у учащихся умение решать примеры на табличное деление в пределах 20;
- учить учащихся делению чисел на 4;
- совершенствовать предметные умения решать задачи.
Развивающая:
- способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Воспитательная:
- воспитывать чувство товарищества, аккуратность, усидчивость и уважительное отношение к изучаемому предмету.
Универсальные Учебные Действия:
Познавательные:
- определять компоненты и результат действия умножения;
- определять взаимосвязь между действием деления и действием умножения при вычислении арифметического выражения и обосновывать своё суждение;
- применять приобретённые умения при решении арифметического выражения и задач на деление.

Регулятивные:
- выполнять учебное задание в соответствии с правилом.
Коммуникативные:
- формировать умения сотрудничать с учителем и сверстниками при решении учебных проблем;
- формулировать высказывания, используя математические термины.
Личностные:
- знать таблицу умножения чисел от 2 до 10 в пределах 20;
- вычислять арифметическое выражение, используя действие умножения и деления;
- комментировать арифметическое выражение, используя разные варианты представления;
- решать задачи, применяя рациональный способ вычисления.
- проявлять интерес к содержанию урока.
Оборудование: компьютер, экран, проектор, учебная презентация.
Ход урока
| Этап урока | Вре | Содержание урока. |
Мотивация учебной деятельности | 1 мин | Здравствуйте, ребята! Я рада Вас видеть на уроке. Меня зовут Наталья Александровна. Как люди могут приветствовать друг друга, не разговаривая? Поприветствуем друг друга. Поприветствуем гостей. Улыбнитесь, подарите свои улыбки мне и друг другу! А теперь настроимся на работу — откроем ладошки новым знаниям и произнесём волшебную фразу: я хочу много знать! Будьте старательными, активными, внимательными и у вас все получится. А помогут нам в этом числа. Откройте тетради и запишите число. |
Устный счёт | 3 мин | Сегодня мы не просто с вами будем работать, а отправимся в путешествие. Какой праздник уже заглядывает в нам в окна? Без чего не бывает Нового года? (без ёлки, Деда Мороза, Снегурочки). Мы отправимся в зимний лес к Деду Морозу и Снегурочке за ёлкой. (слайд, зимний лес) А там нас ждут испытания. Справимся? Хочу напомнить вам, что в лесу нужно вести себя тихо, чтобы не распугать зверей и птиц. Дед Мороз передал мне вот этот колокольчик. Если вы его услышите, значит надо установить тишину. А вот и тропинка, ведущая в лес, и первое наше испытание. А называется оно «Гонка за лидером» Работать будем по рядам. На доске вы видите 3 тропинки. Одна тропинка для каждого ряда. По одному с каждого ряда одновременно вы будете выбегать, записывать ответ (решаем одно РАВЕНСТВО) и возвращаемся на место. Если вы увидели ошибку своего товарища, смело исправляйте. Кто быстрее пройдёт по тропинке. На старт! Внимание! Марш! (ДЕТИ ВЫПОЛНЯЮТ ЗАДАНИЕ) Итак, давайте проверим. Если ответ правильный – поднимите руки. Если ответ неправильный – закройте глаза руками. Молодцы! Можно положить руку на голову, погладить себя и сказать: «Ах, какой я молодец!» |
Минутка чистописания | 1 мин | Холодно в лесу. Но нам холод не страшен. Разогреем немного наши руки (руки растираем) 4 44 444 Запись на доске |
Самоопределение к деятельности | 6 мин | Что вы знаете о числе четыре? А таблицу умножения на 4 знаете? Как называются компоненты при умножении? Вывешиваю на доску названия компонентов при умножении. 1-й множитель 2-й множитель Значение произведения (слайд, зимний лес, появление Бабы Яги) Посмотрите, ребята, кто это? Любительница вредить, жительница леса, Баба Яга предлагает нам поиграть в игру «Мешалки». Для этого мне нужно 5 человек. Раздаю листы с записанными числами и знаками. Вы должны внимательно меня послушать и найти каждый своё место. 3 х 4 = 12 Каким компонентом в этом РАВЕНСТВЕ является 3? А 4? А 12? Какие еще РАВЕНСТВА можно составить с помощью этих чисел, используя знак деления? Забираю лист со знаком «умножить», даю лист со знаком «разделить» 12: 3 = 4 12:4 = 3 Каким компонентом в этом РАВЕНСТВЕ является 12? А 4? А3? Вывешиваю на доску названия компонентов при делении. Запишите в тетради РАВЕНСТВО 12: 4 = 3 Кто догадался, над какой темой мы будем сегодня работать? Какие задачи перед собой поставим? Задачи
|
Работа над новой темой | 5 мин | Баба Яга пока пускать нас дальше в лес не хочет. Как-то надо ее задобрить. Перед нами 4 метлы. Их нужно раздать четырём сёстрам Бабы Яги поровну. Презентация с анимацией. 4: 4 = 1 По сколько новых метелок окажется у каждой Яги? Как это записать выражением? Назовите, как называются компоненты при делении? 4 – это…. делимое 4 – это…. делитель 1 – это…значение частного Запишите это выражение в тетрадь. Подобрела Баба Яга и решила угостить зайцев мороженым. Она точно знает, что для каждого зайца у нее запасено 4 порции мороженого. Скольких же зайцев сможет угостить Баба Яга, если у неё 16 порций мороженого? Как это записать выражением? 16:4=4 Но какой же Новый год без ёлки и подарков? Но мы ёлку рубить не будем. Под новогодней ёлкой стояли подарки. 4 подарка справа и 4 подарка слева. Сколько всего подарков? Как узнать? 4х2=8 Как называются компоненты при умножении? Вы, наверно, знаете, что новогодние подарки принято дарить. А как записать это выражением? 8:4=2 Запишите в тетрадь это выражение. |
Физминутка | 1 мин | Устала Баба Яга делить подарки. Отдохнуть хочет. И нам отдохнуть надо, чтобы плодотворно продолжить работать и быть внимательными, мы должны отдохнуть. 4:2 — Сколько раз ногами топнем? 9:3 — Сколько раз руками хлопнем? 2х2 -Мы присядем сколько раз? 4:4 -Мы наклонимся сейчас. 3х1 — Мы подпрыгнем ровно столько. Ай да счёт, игра и только! |
Закрепление | 10 мин | Не хочет пускать нас Баба Яга к Деду Морозу и Снегурочке. Снова хочет вас испытать, хочет понять, справитесь ли вы, всё ли вам понятно. Работа у доски Для работы мне необходимо 4 человека. Попробуйте выполнить такое задание. Разделите поровну 20 подарков между четырьмя зайцами. Сколько подарков получит каждый зайчик? По одному подарку берём для своего зайца. Как это записать равенством? 20: 4 = 5 Запишите в тетрадь это РАВЕНСТВО. Что же у нас получилось? А записали мы с вами таблицу деления на 4 (в пределах 20). А сейчас попробуйте поработать в парах. Вам необходимо прочитать задачу, дополнить рисунок и записать решение задачи. 1)16 морковок Баба Яга связала в пучки, по 4 морковки в каждом. Сколько пучков получилось? 2) Для украшения Баба Яга разложила 12 вишенок поровну на 4 новогодних торта. Сколько вишенок на каждом торте? Проверка (опора презентацию) Со всеми заданиями справились. Молодцы! |
Рефлексия Итог урока | 1 мин | Ребята, давайте вернёмся к задачам, поставленным на уроке. 1-я задача: закрепить умение решать примеры на табличное деление в пределах 20; 2-я: учиться делить числа на 4; 3-я: закрепить умения решать задачи. Со всеми задачами мы справились? Можно себя похвалить? «Ах, какой я молодец!» Посмотрите на слайд. Прочитайте начало фразы и закончите её. Посмотрите, кто встречает нас. Путешествие наше заканчивается. Подарки сегодня получили и зайцы, и лисички, и даже сёстры Бабы Яги. И вы, ребята, без подарков не останетесь. Достаю красивую подарочную коробку в закладки с таблицей умножения. Спасибо за работу на уроке! Мне приятно было с вами работать! |
16 тыс изображений найдено в Яндекс.Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
ВСЕ ПРОГРАММЫ
Математика
Рабочие листы для 4 класса
1 цикл: Космос
Сложение, вычитание, умножение и деление в пределах 100 (устно и письменно). Название компонентов действия при сложении, вычитании, умножении и делении. Алгоритм решения текстовых задач. Значение переменной. Простейшие виды письменного сложения и вычитания в пределах 10 000. Скобки и порядок действий. Вычитание суммы и разности из числа. Умножение и деление суммы на число.
Название компонентов действия при сложении, вычитании, умножении и делении. Алгоритм решения текстовых задач. Значение переменной. Простейшие виды письменного сложения и вычитания в пределах 10 000. Скобки и порядок действий. Вычитание суммы и разности из числа. Умножение и деление суммы на число.
1. Сложение и вычитание в пределах 100
2. Решение текстовых заданий
3. Значение переменной
4. Письменное сложение и вычитание
5. Переместительный закон сложения
6. Сочетательный закон умножения
7. Вычитание суммы из числа
8. Умножение в пределах 100
9. Деление в пределах 100
10. Деление — действие, обратное умножению
11. Переместительный закон умножения
12. Законы умножения
13. Умножение суммы на число
14. Умножение суммы на число
15. Деление суммы на число
16. Деление суммы на число
17. Вычисление удобным способом. Порядок действий
Порядок действий
18. Вычисление удобным способом. Порядок действий
19. Повторение
2 цикл: Было время…
Величины (единицы длины, массы, времени, площади) и их соотношения. Периметр квадрата и прямоугольника. Числа до 1 000 000 и их состав.
1. Деление с остатком
2. Повторение
3. Единицы длины
4. Периметр прямоугольника
5. Единицы массы
6. Денежные единицы
7. Единицы времени
8. Скорость, время и расстояние
9. Повторение
10. Разряды числа. Сумма разрядных слагаемых.
11. Разряды. Сумма разрядных слагаемых.
12. Разряды тысяч
13. Десятки тысяч
14. Сотни тысяч
3 цикл: Земля в огненном кольце
Сравнение площадей предметов, вычисление площади квадрата и прямоугольника. Письменное сложение и вычитание 5- и 6-значных чисел. Проверка суммы и разности при письменном сложении и вычитании. Порядок действий и скобки. Письменное сложение и вычитание именованных величин.
Порядок действий и скобки. Письменное сложение и вычитание именованных величин.
1-1. Сравнение площадей фигур. Равные по площади фигуры
1-2. Квадратный сантиметр. Площадь прямоугольника
2. Площадь квадрата
3. Единицы площади
4. Повторение
5. Повторение
6. Алгоритм устного счета
7-1. Алгоритм письменных вычислений
7-2. Алгоритм письменных вычислений
8-1. Сравнение алгоритмов устного и письменного вычислений
8-2. Сравнение алгоритмов устного и письменного вычислений
9-1. Повторение
9-2. Повторение
10. Письменное значение пяти- и шестизначных чисел
11-1. Письменное значение пяти- и шестизначных чисел
11-2. Письменное значение пяти- и шестизначных чисел
12. Сложение нескольких чисел
13. Сложение нескольких чисел
14. Письменное значение пяти- и шестизначных чисел
15-1. Письменное значение пяти- и шестизначных чисел
15-2. Письменное значение пяти- и шестизначных чисел
Письменное значение пяти- и шестизначных чисел
16. Закрепление
18. Проверка письменного сложения и вычитания
19. Повторение
20. Повторение
4 цикл: Кукольный театр
Анализ и решение задач до трех действий. Устное умножение с числами 10, 100, 1000. Умножение однозначного числа на числа, оканчивающиеся на 0. Письменное умножение на однозначное число.
1-1. Значение выражений. Скобки и порядок действий
1-2. Значение выражений. Скобки и порядок действий
2-1. Значение выражений. Скобки и порядок действий
2-2. Значение выражений. Скобки и порядок действий
3-1. Письменное сложение и вычитание величин
3-2. Письменное сложение и вычитание величин
4-1. Письменное сложение и вычитание величин
4-2. Письменное сложение и вычитание величин
5-1. Повторение
5-2. Повторение
6-1. Решение текстовых заданий
6-2. Решение текстовых заданий
7-1. Решение текстовых заданий
Решение текстовых заданий
7-2. Решение текстовых заданий
8-1. Повторение
8-2. Повторение
9-1. Повторение
9-2. Повторение
10. Сложение в уме
11. Умножение в уме
12. Деление в уме
13. Деление в уме
14-1. Повторение
14-2. Повторение
15-1. Повторение
15-2. Повторение
5 цикл: Секреты энергии
Повторение письменного умноженияна на однозначное число. Решение выражений (порядок действий). Письменное деление на однозначное число.
1-1. Письменное умножение многозначного числа на однозначное число
1-2. Письменное умножение многозначного числа на однозначное число
2. Письменное умножение многозначного числа на однозначное число
3. Письменное умножение многозначного числа на однозначное число
4. Письменное умножение многозначного числа на однозначное число
5-1. Письменное умножение многозначного числа на однозначное число
5-2. Письменное умножение многозначного числа на однозначное число
Письменное умножение многозначного числа на однозначное число
6. Значение выражений. Порядок действий
7. Повторение
8. Письменное деление многозначного числа на однозначное число
9. Письменное умножение многозначных чисел с 0 на однозначное число
10. Письменное умножение многозначных чисел с 0 на однозначное число
11. Письменное деление многозначного числа на однозначное число
12. Письменное деление многозначного числа на однозначное число
13. Письменное деление многозначного числа на однозначное число
14. Письменное деление многозначного числа на однозначное число
15-1. Повторение
15-2. Повторение
6 цикл: Кем быть?
Решение выражений (порядок действий). Письменное умножение и деление на двузначное число.
1-1. Решение выражений (порядок действий)
1-2. Значение выражений (порядок действий)
2-1. Письменное умножение на двузначное число
Письменное умножение на двузначное число
2-2. Письменное умножение на двузначное число
3-1. Письменное умножение множителей, оканчивающихся на ноль
3-2. Письменное умножение множителей, оканчивающихся на ноль
4-1. Письменное умножение на двузначное число
4-2. Повторение
5-1. Значение выражений
5-2. Значение выражений
6-1. Значение выражений
6-2. Значение выражений
7-1. Письменное деление на двузначное число
7-2. Письменное деление на двузначное число
8-1. Письменное деление на двузначное число с 0 в частном
8-2. Письменное деление на двузначное число с 0 в частном
9-1. Письменное деление на двузначное число с 0 в частном
9-2. Письменное деление на двузначное число с 0 в частном
10-1. Письменное деление на двузначное число
10-2. Письменное деление на двузначное число
11. Письменное деление на двузначное число
12-1. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
12-2. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
13. Письменное деление на двузначное число в случае, когда делимое и делитель оканчиваются на 0
7 цикл: Государство сквозь века
Повторение умножения на двузначное число. Решение выражений (порядок действий). Письменное деление с остатком. Письменное умножение на трехзначное число. Умножение именных величин на одно- и двузначное число. Решение текстовых заданий путем составления выражений и уравнений.
1-1. Письменное деление на двузначное число
1-2. Письменное деление на двузначное число
2. Значение выражения и порядок действий
3. Значение выражения и порядок действий
4. Письменное деление с остатком
5. Письменное деление с остатком
6. Повторение письменного деления и умножения
7. Умножение на трехзначное число
8. Умножение на трехзначное число
Умножение на трехзначное число
9. Письменное умножение множителей, содержащих 0
10. Письменное умножение множителей, содержащих 0
11. Повторение письменного умножения на трехзначное число
12. Умножение величин
13. Деление величин
14. Составление и решение уравнений
15. Решение текстовых заданий
16. Решение текстовых заданий
17. Повторение
18-1. Дроби
18-2. Дроби
18-3. Дроби
8 цикл: Рука об руку в политике
Решение текстовых заданий путем составления выражений и уравнений. Дроби (числительное, знаменательное, дробная черта; деление фигур на равные части; 1/2, 1/3 и 1/4 фигуры). Нахождение половины, трети и четверти числа. Нахождение части заданных величин. Нахождение дроби по закрашенной или незакрашенной части фигуры. Решение текстовых задач с дробями. Повторение и углубление: счет, составление и чтение чисел до миллиона, сравнение чисел, устное и письменное сложение и вычитание.
1. Нахождение части величин
2. Нахождение дроби по раскрашенной части
3. Текстовые задания с дробями
4. Повторение
5. Повторение
6. Счет
7-1. Состав, чтение и запись чисел до миллиона
7-2. Сравнение чисел
8. Письменное и устное сложение в пределах миллиона
9. Устное и письменное вычитание в пределах миллиона
10. Связь сложения и вычитания
11. Устное и письменное умножение
12. Письменное умножение на двузначное число
13-1. Устное и письменное деление на однозначное число
13-2. Письменное деление на двузначное число
9 цикл: Классифицируем природу
Связь сложения и вычитания. Устное и письменное умножение на одно- и двузначное число в пределах миллиона. Письменное умножение на двузначное число в пределах миллиона. Устное и письменное деление на одно- и двузначное число в пределах миллиона. Письменное деление на двузначное число в пределах миллиона. Связь умножения и деления. Выражения и равенства. Буква в равенстве. Числа 0 и 1 и действия с ними. Порядок действий и скобки. Измерение величин (длина, вес, скорость, время, вычисление площади). Различение, называние и черчение геометрических фигур — точка, отрезок, ломаная, треугольник, четырехугольник, квадрат, прямоугольник. Вычисление периметра треугольника и четырехугольника. Решение текстовых задач до трех действий. Задачи на самоконтроль и смекалку.
Письменное деление на двузначное число в пределах миллиона. Связь умножения и деления. Выражения и равенства. Буква в равенстве. Числа 0 и 1 и действия с ними. Порядок действий и скобки. Измерение величин (длина, вес, скорость, время, вычисление площади). Различение, называние и черчение геометрических фигур — точка, отрезок, ломаная, треугольник, четырехугольник, квадрат, прямоугольник. Вычисление периметра треугольника и четырехугольника. Решение текстовых задач до трех действий. Задачи на самоконтроль и смекалку.
1. Связь деления и умножения
2. Выражение и равенство. Переменная в равенстве.
3. Числа 0 и 1
4. Скобки и порядок
5. Измерение длины
6. Измерение массы
7. Измерение времени
8. Измерение скорости
9. Измерение стоимости
10. Измерение площади
11. Геометрические фигуры
12. Периметр прямоугольника и четырехугольника
13. Периметр и площадь треугольника и четырехугольника
14. Решение текстовых заданий
Решение текстовых заданий
15. Задания на повторение и смекалку
Содержание
” Алгоритм умножения и деления на трехзначное число. 4 класс – Балабақша әлемі
Математика.
Краткосрочный план урока № 60.
Предмет: Математика
Урок: 60 Школа: Х. Бижанова
Дата:
05.12.19 ФИО учителя:
Отамурадова А.А
Класс: 4 А Количество
присутствующих: Количество
отсутствующих:
Раздел (сквозная тема): Раздел 2А. Умножение и деление «Культурное наследие».
Тема урока: Обобщение изученного.
Алгоритм умножения и деления на трехзначное число.
Древние города
Цели обучения, которым посвящен урок: 4.1.2.12** – применять алгоритм умножения и деления многозначных чисел, оканчивающихся нолями, на трехзначное число;
4.1.2.13** – применять алгоритм деления многозначных чисел на двух/трехзначное число, когда в записи частного есть ноли и алгоритм обратного действия умножения
Развитие навыков: 1. 2 Операции над числами
2 Операции над числами
Языковые цели
Учащиеся могут:
применять алгоритм умножения и деления многозначных чисел на двузначные и трехзначные.
Предметная лексика и терминология:
названия компонентов действий, неполное произведение, неполное делимое, пробная цифра частного.
Полезные выражения для диалогов и письма:
Обсуждение
Для чего нужно определить количество цифр в частном?
Почему используется пробная цифра частного?
Письмо
Запись умножения и деления столбиком
Критерии оценивания
Применяет алгоритм деления многозначных чисел на двузначное и трехзначное. Проверяет вычисления.
Материал прошедших уроков: Алгоритм умножения и деления.
Ход урока:
Этапы урока Запланированная деятельность на уроке Ресурсы
0-1 мин Создание положительного эмоционального настроя:
– Здравствуйте, те, кто родился зимой! (те, кто родился зимой, здороваются и садятся)
– Здравствуйте, те, кто родился летом! (те, кто родился летом, здороваются и садятся)
– Здравствуйте, те, кто родился весной! (те, кто родился весной, здороваются и садятся)
– Здравствуйте, те, кто родился осенью! (те, кто родился осенью, здороваются и садятся)
– Ещё раз, все, здравствуйте!
– Здороваться – это желать здоровья!
Я желаю, чтобы во все времена года у вас было отличное здоровье и мы могли дружно общаться и выполнять работу.
Эмоциональный настрой
Середина урока
2-5 мин
21-22 мин
23-28 мин
29-30 мин
31-37 мин
38-40 мин 1.Актуализация жизненного опыта.
1) Записать число, классная работа
2) Минутка чистописания
Назовите самое большое трехзначное число? (999)
– Давайте это число пропишем в мин. чистописания
3)(К) Математический диктант:
1)Какое число надо прибавить к 12560, чтобы получить 13000? (440)
2)На сколько 10ч. меньше 1 суток? ( на 14 ч)
3) Произведение 490, первый множитель 7. Чему равен второй множитель? (70)
4)Увеличьте 67 в 100 раз (6700)
5)Найдите разность чисел 930 и 200. (730)
6)Найдите восьмую часть числа от числа 800. (100)
7)Сумма двух чисел 650, одно из них 250. Найдите другое число. (400)
8)Сколько минут составляют 180 с.? (3 мин)
9) Частное 6, делитель 50. Чему равно делимое? (300)
10)Найдите частное чисел 54000 и 6. (9000)
Проверка работы. Взаимооценивание в парах. ( на полях оценивают себя карандашами светофор)
2. Постановка цели (проблемная ситуация).
Постановка цели (проблемная ситуация).
Вспомните алгоритм умножения и деления, найдите ошибки в примерах.
1235 * 201 = 248235 29200 : 73 = 4
Учащиеся находят ошибки в записи первого примера и в ответе второго.
( на доске листы с примерами дети подходят и устраняют ошибки красным маркером)
– Какова тема и цель нашего урока?
Обобщить всё, что мы изучали.
3. Выполнение задания №1 с. 72
Определи количество цифр в частном, не выполняя вычислений.
Расположи ответы (количество цифр в частном) в порядке возрастания, и ты прочтёшь, какое второе название имел древний город Испиджаб.
Р-5. А-3. М-7. С-2. А-6. Й-4 Сайрам
Выступление детей и просмотр видеоролика
4.Работа по теме урока.
Выполнение №3 с. 72 второй столбик у доски с объяснением
2210 * 402 = 888420 181944 : 361 = 504
Оценивание работы учащимися.
Физминутка
Руки в стороны и вверх
Повторяем дружно
Засиделся ученик
Разминаться нужно
Мы сначала всем в ответ
Головой покрутим НЕТ!
Энергично, как всегда
Головой покрутим ДА!
Чтоб коленки не скрипели
Чтобы ножки не болели
Приседаем глубоко
Поднимаемся легко
Раз, два, три чеканим шаг
Подает учитель знак
Это значит что пора
Нам за парты сесть УРА!
5. (И) Самостоятельная работа.
(И) Самостоятельная работа.
Выполнение №3 с. 72 третий столбик.
• критерии оценивания:
Знать алгоритм деления на двузначное и трехзначное числа
Применить алгоритм при вычислениях.
Я могу
Могу применить алгоритм деления многозначных чисел на двузначное и трехзначное числа.
Могу выполнить проверку
Проверка работы. Лист оценивания.
6. (П) Работа в парах.
Исследуй.
Составь выражение по схеме и обозначь в нём порядок действий.
( 2.432*203+ 40.000)+ (60.950:50+14.000)- (7.809:3*2)
Проверка работы. Самооценивание.
(Молодец, если допустили ошибку напишите старайся) Дети пишут в тетрадках сами
-Давайте повторим вместе правила работы в группе
7. Работа в группах. Решить примеры, составить слово.
4167 : 463 = 9 (о) 3918:653=6(м)
2541*205=520905 (ы) 2311*203=469133 (ц)
8400:28=300 (л) 1261*324=408564 (д)
3200*12=38400 (о)
С каждой группы выходят по два ученика находят свои ответы
Выступление групп.
– Расположите ответы в порядке возрастания и прочитайте слово «МОЛОДЦЫ»
Резерв стр 73 № 6 (устно)
Нам надо узнать сколько раз по 11л входит в 55 литров.
55:11=5(раз)
100*5=500(км)
Щучинск 239+239=478(км)
2 слайд
3 слайд
4 слайд
Учебник
тетрадь
5 слайд
Учебник
На доске
На доске
Тетрадь
6 слайд
Учебник
7 слайд
Учебник
8 слайд
9 слайд(проверка)
10 слайд
11 слайд(проверка)
Конец урока
Итог урока.
-Какую цель мы поставили на сегодняшнем уроке?
– Достигли ли мы этой цели?
– Какие затруднения были у вас на уроке?
– Что нужно сделать чтобы эти затруднения не
повторялись?
Рефлексия.
Предлагает оценить свою работу при помощи смайликов Картинки к рефлексии.
Дифференциация Оценивание Межпредметные
связи
Мотивированные дети рассказывают по схеме о живой и неживой природе о взаимосвязи в природе Формативное оценивание.
Самооценивание по «Шкале трудности» в тетради.
Взаимооценивание при работе в паре, группе классом
Результаты наблюдения учителем качества ответов учащихся
на уроке.
Определение уровня усвоения навыка по (Творческая тетрадь) – литература
– физическая культура
– самопознание
– познание мира
Рефлексия для учителя:
Важные вопросы
по уроку:
Итоговая оценка (с точки зрения преподавания и обучения)
Какие два момента были наиболее успешны?
Какие два момента улучшили урок?
Что я узнал из урока о классе и отдельных людях, что я расскажу на следующем уроке?
Приемы умножения и деления на 10. 2-й класс, «Школа России»
Тип урока: овладение новыми знаниями.
Цели: познакомить с приемами умножения и деления на 10. Совершенствовать вычислительные навыки навыки устного счёта, умение решать задачи, развивать внимание и логическое мышление.
Педагогические задачи: дать первичное представление об умножении и делении числа на 10, продолжать формировать умения находить результат действия деления с помощью примера на умножение, развивать вычислительные навыки, продолжать работу над задачами.
Планируемые образовательные результаты:
Предметные УУД: умение правильно умножать и делить на число 10, знание названия компонентов умножения и деления, понимание сути переместительного закона умножения, умение выделять геометрические фигуры, применение формулы периметра квадрата.
Метапредметные УУД:
- Регулятивные: умение формулировать учебную задачу урока на основе соотнесения того ,что уже известно и усвоено, и того, что еще неизвестно, умение контролировать и оценивать учебные действия в соответствии с поставленной задачей; способность к самопроверке, самооценке, проверке по образцу и корректировке, взаимопроверке.
- Познавательные: проявлять познавательную инициативу в учебном сотрудничестве, умение выделять необходимую информацию, создавать алгоритм деятельности, сравнивать, анализировать, устанавливать причинно-следственные связи, делать выводы.
- Коммуникативные: оказывать необходимую взаимопомощь, договариваться и приходить к общему решению в совместной деятельности, слушать, слышать и понимать партнеров, планировать учебное сотрудничество с учителем и сверстниками, достаточно полно и четко выражать свои мысли.

- Личностные УУД: принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения; развитие навыков сотрудничества с взрослыми и сверстниками в разных социальных ситуациях, проявление самостоятельности, личной ответственности.
Методы и формы обучения: частично-поисковый, фронтальная и групповая работа, индивидуальная.
Оборудование: компьютер, электронная доска, доска, карточки с заданием, математический веер, карта путешествия, сундучок с призами.
1. Организационный момент
— Ребята, сегодня у нас необычный урок. Мы с вами отправимся в увлекательное морское путешествие и побудем командой моряков. С нами на борту присутствуют пассажиры. Только от нашей слаженной, дружной работы, зависит найдем ли мы сегодня клад.
2. Актуализация знаний
— Давайте вспомним правила поведения на корабле (Отвечаем по руке, задание дослушиваем до конца, сидим ровно прямо).
— Чтобы отправиться в путь нам нужно проложить курс корабля. Найдем значение данных математических выражений, показывая ответы на математическом веере.
(Выводим картинку корабля на электронную доску).
— Ребята, прочитайте данные математические выражения, назвав их компоненты и найдите значение (если дети затрудняются, необходимо напомнить арифметическое действие).
— 14 + 6 (1 слагаемое — 14, 2 слагаемое – 6, сумма равна 20).
— 43 — 4 (Уменьшаемое – 43, вычитаемое – 4, разность равна 39).
— 16 : 4 (Делимое – 16, делитель – 4, частное равно 4).
— 4 * 3 (1 множитель – 4, 2 множитель -3, произведение равно 12).
— 8 * 0 (1 множитель – 8, 2 множитель — 0, произведение равно 0).
— 40 — 33 (Уменьшаемое – 40, вычитаемое – 33, разность равна 7).
— 5 * 10 (1 множитель – 5, 2 множитель -10, произведение равно 50).
— 24 : 4 (Делимое – 24, делитель – 4, частное равно 6).
— 10 * 5 (1 множитель – 10, 2 множитель — 5, произведение равно 50).
— 17 + 15 (1 слагаемое — 17, 2 слагаемое – 17, сумма равна 32).
— Ребята, что мы сейчас с вами делали? (Считали математические выражения, вспоминали название математических компонентов).
— Молодцы! Мы отправляем наш корабль в добрый путь!
3. Самоопределение к деятельности
— Ребята, а что вы заметили, работая с данными математическими выражениями? (Мы заметили, что два выражения с одинаковыми числами и одинаковым результатом. Это 5*10 и 10*5).
Учитель записывает выражение на доске (5*10 … 10*5).
— Ребята, сравните это выражение. Какой знак мы поставим? (Равно.)
— Какое математическое свойство вы использовали для сравнения выражения? (Переместительное свойство умножения. От перестановки множителей результат умножения не изменяется).
— Вычислите значение этих выражений, заменяя умножение сложением (Один ребенок работает у доски. 5* 10 = 5+5+5+5+5+5+5+5+5+5 = 50 и 10 * 5 = 10+10+10+10+10 = 50)
5* 10 = 5+5+5+5+5+5+5+5+5+5 = 50 и 10 * 5 = 10+10+10+10+10 = 50)
— Хорошо. Ребята, чтобы дальше отправиться в путь на нашем корабле, нам нужно составить по этим выражениям два примера на деление (50 : 10 = 5 и 50 : 5 = 10)
— А как вы нашли значение выражений? (Зная значение произведения чисел 5 и 10, можно найти их частное)
— Какое правило взаимосвязи компонентов и результата действия вам помогло? (Если произведение разделить на один из множителей, то получится другой множитель)
— На сегодняшнем уроке мы продолжим учиться выполнять умножение и деление чисел и познакомимся с новым приёмом.
А кто догадался, что это за приём? (Приём умножения и деления на число 10)
— Ребята, что мы сейчас с вами делали? (Сравнивали выражения, повторяли переместительное свойство умножения и деления).
— Молодцы, отправляемся далее в наше путешествие.
— Проверьте своё предположение, откройте с. 74 и прочитайте задачи урока.
— Прочитайте объяснение вычислительного приема рядом с красной чертой.
— Послушаем объяснение и обратим наше внимание на электронную доску (Числа от 1 до 100. Приемы умножения и деления на 10).
— Что вы можете сказать о наших выводах и выводах в учебнике? (От перестановки множителей результат умножения не изменяется. Если произведение разделить на один из множителей, то получится другой ).
— Хорошо, что мы сейчас с вами сделали? (Убедились, что наши предположения правильны).
— Отправляемся дальше в наше увлекательное путешествие.
4. Физминутка
— Мы с вами моряки и нам необходимо быть внимательными, чтобы не попасть в руки к пиратам или не наткнуться на айсберг.
Игра «Запрещенное движение». Учитель говорит запретное движение, а дети должны быть внимательными и не повторять его, если учитель сказал или показал его.
5. Работа по учебнику
Работа по учебнику
Минутка чистописания.
— Откройте тетради, запишите: сегодняшнее число, Классная работа.
Цифра вроде буквы О —
Это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки!
Если ж слева рядом с ним
Единицу примостим,
Он побольше станет весить,
Потому что это — десять.
— Какое число будем прописывать? (10)
— Что можно сказать о числе 10? (чётное, двузначное, круглое, 1 десяток, 0 ед., в числовом ряду стоит после числа 9, перед числом 11)
— Что в жизни бывает круглым? (Солнце, арбуз, мяч, часы, пуговица и т.п.)
— А в математике? (Круг, шар, числа)
— Какие числа называют круглыми? (Круглыми называют числа, оканчивающиеся на ноль).
— Назовите все круглые числа в числовом ряду до 100? (10, 20, 30, 40, 50, 60, 70, 80, 90).
— Назовите самое маленькое круглое двузначное число? Самое маленькое круглое трехзначное число? (10; 100).
— Прописываем число 10 через клеточку.
(Прописная цифра 1. — Начинают писать маленькую палочку немного выше и правее центра клетки, ведут линию вверх к правому верхнему углу клетки. Затем пишут большую палочку от верхнего правого угла почти до середины нижней стороны клетки.
Прописная цифра 0. — Овал начинают писать немного левее правого верхнего угла клетки. Ведут линию вниз, закругляя на середине нижней стороны клетки. Затем ведут руку вверх к началу овала.)
— Молодцы, наш корабль плывет дальше.
— №1 стр.74 – фронтальная работа.
Составление таблицы. Дети устно поочередно читают примеры.
— Как связаны между собой четыре столбика примеров? (При составлении 2 столбика используется переместительное свойство умножения, при составлении 3 и 4 столбика – правило о том, что если значение произведения разделить на один множитель, то получится другой множитель).
| 10 * 2 = 20 | 2 * 10 = 20 | 20 : 2 = 10 | 20 : 10 = 2 |
10 * 3 = 30 | 3 * 10 = 30 | 30 : 3 = 10 | 30 : 10 = 3 |
10 * 4 = 40 | 4 * 10 = 40 | 40 : 4 = 10 | 40 : 10 = 4 |
10 * 5 = 50 | 5 * 10 = 50 | 50 : 5 = 10 | 50 : 10 = 5 |
10 * 6 = 60 | 6 * 10 = 60 | 60 : 6 = 10 | 60 : 10 = 6 |
10 * 7 = 70 | 7 * 10 = 70 | 70 : 7 = 10 | 70 : 10 = 7 |
10 * 8 = 80 | 8 * 10 = 80 | 80 : 8 = 10 | 80 : 10 = 8 |
10 * 9 = 90 | 9 * 10 = 90 | 90 : 9 = 10 | 90 : 10 = 9 |
10 * 10 = 100 | 10 * 10 = 100 | 100 : 10 = 10 | 100 : 10 = 10 |
— Ребята, какой вывод мы можем сделать об умножении и делении на 10? (Вывод: при умножении на 10 к числу справа дописывается 0.
При делении на 10 у числа 0 убирается!)
Дети читают на электронной доске стихотворение-правило.
— Наш корабль доплыл до середины пути, продолжаем наш путь. Что мы сейчас делали? (Выявили правило умножения и деления на 10.)
6. Физминутка
— Моряки должны быть не только внимательными, но и ловкими и смелыми.
— Как мы будем плыть на спасательной шлюпке? (Упражнение гребля)
— Как будем залезать по висячей лестнице? (Упражнение как будто лезем по лестнице руками)
— Как будем смотреть вдаль? (Упражнение тянемся на мысочках)
7. Закрепление изученного материала
— Ребята, как называется кухня на корабле? (Камбуз)
— Как называют повара на корабле? (Кок)
— Кок приготовил нам пирожки, но (скажу вам по секрету) кок – это бывший пират и он не умеет считать. Нам ему необходимо помочь разложить пирожки. Читаем условие задачи на стр.74 № 3.
Нам ему необходимо помочь разложить пирожки. Читаем условие задачи на стр.74 № 3.
Задача №3.
— Прочитай задачу про себя.
— Прочитай вслух.
— Сколько пирожков раскладывал повар? (40)
— Как он их раскладывал? (Поровну).
— Что значит «поровну»? (На каждую тарелку одинаковое количество).
— Как будем раскладывать пирожки на 10 тарелок? (По 1 пирожку на каждую тарелку).
(Один ученик работает у доски. 10 магнитных тарелок закрепляем на доске, раскладываем пирожки (из бумаги) по тарелкам).
— Сколько пирожков оказалось на каждой тарелке? (1)
— Поровну разложили все 40 пирожков? (Нет).
— Уточните, как будем раскладывать пирожки? (До тех пор, пока все не закончатся).
— Сколько пирожков стало на каждой тарелке? (По 4 пирожка).
— Запишите решение задачи и ответ.
40:10=4 (п.)
Ответ: на каждой тарелке по 4 пирожка.
— Что обозначает число 40? (Количество пирожков)
— Что обозначает число 10? (Количество тарелок)
-Что обозначает число 4? (Сколько пирожков на каждой тарелке).
— Решим 2 задачи обратные данной (с помощью магнитных рисунков составляем условие задач).
1. Повар разложил 40 пирожков на тарелки. В каждой тарелке получилось по 4 пирожка. На сколько тарелок повар разложил пирожки?
40: 4 = 10 (т.)
Ответ: на 10 тарелок.
— Что обозначает число 40? (количество пирожков)
— Что обозначает число 4? (Сколько пирожков на каждой тарелке).
— Что обозначает число 10? (Количество тарелок)
2. Повар разложил на 10 тарелок пирожки. В каждой тарелке получилось по 4 пирожка. Сколько всего пирожков было?
10 * 4 = 40 (п.)
Ответ: 40 пирожков всего.
— Что обозначает число 10? (Количество тарелок)
— Что обозначает число 4? (Сколько пирожков на каждой тарелке).
— Что обозначает число 40? (Количество пирожков)
— Молодцы! Что мы сейчас с вами делали? (Решали задачу и составляли задачи обратной данной).
— Хорошо, наш корабль следует дальше. И перед нами разрушенный мост. Чтобы проплыть дальше, нам необходимо восстановить мост, решая примеры самостоятельно (Выводим картинку моста с примерами на электронную доску. Примеры из №5 с.74. Решаем в столбик. После выполнения задания проверка.)
- 74 – 58 = 16
- 46 + 37 = 83
- 83 – 29 = 54
- 64 + 36 = 100
— Молодцы! Корабль наш держит путь далее и мы с вами находим сундук с сокровищами. Чтобы открыть сундук нам надо узнать длину его стороны, зная уже периметр.
— Какую фигуру представляет сундук? (Квадрат)
— Что такое квадрат? (Прямоугольник, у которого все стороны равны)
— Что такое периметр? (Сумма длин всех сторон)
— Как найти периметр квадрата? (Сложить длины всех сторон)
— Прочитайте задание №4 на стр. 74.
74.
— Какая формула периметра квадрата?
(Р = а + а +а +а
Р = а * 4)
— Чему равен периметр квадрата по условию задачи? (20 см.)
— Подставьте это значение в равенство (а * 4 = 20.)
— Что у вас получилось? (Уравнение.)
— Решите уравнение и узнайте длину стороны этого квадрата.
а * 4 =20
а = 20:4
а =5
Ответ: а = 5 см.
— Молодцы! Что мы сейчас делали? (Закрепляли изученный материал)
8. Рефлексия
— Решение задания по компьютеру № 1.
Работа в группах.
— Мы продолжаем наше путешествие и находим на острове бутылку с посланием. На листочках детям дается задание составить числовые выражения на деление. Проверка проходит фронтально.
— Составьте числовые выражения на деление.
1) 3, 30, 10 0, 50, 4, 10, 40 60, 6, 5
30 : 3 = 10
100 : 10 = 10
50 : 5 = 10
40 : 4 = 10
60 : 6 = 10
2) 90, 70, 7, 80,9 ,10, 100, 20, 8, 2
90 : 9 = 10
70 : 7 = 10
80 : 8 = 10
100 : 10 = 10
20 : 2 = 10
Фронтальная проверка.

9. Подведение итогов урока
— Ребята, мы с вами возвращаемся домой из нашего увлекательного путешествия.
— Какую тайну математики вы сегодня открыли? Чему научились? Всем ли было легко? Какие трудности испытывали? (Мы освоили приемы умножения и деления на 10.)
— Какое правило использовали при умножении числа на 10? (При умножении на 10 к числу справа дописывается 0.)
— Как находить результат при делении круглого числа на 10? (При делении на 10 у числа 0 убирается.)
— Молодцы! Вы были сегодня активны, внимательны, сообразительны, поэтому мы справились со всеми заданиями и нашли сундук с сокровищами. Спасибо вам за хорошую работу.
Выставление отметок.
10. Домашнее задание
— Открываем наш бортовой журнал – дневник и записываем домашнее задание. Учебник – стр.74 № 6.
Сундучок с призами – шоколадные монеты.
Применение распределительного свойства умножения 6 класс онлайн-подготовка на Ростелеком Лицей
51. Применение распределительного свойства умножения.
Применение распределительного свойства умножения.
Напомню, что распределительное свойство умножения относительно сложения и вычитания записывается так.
(a + b) · c = a · c + b · c = ac + bc;
(a — b) · c = a · c — b · c = ac — bc.
Распределительное свойство умножения относительно сложения и относительно вычитания позволяет решать примеры.
Пример 1. 35-13∙15=35∙15-13∙15=3∙155-1∙153=9-5=4.
Пример 2. Найдем значение произведения
2314∙7=2+314∙7=2∙7+314∙7=14+3*714=1512.
Чтобы умножить смешанное число на натуральное число, можно:
- Умножить целую часть на это число.
- Умножить дробную часть на это число.
- Сложить полученные результаты.
Пример 3. Найдем значение выражения
538∙28+258∙28=538+258∙28=8∙28=2.
Используя распределительное свойство умножения, можно упрощать выражения вида:
58a+34a=58+34∙a=148а=134 а
34x-15x=34-15x=1520-420x=1120x.
Пример 4. Квартира состоит из двух комнат. Длина большей комнаты 5110, а ширина 4 м. Длина меньшей комнаты 4 м, а ширина 3110 м. На сколько площадь одной комнаты меньше площади другой?
Площадь первой комнаты
S=a∙b=5110∙4=5+110∙4=5∙4+110∙4=20+25=2025 м2.
Площадь второй комнаты
S=a∙b=3110∙4=3+110∙4=3∙4+110∙4=12+25=1225 м2.
Разница площадей 2025-1225=8 м2.
Чтобы умножить смешанное число на смешанное число, можно:
- Перевести одно смешанное число в неправильную дробь.
- Умножить целую часть второго множителя на неправильную дробь.
-
Умножить дробную часть второго множителя на неправильную дробь.

- Сложить полученные результаты.
Пример 5. Найдем значение выражения
225∙412=225∙92=2∙92+25∙92=9+95=1045 .
Урок математики 4 класс «Деление числа на произведение»
Слайды и текст этой онлайн презентации
Слайд 1
УРОК
МАТЕМАТИКИ
4 КЛАСС
Автор: Четкина Г. В.
учитель начальных классов
МБОУ «Атратская СОШ»
Слайд 2
1
4
55
+
23
99
100
5
=
Слайд 3
560 : 7
250 * 200
15 0* 200
20180 : 10
800 * 60
200 : 2
3500 : 5
30 * 20
50150 : 10
90 * 3000
500 * 40
320 : 8
810 : 9
5400 : 6
600
5015
70
80
900
270000
40
20000
90
48000
100
30000
2018
50000
30000
2018
700
100
48000
50000
5015
900
270000
40
20000
90
Слайд 4
ВСЕХ
2
5
3
4
,
ЦАРИЦА
,
МАТЕМАТИКА
,
НАУК.
Вычислите, запишите ответ:
355 – 50*7
Реши задачу, запиши ответ:
Ученик решает 10 примеров за 40 минут. Сколько
минут в среднем идёт на решение одного примера?
Запишите номер примера, в котором допущена
ошибка: 1. 96000 : 100 = 960
2. 1250 : 10 = 125
3. 95000 : 1000 = 950
Запишите номер верного утверждения:
Чтобы найти делитель, нужно:
1. Делимое умножить на частное.
2. Делимое разделить на частное.
—
3, 5, 2, 4.
Слайд 5
Чтоб врачом, моряком
Или лётчиком стать,
Надо твёрдо на «5»
Математику знать!
Добро
пожало
вать!
МАТЕМАТИКА
Слайд 6
Частное чисел 350 и 7 увеличь на 20.
Из 800 вычти произведение чисел 30 и 9.
К 50 прибавь частное чисел 36 и 6.
Чему равно 3/5 тонны?
Найди периметр квадрата со стороной 9 см.
Чему равна ширина сада, если его S=54 кв.м, а его
длина 9 м?
70
530
56
600 кг
36 см
6 м
Сколько дм в 240 см?
24 дм
Слайд 7
500 * 6 : 100
4000 * 3 : 100
950 – 720 + 42
140 : 7 * 2
(270 – 50) * 10
Е
Н
Д
И
Л
272
30
2200
30
120
40
30
Д е л е н и е
Слайд 8
Деление числа
на произведение
познакомиться и отработать
приёмы деления числа
на произведение
Слайд 9
Составь задачу и реши её.
12км/ч t=2ч 13км/ч
?
Слайд 10
Слайд 11
Слайд 12
Молодцы!
Спасибо
за урок!
Д/З
№ 90, с. 20
20
Слайд 13
Рефлексия
ВО ВРЕМЯ ПУТЕШЕСТВИЯ БЫЛО ИНТЕРЕСНО И ЛЕГКО, ПОТОМУ ЧТО УМЕЮ БЫСТРО И ПРАВИЛЬНО ВЫЧИСЛЯТЬ, РЕШАТЬ ЗАДАЧИ
ПУТЕШЕСТВИЕ БЫЛО ИНТЕРЕСНОЕ,
НО НЕКОТОРЫЕ ЗАДАНИЯ ВЫЗЫВАЛИ
ЗАТРУДНЕНИЯ
МНЕ БЫЛО СКУЧНО! Я МЕДЛЕННО
СЧИТАЮ, МНЕ ТРУДНО БЫЛО
ВЫПОЛНИТЬ ЗАДАНИЯ.
Поколения компьютеров — история развития вычислительной техники
☰
В короткой истории компьютерной техники выделяют несколько периодов на основе того, какие основные элементы использовались для изготовления компьютера. Временное деление на периоды в определенной степени условно, т.к. когда еще выпускались компьютеры старого поколения, новое поколение начинало набирать обороты.
Можно выделить общие тенденции развития компьютеров:
- Увеличение количества элементов на единицу площади.
- Уменьшение размеров.
- Увеличение скорости работы.
- Снижение стоимости.
- Развитие программных средств, с одной стороны, и упрощение, стандартизация аппаратных – с другой.

Нулевое поколение. Механические вычислители
Предпосылки к появлению компьютера формировались, наверное, с древних времен, однако нередко обзор начинают со счетной машины Блеза Паскаля, которую он сконструировал в 1642 г. Эта машина могла выполнять лишь операции сложения и вычитания. В 70-х годах того же века Готфрид Вильгельм Лейбниц построил машину, умеющую выполнять операции не только сложения и вычитания, но и умножения и деления.
В XIX веке большой вклад в будущее развитие вычислительной техники сделал Чарльз Бэббидж. Его разностная машина, хотя и умела только складывать и вычитать, зато результаты вычислений выдавливались на медной пластине (аналог средств ввода-вывода информации). В дальнейшем описанная Бэббиджем аналитическая машина должна была выполнять все четыре основные математические операции. Аналитическая машина состояла из памяти, вычислительного механизма и устройств ввода-вывода (прямо таки компьютер … только механический), а главное могла выполнять различные алгоритмы (в зависимости от того, какая перфокарта находилась в устройстве ввода). Программы для аналитической машины писала Ада Ловлейс (первый известный программист). На самом деле машина не была реализована в то время из-за технических и финансовых сложностей. Мир отставал от хода мыслей Бэббиджа.
Программы для аналитической машины писала Ада Ловлейс (первый известный программист). На самом деле машина не была реализована в то время из-за технических и финансовых сложностей. Мир отставал от хода мыслей Бэббиджа.
В XX веке автоматические счетные машины конструировали Конрад Зус, Джорж Стибитс, Джон Атанасов. Машина последнего включала, можно сказать, прототип ОЗУ, а также использовала бинарную арифметику. Релейные компьютеры Говарда Айкена: «Марк I» и «Марк II» были схожи по архитектуре с аналитической машиной Бэббиджа.
Первое поколение. Компьютеры на электронных лампах (194х-1955)
Быстродействие: несколько десятков тысяч операций в секунду.
Особенности:
- Поскольку лампы имеют существенные размеры и их тысячи, то машины имели огромные размеры.
- Поскольку ламп много и они имеют свойство перегорать, то часто компьютер простаивал из-за поиска и замены вышедшей из строя лампы.
- Лампы выделяют большое количество тепла, следовательно, вычислительные машины требуют специальные мощные охладительные системы.

Примеры компьютеров:
Колоссус – секретная разработка британского правительства (в разработке принимал участие Алан Тьюринг). Это первый в мире электронный компьютер, хотя и не оказавший влияние на развитие компьютерной техники (из-за своей секретности), но помог победить во Второй мировой войне.
Эниак. Создатели: Джон Моушли и Дж. Преспер Экерт. Вес машины 30 тонн. Минусы: использование десятичной системы счисления; множество переключателей и кабелей.
Эдсак. Достижение: первая машина с программой в памяти.
Whirlwind I. Слова малой длины, работа в реальном времени.
Компьютер 701 (и последующие модели) фирмы IBM. Первый компьютер, лидирующий на рынке в течение 10 лет.
Второе поколение. Компьютеры на транзисторах (1955-1965)
Быстродействие: сотни тысяч операций в секунду.
По сравнению с электронными лампами использование транзисторов позволило уменьшить размеры вычислительной техники, повысить надежность, увеличить скорость работы (до 1 млн. операций в секунду) и почти свести на нет теплоотдачу. Развиваются способы хранения информации: широко используется магнитная лента, позже появляются диски. В этот период была замечена первая компьютерная игра.
операций в секунду) и почти свести на нет теплоотдачу. Развиваются способы хранения информации: широко используется магнитная лента, позже появляются диски. В этот период была замечена первая компьютерная игра.
Первый компьютер на транзисторах TX стал прототипом для компьютеров ветки PDP фирмы DEC, которые можно считать родоначальниками компьютерной промышленности, т.к появилось явление массовой продажи машин. DEC выпускает первый миникомпьютер (размером со шкаф). Зафиксировано появление дисплея.
Фирма IBM также активно трудится, производя уже транзисторные версии своих компьютеров.
Компьютер 6600 фирмы CDC, который разработал Сеймур Крей, имел преимущество над другими компьютерами того времени – это его быстродействие, которое достигалось за счет параллельного выполнения команд.
Третье поколение. Компьютеры на интегральных схемах (1965-1980)
Быстродействие: миллионы операций в секунду.
Интегральная схема представляет собой электронную схему, вытравленную на кремниевом кристалле. На такой схеме умещаются тысячи транзисторов. Следовательно, компьютеры этого поколения были вынуждены стать еще мельче, быстрее и дешевле.
На такой схеме умещаются тысячи транзисторов. Следовательно, компьютеры этого поколения были вынуждены стать еще мельче, быстрее и дешевле.
Последнее свойство позволяло компьютерам проникать в различные сферы деятельности человека. Из-за этого они становились более специализированными (т.е. имелись различные вычислительные машины под различные задачи).
Появилась проблема совместимости выпускаемых моделей (программного обеспечения под них). Впервые большое внимание совместимости уделила компания IBM.
Было реализовано мультипрограммирование (это когда в памяти находится несколько выполняемых программ, что дает эффект экономии ресурсов процессора).
Дальнейшее развитие миникомпьютеров (PDP-11).
Четвертое поколение. Компьютеры на больших (и сверхбольших) интегральных схемах (1980-…)
Быстродействие: сотни миллионов операций в секунду.
Появилась возможность размещать на одном кристалле не одну интегральную схему, а тысячи. Быстродействие компьютеров увеличилось значительно. Компьютеры продолжали дешеветь и теперь их покупали даже отдельные личности, что ознаменовало так называемую эру персональных компьютеров. Но отдельная личность чаще всего не была профессиональным программистом. Следовательно, потребовалось развитие программного обеспечения, чтобы личность могла использовать компьютер в соответствие со своей фантазией.
Компьютеры продолжали дешеветь и теперь их покупали даже отдельные личности, что ознаменовало так называемую эру персональных компьютеров. Но отдельная личность чаще всего не была профессиональным программистом. Следовательно, потребовалось развитие программного обеспечения, чтобы личность могла использовать компьютер в соответствие со своей фантазией.
В конце 70-х – начале 80-х популярностью пользовался компьютера Apple, разработанный Стивом Джобсом и Стивом Возняком. Позднее в массовое производство был запущен персональный компьютер IBM PC на процессоре Intel.
Позднее появились суперскалярные процессоры, способные выполнять множество команд одновременно, а также 64-разрядные компьютеры.
Пятое поколение?
Сюда относят неудавшийся проект Японии (хорошо описан в Википедии). Другие источники относят к пятому поколению вычислительных машин так называемые невидимые компьютеры (микроконтроллеры, встраиваемые в бытовую технику, машины и др. ) или карманные компьютеры.
) или карманные компьютеры.
Также существует мнение, что к пятому поколению следует относить компьютеры с двухядерными процессорами. С этой точки зрения пятое поколение началось примерно с 2005 года.
| Домен | Кластер | Код | Единое ядро ГОСТ |
|---|---|---|---|
| Операции и алгебраическое мышление | Используйте четыре операции с целыми числами для решения проблем. | 4. OA.1 OA.1 | Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 x 7 как утверждение, что 35 в 5 раз больше 7 и 7 раз больше 5. Представьте словесные утверждения мультипликативных сравнений как уравнения умножения. |
| 4.OA.2 | Умножение или деление для решения словесных задач, включающих мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного сравнения. | ||
| 4.OA.3 | Решайте многоступенчатые задачи со словами, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление. | ||
Ознакомьтесь с факторами и мультипликаторами. | 4.OA.4 | Найдите все пары факторов для целого числа в диапазоне 1–100. Помните, что целое число является кратным каждому из его факторов. Определите, является ли данное целое число в диапазоне 1–100 кратным заданному однозначному числу. Определите, является ли данное целое число в диапазоне 1–100 простым или составным. | |
| Создание и анализ шаблонов. | 4.OA.5 | Создает рисунок числа или фигуры в соответствии с заданным правилом.Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например: учитывая правило «сложить 3» и начальное число 1, сгенерируйте термины в результирующей последовательности и обратите внимание, что термины кажутся чередующимися между нечетными и четными числами. Неформально объясните, почему числа будут и дальше меняться таким образом. | |
| Число и операции в базе Ten | Обобщить понимание разрядов для многозначных целых чисел. | 4.NBT.1 | Помните, что в многозначном целом числе цифра в одном месте в десять раз больше, чем в месте справа. Например, узнайте, что 700 ÷ 70 = 10, применив концепции числового значения и деления. (Ожидания 4-й степени в этой области ограничены целыми числами, меньшими или равными 1 000 000.) |
| 4.NBT.2 | Чтение и запись многозначных целых чисел с использованием десятичных цифр, числовых имен и расширенной формы.Сравните два многозначных числа на основе значений цифр в каждом месте, используя>, = и | ||
| 4.NBT.3 | Используйте разметку знаков для округления многозначных целых чисел до любого места. (Ожидания 4-й степени в этой области ограничены целыми числами, меньшими или равными 1 000 000.) | ||
| Используйте понимание разряда и свойства операций для выполнения многозначной арифметики. | 4.NBT.4 | Свободно вычисляйте и вычитайте многозначные целые числа, используя стандартный алгоритм. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000. Можно использовать ряд алгоритмов.) (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000. Можно использовать ряд алгоритмов.) | |
| 4.NBT.5 | Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядах и свойствах операций. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000.Может использоваться ряд алгоритмов.) | ||
| 4.NBT.6 | Найдите целочисленные частные и остатки с дивидендами до четырех цифр и однозначными делителями, используя стратегии, основанные на разряде, свойствах операций и / или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет с помощью уравнений, прямоугольных массивов и / или моделей площадей. (Ожидания 4-го класса в этой области ограничены целыми числами, меньшими или равными 1 000 000. Может использоваться ряд алгоритмов.) Может использоваться ряд алгоритмов.) | ||
| Число и операции: дроби | Расширить понимание эквивалентности дробей и упорядочения. | 4.NF.1 | Объясните, почему дробь a / b эквивалентна дроби (n × a) / (n × b), используя модели визуальных дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две дроби являются тот же размер. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби.(Ожидаемые оценки 4-го класса в этой области ограничены дробями со знаменателями 2, 3, 4, 5, 6, 8, 10, 12, 100.) |
| 4.NF.2 | Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов>, = или | ||
Постройте дроби из дробных единиц, применяя и расширяя предыдущие представления об операциях над целыми числами. | 4.NF.3 | Дробь a / b с a> 1 понимается как сумма дробей 1 / b. а. Под сложением и вычитанием дробей следует понимать соединение и разделение частей, относящихся к одному целому. г. Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение по формуле . Обоснуйте разложение, например, используя визуальную модель дроби. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8. г. Сложите и вычтите смешанные числа с одинаковыми знаменателями, например, заменив каждое смешанное число эквивалентной дробью, и / или используя свойства операций и взаимосвязь между сложением и вычитанием. г. Решайте задачи со словами, включающие сложение и вычитание дробей, относящихся к одному целому и имеющих одинаковые знаменатели, , например, используя визуальные модели дробей и уравнения для представления проблемы. | |
| 4.NF.4 | Применяйте и расширяйте предыдущие представления об умножении, чтобы умножать дробь на целое число. а. Дробь a / b следует понимать как кратное 1 / b. Например, используйте модель визуальной дроби, чтобы представить 5/4 как произведение 5 × (1/4), записав вывод по уравнению 5/4 = 5 × (1/4). г. Поймите, что кратное a / b является кратным 1 / b, и используйте это понимание для умножения дроби на целое число. Например, использует модель визуальной дроби, чтобы выразить 3 × (2/5) как 6 × (1/5), распознавая этот продукт как 6/5. (Как правило, n × (a / b) = (n × a) / b.) c. Решать задачи со словами, связанные с умножением дроби на целое число, например.g., используя модели визуальных фракций и уравнения для представления проблемы. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек , сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ? | ||
| Разберитесь в десятичной системе счисления дробей и сравните десятичные дроби. | 4.NF.5 | Выразите дробь со знаменателем 10 как эквивалентную дробь со знаминателем 100 и используйте этот метод для сложения двух дробей с соответствующими знаменателями 10 и 100. Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100. (Учащиеся, которые могут генерировать эквивалентные дроби, могут разработать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями в целом не является обязательным требованием в этом классе.) Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100. (Учащиеся, которые могут генерировать эквивалентные дроби, могут разработать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями в целом не является обязательным требованием в этом классе.) | |
| 4.NF.6 | Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите 0,62 как 1 62/100; опишите длину как 0,62 метра; найдите 0.62 на числовой линейной диаграмме. (Ожидаемые оценки 4-го класса в этой области ограничены дробями со знаменателями 2, 3, 4, 5, 6, 8, 10, 12, 100.) | ||
| 4.NF.7 | Сравните два десятичных знака с сотыми, исходя из их размера. Помните, что сравнения сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов>, = или | ||
| Измерения и данные | Решает проблемы, связанные с измерением и преобразованием измерений из более крупной единицы в меньшую. | 4.MD.1 | Знать относительные размеры единиц измерения в одной системе единиц, включая км, м, см; кг, г; фунт, унция; л, мл; час, мин, сек. В рамках единой системы измерения выразите измерения в большей единице через меньшую единицу. Запишите эквиваленты измерений в таблицу из двух столбцов. Например: знайте, что 1 фут в 12 раз больше 1 дюйма. Выразите длину 4-футовой змеи как 48 дюймов. Создайте таблицу преобразования для футов и дюймов, перечислив пары чисел (1, 12), (2, 24 ), (3, 36),…. |
| 4.MD.2 | Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкости, массами объектов и деньгами, включая задачи, связанные с простыми дробями или десятичными знаками, а также задачи, требующие выражения измерений, данных в большей единице, в меньших Блок. Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерений. | ||
4. MD.3 MD.3 | Применяйте формулы площади и периметра для прямоугольников в реальных и математических задачах. Например, найдите ширину прямоугольной комнаты с учетом площади пола и длины, просмотрев формулу площади как уравнение умножения с неизвестным коэффициентом. | ||
| Представление и интерпретация данных. | 4.MD.4 | Постройте линейный график для отображения набора данных измерений в долях единицы (1/2, 1/4, 1/8). Решайте задачи, связанные с сложением и вычитанием дробей, используя информацию, представленную на линейных графиках.Например, с помощью линейного графика найдите и интерпретируйте разницу в длине между самым длинным и самым коротким экземплярами в коллекции насекомых. | |
| Геометрические измерения — понимание понятий угла и измерения углов. | 4.MD.5 | Распознавать углы как геометрические формы, которые образуются там, где два луча имеют общую конечную точку, и понимать концепции измерения углов: a.  Угол измеряется относительно круга с центром в общем конце лучей, принимая во внимание долю дуги окружности Угол измеряется относительно круга с центром в общем конце лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают круг.Угол, который составляет 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов. г. Угол, который поворачивается на n углов в один градус, называется угловой мерой n градусов. | |
| 4.MD.6 | Измерьте углы в целых градусах с помощью транспортира. Нарисуйте углы указанной меры. | ||
| 4.MD.7 | Распознать угловую меру как добавочную. Когда угол разбивается на неперекрывающиеся части, угловая мера целого является суммой угловых величин частей.Решайте задачи сложения и вычитания, чтобы найти неизвестные углы на диаграмме в реальных и математических задачах, например, используя уравнение с символом для неизвестной угловой меры. | ||
| Геометрия | Нарисуйте и обозначьте линии и углы, а также классифицируйте формы по свойствам их линий и углов. | 4.G.1 | Нарисуйте точки, линии, отрезки, лучи, углы (прямые, острые, тупые), а также перпендикулярные и параллельные линии. Обозначьте их на двухмерных фигурах. |
| 4.G.2 | Классифицируют двумерные фигуры на основании наличия или отсутствия параллельных или перпендикулярных линий либо наличия или отсутствия углов заданного размера. Считайте прямоугольные треугольники категорией и определяйте прямоугольные треугольники. | ||
| 4.G.3 | Распознает линию симметрии двумерной фигуры как линию, пересекающую фигуру, так что фигуру можно сложить вдоль этой линии на совпадающие части.Определите линейно-симметричные фигуры и проведите линии симметрии. |
Оценка: 4 — Расчет 2
Особенности специального образования
Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования. Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
| Универсальные стратегии для учащихся с трудностями | |
|---|---|
Использование манипуляторов |
|
Модель / Рисование рисунка |
|
Строительные ресурсы |
|
Ежедневное подкрепление |
|
Карты памяти |
|
Взаимодействие с точками соприкосновения | |
Визуальные подсказки |
|
Несколько способов доставки |
|
% PDF-1. 5
%
1599 0 объект
>
эндобдж
xref
1599 72
0000000016 00000 н.
0000003056 00000 н.
0000003183 00000 п.
0000003883 00000 н.
0000004106 00000 п.
0000004315 00000 н.
0000004539 00000 н.
0000004747 00000 н.
0000004984 00000 н.
0000005211 00000 н.
0000005438 00000 н.
0000005650 00000 н.
0000005877 00000 н.
0000006100 00000 н.
0000006307 00000 н.
0000006514 00000 н.
0000006721 00000 н.
0000006913 00000 н.
0000007119 00000 н.
0000007345 00000 н.
0000007555 00000 н.
0000007794 00000 н.
0000008120 00000 н.
0000008446 00000 н.
0000008756 00000 н.
0000009082 00000 н.
0000009290 00000 н.
0000009529 00000 н.
0000009755 00000 н.
0000009965 00000 н.
0000010204 00000 п.
0000010426 00000 п.
0000010632 00000 п.
0000010854 00000 п.
0000011078 00000 п.
0000011304 00000 п.
0000011514 00000 п.
0000011753 00000 п.
0000011979 00000 п.
0000012152 00000 п.
0000012287 00000 п.
0000012460 00000 п.
0000012637 00000 п.
0000012877 00000 п.
0000013111 00000 п.
0000013140 00000 п.
5
%
1599 0 объект
>
эндобдж
xref
1599 72
0000000016 00000 н.
0000003056 00000 н.
0000003183 00000 п.
0000003883 00000 н.
0000004106 00000 п.
0000004315 00000 н.
0000004539 00000 н.
0000004747 00000 н.
0000004984 00000 н.
0000005211 00000 н.
0000005438 00000 н.
0000005650 00000 н.
0000005877 00000 н.
0000006100 00000 н.
0000006307 00000 н.
0000006514 00000 н.
0000006721 00000 н.
0000006913 00000 н.
0000007119 00000 н.
0000007345 00000 н.
0000007555 00000 н.
0000007794 00000 н.
0000008120 00000 н.
0000008446 00000 н.
0000008756 00000 н.
0000009082 00000 н.
0000009290 00000 н.
0000009529 00000 н.
0000009755 00000 н.
0000009965 00000 н.
0000010204 00000 п.
0000010426 00000 п.
0000010632 00000 п.
0000010854 00000 п.
0000011078 00000 п.
0000011304 00000 п.
0000011514 00000 п.
0000011753 00000 п.
0000011979 00000 п.
0000012152 00000 п.
0000012287 00000 п.
0000012460 00000 п.
0000012637 00000 п.
0000012877 00000 п.
0000013111 00000 п.
0000013140 00000 п.
Деление на 4 с остатком и без остатка.
 Примеры на порядок действий. Геометрический материал. Решение задач.
Примеры на порядок действий. Геометрический материал. Решение задач.Урок математики в 3 классе. Учитель: Шпанко И.Г.
Тема урока: Деление на 4 с остатком и без остатка. Примеры на порядок действий. Геометрический материал. Решение задач.
Цель урока: 1) закрепить умение делить числа на 4 без остатка; совершенствовать умение решать примеры на порядок действий;закреплять умения решать задачи на сравнение.
2)развивать навыки контроля и самоконтроля; умение и навыки устных и письменных вычислений; математические способности и интерес к предмету через доказательства и обоснования ответов учащихся.
3) Способствовать созданию условий обучения, при которых каждый ученик будет чувствовать свою успешность. Формировать культуру межличностных отношений, культуру умственного труда через формы организации обучения, способы взаимодействия учащихся учителя на уроке, контроль и коррекцию ответов детей.
Ход урока:
- Оргмомент ( создать положительный настрой на работу). Слайд №1 «Звонок»№1.
Прозвенел уже звонок,
Он позвал нас на урок.
Мы все дружная семья –
Он и ты, она и я.
Время зря сам не теряй
И соседу помогай.
— Как вы думаете, почему так написано в последней строчке?
— Мы сегодня много будем работать в парах.
— Значит нам понадобятся дружба, взаимопомощь, выручка, поддержка.
2) Целеполагание. Мотивация.
— Прочитайте название темы урока. Так что мы будем делать сегодня на уроке? Зачем нам учиться считать?
3) Устный счет.
— На прошлом уроке мы научились находить четверть от числа.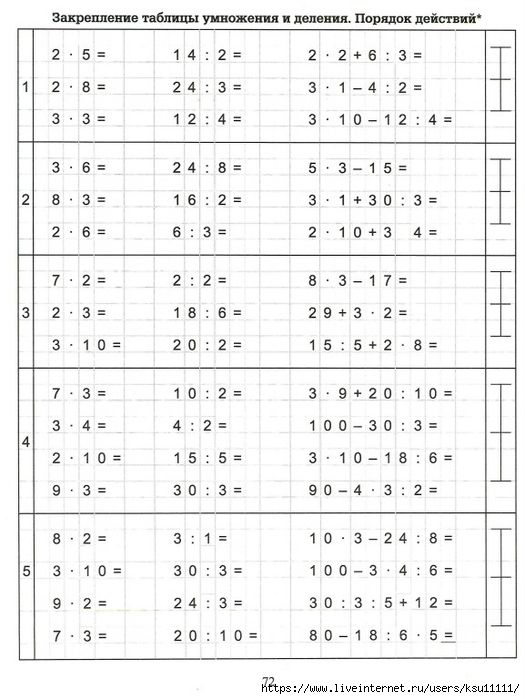 — Другими словами, что мы повторяли на прошлом уроке? — Сегодня мы проверим свои знания и будем находить четверть от чисел, которые вы будете видеть на экране.
— Другими словами, что мы повторяли на прошлом уроке? — Сегодня мы проверим свои знания и будем находить четверть от чисел, которые вы будете видеть на экране.
(На экране через каждые 12 секунд появляются числа. Дети находят четверть от них и записывают результаты в тетрадь.)
Слайды №2 на экране «20, 4, 24, 8, 32, 12, 36, 16, 40, 28»
— Ответы деления будете записывать в тетрадь, а потом проверите друг друга.
( 2 минуты дети пишут ответы, затем меняются тетрадями и проверяют друг друга с помощью слайда « ответы» №3 «5, 1, 6, 2, 8, 3, 9, 4, 10, 7». Затем с помощью слайда « Как оценить работу»№4 оценивают своих товарищей.)
«Без ошибок — 12 баллов
1 ош. — 9
— 9
2 ош. — 6
3 ош. – 2»
— Ребята, кто справился с работой на отлично? ( показывают зелёный сигнал) А кто допустил 1 ошибку? (те, кто не справился с работой – показывают красный си гнал).
— Если вы не справились с работой, не отчаивайтесь. У вас будет время поработать дома самостоятельно над своими ошибками, а также в классе вам помогут ваши одноклассники – консультанты.
— Итак, что мы сейчас повторили? Сегодня нам пондобятся знания этой таблицы, мы будем использовать их на уроке при решении примеров.
— Давайте вспомним, как называются числа при делении?
( на экране слайд «компоненты»№5 «32 : 4 = 8»)
«делимое» «делитель» «частное»
4). Работа в парах. Решение примеров на порядок действий. ( время работы 3 минуты)
Работа в парах. Решение примеров на порядок действий. ( время работы 3 минуты)
А) – Сейчас вы будете работать самостоятельно на своих карточках, но если понадобится помощь, обращайтесь к соседу по парте. Помните слова « Уча – учусь». Помогая товарищу, вы укрепляете свои знания. На каждой карточке есть памятка «Как оценить свою работу». Она поможет вам при оценке работы. (Карточек 4 варианта, примеры разные, но у всех получается в результате одно слово – «успех!» Если слово получилось, работа выполнена без ошибок. Т. К. дети работают в парах работу они заканчивают приблизительно одновременно. )
— Кто справился с заданием самостоятельно? Получают отличный результат. – Тот, кому помогали – оценку пока не получает.
Б) В это же время у компьютера работает один ученик. Он выполняет похожее задание. Слайд «Тропка»№6.
24 : 4 * 1 = 6 т
1 * (36 : 4) = 9 р
12 + 8 : 4 = 14 о
32 : 4 + 8 = 16 п
36 : (16 : 4) = 9 к
1 * (20 : 4) = 5 а
В) Через 3 минуты учитель вызывает к доске двух, справившихся с работой учеников. На доске примеры:
На доске примеры:
16 : 4 = 4 17 : 4 = 4 (ост. 1)
36 : 4 = 9 37 : 4 = 9 (ост. 1)
20 : 4 = 5 21 : 4 = 5 (ост. 1)
28 : 4 = 7 29 : 4 = 7(ост. 1)
— Правильно ли решены примеры?
— Чем они отличаются?
— Почему появился остаток?
— Что мы должны помнить при решении примеров с остатком?
(остаток не должен быть больше делителя)
5). Творческая работа над задачей учебника ст. № .
А) Дети читают задачу про себя.
Б) Повторяют условие задачи по слайдам№7 «2 палатки»
№8 «3 палатки».
В) –Какой вопрос поставлен в задаче?
Г) запись краткой записи в тетрадях и на доске:
2 палатки по 7 человек на ? больше (меньше) человек в одной
3 палатки по 4 человека палатке
— А какой ещё ворос можно поставить к задаче?
— Какие это задачи? Почему так думаете? Какого типа первая задача? А вторая? (Первый вариант записывает задачу на сравнение, а второй – на нахождение суммы).
6) Самостоятельная работа по решению задачи по краткой записи. Задачу решают по выбору. Слайд №9« 3 коробки по 4 яблока на ?
2 коробки по 7 яблок
3 коробки по 4 яблока ?
2 коробки по 7 яблок
7). Рефлексия
Рефлексия
— Как вы оцениваете свою работу на уроке?
— Кто сам может оценить свои ответы? (показывают зелёные сигналы)
-А кто может объяснить, как выполнял свои задания? ( показать)
примеры для математики в 5 классе и алгоритм выполнения операции
Математика
12.11.21
13 мин.
Изучение арифметических операций подробно начинается на уроках математики в 5 классе на примерах, а деление с остатком не является исключением. Некоторые ученики не представляют, какой важной для дальнейшего изучения дисциплин с физико-математическим уклоном считается эта тема. Однако сначала требуется рассмотреть теорию, а затем переходить к практическому применению знаний, полученных в процессе обучения.
Оглавление:
- Общие сведения
- Виды величин
- Методика деления с остатком
Общие сведения
Деление с остатком — разновидность арифметической операции, которая также состоит из делимого и делителя, но результат ее выполнения записывается в виде целой части и некоторого значения. Математическая запись выглядит следующим образом: 4 (+1) или 5 (-1). Следует отметить, что в алгебре встречаются два вида представления результата с остатком:
Математическая запись выглядит следующим образом: 4 (+1) или 5 (-1). Следует отметить, что в алгебре встречаются два вида представления результата с остатком:
- Положительным.
- Отрицательным.
В первом случае запись имеет такой вид: 36 (+1). Если рассмотреть операцию деления «73/2», то, зная частное и делитель, можно вычислить искомое значение. Для этого нужно умножить частное на делитель, а затем к полученному произведению прибавить остаток, т. е. 36*2+1=73. Положительная форма представления применяется довольно часто и считается наиболее распространенной.
Однако существует и другой вид представления остатка — отрицательный. Его суть заключается в необходимой подстройке частного. Например, для написания компьютерной программы или удобной записи какого-либо параметра физического явления. Например, при делении 71 на 2 результат можно записать в положительной и отрицательной формах, т. е. 71/2=35 (+1) и 71/2=36 (-1) соответственно.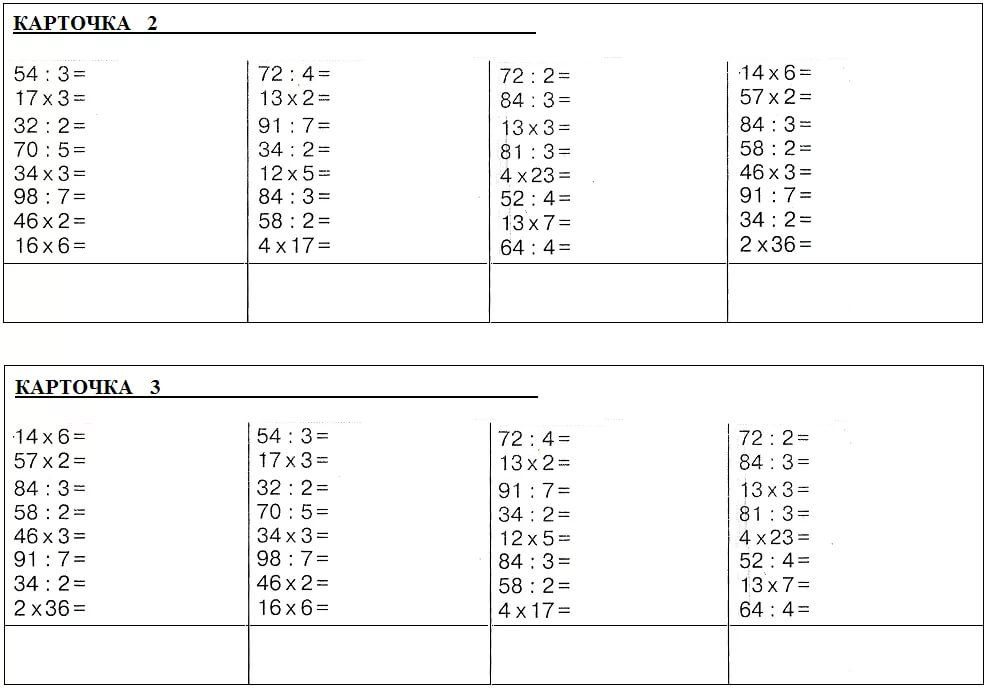
При выполнении обратной конвертации искомая величина не изменяется, т. е. 35*2+1=71 и 36*2−1=71. Иными словами, обе формы представления применяются для удобства записи. Каждый сам определяет тип частного с остатком и использует его в конкретной ситуации.
Математики называют операцию деления обратной умножению, т. е. произведение — делимое, частное и делитель — I и II множители. Не каждое число делится нацело на другое. Чтобы правильно подобрать соответствующий сомножитель, нужно ознакомиться с признаками делимости для двух чисел.
Виды величин
Перед подробным рассмотрением правил делимости одной величины на другую следует разобраться с классификацией чисел. Последние бывают двух типов: простыми и составными. Для идентификации первых необходимо использовать определенный алгоритм, базой которого являются правила делимости. Простые значения имеют одно важное свойство: делителем является единица или эквивалентное значение исходной величине. Например, 13 делится только на 1 и 13.
Например, 13 делится только на 1 и 13.
Составным называется значение, которое может представляться в виде сомножителей, отличных от единицы и самого себя. Например, 12=2*3*2. Для идентификации такого числа также нужны также признаки делимости.
Признаки делимости
Правила делимости — совокупность критериев, указывающих на принадлежность некоторого сомножителя определенному значению. В книге советского математика Виленкина Н. Я., изданной с разрешения ФГОС (федеральных государственно-образовательных стандартов), они подробно описываются. Автор выделяет девять основных критериев деления величины на однозначное число, принимающее значения от 2 до 9:
- Все четные величины делятся на двойку. Первые заканчиваются только на 2, 4, 6, 8 и 0.
- Число можно разделить на три, когда сумма всех элементов разрядной сетки содержит делитель, эквивалентный трем.

- Условие деления на 4: сумма последних 2 цифр делится на это значение.
- На 5 можно поделить в том случае, когда последний разряд заканчивается на нуль или пятерку.
- При целочисленном делении величины на шестерку должны соблюдаться второе и третье правила (на 2 и 3, т. к. их произведение эквивалентно шести).
- Если количество цифр превышает 7, то правило имеет такой вид: выполнить разбивку по три элемента (справа налево), просуммировать компоненты триад и разделить на 7. Когда величина разрядов меньше семи, то критерий формулируется по-другому: отнять от числа без разряда единиц удвоенное значение последнего компонента, а затем попробовать разделить на 7. В обоих случаях частное должно быть целым.
- Величина делится на 8 только при выполнении сразу первого и третьего признаков (для 2 и 4, т. к. 2*4=8).
- Частное является целочисленным значением при выполнении операции деления искомого числа на 9, только когда сумма разрядов делителя также делиться на 9 без остатка.

- На 10 можно разделить величину при условии, что она заканчивается на нуль.
Однако для новичков не все критерии понятны. Для понимания материала нужно разобрать примеры на деление без остатка для 5 класса.
Применение правил
Для первого пункта (деления на двойку) можно привести следующий пример деления 5226 на 2. Частное при операции деления 5226 на 2 является целым числом, т. к. делимое заканчивается на четную цифру. На тройку 5226 делится, поскольку 5+2+2+6=15. Кроме того, 5226 можно также поделить на 4, т. е. 2+6=8.
Пятерка не является делителем 5226, поскольку величина заканчивается на 6. На последнее значение не делится, т. к. сумма компонентов разрядной сетки составляет 15. Чтобы определить делимость на 7, нужно воспользоваться следующим алгоритмом:
- Число разрядов меньше 7: 522−6*2=510.
- Величина 510 не делится на 7, т. к. последняя не является делителем 51 (можно нуль не учитывать).

Следует отметить, что на 8 число 5226 делится, поскольку соблюдаются условия для четверки и двойки. Если сложить все компоненты разрядной сетки, то они не будут нацело делиться на 9, т. к. в сумме дают 15. Кроме того, десятка не является сомножителем 5226. Последнее заканчивается на «6».
Специалисты рекомендуют записать все правила на карточки из плотной бумаги. Далее следует ознакомиться с алгоритмом определения принадлежности числа к простому или составному.
Методика идентификации значений
Многие начинающие математики сталкиваются с проблемой правильной идентификации типа числового значения. Для этих целей были разработаны специальные способы. К ним относятся следующие:
- Таблицы.
- Компьютерное программное обеспечение.
- Ручной метод.
В первом случае в конце каждого учебника находятся специальные дополнения, в которых содержится информация о простых числах в виде табличных данных. Как правило, указываются величины до 1000. Однако при выполнении сложных расчетов (решения различных уравнений, сокращение дробных выражений и т. д) информации в учебнике будет недостаточно. В этом случае математики рекомендуют воспользоваться специализированным программным обеспечением или онлайн-калькуляторами простых значений.
Однако при выполнении сложных расчетов (решения различных уравнений, сокращение дробных выражений и т. д) информации в учебнике будет недостаточно. В этом случае математики рекомендуют воспользоваться специализированным программным обеспечением или онлайн-калькуляторами простых значений.
Однако иногда возникают ситуации, когда нет ни учебника, ни компьютера. В этом случае будет полезен алгоритм идентификации числа. Он имеет следующий вид:
- Написать величину.
- Определить ее сомножители, используя признаки делимости двух чисел.
- Если множитель найден, то остановится или продолжить, когда стоит задача о нахождении всех делителей. В противном случае число — простое.
Следует отметить, что специалисты после изучения методики, рекомендуют разобрать ее на практике. Это хороший тренажер для мозга, направленный на приобретение опыта. Реализация алгоритма выглядит следующим образом:
- Число: 329.
- На 2: не делится, т.
 к. последняя цифра нечетная (-).
к. последняя цифра нечетная (-). - 3: 3+2+9=14 (-).
- 4: 2+9=11 (-).
- 5: (-), т. к. 9 не эквивалентна 0 или 5.
- 6: (-) — не делится на 2 и 3.
- 7: 32−18=14 (+).
- 8: (-), т. к. не выполняются условия для 2 и 4.
- 9: (-) — сумма цифр не делится на 9.
Следует отметить, что алгоритм можно было прервать на седьмом шаге, поскольку делитель уже был найден. Далее нужно перейти к самой методике деления чисел с остатком.
Очень часто начинающие математики делают много ошибок в задачах на деление с остатком. В 5 классе подробно изучается методика для выполнения этой операции. Она выглядит таким образом:
- Написать искомое число с делителем, разделив их между собой вертикальной чертой. Далее следует подчеркнуть делитель при помощи прямой линии, под которой и будет записываться результат: 7153/2.
- Рассмотреть I разряд: 7. Он больше делителя, т. е. 7>5.
- Разделить I разряд на 5 с выделением целой части: 7/5=1.
 Записать 1 в графу результата.
Записать 1 в графу результата. - Перемножить I разряд частного с делителем, записав их произведение под 7: 5*1=5.
- Осуществить операцию разности: 7−5=2.
- Снести II разряд, т. к. 2 на пятерку не делится: 21.
- Поделить 21 на 5 с получением только целой величины: 21/5=4 (записать к частному).
- Перемножить 5 на 4, а затем отнять их произведение от искомой величины: 21−4*5=1.
- Снести следующий разряд, поскольку 1<5: 15.
- Число, полученное на девятом шаге, нацело делится на 5: 15/5=3 (записать в графе результата).
- Снести последний разряд «1», который остается в остатке. Он не делится на 5. В этом случае нужно поставить нуль в графе частного.
- Искомый результат, который получается при делении: 1430 (+1).
После выполнения двенадцатого пункта обязательно требуется произвести проверку. Это делается следующим образом: 1430*5+1=7152+1=7153. Последнюю операцию необходимо осуществлять всегда после выполнения любого математического действия. Для тренировки нужно проходить материал, а затем решать задания.
Для тренировки нужно проходить материал, а затем решать задания.
Таким образом, операция деления двух чисел с остатком выполняется по определенной методике, предложенной советским математиком Виленкиным Н. Я. Чтобы к ней перейти, нужно изучить правила деления двух чисел и основные критерии идентификации величин.
Что такое деление? Определение, формула, шаги, правило, примеры
Допустим, у вас есть 12 пончиков, и вы хотите поровну раздать их трем своим друзьям. Как вы справедливо решаете, сколько получит каждый?
Просто раздели пончики поровну между друзьями! Этот метод распределения группы вещей на равные части называется делением. Это одна из четырех основных арифметических операций, которая дает справедливый результат обмена.
Раздел Определение
Деление противоположно умножению. Если 3 группы по 4 дают при умножении 12, то 12, разделенные на 3 равные группы, дают по 4 в каждой группе при делении.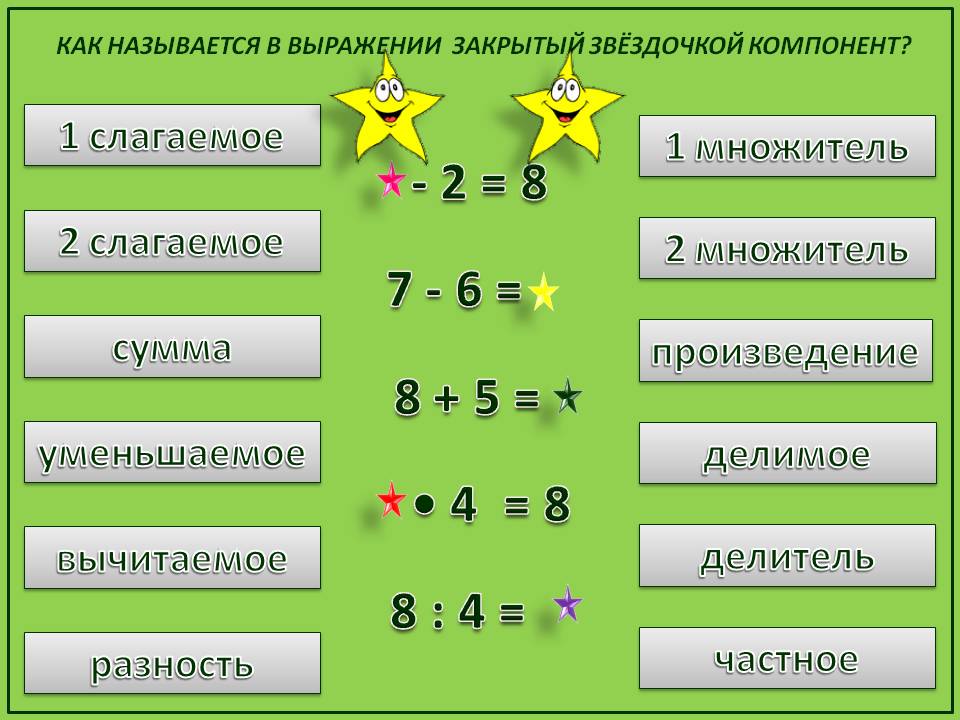
Основная цель деления состоит в том, чтобы увидеть, сколько равных групп образуется или сколько в каждой группе при справедливом разделении.
В приведенном выше примере, чтобы разделить 12 пончиков на 3 одинаковые группы, вам нужно положить по 4 пончика в каждую группу. Таким образом, 12 разделить на 3 даст результат 4.
Математическая запись деления
Существуют различные признаки, которые можно использовать для обозначения дивизии, таких как
- ÷
- /
Например:
- 27 ÷ 3
- 27/3
6620. Числа в уравнении деления
Каждая часть уравнения деления имеет специальное имя.
Дивиденд: Делимое — это число, которое делится в процессе деления.
Делитель: Число, на которое делится делимое, называется делителем.
Частное: Частное — это результат, полученный в процессе деления.
Остаток : Иногда мы не можем точно разделить вещи. Возможно, остался лишний номер. Это оставшееся число называется остатком.
Возможно, остался лишний номер. Это оставшееся число называется остатком.
Отношение между этими четырьмя частями может быть выражено следующим образом:
Дивиденд = Делитель x Частное + Остаток
Это также называется формулой деления для проверки правильности ответа или нет.
Например, давайте разделим 16 на 3. Остаток будет 1.
Здесь делимое = 16, делитель = 3, частное = 5 и остаток = 1
Итак, 16 = 3 × 5 + 1
Свойства деления
Чтобы лучше понять деление, давайте рассмотрим несколько общих правил и свойств деления:
1. Если мы разделим целое число (кроме нуля) само по себе, то в частном или ответе всегда будет 1.
Например:
· 7 ÷ 7 = 1
· 25 ÷ 25 = 1
2. Если разделить целое число на ноль, то ответ будет неопределенным.
Например:
6 ÷ 0 = не определено
325 ÷ 0 = не определено
3. Ноль, разделенный на любое число, даст ответ ноль.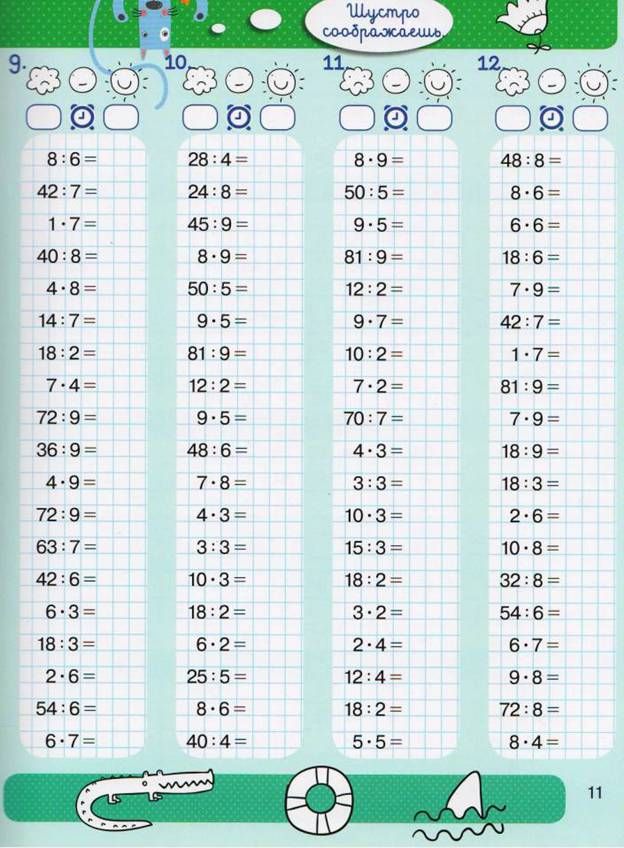
Например:
0 ÷ 5 = 0
0 ÷ 100 = 0
4. Если мы разделим целое число (кроме нуля) на 1, ответом будет само число.
Например:
4 ÷ 1 = 4
11 ÷ 1 = 11
5. Если целое число разделить на другое целое число, частное не обязательно будет целым числом.
Например:
15 ÷ 2 = 7,5
20 ÷ 3 = 6,67
6. В случае точного деления (без остатка) делимым является делитель, умноженный на частное. Это свойство выполняется только в том случае, если все три числа являются целыми числами, отличными от нуля.
Например:
Если 30 ÷ 5 = 6, то 5 × 6 = 30
7. Если есть три ненулевых целых числа a, b и c, и b × c = a, то
a ÷ b = c и a ÷ c = b
Например:
5 × 10 = 50, тогда
· 50 ÷ 5 = 10
· 50÷ 10 = 5
Long Division
7 9000 деление — это математический метод деления больших чисел на более мелкие группы или части. Это помогает разбить проблему на простые и легкие шаги.
Это помогает разбить проблему на простые и легкие шаги.
Длинные шаги деления
Каждое длинное деление можно решить с помощью пяти шагов, указанных ниже.
Вот пример, который поможет вам понять этапы деления.
Давайте рассмотрим несколько примеров деления, чтобы попрактиковаться в длинных шагах деления. Примеры решения себя)
2. Разделение 6148 на 4.
Решение:
С. С. Так, коэффициент = 1537, остаток = 0
3. Разделите 1579 на 6.
Решение:
. Частное = 263, остаток = 1. , R = 0$
Правильный ответ: Q $ = 344 , R = 3$
Частное (целочисленное деление) $1723/5$ равно 344; остаток («остаток») равен 3.
1723 — это делимое, а 5 — делитель.
71
72
73
74
Правильный ответ: 73
Здесь остаток равен 1. Таким образом, если кейтеринг расставляет 72 стола, 1 человек не сможет занять место на свадьбе. Значит, им предстоит расставить 73 стола.
Значит, им предстоит расставить 73 стола.
$\$$2190
$\$$2191
$\$$2192
$\$$2193
Правильный ответ: $\$$2191
Следовательно, каждый получит $\$$2191.
$\$2598
$\$2597
$\$2595
$\$$2594
Правильный ответ: $\$$2594
Следовательно, каждый месяц Гарри зарабатывал $\$$2594.
Часто задаваемые вопросы
Верно ли свойство коммутативности деления?
Коммутативное свойство говорит нам, что если мы можем перемещать или менять местами числа с их позиции при выполнении математических операций, ответ останется прежним.
Это свойство справедливо для умножения и сложения, но не для деления.
Например: 27 × 3 = 3 × 27, но 27 ÷ 3 ≠ 3 ÷ 27
Можно ли разделить путем многократного вычитания?
Да, повторное вычитание — это непрерывное вычитание одного и того же числа из большого числа до тех пор, пока не получится остаток 0 или меньше фактического числа. Разделение — это кратчайший путь к этому процессу.
Разделение — это кратчайший путь к этому процессу.
Есть ли способ проверить частное и остаток в задаче на деление?
Да, вы можете проверить частное и остаток, используя соотношение:
Дивиденд = Делитель x Частное + Остаток
| Интересные факты о делении учим делению в столбик: пошаговый метод В этой статье я объясню, как научить делению в несколько этапов. Вместо того, чтобы показывать студентам весь алгоритм сразу, мы действительно делайте это «шаг за шагом». Перед тем, как ребенок готов к изучению деления в столбик, он должен знать:
Одна из причин, почему деление в длинную затруднительно Длинное деление — это алгоритм, который повторяет основные шаги Из этих шагов № 2 и № 3 могут показаться учащимся трудными и запутанными, потому что похоже, они не связаны с делением — они связаны с нахождением остатка. На самом деле, чтобы указать на это, мне нравится объединять их в одно «умножить и вычесть». шаг. Чтобы избежать путаницы, я рекомендую учить дробное деление в такой мода на то, чтобы дети сначала НЕ подвергались всем этим шагам. Вместо этого вы можете научить этому в несколько «шагов»:
Шаг 1: деление на четное во всех цифрахМы делим числа, у которых каждая из цифр сотен, десятков и единиц делится на делитель без остатка. ЦЕЛЬ этого первого, простого шага состоит в том, чтобы студенты привыкли к двум вещам:
Ниже приведены примеры задач для этого шага. Учащиеся должны проверить каждый
деление умножением.
На этом этапе учащиеся также учатся смотреть на первые две цифры делимого, если делитель не «уходит» в первую цифру:
Ниже приведены другие примеры проблем. Разделять. Проверьте свой ответ по умножение частного и делителя.
Шаг 2: Остаток в единицах Теперь в единицах (единицах) остался остаток.
Далее студенты изучают
на найти
остаток с использованием процесса «умножить и вычесть» . Это
очень важный шаг! Часть «умножить и вычесть» часто очень
сбивает с толку студентов, поэтому здесь мы практикуем это в максимально простом
место: в самом конце раздела, в колонке единиц (вместо
в колонке десятков или сотен). В проблемах раньше вы просто записали остальные. Обычно мы записываем вычитание, которое фактически находит остаток. Смотри внимательно:
Вот несколько примеров проблем. Сейчас учащиеся проверяют ответ, умножая делитель на частное, а затем добавить остаток.
Шаг 3: Остаток в десяткахНа этом этапе учащиеся впервые отрабатывают все основные шаги. алгоритма длинного деления: разделить, умножить и вычесть, выпадающий список следующая цифра. Мы используем двузначные числа для простоты. Умножить & вычитание связано с нахождением остатка, а после нахождения остаток, мы объединяем это со следующим блоком, который мы готовим разделить (опустить цифру вниз). Пример:
Шаг 4: Остаток в любом разряде значенийПосле освоения предыдущего шага учащиеся долго практикуются. деление с трех- и четырехзначными номерами, куда они должны будут попасть через основные шаги несколько раз.
Эти идеи также объясняются в видео на YouTube ниже:
Почему работает длинное делениеЯ чувствую, что алгоритм деления в длину И то, почему он работает, представляет собой довольно сложную вещь для изучения учащимися, поэтому в этом случае я не вижу проблемы в том, чтобы учащиеся сначала изучали алгоритмические шаги («как»), а затем углублялись в «почему». Попытка сделать и то, и другое одновременно может оказаться для некоторых слишком сложным. Однако, как только учащийся освоит как выполнять деление в большую сторону, настало время также изучить, на чем оно основано. Чтобы узнать больше об этом, см.: Длинное деление как многократное вычитание Почему работает длинное деление (на основе многократного вычитания) Рабочие листы Рабочие листы с длинным делением |
Как делать деление в длинное число: простое пошаговое руководство с иллюстрациями
Вы провели свой класс через большинство больших единиц: сложение, деление, вычитание, умножение. Но вот еще одна хитрость:
Как выполнить деление в большую сторону.
Исследование 2012 года, опубликованное в Psychological Science, показало, что понимание пятиклассниками дробей и деления может быть напрямую связано с тем, насколько хорошо они понимают алгебру в старшей школе и успевают ли они на уроках математики более высокого уровня — даже после учета различных социально-экономических факторы. Никакого давления, верно? Если при мысли об обучении делению на длинные лады у вас холодный пот и липкие ладони, не беспокойтесь — мы сделали всю работу за вас.
Как выполнить деление в большую сторону за шесть шагов1.
 Повторить
ПовторитьПервый шаг, который вам следует сделать, это шаг назад.
Для ученика 4-го класса деление в большую сторону представляет собой сложную смесь различных операций. Чтобы успешно научиться выполнять деление в большую сторону, им необходимо повторить эти фундаментальные понятия.
Согласно французскому исследованию, «представление и извлечение математических фактов из долговременной памяти» является одним из наиболее важных факторов, определяющих будущие успехи учащегося в математике. Согласно тому же исследованию, длинное деление — это «синтез всех арифметических знаний».
Убедитесь, что ваши ученики понимают, что умножение — это результат многократного сложения, а деление — это просто противоположное — многократное вычитание.
Используйте блоки с основанием 10 или деньги, чтобы усилить значение места и чувство числа. Запланируйте занятия, в которых учащимся будет предложено создать «семейство фактов», чтобы убедиться, что учащиеся понимают, как взаимодействуют различные функции.
Используйте игры на умножение и другие математические игры, чтобы заинтересовать учащихся в учебе и развить уверенность в математике, прежде чем продолжить.
2. Начните с простогоДавайте начнем с урока словарного запаса. Уравнение деления на деление состоит из множества частей. Убедитесь, что ваши ученики знают, что они имеют в виду и как их идентифицировать.
Дивиденд — это число в правой части уравнения под чертой. Он представляет собой сумму, которую нужно разделить.
Делитель — это число слева — оно выполняет деление.
Частное — номер сверху. Он представляет собой ответ или количество единиц в каждом разряде после завершения уравнения.
Остаток — это число вверху справа. Он представляет оставшиеся единицы, которые не могут быть равномерно разделены на частное. Во-первых, введите уравнение, которое не имеет остатков, чтобы учащиеся могли привыкнуть к формату и начать понимать новый словарный запас, который они только что выучили:
Спросите учащихся, сколько раз 2 умещается в 4. Это может показаться им сложной концепцией, поэтому используйте идею обмена: если вы хотите разделить 4 предмета между двумя людьми, сколько предметов получит каждый?
Это может показаться им сложной концепцией, поэтому используйте идею обмена: если вы хотите разделить 4 предмета между двумя людьми, сколько предметов получит каждый?
Как только они придут к правильному ответу, поставьте 2 выше 4. Затем повторите шаг со второй цифрой в делимом.
Используйте эти простые уравнения, чтобы усилить позиционное значение. Объясните учащимся, что, когда они спрашивают, сколько раз 2 может превратиться в 4, на самом деле они спрашивают, сколько раз 2 превращается в 40. они удобны с основным форматом. Тогда пришло время двигаться дальше.
Вместо того, чтобы сразу перейти к уравнению с остатками, начните с другого предметного урока . Разделите учащихся на группы по три, четыре или шесть человек и дайте каждой группе по 50 ватных шариков (или мармеладок, или помпонов, или зефира — любой маленький предмет, доступный в вашем классе).
Попросите учеников разделить предметы так, чтобы у каждого члена группы было одинаковое количество предметов, а затем наблюдайте и ждите.
В конце концов, они поймут, что не могут разделить его поровну, и всегда будут оставаться какие-то предметы. Вот где вы приходите, чтобы спасти положение и объяснить, как выполнить деление в большую сторону с помощью 9.0041 осталось .
Сначала покажите учащимся задачу с остатком в единицах:
Теперь начните со столбца десятков и проработайте задачу: 5 входит в 5 ровно один раз, так что там ничего не осталось. Но сколько раз 5 входит в 7, и что вы делаете с остатками?
Покажите учащимся новые шаги:
- Разделить столбец единиц делимое на делитель
- Умножить делитель на частное в нужном месте столбец
- Вычтите произведение из столбца единиц
Оставшееся число — это остаток. Обязательно смоделируйте несколько задач всем классом, чтобы учащиеся могли начать понимать этапы и то, как правильно записывать свои ответы.
Это хорошее время на уроке, чтобы научить учащихся проверять свои ответы.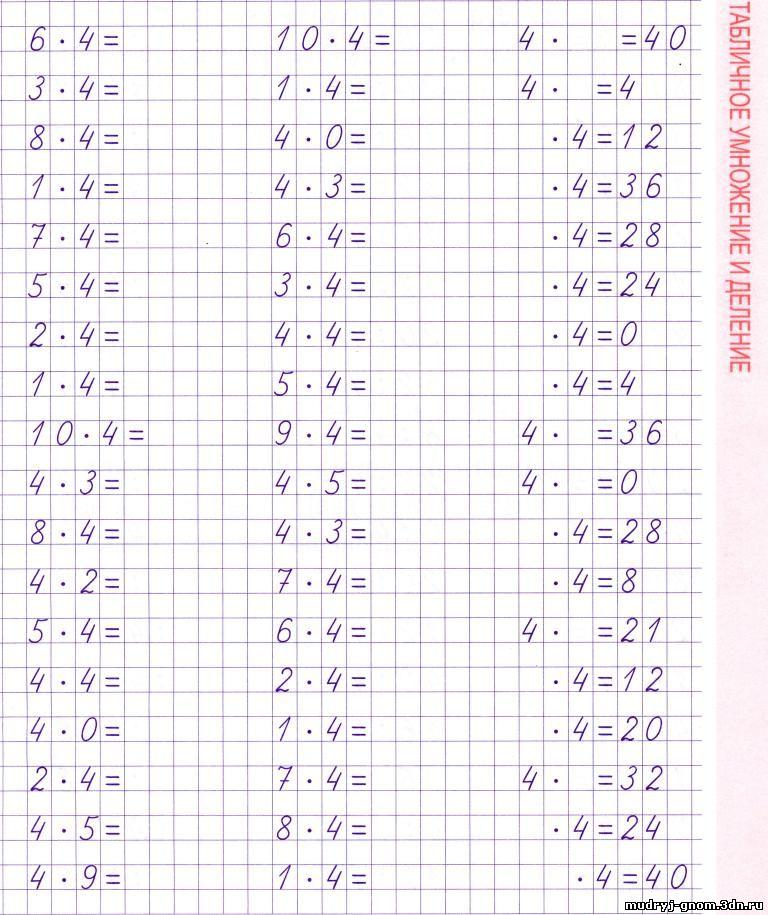 Пусть они умножат делитель на частное и прибавят остаток — ответ должен быть таким же, как и делимое, с которого они начали.
Пусть они умножат делитель на частное и прибавят остаток — ответ должен быть таким же, как и делимое, с которого они начали.
Теперь пришло время учащимся решить задачи, в которых делитель не помещается точно в столбец десятков или единиц. Шаги почти такие же, за исключением одного нового дополнения:
- Разделить делимое в столбце десятков на делитель
- Умножить делитель на частное в столбце десятков
- Вычесть произведение из делителя
- Сократите делимое в столбце единиц и повторить .
Для простоты начните с однозначных делителей и двузначных дивидендов. Помните, что это совершенно новая концепция для учащихся, поэтому найдите время, чтобы смоделировать задачи на доске. Обсудите, почему эти шаги работают, и помогите им понять, какую важную роль в этом процессе играет значение места.
5. Постепенно вводите большие числа Вот и все. Или это?
Или это?
Дайте учащимся освоиться с формулой и поработать над более мелкими задачами. Когда они обретут уверенность и начнут понимать, как выполнять деление в большую сторону, начните предлагать им задачи с трехзначным делимым, а затем задачи с двузначным делителем.
Напомните учащимся, что шаги остаются одинаковыми, независимо от того, насколько велика задача , и предложите им использовать лист бумаги, чтобы «угадать и проверить» свое умножение по ходу дела. Это хороший момент, чтобы убедиться, что у них нет проблем и что они полностью понимают взаимосвязь деления с разрядным значением и умножением.
Посмотрите это видео от Khan Academy:
0042 Если вы рассмотрели весь свой контент на первых пяти шагах, поздравляем! Предложите учащимся продолжать практиковаться в делении больших и малых чисел в длинную и укреплять связь между делением и другими математическими понятиями, которые они изучают. Но процесс еще не завершен — учащиеся должны понять, как делать длинную деление с десятичной дробью.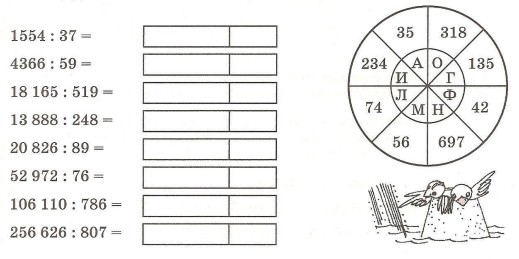 Для начала вернемся к одному из фундаментальных понятий деления: разрядному значению. Однако на этот раз вы будете двигаться назад, а не вперед.
Для начала вернемся к одному из фундаментальных понятий деления: разрядному значению. Однако на этот раз вы будете двигаться назад, а не вперед.
Предложите учащимся решить задачу, как обычно. Когда они дойдут до шага, на котором они обычно останавливаются с остатком, попросите их поставить десятичную точку в конце частного и делимого и написать несколько нулей после делимого.
Предложите им продолжить обычные шаги деления на один или два разряда, опуская нули.
Соедините десятичную дробь с дробью. Попросите их преобразовать частное с десятичной дробью в неправильную дробь. Это должно помочь им понять взаимосвязь между дробями и разрядным значением и может стать хорошей возможностью изучить основы дробей.
Как выполнить деление в длинное число (без деления в длинное число)Поздравляем! Ваш модуль подходит к концу, и вы успешно научили своих учеников выполнять деление в большую сторону.
Но знаете ли вы, что существует несколько способов деления больших чисел? Обучение учащихся другим способам проверки своей работы является важной частью математических стандартов Common Core и может улучшить понимание учащимися того, что на самом деле означает деление в столбцах в данном контексте.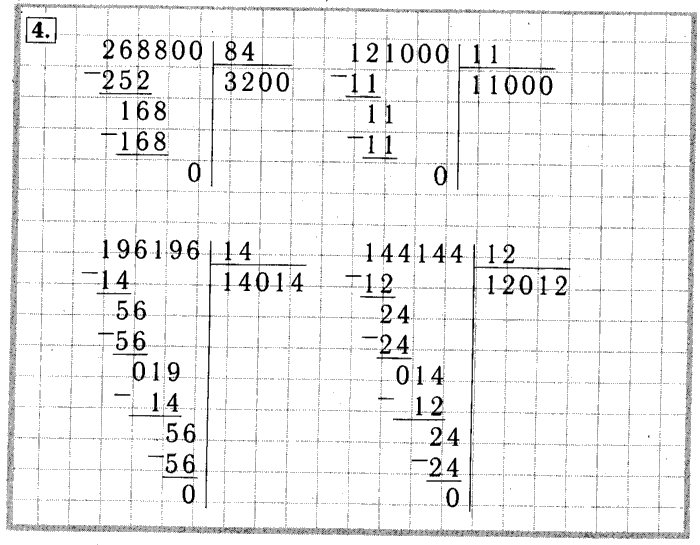
Плоскостные модели — отличный способ для визуалов понять и осмыслить деление, а также улучшить чувство числа.
Этот метод использует сетку, чтобы представить процесс деления как задачу площади: например, 148÷4 будет разделен на сетку высотой 4 единицы, площадью 148 квадратных единиц и неизвестным количеством единиц ширины.
Учащиеся разбивают сетку на более удобные области: 100 квадратных единиц, 40 квадратных единиц и 8 квадратных единиц. 100÷4 равно 25, 40÷4 равно 10, а 8÷4 равно 2. Эти числа идут вверху модели области и могут быть сложены, чтобы получить ответ.
Частичное частноеПодобно модели области, частичное частное побуждает учащихся разбивать вопросы на деление на «более понятные» части. Это помогает учащимся понять, что деление — это нахождение того, сколько раз одно число может перейти в другое число.
Поставьте задачу (в данном случае 450÷23) как уравнение деления на деление. Попросите учащихся умножить делитель на 2 и 5, чтобы использовать его в качестве удобного ориентира.
Попросите учащихся умножить делитель на 2 и 5, чтобы использовать его в качестве удобного ориентира.
Спросите, сколько раз 23 входит в число 400, но не ищите точное ближайшее число: сделайте его простым для работы, например, 230 (десять раз). Вычтите 230 из 450 и поставьте 10 справа, чтобы отслеживать результат.
Возьмите разницу и вычтите ее из делимого. Ответ должен быть 220.
Спросите, сколько раз 23 входит в 220. 5 x 23 равно 115, так что вычтите это из 220 и запишите 5.
Продолжайте, умножая и вычитая, пока окончательное число не станет слишком маленьким. Когда вы достигли этого шага, вы нашли остаток! Сложите числа в правом столбце, чтобы найти частное.
Частичные частные обладают гибкостью, которой нет в длинном делении. Длинное деление нужно делать точно, но с частичными частными можно просто несколько раз вычесть делитель из делимого и все равно прийти к правильному ответу.
Используйте этот метод, чтобы закрепить позиционное значение и концепцию деления как многократного вычитания.
Лучший способ научиться делению в длинное число – практиковаться, практиковаться и еще раз практиковаться.
Вот список из восьми заданий, которые заинтересуют ваш класс делением в длинную и помогут развить прочные математические навыки.
1. ProdigyProdigy — это забавный и увлекательный ресурс для занятий на длинном дивизионе в классе или дома. Учащиеся исследуют мир, полный приключений, где успех зависит от правильных ответов на математические вопросы.
С помощью панели управления учителя вы можете предоставлять контент, ориентированный на урок, в зависимости от оценки, навыков или ученика. Затем учащиеся отвечают на эти вопросы в игре и предоставляют вам обратную связь в режиме реального времени о своем обучении и понимании .
Поощряйте своих учеников практиковать все математические навыки, которые они изучили в классе, включая деление в столбик. Вот как вы можете использовать Prodigy для:
Вот как вы можете использовать Prodigy для:
- усиления уроков в классе
- разнообразия материалов по математике
- Проведение формирующего оценивания
Учащиеся играют в увлекательную игровую платформу, где они могут собирать питомцев, выполнять квесты и сражаться с друзьями. И пока они развлекаются, вы помогаете им развивать навыки длинного деления. Это победа для всех!
Зарегистрируйтесь сейчас 2. Деление в натуральную величинуОживите математику с помощью практической головоломки с делением в длину. Вырежьте квадраты из цветной бумаги со всеми числами, которые нужны учащимся для решения задачи на деление в длину от начала до конца. Используйте клейкую ленту, чтобы разделить линии на полу, и раздайте учащимся пронумерованные карточки.
Начав с заданного уравнения, попросите учащихся разложить все карточки в правильном порядке, чтобы решить уравнение. Это задание побуждает учащихся замедлиться и подумать о своих шагах, и это особенно полезно для класса, который все еще хочет освоить шаги умножения.
Бинго является классикой не просто так. Каждая из цифр в листе учащегося должна соответствовать вопросу, который вы задали перед классом. Напишите задачу на доске, а затем дайте учащимся черновик и возможность решить ее и посмотреть, есть ли она у них на карточках. Как всегда, побеждает тот, кто первым заполнит весь ряд!
Бросьте вызов своим учащимся, но убедитесь, что вы уделяете этому упражнению достаточно времени — некоторые учащиеся могут испытывать трудности с быстрым решением задач и могут расстраиваться или совершать ошибки, если не смогут справиться с заданием.
4. Книги по математике Повысьте уровень грамотности и обучения математике с помощью забавных книг, посвященных сложным математическим понятиям. Используйте их, чтобы объяснить учащимся деление и остатки в веселой и увлекательной форме и даже охватить более основные понятия, прежде чем они начнут учиться выполнять деление в столбик.
Some math books that cover division include:
- A Remainder of One by Elinor J. Pinczes
- Bean Thirteen by Matthew McElligott
- The Doorbell Rang by Pat Hutchins
5. Get creative
В длинном делении много шагов, и их нужно выполнять в правильном порядке, чтобы получить правильный ответ. Учащиеся могут запутаться или расстроиться, если не помнят шагов, что отрицательно сказывается на их уверенности в математике и успеваемости.
Предложите учащимся придумать свой собственный уникальный способ запомнить, как выполнять деление в большую сторону — разделить , умножить , вычесть и свести — чтобы стимулировать творчество в вашем классе.
Предложите им создать постер, песню, мнемоническое устройство или даже небольшую сценку, которую они могут представить своим одноклассникам. Если они заинтересованы в том, чтобы найти способ запомнить шаги, они, скорее всего, быстро научатся.
Превратите практику длинных дивизий в веселую классную игру с эстафетами длинных дивизий. Разделите свой класс на команды и сделайте карточки с задачами на деление в длину.
Объедините учеников в группы. Каждая группа получает карточку для начала, и первые учащиеся выполняют первый набор шагов для своей проблемы.
Когда они закончат, второй учащийся ищет ошибки и продолжает решать задачу. Если они решат задачу, они могут позвонить вам, чтобы проверить их работу и обменять правильный ответ на карточку с новой задачей.
Продолжайте, пока каждая группа не ответит на все свои карточки, и посмотрите, какая команда победит!
7. Сундук с сокровищами
Это задание — веселый способ для вашего класса отпраздновать завершение отряда в дивизионе. Возьмите несколько коробок и наполните их небольшим угощением, которое понравится всем в классе. Включите список задач на умножение, которые учащиеся должны решить в группах, чтобы «открыть» коробку.
В качестве дополнительной задачи сделайте это кодом: пусть каждое частное соответствует букве алфавита, чтобы учащиеся должны были правильно расшифровать ключевую фразу, чтобы открыть коробку.
8. Генератор рабочих листовРабочие листы — это проверенный материал на уроках математики. К счастью для вас, существует множество веб-сайтов, которые сделают всю работу за вас и сгенерируют пользовательский рабочий лист, который даст вашим ученикам возможность практиковаться в делении в большую сторону. Вот некоторые из наших любимых:
- Помощь с математикой
- Пособия по математике
- Гениальный рабочий лист
Самое важное, что следует помнить при обучении студентов делению в столбик, это не торопиться с изучением материала. Это большая концепция, которая отличается от всего, что они изучали раньше, и некоторые (если не все) ваши ученики поначалу могут испытывать затруднения.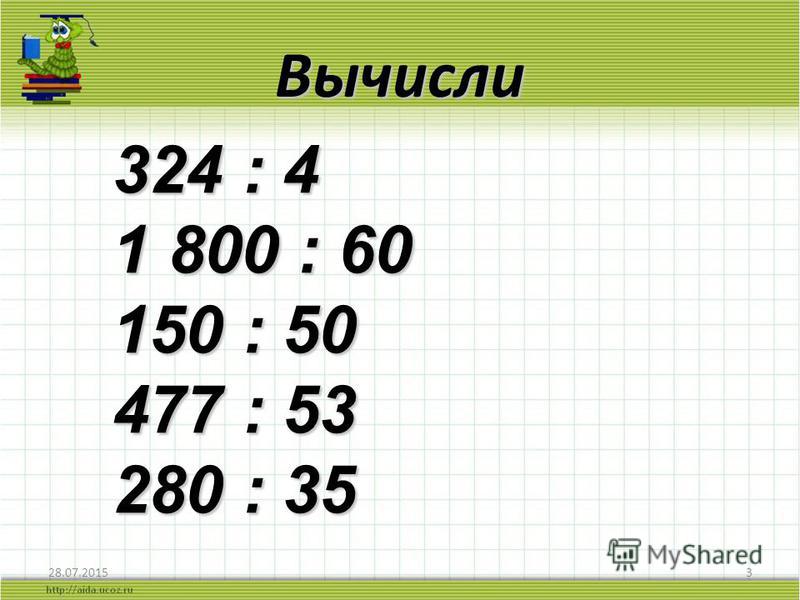 Если вам нужно, вернитесь к более простым уравнениям и некоторым из предыдущих шагов, которые мы описали. для вас и работайте над ними, пока ваши ученики не почувствуют себя уверенно. Продолжайте поощрять и бросать вызов своим ученикам, и они будут готовы разделять и властвовать в кратчайшие сроки!
Если вам нужно, вернитесь к более простым уравнениям и некоторым из предыдущих шагов, которые мы описали. для вас и работайте над ними, пока ваши ученики не почувствуют себя уверенно. Продолжайте поощрять и бросать вызов своим ученикам, и они будут готовы разделять и властвовать в кратчайшие сроки!
Создайте или войдите в свою бесплатную учетную запись учителя в Prodigy – игровой платформе для обучения математике, которую легко использовать как преподавателям, так и учащимся. Он соответствует учебным программам англоязычного мира и используется миллионами учителей и учащихся .
Зарегистрируйтесь сейчасРаздел: Целые числа
Разделение это математическая операция, записанная с помощью символа
÷
, это можно рассматривать двумя способами:
а
÷
б
размер каждой группы, когда
а
объекты делятся на
б
группы одинакового размера, ИЛИ
а
÷
б
это количество групп, когда
а
объекты разбиты на группы
б
объекты каждый.
Например, 20 ÷ 4 можно найти, разделив 20 точки в 4 группы одинакового размера.
Мы находим, что каждая из четырех групп содержит 5 точки, так 20 ÷ 4 знак равно 5 .
В качестве альтернативы мы можем найти 20 ÷ 4 путем формирования групп 4 точки каждая, а затем подсчет количества групп:
Есть 5 группы.
Дивизия – это обратная операция умножения. То есть,
а ÷ б знак равно с если и только если с × б знак равно а .
Здесь
а
называется дивиденд ,
б
называется делитель , а также
с
(результат) называется частное .
Разделение по 0 не определено; чтобы понять почему, замените б знак равно 0 в приведенных выше уравнениях. С с × 0 знак равно 0 независимо от того, какое значение с , так а также должен быть равен 0 ; и если а а также б оба 0 , с может равняться чему угодно!
Деление на целые числа может привести к остатку. Например, если мы разделим 20 ÷ 6 путем деления 20 на группы 6 , мы получаем 3 группы с 2 осталось:
Иногда мы пишем 20 ÷ 6 знак равно 3 р 2 , куда 2 это остаток .
Или мы можем записать один числовой ответ в виде
дробная часть
или десятичное.
Длинный дивизион
Чтобы разделить многозначное число на однозначное, мы можем использовать длинное деление.
Пример 1:
Разделять. 496 ÷ 8
Поместите делимое внутри символа деления, а делитель снаружи символа деления.
8 496
Здесь, 8 не может содержаться в 4 , так что рассмотрим и следующую цифру. Есть 6 восьмерки в 49 , так что пиши 6 в десятках частного.
Умножить 6 на делитель 8 и вычесть.
6 8 49 6 48 _ 1
Теперь снова
8
не может содержаться в
1
, поэтому опустите следующую цифру
6
.
6 8 49 6 48 _ 16
Там 2 восьмерки в 16 , так что пиши 2 на тех местах.
Умножить 2 на делитель 8 и вычесть.
6 2 8 496 48 _ 16 16 _ 0
Чтобы разделить многозначное число на многозначное число, процесс аналогичен.
Пример 2:
Разделять 1036 по 32 . Поместите делимое внутри символа деления, а делитель снаружи символа деления.
32 1036
Здесь, 32 не может содержаться в 1 , рассмотрим следующую цифру, еще 32 не может содержаться в 10 . Итак, рассмотрим также следующую цифру. Есть 3 тридцать два в 103 , так что пиши 3 в десятках частного.
Умножить 3 на делитель 32 и вычесть.
3 32 103 6 96 _ 7
Теперь снова
32
не может содержаться в
7
, поэтому опустите следующую цифру
6
.
3 32 1036 96 _ 76
Там
2
тридцать два в
76
, так что пиши
2
на тех местах.
Умножить 2 на делитель 32 и вычесть.
Вот и остаток 12 .
3 2 32 103 6 96 _ 76 64 _ 12
В отличие от сложения и умножения, для
вещественные числа
, операция деления нет коммутативный
. То есть порядок имеет значение:
40
÷
8
знак равно
5
, но
8
÷
40
знак равно
1
5
(дробное значение).
То есть порядок имеет значение:
40
÷
8
знак равно
5
, но
8
÷
40
знак равно
1
5
(дробное значение).
Точно так же деление нет ассоциативный ; то есть группировка имеет значение. Например,
( 80 ÷ 10 ) ÷ 2 знак равно 8 ÷ 2 знак равно 4 , но
80 ÷ ( 10 ÷ 2 ) знак равно 80 ÷ 5 знак равно 16 .
Длинное полиномиальное деление: Примеры | Purplemath
SimplificationLong Division
Purplemath
В отличие от примеров на предыдущей странице, почти все полиномиальные деления не «выходят четными»; обычно у вас остается остаток.
Я начну с деления деления:
Глядя только на первые члены, я делю 3 x 3 на 3 x , чтобы получить x 2 . This is what I put on top:
Content Continues Below
MathHelp.com
I multiply this x 2 by the 3 x + 1 to get 3 x 3 + 1 x 2 , который я поставил под:
Затем я меняю знаки, добавляю вниз и не забываю нести «+10 9».0173 x — 3″ от исходного делимого, что дает мне новую нижнюю строку −6 x 2 + 10 x — 3:
Деление нового старшего члена, -6 x
Затем я умножаю -2 x на 3 x + 1, чтобы получить -6 x 2 − 2 x , которое я положил под ним. Я меняю знаки, прибавляю и не забываю брать «-3» из делимого:
Моя новая последняя строка: «12 x — 3. Разделив новый старший член 12 x на старший член делителя 3 x , я получаю +4, который я помещаю сверху. Я умножаю 4 на 3 x + 1, чтобы получить 12 x + 4. Я меняю знаки и прибавляю вниз. В итоге получается остаток −7:
Разделив новый старший член 12 x на старший член делителя 3 x , я получаю +4, который я помещаю сверху. Я умножаю 4 на 3 x + 1, чтобы получить 12 x + 4. Я меняю знаки и прибавляю вниз. В итоге получается остаток −7:
Это деление не получилось четным. Что мне делать с остаток?
Вспомните, когда вы делили простые числа в длинное, иногда оставался остаток, например, если вы делите 132 на 5:
…осталось 2. Помните, как вы с этим справились? Вы составили дробь, положив остаток на вершину делителя, и записали ответ как «двадцать шесть и две пятых»:
Первая форма без «плюса» в середине — это как «смешанные числа» пишутся, но смысл смешанного числа — это на самом деле форма с добавлением.
То же самое делаем с полиномиальным делением. Поскольку остаток в этом случае равен −7, а делитель равен 3 x + 1, затем я превращу остаток в дробь (остаток, разделенный на исходный делитель) и добавлю эту дробь к многочлену в верхней части символа деления. Тогда мой ответ таков:
Тогда мой ответ таков:
Предупреждение: , а не запишите полиномиальное «смешанное число» в том же формате, что и числовые смешанные числа! Если вы просто добавите дробную часть к полиномиальной части, это будет интерпретировано как полиномиальное умножение, то есть , а не 9.0174 что ты имеешь в виду!
Примечание. В разных книгах длинный раздел форматируется по-разному. При написании выражений в верхней части раздела в некоторых книгах термины помещаются над термином той же степени, а не над термином, над которым ведется работа. В таком тексте длинное деление выше будет представлено, как показано здесь:
Единственное отличие состоит в том, что термины сверху смещены вправо. В остальном все точно так же; в частности, все вычисления точно такие же. Если вы сомневаетесь, используйте форматирование, которое использует ваш преподаватель.
Вам может быть интересно, как я понял, что надо остановиться, когда дошел до -7 остатка. Это очень похоже на то, как вы знали, когда остановиться при делении в большую сторону (до того, как вы узнали о десятичных разрядах). Как только вы добрались до чего-то, на что делитель был слишком велик, чтобы разделить его, вы зашли так далеко, как только могли, поэтому остановились; все, что осталось, если что, было вашим остатком. То же самое касается полиномиального длинного деления. −7 — это просто постоянный член; 3 x «слишком велико», чтобы войти в него, точно так же, как 5 было «слишком велико», чтобы войти в 2 в приведенном выше примере числового длинного деления. Как только вы получите остаток, который «меньше» (в полиномиальной степени), чем делитель, все готово.
Это очень похоже на то, как вы знали, когда остановиться при делении в большую сторону (до того, как вы узнали о десятичных разрядах). Как только вы добрались до чего-то, на что делитель был слишком велик, чтобы разделить его, вы зашли так далеко, как только могли, поэтому остановились; все, что осталось, если что, было вашим остатком. То же самое касается полиномиального длинного деления. −7 — это просто постоянный член; 3 x «слишком велико», чтобы войти в него, точно так же, как 5 было «слишком велико», чтобы войти в 2 в приведенном выше примере числового длинного деления. Как только вы получите остаток, который «меньше» (в полиномиальной степени), чем делитель, все готово.
Прежде всего отмечу, что в степенях членов делимого имеется разрыв: многочлен 2 x 3 − 9 x 2 + 15 не имеет члена x . Моя работа может усложниться внутри символа деления, поэтому важно, чтобы я на всякий случай оставил место для столбца терминов размером x . (Это похоже на ноль, скажем, в разряде сотен делимого, удерживая этот столбец открытым для вычитания под символом длинного деления.) Я могу создать это пространство, превратив делимое в 2 x 3 − 9 x 2 + 0 x + 15.
(Это похоже на ноль, скажем, в разряде сотен делимого, удерживая этот столбец открытым для вычитания под символом длинного деления.) Я могу создать это пространство, превратив делимое в 2 x 3 − 9 x 2 + 0 x + 15.
чего угодно.)
Теперь, когда у меня есть все «комнаты», которые мне могут понадобиться для работы, я займусь делением. Я начинаю, как обычно, с деления деления в длину:
Разделив 2 x 3 на 2 x , я получаю x 2 , поэтому я помещаю это сверху. Затем я умножаю x 2 на 2 x − 5, чтобы получить 2 x 3 − 5 x 2 , которое я поместил ниже. Затем я меняю знаки, прибавляю и переношу 0 x + 15 от исходного делимого. Это дает мне -4 x 2 + 0 x + 15 в качестве моей новой итоговой строки:
Деление -4 x 2 на 2 x , 01 получается наношу сверху. Умножая это -2 x на 2 x − 5, я получаю −4 x 2 + 10 x , которые я помещаю ниже. Затем я меняю знаки, прибавляю и опускаю +15 от предыдущего делимого. Это дает мне -10 x + 15 в качестве моей новой итоговой строки:
Умножая это -2 x на 2 x − 5, я получаю −4 x 2 + 10 x , которые я помещаю ниже. Затем я меняю знаки, прибавляю и опускаю +15 от предыдущего делимого. Это дает мне -10 x + 15 в качестве моей новой итоговой строки:
Разделив -10 x на 2 x , я получаю -5, которое я помещаю сверху. Умножив −5 на 2 x — 5, я получаю 10 x + 25, которые я помещаю ниже. Затем я меняю знаки и прибавляю, что дает мне остаток −10: 9.0003
Мне нужно запомнить к добавить остаток к полиномиальной части ответа:
Сначала я переставлю делимое, поэтому члены записываются в обычном порядке:
4 x 4 + 3 x 3 + 2 x + 1
Я заметил, что в делимом нет члена x 2 , поэтому я создам его, добавив 2 срок на дивиденд (внутри символа деления), чтобы освободить место для моей работы.
Тогда я сделаю деление в обычном порядке. Разделив 4 x 4 на x 2 , я получаю 4 x 2 , которые я положил сверху. Затем я умножаю и так далее, приводя к новой нижней строке:
Разделив — x 3 на x 2 , я получаю — x , которое я помещаю сверху. Затем я умножаю и т. д. и т. д.:
Деление −7 x 2 на x 2 , я получаю −7, которую ставлю сверху. Затем я умножаю на и т. д. и т. д.:
И затем я закончил деление, потому что остаток линейный (11 x + 15), а делитель квадратичный. Квадратичный не может делиться на линейный многочлен, поэтому я зашел так далеко, как только мог.
Тогда мой ответ:
Чтобы добиться успеха в многочленном длинном делении, вам нужно писать аккуратно, не забывать менять знаки при вычитании и работать осторожно, сохраняя правильное расположение столбцов. Если вы делаете это, то эти упражнения не должны быть очень тяжелыми; раздражает, может быть, но не сильно.
Если вы делаете это, то эти упражнения не должны быть очень тяжелыми; раздражает, может быть, но не сильно.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в нахождении деления на длинные полиномы. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Разделить с использованием длинного полиномиального деления», чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите файлы cookie «предпочтения», чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Страница 1 Страница 2
URL: https://www.purplemath.com/modules/polydiv3.htm
Как делить числа
Домашний
Узнать
Базовая математика
- Дополнение
- Вычитание
- Умножение
- Отдел
- Целые числа
- Натуральные числа
- Четный нечетный
множители и множители Ссылки
Предварительная алгебра Ссылки
Вычитание определенного количества объектов снова и снова — это деление.
Примечание:
- Деление обозначается знаком «÷».
- Результат выражается знаком «=».
- С помощью таблиц мы можем выполнять деление без вычитания объектов.
Пример
Если есть 10 шоколадок. Сколько групп можно составить из этих 10 конфет с поровну в каждой группе?
5 групп по 2 шоколадки в каждойОбъяснение :
Сначала уберём 2 шоколадки из 10. Остаётся 8 шоколадок.
Теперь, когда мы уберем 2 шоколадки из 8, останется 6 шоколадок.
Когда из 6 уберём 2 шоколадки, останется 4 шоколадки.
Из оставшихся 4, когда мы уберем 2 шоколадки, останется 2 шоколадки.
Когда мы удаляем группу из 2 в пятый раз, конфет не остается.
Получаем 5 таких групп по 2 шоколадки в каждой.
Таким образом, мы можем сказать, что 10÷2= 5
Таблицы сообщают нам результат во сколько раз число.
Если мы скажем, что 2 × 5 = 10. Это означает, что для получения 10 в качестве произведения скажем таблицу от 2 до 10, получаем 5.
Так что 10 ÷ 2= 5.
Примечание:
Делимое число и есть делимое. Число, на которое мы делим, и есть делитель.
Если 8 ÷ 2 = 4. Здесь делимое равно 8, делитель 2, частное 4 и остаток 0.
Простой пример
Раздел: задачи Word
Пример 1:
Пример 2:
В книге 64 страницы. Элизабет читает по 2 страницы каждый день. За сколько дней она завершит
книга?
Элизабет читает по 2 страницы каждый день. За сколько дней она завершит
книга?
Элизабет заканчивает книгу за 32 дня.
Объяснение :
Чтобы найти количество дней для завершения книги, нужно разделить 64 на 2.
64 ÷ 2 = Сколько?
Чтобы разделить, сначала посмотрите на цифру слева в делимом. Скажи 2 раза
стол до 6.
Две тройки шесть. Произведение 3 и 2 равно 6. Вычтите это произведение из 6 T.
Осталось ноль десятков.
Запишите цифру 3 над чертой в разряде десятков делимого.
Запишите 4 единицы перед 0. Разделите 4 единицы на 2. Произнесите таблицу умножения на 2.
до 4.
Частное равно 2. Произведение 2 на 2 равно 4. Вычтите это произведение из 4 U.
Осталось ноль десятков.
Остаток 0,
Частное равно 32.
Таким образом, 64 ÷ 2 = 32.
Простой пример
Раздел: задачи Word
3876 рубашек расставлены на 17 полках. Если на каждом лежит одинаковое количество рубашек. полка, сколько рубашек на каждой полке?
На каждой полке 228 рубашек.
Объяснение :
Чтобы найти количество рубашек на каждой полке, разделите 3876 на 17.
Чтобы разделить, сначала посмотрите на разряд тысяч в делимом. что 3.
3 меньше делителя 17. 3 нельзя разделить на 17. Возьмите 38, чтобы разделить на
17.
Разделите 38 на 17. Вычтите 34 из 38. Частное равно 2. Остаток равен 4.
Запишите 7 десятков перед 4. Разделите 47 на 17. Вычтите 34 из 47.
Частное равно 2. Остаток равен 13.
Запишите 6 единиц перед 13. Разделите 136 единиц на 17.
Произнесите таблицу умножения на 17 до 136.
Частное равно 8.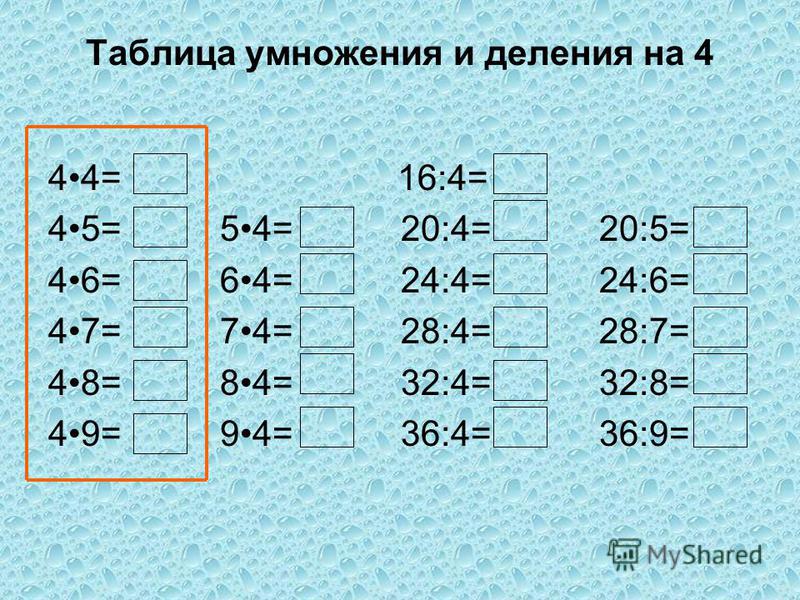 Вычтите это произведение из 136 U. Остаток 0,
Вычтите это произведение из 136 U. Остаток 0,
.
Частное равно 228.
Следовательно, 3876 ÷ 17 = 228
Набор фактов, связанных с делением, составляет семейство фактов.
- Скажем, 35 ÷ 7. Получим 5.
- А также 35 ÷ 5. Получим 7.
- Таким образом, 5,7 и 35 составляют фактическую семью.
Что нужно помнить
Деление на 1
Если мы разделим любое число на 1, мы получим само число.
Допустим, 78 ÷ 1. Получится 78.
Советы
- Мы всегда должны начинать делить числа с первого места заданного числа.

- Порядок деления некоторого числа: тысячи, сотни, десятки… и так далее…
- При делении любого числа делитель должен быть меньше числа делимого.
- Каждый раз вычитайте произведение из числа делимого, а затем берите следующее число, пока все число не закончилось.
- Частное всегда пишется над чертой, а произведение — под числом делимого.
Подумай
- Ручки стоят 60, а сколько тогда стоит каждая ручка?
- Если 20 000 ÷ 20 = 1000, чему равно 20 000 ÷ 200?
- У Рупы 55 шоколадок. Она хочет раздать их своим друзьям как каждому другу
можно получить 5 шоколадок.



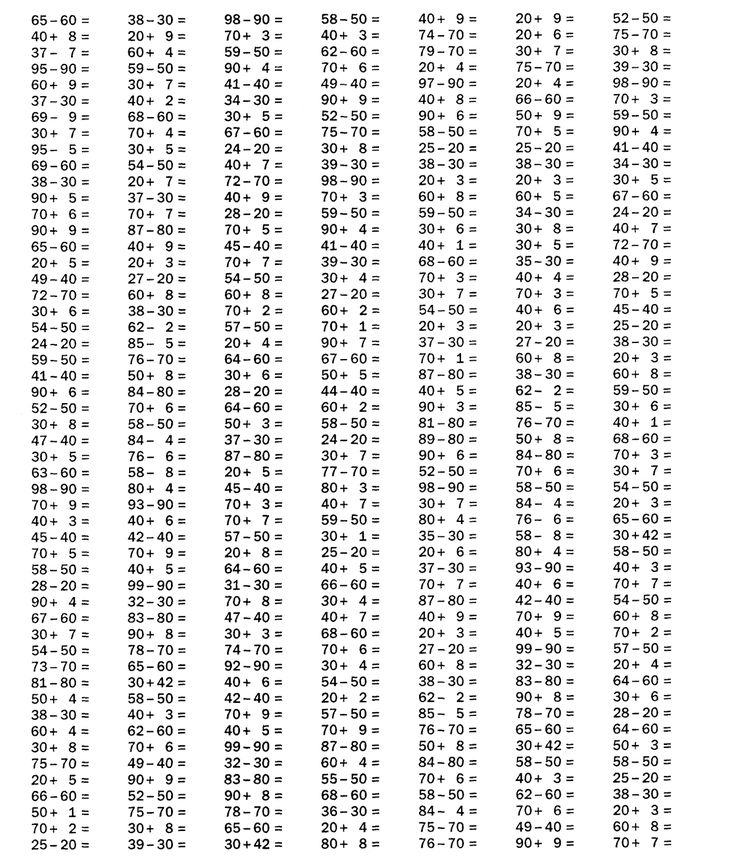

 Деятельность учителя
Деятельность учителя


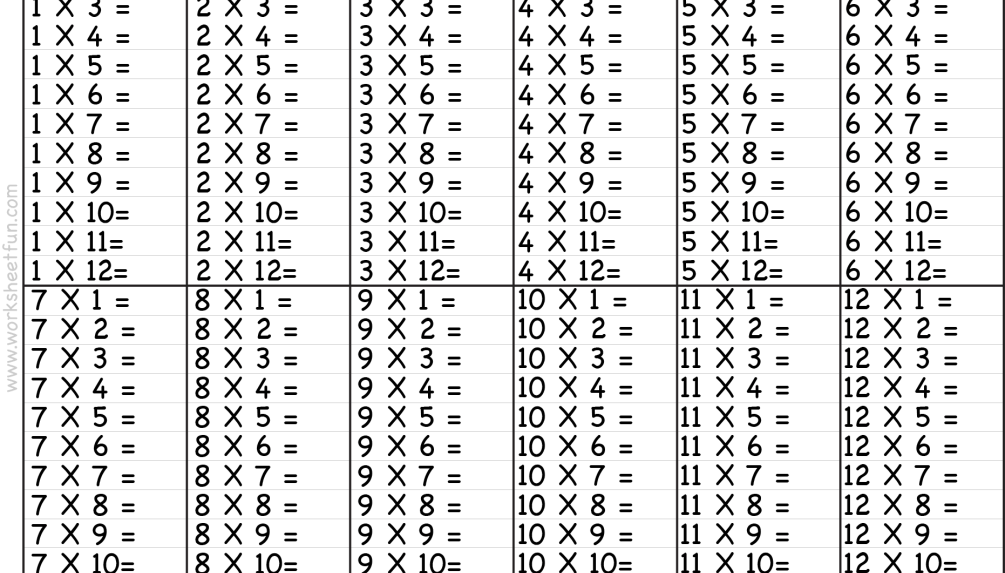
 Почему?
Почему?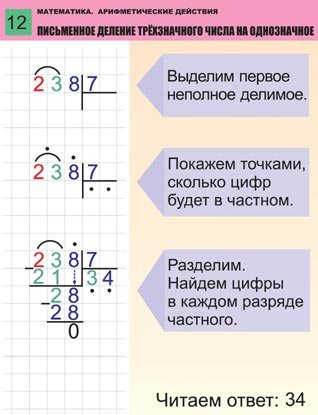






 Они применяют свое понимание моделей умножения (группы равного размера, массивы, модели площадей), разметки и свойств операций, в частности свойства распределения, при разработке, обсуждении и использовании эффективных, точных и универсальных методов для вычислить произведения многозначных целых чисел. В зависимости от цифр и контекста они выбирают и точно применяют соответствующие методы для оценки или мысленного расчета продуктов.Они развивают беглость с помощью эффективных процедур умножения целых чисел; понимать и объяснять, почему процедуры работают на основе числовой стоимости и свойств операций; и используйте их для решения проблем. Учащиеся применяют свое понимание моделей деления, разметки, свойств операций и отношения деления к умножению по мере того, как они разрабатывают, обсуждают и используют эффективные, точные и обобщаемые процедуры для нахождения частных, включающих многозначные дивиденды. Они выбирают и точно применяют подходящие методы для оценки и мысленного вычисления частных, а также интерпретируют остатки в зависимости от контекста.
Они применяют свое понимание моделей умножения (группы равного размера, массивы, модели площадей), разметки и свойств операций, в частности свойства распределения, при разработке, обсуждении и использовании эффективных, точных и универсальных методов для вычислить произведения многозначных целых чисел. В зависимости от цифр и контекста они выбирают и точно применяют соответствующие методы для оценки или мысленного расчета продуктов.Они развивают беглость с помощью эффективных процедур умножения целых чисел; понимать и объяснять, почему процедуры работают на основе числовой стоимости и свойств операций; и используйте их для решения проблем. Учащиеся применяют свое понимание моделей деления, разметки, свойств операций и отношения деления к умножению по мере того, как они разрабатывают, обсуждают и используют эффективные, точные и обобщаемые процедуры для нахождения частных, включающих многозначные дивиденды. Они выбирают и точно применяют подходящие методы для оценки и мысленного вычисления частных, а также интерпретируют остатки в зависимости от контекста.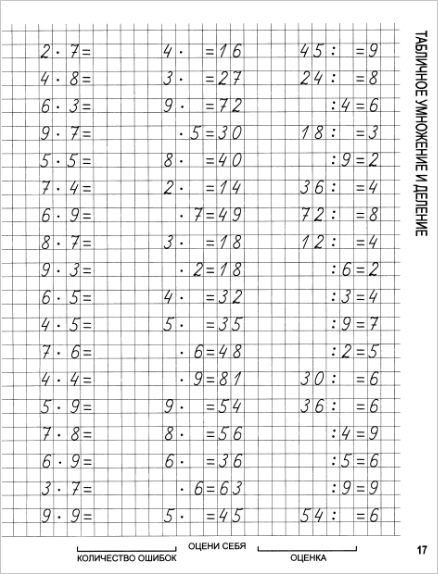
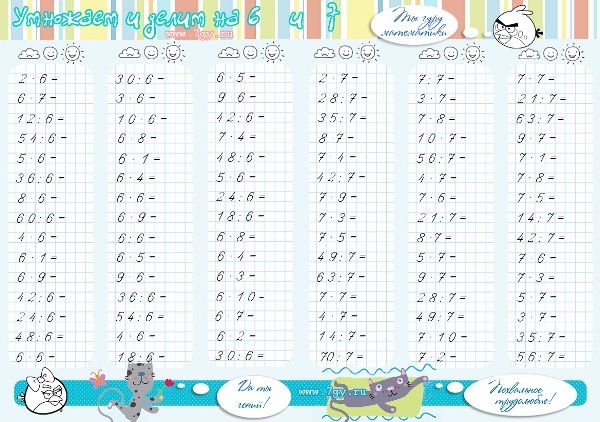


 к. последняя цифра нечетная (-).
к. последняя цифра нечетная (-). Записать 1 в графу результата.
Записать 1 в графу результата.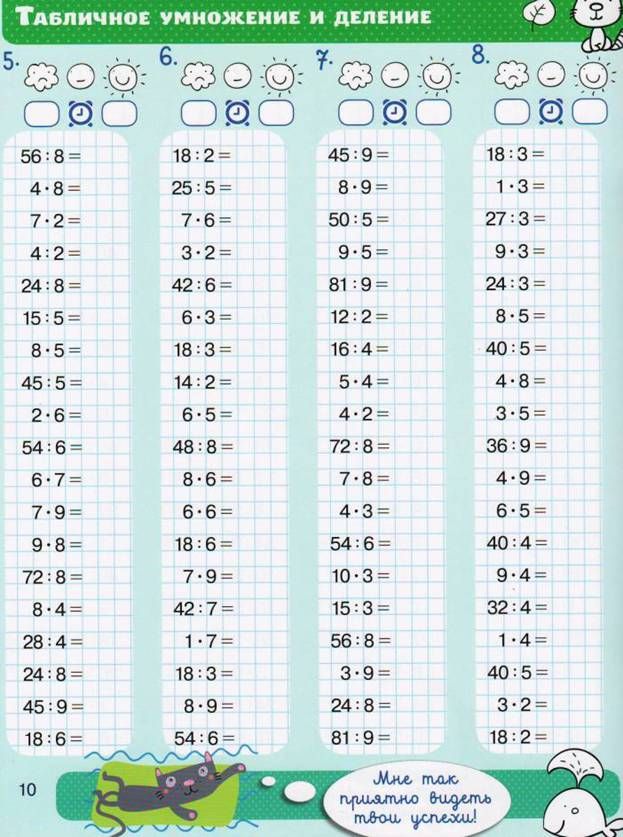


 Вы можете поставить ноль в частном в разряде сотен или опустить его.
Но 4 входит в 24 шесть раз. Подставь 6 в частном.
Вы можете поставить ноль в частном в разряде сотен или опустить его.
Но 4 входит в 24 шесть раз. Подставь 6 в частном.
 Тысячи, сотни,
а также
десятки цифр все равно делятся без остатка на делитель. Во-первых, студенты могут
решите в уме остаток
и просто напишите остаток сразу после
частное:
Тысячи, сотни,
а также
десятки цифр все равно делятся без остатка на делитель. Во-первых, студенты могут
решите в уме остаток
и просто напишите остаток сразу после
частное:
 Конечно, это предполагает, что учащиеся
уже научились находить остаток в простых задачах на деление
которые основаны на таблицах умножения (например, 45 ÷ 7 или 18 ÷ 5).
Конечно, это предполагает, что учащиеся
уже научились находить остаток в простых задачах на деление
которые основаны на таблицах умножения (например, 45 ÷ 7 или 18 ÷ 5).  Умножьте 1 × 4 = 4, напишите, что четыре меньше 7,
и вычесть. Это находит нам остаток от 3.
Умножьте 1 × 4 = 4, напишите, что четыре меньше 7,
и вычесть. Это находит нам остаток от 3.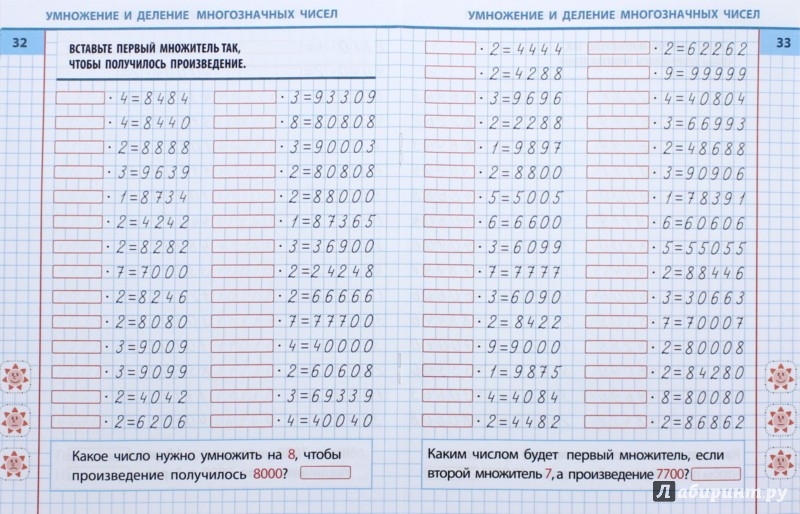 Умножьте 2 × 4 = 8, напишите, что восемь под
9и вычесть. Это находит нам остаток от 1.
Умножьте 2 × 4 = 8, напишите, что восемь под
9и вычесть. Это находит нам остаток от 1.

 Разделять.
Разделять.  Приложите 9 к частному.
Приложите 9 к частному.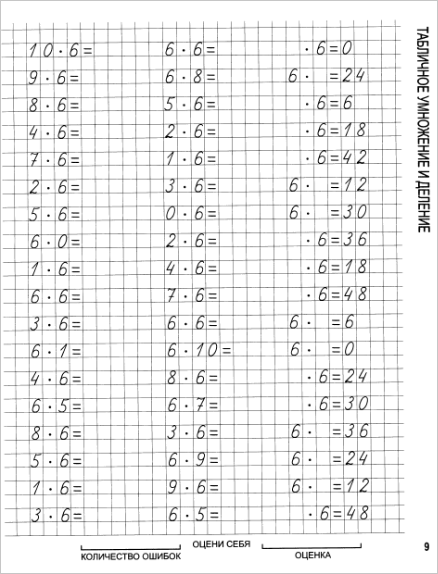
 Частное равно 29.
Частное равно 29.

 Подставь 3 в частное.
Подставь 3 в частное.
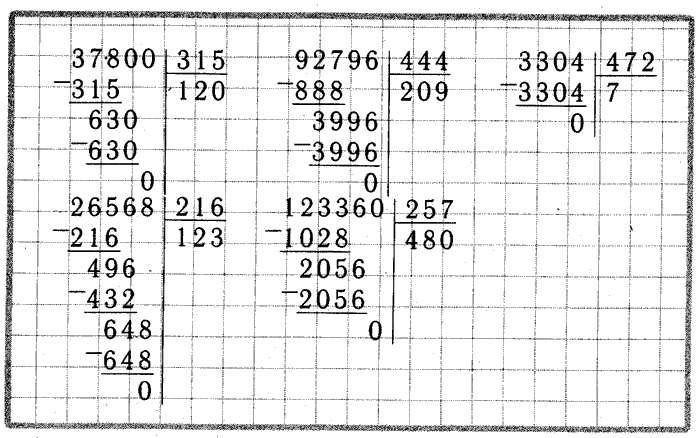
 Приложите 9 к частному.
Приложите 9 к частному.
 Частное равно 139.
Частное равно 139. Рабочие листы могут быть сделаны в формате html или PDF — оба варианта легко распечатать. Вы также можете настроить их с помощью генератора.
Рабочие листы могут быть сделаны в формате html или PDF — оба варианта легко распечатать. Вы также можете настроить их с помощью генератора.

