Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеСЛОВО К УЧАЩИМСЯГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел.  8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами.  30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 47. Отыскание комплексных корней уравнений. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49.  3.112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени.  130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 141. Уравнения, содержащие переменную под знаком модуля. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения.  149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными.  169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. § 17. Решение неравенств с переменной 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188.  Неравенства и системы неравенств с двумя переменными.§ 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21.  Производная и ее применения209. Определение производной. 211. Дифференцирование суммы, произведения, частного. 212. Сложная функция и ее дифференцирование. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226.  Правила вычисления первообразных.227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. 22.  Простейшие задачи на построение.23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники.  49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76.  Понятие движения.§ 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ |
Вся элементарная математика — Средняя математическая интернет-школа
Что такое решение уравнения?
Тождественное преобразование. Основные
виды тождественных преобразований.
Посторонний корень. Потеря корня.
Решение уравнения – это процесс, состоящий в основном в замене заданного уравнения другим
уравнением, ему равносильным .
Такая замена называется тождественным преобразованием .
Основные тождественные преобразования следующие:
| 1. | Замена одного выражения другим,
тождественно равным ему. Например,
уравнение
(
3 x+ 2
) 2 = 15 x+ 10
можно
заменить следующим
равносильным:
9 x 2 + 12 x + 4 = 15 x + 10 . |
| 2. | Перенос членов уравнения из
одной стороны в другую с обратными знаками. Так, в предыдущем
уравнении мы можем перенести все его члены из правой
части в левую со знаком « – »: 9 x 2 + 12 x + 4 – 15 x – 10 = 0,
после чего полу
чим:
9 x 2 – 3 x – 6 = 0 . |
| 3. | Умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля. Это очень важно, так как новое уравнение может не быть равносильным предыдущему, если выражение, на которое мы умножаем или делим, может быть равно нулю. П р и м е р . Уравнение x – 1 = 0 имеет единственный корень x = 1. Умножив обе его части на x – 3 , мы получим уравнение ( x
– 1 )( x
– 3 ) = 0, у которого
два корня: x
= 1 и x = 3. Последнее значение не является корнем заданного уравнения x – 1 = 0. Это так называемый посторонний корень . И наоборот, деление может привести к потере корня . Так в нашем случае, если ( x – 1 )( x – 3 ) = 0 является исходным уравнением, то корень x = 3 будет потерян при делении обеих частей уравнения на x
– 3 . В
последнем уравнении (п.2) мы можем разделить все его члены на 3 (не ноль!) и
окончательно получим: |
Это уравнение равносильно исходному:
Основы решения уравнений в один или несколько шагов (Предварительная алгебра, Подробнее об уравнениях и неравенствах) – Mathplanet
Формулы очень распространены в физике и химии, например, скорость равна расстоянию, деленному на время. Таким образом, мы используем общие символы для скорости ( v ), расстояния ( d ) и времени (t) и выражаем это следующим образом:
$$v=\frac{d}{t}$$
Мы можем просто опишите формулу как переменную и выражение, разделенные знаком равенства между ними.
Другими словами, формула — это то же самое, что и уравнение.
Пример
Книжный клуб требует членский взнос в размере 10 долларов в дополнение к 2 долларам, взимаемым за каждую заказанную книгу. Если бы нам нужно было перечислить стоимость заказа ряда книг, это выглядело бы так:
| Количество книг | Стоимость |
| 1 | 10 + 2 ∙ 1 = 12 |
| 2 | 10 + 2 ∙ 2 = 14 |
| 3 | 10 + 2 ∙ 3 = 16 |
| 4 | 10 + 2 ∙ 4 = 18 |
| 5 | 10 + 2 ∙ 5 = 20 |
| х | 10 + 2x |
Если мы обозначим общую стоимость книжного клуба как C, мы можем вывести следующую формулу выражения:
$$C=10 + 2x$$
из книжного клуба за 30 долларов мы можем либо продолжить заполнение таблицы выше, либо использовать свойства уравнений, которые мы рассмотрели в предыдущем разделе.
Мы можем купить 10 книг за 30 долларов.
Когда мы хотим решить уравнение, включающее одну неизвестную переменную, как x в приведенном выше примере, мы всегда стремимся изолировать неизвестную переменную. Можно сказать, что все остальное мы поставили по ту сторону знака равенства. Всегда полезно сначала изолировать термины, включающие переменную, от констант, как мы делали выше, путем вычитания или сложения перед делением или умножением коэффициента перед переменной. Пока вы делаете одно и то же по обе стороны от знака равенства, вы можете делать все, что хотите и в каком порядке.
Выше мы начали с вычитания константы с обеих сторон. Вместо этого мы могли бы начать с деления на 2. Это выглядело бы как
$$\frac{30}{{\color{blue} {2}}}=\frac{10+2x}{{\color{blue} {2}}}$$
$$\frac{30}{{\color{blue} {2}}}=\frac{10}{{\color{blue} {2}}}+\frac{2x}{{\color{blue} {2}}}$$
$$15=5+x$$
$$15\, {\color{blue} -\, 5}=5+x\, {\color{blue} -\, 5 }$$
$$10=x$$
Снова тот же ответ, просто подтверждающий точку зрения.
Если ваше уравнение содержит одинаковые члены, предпочтительно начать с объединения одинаковых членов, прежде чем продолжить решение уравнения. подобные термины (все термины, включающие одну и ту же переменную x и все константы)
$$\left (5x +2x \right )+\left (14+2 \right )=30$$
$$7x+16=30 $$
Теперь пришло время изолировать переменную от постоянной части. Это делается путем вычитания 16 с обеих сторон
$$7x+16\, {\color{green} -\, {16}}=30\, {\color{green} -\, {16}}$$
$$7x=14$$
Разделите обе части на 7, чтобы выделить переменную
$$\frac{7x}{{\color{green} 7}}=\frac{14}{{\color{green} 7}}$$
$$x=2$$
Если у вас есть уравнение, в котором у вас есть переменные с обеих сторон, вы делаете в основном то же самое, что и раньше. Вы собираете все подобные термины. Прежде чем вы работали, сначала соберите все постоянные члены с одной стороны и сохраните переменные члены с другой стороны. То же самое относится и здесь.
Вы собираете все постоянные термины с одной стороны и переменные термины с другой стороны. Обычно хорошей идеей является собрать все переменные на той стороне, которая имеет переменную с наибольшим коэффициентом, т. е. в приведенном ниже примере больше x:es на левой стороне (4x) по сравнению с правой стороной (2x), и, следовательно, мы собираем все x:es слева.
Пример
$$4x+3=2x+11$$
вычесть 2x с обеих сторон
$$4x+3\, {\color{blue} -\, {2x}}=2x +11\, {\color{blue} -\, {2x}}$$
Теперь это выглядит как любое другое уравнение
$$2x+3=11$$
вычесть 3 из обеих сторон
$$2 x+3{\color{blue} \, -\, {3}}=11{\color{blue} \, -\,{ 3}}2x=8$$
Разделить на 2 с обеих сторон
$$\frac{2x}{{\color{blue} {2}}}=\frac{8}{{\color{blue} {2}}}$$
$$x=4$$
В начале этого раздела мы показали формулу для расчета скорости, где скорость (v) равна расстоянию (d), деленному на время (t), или
$$v=\frac {d}{t}$$
Если мы случайно захотим узнать, какое расстояние проезжает грузовик за 3 часа со скоростью 60 миль в час, мы можем использовать приведенную выше формулу и переписать ее для определения расстояния d.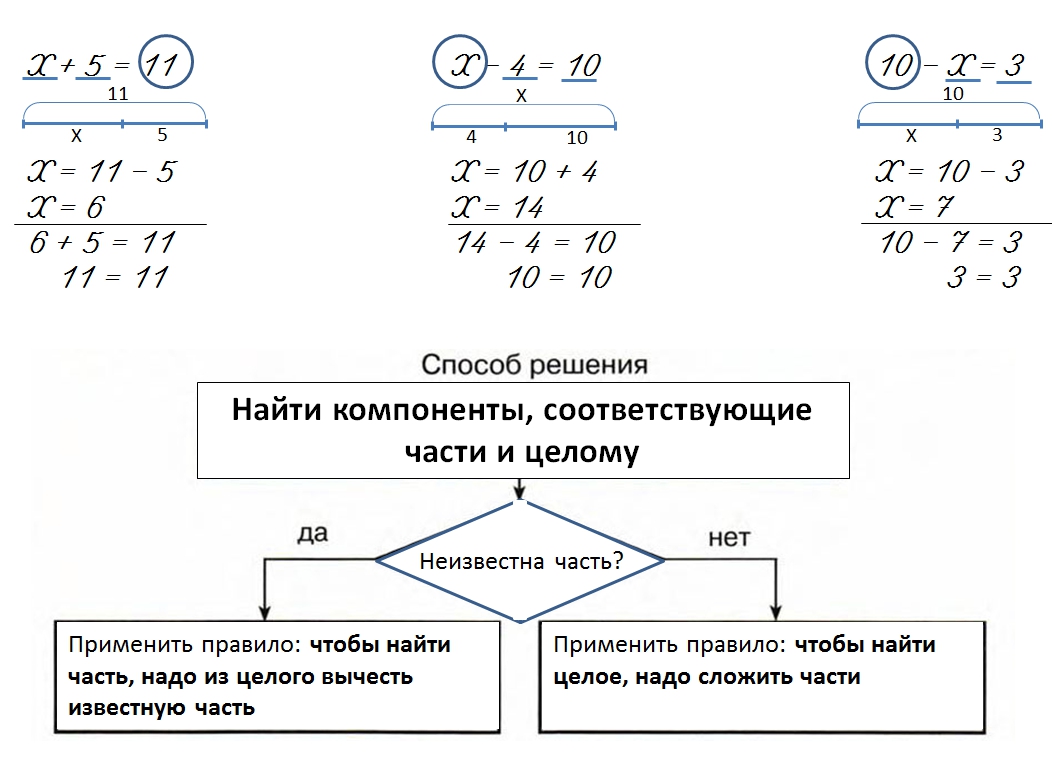
$$\frac{d}{t}{\color{green} ${\, \cdot\, t}}=v{\color{green} {\, \cdot\, t}}$$
$$d=v\cdot t$$
Когда это будет сделано, мы можем просто подставить наши числа в формулу и вычислить ответ
$$d=60\cdot 3=180$$
Грузовик проезжает 180 миль за 3 часа.
Это верно для всех формул и уравнений.
Решите уравнение
Что такое свойство равенства деления? Определение, примеры, факты
Свойство деления равенства говорит нам, что если мы разделим обе части уравнения на одно и то же число, уравнение останется прежним.
Предположим, у вас есть две пиццы одинакового размера. Вы разрезаете каждую из них пополам и отдаете половинку от каждой пиццы своим друзьям. Если вы измерите оставшиеся порции, вы обнаружите, что у вас остались равные порции от обеих пицц.
Здесь исходное уравнение состояло в том, что обе пиццы были равны.
Затем вы разделили их на 2 и обнаружили, что они по-прежнему равны. Это означает, что уравнение осталось прежним, даже если вы разделили обе части уравнения на общее число.
Это основная концепция свойства равенства деления
Свойство равенства определения деления
Свойство равенства деления утверждает, что если обе части уравнения разделить на общее действительное число, не равное коэффициенты остаются равными.
Формула для того же может быть записана следующим образом:
Если a, b и c — действительные числа, где a = b и c ≠ 0, то:
$\frac{a}{c}=\frac {b}{c}$
Это свойство верно для всех действительных чисел и даже для алгебраических выражений, использующих переменные.
Вот пример свойства деления на равенство с использованием целых чисел.
Пример 1 : Рассмотрим уравнение 50 = 20 + 30.
Разделим обе части на 10.
Вот пример использования дробей.
Пример 2 : Возьмем уравнение 2/3 = 4/6
Если мы разделим обе части на 1/3, мы получим
Связанные игры
Свойство, обратное свойству деления, является свойством умножения неравенства.
В нем говорится, что если вы умножите две части уравнения на любое число, результат останется прежним. То есть, если a, b и c — любые три действительных числа и a = b, то это означает, что
Связанные рабочие листы
Как используется свойство равенства деления?Это свойство используется в различных математических контекстах.
- Это свойство помогает определить, эквивалентны ли два выражения в арифметике.
- Используется в алгебре для решения неизвестной переменной.
Например:
Допустим, Мия купила 5 кексов за $\$$30. Как она может узнать цену одного кекса?
Допустим, один кекс стоит z долларов.
Следовательно, 5z = $\$$30.
Разделив обе части этого уравнения на 5, мы получим
Следовательно, каждый кекс стоит $\$$6.
- Он служит основой для изучения логики.
Пример 1: Джеймс может хранить 50 мячей в корзине.
Если у него 300 мячей, сколько корзин ему понадобится, чтобы их хранить?
Решение : общее количество мячей, которое нужно сохранить Джеймсу, равно 300.
Допустим, ему нужно «x» корзин для хранения мячей.
Составляем уравнение в виде 50x = 300.
Разделив обе части уравнения на 5, получим
$\frac{50x}{5}= \frac{300}{5}$
Или, 10x= 60
Разделив обе части уравнения на 10,
$\frac{10x}{10}= \frac{60}{10}$,
Или x= 6 .
Итак, Джеймсу нужно 6 корзин, чтобы хранить 300 мячей.
Пример 2: Гарри проехал на велосипеде 56 км за 7 дней. Используйте свойство равенства деления, чтобы найти расстояние, пройденное Гарри каждый день.
Решение : Допустим, Гарри проезжает «x» км на своем велосипеде за один день.
Составим уравнение в виде 7x = 56.
Разделив обе части уравнения на 7, получим
$\frac{7x}{7}= \frac{56}{7}$
Или, x= 8
Таким образом, мы видим, что Гарри каждый день проезжает на велосипеде 8 км.
Пример 3. Найдите значение y в следующем уравнении:
11 – 38 = 3y
Решение : Начнем с упрощения терминов с каждой стороны.
11 – 38 = 3 года
Или, – 27 = 3 года
Разделив обе части уравнения на 3, мы получим
$-\frac{27}{3}= \frac{3y}{3}$
Или, $y= –9$
Практические задачи
1
Какое из следующих уравнений показывает свойство равенства деления для действительных чисел x, y, z, где y ≠ 0 и x = z?
x + y = z + y
x – y = z – y
$\frac{x}{y} = \frac{z}{y}$
Ничего из вышеперечисленного
Правильный ответ: $\frac{x}{y} = \frac{z}{y}$
В соответствии со свойством равенства деления, если x, y, z — три действительных числа, таких как что x = z и y ≠ 0,
, тогда $\frac{x}{y} = \frac{z}{y}$.
2
Используя свойство деления равенства, решите относительно x следующее уравнение {70x}{7}= \фракция{490}{7}$
Или, $10x$= 70
Разделив обе части уравнения на 10,
$\frac{10x}{10}= \frac{70}{10},
Или x = 7 .
