Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Предыдущую статью о показательных уравнениях мы начали с уравнения 2x = 8. Там всё было ясно: x = 3.
А теперь рассмотрим уравнение 2x = 7.
По графику функции y = 2x мы видим, что это уравнение имеет корень, и притом единственный.
Ясно, что этот корень — не целое число (так как 22 = 4, 23 = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.
Этот корень обозначается log27 (читается: «логарифм семи по основанию два»). Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log27 = 2,807354922057604107…
Итак, наше число log27 — это показатель степени, в которую надо возвести 2, чтобы получить 7.
Теперь дадим общее определение логарифма.
Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).
Определение. Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b.
Иными словами,
Например:
так как ;
, так как ;
так как ;
, так как .
Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.
Логарифм с основанием e называется натуральным и обозначается ln.
Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log2(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.
Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.
Основные формулы
По определению, logab — это показатель степени, в которую надо возвести число a, чтобы получить число b:
alogab=b. | (1) |
Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:
logaax=x.
Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.
Логарифм произведения — это сумма логарифмов:
| loga(bc) = logab + logac. | (2) |
Логарифм частного — это разность логарифмов:
| (3) |
Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:
| (4) |
Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:
| (5) |
Формулы (4) и (5) вместе дают:
. | (6) |
В частности, если m = n, мы получаем формулу:
| . | (7) |
Например, .
Наконец, важнейшая формула перехода к новому основанию:
| . | (8) |
В частности, если c = b, то logbb = 1, и тогда:
| . | (9) |
Приведём несколько примеров из банка заданий.
1. (применили формулу (2) суммы логарифмов).
2. (применили основное логарифмическое тождество(1)).
3. (применили формулу (4)).
4. (применили формулу (9), перейдя к новому основанию 0,8).
5. (применили формулу (3) разности логарифмов).
Немного истории
Теперь вы поняли, что такое логарифмы и как ими пользоваться.
Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?
Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.
Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?
Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.
В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.
Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.
Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу.
Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).
А затем по таблице логарифмов найти само произведение чисел b и c.
Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.
Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Логарифмы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Публикация обновлена: 08.04.2023
Онлайн калькулятор логарифмов двоичного, десятичного, по заданному основанию
- Подробности
Калькулятор онлайн рассчитывает: натуральный логарифм ln(b); двоичный логарифм lg2(b); деcятичный логарифм lg(b); логарифм по заданному основанию loga(b).
| Исходные данные: | Решение: | |
| Основание логарифма a = | вычиление натурального логарифма вычиление двоичного логарифма вычиление деcятичного логарифма вычиление логарифма по основанию | |
| Значение логарифма b = | ||
| округление до 12345 знаков после запятой | ||
Помощь на развитие проекта premierdevelopment.
ru
Send mail и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Для справки:
- натуральный логарифм
- — это логарифм по основанию e, где e — иррациональная константа, приблизительно равная 2,718.
Натуральный логарифм обозначается как ln(b), loge(b) или иногда просто log(b), если основание e подразумевается. - двоичный логарифм
- — логарифм по основанию 2. Двоичный логарифм обозначается как lg2(b). Двоичный логарифм числа b есть решение уравнения 2x = b.
- десятичный логарифм
- — логарифм по основанию 10. Десятичный логарифм обозначается как lg(b). Десятичный логарифм числа b есть решение уравнения 10x = b.
- логарифм числа b по основанию a
- — показатель степени, в которую надо возвести основание a, чтобы получить число b.
Он обозначается как loga(b).
Логари́фм числа b по основанию a есть решение уравнения ax = b.
Он обозначается как loga(b).
Логари́фм числа b по основанию a есть решение уравнения ax = b.II. Примечание:
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолачанию — округление до сотых).
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
ФорумСпециалистыО нас
Ссылка для цитирования в списке литературы: CAE-CUBE: [Электронный ресурс]. URL: https://premierdevelopment.ru/ (дата обращения ) | premierdevelopment.ru, все права защищены, 2015 - 2021 e-mail: Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. |
Log10 Calculator — Online Log10 Calculator
Логарифмы (или) логарифмы определяются как еще один способ выражения показателей степени.
Показатели выражаются в виде логарифмов.
Что такое калькулятор Log10?
‘ Log10 Calculator ‘ представляет собой онлайн-инструмент, который помогает вычислить значение логарифма по основанию 10. Онлайн-калькулятор Log10 поможет вам вычислить значение логарифма по основанию 10 за несколько секунд.
Калькулятор Log10
ПРИМЕЧАНИЕ: Введите значения только до четырех цифр.
Как пользоваться калькулятором Log10?
Чтобы использовать калькулятор, выполните следующие действия:
- Шаг 1: Введите значение в соответствующее поле ввода.
- Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти значение логарифма.
- Шаг 3: Нажмите кнопку «Сброс», чтобы очистить поле и ввести новые значения.
Как найти калькулятор Log10?
Логарифм определяется с использованием показателя = B x = a ⇒ log B A = x ⇒ log 10 A = x, где b — базовый = 10, A — аргумент.
и x — действительное число
Существует два разных типа логарифмических функций. Они:
1. Логарифмическая функция (основание которой равно 10)
2. Натуральная логарифмическая функция (по основанию e)
Десятичный логарифм определяется как логарифм по основанию 10. Он представлен числом 9.0007 журнал 10 .
10 x =a ⇒ log 10 a = x
Хотите находить сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры на калькуляторе Log10Пример 1:
Найти значение логарифма журнала 10 100 и проверьте его с помощью калькулятора log10.
Решение:
Дано: Значение аргумента = 100
log 10 a = x ⇔ 10 x 1 03 = a
3 90 44 100 ⇔ 10 x = 100
x = 2
Следовательно, логарифмическое значение log 10 100 равно 2.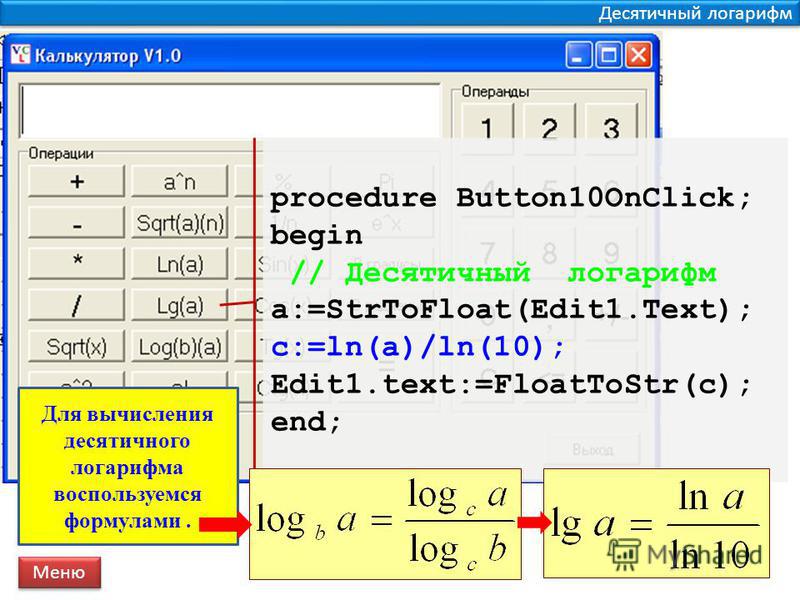
Пример 2:
0043 10 1000 и проверьте его с помощью калькулятора log10.Решение:
Дано: значение аргумента = 1000
log 10 a = x ⇔ 10 x 90 3 log = a 9 00023
3 044
1000 ⇔ 10 x = 1000x = 3
Следовательно, значение логарифма log 10 1000 равно 3.
Пример 3:
3 0043 10 240 и проверьте его с помощью калькулятора log10.
Решение:
Дано: Значение аргумента = 240
log 10 a = x ⇔ 10 x 1 03 = a
3 90 44 240 ⇔ 10 x = 240
x = 2,38
Таким образом, значение логарифма log 10 240 равно 2,38
Аналогично, вы можете попробовать калькулятор log10, чтобы найти значение логарифма
- журнал 10 25
- журнал 10 45
- Логарифмы
- Основные сведения о логарифмах
Калькулятор логарифмов
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обычный логарифм — это логарифм с основанием 10, также известный как десятичный логарифм или десятичный логарифм. В то время как натуральный логарифм является основанием с математической константой «е», которая приблизительно равна 2,718281828459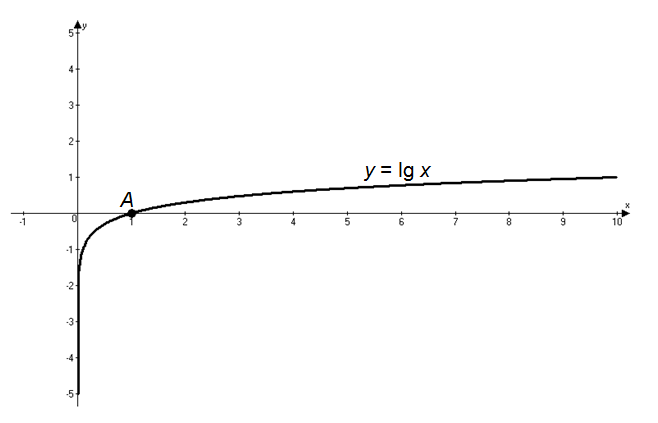
..
..