Геометрическая задача о параллелограмме на доказательство — «Шпаргалка ЕГЭ»
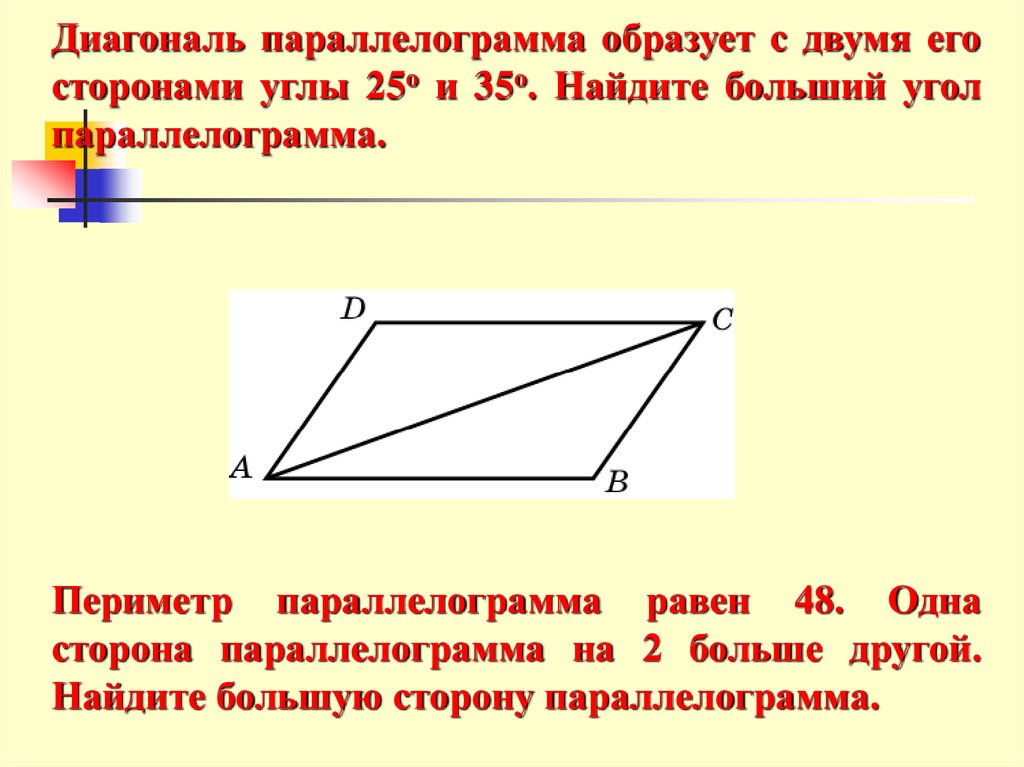
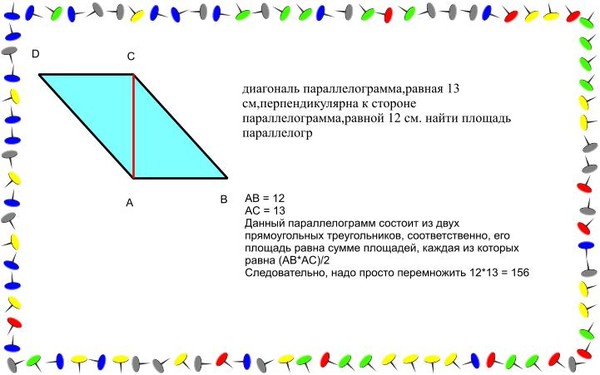
На диагонали параллелограмма взяли точку, отличную от ее середины. Из нее на все стороны параллелограмма (или их продолжения) опустили перпендикуляры.
а) Докажите, что четырёхугольник, образованный основаниями этих перпендикуляров, является трапецией.
б) Найдите площадь полученной трапеции, если площадь параллелограмма равна , а один из его улов равен .
Решение задачи
Данный урок показывает, как правильно доказать, что при проведении перпендикуляров из точки, расположенной на диагонали параллелограмма, получается трапеция, если соединить основания этих перпендикуляров. Решение данной задачи сводится к доказательству равенства накрест лежащих углов (условие параллельности прямых при пересечении их секущей). В данном случае доказательство проводится через доказательство подобия треугольников, которое в свою очередь доказывается через очевидные подобные треугольники, а значит, и через подобие сторон.
Следует помнить, что при решении задача с пересекающимися прямыми всегда получаются вертикальные углы, которые равны по определению, кроме того для доказательства подобия прямоугольных треугольников достаточно доказать равенство одного из острых углов треугольников. Доказав равенство углов, получаем, что две стороны у полученной фигуры параллельны, что дает нам основание утверждать, что полученная фигура – трапеция. Решение пункта а) выполнено, переходим к пункту б). В данной задаче требуется определить площадь, полученной трапеции. Очевидным является тот факт, что для использования стандартной формулы площади трапеции (через стороны основания и высоту) нам не достаточно данных, поэтому на помощь приходит формула площади четырехугольника: , – где d1 и d2 – длины диагоналей, α – угол между диагоналями. Обозначив, боковые стороны параллелограмма через неизвестные можно получить данную по условию площадь параллелограмма по формуле , где а и b – стороны параллелограмма, α – угол между сторонами (который дан нам по условию), после этого можно легко получить диагонали трапеции, если использовать формулу площади трапеции через высоту и боковую сторону.
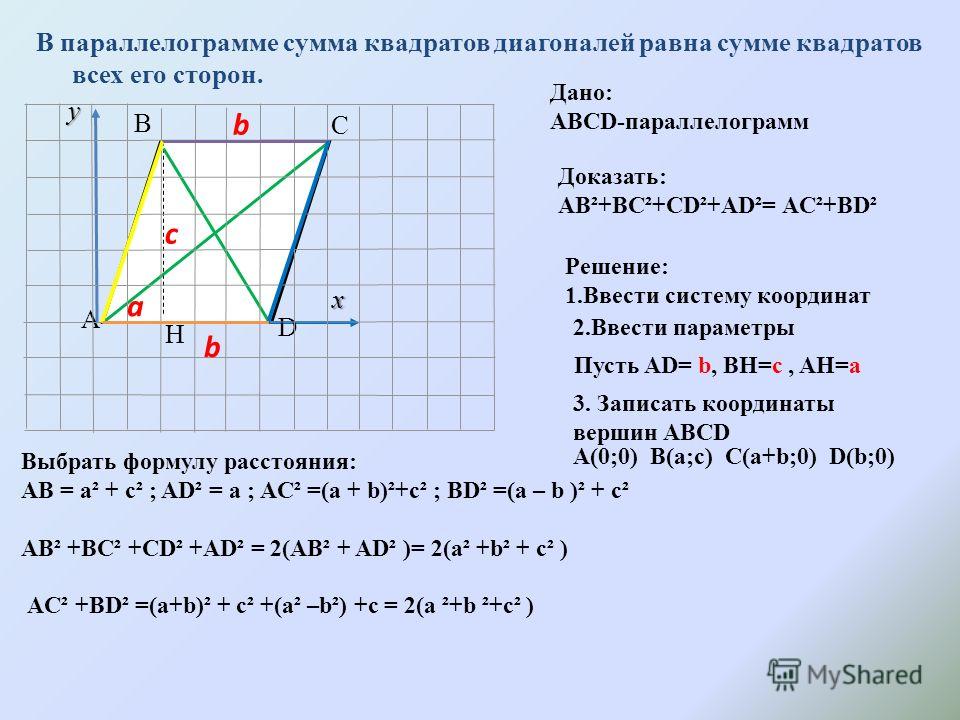
Решение данной задачи рекомендовано для учащихся 8-х классов при изучении тем «Четырехугольники» («Многоугольники», «Параллелограмм», «Трапеция»), «Площадь» («Понятие площади многоугольника», «Площадь параллелограмма», «Площадь трапеции»), «Подобные треугольники» («Первый признак подобия треугольников», «Второй признак подобия треугольников», «Третий признак подобия треугольников», «Пропорциональные отрезки в прямоугольном треугольнике»). При подготовке к ЕГЭ урок рекомендован при повторении темы «Четырехугольники», «Площадь», «Подобные треугольники».
Рекомендуем
Отзывы учеников
- Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
- Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
- Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.
Параллельные прямые, проведенные через диагональ параллелограмма
Главная » Четырехугольники » Параллелограммы » Параллельные прямые, проведенные через точку на диагонали параллелограмма
Последнее обновление: Идо Сариг · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности
Одно из доказательств, сделанных Евклидом в его книге «Элементы», где он положил Основой геометрии является то, что если вы проведете линии, параллельные сторонам параллелограмма и проходящие через любую точку на диагонали параллелограмма, то два параллелограмма выше и ниже этой диагонали будут равны по площади. Мы повторим доказательство здесь.
Задача
ABCD — параллелограмм, а DB — одна из его диагоналей. ФХ || AD и EG || ДК . Покажите, что площадь AEKF равна площади HKGC .
Стратегия
Сначала заметим, что поскольку EG и FH были проведены параллельно двум парам параллельных сторон (AB и DC, AD и BC соответственно), все четыре четырехугольника AEKF , EDHK, FKGB и HKGC сами по себе являются параллелограммами.
Чтобы найти площадь параллелограмма, обычно нам нужно найти длину стороны и высоту, но здесь ничего этого нет.
Значит, нам нужно использовать другую стратегию. Поскольку нам на самом деле не нужно находить площадь AEKF или HKGC , просто чтобы показать, что они равны, мы попробуем сделать это, используя другую технику, которую мы использовали в прошлом, в этом уроке или здесь. — вычитание известных областей для получения неизвестных.
Ранее мы показали в процессе доказательства конгруэнтности двух пар противоположных углов параллелограмма, что диагональ параллелограмма делит его пополам на два конгруэнтных треугольника, поэтому площадь Δ ABD та же, что и площадь Δ BDC .
Но поскольку меньшие четырехугольники EDHK и FKGB сами по себе являются параллелограммами, которые также имеют одну и ту же диагональ, по приведенной выше логике площадь Δ EDK такая же, как площадь Δ КДХ .
А площадь БФК такая же, как площадь БГК .
Вычитание равных площадей меньших треугольников из равных площадей большего треугольника дает нам площади двух параллелограммов, которые равны.
Доказательство
(1) AD||BC //Дано. ABCD — параллелограмм
(2) AB||DC //Дано. ABCD — параллелограмм
(3) FH || AD // Дано
(4) EG || DC // Дано
(5) ЭДХК — параллелограмм //(3), (4), определение параллелограмма
(6) ФКГБ — параллелограмм //(3), (4), определение параллелограмма
( 7) Δ EDK ≅ Δ KDH //(5), Диагональ параллелограмма делит его пополам на два равных треугольника
(8) Δ BFK ≅ Δ BGK //(6), Диагональ параллелограмм делит его пополам на два конгруэнтных треугольника
(9) Δ ABD ≅ Δ BDC //(Диагональ параллелограмма делит его пополам на два конгруэнтных треугольника
(10) Area(ABD) = Area(BDC) //площади конгруэнтных треугольников равны
(11) Area(BFK)=Area(BGK) //площади конгруэнтных треугольников равны
(12) Area(EDK)=площадь (KDH) //площади конгруэнтных треугольников равны
(13) Площадь(ABD)-Площадь(BFK)-Площадь(EDK)=Площадь(BDC)-Площадь(BGK)-Площадь(KDH) //(10), ( 11), (12), переходные и вычитательные свойства равенства
(14) Площадь (S 1 ) = Площадь (S 2 )
Об авторе
Идо Сариг — руководитель отдела высоких технологий со степенью бакалавра наук степень в области вычислительной техники.
Его цель — помочь вам разработать лучший подход к решению геометрических задач. Вы можете связаться с ним по адресу [email protected]
Параллелограмм образован векторами = (2, 3) и = (1, 1). а) Определите длины диагоналей. б) Определить периметр…
Цитата страницы Начать эссе значок-вопрос Спросите репетитораУкажите эту страницу следующим образом:
«Параллелограмм образован векторами = (2, 3) и = (1, 1).
а) Определите длины диагоналей.
б) Определить периметр параллелограмма.
» eNotes Editorial , 9 июня 2013 г., https://www.enotes.com/homework-help/parallelogram-formed-by-vectors-2-3-1-1-determine-439132.
По состоянию на 26 января 2023 г.
Когда параллелограмм образован двумя векторами, одна диагональ представляет собой векторную сумму сторон, а другая диагональ представляет собой разность векторов сторон. 92) = sqrt(2)` .
Периметр параллелограмма равен `2sqrt(13) + 2sqrt(2)` .
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы педагога
Математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 ответа учителя
Математика
Последний ответ опубликован 3 октября 2011 г.