Диагонали параллелограмма формулы: Все формулы диагонали параллелограмма

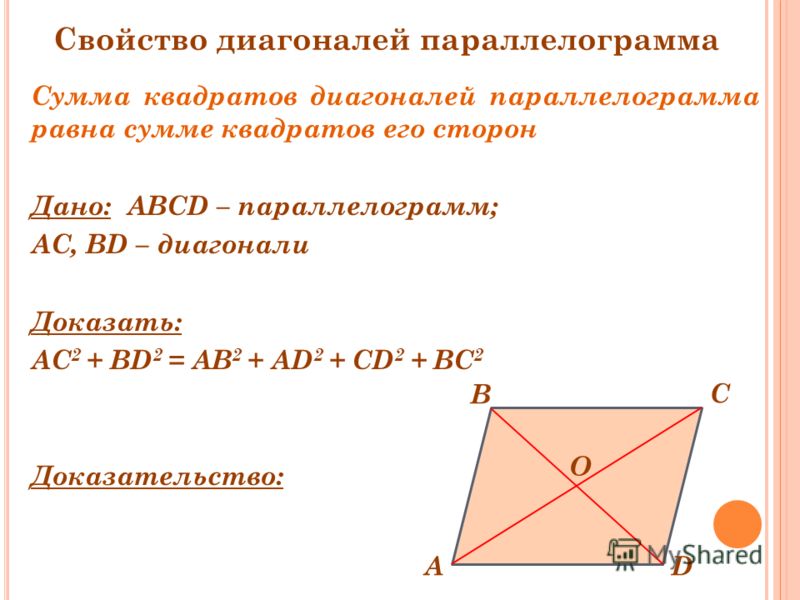
Диагональ параллелограмма: онлайн-калькулятор, формулы и примеры

Параллелограмм представляет собой геометрическую фигуру, где лежащие напротив друг друга ребра взаимно параллельны.

В задачах по геометрии иногда нужно найти длину его диагонали. В некоторых из них это прямой вопрос, а в некоторых диагональ нужно вычислить, чтобы потом через нее вычислять другие геометрические объекты. Например, используя значения длины отрезков, соединяющих вершины, ребер этой геометрической фигуры, ее углов, вычисляется значение ее площади, другая диагональ. Если в параллелограмме неизвестны его углы, но известны стороны и угол между диагоналями, то из этих значений узнаются через расчет углы параллелограмма.

• Длинная диагональ параллелограмма через две стороны и тупой угол
• Короткая диагональ параллелограмма через две стороны и тупой угол
• Длинная диагональ параллелограмма через две стороны и острый угол
• Короткая диагональ параллелограмма через две стороны и острый угол
• Диагональ параллелограмма через две стороны и другую известную диагональ
• Диагональ параллелограмма через площадь, другую известную диагональ и угол между диагоналями

Длинная диагональ через две стороны и тупой угол

В параллелограмме для вычисления длины наибольшей диагонали при имеющихся данных о его ребрах и тупом угле между ними следует рассчитать квадрат ребер, суммировать эти значения. После этого умножить значение одного ребра на другое, на косинус тупого угла между ними, на два. Затем от первой суммы отнять это произведение и найти из этой разности квадратный корень.

D = √(a² + b² – 2 * a * b * cosβ

где D – диагональ этой геометрической фигуры, a, b – ее ребра, cos β – косинус тупого угла между ребрами этой фигуры

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Угол (β):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Значения ребер этого четырехугольника 2 и 4, а косинус тупого угла (120 градусов) между ними -0,5. Диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * (-0,5)) = √(4+16 – 16 *( -0,5)) = √(20 + 8) = 5,3 (ответ округлен)

Диагональ через две стороны и другую известную диагональ

В параллелограмме для вычисления длины проведенной в нем диагонали через его стороны и другую диагональ следует возвести в квадрат каждую его сторону и умножить на 2 оба результата, затем сложить полученные значения (это первый результат).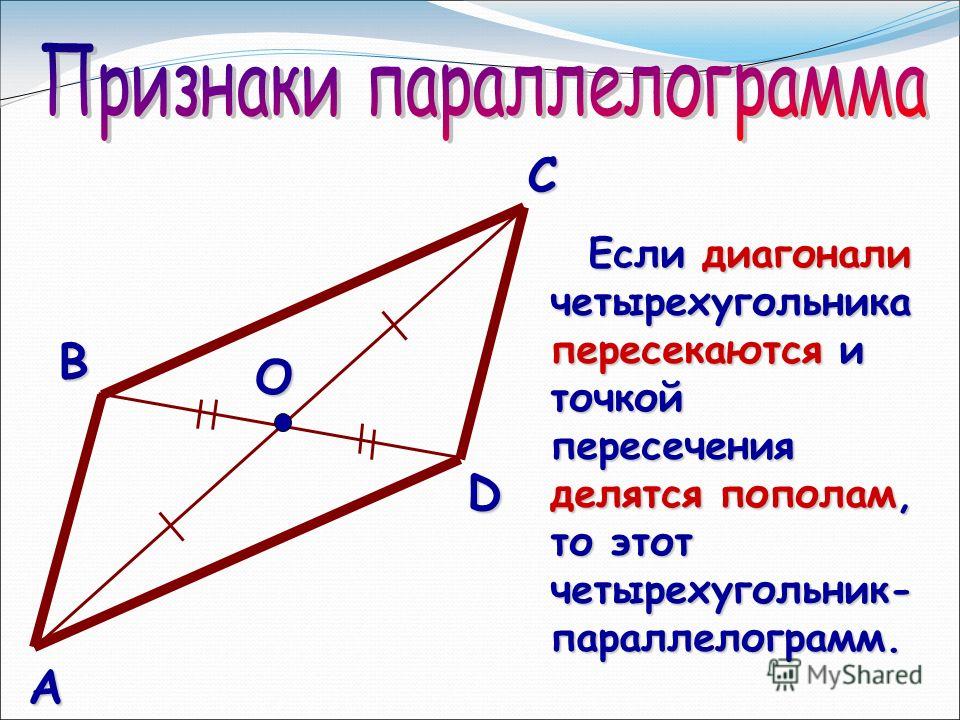

Потом следует возвести в квадрат значение длины другой диагонали (это второй результат). Затем из первого результата вычесть второй и найти из полученного значения квадратный корень.

D = √(2 * a² + 2 * b² – d²)

где D – диагональ параллелограмма, a, b – его стороны, d – другая диагональ параллелограмма

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Диагональ (d):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть стороны параллелограмма 2 и 4, а одна из диагоналей 4. Тогда вторая диагональ равна: D = √(2 * 2²+ 2 * 4² – 4²) = √(8 + 32 – 16) = √24 = 4,9 (ответ округленный)

Короткая диагональ через две стороны и тупой угол

Для нахождения наименьшего отрезка соединяющего противоположные вершины в этой геометрической фигуре через его ребра и тупой угол между ними возводятся в квадрат длины его ребер, складываются полученные числа (один результат).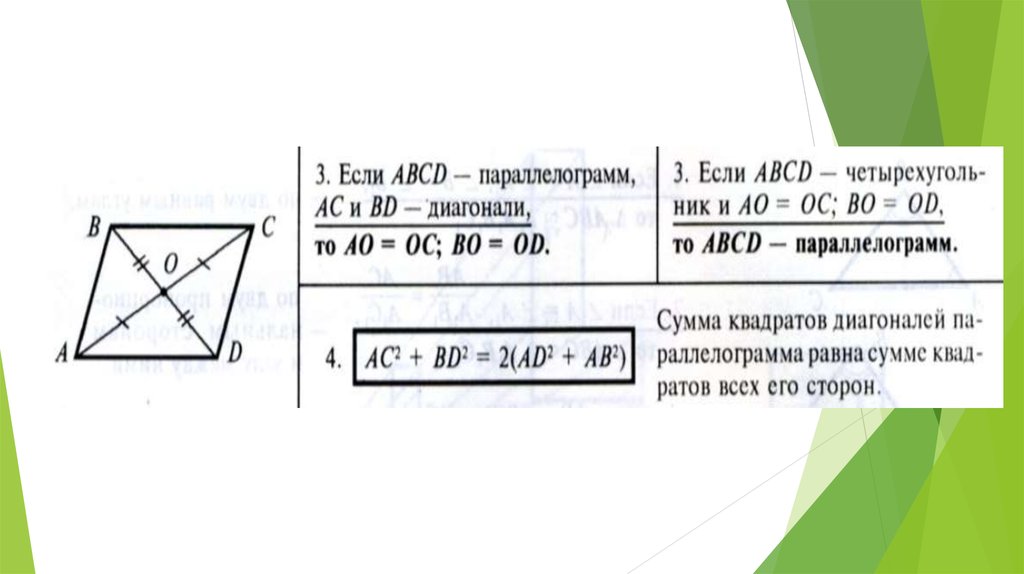 Далее перемножаются значения длины ребер, косинус тупого угла, удваивается полученное число (это другой результат). К одному результату прибавляется другой и находится из полученного значения квадратный корень.

D = √(a² + b² + 2 * a * b * cosβ)

где D – диагональ параллелограмма, a, b – его стороны, cos β – косинус тупого угла между ребрами.

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Угол (β):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Если ребра этой геометрической фигуры 1 и 3, а косинус тупого угла (120) между ними -0,5. Тогда диагональ равна: D = √(1²+ 3² + 2 * 1 * 3 * (-0,5)) = √(1 + 9 + 6 * (-0,5)) = √(10 – 3) = 2,6 (ответ округлен)

Длинная диагональ через две стороны и острый угол

В этом четырехугольнике для расчета значения протяженности большего отрезка, соединяющего в нем расположенные друг напротив друга вершины, через два его ребра и острый угол нужно сначала возвести в квадрат значение длины его ребер, потом складываются результаты этого вычисления (это первое слагаемое для последующего сложения).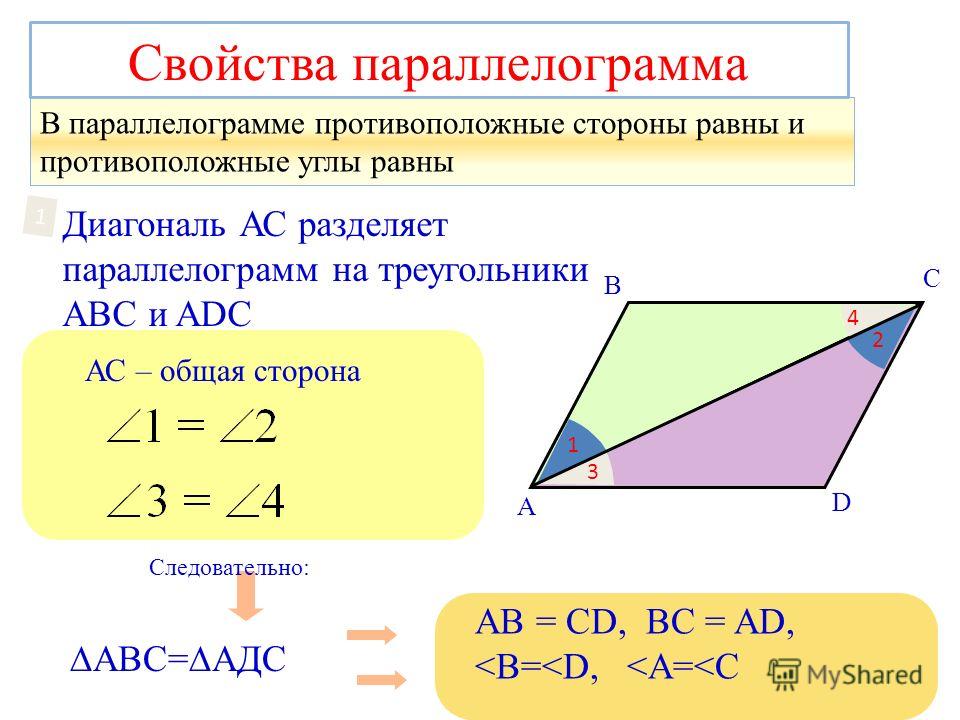

Затем умножаются длины ребер друг на друга, на косинус острого угла, найденное произведение еще на 2 (это второе слагаемое). Затем оба слагаемых складываются и из суммы вычисляется квадратный корень.

D = √(a² + b² + 2 * a * b * cos α)

где D – диагональ этой геометрической фигуры, a, b – его ребра, cos α – косинус острого угла

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Угол (α):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Если ребра этого четырехугольника 2 и 5, а косинус острого угла (60 градусов) 0,5. Тогда диагональ рассчитывается: D = √(2²+ 5² + 2 * 2 * 5 * 0,5) = √(4 + 25 + 20 * 0,5 = √(29 + 10) = 6,2 (округленно)

Короткая диагональ через две стороны и острый угол

В параллелограмме для вычисления длины наименьшей проведенной в нем диагонали через его стороны и острый угол между ними следует возвести в квадрат каждую его сторону, затем сложить полученные значения (это первый результат). Потом следует перемножить между собой стороны, косинус тупого угла между ними, удвоить полученное значение (это второй результат). Затем из первого результата вычесть второй и найти из полученного значения квадратный корень.

D = √(a² + b²– 2 * a * b * cosα)

где D – диагональ параллелограмма, a, b – его стороны, cos α – косинус острого угла между сторонами параллелограмма

Сторона (a):

ммсмдмм

Сторона (b):

ммсмдмм

Угол (α):

градусырадианыcos

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Пусть стороны параллелограмма 2 и 4, а косинус острого угла (60) между ними 0,5. Тогда диагональ равна: D = √(2²+ 4² – 2 * 2 * 4 * 0,5) = √(4 + 16 – 16 * 0,5) = √(20 — 8) = 3,5 (ответ округлен)

Диагональ через площадь, другую известную диагональ и угол между диагоналями

В параллелограмме для вычисления длины проведенного в нем отрезка, соединяющего противоположные вершины, используя значение его площади, другой диагонали и угол между диагоналями, следует удвоить значение его площади (это первый результат). Потом следует умножить значение длины другого отрезка, соединяющего противоположные вершины, на синус угла между диагоналями (это второй результат). Затем следует разделить первый результат на второй.

D = (2 * S) / (d * sin α)

где D – диагональ параллелограмма, S – площадь параллелограмма, d – вторая диагональ этой геометрической фигуры, sinα – синус угла между диагоналями параллелограмма

Площадь (S):

мм²см²дм²м²

Диагональ (d):

ммсмдмм

Угол (α):

градусырадианыsin

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Значение площади составляет 30, одна из диагоналей 4, синус угла (30 градусов) между диагоналями 0,5. Тогда другая диагональ равна: D = 2 * 30 / 4 * 0,5 = 60 / 2 = 30

Как найти площадь параллелограмма abcd формула.

Как найти площадь параллелограмма

Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.

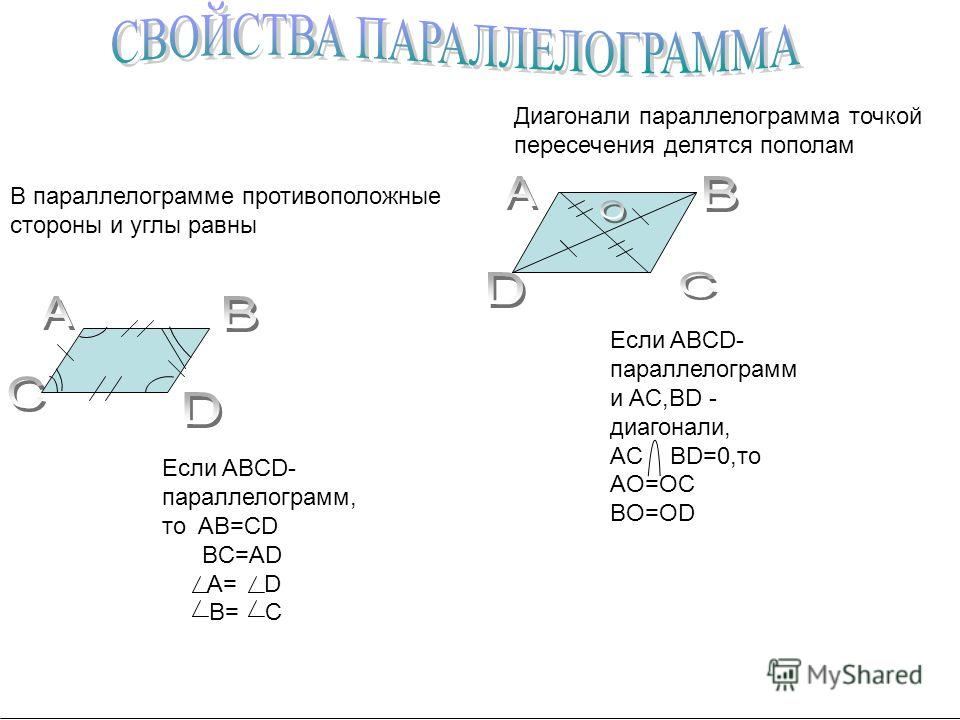
Свойства параллелограмма

Противоположные стороны параллелограмма как и противоположные углы равны между собой:
AB=CD, BC=AD ,

Диагонали параллелограмма в точке пересечения делятся на две равные части:

АО=OC, OB=OD.

Углы прилегающие к любой стороне (соседние углы) в сумме равны 180 градусов.

Каждая из диагоналей параллелограмма делит его на два одинаковые по площади и геометрическими размерами треугольники.

Еще одно замечательное свойство которое часто применяют при решении задач состоит в том, что сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех сторон:

AC^2+BD^2=2*(AB^2+BC^2) .

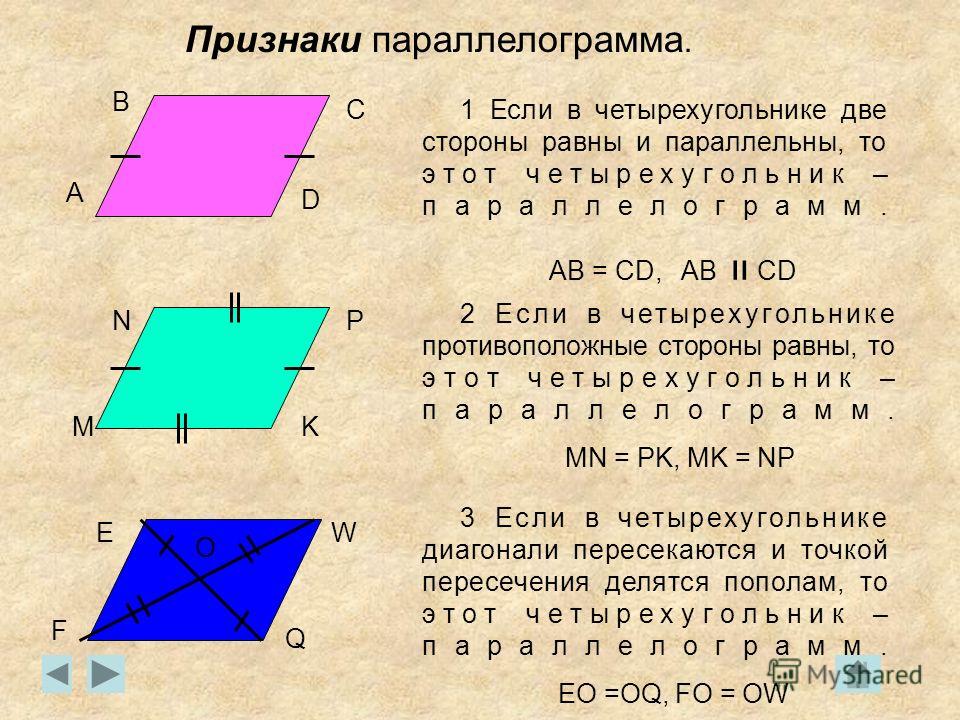
Основные признаки параллелограммов:

1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом

Биссектрисы параллелограмма

Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.

Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).

Высота параллелограмма

Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.

Формула площади параллелограмма

Площадь параллелограмма равна произведению стороны на высоту проведенную к ней. Формула площади следующая

Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними

На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.

Периметр параллелограмма

Формула для вычисления периметру параллелограмма имеет вид

то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

1. Формула площади треугольника по стороне и высоте
   Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
   
2. Формула площади треугольника по трем сторонам и радиусу описанной окружности
   
3. Формула площади треугольника по трем сторонам и радиусу вписанной окружности
   Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
   
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,

Формулы площади квадрата

1. Формула площади квадрата по длине стороны
   Площадь квадрата равна квадрату длины его стороны.
2. Формула площади квадрата по длине диагонали
   Площадь квадрата равна половине квадрата длины его диагонали.
   

   S =	1	2
   	2

где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

где S — Площадь прямоугольника,
— длины сторон прямоугольника.

Формулы площади параллелограмма

1. Формула площади параллелограмма по длине стороны и высоте
   Площадь параллелограмма
2. Формула площади параллелограмма по двум сторонам и углу между ними
   Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

   a · b · sin α

где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.

Формулы площади ромба

1. Формула площади ромба по длине стороны и высоте
   Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
2. Формула площади ромба по длине стороны и углу
   Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
3. Формула площади ромба по длинам его диагоналей
   Площадь ромба равна половине произведению длин его диагоналей.
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.

Формулы площади трапеции

1. Формула Герона для трапеции

   Где S — Площадь трапеции,
   — длины основ трапеции,
   — длины боковых сторон трапеции,
   

При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:

1. Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
2. Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
3. Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
5. Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними

Рассмотрим задачи, при решении которых используются данные свойства.

Задача 1.

Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.

Решение.

1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.

2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.

3. АD = АМ + МD = 7 см.

4. Периметр АВСD = 20 см.

Ответ. 20 см.

Задача 2.

В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.

Решение.

1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.

2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD.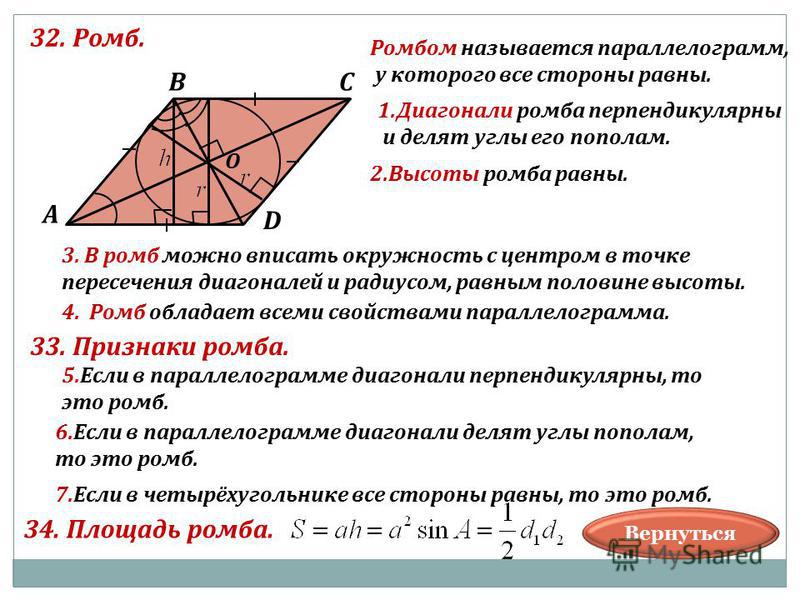 ВЕ = СF. Следовательно, прямая ВС || AD. (*)

3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.

4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)

5. Из условий (*), (**) вытекает – АВСD параллелограмм.

Ответ. Доказано. АВСD – параллелограмм.

Задача 3.

На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;

Решение.

1. В треугольнике DОМ

2. В прямоугольном треугольнике DНС
(

Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).

Но СD = АВ. Тогда АВ: НD = 2: 1.

3.

4.

Ответ: АВ: НD = 2: 1,

Задача 4.

Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.

Решение.

1. АО = 2√6.

2. К треугольнику АОD применим теорему синусов.

АО/sin D = OD/sin А.

2√6/sin 45 о = OD/sin 60 о.

ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.

Ответ: 12.

Задача 5.

У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.

Решение.

Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.

1. Посчитаем двумя разными
способами его площадь.

S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,

S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.

Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или

2 · 5√2 · 7√2 = d 1 d 2 ;

2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство

(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .

((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .

d 1 2 + d 2 2 = 296.

3. Составим систему:

{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.

Умножим второе уравнение системы на 2 и сложим с первым.

Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.

Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.

Ответ: 24.

Задача 6.

Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.

Решение.

1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.

АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.

4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;

d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.

d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.

2. Аналогично запишем соотношение для треугольника АОD.

Учтем, что

Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.

3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.

Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или

d 1 · d 2 = 80/(2√2) = 20√2

4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.

Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.

Ответ: 10.

Задача 7.

Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.

Решение.

1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.

Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .

2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.

(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .

По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.

3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.

ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.

ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.

Ответ: 145.

Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Параллелограмм – это четырехугольник, у которого стороны попарно параллельны.

В этой фигуре противоположные стороны и углы равны между собой. Диагонали параллелограмма пересекаются в одной точке и делятся ей пополам. Формулы площади параллелограмма позволяют найти значение через стороны, высоту и диагонали.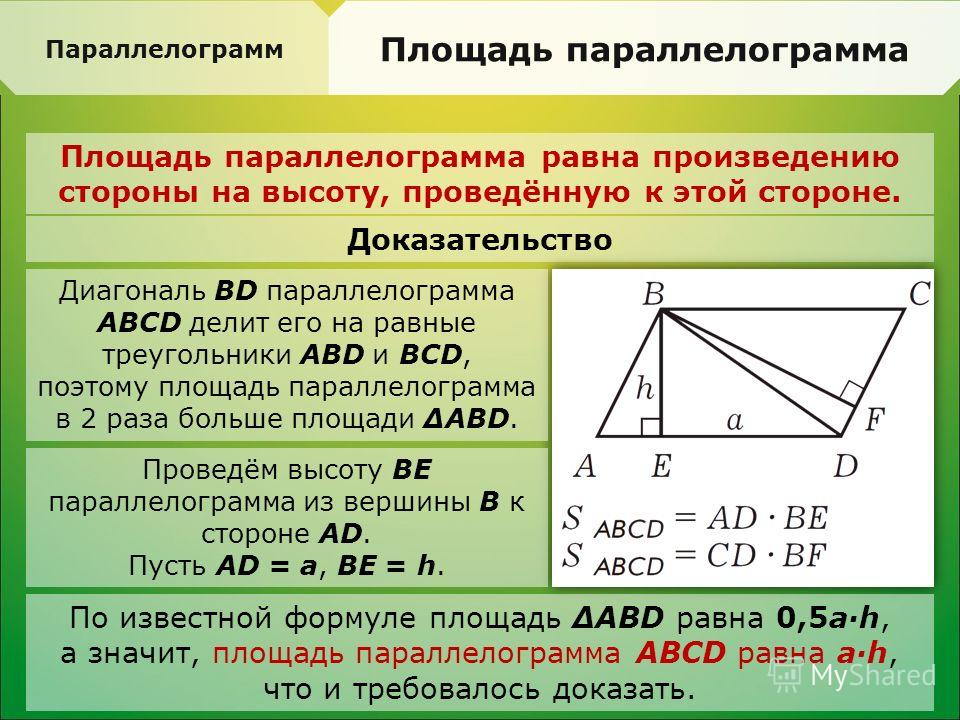 Параллелограмм также может быть представлен в частных случаях. Ими считаются прямоугольник, квадрат и ромб.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, к которой она опущена.

Этот случай считается классическим и не требует дополнительного разбирательства. Лучше рассмотрим формулу вычисления площади через две стороны и угол между ними. Этот же способ применяется в расчете . Если даны стороны и угол между ними, то площадь рассчитывается так:

Допустим, дан параллелограмм со сторонами a = 4 см, b = 6 см. Угол между ними α = 30°. Найдем площадь:

Площадь параллелограмма через диагонали

Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.

Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D = 7 см, d = 5 см. Угол, лежащий между ними α =30°.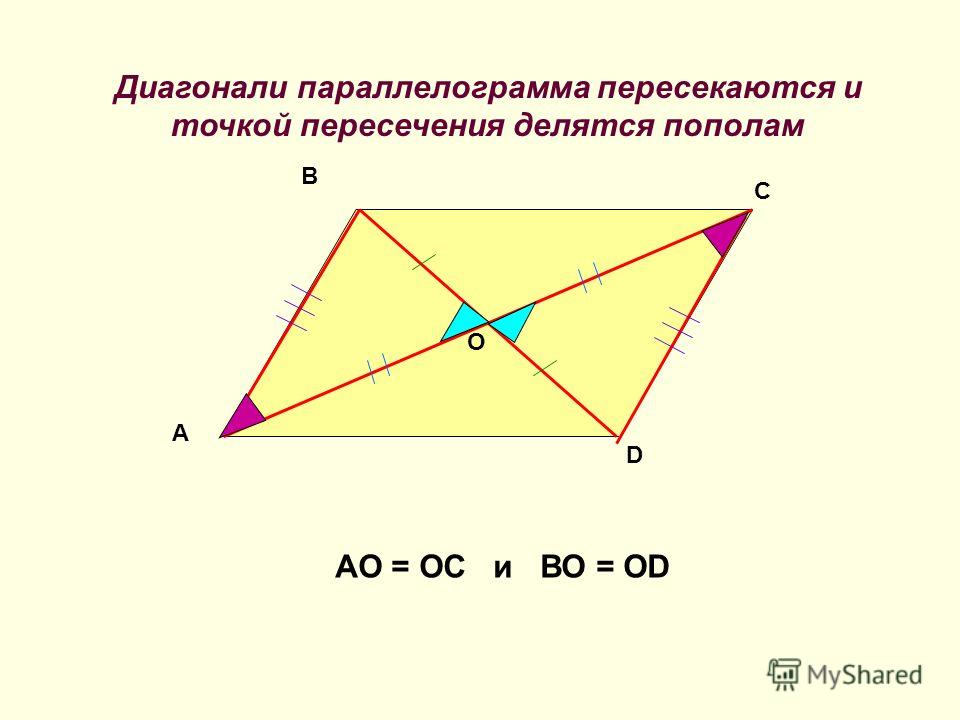 Подставим данные в формулу:

Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.

Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.

Задача: Дан параллелограмм с площадью 92 кв. см. Точка F расположена на середине его стороны ВС . Давайте найдем площадь трапеции ADFB , которая будет лежать в нашем параллелограмме. Для начала нарисуем все, что получили по условиям.
Приступаем к решению:

По нашим условиям ah =92, а соответственно, площадь нашей трапеции будет равняться

Совместимость Водолей (женщина) — Весы (мужчина)

К чему снится шуба во сне?

Урок Длина диагоналей параллелограмма

Этот Урок (Длина диагоналей параллелограмма) создан пользователем ikleyn(46406)   : Просмотр исходного кода, Показать
О ikleyn :20 20 На этом уроке вы узнаете формулу, связывающую длины диагоналей и сторон параллелограмма.
Вывод формулы основан на законе косинусов (см. урок Доказательство закона косинусов, повторно рассмотренный в теме Тригонометрия из
раздел Алгебра-II на этом сайте). Также приведены примеры, показывающие, как использовать формулу.

Теорема
Пусть a , b , c и d — длины сторон параллелограмма и и — длины его диагоналей. затем
= = . Доказывать.

Доказательство На рисунке 1 показан параллелограмм ABCD со сторонами a (BC) , b (DC) ,         c (AD) и d (AB) и диагоналями ( AC 0) и (3 BD 9090). Пусть угол DAB и угол ABC параллелограмма ABCD . Примените Закон косинусов , чтобы выразить длину диагонали как сторону AC треугольника ABC = .

Рисунок 1 . К теореме

Примените Закон косинусов , чтобы выразить длину диагонали как сторону BD треугольника ABD
= .

Теперь возьмем сумму двух последних равенств. Обратите внимание, что , поскольку углы и являются дополнительными углами в соответствии с уроком
Последовательные углы параллелограмма, который находится в теме Параллелограммы раздела Геометрия на этом сайте.

Также обратите внимание, что это как противоположные стороны параллелограмма.
Следовательно, при взятии суммы слагаемые и сокращают друг друга. Итак, после суммирования получаем
+ = + .
Поскольку противоположные стороны параллелограмма имеют одинаковую длину, вот что нужно доказать. Доказательство завершено.

Другое доказательство той же Теоремы представлено ниже. В нем используется формула длины медианы треугольника, доказанная в уроке Длина медианы треугольника (по текущей теме Геометрия раздела Задачи Word на этом сайте).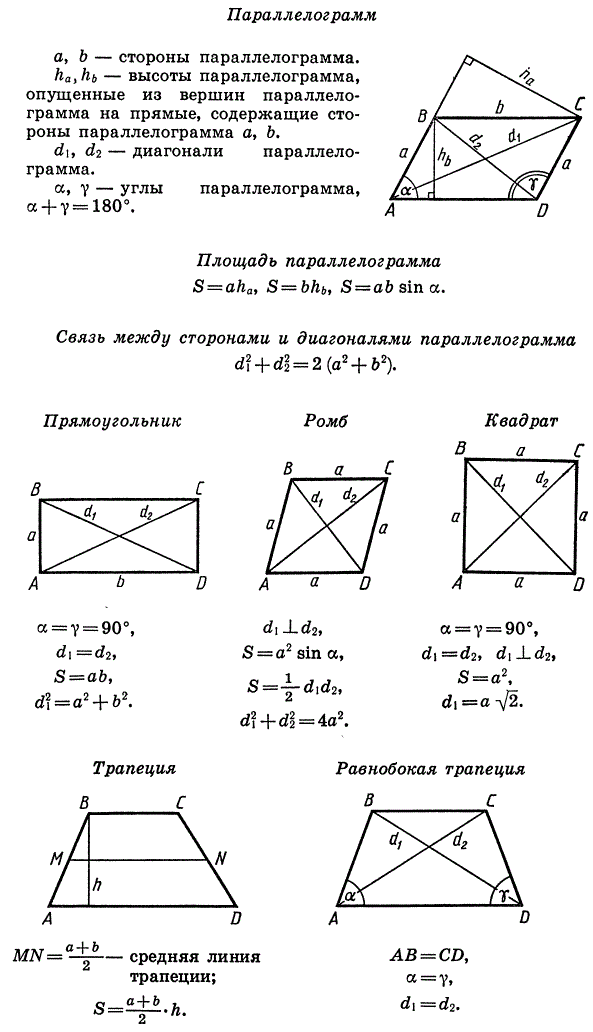 Он также использует тот факт, что диагонали параллелограмма делят друг друга пополам. Этот факт был доказан в уроке Свойства диагоналей параллелограммов (по теме Треугольники раздела Геометрия на этом сайте).

Доказательство 2 На рис. 2 показан параллелограмм ABCD со сторонами a (BC) , b (DC) ,         c (AD) и d (AB) и диагонали ( AC ) и ( BD ) с O точкой пересечения. Рассмотрим треугольник ACD . Так как в параллелограмме ABCD диагонали AC и BD делят пополам других, то часть диагонали DO является медианой в треугольнике ACD , и длиной отрезка DO составляет половину длины диагонали DB .

Рисунок 2 . К другому доказательству теоремы

Примените формулу длины медианы из урока Длина медианы треугольника. Мы получаем

= .

Теперь возведите это равенство в квадрат (обе стороны). Мы получаем

= .

Умножить обе части на 4 и переместите термин с правой стороны на левую, поменяв знак. Мы получаем
= .

Это именно то, что утверждает Теорема . Доказательство завершено.

Итак, теперь вы знаете формулу суммы квадратов длин диагоналей параллелограмма и знаете, что она тесно связана с формулой
для длины медианы треугольника.

Пример
Стороны параллелограмма 8 см и 6 см длиной . Одна диагональ 5 см длины.
Найдите длину второй диагонали параллелограмма.

Раствор
Пусть х — длина второй диагонали параллелограмма.
Применить формулу из теоремы . Вы получаете уравнение

= .

Сделайте все необходимые расчеты и шаг за шагом упростите их:

= = ,
= ,
= 175,
= = ~ 13,23 (приблизительно).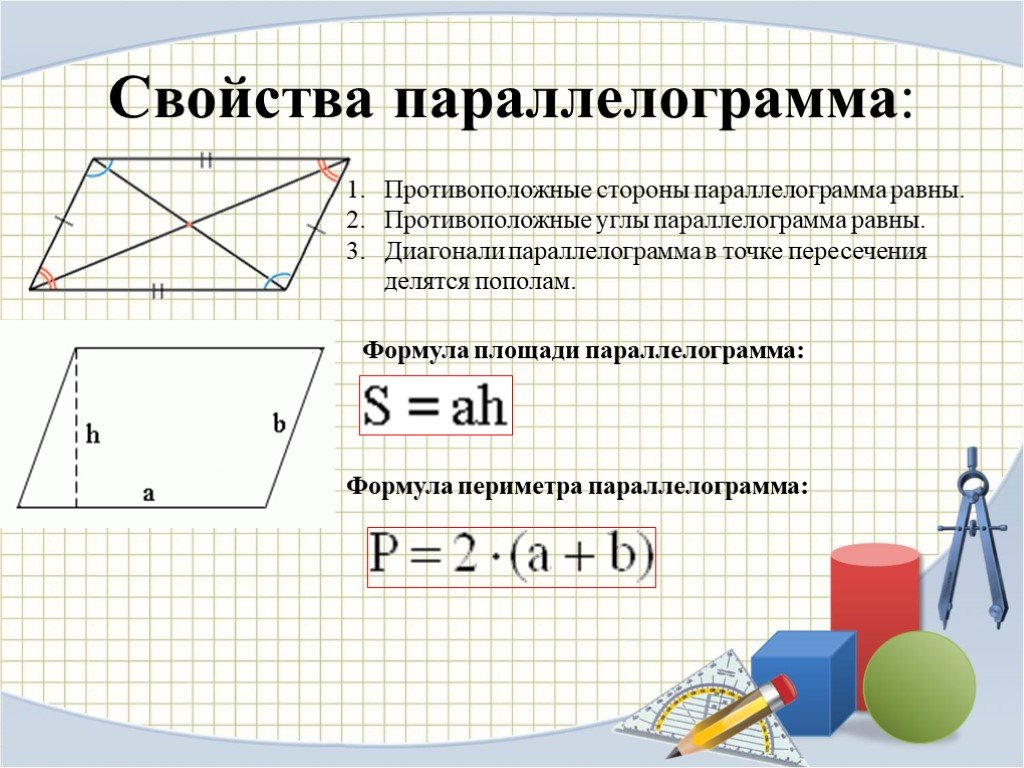

Ответить . Длина второй диагонали параллелограмма см ~ 13,23 см (приблизительно).

Другие мои уроки по параллелограммам на этом сайте
    — В параллелограмме каждая диагональ делит его на два равных треугольника.
    — Свойства сторон параллелограмма
    — Свойства сторон параллелограмма
    — Свойства диагоналей параллелограмма
    — Противоположные углы параллелограмма
    — Последовательные углы параллелограмма
    — Середины четырехугольника являются вершинами параллелограмма
    — Замечательные сложные задачи на параллелограммы
    — КАК РЕШАТЬ задачи на меры сторон параллелограмма — Примеры
    — КАК РЕШАТЬ задачи на углы параллелограмма — Примеры
    — СВОЙСТВА ПАРАЛЛЕЛОГРАММОВ

Для навигации по всем темам/урокам онлайн-учебника по геометрии используйте этот файл/ссылку  ГЕОМЕТРИЯ — ВАШ ОНЛАЙН-УЧЕБНИК.

Измерения параллелограммов, включая углы, стороны и диагонали — Krista King Math

Определение всех мер параллелограмма

Параллелограмм  – это четырехугольник, противоположные стороны которого параллельны.

Параллельные стороны позволяют многое узнать о параллелограмме.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. 9\циркуляр???

Диагонали делят друг друга пополам (разрезают друг друга пополам)

Как решить для каждой меры параллелограмма, включая углы, длины сторон и длины диагоналей

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂 9\циркуляр???

Теперь мы можем использовать тот факт, что противоположные стороны параллелограмма параллельны, чтобы утверждать, что ???JK\parallel ML???. Это означает, что диагональ ???JL??? параллелограмма также является секущей этих двух параллельных прямых.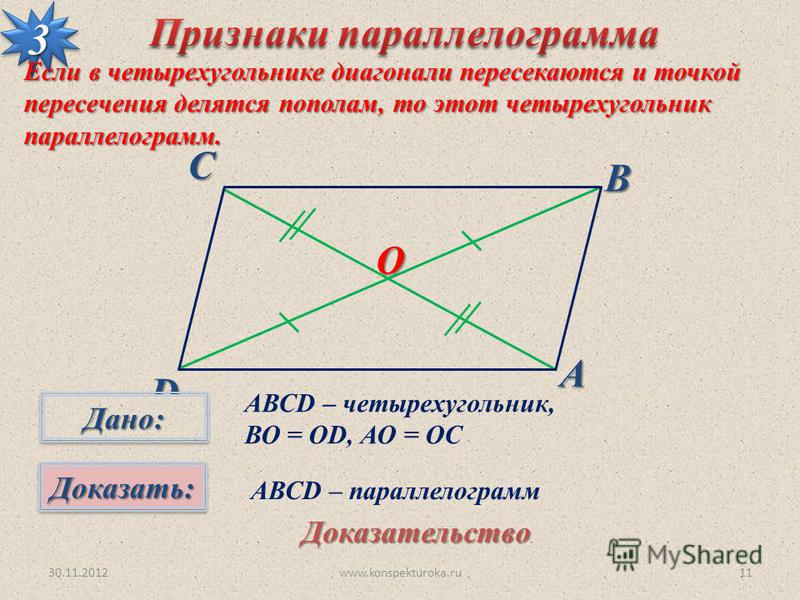 Это означает, что ???\угол KLJ??? и ???\угол MJL??? являются альтернативными внутренними углами. Пары чередующихся внутренних углов конгруэнтны, поэтому ???m\угол KLJ=m\угол MJL=y???.

9\циркуляр???

Параллелограмм  – это четырехугольник, у которого противоположные стороны параллельны.

Пример

Если ???STUV??? является параллелограммом, и если ???VT=4n+34??? и ???VE=7n-3???, какова длина ???ET????

Мы знаем, что диагонали параллелограмма делят друг друга пополам. Добавим эту информацию на схему.

Теперь мы можем увидеть нужные отношения. Поскольку диагонали делятся пополам, ???VE=ET??? и???VE=(1/2)VT???. Мы можем использовать то, что мы знаем, чтобы найти длину ???VE??? и тогда мы узнаем длину ???ET??? также.