Диаметр и хорда окружности: Окружность: радиус, хорда, диаметр и дуга

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. 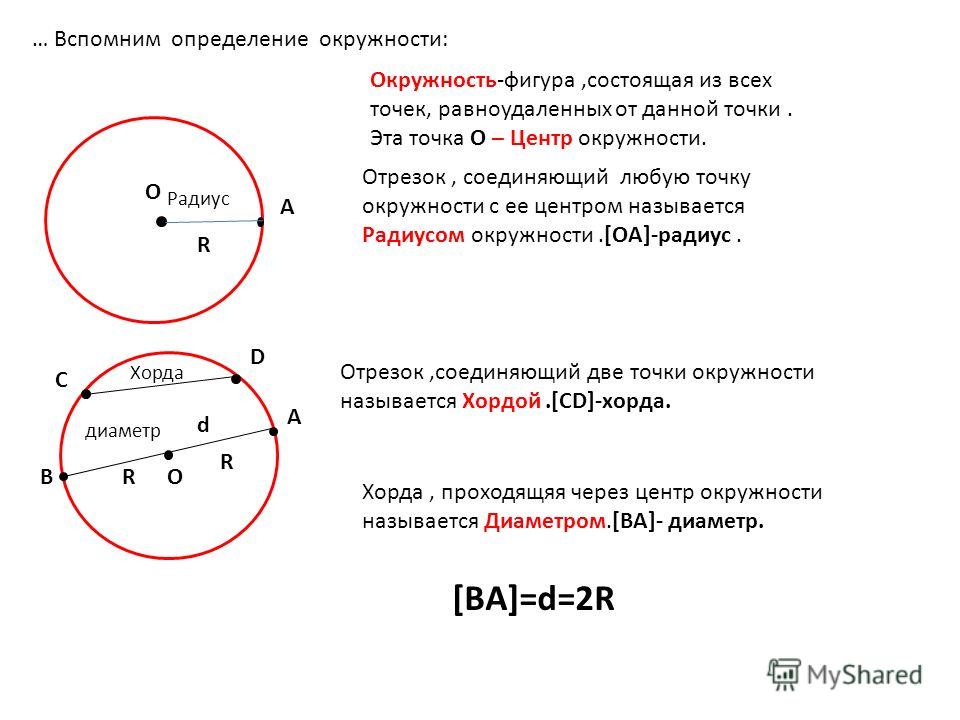Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 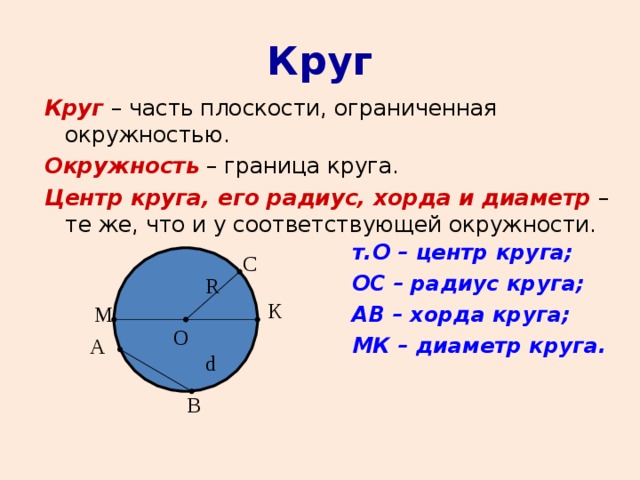94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. 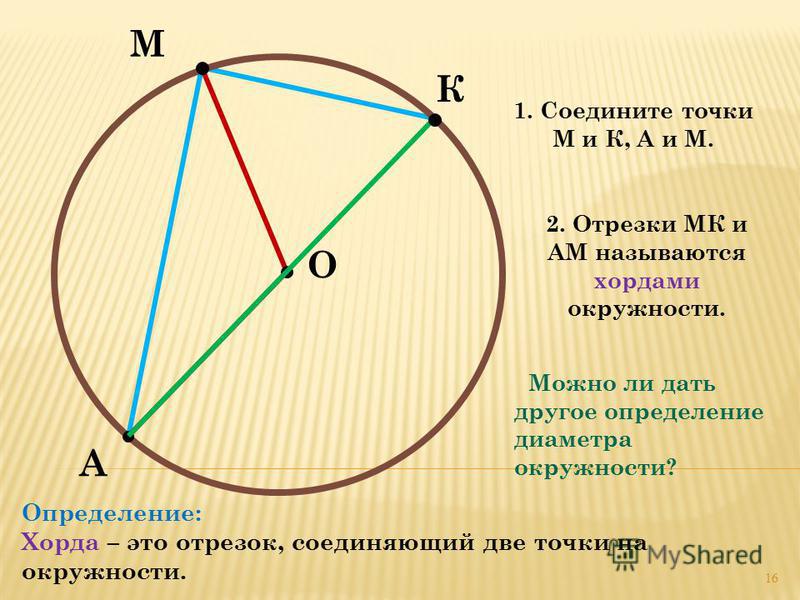Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 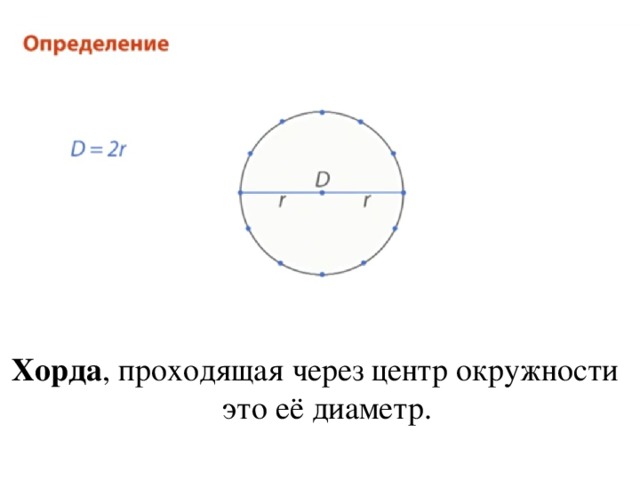155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 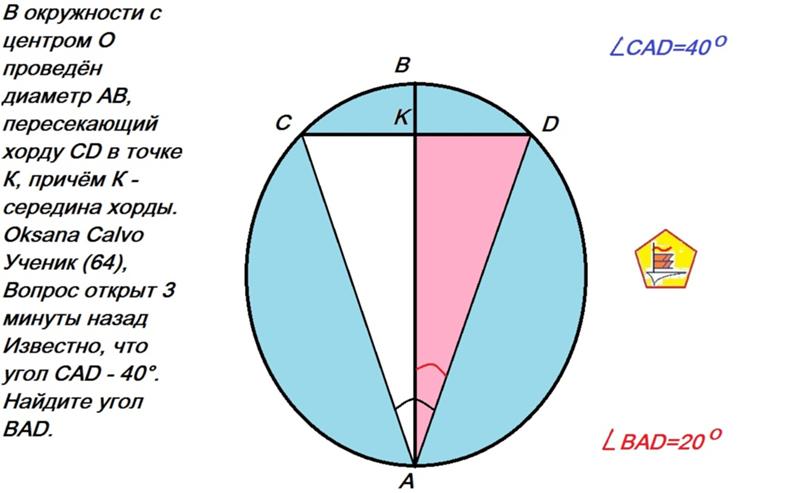176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. 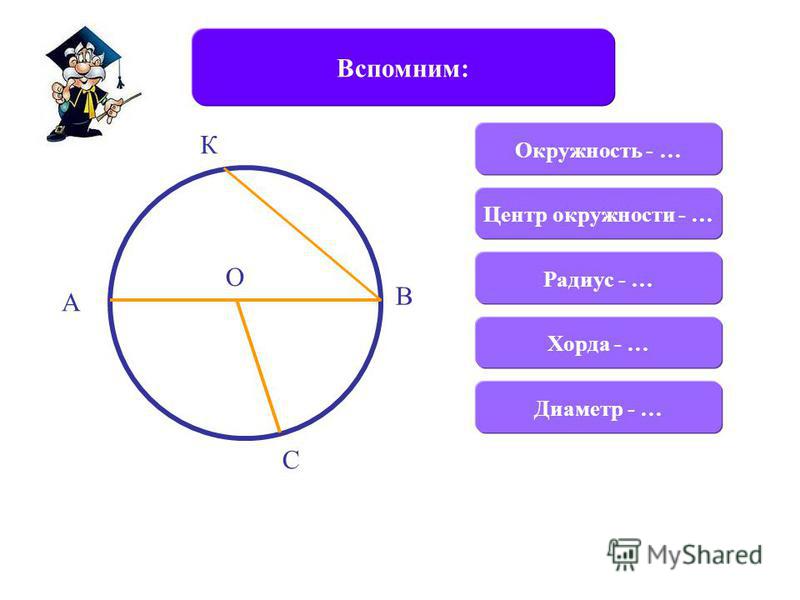§ 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. 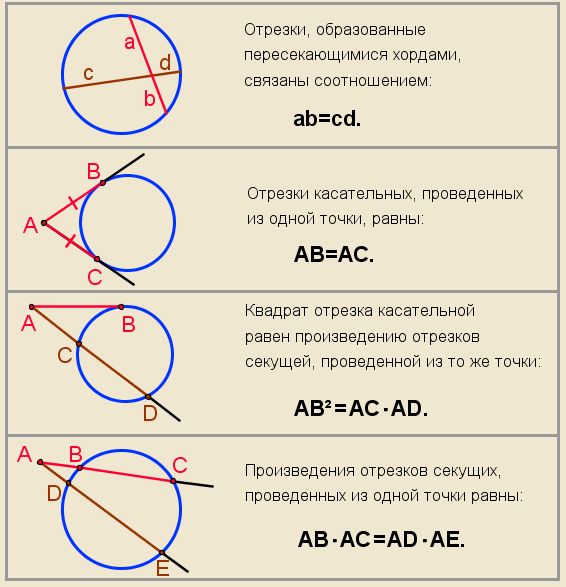Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

Что называется хордой окружности в математике и геометрии: определение, основные свойства

Главная » Наука

Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.

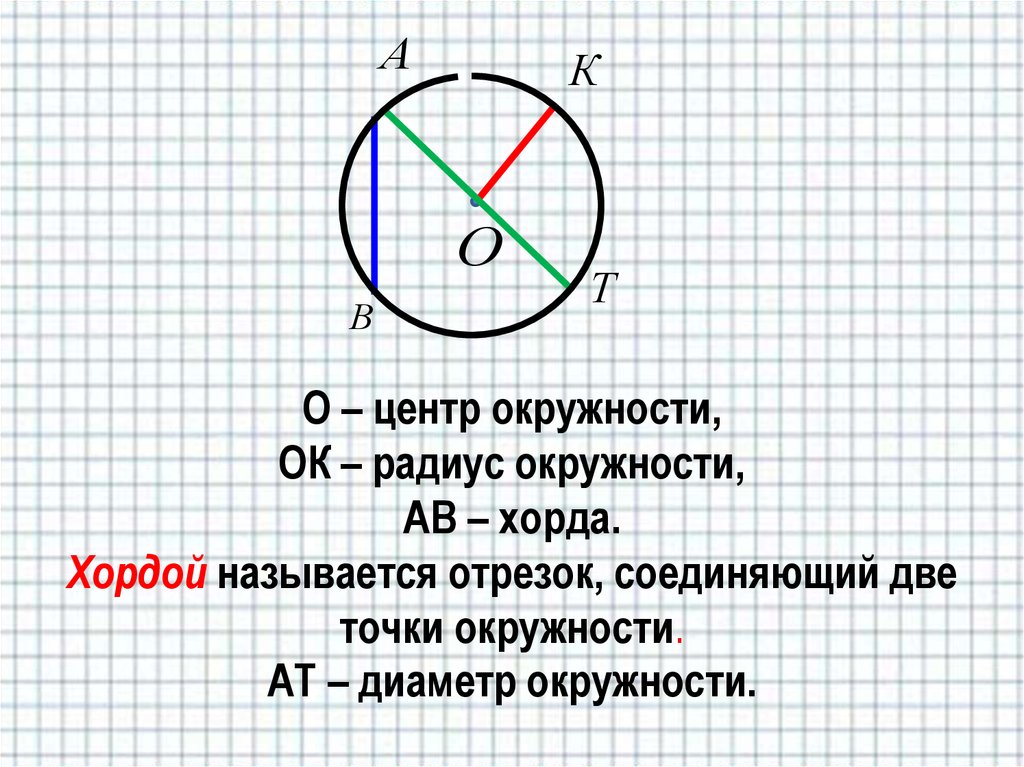
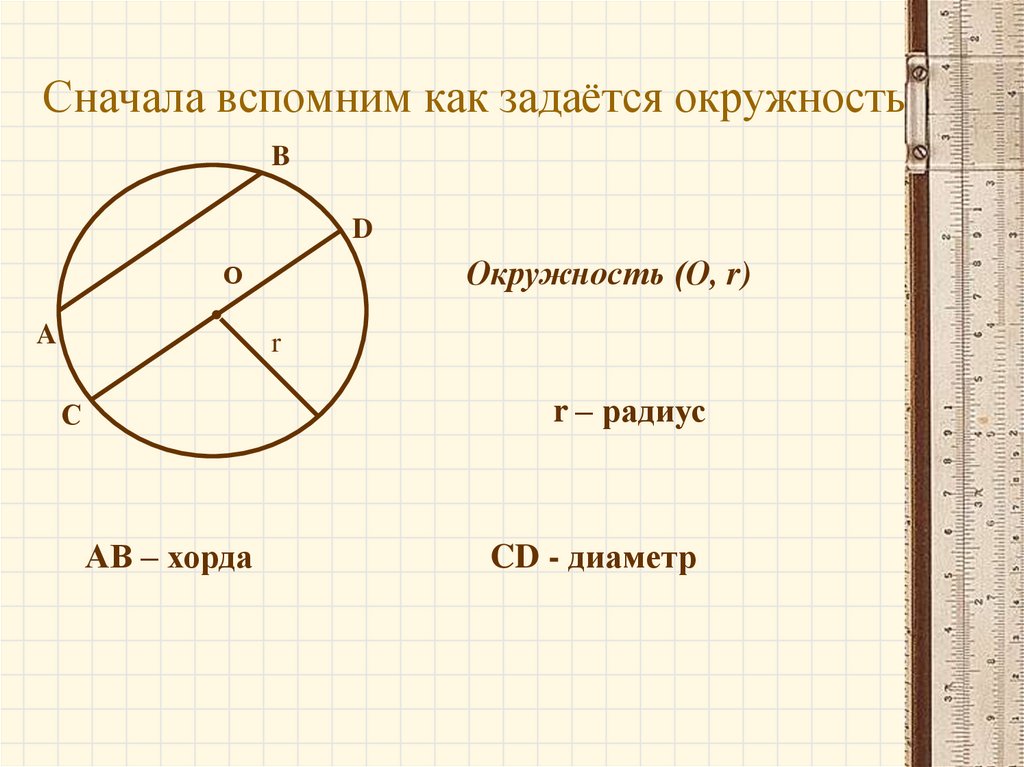
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.

Оглавление:

• Как построить геометрическую хорду
• Свойства
• Взаимосвязь с радиусом и диаметром
• Хорда и радиус
• Отношения со вписанными углами
• Взаимодействия с дугой

Содержание

Как построить геометрическую хорду

Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.

Это интересно: в геометрии луч это что такое, основное понятие.

Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.

Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.

Свойства

Существует ряд закономерностей, связывающих между собой хорды и центр круга:

1. Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
2. Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
3. Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
4. Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
5. Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
6. Отрезок с наименьшей длиной представляет собой точку.
7. Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.

Это интересно: разность векторов, определение разности.

Взаимосвязь с радиусом и диаметром

Вышеуказанные математические понятия связаны между собой следующими закономерностями:

1. Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
2. С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
3. Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
4. Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
5. Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
6. Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.

Хорда и радиус

Между этими понятиями существуют следующие связи:

1. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
2. Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
3. Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
4. Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
5. Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
6. Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.

Отношения со вписанными углами

Углы, вписанные в окружность, подчиняются следующим правилам:

1. Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
2. Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
3. Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
4. Вписанный угол, который опирается на диаметр круга, является прямым.
5. Равные между собой по размеру отрезки стягивают равные центральные углы.
6. Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
7. Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.

Взаимодействия с дугой

Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:

1. Две равные между собой хорды стягивают равные дуги.
2. Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
3. Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.

Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.

Диаметр и хорды — PSAT Math

Все математические ресурсы PSAT

10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept

PSAT Math Help » Геометрия » Плоская геометрия » Круги » Диаметр и хорды

Радиус круга выше равен , а мера – . Какова длина хорды?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить задачу с хордами, нарисуйте прямоугольные треугольники, используя хорду, радиусы и линию, соединяющую центр окружности с хордой под прямым углом.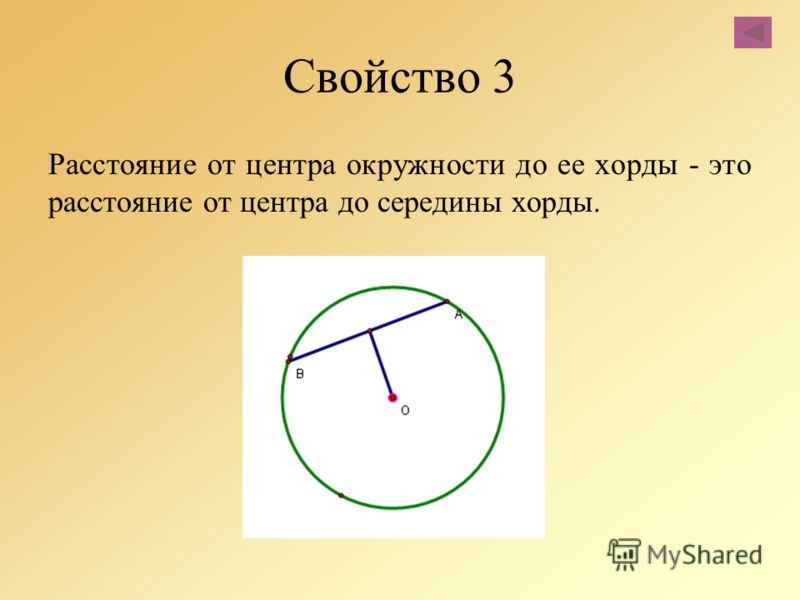

 

Теперь хорда делится на две равные части, а угол AOB делится пополам. Вместо одного угла в 120 градусов теперь у вас есть два треугольника 30-60-90. Треугольники 30-60-90 характеризуются соотношением сторон:

Итак, чтобы найти длину хорды, сначала найдите длину каждой половины. Поскольку треугольники в вашем круге подобны треугольнику 30-60-90 выше, вы можете установить пропорцию. Гипотенуза нашего треугольника равна 6 (радиус окружности), поэтому она больше 2 (гипотенуза нашего модельного треугольника 30-60-90). Половина хорды окружности – это катет треугольника, расположенный напротив угла 60 градусов (120 / 2), поэтому он соответствует стороне модельного треугольника.

Следовательно, 

Поскольку x равен половине хорды, ответ равен .

Сообщить об ошибке

Пусть представляет собой площадь круга и представляет его длину окружности. Какое из следующих уравнений выражается через ?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула площади круга , а формула длины окружности .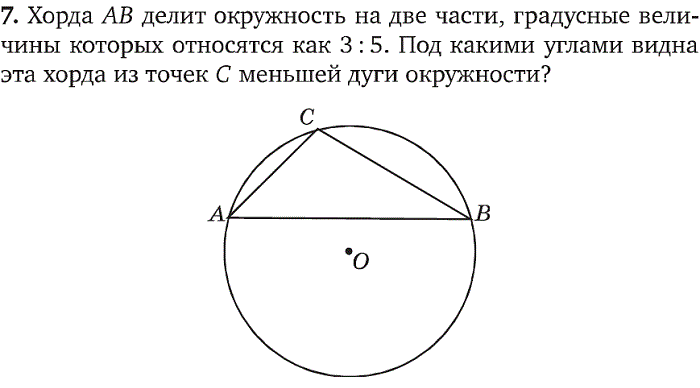 Если мы решим для C через r, мы получим
.

Затем мы можем подставить это значение r в формулу площади: круг в четыре раза больше окружности того же самого круг, каков диаметр круга?

Возможные ответы:

16

8

4

2

32

Правильный ответ:

16

Объяснение:

Задайте площадь круга, равную четырехкратной длине окружности πr ² = 4(2 πr ).

Вычеркните оба символа π  и по одному r с каждой стороны, и у вас останется r = 4(2), поэтому r = 8 и, следовательно, d  = 16.

Сообщить об ошибке

периметр круга равен 36 π. Каков диаметр круга?

Возможные ответы:

36

18

72

6

3

Правильный ответ:

36

Объяснение:

Периметр круга = 2 πr = πd

Следовательно, d = 36

Сообщить об ошибке

Если площадь круга, касающегося квадрата на рисунке выше, равна , каково ближайшее значение к площадь квадрата?

Возможные ответы:

Правильный ответ:

Объяснение:

Получите радиус круга из площади.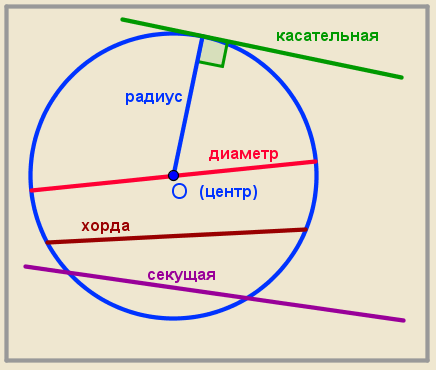

Разделите квадрат на 4 треугольника, соединив противоположные углы. Эти треугольники будут иметь прямой угол в центре квадрата, образованный двумя радиусами круга, и двумя углами по 45 градусов в углах квадрата. Поскольку у вас есть треугольник 45-45-90, вы можете рассчитать стороны треугольников как , , и . Радиусы окружности (от центра до углов квадрата) будут 9. Гипотенуза (сторона квадрата) должна быть .

Тогда площадь квадрата равна .

Сообщить об ошибке

Две стороны прямоугольного треугольника имеют соответственно 3 и 4 длины. Чему равна площадь окружности, описанной около треугольника?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы окружность содержала все 3 вершины, гипотенуза должна быть равна диаметру окружности. Гипотенуза и, следовательно, диаметр равны 5, так как это должен быть прямоугольный треугольник 3-4-5.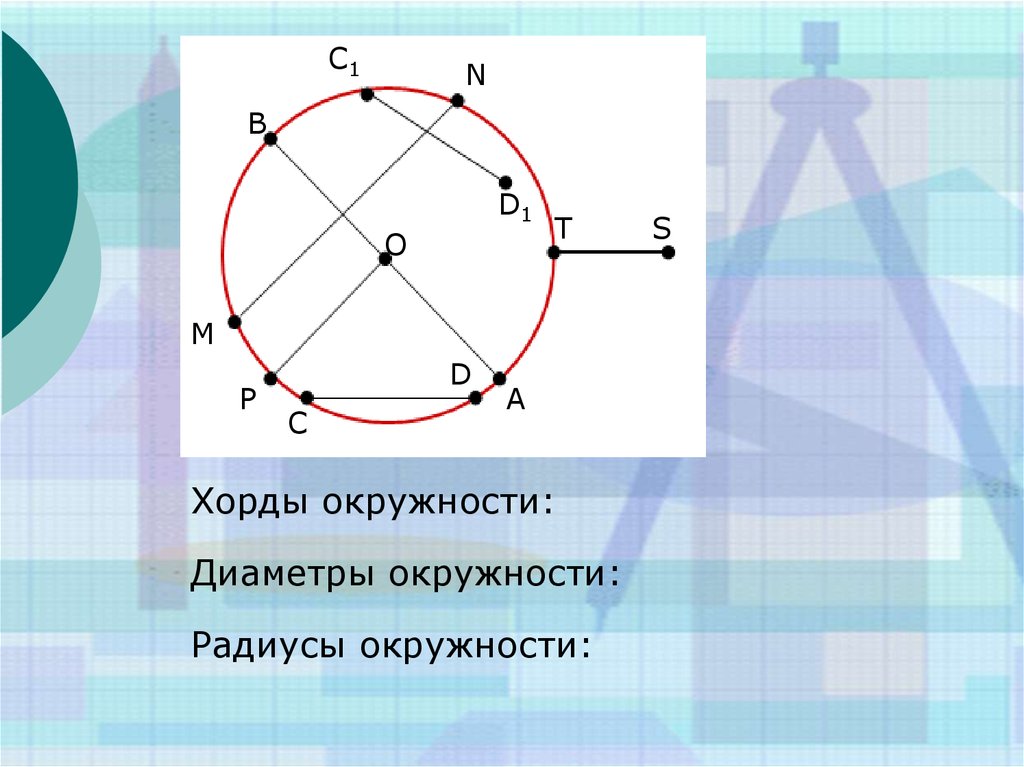

Уравнение площади круга: A = πr ² .

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе.

В приведенном выше круге длина дуги  равна и . Каков диаметр круга?

Возможные ответы:

Правильный ответ:

Объяснение:

Назовите диаметр . Так как ,  является кругом и  является кругом с окружностью .

 – это длина, поэтому

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе.

В приведенном выше круге длина дуги равна 10 и . Укажите диаметр круга. (Ближайшая десятая).

Возможные ответы:

Недостаточно информации для ответа на вопрос.

Правильный ответ:

Объяснение:

Назовите диаметр . Так как ,  это круг с окружностью . Поскольку его длина равна 10, длина окружности в 5 раз больше, или 50. Следовательно, установите в формуле длины окружности:

Сообщить об ошибке

Уведомление об авторских правах

Все математические ресурсы PSAT

10 диагностических тестов 421 практический тест Вопрос дня Карточки Учитесь по концепции

Аккорд круга — GCSE по математике

Введение

Что такое хорда окружности?

Ключевые части круга

Доказательство того, что серединный перпендикуляр из центра окружности к хорде делит хорду пополам

Как найти недостающие длины с помощью хорд

Хорда окружности рабочий лист

Распространенные заблуждения

Практикуйте аккорд круга вопросы

Хорда круга Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое хорда окружности?

Ключевые части круга

Доказательство того, что серединный перпендикуляр из центра окружности к хорде делит хорду пополам

Как найти недостающие длины с помощью хорд

Хорда окружности рабочий лист

Распространенные заблуждения

Практические вопросы по аккорду круга

Хорда круга Вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о теоремах о кругах, включающих хорд окружности , включая их применение, доказательство и использование для решения более сложных задач.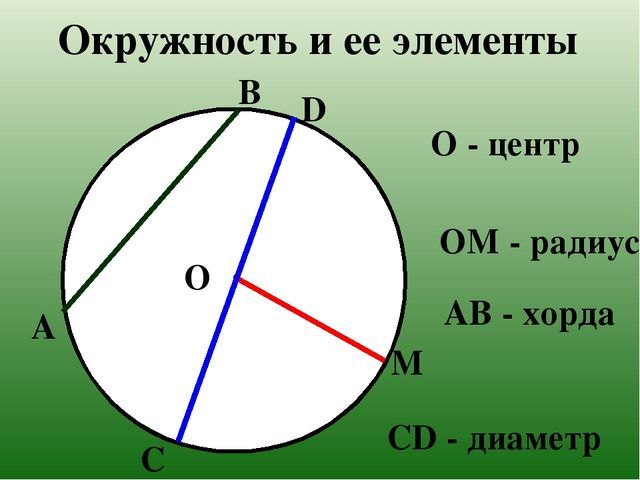

Существует также рабочих листов с теоремой о круге , основанных на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое хорда окружности?

Хорда окружности — это прямая линия, соединяющая две точки на окружности окружности. Самая длинная хорда в окружности — это диаметр окружности.

Перпендикуляр из центра окружности к хорде делит хорду пополам (разделяет хорду на две равные части).

На приведенной выше диаграмме AB — это хорда, а CE — радиус. Здесь мы видим, что радиус CE делит хорду AB пополам под углом 90 градусов, а длины AD = BD = x.

Что такое хорда окружности?

Ключевые части круга

Ниже приведена диаграмма, показывающая ключевые части круга для этой теоремы:

• Диаметр круга — это ширина круга через центр. Концы диаметра лежат на окружности окружности. Диаметр в два раза больше длины радиуса окружности.
• Дуга является частью окружности.
• Большой сегмент является большей частью круга, когда он окружен хордой и большой дугой .
• Младший сегмент — это меньшая часть окружности, когда она пересекается хордой и малой дугой .
• радиус круга — это расстояние между центром круга и окружностью круга.

Стягивающие углы

Угол внутри окружности образуется двумя хордами, сходящимися в одной точке на окружности. На рисунках ниже показан вписанный угол, опирающийся на дугу AC из точки B для двух разных окружностей.

Полезный совет: слово «подтягивать» часто используется в круговых теоремах, поэтому убедитесь, что вы знаете, что оно означает.

Доказательство того, что серединный перпендикуляр из центра окружности к хорде делит хорду пополам

Чтобы доказать эту теорему, вам не нужно знать никакие другие теоремы об окружности.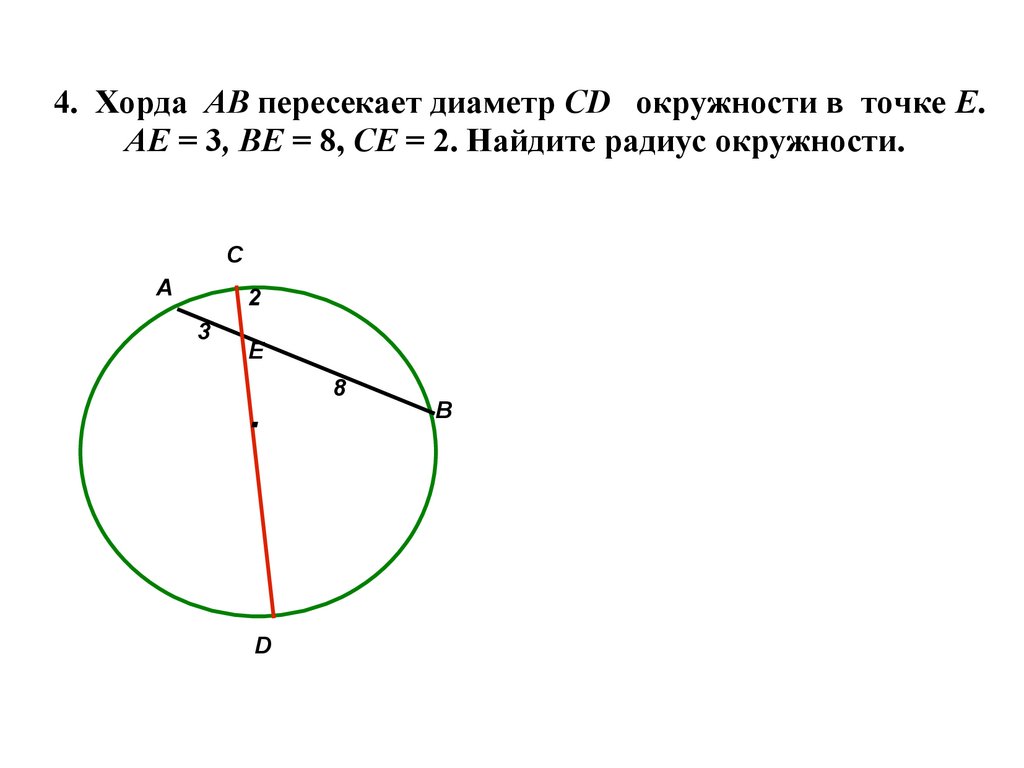 Вам просто нужно быть уверенным в углах треугольника и конгруэнтности .

Шаг	Диаграмма	Описание
1		Начнем с окружности с центром C. Линия AB — это хорда, а CE — радиус. Прямые CE и AB пересекаются в точке D под углом 90 градусов друг к другу, потому что они перпендикулярны.
2		Затем проводим линии AC и BC. Длина AC = BC, так как они оба являются радиусами окружности. Треугольники ACD и BCD, таким образом, являются прямыми углами, их гипотенузы равны, а прямая CD совпадает, поскольку она является общей для обоих треугольников. Это означает, что треугольники конгруэнтны, поэтому отрезок BD и отрезок AD имеют одинаковую длину или BD = AD.

Как найти недостающие длины с помощью хорд

Чтобы найти недостающие углы или длину хорды:

1. Найдите ключевые части круга для соответствующей теоремы круга.
2. Используйте другие данные об углах, чтобы определить недостающие углы .
3. Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .

Как найти недостающие длины с помощью хорд

Рабочий лист «Хорда круга»

Получите бесплатный рабочий лист «Хорда круга», содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист «Хорда круга»

Получите бесплатный рабочий лист «Хорда круга», содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры хорды окружности

Пример 1: отношение косинуса

Внизу круг с центром C . Точки А, В, С и D лежат на окружности. Хорда АВ перпендикулярна прямой CD в точке Е. Прямая AE равна 5 см, а угол ADE = 71°.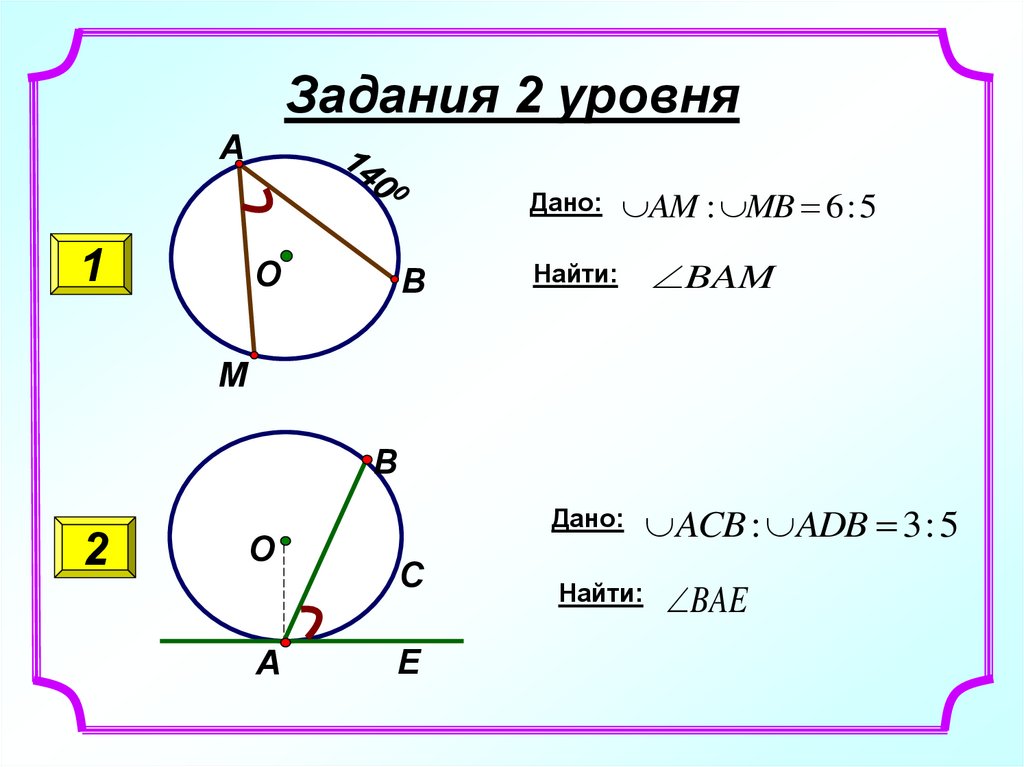 Вычислите длину прямой до н.э. с точностью до 1 знака после запятой.

1. Найдите ключевые части круга для соответствующей теоремы круга .

Здесь имеем:

• CD диаметр
• AB — хорда, перпендикулярная CD
• Угол ADE = 71°
• Угол BEC = 90°
• Линия AE = 5см
• Линия ВС = х

2 Используйте другие данные об углах для определения других необходимых углов .

Поскольку углов в одном отрезке равны , угол ADE равен углу ABC, значит, угол ABC = 71° . Кроме того, поскольку , перпендикулярный из центра окружности к хорде, делит пополам хорду , линия BE равна AE, поэтому BE = 5 см.

3 Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .

Чтобы вычислить длину хорды BC, нам нужно использовать тригонометрию, так как мы знаем длину одной стороны и два угла, где один угол равен 90°.

Поскольку мы знаем сторону, прилегающую к углу, и хотим вычислить гипотенузу, нам нужно использовать \cos(\theta)=\frac{A}{H}  с H в качестве подлежащего.

H=\frac{A}{\cos(\theta)}

x=\frac{5}{\cos(71)}

x=15,4 см (1 дп)

Пример 2: коэффициент синуса

Ниже показана окружность с центром O . А, В, С и D лежат на окружности. AC и BD — перпендикулярные прямые. Вычислите длину AE с точностью до 1 знака после запятой.

Найдите ключевые части круга для соответствующей теоремы круга .

Здесь имеем:

• BD диаметр
• AC — хорда, перпендикулярная BD
.
• Угол CDE = 35°
• Угол CED = 90°
• Линия CD = 8см
• Линия АЕ = х

Используйте другие данные об углах для определения других необходимых углов .

Поскольку , перпендикулярный из центра окружности к хорде, делит пополам хорду , это означает, что длина AE равна длине CE.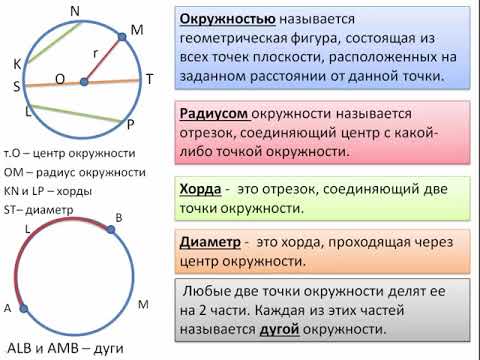

Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .

Мы можем вычислить длину CE, используя прямоугольный треугольник DEC, поскольку мы знаем гипотенузу, угол и находим недостающую сторону:

\[CE=Синь\раз(\тета)\\ CE=8\times\sin(35)\\ CE=4,6 см (1 dp)\]

Пример 3: отношение касательной

Ниже показана окружность с центром O . А, В, С и D лежат на окружности. AC и BD — перпендикулярные прямые. FG является касательной в точке B и параллельна прямой AC. Вычислите длину BE с точностью до 1 знака после запятой.

Найдите ключевые части круга для соответствующей теоремы круга .

Здесь имеем:

• BD диаметр
• AC — хорда, перпендикулярная BD
.
• Угол ABF = 77°
• Линия СЕ = 12см
• Линия ВЕ = х

Используйте другие данные об углах для определения других необходимых углов .

Поскольку , перпендикулярный из центра окружности к хорде, делит пополам хорду , это означает, что длина AE равна длине CE.

Поскольку тангенс и радиус пересекаются в точке 9{\circ}\]

Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .

Мы можем рассчитать длину хорды BE, используя прямоугольный треугольник ABE, поскольку мы знаем сторону, противоположную углу ABE , угол ABE и находим отсутствующую соседнюю сторону BE :

BE=\frac{O} {\tan(\theta)}

x=\frac{12}{\tan(13)}

x=52,0 см (1dp)

Пример 4. Теорема Пифагора

A, B, C и D точки на окружности с центром O . Радиус ОА = 6см, хорда АВ = 13см. Хорда BD перпендикулярна диаметру AC в точке E .

ОЕ:ОС = 1:1 . Вычислите длину BE с отметкой x.

Найдите ключевые части круга для соответствующей теоремы круга .

Здесь имеем:

• AC это диаметр
• BD — хорда, перпендикулярная AC
• Линия АВ = 13см
• Линия ОА = 6см
• Линия ВЕ = х

Используйте другие данные об углах для определения других необходимых углов .

AEB равно 92=88\\ x=9.38cm (2dp)\]

Пример 5: равнобедренный треугольник

Окружность с центром O имеет перпендикулярные диаметры AC и BD . Используйте информацию на диаграмме, чтобы вычислить значение x .

Найдите ключевые части круга для соответствующей теоремы круга .

Здесь имеем:

• AC = BD диаметр
• AC и BD перпендикулярны
• Линия ОС = 4см
• Линия АВ = х

Используйте другие данные об углах для определения других необходимых углов .

OA = OB = OC = OD — это все радиусы, поэтому мы можем утверждать, что OA = OB = 4 см. AOB равен 90°, так как AC и BD перпендикулярны.

Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .

Поскольку мы знаем две стороны прямоугольного треугольника AOB , нам нужно использовать теорему Пифагора, чтобы найти значение x (длину хорды AB ).

\[х^2=4^2+4^2\\ х^2=16+16\\ х^2=32\\ х=4\квадрат{2}см\]

Пример 6: полукруг

На приведенном ниже рисунке показан полукруг.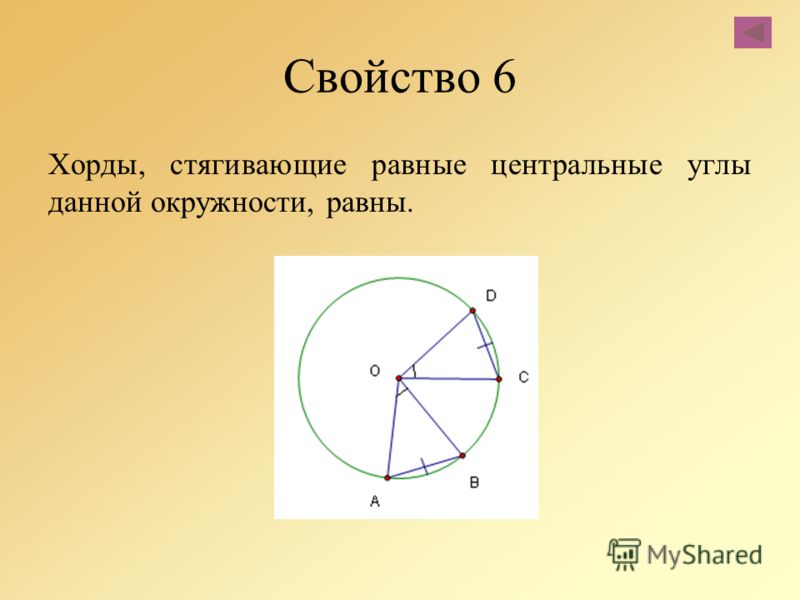 Линия BF является хордой, перпендикулярной диаметру. Вычислите длину диаметра AD.

Найдите ключевые части круга для соответствующей теоремы круга .

Здесь имеем:

• AD это диаметр
• BF — хорда, перпендикулярная AD
.
• Угол BGE = 112°
• Линия DE = 3см
• Строка AD = x

Используйте другие данные об углах для определения других необходимых углов .

Угол полуокружности равен 90° поэтому угол AEB = 90° . Углы на прямой составляют 180° , поэтому BGA = 180 — 112 = 68° . Поскольку угол ABG = 90°, угол BAG = 180 — (90 + 68) = 22°. Теперь мы знаем

Используйте теорему Пифагора или тригонометрию, чтобы найти недостающую длину .

Поскольку ADE — прямоугольный треугольник с DE = 3 см и DAE = 22°, мы можем использовать тригонометрию для вычисления стороны AD:

\[H=\frac{Opp}{\sin(\theta)}\\ H=\frac{3}{\sin(22)}\\ H=8. 0cm (1dp)\]

Распространенные заблуждения

• Теорема Пифагора отсутствует сторона

Недостающая сторона вычисляется путем неправильного сложения квадрата гипотенузы и меньшей стороны, или путем вычитания квадрата меньшей стороны.

• Неверная тригонометрическая функция

Используется неверная тригонометрическая функция, поэтому вычисляемая сторона или угол неверны. Это также включает в себя обратные тригонометрические функции. 9{\circ} (BC перпендикулярна AF)

(1)

x=\frac{6.2}{\cos(55)}=10.8cm\quad(1dp)

(1)

2. (a) Окружность внизу имеет центр O. Диаметр BD перпендикулярен хорде AC в точке E. CE = 5,4 см, а угол AB = 8,1 см. Вычислите длину линии BE.

(b) Вычислите величину угла ABE. Запишите свой ответ с точностью до 1 знака после запятой.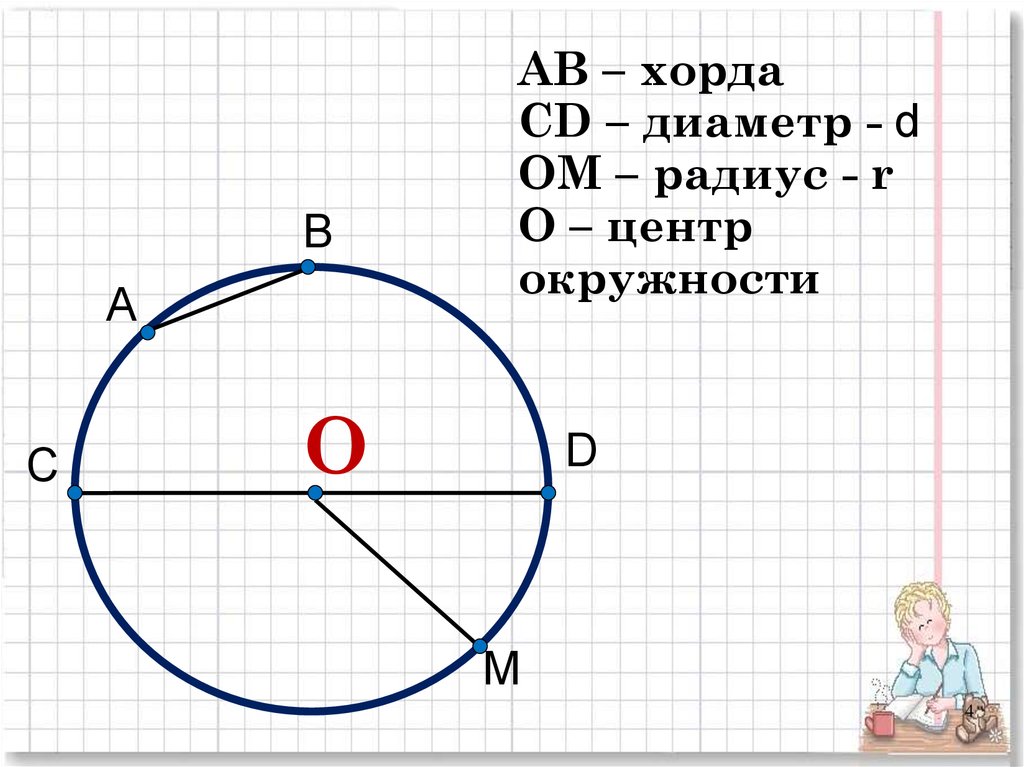

 

(5 баллов) 9{2}}=8\sqrt{2}

(1)

AD = CD = 11 см
Масштабный коэффициент увеличения: 11\div8=1,375

(1)

900 12 AC=8\sqrt{2}\times{1,375}=11\sqrt{2}

(1)

11\кв{2}-8\кв{2}=3\кв{2} см

(1)

Контрольный список для обучения

Теперь вы научились:

• Применять и доказывать стандартные теоремы о окружностях, касающиеся углов, радиусов, касательных и хорд, и использовать их для доказательства связанных результатов

Все еще застряли?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта.

No related posts.