Дифференциал и интеграл: Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?

Содержание

Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?

Дифференциал. Геометрический смысл. Связь приращения и дифференциала функции

Признаки постоянства, монотонности функции.

Постоянство

Если на некотором промежутке производная тождественно равна нулю, то функция на этом промежутке постоянна

Монотоность

Промежутки монотонности функции совпадают с промежутками постоянного знака ее производной.

Частные производные первого порядка.

Частные производные первого порядка. Пусть функция определена в области и . Тогда при малых определено ее частное приращение по : .

Определение. Частной производной функции по переменной в точке называют предел

если он существует.

Частную производную по обозначают одним из следующих символов:

Аналогично определяется частная производная по и вводятся ее обозначения.

Полный дифференциал.

Полным дифференциалом функции многих переменных называется главная линейная относительно приращений аргументов часть малого полного приращения функции.

Теорема. Полный дифференциал равен сумме попарных произведений частных производных на дифференциалы соответствующих переменных.

Первообразный интеграл, свойсва интегралов, таблица интегралов.

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).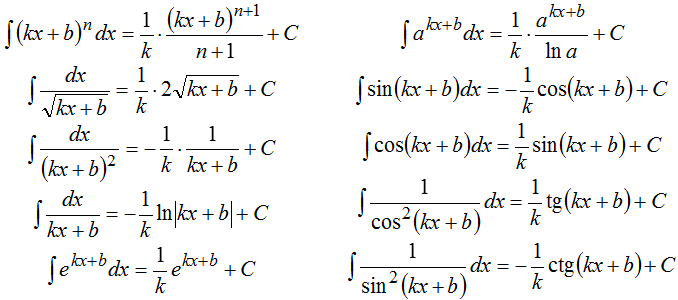

Обозначение

где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx — подынтегральным выражением.

Свойства:

Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Интегрирование по частям в неопределенном интеграле (формулы)

Функции и гладкие, следовательно, возможно дифференцирование:

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

Не стоит, однако, забывать, что это равенство подразумевается в смысле равенства множеств, то есть, грубо говоря, с точностью до константы, возникающей во время интегрирования.

Типичную ошибку «потери» константы при обращении с неопределенным интегралом иллюстрирует следующий пример-софизм:

Отсюда «следствие»: , что очевидно неверно.

Определение интеграла (определение)

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции

Геометрический смысл определенного интеграла

Пусть функция y = f(x) непрерывна на отрезке [a; b] и не меняет знак на нем (то есть, неотрицательная или неположительная). Фигуру G, ограниченную линиями y = f(x), y = 0, x = aи x = b, называют криволинейной трапецией. Обозначим ее площадь S(G).

Подойдем к задаче вычисления площади криволинейной трапеции следующим образом. В разделе квадрируемые фигуры мы выяснили, что криволинейная трапеция является квадрируемой фигурой. Если разбить отрезок [a; b] на n частей точками и обозначить , а точки выбирать так, чтобы при , то фигуры, соответствующие нижней и верхней суммам Дарбу, можно считать входящей P и объемлющей Q многоугольными фигурами для G.

Таким образом, и при увеличении количества точек разбиения n, мы придем к неравенству , где — сколь угодно малое положительное число, а s и S – нижняя и верхняя суммы Дарбу для данного разбиения отрезка [a; b]. В другой записи . Следовательно, обратившись к понятию определенного интеграла Дарбу, получаем .

Последнее равенство означает, что определенный интеграл для непрерывной и неотрицательной функции y = f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.

То есть, вычислив определенный интеграл , мы найдем площадь фигуры, ограниченной линиями y = f(x), y = 0, x = a и x = b.

Замечание.

Если функция y = f(x) неположительная на отрезке [a; b], то площадь криволинейной трапеции может быть найдена как .

Дифференциальное и интегральное исчисление — Дифференцируйте относительно чего угодно

Интегральное исчисление было одним из величайших открытий Ньютона и Лейбница. Их работа независимо привела к доказательству и признанию важности фундаментальной теоремы исчисления, связывающей интегралы с производными. С открытием интегралов впоследствии можно было изучать площади и объемы.

Интегральное исчисление — это вторая половина пути исчисления, который мы будем исследовать.

В этом уроке вы откроете для себя связь между дифференциальным и интегральным исчислением.

После прохождения этого урока вы будете знать:

Понятия дифференциального и интегрального исчисления связаны между собой основной теоремой исчисления.
Применяя основную теорему исчисления, мы можем вычислить интеграл, чтобы найти площадь под кривой.
В машинном обучении применение интегрального исчисления может предоставить нам метрику для оценки производительности классификатора.

Начнем.

Дифференциальное и интегральное исчисление. Дифференцируйте относительно чего угодно
Фото Максима Лебрена, некоторые права защищены.

Обзор учебника

Это руководство разделено на три части; они:

Дифференциальное и интегральное исчисление – какая связь?
Основная теорема исчисления
- Аналогия подметания
- Основная теорема исчисления. Часть 1
- Основная теорема исчисления. Часть 2
Пример интеграции
Применение интеграции в машинном обучении

Дифференциальное и интегральное исчисление – какая связь?

В нашем путешествии по исчислению до сих пор мы узнали, что дифференциальное исчисление связано с измерением скорости изменения. Мы также открыли дифференциацию и применили ее к различным функциям из первых принципов. Мы даже поняли, как применять правила, чтобы быстрее получить производную.

Но мы только на полпути.

С точки зрения двадцать первого века исчисление часто рассматривается как математика изменений. Он измеряет изменения с помощью двух больших понятий: производных и интегралов. Производные моделируют темпы изменений… Интегралы моделируют накопление изменений…
— Страница 141, Бесконечные силы, 2020.

Вспомним, что исчисление состоит из двух фаз: вырезание и перестроение.

Фаза резки разбивает изогнутую форму на бесконечно малые и прямые части, которые можно изучать отдельно, например, применяя производные для моделирования скорости их изменения или наклона .

Эта половина путешествия по исчислению называется дифференциальным исчислением, и мы уже рассмотрели его в деталях.

Фаза восстановления собирает бесконечно малые и прямые части и суммирует их вместе в попытке изучить исходное целое. Таким образом, мы можем определить площадь или объем правильных и неправильных форм, разрезав их на бесконечно тонкие ломтики. Эту вторую половину пути исчисления мы и будем исследовать дальше. Это называется интегральное исчисление.

Важная теорема, связывающая эти два понятия вместе, называется фундаментальной теоремой исчисления .

Основная теорема исчисления

Чтобы лучше понять фундаментальную теорему исчисления, давайте вернемся к примеру с положением и скоростью автомобиля:

Линейный график положения автомобиля в зависимости от времени

Линейный график зависимости скорости автомобиля от времени

При вычислении производной мы решили задачу вперед , в которой мы нашли скорость по наклону графика положения в любой момент времени, t . Но что, если мы хотим решить обратную задачу , где нам дан график скорости, v ( t ), и мы хотим найти пройденное расстояние? Решение этой задачи заключается в вычислении площади под кривой (заштрихованная область) с точностью до времени т :

Заштрихованная область — это область под кривой

У нас нет специальной формулы для прямого определения площади заштрихованной области. Но мы можем применить математическую математику, чтобы разрезать заштрихованную область под кривой на множество бесконечно тонких прямоугольников, для чего у нас есть формула:

Разрезание заштрихованной области на множество прямоугольников шириной Δt

Если мы рассмотрим прямоугольник i ^th, произвольно выбранный для охвата временного интервала Δ t , мы можем определить его площадь как длину, умноженную на ширину:

площадь_прямоугольника = v ( t _i ) Δ t _i

У нас может быть столько прямоугольников, сколько необходимо, чтобы охватить интересующий интервал, которым в данном случае является заштрихованная область под кривой. Для простоты обозначим этот замкнутый интервал как [ a , b ]. Нахождение площади этой заштрихованной области (и, следовательно, пройденного расстояния) сводится к нахождению суммы n количество прямоугольников:

total_area = V ( T ₀) Δ T ₀ + V ( T ₁) Δ T 9014 ₁) Δ T 9014 _{1 9014. _{.9014 9014}}

_{_{9014 9.9014 9.9014 9.9064 ₁). _n ) Δ t _n
Мы можем выразить эту сумму еще более компактно, применив сумму Римана в сигма-обозначении:
Если мы разрежем (или разделим) область под кривой на конечное число прямоугольников, то мы обнаружим, что сумма Римана дает нам приближение площади, так как прямоугольники не будут точно соответствовать площади под кривой. Если нам нужно расположить прямоугольники так, чтобы их верхний левый или верхний правый углы касались кривой, сумма Римана дает нам либо заниженную, либо завышенную оценку истинной площади соответственно. Если бы середина каждого прямоугольника должна была касаться кривой, то часть прямоугольника, выступающая над кривой примерно , компенсирует зазор между кривой и соседними прямоугольниками:
Аппроксимация площади под кривой левыми суммами
Аппроксимация площади под кривой правильными суммами
Аппроксимация площади под кривой с суммой средних точек

Решение для нахождения точной площади под кривой состоит в том, чтобы уменьшить ширину прямоугольников настолько, чтобы они стали бесконечно тонкими (вспомните принцип бесконечности в исчислении). Таким образом, прямоугольники будут покрывать всю область, и суммируя их площади, мы найдем определенный интеграл .
Определенный интеграл («простое» определение): Точная площадь под кривой между t = a и t = b определяется определенным интегралом, который определяется как предел суммы Римана …
– Страница 227, Исчисление для чайников, 2016.
Тогда определенный интеграл может быть определен суммой Римана, когда число прямоугольников n стремится к бесконечности. Обозначим также площадь под кривой через А ( т ). Тогда:
Обратите внимание, что обозначение теперь меняется на целочисленный символ ∫, заменяя сигму, Σ. Причина этого изменения состоит просто в том, чтобы показать, что мы суммируем огромное количество тонко нарезанных прямоугольников. Выражение в левой части читается как интеграл v ( t ) от a до b , а процесс нахождения интеграла называется интегрированием .
Аналогия подметания Возможно, более простая аналогия, которая поможет нам связать интеграцию с дифференциацией, состоит в том, чтобы представить себе, что вы держите один из тонко нарезанных срезов и перетаскиваете его вправо под кривой бесконечно малыми шагами. По мере движения вправо тонкий срез подметает большую площадь под кривой, а его высота будет меняться в зависимости от формы кривой. Вопрос, на который мы хотели бы ответить, заключается в том, с какой скоростью площадь накапливается по мере того, как тонкий срез смещается вправо?
Пусть dt обозначает каждый бесконечно малый шаг, пройденный заметающим срезом, а v ( t ) его высоту в любой момент времени, t . Тогда бесконечно малая площадь дА ( t ) этого тонкого среза может быть найдена путем умножения его высоты v ( t ) на бесконечно малую ширину dt :
. дА ( t ) = v ( t ) dt
Деление уравнения на dt дает нам производную от A ( t ) и говорит нам, что скорость накопления площади равна высоте кривой, v ( t ), в момент времени т :
дА ( t ) / dt = v ( t )
Наконец мы можем определить основную теорему исчисления.
Основная теорема исчисления. Часть 1 Мы обнаружили, что площадь, A ( t ), развертка под функцией, v ( t ), может быть определена с помощью:
Мы также обнаружили, что скорость, с которой подметается площадь, равна исходной функции, v ( t ):
дА ( t ) / dt = v ( t )
Это подводит нас к первой части фундаментальной теоремы исчисления, которая говорит нам, что если v ( t ) непрерывна на отрезке [ a , b ], и если она также является производной от A ( t ), то A ( t ) является первообразной 9064 из против ( т ):
A’ ( t ) = v ( t )
Или, проще говоря, интегрирование — это операция, обратная дифференцированию. Следовательно, если бы нам сначала пришлось интегрировать v ( t ), а затем продифференцировать результат, мы получим исходную функцию, v ( t ):
Основная теорема исчисления. Часть 2 Вторая часть теоремы позволяет нам сократить путь вычисления интеграла, не прибегая к более длинному пути вычисления предела суммы Римана.
Утверждается, что если функция v ( t ) непрерывна на интервале, [ a , б ], затем:
Здесь F ( t ) представляет собой любую первообразную v ( t ), а интеграл определяется как вычитание первообразной, оцененной в a и b .
Следовательно, вторая часть теоремы вычисляет интеграл путем вычитания площади под кривой между некоторой начальной точкой C и нижним пределом a из площади между той же начальной точкой C и верхний предел, b . Это фактически вычисляет область интереса между a и b .
Поскольку константа C определяет точку на оси x , в которой начинается развертка, простейшей первообразной для рассмотрения является та, где C = 0. Тем не менее, любая первообразная с любым значением C Можно использовать , который просто устанавливает начальную точку в другое положение на x -ось.
Пример интеграции Рассмотрим функцию v ( t ) = x ³ . Применяя степенное правило, мы можем легко найти его производную: v’ ( t ) = 3x ² . Первопроизводная от 3 х ² снова равна х ³ — выполняем обратную операцию для получения исходной функции.
Теперь предположим, что у нас есть другая функция, г ( t ) = x ³ + 2. Его производная также равна 3x ² , как и производная еще одной функции: 3 – 5. Обе эти функции (и другие подобные) имеют первообразную x ³. Следовательно, мы задаем семейство всех первообразных 3x ² неопределенным интегралом :
Неопределенный интеграл не определяет границы, в которых вычисляется площадь под кривой. Постоянная, C , включен для компенсации отсутствия информации о пределах или начальной точке развертки.
Если мы знаем пределы, то мы можем просто применить вторую фундаментальную теорему исчисления, чтобы вычислить определенный интеграл:
Мы можем просто установить C равным нулю, потому что в данном случае это не изменит результат.
Применение интеграции в машинном обучении Мы рассмотрели кривую скорости автомобиля v ( t ) в качестве знакомого примера, чтобы понять взаимосвязь между интегрированием и дифференцированием.
Но вы можете использовать эту схему сложения площадей прямоугольников, чтобы складывать крошечные кусочки чего угодно — расстояния, объема или энергии, например. Другими словами, площадь под кривой не обязательно должна обозначать фактическую площадь.
– Страница 214, Исчисление для чайников, 2016.
Одним из важных шагов успешного применения методов машинного обучения является выбор подходящих показателей производительности. Например, в глубоком обучении обычной практикой является измерение точности и отзыва .
Точность — это доля правильных обнаружений, о которых сообщила модель, а полнота — это доля обнаруженных истинных событий.
— Страница 423, Глубокое обучение, 2017.
Также общепринятой практикой является нанесение точности и полноты на кривую Precision-Recall (PR), помещая полноту на x -оси и точность по оси y . Было бы желательно, чтобы классификатор характеризовался как высокой полнотой, так и высокой точностью, что означает, что классификатор может правильно обнаруживать многие истинные события. Такая хорошая эффективность классификации будет характеризоваться более высокой площадью под кривой PR.
Вероятно, вы уже можете сказать, к чему все идет.
Площадь под кривой PR действительно может быть рассчитана путем применения интегрального исчисления, что позволяет нам охарактеризовать работу классификатора.
Дополнительная литература В этом разделе содержится больше ресурсов по теме, если вы хотите углубиться.
Книги Одно- и многомерное исчисление, 2020.
Исчисление для чайников, 2016.
Бесконечные силы, 2020.
Автостопом по вычислениям, 2019.
Глубокое обучение, 2017.
Сводка В этом уроке вы открыли связь между дифференциальным и интегральным исчислением.
В частности, вы узнали:
Понятия дифференциального и интегрального исчисления связаны между собой основной теоремой исчисления.
Применяя основную теорему исчисления, мы можем вычислить интеграл, чтобы найти площадь под кривой.
В машинном обучении применение интегрального исчисления может предоставить нам метрику для оценки производительности классификатора.
Есть вопросы?
Задавайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Получите доступ к вычислениям для машинного обучения!
Почувствуйте себя умнее с концепциями исчисления
…чтобы лучше понять символы и термины исчисления
Узнайте, как в моей новой электронной книге:
Исчисление для машинного обучения
Он содержит учебных пособий для самостоятельного изучения с полными рабочий код на:
дифференцирование , градиент , лагранжев множитель подход , матрица Якоби ,
и многое другое…
Предоставьте достаточно знаний по математическому анализу для

ваших проектов машинного обучения Посмотрите, что внутри
О Стефании Кристине
Стефания Кристина, доктор философии, преподаватель кафедры систем и техники управления Мальтийского университета.
Просмотреть все сообщения Стефании Кристины →
площадь под кривой, дифференциальное исчисление, фундаментальная теорема, интегральное исчисление, точность, кривая точности-отзыва, скорость изменения, отзыв, скорость
Нежное введение в многомерное исчисление
Нежное введение в векторнозначные функции
Курс дифференциального и интегрального исчисления
Чему вы можете научиться.
Введение в дифференциальное и интегральное исчисление с одной переменной
Приобретите математические инструменты, чтобы применить их к последующим курсам по математике, естественным наукам или экономике
Найти и использовать производные
Решение прикладных и оптимизационных задач
Нахождение первообразных различных алгебраических и тригонометрических функций
Использовать фундаментальные теоремы исчисления
Использование интегралов для решения различных прикладных задач
Об этом курсе:
Этот курс охватывает дифференциальное исчисление, его приложения и введение в интеграцию. Передается для кредита UC.
Предпосылки
МАТЕМАТИКА XL 1 Precalculus с оценкой C- или выше, или три с половиной года обучения математике в средней школе, включая некоторую координатную геометрию и тригонометрию.
Расписание на зиму 2023 г.
11 января — 15 февраля
Среда, суббота
Доступен
Подробнее
Преподаватель:
Эсмаил Никье
3
Плата:
$955,00
Удаленный
Расположение:
Удаленный класс
Обновление…
ЗАПИСАТЬСЯ ДО: 11 января 2023 г.
См. подробности
Примечания
Учащиеся, не допущенные к прохождению этого курса, должны записаться на курс MATH XL 1 Precalculus.
Зачисление/участие в классе зависит от сдачи вступительного экзамена ALEKS.
Посетители не допускаются. Крайний срок регистрации: 13 января 2023 г. Требуется доступ в Интернет. Требуемые материалы.
Учащиеся, зачисленные на этот курс, должны сдать вступительный экзамен по математике перед первым занятием. Пожалуйста, зарегистрируйтесь на вступительный экзамен по математике http://www.aleks.com/sign_up/class?class_code=DGXAY-LLNLE С каждого учащегося взимается плата в размере 20 долларов США (невозмещаемая), которая покрывает 12 месяцев доступа к подготовительному и Учебный модуль, который является ресурсом для обновления ваших математических навыков.
Длина экзамена: 30 вопросов
Время: Вы должны спланировать сдачу вступительного экзамена в течение двух часов без перерыва.
Если вы набрали 80% или выше, мы рекомендуем вам пройти курс Calculus MATH XL 31A
Если вы набрали от 60% до 79%, мы рекомендуем вам записаться на Pre-Calculus MATH XL 1
Если вы набрали менее 60%, мы рекомендуем вам записаться на курс алгебры
После сдачи вступительного экзамена вам предоставляется возможность ознакомиться с определенными темами с помощью специальных учебных упражнений в модуле «Подготовка и обучение».
Повторная сдача экзамена, если необходимо
После изучения Модуля подготовки и обучения в течение не менее 3 часов вы можете снова сдать вступительный экзамен
Пересдача экзамена будет доступна через 24 часа после сдачи первого экзамена.
У вас будет доступ к модулю «Подготовка и обучение» в течение 12 месяцев после сдачи начального экзамена.
Крайний срок возврата средств
После 18 января 2023 г. возврат средств невозможен
Требования к курсу
Для получения материалов курса требуется доступ в Интернет.
Книга:
ВЫЧИСЛЕНИЕ ОДНОЙ ПЕРЕМЕННОЙ
by ROGAWSKI
ISBN 9781319328283
Schedule
Lecture
Wed Jan 11, 2023
6:30PM PT — 9:30PM PT
Remote Classroom
Lecture
Sat Jan 14, 2023
9:00AM PT — 12:00 PT
Дистанционный класс
Лекция
Среда, 18 января 2023 г.
18:30 Pt — 21:30 Pt
Удаленный класс
Лекция
SAT 21 января 2023
9:00 утра PT — 12:00 Pt
Отдаленная класс
. Сд.
18:30 Pt — 21:30 Pt
Удаленный класс
Лекция
SAT 28 января 2023
9:00 утра PT — 12:00 Pt
Отдаленный класс
WED FEB 1, 2023333.
18:30 по тихоокеанскому времени — 21:30 по тихоокеанскому времени
Удаленный класс
Лекция
Сб 4 февраля, 2023
9:00 утра по тихоокеанскому времени — 12:00 Pt
Удаленный класс
Лекция
Ср.
Удаленный класс
Лекция
Сб 11 февраля, 2023
9:00 Pt — 12:00 Pt
Удаленный класс
Лекция
Ср.
Удаленный класс
9 января — 20 марта
Понедельник 18:00 — 21:15 по тихоокеанскому времени
Доступно
Подробнее
Преподаватель:
Райан Валлес
3
Плата:
955,00 долларов США
Лично
Местонахождение:
UCLA
Обновление…
РЕГИСТРАЦИЯ: 9 января 2023 г.
См. подробности
Примечания
Нет собрания 16 января; 20 февраля 2023 г.
Учащиеся, не допущенные к прохождению этого курса, должны записаться на курс MATH XL 1 Precalculus.
Зачисление/участие в классе зависит от сдачи вступительного экзамена ALEKS.
Посетители не допускаются. Крайний срок регистрации: 16 января 2023 г. Требуется доступ в Интернет. Требуемые материалы.
Учащиеся, зачисленные на этот курс, должны сдать вступительный экзамен по математике перед первым занятием. Пожалуйста, зарегистрируйтесь на вступительный экзамен по математике http://www.aleks.com/sign_up/class?class_code=DGXAY-LLNLE С каждого учащегося взимается плата в размере 20 долларов США (невозмещаемая), которая покрывает 12 месяцев доступа к подготовительному и Учебный модуль, который является ресурсом для обновления ваших математических навыков.
Длина экзамена: 30 вопросов
Время: Вы должны спланировать сдачу вступительного экзамена в течение двух часов без перерыва.
Если вы набрали 80% или выше, мы рекомендуем вам пройти курс Calculus MATH XL 31A
Если вы набрали от 60% до 79%, мы рекомендуем вам записаться на Pre-Calculus MATH XL 1
Если вы набрали менее 60%, мы рекомендуем вам записаться на курс алгебры
После сдачи вступительного экзамена вам предоставляется возможность ознакомиться с определенными темами с помощью специальных учебных упражнений в модуле «Подготовка и обучение».
Повторная сдача экзамена, если необходимо
После изучения Модуля подготовки и обучения в течение не менее 3 часов вы можете снова сдать вступительный экзамен
Пересдача экзамена будет доступна через 24 часа после сдачи первого экзамена.
У вас будет доступ к модулю «Подготовка и обучение» в течение 12 месяцев после сдачи начального экзамена.
Крайний срок возврата средств
После 22 января 2023 г. возврат средств невозможен
Требования к курсу
Для получения материалов курса требуется доступ в Интернет.
Книга:
ВЫЧИСЛЕНИЕ ОДНОЙ ПЕРЕМЕННОЙ
by ROGAWSKI
ISBN 9781319328283
Schedule
Lecture
Mon Jan 9, 2023
6:00PM PT — 9:15PM PT
UCLADodd Hall 170
Lecture
Mon Jan 23, 2023
6:00PM PT – 21:15 PT
UCLDodd Hall 170
Лекция
Пн, 30 января 2023 г.
18:00 Pt — 9:15 вечера Pt
Ucladodd Hall 170
Лекция
понедельник 6 февраля, 2023
18.00 Pt — 9:15 Pt
Ucladodd Hall 170
Lecture
Mon Feb 13 Feb 130
Mon Feb 13 Feb 130 0009
Mon Feb 130
Mon Feb 130
Mon Feb 130
Mon Feb 130
. , 2023
6:00PM PT — 9:15PM PT
UCLADodd Hall 170
Lecture
Mon Feb 27, 2023
6:00PM PT — 9:15PM PT
UCLADodd Hall 170
Lecture
Mon 6 марта 2023 г.
18:00 по тихоокеанскому времени — 21:15 по тихоокеанскому времени
Ucladodd Hall 170
Лекция
понедельник 13, 2023
18:00. 15:00 по тихоокеанскому времени
UCLDodd Hall 170
Домедицинские и общенаучные исследования
Готов начать
свое будущее?
Будьте в курсе последних новостей и предложений по математике и статистике
Имя
Фамилия
Проценты
Выберите интересБухгалтерский учет, налогообложение и внутренний аудитАрхитектура и дизайн интерьераБизнес и менеджментДизайн и искусствоЦифровые технологииОбразованиеИнжинирингРазвлеченияЭкология и государственная политикаФинансы и инвестицииЗдравоохранение и консультированиеГуманитарные и социальные наукиЛандшафтная архитектура и садоводствоЯзыкиЮридические программыOsher (OLLI)PathwayНедвижимостьНауки и математикаПисьмо и журналистика
Электронная почта
Компания (опционально)
Политика конфиденциальности Флажок
Регистрируясь, вы соглашаетесь с Политикой конфиденциальности UCLA Extension.
No related posts.}}