Как решать задачи по динамическому программированию
Методы динамического программирования применяются при решении оптимизационных задач, в которых целевая функция или ограничения, или же и первое, и второе одновременно характеризуются нелинейными зависимостями.Данный раздел представлен следующими калькуляторами:
- Задача распределения инвестиций. Распределении инвестиций между предприятиями П1, П2,…, Пn. Инвестируемая сумма E усл. ден. ед.
- Задача распределения ресурсов. Планируется работа двух предприятий на n лет. Начальные ресурсы равны s0.
- Метод прогонки.
- Задача замены оборудования.
- Складская задача: составить оптимальную программу выпуска продукции X, которая минимизирует суммарные издержки предприятия.
- Задача Джонсона.
- Задача о рюкзаке (решение задачи о загрузке транспортного средства).

- Динамическая оптимизация в планировании работ
В условиях задачи производственного планирования найти оптимальные сроки начала строительства каждого из объектов так, чтобы суммарный срок строительства всех объектов был бы минимальным.Объекты / Стадии №1 №2 №3 №4 A1 2 5 4 3 A2 1 4 2 6 A3 3 4 3 4
Задача распределения инвестиций
В задачах данного типа заданы сумма инвестиций (или сумма для распределения) и таблица планируемой прибыли.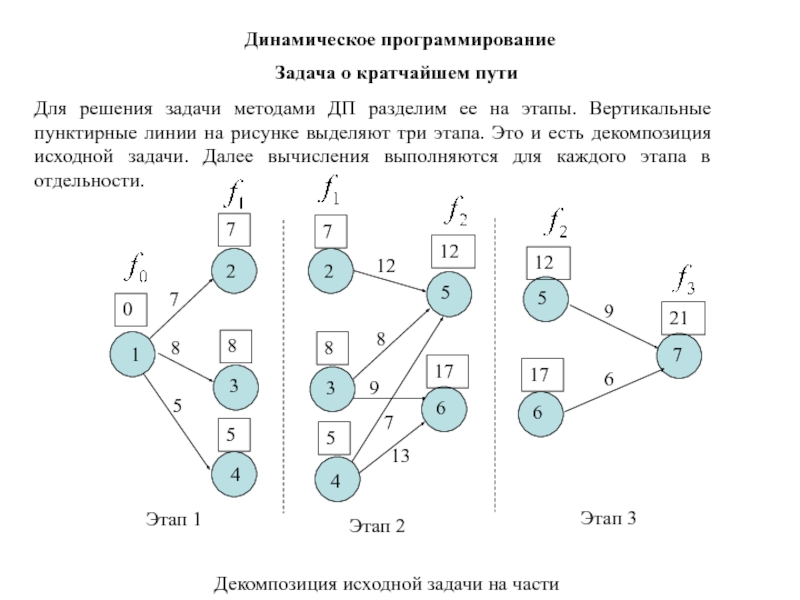 Если сумма для распределения явно не задана, то ее можно найти из таблицы — она равна максимальному значению xi (последняя строчка таблицы).
Если сумма для распределения явно не задана, то ее можно найти из таблицы — она равна максимальному значению xi (последняя строчка таблицы).
Таблицы могут иметь разный вид.
Таблица 1 — Первый вариант таблицы исходных данных
| x | f1(x) | f2(x) | f3(x) |
| 1 | 6.3 | 4 | 5 |
| 2 | 5.2 | 6 | 7 |
| 3 | 4.3 | 4.6 | 7.8 |
| 4 | 5 | 6 | 3 |
| 5* | 7 | 6.3 | 8.2 |
Таблица 2 — Второй вариант таблицы исходных данных
| x | 0 | 10 | 20 | 30 | 40 |
| f1(x) | 0 | 4 | 5 | 7 | 8 |
| f2(x) | 0 | 3 | 3 | 4 | 6 |
| f3(x) | 0 | 4 | 4 | 5 | 6 |
Пример задачи.
Для двух предприятий выделено A единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от x единиц средств, вложенных в первое предприятие, равен f1(х), а доход от y единиц средств, вложенных во второе предприятие, равен f2(y). Остаток средств к концу года составляет g1(x) для первого предприятия и g2(y) для второго предприятия. Задачу решить методом динамического программирования.
При вводе данных первую нулевую строку можно не заполнять.
В сервисе Задача распределения инвестиций используется метод обратной прогонки.
Метод прогонки
Данная задача соответствует задаче распределения инвестиций. Разница состоит в оформлении результатов полученного решения и применения метода прямой прогонки.В сервисе Метод прогонки необходимо также выбрать метод решения: процедура прямой или обратной прогонки.
Задача замены оборудования
Цель решения — определить на каких шагах алгоритма (в какие годы) необходимо заменить оборудование. Для этого вводятся Период эксплуатации (в годах) и Стоимость нового оборудования. После этого необходимо заполнить таблицу дохода r(t) и остаточной стоимости S(t).
Для этого вводятся Период эксплуатации (в годах) и Стоимость нового оборудования. После этого необходимо заполнить таблицу дохода r(t) и остаточной стоимости S(t).
Задача замены оборудования
Планирование производственной линии
Задача последовательной обработки на двух машинах N различных деталей, если известно время AЗадача Джонсона
Mетод динамического программирования. Примеры решения задач
Mетод динамического программирования
Задача1. Для двух предприятий выделено 1400 единиц денежных средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от х единиц, вложенных в первое предприятие равен , а доход от у единиц, вложенных в первое предприятие равен . Остаток средств к концу года составляет - для первого предприятия, - для второго предприятия. Решить задачу методом динамического программирования.
Остаток средств к концу года составляет - для первого предприятия, - для второго предприятия. Решить задачу методом динамического программирования.Решение
Процесс распределения средств разобъем на 4 этапа – по соответствующим годам.
Суммарный доход от обоих предприятий на к–ом шаге:
Остаток средств от обоих предприятий на к–ом шаге:
Обозначим — максимальный доход, полученный от распределения средств между двумя предприятиями с к-го шага до конца рассматриваемого периода.
Рекуррентные соотношения Беллмана для этих функций
Проведем оптимизацию, начиная с четвертого шага:
4-й шаг.
Оптимальный доход равен: , т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т. е. при .
е. при .
3-й шаг.
т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.е. при .
2-й шаг.
т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при .
1-й шаг.
т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при .
Результаты оптимизации:
Определим количественное распределение средств по годам:
Т.к. , получаем
Представим распределение средств в виде таблицы:
предприятие | год | |||
1 | 2 | 3 | 4 | |
1 | 1400 | 700 | 0 | 0 |
2 | 0 | 0 | 350 | 105 |
При таком распределении средств за 4 года будет получен доход, равный
Задача 2. Предприятие изготавливает продукцию, спрос на которую в каждом из месяцев планируемого периода Dt (t
Предприятие изготавливает продукцию, спрос на которую в каждом из месяцев планируемого периода Dt (t
=) тыс. ед. Запас продукции на складе на начало планируемого периода i0 тыс.ед. Затраты на производство продукции складываются из условно постоянных затрат, равных kден.ед., и пропорциональных затрат, равных Lxt. Затраты на хранение 1 тыс. ед. продукции составляют h ден.ед. Складские площади позволяют хранить не более М тыс.ед. продукции. Производственные мощности ограничены, и в каждом месяце предприятие может произвести не более В тыс.ед. продукции. Требуется разработать производственную программу изготовления продукции xt удовлетворяющую спрос в каждом из месяцев планируемого периода и обеспечивающую минимальные затраты на производство продукции и содержание запасов. Запас продукции на складе в конце планируемого периода должен быть равен нулю.
Все необходимые числовые данные приведены в таблице. T D1
D2
D3
D4
i0
k
L
h
M
B
3
3
5
4
-
2
4
1
1
6
7
Решение
Для решения задачи методом динамического программирования и записи рекуррентного соотношения будем использовать следующие обозначения: n — номер планового отрезка времени периода; j — уровень запаса на конец отрезка;
cn(x,j)= c(x)+j h — затраты, связанные с выпуском х единиц продукции на n-м отрезке и содержанием запасов, объем которых на конец n-го отрезка равен единицу j; fn(i)— значение функции, равное затратам на производство и хранение продукции за последние n месяцев при условии, что уровень запасов на начало n-гo месяца составляет i единиц; xn(i)— производство продукции на n-м отрезке, если уровень запасов на начало отрезка равен i единиц. Изобразим плановый период на рисунке и для наглядности нанесем на него числовые данные
Изобразим плановый период на рисунке и для наглядности нанесем на него числовые данные
D1 = 3 D2 = 5 D3 = 4
i 0 = 2 n =3 n = 2 n = 1 j 4 = 0
d3 = 3 d2 = 5 d1 = 4
x3 x2 x1
Т.к. c(x)=k+Lxто c(0)=0; c(l)=5; c(2)=6; c(3)=7; c (4)=8; c(5)=9; c(6)=10; c(7)=11; Уровень запасов на конец планового периода должен быть равен нулю, то для n=0 имеем f0(0)=0. Перейдем к рассмотрению первого отрезка, т.е. n=1.
Тогда функциональные уравнения Беллмана для рассматриваемой задачи имеют следующий вид: для n =1
f1(i)=c1(d1-i, 0) = c1(d1-i, 0) , где i может принимать значения 0, 1, 2, 3, 4.
Расчет всех значений выполним в виде таблицы.
| x i | X1* (i) | f1 (i) |
0 | 4 | 8 |
1 | 3 | 7 |
2 | 2 | 6 |
3 | 1 | 5 |
4 | 0 | 0 |
Переходим к анализу периода, состоящего из двух последних месяцев, т. е. n= 2. Тогда уравнение Беллмана примет вид:
е. n= 2. Тогда уравнение Беллмана примет вид:
(с2(x) + h(i +x- d2 ) + f1(i +x — d2)) , где i — уровень запаса сырья на начало предпоследнего месяца может принимать значения 0, 1, 2, 3, 4, 5, 6,
x будет равняться 7, 6, 5, 4 ,3, 2, 1, 0.
Расчет всех значений выполним в виде таблицы.
| x i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X2(i) | f2(i) |
0 | — | — | — | — | — | 9+0+8=17 | 10+1+7=18 | 11+2+6=19 | 5 | 17 |
1 | — | — | — | — | 8+0+8=16 | 9+1+7=17 | 10+2+6=18 | 11+3+5=19 | 4 | 16 |
2 | — | — | — | 7+0+8=15 | 8+1+7=16 | 9+2+6=17 | 10+3+5=18 | 11+4+0=15 | 3 | 15 |
3 | — | — | 6+0+8=14 | 7+1+7=15 | 8+2+6=16 | 9+3+5=17 | 10+4+0=14 | — | 2 | 14 |
4 | — | 5+0+8=13 | 6+1+7=14 | 7+2+6=15 | 8+3+5=16 | 9+4+0=13 | — | — | 1 | 13 |
5 | 0+0+8=8 | 5+1+7=13 | 6+2+6=14 | 7+3+5=15 | 8+4+0=12 | — | — | — | 0 | 8 |
6 | 0+1+7=8 | 5+2+6=13 | 6+3+5=14 | 7+4+0=14 | — | — | — | — | 0 | 8 |
Последнему шагу (n=3) будет соответствовать функциональное уравнение,
(с3(x) + h(2 +x- d3 ) + f2(2 +x – d3)), где i — уровень запаса сырья на начало предпоследнего месяца может принимать значение 2, а x будет равняться 7, 6, 5, 4 , 3, 2, 1.
Расчет всех значений выполним в виде таблицы. Таб. 4.4
| x i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | x4(i) | f4(х) |
i 0 = 2 | 5+0+17 | 6+1+16 | 7+2+15 | 8+3+14 | 9+4+13 | 10+5+8 | 11+6+8 | 1 | 22 |
Из таблицы видно, что в первом месяце оптимальной будет поставка x3(2)=1 единицам. С учетом запаса 2 единиц, общее количество составит 3. За этот месяц будет израсходовано 3 единицы, так что к началу второго месяца запас составит i=0 единиц. По таб. 4.3 находим x2(0)=5, за этот месяц будет израсходовано 5 единиц. Останется 0 единица. В третьем месяце с учетом остатка 0 единиц будет поставка x1(0)=4 единицы, что достаточно для удовлетворения потребностей в третьем месяце. При этом к концу третьего месяца уровень запаса будет равен 0 ед.
С учетом запаса 2 единиц, общее количество составит 3. За этот месяц будет израсходовано 3 единицы, так что к началу второго месяца запас составит i=0 единиц. По таб. 4.3 находим x2(0)=5, за этот месяц будет израсходовано 5 единиц. Останется 0 единица. В третьем месяце с учетом остатка 0 единиц будет поставка x1(0)=4 единицы, что достаточно для удовлетворения потребностей в третьем месяце. При этом к концу третьего месяца уровень запаса будет равен 0 ед.
Минимальные затраты, связанные с производством и хранением продукции за три месяца, составят 22 единицы.
Топ-10 задач динамического программирования для собеседований — Techie Delight
Топ-10 задач динамического программирования для интервью — Techie Delight — Medium Опубликовано в·
12 декабря 2018 г. разбить на набор более простых подзадач, решая каждую из этих подзадач только один раз и сохраняя их решения. В следующий раз, когда возникает та же самая подзадача, вместо повторного вычисления ее решения просто просматривается ранее вычисленное решение, тем самым экономя время вычислений. Этот метод хранения решений подзадач вместо их пересчета называется мемоизацией.
Этот метод хранения решений подзадач вместо их пересчета называется мемоизацией.
Ниже приведены 10 основных задач, которые можно легко решить с помощью динамического программирования:
- Самая длинная общая подпоследовательность
- Самая короткая общая суперпоследовательность
- Задача о самой длинной возрастающей подпоследовательности
- Задача о расстоянии Левенштейна (расстоянии редактирования) 90 014
- Умножение цепочки матриц
- 0–1 Задача о рюкзаке
- Задача о перегородках
- Резка стержня
- Задача о размене монет
- Задача о разрыве слов
Спасибо.
Программирование
Динамическое программирование
Алгоритмы
Структуры данных
Вопросы для интервью
Написано Coding Freak
6 .4K Followers
· Writer forЕще от Coding Freak и Techie Delight
Coding Freak
in
25 лучших алгоритмов, которые должен знать каждый программист
Хорошее знание стандартных алгоритмов так же важно, как и выбор правильной структуры данных.
Чтение через 1 мин·11 июня 2020 г.
Coding Freak
in
Более 500 структур данных и алгоритмов Интервью Вопросы и практические задачи
90 067 Массив
28 минут чтения · 15 июля 2018 г.
Coding Freak
in
Структура данных стека Практические задачи и вопросы для интервью
Стек — это абстрактный тип данных, который служит набором элементов с двумя основными операциями: push, которая добавляет элемент в…
2 минуты чтения · 26 декабря 2018 г.
Coding Freak
in
Топ-50 практических проблем динамического программирования
Динамическое программирование — это метод решения сложную задачу, разбив ее на набор более простых подзадачи, решение каждой из…
3 минуты чтения·3 августа 2018 г.
Просмотреть все от Coding Freak
Рекомендовано на Medium
Nitin Kishore
в
900 47 Вы неправильно делаете Leetcode — Вот как получить максимальная выгода
Теперь вам может быть интересно: «Общий пост в блоге о leetcode? Люди до сих пор так делают? Возраст не проверял.
 Нужно ли мне это… ·14 минут чтения·4 декабря 2022 г.
Нужно ли мне это… ·14 минут чтения·4 декабря 2022 г.Арслан Ахмад
в
Не просто LeetCode; Вместо этого следуйте шаблонам кодирования
Что, если вам не нравится практиковаться в сотнях вопросов по кодированию перед собеседованием?
·5 мин чтения·15 сентября 2022 г.Списки
Истории, которые помогут вам расти как разработчику программного обеспечения
19 историй·46 сохранений
Лидерство
30 историй·16 сохранений
Как проводить более содержательные встречи 1:1
11 историй·2 2 сохраняет
историй в Help You Level Up at Work
19 историй·36 сохранений
Santal Tech
in
Все ресурсы, которые я использовал, чтобы получить предложения по разработке программного обеспечения на сумму более 500 тысяч долларов
Список всех ресурсов, которые я использовал четкий технический интервью ведущих технологических компаний.
 Если я могу это сделать, то сможете и вы. ·Чтение 4 мин·6 января
Если я могу это сделать, то сможете и вы. ·Чтение 4 мин·6 январяЭнтони Д. Мэйс
Как решать задачи LeetCode (правильный путь)
tl;dr: Вы делаете это неправильно. Используйте «Шесть шагов» каждый раз, когда тренируетесь с вопросами LeetCode, желательно с другим человеком. Держите…
·13 min read·May 10, 2022Arslan Ahmad
in
Станьте профессионалом на собеседовании по кодированию в 2023 году с помощью этих 20 обязательных алгоритмических паттернов!
Мастер-собеседование по программированию: как изучение шаблонов интервью по кодированию может помочь вам подготовиться с умом.
·6 мин чтения·9 январяАрслан Ахмад
в
Руководство по выживанию на собеседовании по проектированию системы (2023): стратегии подготовки и практические советы
Подготовка к собеседованию по системному дизайну: овладение искусством системного проектирования.



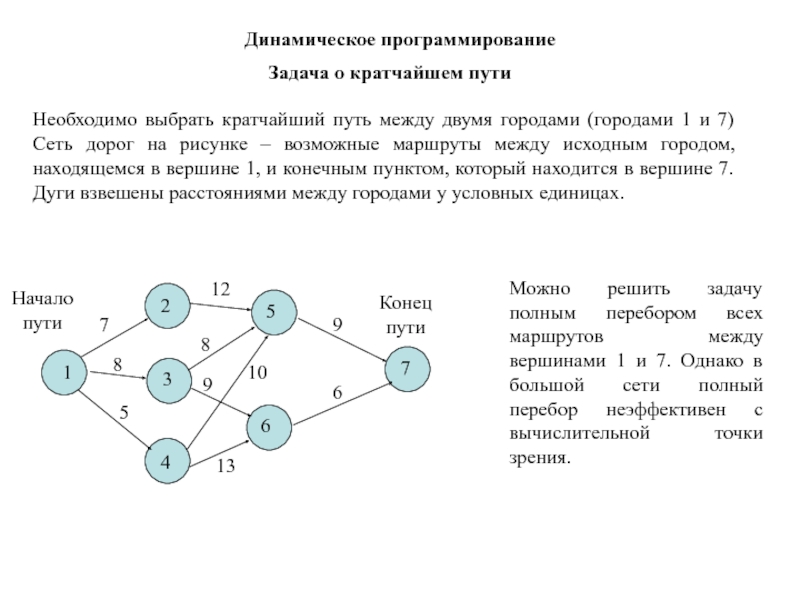 Остаток средств к концу года составляет - для первого предприятия, - для второго предприятия. Решить задачу методом динамического программирования.
Остаток средств к концу года составляет - для первого предприятия, - для второго предприятия. Решить задачу методом динамического программирования. Предприятие изготавливает продукцию, спрос на которую в каждом из месяцев планируемого периода Dt (t
Предприятие изготавливает продукцию, спрос на которую в каждом из месяцев планируемого периода Dt (t