Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации в Excel
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно.
Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании.
Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Расчет дисперсии в Excel
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета.
Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной.
В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Дисперсия, формула дисперсии, виды дисперсии, простая дисперсия, взвешенная дисперсия
Понятие дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2.
Взвешенная дисперсия (для вариационного ряда):
где n — частота (повторяемость фактора Х)
Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию
Построим интервальную группировку. Определим размах интервала по формуле:
где X max– максимальное значение группировочного признака;
X min–минимальное значение группировочного признака;
n – количество интервалов:
Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6
Составим интервальную группировку
Для дальнейших расчетов построим вспомогательную таблицу:
X’i– середина интервала.
(например середина интервала 159 – 165,6 = 162,3)
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
Пример 2. Определение групповой, средней из групповой, межгрупповой и общей дисперсии
Пример 3. Нахождение дисперсии и коэффициента вариации в группировочной таблице
Пример 4. Нахождение дисперсии в дискретном ряду
Формулу дисперсии можно преобразовать так:
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m2 — момент второго порядка
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:
Подставляя в данную формулу дисперсии q =1- р, получаем:
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию.
Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя;
ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.
д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
2 раз.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Что такое дисперсия в статистике? Определение, формула и пример
Оглавление
Содержание
Что такое дисперсия?
Понимание дисперсии
Преимущества и недостатки
Пример
Часто задаваемые вопросы
Часто задаваемые вопросы о различиях
К
Адам Хейс
Полная биография
Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов. Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень.
Узнайте о нашем редакционная политика
Обновлено 14 марта 2023 г.
Рассмотрено
Майкл Дж. Бойл
Рассмотрено Майкл Дж. Бойл
Майкл Бойл — опытный специалист в области финансов, более 10 лет занимающийся финансовым планированием, деривативами, акциями, фиксированным доходом, управлением проектами и аналитикой.
Узнайте о нашем Совет финансового контроля
Факт проверен
Викки Веласкес
Факт проверен Викки Веласкес
Полная биография
Викки Веласкес — исследователь и писатель, которая руководила, координировала и руководила различными общественными и некоммерческими организациями.
Она провела углубленное исследование социальных и экономических вопросов, а также пересмотрела и отредактировала учебные материалы для района Большого Ричмонда.
Узнайте о нашем редакционная политика
Инвестопедия / Алекс Дос Диас
Что такое дисперсия?
Термин дисперсия относится к статистическому измерению разброса между числами в наборе данных. В частности, дисперсия измеряет, насколько далеко каждое число в наборе от среднего (среднего) и, следовательно, от любого другого числа в наборе. Дисперсия часто обозначается этим символом: σ 2 . Он используется как аналитиками, так и трейдерами для определения волатильности и безопасности рынка.
Квадратный корень из дисперсии представляет собой стандартное отклонение (SD или σ), которое помогает определить постоянство доходности инвестиций в течение определенного периода времени.
Ключевые выводы
- Дисперсия — это измерение разброса между числами в наборе данных.
- В частности, он измеряет степень разброса данных относительно среднего значения выборки.
- Инвесторы используют дисперсию, чтобы увидеть, насколько рискованно вложение и будет ли оно прибыльным.
- Дисперсия также используется в финансах для сравнения относительной эффективности каждого актива в портфеле для достижения наилучшего распределения активов.
- Квадратный корень из дисперсии является стандартным отклонением.
Смотреть сейчас: что такое дисперсия?
Понимание разницы
В статистике дисперсия измеряет отклонение от среднего или среднего значения. Он рассчитывается путем взятия разностей между каждым числом в наборе данных и средним значением, затем возведения в квадрат разностей, чтобы сделать их положительными, и, наконец, деления суммы квадратов на количество значений в наборе данных.
Дисперсия рассчитывается по следующей формуле:
о 2 «=» ∑ я «=» 1 н ( Икс я − Икс ‾ ) 2 Н где: Икс я «=» Каждое значение в наборе данных Икс ‾ «=» Среднее значение всех значений в наборе данных Н «=» Количество значений в наборе данных \begin{align}&\sigma^2 = \frac { \sum_{i = 1} ^ { n } \big (x_i — \overline { x } \big ) ^ 2 }{ N } \\&\textbf{ где:} \\&x_i = \text{Каждое значение в наборе данных} \\&\overline { x } = \text{Среднее значение всех значений в наборе данных} \\&N = \text{Количество значений в наборе данных набор данных} \\\end{выровнено} σ2=N∑i=1n(xi−x)2где:xi=Каждое значение в наборе данныхx=Среднее значение всех значений в наборе данныхN=Количество значений в наборе данных
Вы также можете использовать приведенную выше формулу для расчета дисперсии в других областях, кроме инвестиций и торговли, с некоторыми небольшими изменениями.
Например, при расчете выборочной дисперсии для оценки дисперсии совокупности знаменатель уравнения дисперсии становится равным N — 1, так что оценка является несмещенной и не занижает дисперсию совокупности.
Преимущества и недостатки вариантов
Статистики используют дисперсию, чтобы увидеть, как отдельные числа соотносятся друг с другом в наборе данных, а не используют более широкие математические методы, такие как распределение чисел по квартилям. Преимущество дисперсии в том, что она рассматривает все отклонения от среднего значения как одинаковые, независимо от их направления. Квадраты отклонений не могут в сумме равняться нулю и вообще не создают видимость изменчивости данных.
Однако одним из недостатков дисперсии является то, что она придает дополнительный вес выбросам. Это цифры, далекие от среднего. Возведение этих чисел в квадрат может исказить данные. Еще одна ловушка использования дисперсии заключается в том, что ее нелегко интерпретировать. Пользователи часто используют его в первую очередь для извлечения квадратного корня из его значения, которое указывает на стандартное отклонение данных.
Как отмечалось выше, инвесторы могут использовать стандартное отклонение, чтобы оценить, насколько постоянна доходность с течением времени.
В некоторых случаях риск или волатильность могут быть выражены в виде стандартного отклонения, а не дисперсии, поскольку первое часто легче интерпретировать.
Пример отклонения по финансам
Вот гипотетический пример, демонстрирующий, как работает дисперсия. Допустим, доходность акций компании ABC составляет 10 % в первый год, 20 % в год 2 и −15 % в год 3. Среднее значение этих трех доходностей составляет 5 %. Различия между каждой доходностью и средним значением составляют 5%, 15% и -20% за каждый последующий год.
Возведение этих отклонений в квадрат дает 0,25%, 2,25% и 4,00% соответственно. Если мы сложим эти квадраты отклонений, то получим в сумме 6,5%. Когда вы делите сумму 6,5% на единицу меньше количества возвратов в наборе данных, поскольку это выборка (2 = 3-1), это дает нам дисперсию 3,25% (0,0325).
Извлечение квадратного корня из дисперсии дает стандартное отклонение 18% (√0,0325 = 0,180) для доходности.
Часто задаваемые вопросы
Как рассчитать дисперсию?
Чтобы вычислить дисперсию, выполните следующие действия:
- Вычислите среднее значение данных.
- Найдите отличие каждой точки данных от среднего значения.
- Возведение в квадрат каждого из этих значений.
- Сложите все квадраты значений.
- Разделите эту сумму квадратов на n – 1 (для выборки) или N (для генеральной совокупности).
Для чего используется дисперсия?
Дисперсия — это, по сути, степень разброса в наборе данных относительно среднего значения этих данных. Он показывает количество вариаций, существующих между точками данных. Визуально, чем больше дисперсия, тем «жирнее» будет распределение вероятностей. В финансах, если что-то вроде инвестиций имеет большую дисперсию, это может быть интерпретировано как более рискованное или волатильное.
Почему стандартное отклонение часто используется больше, чем дисперсия?
Стандартное отклонение — это квадратный корень из дисперсии. Иногда это более полезно, так как при извлечении квадратного корня единицы измерения удаляются из анализа. Это позволяет проводить прямое сравнение между разными вещами, которые могут иметь разные единицы измерения или разные величины. Например, если сказать, что увеличение X на одну единицу увеличивает Y на два стандартных отклонения, это позволяет понять взаимосвязь между X и Y независимо от того, в каких единицах они выражены.
Как рассчитать дисперсию | Калькулятор, анализ и примеры
Опубликован в 18 января 2023 г. к Прита Бхандари.
Дисперсия является мерой изменчивости. Он рассчитывается путем взятия среднего квадрата отклонений от среднего.
Дисперсия говорит вам о степени разброса в вашем наборе данных.
Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению.
Содержание
- Дисперсия по сравнению со стандартным отклонением
- Популяция по сравнению с выборочной дисперсией
- Калькулятор дисперсии
- Шаги для расчета дисперсии вручную
- Почему дисперсия имеет значение?
- Часто задаваемые вопросы
Дисперсия по сравнению со стандартным отклонением
Стандартное отклонение выводится из дисперсии и показывает, в среднем, насколько далеко каждое значение отстоит от среднего. Это квадратный корень из дисперсии.
Обе меры отражают изменчивость распределения, но их единицы различаются:
- Стандартное отклонение выражается в тех же единицах, что и исходные значения (например, в метрах).
- Дисперсия выражается в более крупных единицах (например, в квадратных метрах)
Поскольку единицы дисперсии намного больше, чем единицы типичного значения набора данных, сложнее интуитивно интерпретировать число дисперсии.
Вот почему стандартное отклонение часто предпочитают в качестве основной меры изменчивости.
Однако дисперсия более информативна в отношении изменчивости, чем стандартное отклонение, и она используется для статистических выводов.
Население и дисперсия выборки
Для расчета дисперсии используются разные формулы в зависимости от того, есть ли у вас данные из всей совокупности или из выборки.
Дисперсия населения
Когда вы соберете данные о каждом члене интересующей вас совокупности, вы сможете получить точное значение дисперсии совокупности.
Формула дисперсии населения выглядит следующим образом:
| Формула | Пояснение |
|---|---|
|
Выборочная дисперсия
При сборе данных из выборки выборочная дисперсия используется для оценок или выводов о дисперсии генеральной совокупности.
Формула выборочной дисперсии выглядит следующим образом:
| Формула | Пояснение |
|---|---|
|
Для выборок мы используем n – 1 в формуле, потому что использование n дало бы нам смещенную оценку, которая последовательно занижает изменчивость. Выборочная дисперсия, как правило, ниже, чем реальная дисперсия генеральной совокупности.
Уменьшение выборки n до n – 1 делает дисперсию искусственно большой, давая вам объективную оценку изменчивости: лучше переоценить, чем недооценить изменчивость в выборках.
Важно отметить, что выполнение того же действия с формулами стандартного отклонения не приводит к полностью объективным оценкам.
Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.
Получение отзывов о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
- Академический стиль
- Расплывчатые предложения
- Грамматика
- Согласованность стиля
См. пример
Калькулятор дисперсии
Вы можете рассчитать дисперсию вручную или с помощью нашего калькулятора дисперсии ниже.
Шаги для расчета дисперсии вручную
Дисперсия обычно рассчитывается автоматически любым программным обеспечением, которое вы используете для статистического анализа. Но вы также можете рассчитать его вручную, чтобы лучше понять, как работает формула.
Существует пять основных шагов для нахождения дисперсии вручную.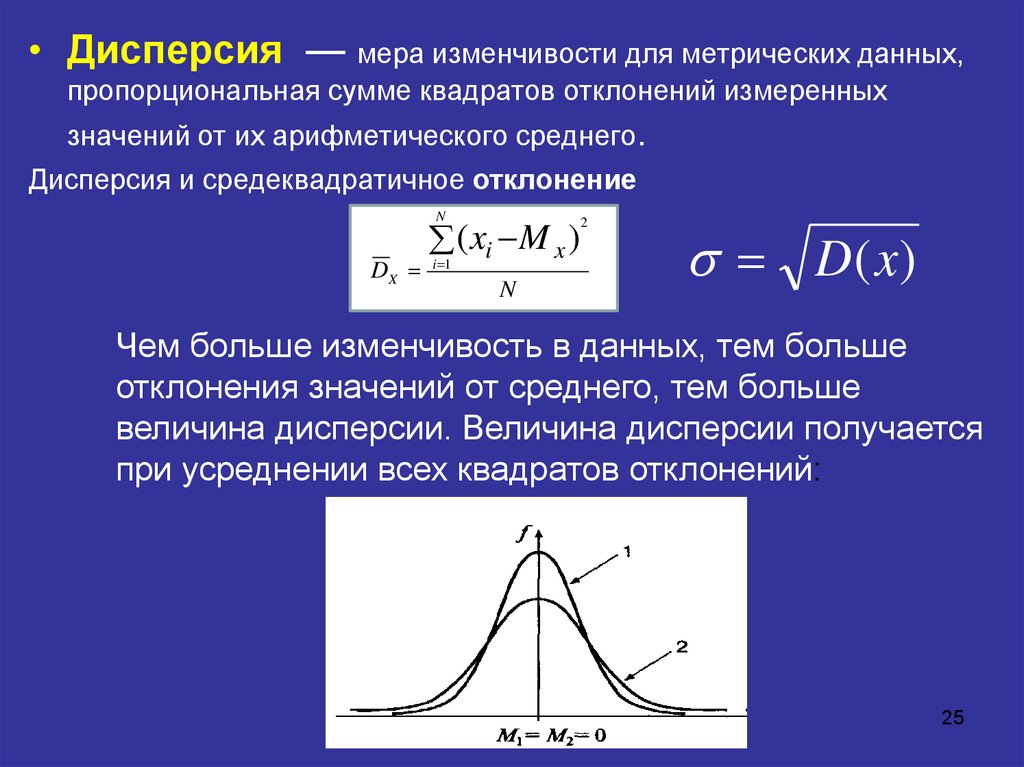
Мы будем использовать небольшой набор данных из 6 баллов, чтобы пройти по шагам.
| Набор данных | |||||
|---|---|---|---|---|---|
| 46 | 69 | 32 | 60 | 52 | 41 |
Чтобы найти среднее значение, сложите все баллы, а затем разделите их на количество баллов.
| Среднее () |
|---|
| = (46 + 69 + 32 + 60 + 52 + 41) 6 = 50 |
Вычтите среднее из каждой оценки, чтобы получить отклонения от среднего.
Поскольку x̅ = 50, отнимите 50 от каждого результата.
| Оценка | Отклонение от среднего |
|---|---|
| 46 | 46 – 50 = -4 |
| 69 | 69 – 50 = 19 |
| 32 | 32 – 50 = -18 |
| 60 | 60 – 50 = 10 |
| 52 | 52 – 50 = 2 |
| 41 | 41 – 50 = -9 |
Умножить каждое отклонение от среднего само на себя.
| Квадрат отклонения от среднего |
|---|
| (-4) 2 = 4 × 4 = 16 |
| 19 2 = 19 × 19 = 361 |
| (-18) 2 = -18 × -18 = 324 |
| 10 2 = 10 × 10 = 100 |
| 2 2 = 2 × 2 = 4 |
| (-9) 2 = -9 × -9 = 81 |
Сложите все квадраты отклонений. Это называется сумма квадратов.
| Сумма квадратов |
|---|
| 16 + 361 + 324 + 100 + 4 + 81 = 886 |
Разделить сумму квадратов на 
Так как мы работаем с образцом, мы будем использовать n – 1, где n = 6.
| Разница |
|---|
| 886 (6 – 1) = 886 5 = 177,2 |
Почему дисперсия имеет значение?
Разница имеет значение по двум основным причинам:
- Параметрические статистические тесты чувствительны к дисперсии.
- Сравнение дисперсии выборок помогает оценить групповые различия.
Однородность дисперсии в статистических тестах
Важно учитывать дисперсию перед выполнением параметрических тестов. Эти тесты требуют равных или близких дисперсий, также называемых однородностью дисперсии или гомоскедастичностью, при сравнении разных выборок.
Неравномерная дисперсия между образцами приводит к смещенным и искаженным результатам теста. Если у вас неравномерная дисперсия по выборкам, более подходящими являются непараметрические тесты.
Использование дисперсии для оценки групповых различий
Статистические тесты, такие как дисперсионные тесты или дисперсионный анализ (ANOVA), используют выборочную дисперсию для оценки групповых различий. Они используют дисперсии выборок, чтобы оценить, отличаются ли друг от друга совокупности, из которых они взяты.
Пример исследования Как исследователь в области образования вы хотите проверить гипотезу о том, что разная частота проведения тестов приводит к разным итоговым баллам студентов колледжа. Вы собираете окончательные баллы от трех групп по 20 студентов в каждой, которые часто, нечасто или редко участвовали в викторинах в течение семестра.- Образец A: один раз в неделю
- Образец B: один раз в 3 недели
- Образец C: один раз каждые 6 недель
Чтобы оценить групповые различия, вы выполняете дисперсионный анализ.
Основная идея дисперсионного анализа состоит в том, чтобы сравнить дисперсии между группами и дисперсии внутри групп, чтобы увидеть, лучше ли результаты объясняются групповыми различиями или индивидуальными различиями.
Если дисперсия между группами выше, чем внутригрупповая дисперсия, то группы, вероятно, будут отличаться в результате вашего лечения. Если нет, то вместо этого результаты могут быть получены из индивидуальных различий членов выборки.
Пример исследованияВаш дисперсионный анализ оценивает, обусловлены ли различия в средних итоговых баллах между группами различиями в частоте опросов или индивидуальными различиями учащихся в каждой группе.Для этого вы получаете соотношение межгрупповой дисперсии окончательных оценок и внутригрупповой дисперсии окончательных оценок — это F-статистика. При большой F-статистике вы найдете соответствующее значение p и сделаете вывод, что группы значительно отличаются друг от друга.
Часто задаваемые вопросы
- В чем разница между стандартным отклонением и дисперсией?
- Стандартное отклонение выражается в тех же единицах, что и исходные значения (например, минуты или метры).
- Дисперсия выражается в более крупных единицах (например, в квадратных метрах).
org/Answer»>Дисперсия — это среднеквадратичное отклонение от среднего значения, а стандартное отклонение — это квадратный корень из этого числа. Обе меры отражают изменчивость распределения, но их единицы различаются:
Хотя единицы дисперсии сложнее интуитивно понять, дисперсия важна в статистических тестах.
Процитировать эту статью Scribbr
Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.
Бхандари, П. (2023, 18 января). Как рассчитать дисперсию | Калькулятор, анализ и примеры.
