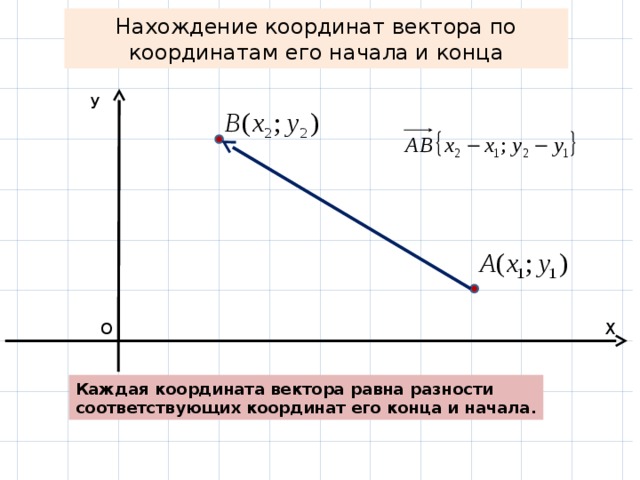
Нахождение длины вектора по теореме косинусов
Однако по условию задач координаты вектора не всегда известны. Тогда приходится искать иные пути решения.
К примеру, известны длины двух векторов\( \vec AB\) и \(\vec AC\), а также угол между ними. Необходимо выяснить, длину вектора \(\vec BC\). В этом случае, чтобы определить векторное значение, следует можно обратиться к теореме косинусов.
Определение
Теорема косинусов — квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Пример:
Длина вектора \(\vec AB=2\), \(\vec AC=4\), а угол между ними \(=\frac\pi4.\)
Вычислить длину вектора \(\vec BC.\)
Длина вектора \(\vec BC\) равна длине стороны BC треугольника ΔABC.
Исходные данные позволяют воспользоваться теоремой косинусов, так как длины стороны треугольника известны из условия (они равны длинам векторов \(\vec AB\) и \(\vec AC\)).
\(BC=\sqrt{20-8\sqrt2}\)
\(\left|\vec BC\right|=\sqrt{20-8\sqrt2}\)
Длина вектора по координатам с примером решения
Содержание:
- Сложение векторов
- Разность векторов
- Умножение вектора на число
Пусть вектор задан своими проекциями: Перенесем его параллельно себе так, чтобы его начало совпало с началом координат. Получим Из рис. 1.9 видно, что
Согласно (1.5) аналогично и Эти числа подставим в предыдущую формулу и получим Извлечем квадратный корень и найдем длину вектора:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Пример с решением
Задача:
Пусть в пространстве Oxyz точки А и В заданы координатами (рис.
Так как координаты точки равны проекциям на оси координат радиус-вектора этой точки, то Согласно (1.8) Значит, — Отсюда видно, что проекции вектора на оси координат равны разностям соответствующих координат его конца и начала. Зная проекции , по формуле (1.10) найдем длину вектора следовательно, и расстояние между точками А и В:
Скалярной называется величина, которая полностью определяется своим численным значением. Примерами скалярных величин являются длина, площадь, объем, масса. Вектором называется направленный отрезок прямой, соединяющий две точки в пространстве (рис. 1.4). Если А и В — начало и конец вектора, то он обозначается или
Возможно вам будут полезны данные страницы:
Линейная комбинация векторов |
Найти угол между векторами: пример решения |
Уравнение плоскости по трем точкам |
Метод Симпсона |
Длиной (модулем) вектора называется число, равное длине отрезка, соединяющего начало и конец вектора. Длина вектора обозначается Если начало вектора совпадает с концом, то вектор называется нулевым и обозначается Рис. 1.4 Ненулевые векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называют равными (в этом случае пишут ), если:
Длина вектора обозначается Если начало вектора совпадает с концом, то вектор называется нулевым и обозначается Рис. 1.4 Ненулевые векторы называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Векторы называют равными (в этом случае пишут ), если:
— равны их длины
— они коллинеарны;
— они сонаправлены.
Следовательно, при параллельном переносе вектора получим вектор, равный исходному.
Сложение векторов
Даны векторы Вектор перенесем параллельно самому себе и поместим его начало в конец вектора Тогда вектор, начало которого совпадает с началом вектора а конец — с концом вектора Ь, называется суммой векторов и обозначается Ясно, что сумму двух векторов можно получить иначе: построить с началом в общей точке, затем достроить на этих векторах, как на сторонах, параллелограмм. Тогда его диагональ, выходящая из общего начала, будет суммой исходных векторов (рис. 1.5). Указанный метод легко распространяется на случаи трех
и большего числа векторов: от конца первого строим второй, от конца второго — третий и т. д., тогда вектор, начало которого совпадает с началом первого, а конец — с концом последнего, и будет суммой рассматриваемых векторов (рис. 1.6).
д., тогда вектор, начало которого совпадает с началом первого, а конец — с концом последнего, и будет суммой рассматриваемых векторов (рис. 1.6).
Свойства сложения векторов: Эти свойства проверяются с помощью построения.
Разность векторов
Даны векторы Построим эти векторы с началом в общей точке. Тогда вектор, начало которого совпадает с концом вектора а конец — с концом вектора , называется разностью векторов и обозначается (рис. 1.7). Из рисунка видно, что
Умножение вектора на число
Даны ненулевой вектор и число Произведением вектора на число называется вектор который:
— коллинеарен
— имеет длину
— направлен так же, как и при , и противоположно при
Свойства умножения вектора на число:
Эти свойства доказываются построением.
линейная алгебра — О величине векторов
Вопрос
Изменено 8 лет, 3 месяца назад
Просмотрено 291 раз
$\begingroup$
Представьте себе вектор a в трехмерных декартовых координатах, координаты конечной точки вектора ($X_a,Y_a,Z_a$). 2.$$ 92}$
2.$$ 92}$
Действительно, величина такого вектора $|\vec v| = д$.
$\endgroup$
0
$\begingroup$
Да, вы правильно поняли, d — это, по сути, расстояние от начала вектора до его конечной точки, что делает его величиной рассматриваемого вектора
$\endgroup$
Зарегистрируйтесь или войдите
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
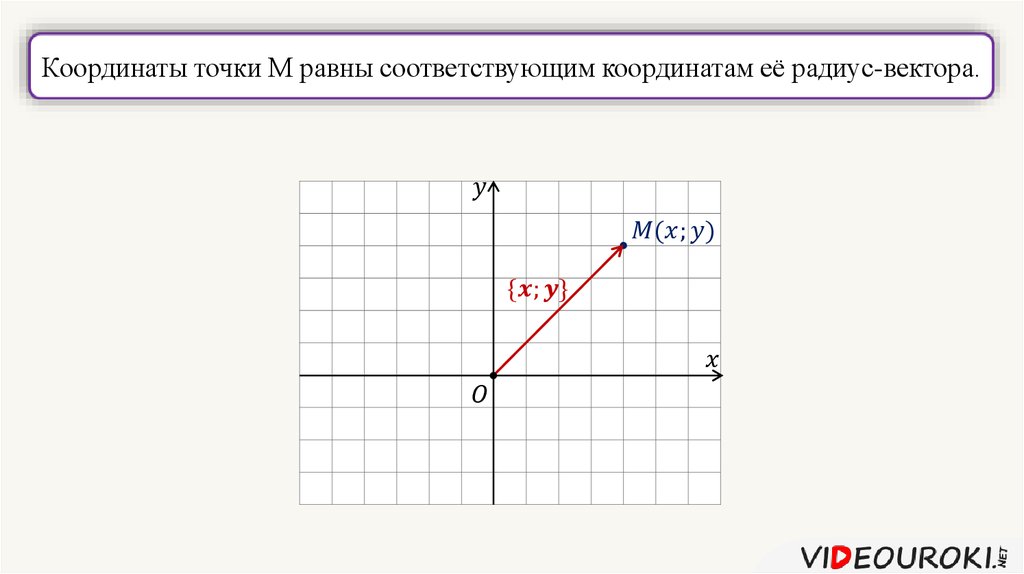
Вектор положения – объяснение и примеры
Мы можем использовать вектор положения , чтобы сообщить нам положение одного объекта относительно другого.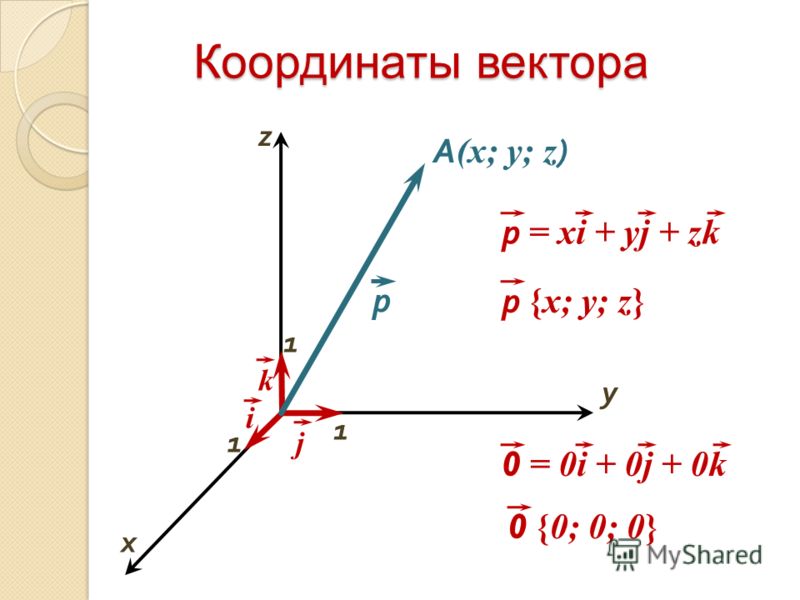 В частности, вектор положения:
В частности, вектор положения:
«Вектор, который указывает местоположение или положение данной точки относительно произвольной контрольной точки, такой как начало координат».
В этом разделе мы обсудим следующие аспекты векторов положения:
- Что такое вектор положения?
- Как найти вектор положения
Что такое вектор положения?
Часто векторы, которые начинаются в начале координат и заканчиваются в любой произвольной точке, называются векторами положения. Они используются для определения положения точки относительно начала координат.
Направление вектора положения указывает от начала координат к заданной точке. В c\декартовой системе координат, если точка O является началом координат, а Q является некоторой точкой (x1, y1), то вектор положения, направленный из точки O в точку Q, представляется как ОК . В трехмерном пространстве, если O = (0,0,0) и Q = (x1, y1, z1), то вектор положения r точки Q представляется следующим образом:
r = x1i + y1j + z1k
Предположим, у нас есть два вектора, A и B, с векторами положения a = (2,4) и b = (3, 5) соответственно. Тогда мы можем записать координаты векторов A и B как:
Тогда мы можем записать координаты векторов A и B как:
A = (2,4), B = (3, 5)
Как найти вектор положения
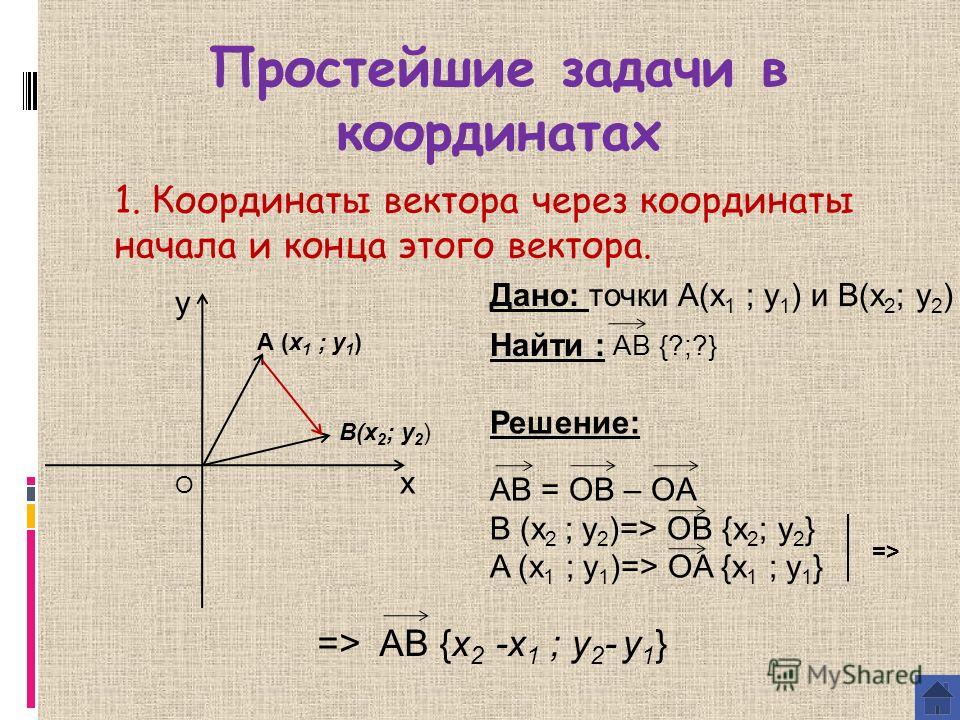
Перед определением вектора положения точки нам сначала нужно определить координаты этой точки. Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Далее мы хотим найти вектор положения из точки M в точку N, вектор MN . Чтобы определить этот вектор положения, мы вычитаем соответствующие компоненты M из N :
MN = (x2-x1, y2-y1)
Формула вектора положения
Используя приведенную выше информацию, мы можем обобщить формулу, которая будет определять вектор положения между двумя точками, если бы мы знали положение точек в плоскости xy .
Например, рассмотрим точку P с координатами (xk, yk) в плоскости xy и другую точку Q с координатами (xk+1, yk+1). Формула для определения вектора положения от P до Q:
PQ = ((xk+1)-xk, (yk+1)-yk)
Помните, что вектор положения PQ относится к вектору, который начинается в точке P и заканчивается в точке Q.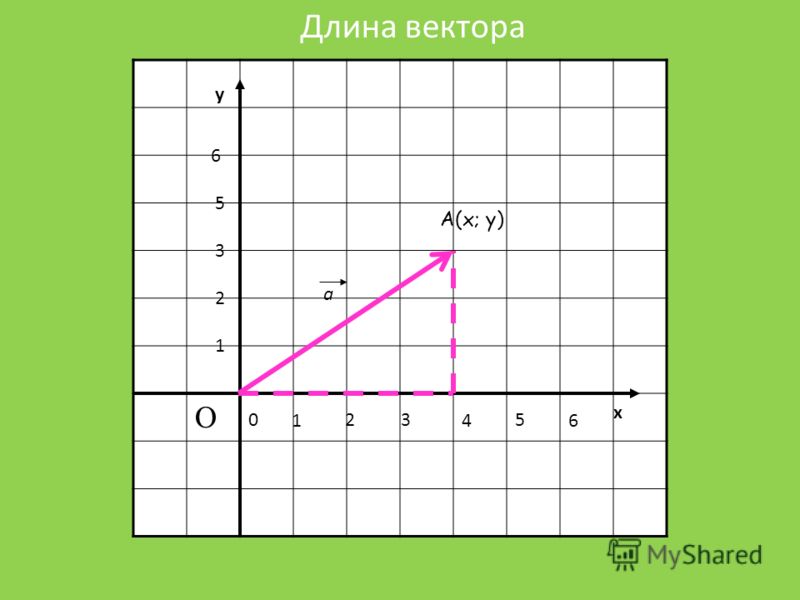 Точно так же, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
Точно так же, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
QP = (xk – (xk+1), yk – (yk+1))
Примеры
В этом разделе мы обсудим некоторые примеры задач вектора положения и их пошаговые решения. Это поможет глубже понять векторы положения.
Пример 1
Для двух точек A = (-4, 6) и B = (5, 12) определите вектор положения AB. Затем , вычисляют величину вектора AB .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для нахождения вектора положения AB :
AB = (x2-x1, y2-y1)
25
252 x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B. Таким образом, просто подставив значения точек A и B в приведенное выше уравнение, мы можем найти вектор положения 92
| АВ | = √81 + 36
| АВ | = √117
| АВ | = 3√13
Пример 2
Имея две точки A = (-4, 6) и B = (5, 12), определите вектор положения BA. Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Решение
Имея две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения BA :
BA = (x1-x2, y1-y2)
Где x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B. Обратите внимание, что вектор положения BA представляет собой вектор, направленный из точки B в сторону точки A. Он отличается от вектора положения AB, , который направлен из A в B. Таким образом, просто поместив значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA:
92 | ВА | = √81 + 36
| ВА | = √117
| ВА | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, отношение между ними следующее:
Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, отношение между ними следующее:
BA = -1 * (9, 6)
BA = -1 * AB
BA = – AB
Таким образом, два вектора положения параллельны друг другу и противоположны друг другу. То есть они являются негативами друг друга.
Пример 3
Учитывая, что вектор положения точки S1 равен OS1 = (2, 3) и что вектор точка S2, OS2 .
Раствор
Сначала мы наносим вектор OS1 с начальной точкой в начале координат (0,0) и конечной точкой в (2,3). Мы также наносим вектор OS2, , который начинается в начале координат и заканчивается в точке S2. Обозначим неизвестное положение S2 произвольными координатными точками (x,y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает связь между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник, 0С1С2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник, 0С1С2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Подставляя данные значения в это уравнение, получаем:
OS2 = (-3, 6) – (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 =(-5, 3) — вектор положения точки S2.
Пример 4
Имея две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .
Так как мы не знаем координаты QM или значения n и m, мы не можем упростить уравнение. Пример 5
Зная точку q, мы можем определить вектор ее положения:
R = -10i + 5j -3k.
Чтобы определить его величину, мы используем следующее уравнение:
| 92
| Р | = √100 + 25 + 9
| Р | = √100 + 25 + 9
| Р | = √134
Пример 6
Учитывая точки c = 5i + 6j +3k и d = 2i +5j – 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Имея две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
33 Практические вопросы - Пусть u = (-1, 4) и v = (2, 5).
 Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV . - Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный VU .
- Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
- Учитывая b = (3,2,5), определите его вектор положения, R. Затем найдите длину вектора
- Пусть вектор AB начинается в a = (1, 2) и заканчивается в б = (2, 3). Определите его вектор положения и его длину.
- Пусть вектор OB начинается в точке o = (0,0) и заканчивается в точке b = (-2, 6). Определите вектор его положения.
Ответы
- УФ = (3,1). Направление UV — на 3 единицы вправо по оси X и на 1 единицу вверх.
- ВУ = (-3,-1). Направление ВУ на 3 единицы влево по оси абсцисс и на 1 единицу вниз. Два вектора УФ и ВУ, противоположны по направлению.

 Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .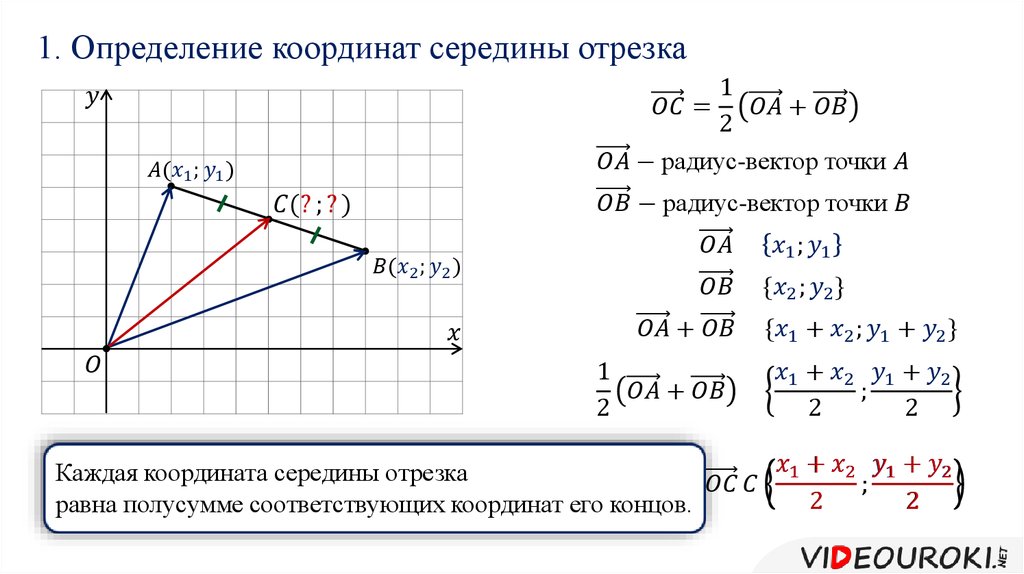 Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, отношение между ними следующее:
Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, отношение между ними следующее: Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник, 0С1С2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1
Это направленный вектор, начальная точка которого находится в точке S1 и который направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник, 0С1С2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом: S1S2 – OS1 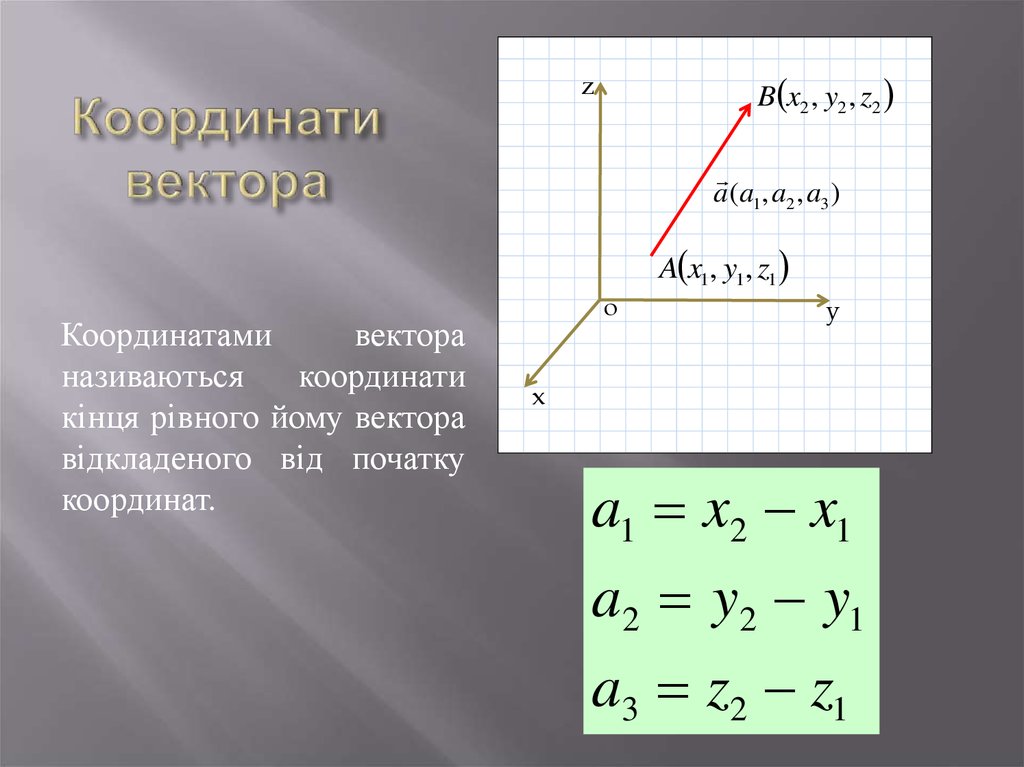
 Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV .