Логические схемы. Переход от логического выражения к логической схеме и наоборот
Цели:
1. Образовательные
- Основные логические операции.
- Построение таблиц истинности сложных высказываний.
- Логические схемы и логические выражения.
2. Развивающие
- Развитие исследовательской и познавательной деятельности.
- Лаконично, полно и содержательно отвечать и делать обобщающие выводы.
3. Воспитательные
- Формирование аккуратности при работе с компьютером.
- Понимание связей между другими учащимися, культурой поведения.
Тип урока: комбинированный
Методы организации учебной деятельности:
- фронтальная
- индивидуальная
- ученик-компьютер
Программно-дидактическое обеспечение: ПК,
презентация, задание для практической работы,
раздаточный материал, Electronics Workbench (EWB512), PowerPoint.
I. Организационный момент.
II. Актуализация ранее изученного материала и проверка домашнего задания.
Задания для выполнения в тетради и у доски.
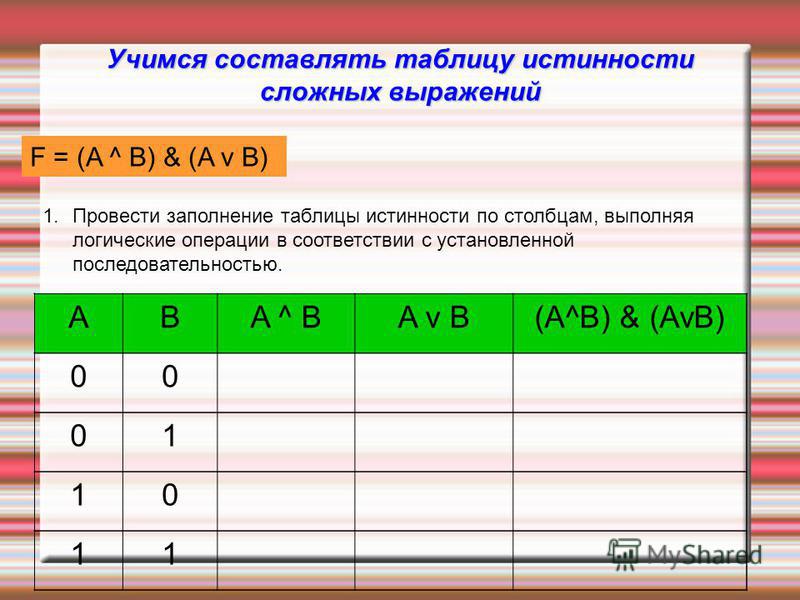
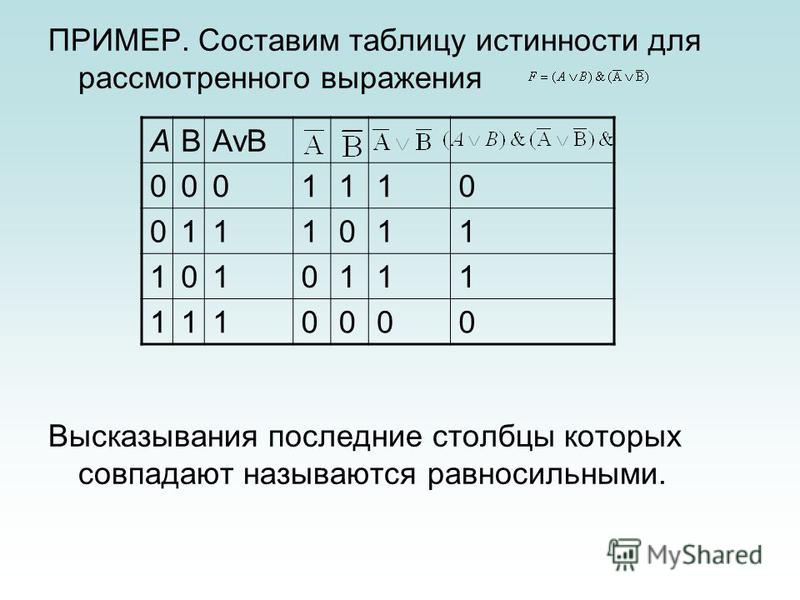
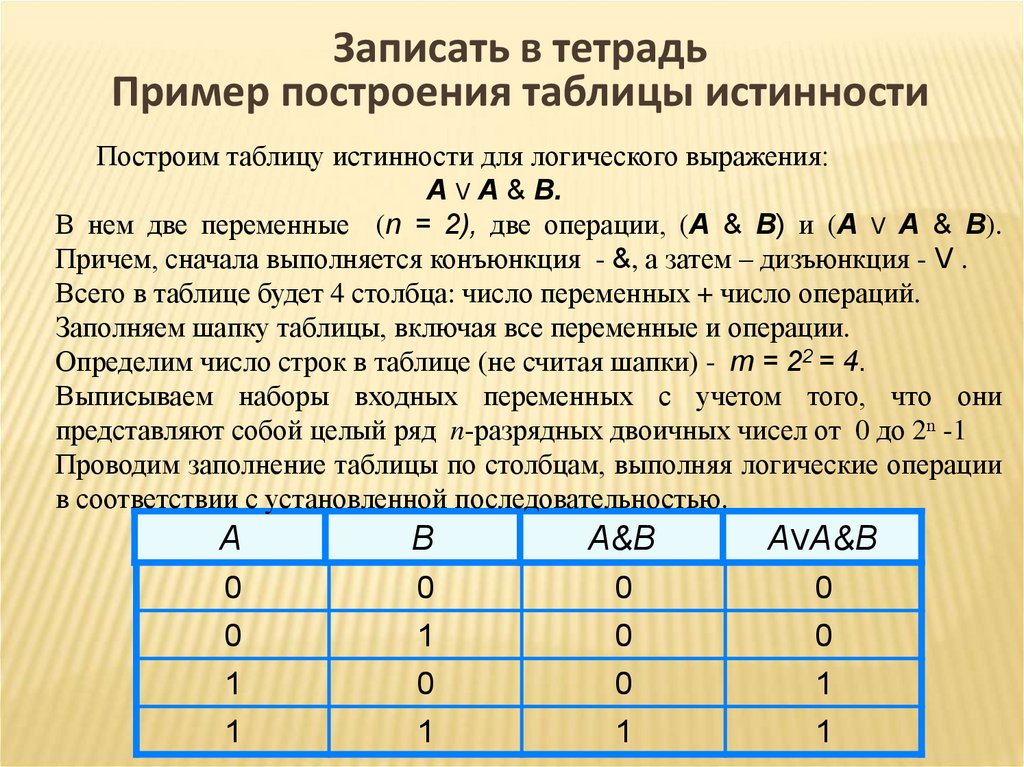
№1. Составьте таблицы истинности для следующих логических выражений:
№3. Нарисовать на доске логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ.
III. Новый материал.
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 - 1933), еще в 1910 году писал: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить:
1) будет ли она правильно функционировать при
любой комбинации, могущей встретиться в ходе
деятельности станции;
2) не содержит ли она излишних усложнений.
Каждая такая комбинация является посылкой,
каждый маленький коммутатор есть логическое
«или-или», воплощенное в эбоните и латуни;
все вместе — система чисто качественных.
Созданная позднее М.А. Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему. На первый взгляд
ничего того, что нас бы удивило, мы не видим!
Но если рассматривать ее при сильном увеличении,
она поразит нас своей стройной архитектурой.
Чтобы понять, как она работает, вспомним, что
компьютер работает на электричестве, то есть
любая информация представлена в компьютере в
виде электрических импульсов.
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более
сложные схемы, которые позволяют выполнять
арифметические операции и хранить информацию.
Причем схему, выполняющую определенные функции,
можно построить из различных по сочетанию и
количеству вентилей.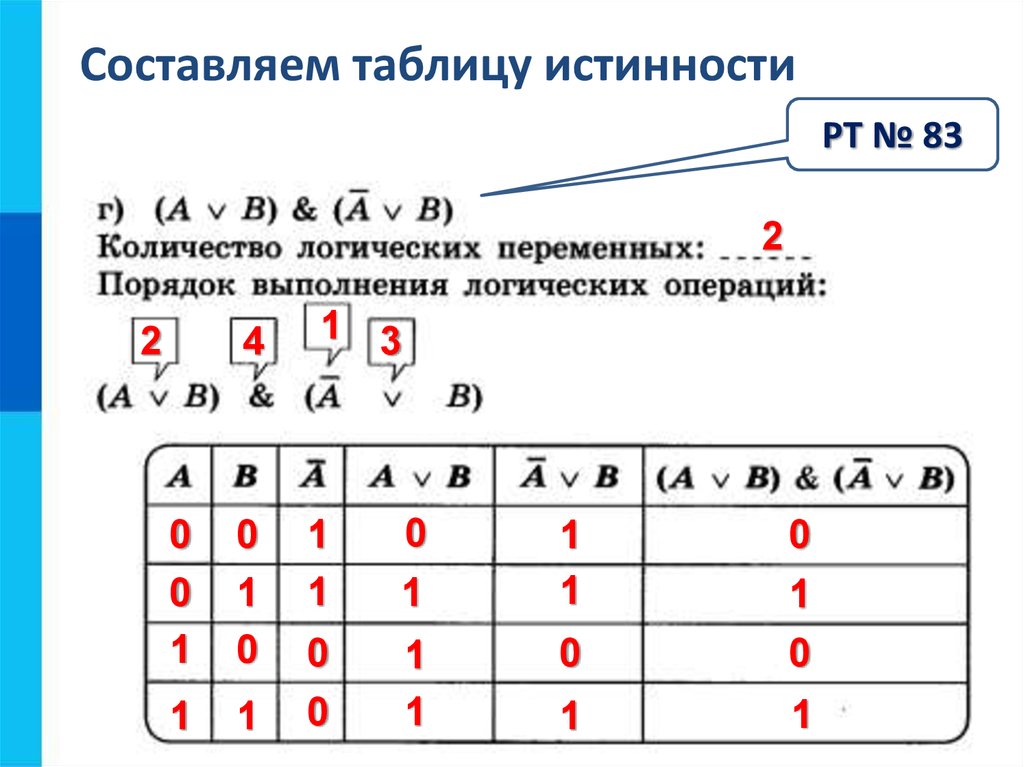
Поэтому значение
формального представления логической схемы
чрезвычайно велико. Оно необходимо для того,
чтобы разработчик имел возможность выбрать
наиболее подходящий ему вариант построения
схемы из вентилей. Процесс разработки общей
логической схемы устройства (в том числе и
компьютера в целом), становится иерархическим,
причем на каждом следующем уровне в качестве
«кирпичиков» используются логические схемы,
созданные на предыдущем этапе.
Логические схемы необходимо строить из
минимально возможного количества элементов, что
в свою очередь, обеспечивает большую скорость
работы и увеличивает надежность устройства.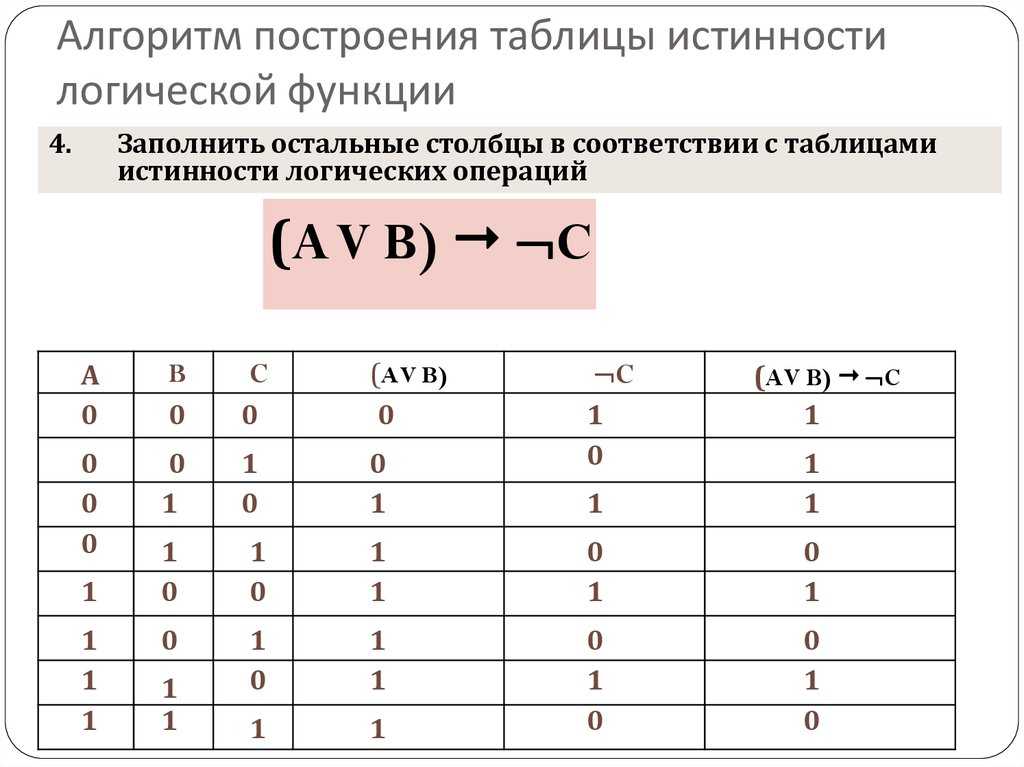
Правило построения логических схем:
1) Определить число логических переменных.
2) Определить количество базовых логических
операций и их порядок.
3) Изобразить для каждой логической операции
соответствующий ей вентиль и соединить вентили в
порядке выполнения логических операций.
Рассмотрение двух примеров перехода от выражения к схеме. (Презентация)
Рассмотрение двух примеров перехода от схемы к выражению. (Презентация)
Чаще в жизни возникает ситуация, когда известен результат и для его реализации необходимо построить устройство.
Рассмотрим следующую задачу: (Презентация)
Задача 1. В двухэтажном доме лестница
освещается одной лампой Х. На первом этаже
установлен один выключатель А, на втором этаже -
выключатель В. Если включают А, то лампа
загорается. При поднятии на второй этаж и
включении В лампа гаснет. Если кто-то выходит и
нажмет В, то лампа включается, при спуске на
первый этаж и нажатии А лампа должна погаснуть.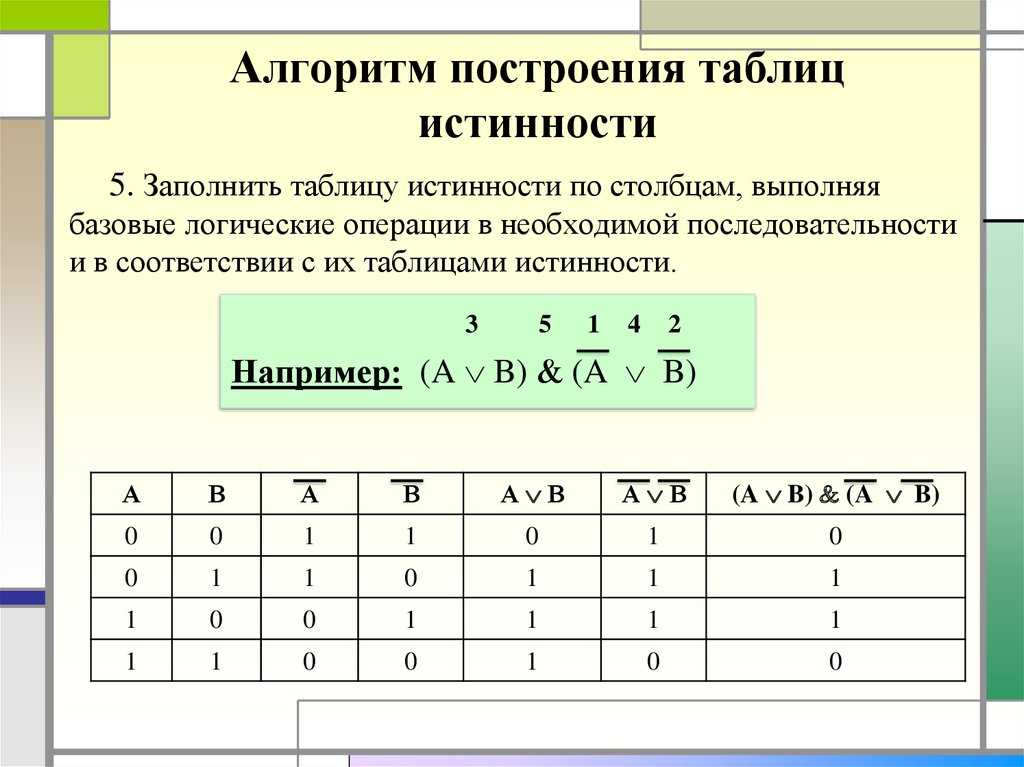
Алгоритм решения:
- Составить таблицу истинности.
- Определить логическую функцию.
- Построить логическую схему.
| A | B | X |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Чтобы создать логическую функцию по таблице
истинности, надо записывать значения выходной
переменной.
Между строками таблицы будет стоять знак логического сложения, а между столбцами — знак логического умножения .
Задача 2. (Презентация)
IV. Закрепление изученного материала.
Работа у доски и в тетради по карточкам.
№1. По логическому выражению построить логическую схему:
№2. По логической схеме составьте логическое выражение:
V. Компьютерный практикум.
Практическая работа с использованием электронной лаборатории Electronics Workbench (EWB512).
Вариант 1
1. Упростите логическое выражение
2. Проверьте свою работу, используя программу Electronics Workbench:
— Запишите исходное выражение в Logic Converter;
— Составьте таблицу истинности
— Упростите выражение используя
3. Проверьте правильность выполненных упрощений.
VI.
Домашнее задание:
а) упростите логическое выражение, постройте
логическую схему и таблицу истинности
б) по таблице истинности (00001011) составьте
выражение, упростите его, нарисуйте схему.
НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Ключевые слова: логический, выражение, истина, ложь, алгебра, представление, переменная, значение, функция, инверсия, дизъюнкция, конъюнкция, таблица, очередь
Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами.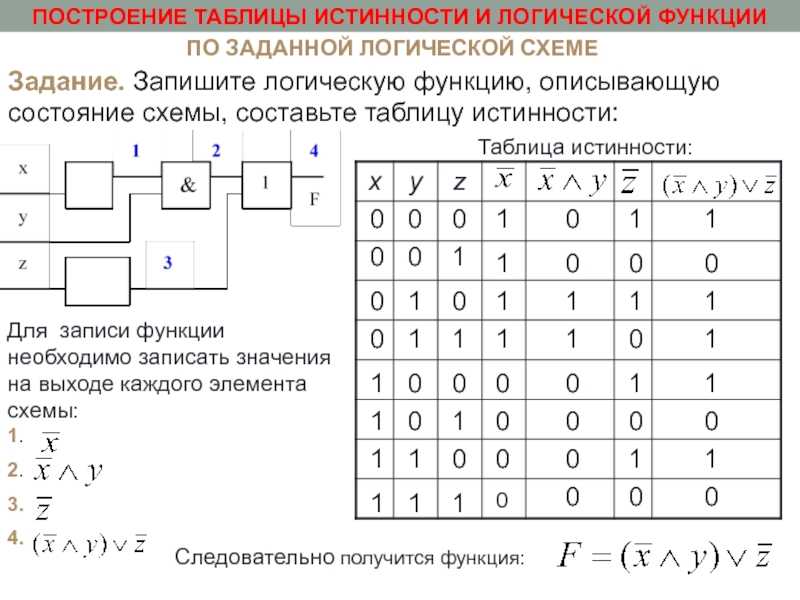
Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) — функция И
intuit.ru/2010/edi»> Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:- на входе схемы разомкнутое состояние соответствующего ключа, например, ;
- на выходе схемы ( ) — такое ее состояние, когда через сопротивление R ток не протекает.
Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.
Рис. 1.1. Трёх-входовой логический элемент И
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — , и . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1.
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
- либо ;
- либо — с использованием знака конъюнкции;
- либо , но при этом из контекста должно быть ясно, что между переменными , и производится логическое умножение.
intuit.ru/2010/edi»>либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа — и . Количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или , или . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис.
1.2,в.
Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая , то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо — с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ
intuit.ru/2010/edi»>Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход — . Количество вариантов для единственной логической переменной равно . Очевидно, что через сопротивление R ток протекает ( ) тогда, когда не замкнут, т.е. . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет
только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.Рис. 1.3. Логический элемент НЕ
intuit.ru/2010/edi»>Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.В логических выражениях применяется единственный вариант обозначения инверсии:
К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
Рис. 1.4. Логический элемент И-НЕ на три входа
intuit.ru/2010/edi»>Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
- либо ;
- либо ;
- либо .
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.
В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо .
Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
Генератор таблиц истинности — онлайн-калькулятор логической алгебры для таблиц
Генератор таблиц истинности
Логическое/логическое выражениеОтображение
Полная таблица истинности (входные переменные + выходные значения)
Таблица истинности с этими переменными
Только выходные значения (список 0 и 1)
Соответствующие minterms $ Σm(…) $ (0-индексированные)
Соответствующие Maxterms $ ΣM(…) $ (0-индексированные)
См. также: Калькулятор логических выражений — Boolean Minterms и Maxterms
Найти уравнение по таблице истинности
Указывать только выходные значения функции (последний столбец из булевой таблицы истинности)
Выходные значения (список 0 и 1)| Таблица упорядочена (входные значения) | От 0,…,0 до 1,…,1 От 1,…,1 до 0,…,0 |
| Булева запись | Литеральная (И, ИЛИ, НЕ) Логическая (∧, ∨, ¬) Программирование (&&, ||, ~) Алгебраическая (*, +, !) |
См.
также: Калькулятор логических выражений
Ответы на вопросы (FAQ)
Что такое таблица истинности? (Определение)
Таблица истинности представляет собой таблицу, представляющую выходные логические значения логического выражения на основе их записей. Таким образом, таблица отображает все возможные комбинации $n$ входных логических переменных (обычно 0/FALSE и 1/TRUE по $n$ столбцам) и результат уравнения в качестве вывода (последний столбец).
Пример: Таблица функции логического НЕ с 1 входом А (1-й столбец) и выходным значением НЕ А (последний столбец):
| А | НЕ А | 01 |
|---|---|
| 1 | 0 |
Каждая электронная схема связана с таблицей истинности , которая описывает ее.
Обычно массив начинается с входных значений в $ 0 $ и заканчивается входными значениями в $ 1 $, но иногда это наоборот.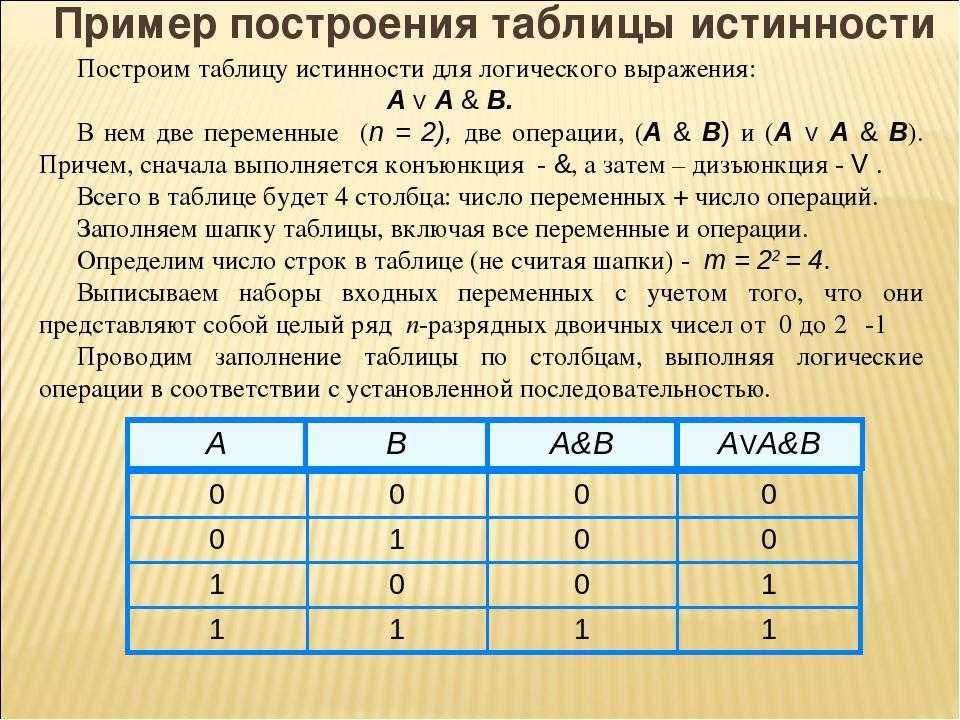
Как работает калькулятор таблицы истинности?
dCode Генератор таблицы истинности интерпретирует булевское логическое выражение и вычисляет (используя булеву алгебру) все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных логических переменных), чтобы составить таблицу истинности .
dCode также позволяет найти булеву логическую функцию/выражение из таблицы истинности .
Как найти уравнение из таблицы истинности?
Единственным важным столбцом таблицы истинности является последний, который описывает выходные значения (первые столбцы всегда идентичны для заданного количества входных данных) и который позволяет преобразовать в логическое выражение.
Существует 2 метода нахождения логического уравнения из таблицы истинности : либо с использованием выходных значений 0 (расчет Maxterms), либо с использованием выходных значений 1 (расчет Minterms).
Пример: Выходные значения: 0,1,1,0 , (и таблица упорядочена от 00 до 11), поэтому таблица истинности :
X
Вот различные вычисления (которые дают тот же результат для данного примера) 1 , запишите соответствующие входные значения, разделенные логическими И , затем сгруппируйте эти результаты с помощью логических ИЛИ .
Пример: Строки 2 и 3 равны 1 , строка 2 записывается как A AND NOT(B) (поскольку A равно 1 , а B равно 0 ), строка 3 записывается как NOT(A) AND B , поэтому уравнение равно (A AND NOT (B)) OR (NOT(A) AND B) , что, возможно, упрощается до A XOR B
Вычисление на основе выходных значений 0 таблицы истинности (Maxterms): для каждого 0 напишите соответствующие входные значения, разделенные логическим ИЛИ , затем сгруппируйте эти результаты с помощью логического И .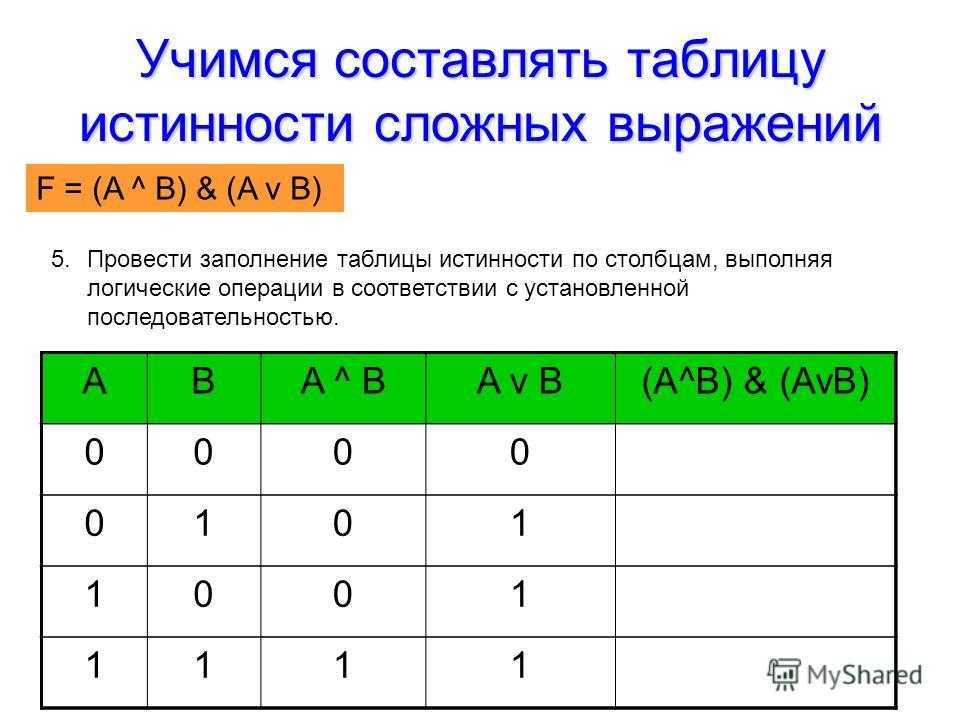
Пример: Строки 1 и 4 равны 0 , строка 1 записывается как A ИЛИ B , строка 4 записывается как НЕ(А) ИЛИ НЕ(В) и поэтому уравнение равно (A OR B) AND (NOT(A) OR NOT(B)) , что, возможно, упрощается до A XOR B
Какая таблица истинности для логического И?
Таблица истинности для функции И:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Что такое таблица истинности для логического ИЛИ?
Таблица истинности для функции ИЛИ:
| A | B | A OR B |
|---|---|---|
| 0 | 0032 0||
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
What is the truth table for logical XOR?
The truth table for the XOR function is:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
What The Prame Table Table Tabil Talecil?
The truth table for the NAND function is:
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Какая таблица истинности для логического НЕ-ИЛИ?
The truth table for the NOR function is:
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Какая таблица истинности для логического ИСТИНА?
The truth table for the TRUE (=1) function is:
| A | TRUE |
|---|---|
| 0 | 1 |
| 1 | 1 |
What is the таблица истинности для логического FALSE?
Таблица истинности для функции ЛОЖЬ (=0):
| A | ЛОЖЬ | ||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 1 | 0 |
д.) и загрузка всех данных, скрипт, или API-доступ к «Таблице правды» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android! 
также: Калькулятор логических выражений — Boolean Minterms и Maxterms| Таблица упорядочена (входные значения) | От 0,…,0 до 1,…,1 От 1,…,1 до 0,…,0 |
| Булева запись | Литеральная (И, ИЛИ, НЕ) Логическая (∧, ∨, ¬) Программирование (&&, ||, ~) Алгебраическая (*, 7 3 6 9 003 | 4 | 4 | 4 | 4 |
См. также: Калькулятор логических выражений
Ответы на вопросы (FAQ)
Что такое таблица истинности? (Определение)
Таблица истинности представляет собой таблицу, представляющую выходные логические значения логического выражения на основе их записей.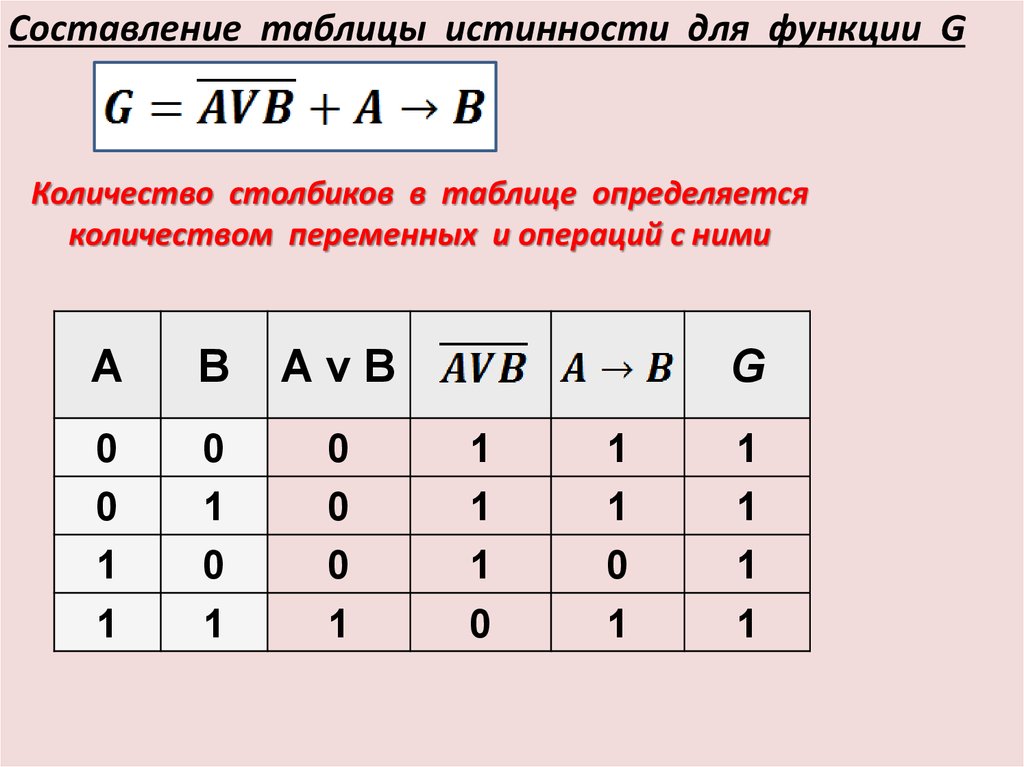
Таким образом, таблица отображает все возможные комбинации $n$ входных логических переменных (обычно 0/FALSE и 1/TRUE по $n$ столбцам) и результат уравнения в качестве вывода (последний столбец).
Пример: Таблица логической функции НЕ с 1 входом A (1-й столбец) и выходным значением NOT A (last column):
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Every electronic circuit is associated with a truth table , который описывает это.
Обычно массив начинается с входных значений в $ 0 $ и заканчивается входными значениями в $ 1 $, но иногда это наоборот.
Как работает калькулятор таблицы истинности?
дКод 9Генератор таблицы истинности 0060 интерпретирует логическое выражение логического типа и вычисляет (используя алгебру логики) все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных переменных логического характера), чтобы составить таблицу истинности .
dCode также позволяет найти булеву логическую функцию/выражение из таблицы истинности .
Как найти уравнение из таблицы истинности?
Единственный важный столбец таблицы истинности является последним, который описывает выходные значения (первые столбцы всегда идентичны для заданного количества входных данных) и который позволяет преобразовать в логическое выражение.
Существует 2 метода нахождения логического уравнения из таблицы истинности : либо с использованием выходных значений 0 (расчет Maxterms), либо с использованием выходных значений 1 (расчет Minterms).
Пример: Выходные значения: 0,1,1,0 , (and the table is ordered from 00 to 11), so the truth table is:
| input A | input B | output X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Вот различные вычисления (которые дают тот же результат для данного примера)
Расчет на основе выходных значений 1 таблицы истинности (Minterms): для каждого 1 запишите соответствующие входные значения отдельно логическими И , затем сгруппируйте эти результаты с логическими ИЛИ .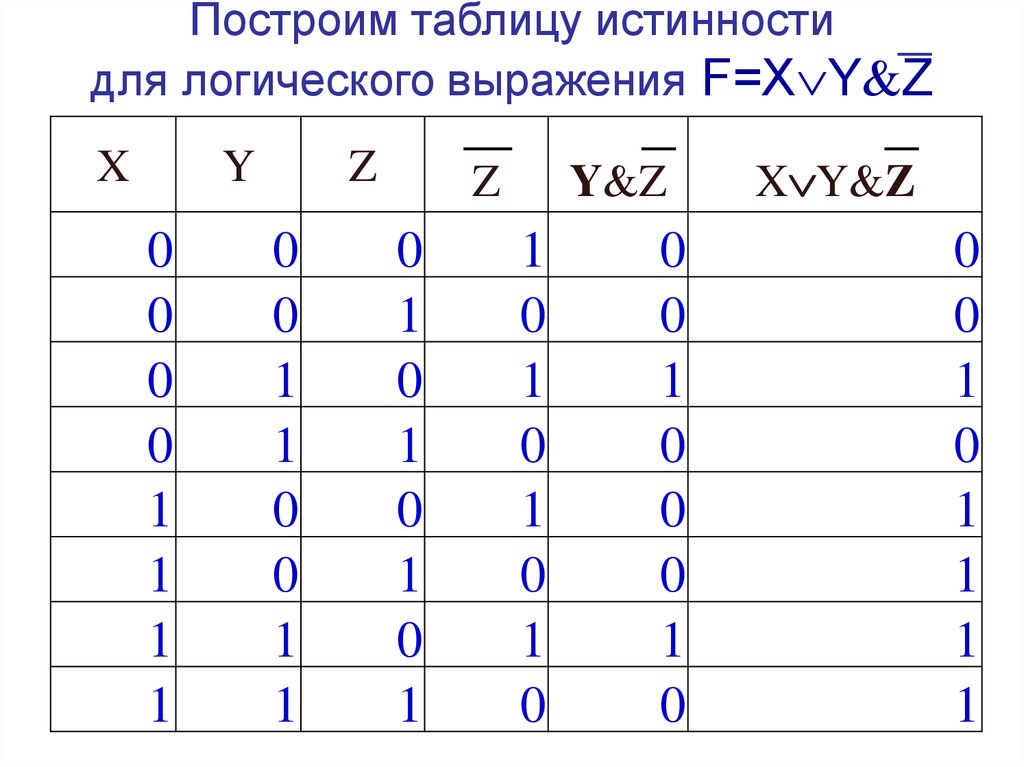
Пример: Строки 2 и 3 равны 1 , строка 2 записывается как A И НЕ(B) (потому что A равно 1 и B равно 0 ), строка 3 записывается как НЕ(А) И В и, следовательно, уравнение имеет вид (А И НЕ(В)) ИЛИ (НЕ(А) И B) , который, возможно, упрощается до A XOR B
Вычисление на основе выходных значений 0 таблицы истинности (Maxterms): для каждого 0 запишите соответствующие входные значения, разделенные логическим ИЛИ , затем сгруппируйте эти результаты с логической И .
Пример: Строки 1 и 4 равны 0 , строка 1 записывается как A ИЛИ B , строка 4 записывается как НЕ(А) ИЛИ НЕ(В) и поэтому уравнение равно (A OR B) AND (NOT(A) OR NOT(B)) , что, возможно, упрощается до A XOR B
Какая таблица истинности для логического И?
Таблица истинности для функции И:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Что такое таблица истинности для логического ИЛИ?
Таблица истинности для функции ИЛИ:
| A | B | A OR B |
|---|---|---|
| 0 | 0032 0||
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
What is the truth table for logical XOR?
The truth table for the XOR function is:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
What The Prame Table Table Tabil Talecil?
The truth table for the NAND function is:
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Какая таблица истинности для логического НЕ-ИЛИ?
The truth table for the NOR function is:
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Какая таблица истинности для логического ИСТИНА?
The truth table for the TRUE (=1) function is:
| A | TRUE |
|---|---|
| 0 | 1 |
| 1 | 1 |
What is the таблица истинности для логического FALSE?
Таблица истинности для функции ЛОЖЬ (=0):
| A | ЛОЖЬ |
|---|---|
| 0 | 0 |
| 1 | 0 |
