Мат. логика, основания математики, теория алгоритмов
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| |||
01/12/15 |
| ||
| |||
| iifat |
| |||
16/02/13 |
| |||
| ||||
| garin99 |
| ||
12/02/09 |
| ||
| |||
| OneMore |
| ||
29/12/12 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| svv |
| |||
23/07/08 |
| |||
| ||||
| default |
| ||
01/12/15 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| default |
| ||
01/12/15 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Что такое Аксиома и Теорема? Определение, примеры, доказательства.
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
|
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.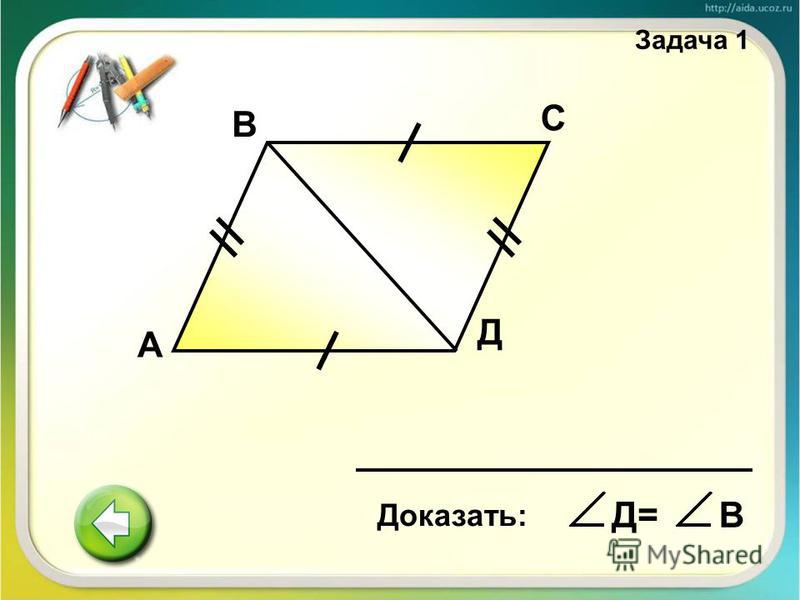
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
- прямая, которая пересекает одну параллельную прямую, обязательно пересекает и другую;
- если две прямые параллельны третьей, то между собой они также параллельны.
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
- если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
- если две прямые параллельны третьей прямой, то они параллельны.
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
|
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
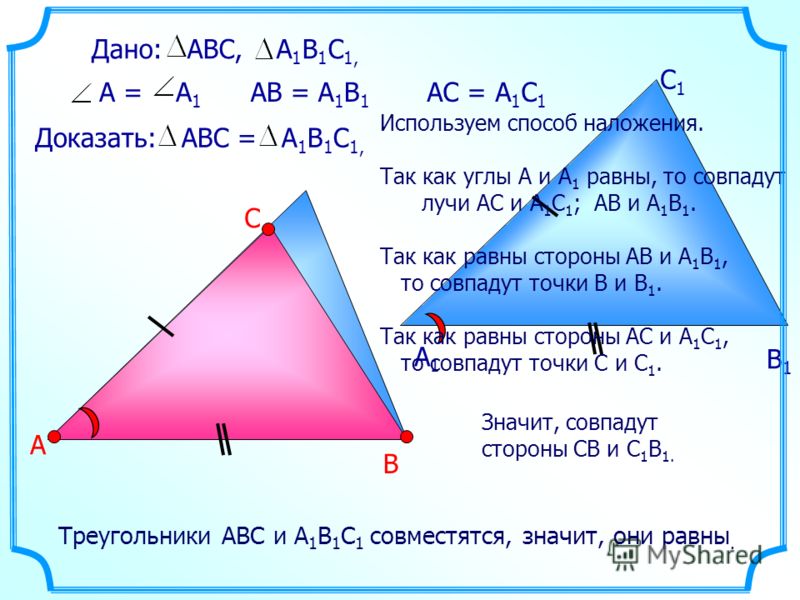
Приемы для доказательства в геометрии:
- Способ наложения — когда одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений в зависимости от того, совмещаются они или нет при наложении.

- Способ пропорциональности — применение свойств пропорций. Этот способ пригодится для доказательства теорем про подобные фигуры и пропорциональные отрезки.
- Способ пределов — когда вместо данной величины берут свойства другой, близкой к ней. А потом перекладывают эти выводы на исходные данные.
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
- прямая теорема: в треугольнике против равных сторон лежат равные углы.
- обратная теорема: в треугольнике против равных углов лежат равные стороны.
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов.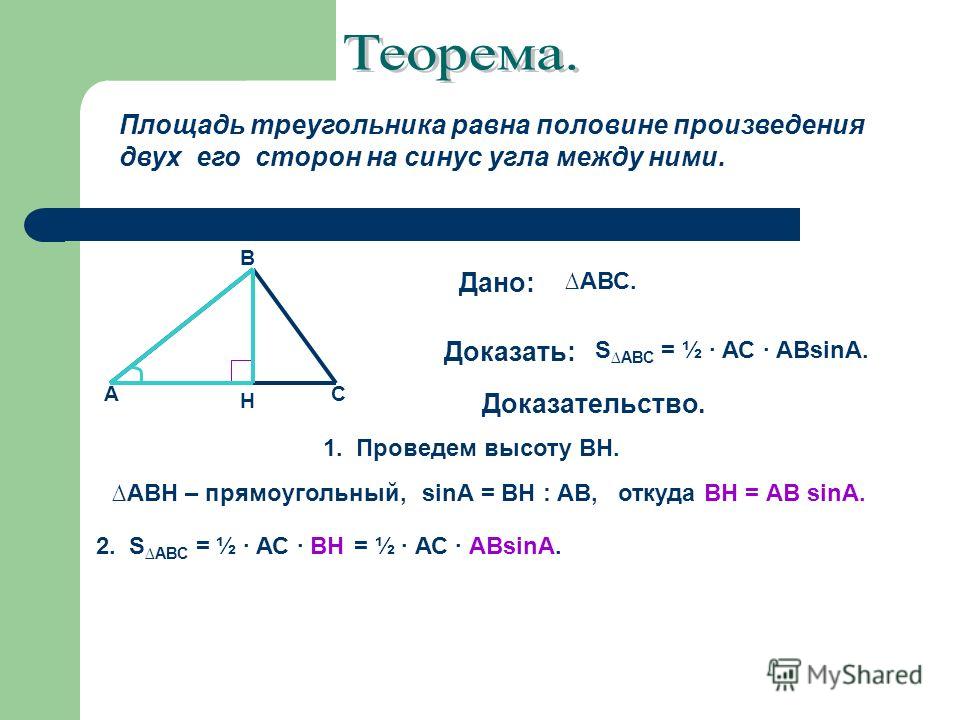 А во второй всё наоборот.
А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
- Прямая: если при пересечении двух прямых третьей соответственные углы равны, то данные прямые параллельны.
- Обратная: если две прямые параллельны, то при пересечении их третьей, соответственные углы равны.
- Противоположная: если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
- Обратная противоположной: если прямые не параллельны, соответственные углы не равны.
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).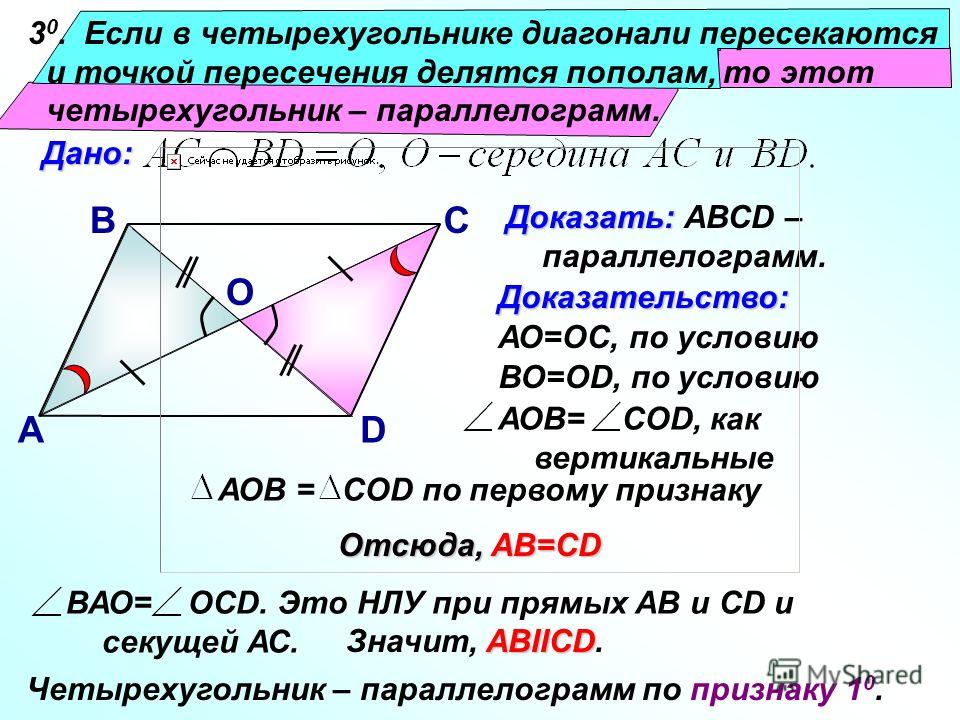
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол, противолежащий стороне а.
Следствия из теоремы косинусов:
- при b² + c² – a² > 0 угол α будет острым;
- при b² + c² – a² = 0 угол α будет прямым, что соответствуем теореме Пифагора;
- при b² + c² – a² < 0 угол α будет тупым.

Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Формула:
где a, b, c — стороны треугольника,
α, β, γ — углы, противоположные сторонам a, b, c соответственно.
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны.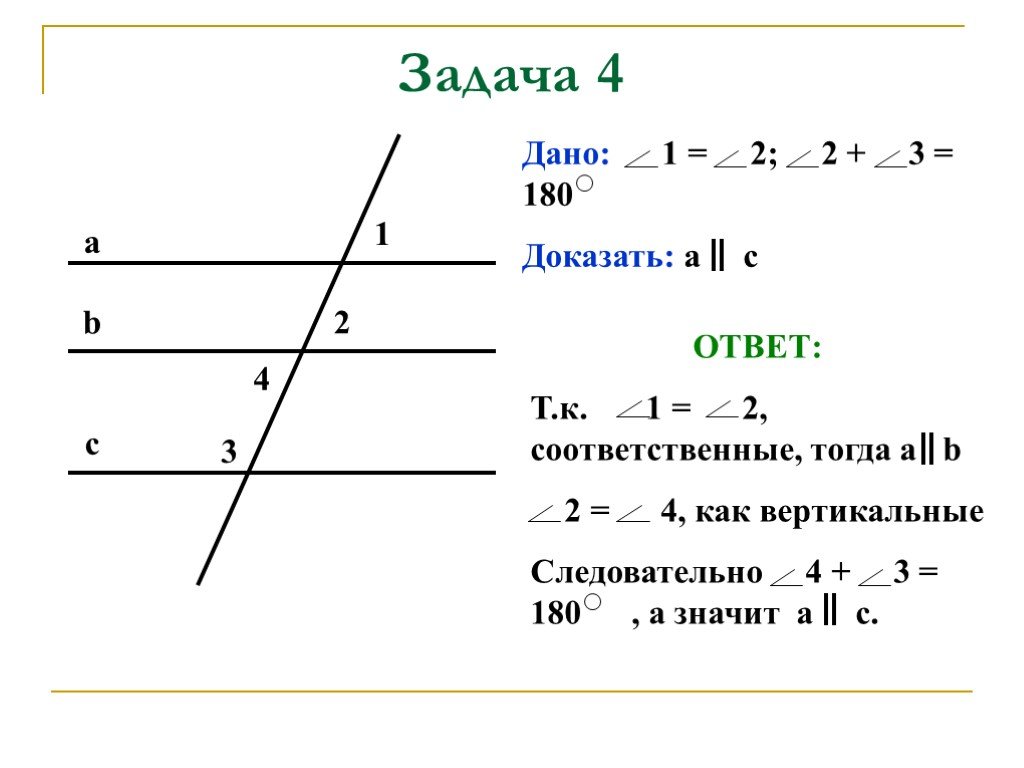 Это верно для любого квадрата, поэтому это — свойство.
Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
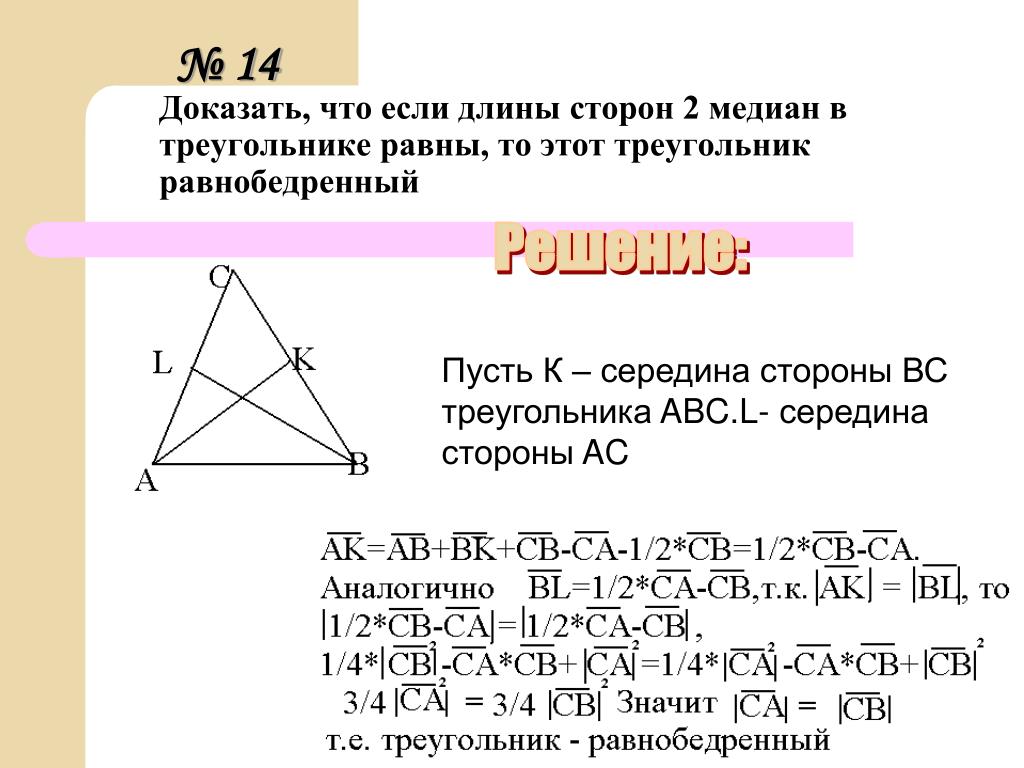
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AC = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AC = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AC = BD, то это уже верный признак прямоугольника.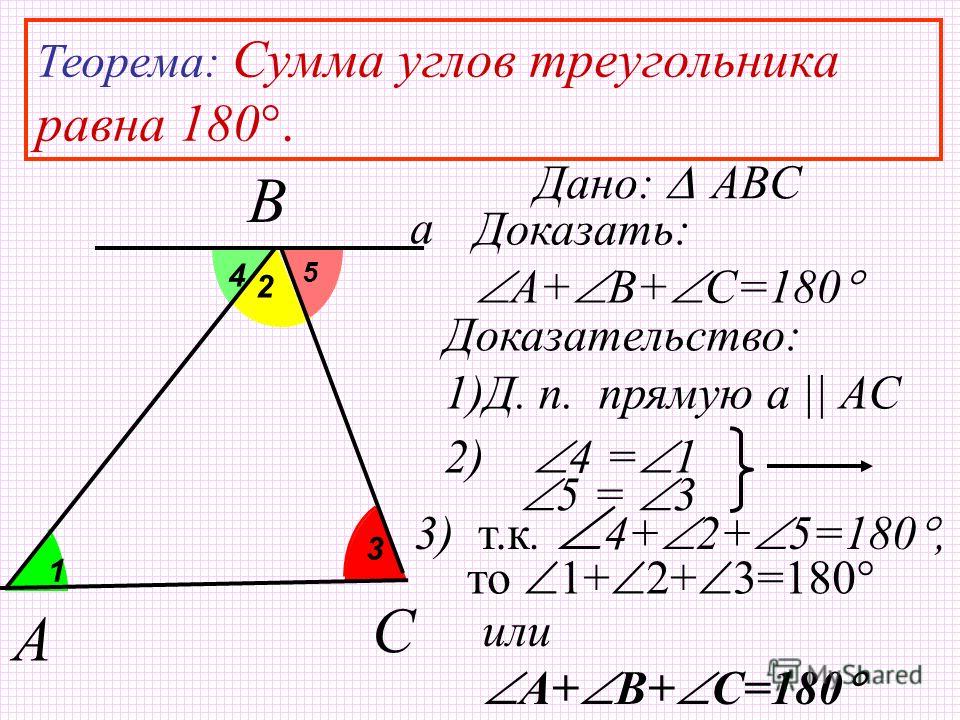 Смотрите рисунок:
Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.
линейная алгебра. Найдите C такое, что CAC’ = B
Редактировать: я дал первый ответ в форме контрпримера. Я откладываю это как вторую часть, потому что теперь у меня есть полный ответ, который я описываю в первой части.
Он дает такие условия, что при заданных матрицах $A$ и $B$ (соответственно $N \times N$ и $(N+1) \times (N+1)$) можно найти $N \times (N+1)$ матрица $C$ такая, что:
$$C’AC = B \ \ \ (1)$$
с дополнительным условием, что $A$, по крайней мере, необратима ( Я поменяю здесь роли $C$ и $C’$, потому что это обозначение будет более практичным в следующих строках) 9N$ и $g \in \mathbb{R}$.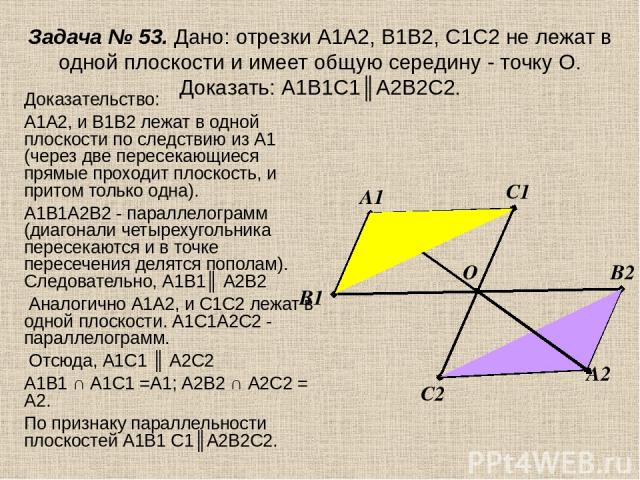
При этих обозначениях соотношение (1) принимает следующий вид:
$$\begin{bmatrix} D’AD&D’AV\\V’AD&V’AV\end{bmatrix}=\begin{bmatrix} E&F\\F’&g \end{bmatrix} \ \ \ (3)$$
Теперь мы имеем 3 соотношения:
$$D’AD=E \ \ \ (4a), \ \ \ \ \ \ \ (D’A )V=F \ \ \ (4b), \ \ \ \ \ \ \ V’AV=g \ \ \ (4c)$$
т.е. 3 ограничения на два неизвестных, матрицу $D$ и вектор $V$ .
Согласно закону инерции (en.wikipedia.org/wiki/Sylvester’s_law_of_inertia), необходимым и достаточным условием существования $D$ является то, что $A$ и $E$ ($N \ раз N$ верхний левый блок $B$ имеет одинаковую сигнатуру (одинаковое количество отрицательных, нулевых и положительных собственных значений).0003
Если выполнено это условие идентичности подписи:
Условие (4b) выполнено, так как $D’A$ необратима (поскольку это так для $A$), дает бесконечное число решений, и среди них решения вида $V=V_1+\mu V_2$ (где ненулевой вектор $V_2 \in Null(D’A)$).

Условие (4c) будет выполнено при условии: квадратное уравнение в $\mu$, полученное путем разложения $(V’_1+\mu V’_2)A(V_1+\mu V_2)=g$, имеет хотя бы одну вещественную решение. 92\конец{bmatrix}$$ Но если матрица $B$ не имеет такой структуры, например, если
$$B=\begin{bmatrix} 1 & 0 & 0\\0 & 1 & 0\\ 0& 0&0\end{bmatrix}$$
невозможно совпадение с предыдущим продуктом, какими бы ни были значения $a,b,c,d,e,f$.
Почему это было предсказуемо? Потому что верхний левый блок $2 \times 2$ $B$ имеет сигнатуру (0 отрицательных, 0 нулевых, 2 положительных), тогда как для $A$ это (0 отрицательных, один нулевой, 1 положительный).
элементарная теория чисел — Докажите, что $(ab,cd)=(a,c)(b,d)\left(\frac{a}{(a,c)},\frac{d}{(b,d )}\right)\left(\frac{c}{(a,c)},\frac{b}{(b,d)}\right)$
Теорема 1. Пусть $x$ и $ y$ — два целых числа. Тогда существуют целые числа $p$ и $q$ такие, что $px+qy=\gcd\left( x,y\right) $.
Теорема 1 — это теорема Безу, и мы предполагаем, что она известна.
 Обратите внимание, что
целые числа $x$ и $y$ могут быть равны $0$ (даже оба, в этом случае
мы используем соглашение $\gcd\left( 0,0\right) =0$).
Обратите внимание, что
целые числа $x$ и $y$ могут быть равны $0$ (даже оба, в этом случае
мы используем соглашение $\gcd\left( 0,0\right) =0$).Предложение 2. Пусть $n$ и $m$ — два таких целых неотрицательных числа, что $n\mid m$ и $m\mid n$. Тогда $m=n$.
Предложение 2 очевидно. Равенства между НОД обычно доказываются с помощью помощи предложения 2.
Лемма 3. Пусть $x$, $y$, $z$ и $w$ — четыре целых числа такие, что $\gcd\left( x,z\right) =1$ и $\gcd\left( y,w\right) =1$. Затем $\gcd\left( xy,zw\right) =\gcd\left( y,z\right) \cdot\gcd\left( x,w\right) $.
Доказательство леммы 3. Теорема 1 (примененная к $w$ вместо $y$) показывает, что существуют целые числа $p$ и $q$ такие, что $px+qw=\gcd\left( x,w\right) $. Давайте обозначим эти $p$ и $q$ через $p_{1}$ и $q_{1}$. Таким образом, $p_{1}$ и $q_{1}$ целые числа, удовлетворяющие $p_{1}x+q_{1}w=\gcd\left( x,w\right) $.
Теорема 1 (примененная к $y$ и $z$ вместо $x$ и $y$) показывает, что существуют целые числа $p$ и $q$ такие, что $py+qz=\gcd\left( y,z\right) $.
 {\prime}w=\gcd\left( x,z\right) =1$. 9{\prime}+q_{1}q_{2}\right) zw$ (через a
простое вычисление)
{\prime}w=\gcd\left( x,z\right) =1$. 9{\prime}+q_{1}q_{2}\right) zw$ (через a
простое вычисление)является $\mathbb{Z}$-линейной комбинацией $xy$ и $zw$ и поэтому делится на $\gcd\left( xy,zw\right) $ (поскольку и $xy$, и $zw$ делятся на $\gcd\left(xy,zw\right) $). Другими словами,
(1) $\gcd\left( xy,zw\right) \mid\gcd\left( y,z\right) \cdot \gcd\left( x,w\right) $.
С другой стороны, умножая соотношения $\gcd\left( y,z\right) \mid y$ и $\gcd\left( x,w\right) \mid x$, получаем $\gcd\left( y,z\right) \cdot\gcd\left( x,w\справа) \mid yx=xy$. Кроме того, умножая отношения $\gcd\left( y,z\right) \mid z$ и $\gcd\left( x,w\right) \mid w$, получаем $\gcd\left( y,z\right) \cdot \gcd\left( x,w\right) \mid zw$. Таким образом, мы знаем, что и $xy$, и $zw$ делится на $\gcd\left( y,z\right) \cdot\gcd\left( x,w\right) $. Следовательно, наибольший общий делитель $xy$ и $zw$ также делится на $\gcd\left( y,z\right) \cdot\gcd\left( x,w\right) $. Другими словами, у нас есть
(2) $\gcd\left( y,z\right) \cdot\gcd\left( x,w\right) \mid\gcd\left( ху, zw\вправо) $.

Теперь мы доказали (1) и (2) . Таким образом, мы можем применить предложение 2 к $n=\gcd\left( y,z\right) \cdot\gcd\left( x,w\right) $ и $m=\gcd\left( ху, zw\вправо) $. Таким образом, мы получаем $\gcd\left( xy,zw\right) =\gcd\left( y,z\right) \cdot\gcd\left( x,w\right) $. Лемма 3 доказана.
Теорема 4. Пусть $a$, $b$, $c$ и $d$ — четыре целых числа. Пусть $n=\gcd\left( a,c\right) $ и $m=\gcd\left( b,d\right) $; предположим, что $n\neq0$ и $m\neq0$. Затем
$\gcd\left( ab,cd\right) =\gcd\left( a,c\right) \cdot\gcd\left( b,d\right) \cdot\gcd\left( \dfrac{a}{n},\dfrac{d}{m}\right) \cdot \gcd\left( \dfrac{c}{n},\dfrac{b}{m}\right) $.
Доказательство теоремы 4. Пусть $x=\dfrac{n}{a}$, $y=\dfrac{m}{b}$, $z=\dfrac{n}{c}$ и $w=\dfrac{n}{d}$. Тогда $a=nx$, $b=my$, $c=nz$ и $d=nw$. Также, $x=\dfrac{n}{a}$ — целое число (поскольку $n=\gcd\left( a,c\right) \mid a$), и аналогично $y$, $z$ и $w$ являются целыми числами.

Теперь $n=\gcd\left( \underbrace{a}_{=nx},\underbrace{c}_{=nz}\right) =\gcd\left( nx,nz\right) =n\gcd\left( x,z\right) $. Поскольку $n\neq0$, мы можем делим это равенство на $n$ и получаем $1=\gcd\left( x,z\right) $. Одинаковый Аргумент (с использованием $m,b,d,y,w$ вместо $n,a,c,x,z$) показывает, что $1=\gcd\left( у,ж\справа) $. Таким образом, лемма 3 дает
$\gcd\left(xy,zw\right) =\underbrace{\gcd\left(y,z\right)} _{=\gcd\left( z,y\right) }\cdot\gcd\left( x,w\right) =\gcd\left( z,y\right) \cdot\gcd\left( x,w\right) $
$=\gcd\left( x,w\right) \cdot\gcd\left( z,y\right) $.
Но
$\gcd\left( \underbrace{a}_{=nx}\underbrace{b}_{=my},\underbrace{c} _{=nz}\underbrace{d}_{=mw}\right) =\gcd\left( nxmy,nzmw\right) =\gcd\left( nm\cdot xy,nm\cdot zw\right) $
$=nm\cdot\underbrace{\gcd\left( xy,zw\right)}_{=\gcd\left(w,x\right) \cdot\gcd\left( z,y\right) }=\underbrace{n}_{=\gcd\left( a,c\right) }\underbrace{m}_{=\gcd\left( b,d\right) }\cdot\gcd\left( \underbrace{x} _{=\dfrac{a}{n}},\underbrace{w}_{=\dfrac{d}{m}}\right) \cdot\gcd\left( \underbrace{z}_{=\dfrac{c}{n}},\underbrace{y}_{=\dfrac{b}{m}}\right) $
$=\gcd\left( a,c\right) \cdot\gcd\left( b,d\right) \cdot\gcd\left( \dfrac{a}{n},\dfrac{d}{m}\right) \cdot\gcd\left( \dfrac{c}{n},\dfrac{b} {м}\справа) $.

Теорема 4 доказана.
Вероятно, это не самое простое или короткое доказательство, но самое простое. писать (мне почти не нужно было концентрироваться и очень мало редактировалось, просто много копировать вставить). Досадные вычисления в доказательстве леммы 3 могли бы был упрощен с использованием идеальных обозначений, но я не знаю, есть ли у вас это фон. Безусловно, существует альтернативное доказательство путем сравнения показателей степени простых чисел, но мой аргумент обобщает лучше. Например, приведенную выше лемму 3 можно непосредственно обобщить до следующего результата:
Лемма 5. Пусть $A$ — коммутативное кольцо. Пусть $X$, $Y$, $Z$ и $W$ — четыре идеала $A$, такие что $X+Z=A$ и $Y+W=A$. Тогда $XY+ZW = \left(Y+Z\right)\left(X+W\right)$.
Лемму 3 можно восстановить из леммы 5, полагая $A = \mathbb Z$, $X = x \mathbb Z$, $Y = y \mathbb Z$, $Z = z \mathbb Z$ и $W = ш \mathbb Z$. Доказательство, которое я дал для леммы 3, по существу является доказательством леммы 5, искусственно ограниченным случаем главных идеалов в $\mathbb Z$.



 Значит .
Значит . Наличие трёх множеств делит универсум на 8 (возможно, пустых) частей, элементы которых равноправны относительно выражений.
Наличие трёх множеств делит универсум на 8 (возможно, пустых) частей, элементы которых равноправны относительно выражений.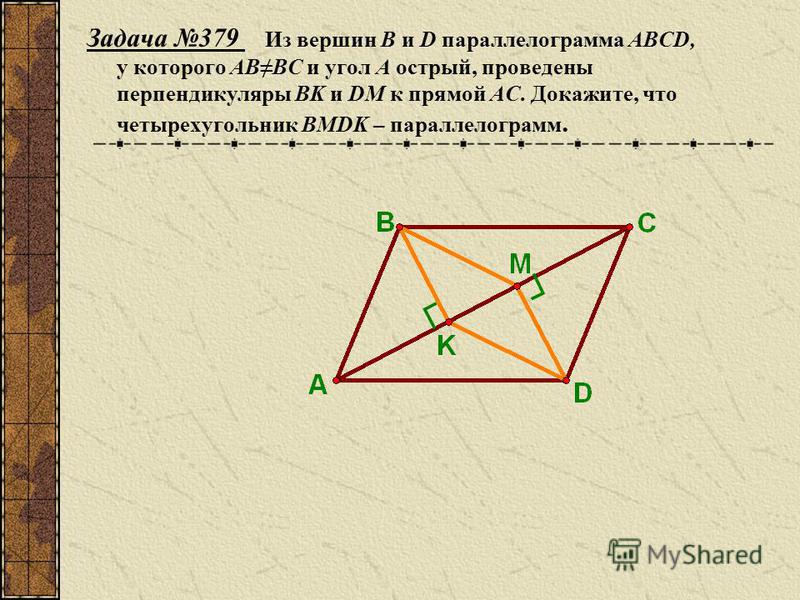


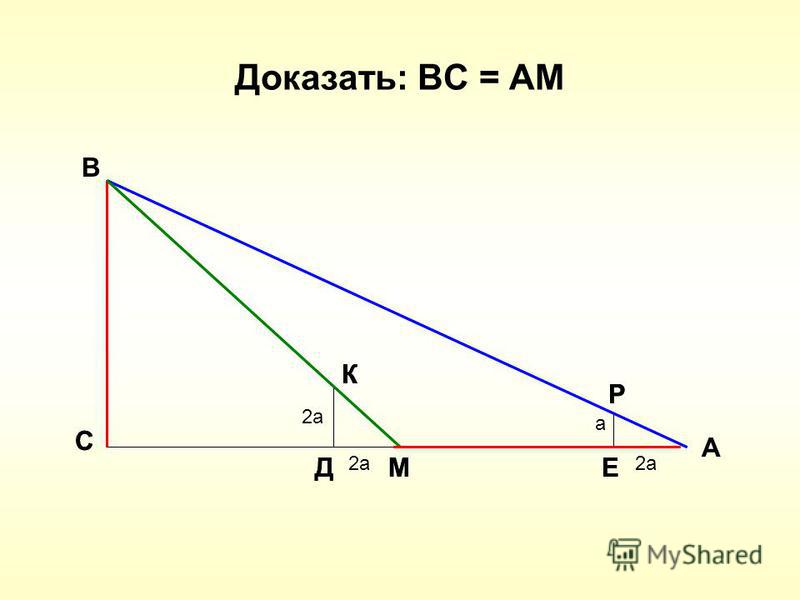


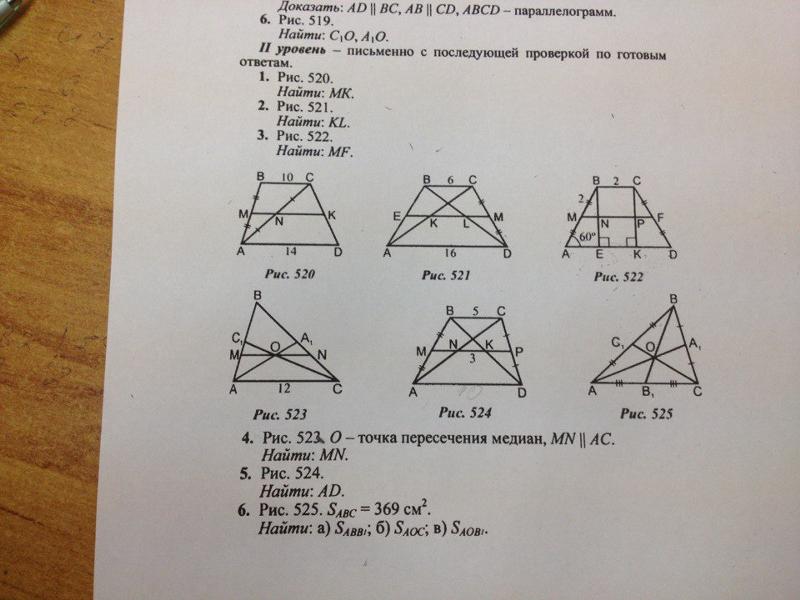 Включение превратится в a , что можно снова упростить, а потом, идя в обратную сторону, подбирать слова и построить таким образом «вывод в словах».
Включение превратится в a , что можно снова упростить, а потом, идя в обратную сторону, подбирать слова и построить таким образом «вывод в словах». А вот рассуждениями не получается у меня понять, почему справа от равно , в частности . Предполагаю, потому что ?
А вот рассуждениями не получается у меня понять, почему справа от равно , в частности . Предполагаю, потому что ?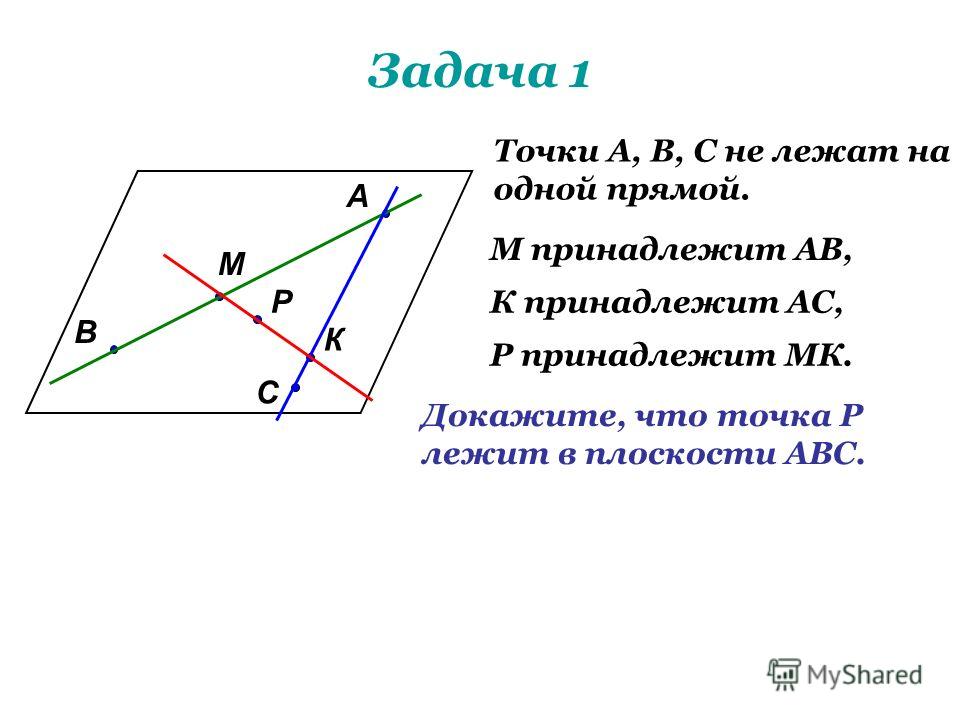 Предполагаю, потому что ?
Предполагаю, потому что ?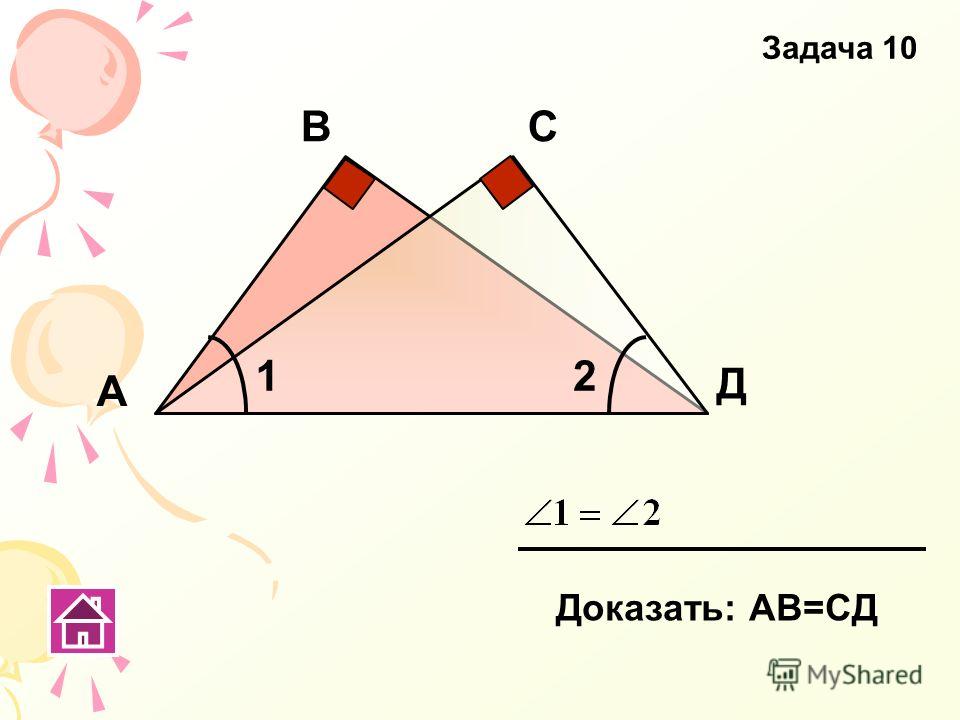
 Обратите внимание, что
целые числа $x$ и $y$ могут быть равны $0$ (даже оба, в этом случае
мы используем соглашение $\gcd\left( 0,0\right) =0$).
Обратите внимание, что
целые числа $x$ и $y$ могут быть равны $0$ (даже оба, в этом случае
мы используем соглашение $\gcd\left( 0,0\right) =0$). {\prime}w=\gcd\left( x,z\right) =1$. 9{\prime}+q_{1}q_{2}\right) zw$ (через a
простое вычисление)
{\prime}w=\gcd\left( x,z\right) =1$. 9{\prime}+q_{1}q_{2}\right) zw$ (через a
простое вычисление)