Третий признак подобия треугольников / Подобные треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Третий признак подобия треугольников
Теорема
| Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны |
Доказательство
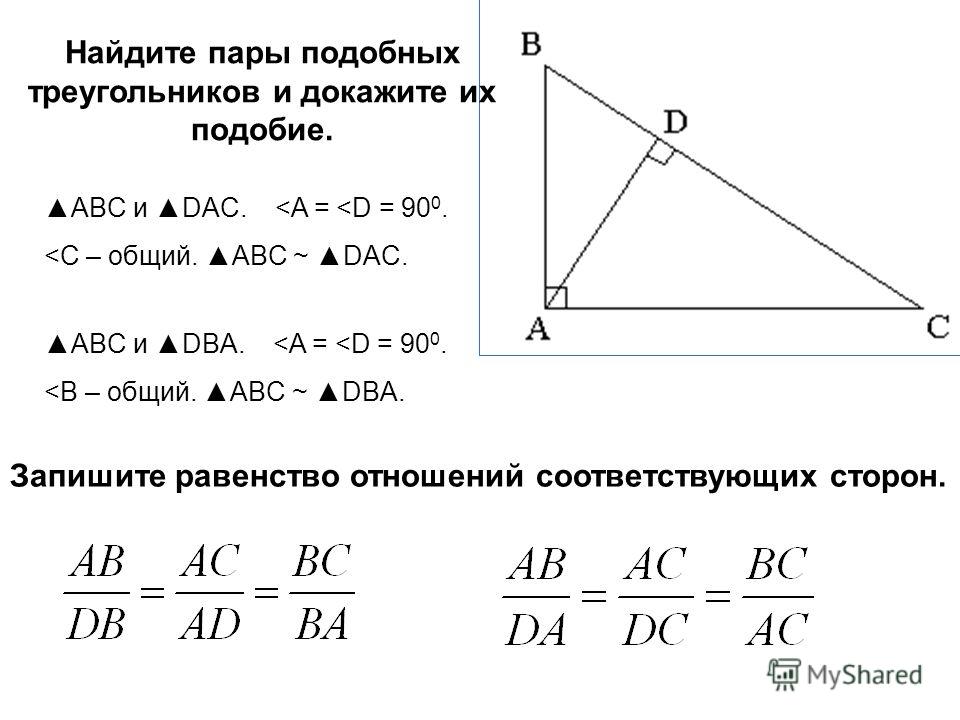
Дано: АВС и А1В1С1,
Доказать: АВСА1В1С1
Доказательство:
Рассмотрим АВС и А1В1С1, у которых (1)
Для доказательства теоремы, учитывая второй признак подобия треугольников, достаточно доказать, что 
Рассмотрим АВС2, у которого 1 = А1, 2 = В1.
АВС2А1В1С1 по первому признаку подобия треугольников, поэтому (2).
Сравнивая равенства (1) и (2), получаем: ВС = ВС2, СА =С2А. АВС =АВС2 по трем сторонам. Отсюда следует, что А = 1, а так как 1 = А1
, то А = А1. Теорема доказана.Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 560, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 613, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 626*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Признаки подобия треугольников
При изучении геометрии вы непременно обращали внимание, что часть фигур очень похожа на другие.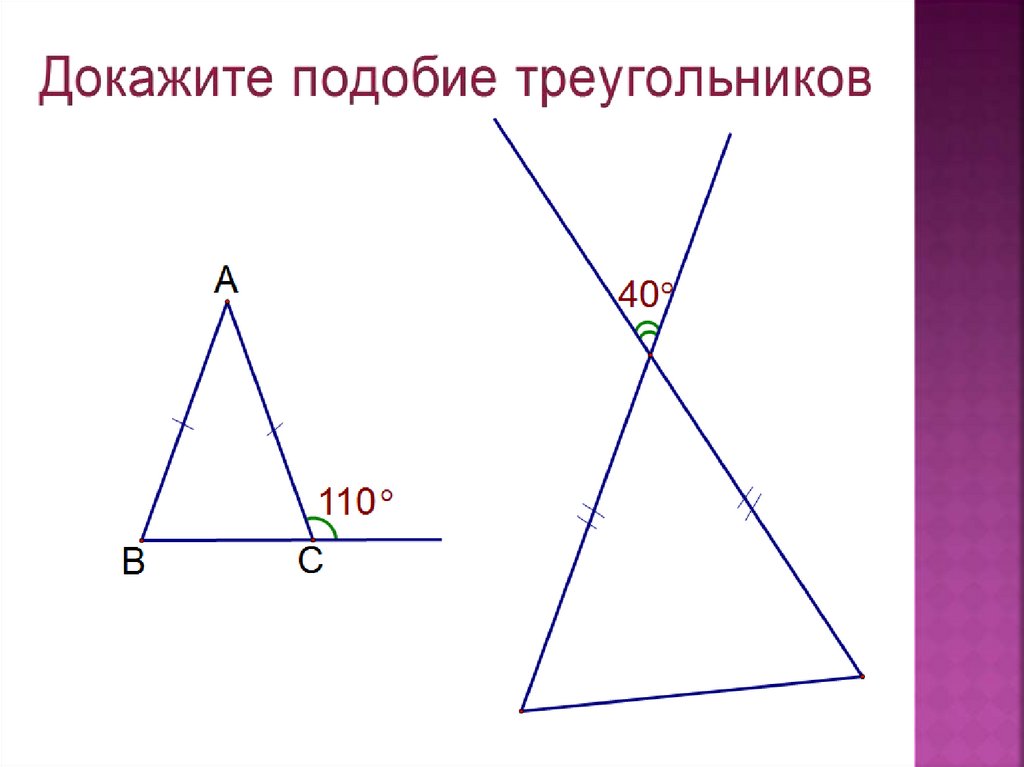
Отличаются только размеры. Но геометрия — наука точная и слово «похожие» не всегда определяет реальное положение вещей. Например, прямоугольный треугольник похож на равносторонний, но при ближайшем рассмотрении легко обнаружить различия, — отличаются углы, длины сторон, конфигурация.
В геометрии применяется другое понятие — «подобие». Это более узкий термин, который определяет фигуры, которые идентичны по всем параметрам, кроме размера. Если увеличить, или уменьшить одну из фигур, то получится другая, с полным соответствием. Знак подобия в геометрии «~» имеет очень большой смысл. Это не просто обозначение «похожести», а специальный термин. Он говорит о том, что из одной фигуры можно получить другую, если преобразовать ее особым образом.
Самый простой способ — увеличение размеров. Но не простое увеличение, а пропорциональное. То есть, каждая сторона фигуры увеличивается на строго определенную величину. Соотношение новой длины и исходной называется коэффициентом подобия.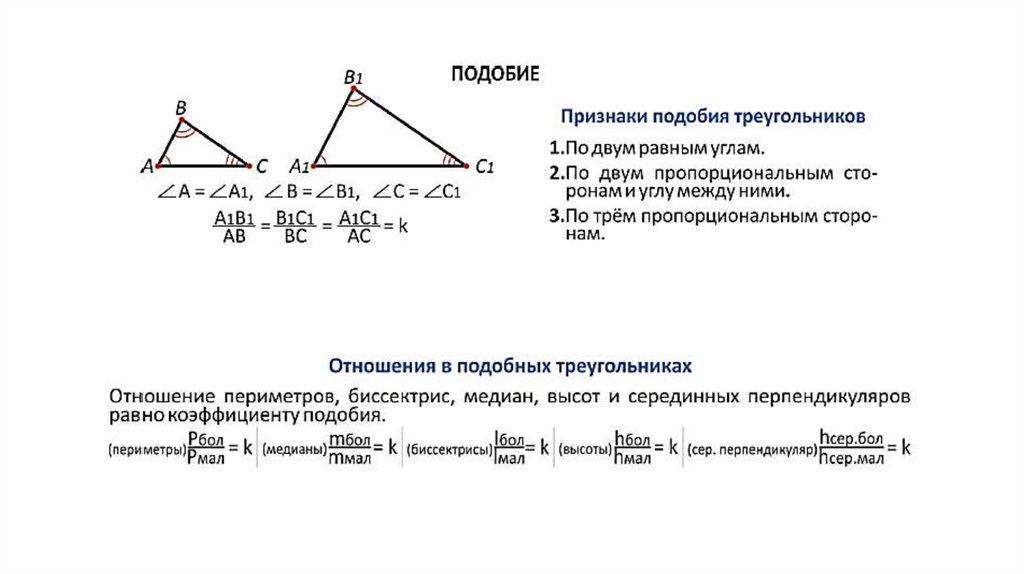
Согласно правилам математики К≠ 0. Смысл ясен, на ноль делить нельзя. В остальном значение К может принимать любое значение, в том числе, и дробное. Если в десятичном исчислении коэффициент находится в диапазоне от ноля до единицы, то фигура уменьшается при проецировании, если К ≥ 1, то фигура получится больше, или идентичной исходной.
Содержание
- Подобие треугольников
- Первый признак подобия
- Второй признак подобия
- Третий признак подобия треугольников
- Примеры прикладного применения признаков подобия треугольников
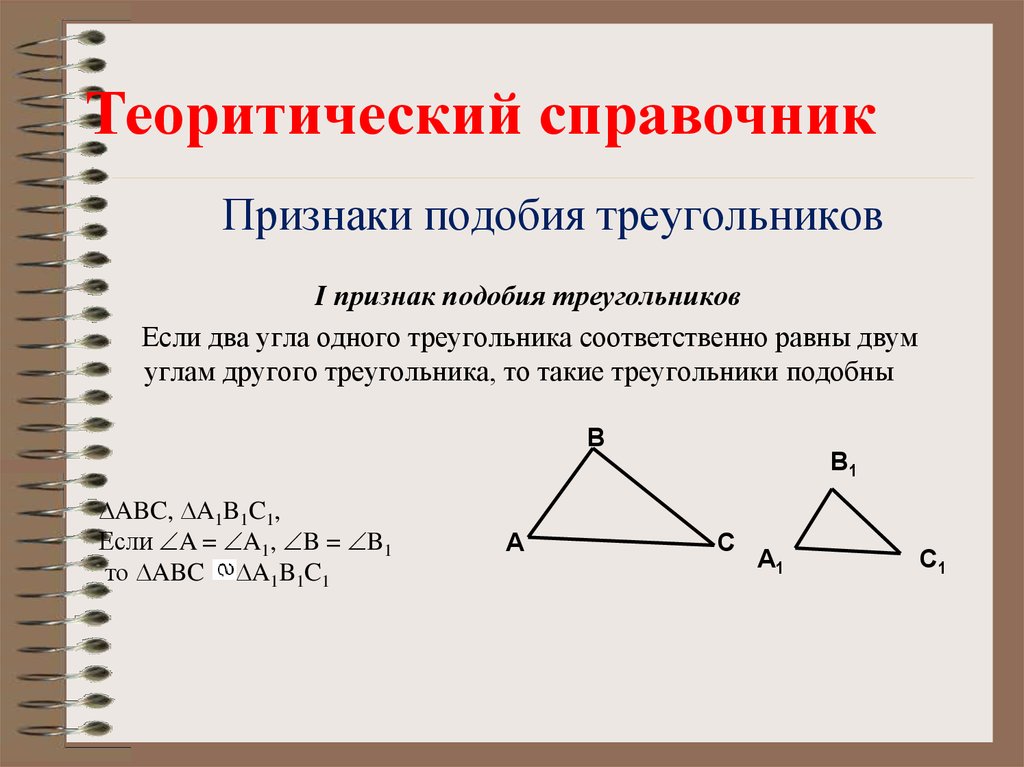
Каждая из геометрических фигур имеет ряд признаков, по которым ее можно сравнить с другой и определить, подобные фигуры, или просто похожие. У треугольников таких признаков три. Рассмотрим их более подробно. В идеале, треугольники называются подобными, если у них три угла одинаковые, а три стороны пропорциональны, согласно коэффициенту К. Но не всегда есть возможность измерить углы и стороны. Есть ряд признаков, требующих меньшего числа измерений, по которым легко определить, подобные треугольники, или нет.
Если два угла произвольного треугольника равны двум углам другого, значит, фигуры подобные. В геометрической графике это записывается так:
ΔАВС ~ΔА1В1С1 А=∠А1, ∠В=∠В1, ∠С=∠С1.
Доказательство первого признака подобия приводить не будем, ввиду того, что признак проверен и доказан, информация об этом есть в любом учебнике. Намного важнее, что из этого признака вытекает следствие, которое не менее важно, чем сам признак. Во многих задачах на ЕГЭ и в учебниках упор делается именно на знание этого правила. «Если три стороны одного треугольника попарно параллельны трем сторонам другого, то эти фигуры подобны».
Утверждение не менее очевидно, чем первый признак подобия. Формулируется оно так:
Если две соответствующие стороны треугольников пропорциональны, а углы между ними равные, то фигуры подобные.
Это правило называется признаком подобия по двум сторонам и углу между ними. Геометрическая запись выглядит так:
ΔАВС ~ΔА1В1С1 ↔ ∠ А=∠А1, АВ/А1В1 = АС/А1С1.
Самый простой и наиболее понятный признак подобия: если три стороны одной фигуры пропорциональны трем сторонам другой с одинаковым коэффициентом К, то треугольники подобные. Записывается такое утверждение таким образом:
ΔАВС ~ΔА1В1С1↔АВ/А1В1 = АС/А1С1= ВС/В1С1..
Доказательство этого утверждения опять же приводить не будем вследствие дефицита размера статьи. Лучше остановимся на следствиях, которые вытекают из этих утверждений. Многие из параметров геометрических фигур можно определить, пользуясь названными правилами.
Один из способов применения признаков подобия демонстрирует теорема об отношении периметров подобных треугольников. В формулировке говорится о том, что отношение периметров подобных треугольников равно коэффициенту пропорциональности сторон. На практике это выглядит так — вам нужно найти периметр треугольника со сторонами в несколько километров, что часто требуется в строительстве, агротехнике и геодезии.
Если нарисовать подобный треугольник на бумаге, со сторонами в несколько сантиметров и вычислить периметр, то он будет ровно настолько же меньше, как и стороны треугольников. То есть, коэффициент К работает и в случае с периметром.
Вторая задача — найти соотношение площадей подобных треугольников. Здесь тоже существует определенная пропорция, но уже квадратичная. То есть, соотношение площадей фигур равно квадрату К.
S1/S = k2.
При решении задач поможет также лемма о подобных треугольниках, говорящая о том, что любая прямая, пересекающая треугольник параллельно одной из сторон, отсекает от него подобную фигуру.
Пользуясь полученной информацией, несложно решить любую задачу по определению параметров подобных треугольников.
Подобные треугольники — Доказательство сходства треугольников
Предыдущий СледующийДоказательство сходства треугольников
Представьте, что вы попали в смерч, который бросает вас и вашу собачку посреди незнакомой новой земли.
Чтобы вернуться домой, вы должны доказать, что два треугольника подобны. Как вы это сделаете?
Просто трижды щелкните каблуками и скажите: «Нет места лучше моего класса геометрии. Нет места лучше моего класса геометрии. Нет места лучше моего класса геометрии».
Если бы только!
Вернувшись сюда, в реальный мир, мы можем использовать три метода, чтобы доказать, что два треугольника подобны. К счастью, они очень похожи на , о которых мы уже узнали. Видишь, что мы там делали? Разве мы не придурки?
Когда мы впервые увидели эти методы, они выглядели как услужливые батраки, ухаживающие за конгруэнтными свиньями и вспахивающие конгруэнтные поля. Теперь они пугало, оловянный человек и лев, и все они помогут вам добраться до волшебника подобия в конце Дороги из желтого кирпича. Они могут выглядеть как одни и те же теоремы (в некоторых случаях они даже имеют одинаковые названия), но это не одно и то же. Те другие были около конгруэнтных треугольников, а эти примерно подобных треугольников.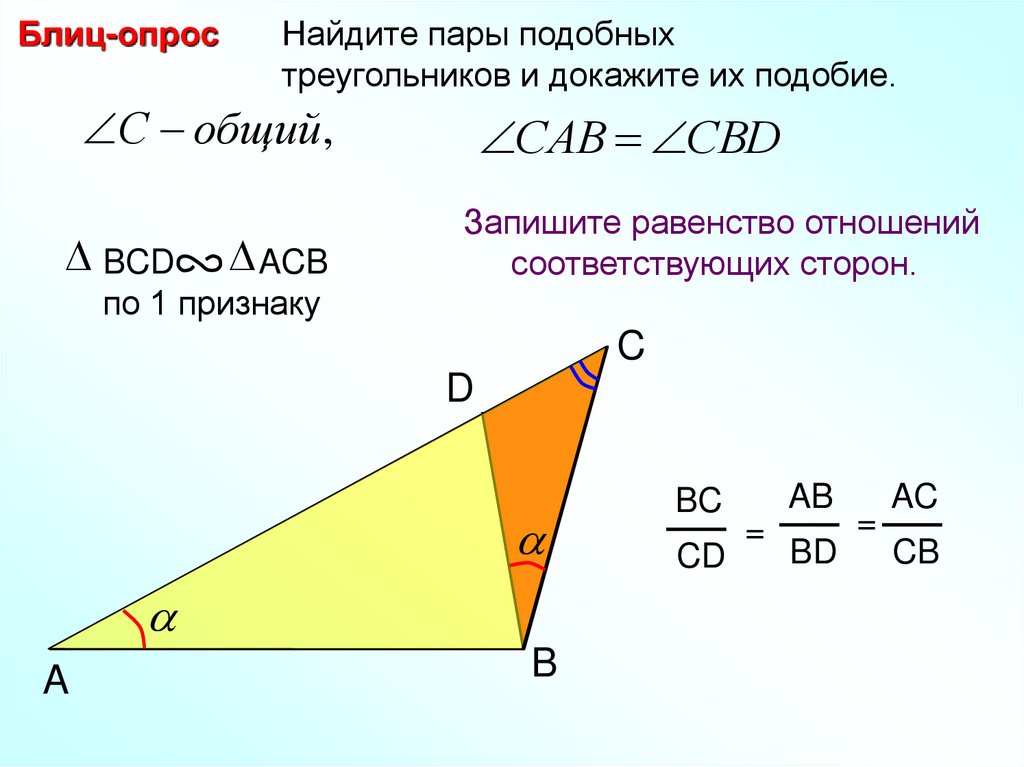
Первый метод доказательства сходства — это постулат Side-Side-Side (SSS) . Вот что говорится о подобных треугольниках:
Если три стороны двух треугольников пропорциональны по длине, то треугольники подобны.
Пример задачи
Докажите, что эти треугольники подобны.
| Заявление | Reason |
| 1. DO = 8, WI = 6 | Given |
| 2. OR = 12, IZ = 9 | Given |
| 3. RD = 16, ZW = 12 | Given |
| 4. | Algebra |
| 5. ∆ DOR ~ ∆ WIZ | Side-Side-Side Postulate (4 ) |
Вторым способом доказательства подобия треугольников является постулат Угол-Угол (AA) .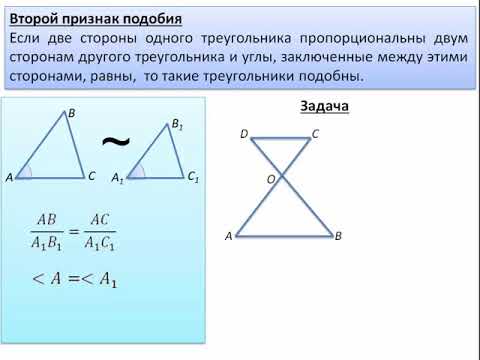
Это выглядит примерно так:
Если два треугольника имеют две пары равных углов, то такие треугольники подобны.
Пример задачи
Докажите, что эти треугольники подобны.
| Заявление | Причина |
| 1. ∠ M 9 0 ≥0014 | Приведен (на рисунке) |
| 2. тий TNI ≅ тий MNA | Вертикальные углы. 1, 2) |
Есть еще один способ доказать, что два треугольника подобны: постулат Сторона-Угол-Сторона (SAS) . SAS — это небольшая смесь AA и SSS. Похоже на то, что летающие обезьяны — это смесь птиц и обезьян, за исключением того, что SAS намного более цивилизован и не подчиняется приказам водорастворимой ведьмы. Мы думаем.
По сути, он говорит следующее:
Если длины двух сторон пропорциональны, а угол между этими двумя сторонами равен, то треугольники подобны.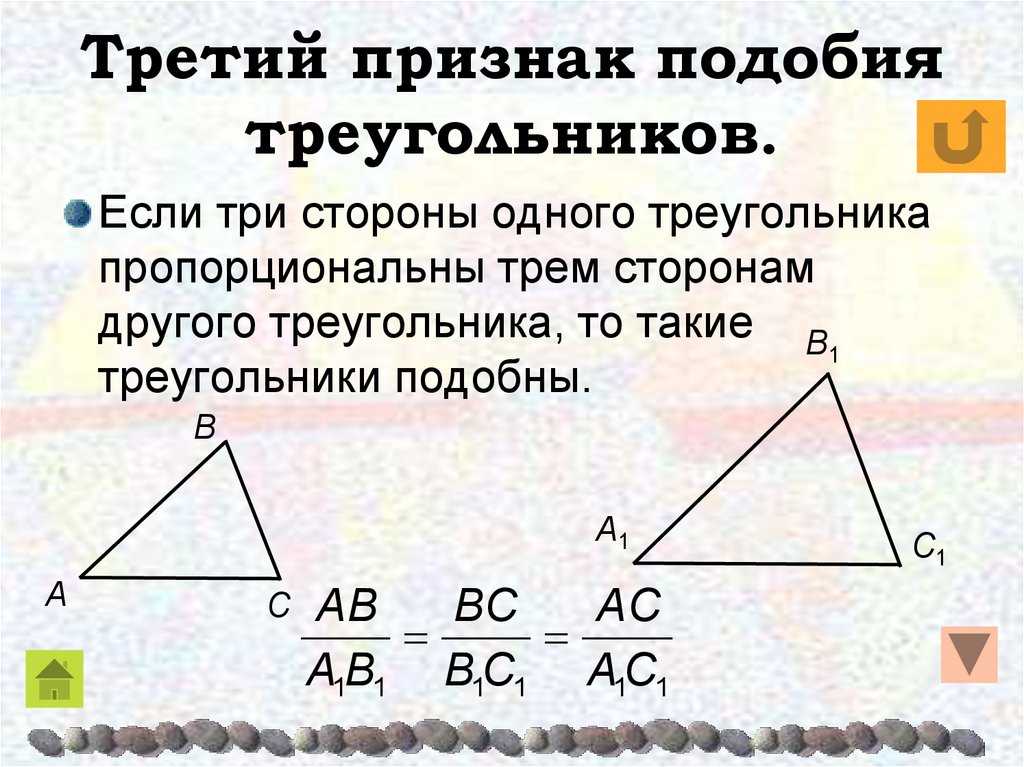
Пример задачи
Докажите, что эти треугольники подобны.
| Заявление | Разум |
| 1. WI = 12, WC = 15, KE = 8, 8, WC = 15, KE = 8, 8, WC = 15, KE = 8, 8, WC = 15, KE = 8, WC = 15, KE = 8, WC = 15, KE .0042 | Given |
| 2. | Algebra |
| 3. | Substitution Property |
| 4. m∠ W = 35, m∠ K = 35 | Given |
| 5. T W ≅ тий K | Переходная свойство |
| 6. ∆ WIC ~ ∆ KED | СДЕЛА
Предыдущий
Следующий Подробнее о подобных треугольниках Навигация Это продукт премиум-классаРазблокировать эти функции Устали от рекламы? Присоединяйтесь сегодня и никогда больше их не увидите. Начало работы Ярлыки подобия — Концепция — Геометрия Видео от BrightstormСуществует четыре ярлыка сходства треугольников: SSS, SAS, ASA и AAS. Мы имеем подобие треугольника, если (1) две пары углов конгруэнтны (AA) (2) две пары сторон пропорциональны и углы между ними конгруэнтны (SAS) или (3) если три пары сторон пропорциональны (SSS) . Обратите внимание, что AAA, AAS и ASA не указаны — их включение было бы излишним, поскольку все они имеют два равных угла. подобных треугольников АА САС ССС пропорция конгруэнтность Если бы вам нужно было доказать, что два треугольника подобны, мы проведем сравнение с конгруэнтностью, о чем мы говорили ранее. Мы сказали, что есть 4 способа доказать конгруэнтность двух треугольников.  Итак, под нашими ярлыками сходства я собираюсь использовать здесь другой маркер. Тот на исходе. Мы собираемся сказать, что угловой угол — это сокращение. Давайте рассмотрим второй случай. Допустим, все, что вы знали, это сторона, угол и еще одна сторона. А еще вы знали, что соответствующие стороны пропорциональны. Что ж, этой информации было бы достаточно, чтобы сказать, что эти два треугольника подобны. Итак, мы собираемся включить сторону угла в наш список сокращений подобия. И наконец, скажем, если бы все, что мы знали, было то, что 3 стороны 2-х разных треугольников, которые соответствуют, пропорциональны. Таким образом, мы могли бы записать эту пропорцию как постоянную между соответствующими сторонами.  |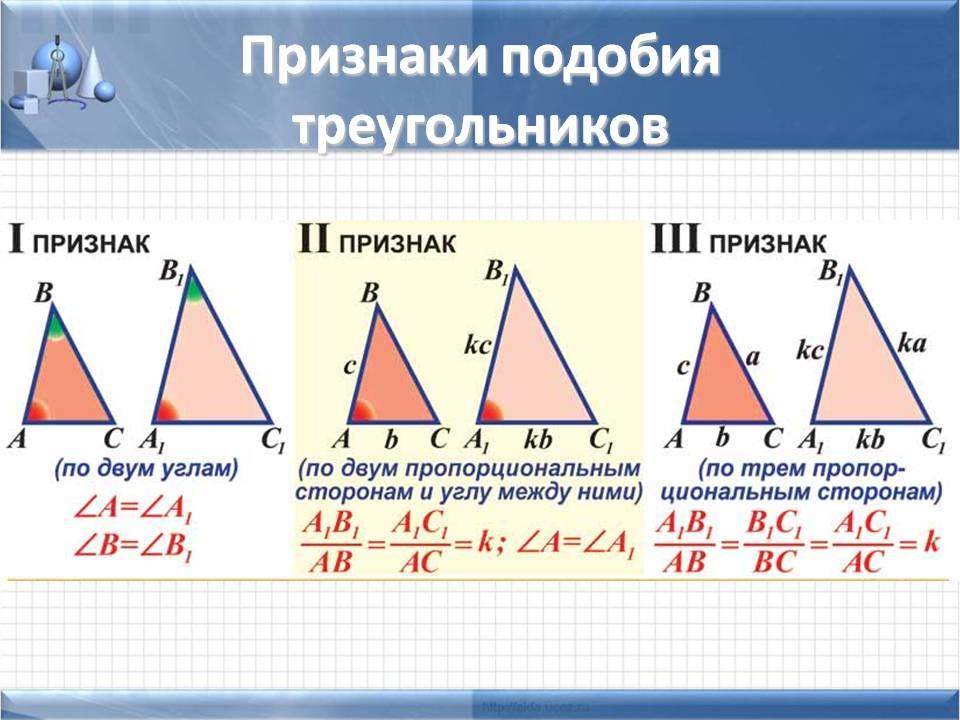
И эти 4 ярлыка были угол сторона угол, сторона угол сторона, сторона сторона угол и угол угол сторона.