Попробуйте решить уравнение с дробью и вспомнить школьный курс математики
Эта математическая головоломка ввела в ступор даже самых уверенных в себе умников в интернете. Вам выпал шанс доказать, что вы умнее десятков пользователей сети. Сможете ли вы решить этот пример с дробью? Даже если не справитесь с первого раза, мы подготовили для вас объяснение, как решать уравнения и примеры с дробями.
Теги:
Нетленка
Тест
Головоломки
Занимательная математика
Соцсети
Попробуйте решить этот пример с дробью. Калькулятор прочь: напрягаем мозг и решаем сами!
ВОПРОС 1 ИЗ 1
Теперь давайте попробуем решить уравнения с дробями. Напоминаем, что уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Его решение заключается в нахождении неизвестных чисел. При их подстановке должно получиться верное числовое равенство.
Чаще всего при решении уравнений с дробями неизвестная стоит в знаменателе. Такие уравнения называют дробно-рациональными. Если неизвестная находится в числителе, то это либо линейные, либо квадратные уравнения. Важно помнить следующее: если значение переменной обращает знаменатель в 0, значит это неверное значение. Также делить и умножать уравнение на 0 нельзя.
Давайте вспомним основные математические правила, которые помогут нам решить уравнение с дробями. Так, сокращение дроби — это деление числителя и знаменателя на одно и то же натуральное число. Сокращение делает дробь короче и проще для восприятия. Вспомним и правило сложении и вычитании дробей с одинаковыми знаменателями. При этих действиях к числителю первой дроби прибавляют числитель второй дроби (или из числителя первой вычитают числитель второй при вычитании) и оставляют тот же знаменатель. Произведение двух дробей вычисляется так: числитель одной дроби умножается на числитель другой, то же происходит и со знаменателями.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Попробуйте справиться с таким уравнением: 3/8*x − 5/6 = 7/12*x − 2/3. Что у вас получилось?
Вот объяснение решения этого линейного уравнения с дробями. Для начала умножим обе части уравнения (каждый член) на наименьший общий знаменатель всех дробей. В нашем случае он равен 24. При умножении дроби сокращаются, в знаменателе остается единица, её мы не пишем. В итоге получилось уравнение с целыми числами: 9x − 20 = 14x − 16. Неизвестные отправим в одну сторону, а известные — в другую с противоположными знаками: 9x − 14x = −16 + 20. Получаем следующее: −5x = 4. Остается разделить обе части уравнения на −5. Ответ таков: −4/5. Можно представить его в виде конечной десятичной дроби, тогда получим −0,8.
Решение систем уравнений с дробями повышенного уровня сложности
Решение систем уравнений с дробями повышенного уровня сложности
Решение систем уравнений с дробями повышенного уровня сложности
Преобразуем уравнение.
Приводим дроби к общему знаменателю.
Производим сложение дробей с одинаковыми знаменателями.
Раскрываем скобки.
Раскрываем скобки.
Приводим подобные члены.
Изменяем порядок действий.
Преобразуем уравнение.
Что сделать решение систем уравнений быстрее, приводим дроби к общему знаменателю.
Производим сложение дробей с одинаковыми знаменателями.
Раскрываем скобки.
Раскрываем скобки.
Приводим подобные члены.
Дальше чтобы провести решение систем уравнений, мы изменяем порядок действий.
Перенесем все в левую часть.
Преобразуем уравнение.
Приводим дроби к общему знаменателю.
Производим сложение дробей с одинаковыми знаменателями.
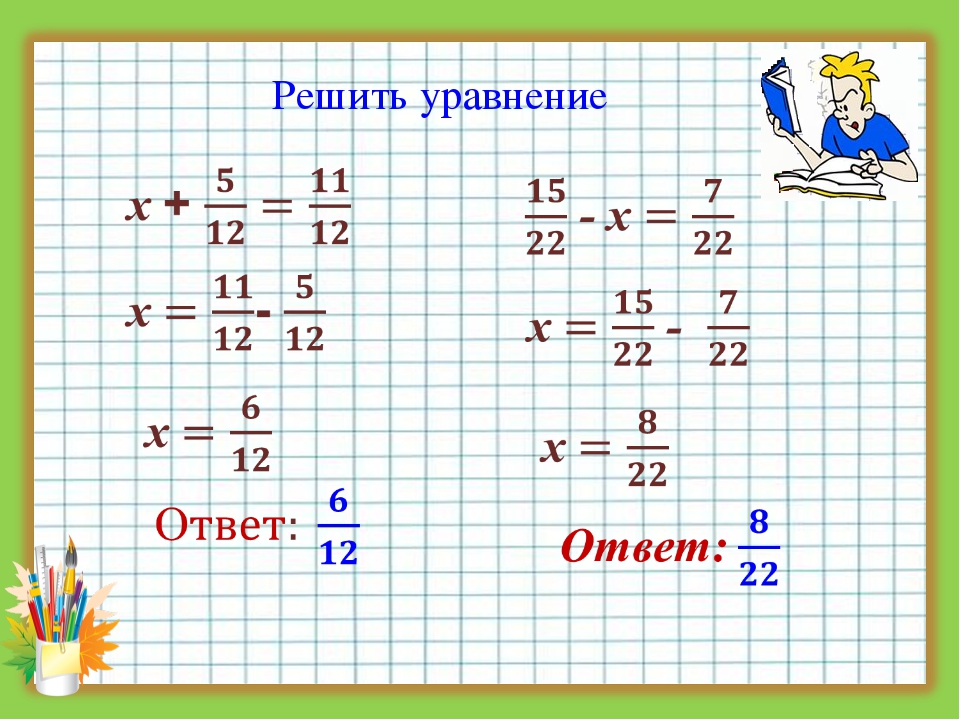
Воспользуемся свойством степеней.
Изменяем порядок действий.
Преобразуем уравнение.
Приводим дроби к общему знаменателю.
Производим сложение дробей с одинаковыми знаменателями.
Изменяем порядок действий.
Преобразуем уравнение.
Преобразуем уравнение.
Из уравнения 1 выразим переменную x
Подставим вместо переменной x найденное выражение.
Решаем вспомогательное уравнение.
Изменим знаки выражений на противоположные.
Для окончательного решения ситемы уранвений раскрываем скобки
Раскрываем скобки.
Приводим подобные члены.
Перенесем известные величины в правую часть уравнения.
Изменим знаки выражений на противоположные.
| PHP |
| Алгебраические преобразования, уравнения, неравенства |
| Другое |
| Логарифмические, показательные уравнения , неравенства |
| Начала анализа |
| Планиметрия |
| Прогрессии |
| Стереометрия |
| Текстовые задачи |
| Тригонометрия |
| Числа и выражения |
Как вычислить переменную как часть дроби
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 Следующая →
ACT Math Help » Алгебра » Алгебраические дроби » Как найти переменную в составе дроби
Решить для .
Возможные ответы:
Правильный ответ:
Пояснение:
Перекрестное умножение.
Рассылка.
Решите для .
Сообщить об ошибке
Частное дроби равно . Если числитель , каково значение знаменателя?
Возможные ответы:
Правильный ответ:
Объяснение:
Шаг 1: Задайте уравнение
Шаг 2: Найдите D
Сообщите об ошибке
Найдите :
9 0016 Возможные ответы:Правильный ответ:
Объяснение:
Найдите x:
Шаг 1: Найдите наименьший общий знаменатель и соответствующим образом сопоставьте дроби:
Найдите :
Сообщить об ошибке
Если , то каково значение ?
Возможные ответы:
9/114
7/12
38/3
ни один из этих
3/38
900 16 Правильный ответ:38/3
Объяснение:
перекрестное умножение:
(6)(19) = 9x
114=9x
x = 38/3
Сообщить об ошибке
Найти х.
Возможные ответы:
Правильный ответ:
Объяснение:
Перекрестное умножение:
Сообщить об ошибке
Числитель дроби равен сумме знаменателя, умноженного на 4 и 5. Если дробь разделить на 2, то числитель в 3 раза больше знаменателя. Найдите упрощенную версию дроби.
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть числитель = N и знаменатель = D.
Согласно первому утверждению,
N = (D x 5) + 4.
Согласно второму утверждению, N / 2 = 3 * D.
Умножим второе уравнение на –2 и сложим его с первым уравнением:
–N = –6D
+[N = (D x 5) + 4]
=
–6D + (D x 5) + 4 = 0
–1D + 4 = 0
D = 4
Таким образом, N = 24.
Следовательно, N/D = 24/4 = 6.
Сообщить об ошибке
Решите следующее уравнение для заданной переменной :
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить это уравнение, мы должны умножить обе части на знаменатель, чтобы избавиться от дроби.
Это дает
Затем, чтобы решить, последний шаг состоит в том, чтобы изолировать переменную, разделив обе части на 12.
Таким образом,
.
Сообщить об ошибке
При каком значении уравнение верно?
Возможные ответы:
Правильный ответ:
Объяснение:
При перекрестном умножении уравнения получается
.
Следовательно,
или .
Сообщить об ошибке
Решите следующее уравнение для :
.
Сократите любые дроби в окончательном ответе.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить уравнение с переменной в дроби, примите знаменатель как постоянное значение и умножьте обе части уравнения на знаменатель, чтобы исключить его.
Сообщить об ошибке
Найдите:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти ответ, умножьте правую часть на . Результат есть.
Сообщить об ошибке
← Назад 1 2 3 4 5 Далее →
Уведомление об авторских правах
Все ресурсы ACT Math
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Решение уравнений путем удаления дробей
Результаты обучения
- Использование наименьшего общего знаменателя для исключения дробей из линейного уравнения перед его решением
- Решение уравнений с дробями, требующее нескольких шагов
Вы можете чувствовать себя ошеломленным, когда видите дроби в уравнении, поэтому мы собираемся показать метод решения уравнений с дробями, в котором вы используете общий знаменатель, чтобы исключить дроби из уравнения.
Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей.
Обратите внимание, что каждый член уравнения умножается на наименьший общий знаменатель. Вот что делает его равным оригиналу!
ПРИМЕР
Решите: [латекс]\Большой\фракция{1}{8}\нормальный размер х+\Большой\фракция{1}{2}=\Большой\фракция{1}{4}[/латекс]
Решение:
| [латекс]\Large\frac{1}{8}\normalsize x+\Large\frac{1}{2}=\Large\frac{1}{4}\normalsize\quad{LCD=8}[/latex ] | |
| Умножьте обе части уравнения на этот LCD, [латекс]8[/латекс]. Это очищает дроби. | [латекс]\color{red}{8(}\Large\frac{1}{8}\normalsize x+\Large\frac{1}{2}\color{red}{)}=\normalsize\color{ красный {8(}\Large\frac{1}{4}\color{red}{)}[/latex] |
| Используйте свойство Distribution. | [латекс]8\cdot\Large\frac{1}{8}\normalsize x+8\cdot\Large\frac{1}{2}\normalsize=8\cdot\Large\frac{1}{4} [/латекс] |
| Упростите — и заметьте, больше никаких дробей! | [латекс]x+4=2[/латекс] |
Решите, используя общую стратегию решения линейных уравнений. | [латекс]x+4\цвет{красный}{-4}=2\цвет{красный}{-4}[/латекс] |
| Упрощение. | [латекс]x=-2[/латекс] |
| Проверить: пусть [латекс]x=-2[/латекс][латекс] \большой\фрак{1}{8}\нормальный размер х+ \большой\фракция{1}{2}= \большой\фрак{1 {4}[/латекс] [латекс] \Large\frac{1}{8}\normalsize(\color{red}{-2})+ \Large\frac{1}{2}\normalsize\stackrel{\text{?}}{ =} \Large\frac{1}{4}[/latex] [латекс] \Large\frac{-2}{8}+ \Large\frac{1}{2}\normalsize\stackrel{\text{?}}{=} \Large\frac{1}{4} [/латекс] [латекс] \Large\frac{-2}{8}+ \Large\frac{4}{8}\normalsize\stackrel{\text{?}}{=} \Large\frac{1}{4} [/латекс] [латекс] \Large\frac{2}{8}\normalsize\stackrel{\text{?}}{=} \Large\frac{1}{4}[/latex] [латекс] \Large\frac{1}{4}= \Large\frac{1}{4}\quad\checkmark[/latex]
|
В последнем примере наименьший общий знаменатель был [латекс]8[/латекс]. Теперь ваша очередь найти ЖК-дисплей и очистить дроби, прежде чем решать эти линейные уравнения.
Попробуйте
https://ohm.lumenlearning.com/multiembedq.php?id=71948&theme=oea&iframe_resize_id=mom1
Обратите внимание, что после очистки уравнения дробей оно стало таким же, как те, которые мы решали ранее в этой главе. . Мы изменили задачу на ту, которую уже знали, как решить!
Решите уравнения, очистив знаменатели
- Найдите наименьший общий знаменатель всех дробей в уравнении.
- Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
- Изолируйте переменные члены с одной стороны и постоянные члены с другой стороны.
- Упростите обе стороны.
- Используйте свойство умножения или деления, чтобы сделать коэффициент переменной равным [latex]1[/latex].
Вот пример с тремя переменными терминами. После того, как вы очистите дроби с помощью ЖК-дисплея, вы упростите три члена переменных, а затем изолируете переменную.
Пример
Решите: [латекс]7=\Большой\фракция{1}{2}\нормальный размер х+\Большой\фракция{3}{4}\нормальный размер х-\Большой\фракция{2}{3}\ нормальный размер х[/латекс]
Показать решение
А теперь попробуйте решить похожую задачу.
Очистите дроби, упростите, затем решите.
Попробуйте
https://ohm.lumenlearning.com/multiembedq.php?id=71948&theme=oea&iframe_resize_id=mom2
Внимание!
Одна из самых распространенных ошибок при очистке дробей — это забывание умножить ОБЕ части уравнения на ЖК-дисплей. Если ваш ответ не проходит проверку, убедитесь, что вы умножили обе части уравнения на LCD.
В следующем примере у нас будут переменные и дроби с обеих сторон уравнения. После того, как вы очистите дроби с помощью ЖК-дисплея, вы увидите, что это уравнение похоже на уравнения с переменными с обеих сторон, которые мы решали ранее. Не забудьте выбрать переменную сторону и постоянную сторону, чтобы помочь вам организовать свою работу.
Пример
Решите: [latex]x+\Large\frac{1}{3}=\Large\frac{1}{6}\normalsize x-\Large\frac{1}{2}[/latex]
Показать решение
Теперь вы можете попробовать решить уравнение с дробями, в котором переменные стоят по обе стороны от знака равенства.