Дроби примеры для решения с разными знаменателями: Сложение и вычитание дробей с разными знаменателями

Как правильно вычитать обыкновенные дроби?

Оглавление

Время чтения:  5 минут

560

Дроби можно складывать, умножать, делить, а также вычитать. В этой статье мы рассмотрим вычисление разности таких дробей, которые имеют одинаковый или разный знаменатель. Также будет вычисление дроби из натурального числа и наоборот.

Вычитание дробей с одинаковыми знаменателями

Для нахождения разности дробей с одинаковыми знаменателями, необходимо вычесть один числитель из другого. Знаменатели не вычитаются.

Примеры

Найдите разность 4/8 – 3/8.

Решение:

Представьте, что у вас есть большая пицца, которая поделена на восемь частей. Вы взяли 4 куска, но съели лишь 3. Чтобы узнать, сколько осталось, нужно записать это так:

4/8 – 3/8 = 4-3/8 = 1/8

Выходит, что на тарелке остался 1 восьмой доли кусок пиццы. Из этого примера можно вывести формулу, которая подойдет для решения подобных примеров.

---

Рассмотрим ещё одно задание.

Пример 2:

Найдите разность 6/12 – 3/12.

Решение:

6/12 – 3/12 = 6-3/12 = 3/12 = 1/4 = 0.25

У этих дробей одинаковые знаменатели, поэтому нам нужно лишь вычесть 3 из 6. Мы получили 3/12 и сократили дробь делением на 3. Знак дроби означает деление, поэтому делим 1 на 4 и получаем 0.25.

Вычитание дробей с разными знаменателями

Если знаменатели разные, то нужно сделать так, чтобы они стали одинаковыми, т.е. привести дроби к общему знаменателю. После этого совершаем те же действия, что и выше.

Примеры

Пример 3:

Найдите разность 5/10 – 2/5.

Решение:

5/10 – 2/5 = 5/10 – 2•2/2•5 = 5/10 – 4/10 = 5-4/10 = 1/10 = 0.1

Чтобы найти общий знаменатель, нужно числитель и знаменатель второй дроби умножить на 2. Получим 4/10. Теперь можно находить разность как в прошлом примере.

---

Перейдем к следующему примеру.

Пример 4:

Найдите разность 52/24 – 14/12.

Решение:

52/24 – 14/12 = 52/24 – 2•14/2•12 = 52/24 – 28/24 = 52-28/24 = 24/24 = 1

Для того, чтобы привести к общему знаменателю, нужно умножить числитель и знаменатель второй дроби на 2. Будь в двух знаменателях 7 и 49, то мы бы умножали 7 не на 2, а на 7, чтобы получить в обоих знаменателях 49. Дальше все по формуле.

Вычитание натурального числа из обыкновенной дроби

Для того чтобы вычесть натуральное число из обыкновенной дроби, нужно представить натуральное число в виде обыкновенной дроби.

Рассмотрим на примере.

Примеры

Пример 5:

Найдите разность 288/36 – 6.

Решение:

288/36 – 6 = 288/36 – 6/1 = 288/36 – 36•6/36•1 = 288/36 – 216/36 = 288-216/36 = 72/36 = 2

Может показаться, что это сложно, но это не так. Число 6 можно представить в виде обыкновенной дроби: 6/1. Далее будем находить разность этих дробей. Приводим дроби к общему знаменателю, умножая знаменатель и числитель второй дроби на 36. Вычитаем, делим и получаем ответ.

Есть и второй вариант решения (для неправильных дробей, где числитель больше знаменателя) такого примера, более удобный и простой. Возьмем новые числа.

---

Пример 6:

Найдите разность 72/27 – 2.

Решение:

72/27 – 2 = 2 2/3 – 2 = 2/3

В этом случае не пришлось превращать натуральное число в дробь, 72/27 мы сделали смешанным числом, отняли двойки и получили ответ. Можно решать на основе прошлого примера, однако, это будет дольше и сложнее.

Понятия

• Смешанное число – это такая правильная дробь, в состав которой входит целое число.
• Неправильная дробь – это дробь, в которой числитель равен знаменателю или больше его.
• Правильная дробь – это дробь, в которой знаменатель больше числителя.

Для того, чтобы преобразовать неправильную дробь в смешанное число, необходимо поделить ее числитель на знаменатель. Неполное частное станет целой частью смешанной дроби, остаток будет числителем дробной части, а знаменатель неправильной дроби – знаменателем дробной части.

Вычитание обыкновенной дроби из натурального числа

Примеры

Сразу перейдем к примеру.

Пример 7:

Найдите разность 6 – 7/5.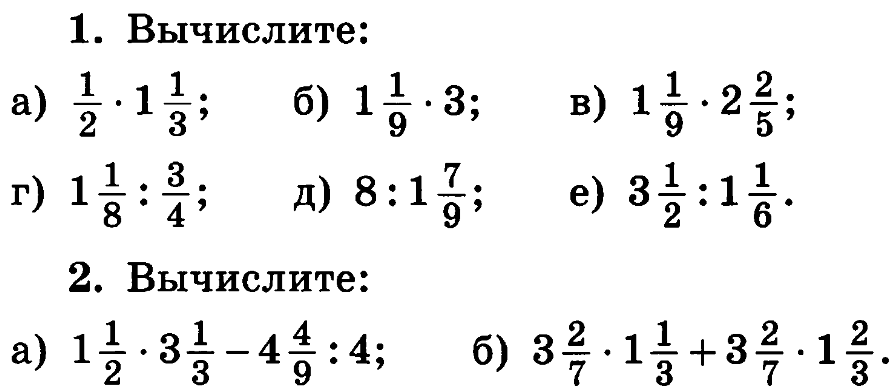

Решение:

6 – 7/5 = 6/1 – 7/5 = 5•6/5•1 – 7/5 = 30/5 – 7/5 = 30-7/5 = 23/5 = 4 3/5 = 4.6

Все, как и ранее, натуральное число 6 представляем в виде дроби, приводим к общему знаменателю, а после
находим разность.

Есть ещё один способ. Он хорош в том случае, если приходится работать с большими числами.

Если вычитаемая дробь – правильная, то натуральное число необходимо предоставить как сумму двух чисел, где
одно из них равно 1. Последним действием является вычитание дроби из этой единицы. Рассмотрим на
примере.

---

Пример 8:

Найдите разность 1040 – 20/55.

Решение:

Отнимем от 1040 единицу и вычтем дробь:

1040 – 20/55 = (1039 + 1) – 20/55

Перейдем к поиску ответа. Для этого вспомним свойства вычитания, согласно которым можно записать получившееся
выражение как 1039 + (1 – 20/55). Просто так отнять единицу в виде натурального числа мы не можем, поэтому
предоставим ее как дробь 1/1.

А теперь можно находить разность:

1 – 20/55 = 1/1 – 20/55 = 55/55 – 20/55 = 35/55.

Но это не конец, ведь у нас ещё осталось число 1039. Здесь все легко, просто приписываем это число к нашей дроби и получаем ответ: 1039 35/55. Здесь можно сократить дробь и выйдет 1039 7/11.

Рассмотрим решение этого примера с помощью прошлого способа, чтобы определить то, какой из них более удобный:

1040 – 20/55 = 1040/1 – 20/55 = 55•1040/55•1 — 20/55 = 57200/55 = 11436•5/11•5 = 11436/11 = 1039 7/11.

Ответ одинаковый, но решение, очевидно, побольше.

---

Но что же делать с неправильной дробью? Нужно заменить ее смешанным числом, а далее все про инструкции.

Пример 9:

Найдите разность 378 – 35/6.

Решение:

Отделяем целую часть: 35/6 = 5 5/6

Теперь, как и ранее, совершаем следующие действия:

373 – 5/6 = (372 + 1) – 5/6 = 372 + (1 – 5/6) = 372 + 1/6 = 372 1/6.

Свойства, необходимые для вычитания дробей

Примеры

Свойства вычитания натуральных чисел действуют и на вычитание обыкновенных дробей.

Пример 10:

Найдите разность 16/6 – 2/4 – 6/3.

Решение:

Сначала находим разность первых двух дробей, а после уже отнимаем и третью:

16/6 – 2/4 = 2•16/2•6 – 3•2/3•4 = 32/12 – 6/12 = 32-6/12 = 26/12 – 6/3 = 26/12 – 4•6/4•3 = 26/12 – 24/12 = 2/12 = 1/6

Когда необходимо работать с дробями и натуральными числами, то следует их распределять по типам в группы.

---

Пример 11:

Найдите разность (86 + 15/24) – (4 + 2/4).

Решение:

Сгруппируем числа.

(86 + 15/24) – (4 + 2/4) = 86 + 15/24 – 4 – 2/4 = (86 – 4) + (15/24 – 2/4)

Теперь можно решать дальше:

(86 – 4) + (15/24 – 2/4) = 82 + (15/24 – 12/24) = 82 + 3/24 = 82 + 1/8 = 82 1/8.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Задания для практики

Задание 1: Найдите разность 20/10 – 15/10.

Задание 2: Найдите разность 54/6 – 9/6.

Задание 3: Выделите целую часть из неправильной дроби 7/3.

Задание 4: Выделите целую часть из неправильной дроби 9/5.

Задание 5: Найдите разность 63/2 – 42/8.

Задание 6: Найдите разность 101/25 – 4.

Задание 7: Найдите разность 1096 – 25/40.

Задание 8: Найдите разность 46/6 – 2/2 – 189/36.

Задание 9: Найдите разность (65 + 56/45) – (10 + 4/9).

Ответы

Решение задания 1: 20/10 – 5/10 = 20-15/10 = 5/10 = 1/2 = 0.5.

Решение задания 2: 54/6 – 9/6 = 54-9/6 = 45/6 = 15/2 = 7.5.

Решение задания 3: 7/3 = 7:3 = 2 (остаток 1) = 2 1/3.

Решение задания 4: 9/5 = 9:5 = 1 (остаток 4) = 1 4/5.

Решение задания 5: 63/2 – 42/8 = 4•63/4•2 – 42/8 = 252/8 – 42/8 = 252-42/8 = 210/8 = 26.25.

Решение задания 6: 101/25 – 4 = 101/25 – 4/1 = 101/25 – 100/25 = 101-100/25 = 1/25 = 0. 04.

Решение задания 7: 1096 – 25/40 = (1095 + 1) – 25/40 = 1095 + (1 — 25/40) = 1/1 – 25/40 = 40/40 – 25/40 = 15/40 = 1095 15/40 = 1095 3/8 = 1095.375.

Решение задания 8: 46/6 – 2/2 – 189/36 = 46/6 – 2/2 = 46/6 – 3•2/3•2 = 46/6 – 6/6 = 46-6/6 = 40/6 – 189/36 = 6•40/6•6 – 189/36 = 240/36 – 189/36 = 240-189/36 = 51/36 = 1.416.

Решение задания 9: (65 + 56/45) – (10 + 4/9) = 65 + 56/45 – 10 – 4/9 = (65 – 10) + (56/45 – 4/9) = 55 + 36/45 = 55 + 4/5 = 55 4/5.

Оценить статью (55 оценок):

Поделиться

Как сложить обыкновенные дроби: с одинаковыми/разными знаменателями

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Сложение обыкновенных дробей

В данной публикации мы рассмотрим, каким образом можно сложить обыкновенные (простые) дроби с одинаковыми/разными знаменателями и смешанные дроби. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

• Сложение дробей
  • С одинаковыми знаменателями
  • С разными знаменателями
• Сумма смешанных дробей
• Примеры задач

Сложение дробей

С одинаковыми знаменателями

В данном случае все предельно просто. При сложении дробей с одинаковыми знаменателями суммируются числители, а знаменатель остается неизменным.

a/c

+

b/c

=

a+b/c

 
Примечание: полученную путем сложения новую дробь в некоторых случаях можно сократить.

С разными знаменателями

Для того, чтобы сложить дроби с разными знаменателями, выполняем следующие действия:

1. Приводим заданные дроби к наименьшему общему знаменателю.
2. Складываем полученные результаты как дроби с одинаковыми знаменателями.

Сумма смешанных дробей

Чтобы сложить смешанные дроби, необходимо отдельно просуммировать целые части, и отдельно дробные.

X

a/b

+ Y

c/d

= (X + Y) + (

a/b

+

c/d

)

 
Примечание: Если дробные части имеют разные знаменатели, значит их сперва нужно привести к наименьшему общему знаменателю, и только после этого складывать.

Примеры задач

Задание 1

Найдите сумму дробей 

4/11

 и 

7/11

.

 
Решение

Т.к. у нас дроби с одинаковыми знаменателями, то:

4/11

+

7/11

=

4+7/11

=

11/11

=1

 
Задание 2

Найдите сумму дробей 

5/12

 и 

4/7

.

 
Решение

В данном случае нам сначала нужно привести дроби к наименьшему общему знаменателю.
Наименьшее общее кратное обоих знаменателей равняется 84, следовательно, дополнительный множитель для первой дроби – число 7, для второй – 12.

5/12

=

5⋅7/12⋅7

=

35/84

4/7

=

4⋅12/7⋅12

=

48/84

 
Таким образом, мы получили дроби с одинаковыми знаменателями, и теперь их можно сложить:

35/84

+

48/84

=

35+48/84

=

83/84

 
Задание 3

Найдите сумму дробей 2

6/13

 и 5

3/13

.

 
Решение

Дробные части имеют один и тот же знаменатель, значит мы сразу же можем выполнить сложение:

2

6/13

 + 5

3/13

 = 2 + 5 + (

6/13

 + 

3/13

) = 7 + 

6+3/13

 = 7

9/13

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Как вычитать дроби с разными знаменателями? Определение

• Вычитание дробей с разными знаменателями
• Этапы вычитания дробей с разными знаменателями:

Вычитание дробей с разными знаменателями

Дроби с разными знаменателями — это дроби, имеющие разные знаменатели.

Например, у дробей 1 4 и 1 3 разные знаменатели.

Другой пример: у Тома 34 пиццы, и он съел 1 8 Нам нужно отнять 1 8 от 34, чтобы узнать, сколько пиццы он съел.

Аналогично, если бы у Мэйси была половинка яблока, и она съела бы четверть этого утром. Чтобы вычислить оставшуюся часть оставшегося яблока, нам нужно от 1 отнять 4 от 1 2 .

Рекомендуемые рабочие листы:

Этапы вычитания дробей с разными знаменателями:

(i) Определите неодинаковые дроби, которые нам нужно вычесть.

(ii) Преобразуйте обе дроби в эквивалентные дроби так, чтобы они имели одинаковые знаменатели.

(iii) Замените обе фракции на этапе (i) их эквивалентными фракциями, полученными на этапе (ii).

(iv) Поскольку у нас есть дроби с одинаковыми знаменателями, мы можем вычесть числители напрямую, чтобы получить ответ, и знаменатель останется прежним.

(v) Если возможно, упростите дробь, полученную на шаге (iv).

Случай-1: Когда один из знаменателей кратен другому.

Пример 1 900:25: Тренировка: 12-28.

Solution :

Step Number	Observation	Working Out
Step (i)	Unlike Denominators	1 2 – 2 8
Шаг (ii)	Общий знаменатель для приведенных выше дробей равен 8. Вычисление эквивалентных дробей.	1 × 42 × 4 = 48 ; 2 8 = 2 8
Step (iii)	Replacing the fractions in (i) by equivalent fractions from (ii)	4 8 – 28
Step (iv)	Теперь у нас одинаковые знаменатели. Итак, мы напрямую отнимаем числители.	48 – 28 = 2 8
Шаг (v)	Упрощение ответа из (iv)	2 ÷ 2 8 ÷ 2 = 14

Следовательно, 12 – 28 = 14

Случай 2: Когда оба знаменателя различны.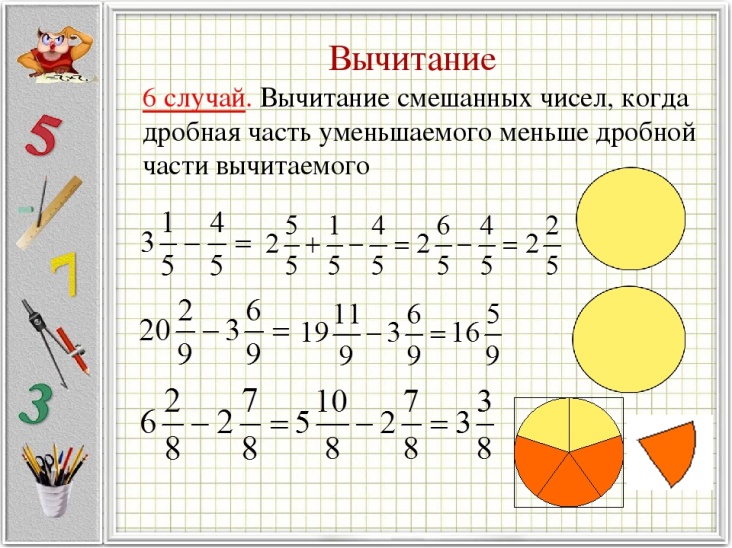

Пример 2 : У Джека 45 штук папайи. Если он отдаст 13 из них Люси, какая часть папайи останется у Джека?

Решение :

0025

Номер шага	Наблюдение
Шаг (I)	В отличие от знаменателей	45 — 13
Шаг (II). дроби.	4 × 35 × 3 = 1215; 1 × 5 3 × 5  =  515
Шаг (iii)	Замена дробей в (i) эквивалентными дробями из (ii)	12 15 – 5 15
Шаг (iv)	Теперь у нас одинаковые знаменатели. Итак, мы напрямую отнимаем числители.	12 15 – 515 = 715
Шаг (v)	Ответ уже в самой простой форме.	2 ÷ 28 ÷ 2 = 14

Значит, у Джека осталось 14  папайи.

Пример 3 : Элли и Джозеф участвуют в велогонке. Если Элли преодолела 34 из общего расстояния, а Джозеф преодолел 15 из общего расстояния. Какова разница в расстоянии, пройденном ими обоими?

Solution :

Step Number	Observation	Working Out
Step (i)	Unlike Denominators	34 – 1 5
Этап (ii)	Общий знаменатель для приведенных выше дробей равен 20. Вычисление эквивалентных дробей.	3 × 54 × 5 = 1520; 1 × 45 × 4 = 420
Шаг (iii)	Замена дробей в (i) эквивалентными дробями из (ii)	1520 – 420
Шаг (iv)	Теперь у нас одинаковые знаменатели. Итак, мы напрямую отнимаем числители.	1520 – 4 20 = 1120
Шаг (v)	Ответ уже в простейшей форме.	1120

Следовательно, разница между расстоянием, пройденным Элли и Джозефом, составляет 1120 от общего расстояния.

Забавные факты Любое целое число можно записать в виде дроби. Например, : 2 можно записать как 2 1 или 3 как 31 и так далее.

Как вычитать дроби с разными знаменателями?

Вычитание дробей с разными знаменателями кажется сложным, особенно при работе с большими числами. Однако, как только вы ознакомитесь с шагами и советами, такие расчеты не так сложны, как кажутся. Ниже мы предоставим вам четырехэтапный подход и несколько советов, которые помогут вам легко решить задачу вычитания дробей.

Вычитание дробей в четыре шага

Четырехэтапный подход — это традиционный метод, применимый ко всем случаям , независимо от того, с какими типами дробей вы будете иметь дело.

Прежде чем перейти к первому шагу, необходимо понять структуру дроби . Дробь состоит из двух частей: числителя и знаменателя , разделенных разделительной чертой. При вычитании или сложении с дробями нам необходимо убедиться, что знаменатели двух или более дробей в вычислениях совпадают, прежде чем приступать к фактическим вычислениям.

Ниже подробно описаны четыре шага, которые помогут вам в вычислении дробей. Чтобы вы лучше поняли наш четырехэтапный подход, мы разработаем один и тот же пример на всех четырех этапах.

Шаг 1. Найдите наименьший общий знаменатель

Наименьший общий знаменатель — это наименьшее общее кратное двух или более знаменателей в вычитании дробей, над которым вы работаете.

Чтобы найти наименьший общий знаменатель, мы находим наименьшее число, которое делится на оба знаменателя. В этом случае наименьший общий знаменатель равен 9.0012

17 x 6 = 106.

Шаг 2. Вычислите эквивалентные дроби

После нахождения наименьшего общего знаменателя вам нужно выяснить, что представляют собой новые дроби, когда обе дроби теперь имеют новые знаменатели.

Работая с тем же примером из шага 1, мы получаем, что новый знаменатель обеих дробей равен 106. знаменатель с 6. 

Шаг 3: Выполните вычитание

Теперь с новыми дробями нам просто нужно выполнить вычитание числителей для результата.

Шаг 4: При необходимости упростите результат

Для окончательного ответа вам нужно будет упростить результат дроби, если это необходимо. В данном примере 167106 нельзя упростить, так как числитель и знаменатель не делятся ни на одно целое число.

В других случаях, когда числители и знаменатели делятся на целое число, необходимо упростить дробь, разделив и числитель, и знаменатель на это число. Вы продолжаете такой процесс до тех пор, пока числитель и знаменатель не перестанут делиться ни на одно целое число.

Советы по вычитанию дробей с разными знаменателями

Хотя вы можете использовать четырехэтапный подход для вычитания всех дробей, иногда это не самый быстрый метод вычитания дробей. Ниже мы приводим несколько советов, которые помогут вам выполнять вычитание дробей намного быстрее.

Совет 1: перекрестное умножение перед вычитанием

Это самый простой способ выполнять вычитание дробей с разными знаменателями. Вот детали шага с примером.

Шаг 1: Находим значение перекрестного умножения дробей, которое равно (2×7) и (1×5)

Шаг 2: Находим значение вычитания между вышеуказанным результатом, которое равно

(2×7) – (1×5) = 9. Это число является числителем окончательного ответа.

Шаг 3: Найдите знаменатель окончательного ответа, умножив знаменатели двух дробей при вычитании, что равно 5 x 7 = 35.

Совет 2: Найдите наименьший общий знаменатель при вычитании

Вам не нужно постоянно умножать знаменатели, чтобы найти наименьший общий знаменатель. Иногда наименьший общий знаменатель может быть одним из знаменателей дробей. Вам нужно посмотреть, делится ли один из знаменателей дробей на другой знаменатель.

No related posts.