Центральные и вписанные углы 8 класс онлайн-подготовка на Ростелеком Лицей
Тема 4: Окружность
- Видео
- Тренажер
- Теория
Заметили ошибку?
Центральные и вписанные углы
Угол с вершиной в центре окружности называется ее центральным углом.
Центральный угол – угол между двумя радиусами.
Центральному углу АОВ соответствуют две дуги с концами А и В. Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ. Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 360°-∠AOB.
Центральный угол измеряется дугой, на которую опирается.
Сумма градусных мер дуг окружности с общими концами равна 3600.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом

Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.
При этом говорят, что вписанный угол ABC опирается на дугу AC.
Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство.
Пусть ∠АВС – вписанный угол окружности с центром О, опирающийся на дугу АС. Докажем, что ∠АВС=12AC. Рассмотрим три возможных случая расположения луча ВО относительно угла АВС.
-
Луч ОВ совпадает с одной из сторон угла АВС, например со стороной ВС. В этом случае дуга АС меньше полуокружности, поэтому центральный угол АОС равен дуге АС. Так как угол АОС – внешний угол равнобедренного треугольника АВО, а углы 1 и 2 при основании равнобедренного треугольника равны, то ∠АОС=∠1+∠2=2·∠1.
Отсюда следует, что удвоенный ∠1 равен дуге АС или ∠АВС=∠1=12AC.
-
Луч ВО делит угол АВС на два угла.
 В этом случае ВО пересекает дугу АС в некоторой точке D. Точка D разделяет дугу АС на две дуги: АD и DC. По доказанному в теореме о вписанном угле ∠ABD=12AD, ∠DBC=12DC. Складывая эти равенства попарно, получаем ∠ABD+∠DBC=12AD+12DC или ∠ABC=12AC.
В этом случае ВО пересекает дугу АС в некоторой точке D. Точка D разделяет дугу АС на две дуги: АD и DC. По доказанному в теореме о вписанном угле ∠ABD=12AD, ∠DBC=12DC. Складывая эти равенства попарно, получаем ∠ABD+∠DBC=12AD+12DC или ∠ABC=12AC. -
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла. Этот случай доказывается аналогично двум предыдущим.
Из теоремы о вписанном угле следует два утверждения:
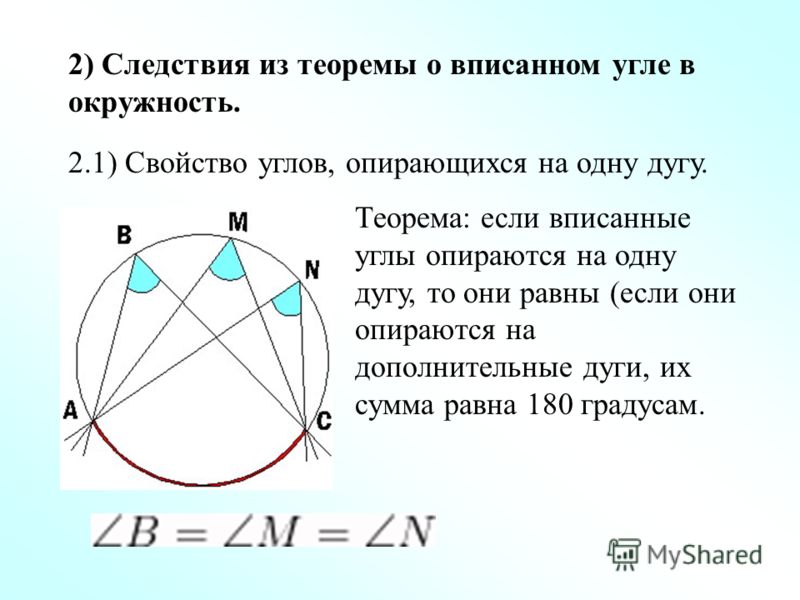
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Вписанный угол, опирающийся на полуокружность – прямой.
Докажем еще одну теорему, которая пригодится для решения задач.
Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.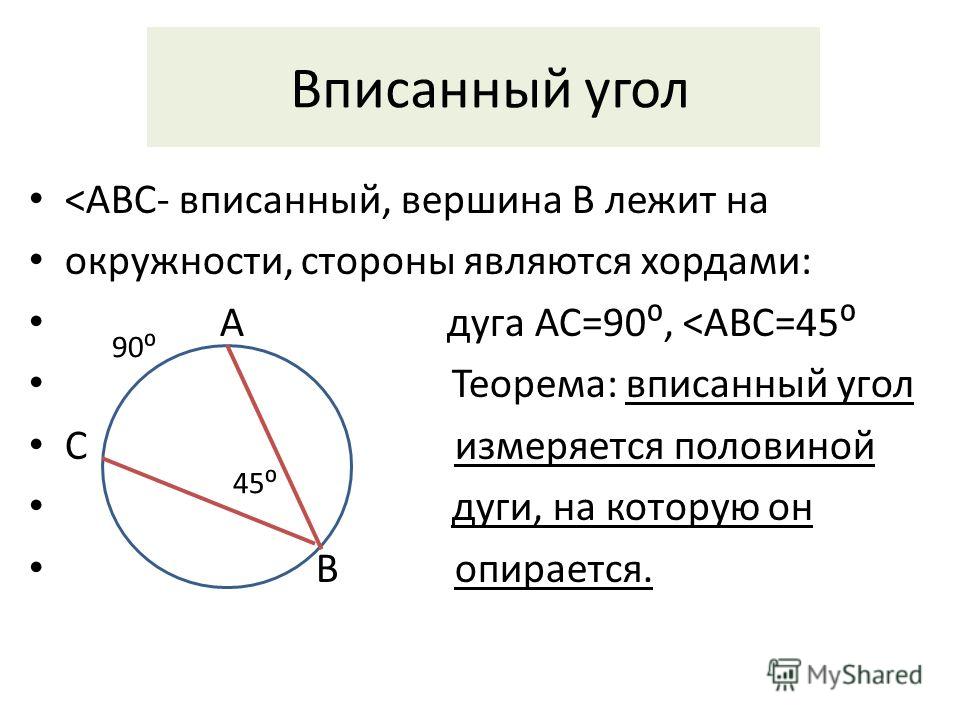
Пусть хорды АВ и СD пересекаются в точке Е. Докажем, что АЕ·ВЕ = СЕ·DE.
Рассмотрим треугольники ADE и CBE. В этих треугольниках углы 1 и 4 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 2 и 3 равны как вертикальные. По первому признаку подобия треугольников △ADE ∼△CBE. Отсюда следует, что АЕСЕ=DEBE, или AE·BE = CE·DE.
Решим задачу, используя изученные свойства центральных и вписанных углов.
Центральный угол на 17° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Пусть центральный угол равен х, а вписанный угол, опирающийся на ту же дугу, равен у:
Мы знаем, что х = 2у. Отсюда 2у = 17+у; у = 17.
Ответ: 17.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Углы в окружности, центральный и вписанный. Свойства и способы нахождения
Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?
К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?
Что такое центральный угол?
Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).
Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.
Рассмотрим пример №1.
На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О.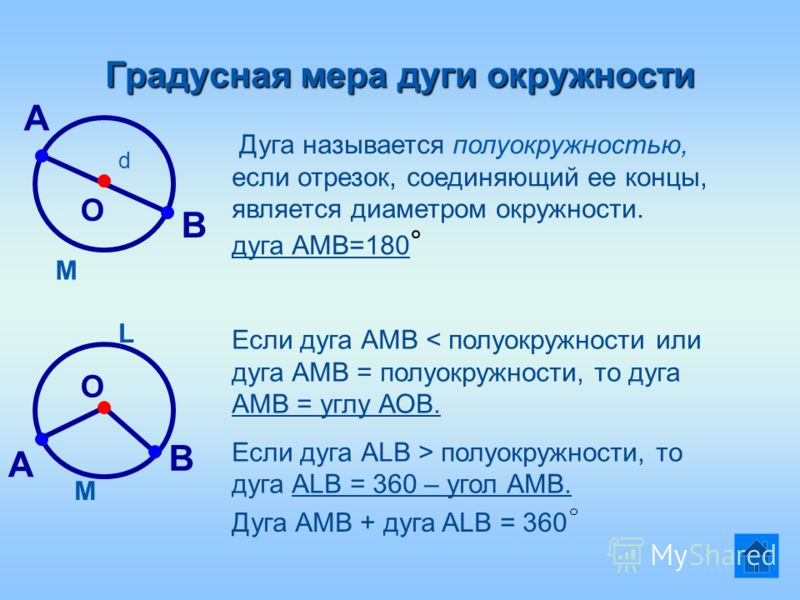 Он опирается на дугу AB, не содержащую точку С.
Он опирается на дугу AB, не содержащую точку С.
Чем вписанный угол отличается от центрального?
Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.
Приведем следующий пример.
Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.
Чему равен центральный угол
Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.
Итак, центральный угол равен градусной мере дуги, на которую он опирается.
На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.
Таким образом, центральные углы, опирающиеся на равные дуги, равны.
На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.
Как найти вписанный угол
Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?
Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.
Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.
Значит, угол АСВ = 66° : 2 = 33°
Рассмотрим некоторые следствия из этой теоремы.
- Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
- Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
- Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
- Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения
Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.
Углы, опирающиеся на одну дугу
Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.
Задача №1
Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.
Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла — общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,
1) АОВ = 54° : 2 = 27°.
Ответ: 54°.
Углы, опирающиеся на разные дуги одной окружности
Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.
Задача 2
В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.
Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий.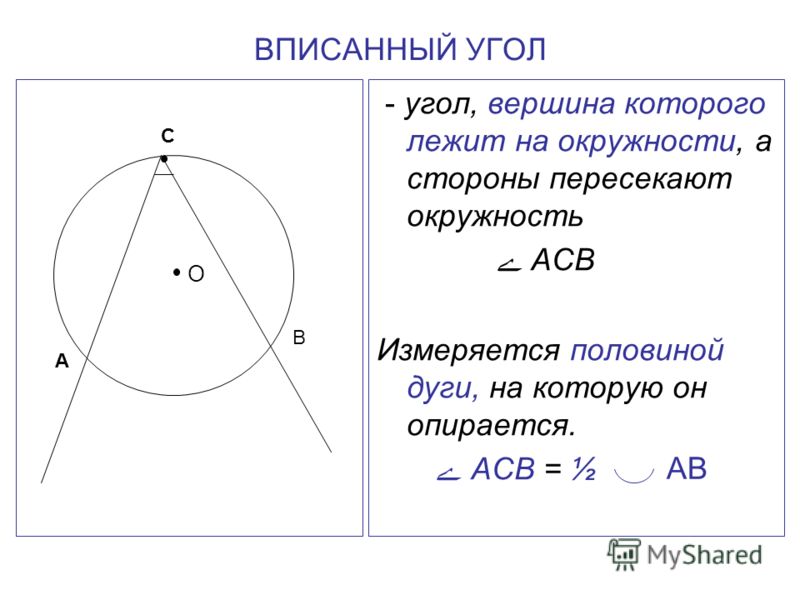 Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.
Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.
Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.
АС = 120°
Точно так же угол АОВ опирается на дугу АВ.
АВ = 30°.
Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.
ВС = 360° — АС — АВ
ВС = 360° — 120° — 30° = 210°
Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.
Угол САВ = 210° : 2 = 110°
Ответ: 110°
Задачи, основанные на соотношении дуг
Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.
Задача 1
Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.
Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник.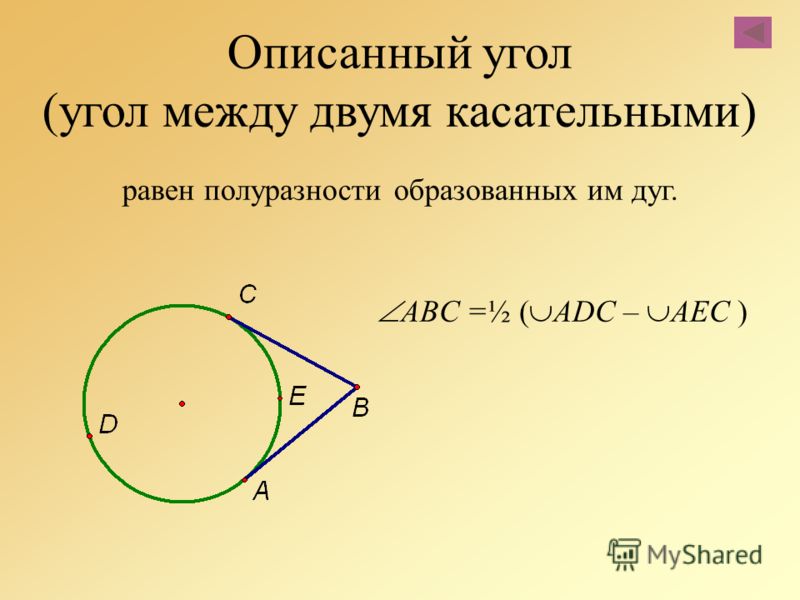 Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.
Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.
АВ = 360° — 60° = 300°
Угол АВС = 300° : 2 = 150°
Ответ: 150°
Задача 2
В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.
Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.
3Х + 7Х = 360°
10Х = 360°
Х = 36°
По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.
Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°
Ответ: 54°
Задача 3
В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги — 50. Вычислите длину большей дуги.
Вычислите длину большей дуги.
Для того чтобы вычислить длину большей дуги, нужно составить пропорцию — как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.
Большая дуга равна 360° — 60° = 300°.
Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.
Большая дуга = 50 * 5 = 250
Ответ: 250
Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.
Как идентифицировать дуги, центральные углы и длины дуг
БА: Марк Райан и
Обновлены: 09-17-2021
Из книги: Геометрия для майки
Геометрия для Dummies
.
Исследовать книгу Купить на Amazon
Центральные углы круга и дуги, которые они вырезают, являются частью многих доказательств круга. Они также возникают во многих территориальных проблемах. На следующем рисунке показано, как взаимосвязаны угол и дуга.Центральный угол в 60 градусов образует дугу в 60 градусов.
- Дуга: Дуга — это просто изогнутая часть круга. Любые две точки на окружности делят окружность на две дуги: малая дуга (меньшая часть) и большая дуга (большая часть) — если только эти точки не являются конечными точками диаметра, в этом случае обе дуги полукруги.
Обратите внимание, что для обозначения второстепенной дуги используются две ее конечные точки; чтобы назвать большую дугу, вы используете две ее конечные точки плюс любую точку вдоль дуги.
- Центральный угол: Центральный угол — это угол, вершина которого находится в центре окружности.
 Две стороны центрального угла — это радиусы, которые пересекаются с окружностью на противоположных концах дуги, или, как говорят математики, угол пересекает дугу .
Две стороны центрального угла — это радиусы, которые пересекаются с окружностью на противоположных концах дуги, или, как говорят математики, угол пересекает дугу .
Мера дуги такая же, как градусная мера центрального угла, который ее пересекает.
Определение длины дуги
Длина дуги означает то же самое, что всегда означает длина здравого смысла — знаете, как длину куска веревки (конечно, с дугой это будет изогнутый кусок веревки). Убедитесь, что вы не перепутали длину дуги с мера дуги, равная размеру ее центрального угла в градусах.Круг равен 360° по всей окружности; следовательно, если вы разделите градусную меру дуги на 360°, вы найдете долю длины окружности, которую составляет дуга. Затем, если вы умножите длину всей окружности (длину окружности) на эту дробь, вы получите длину вдоль дуги. Итак, наконец, вот формула, которую вы так долго ждали.
Длина дуги:
Ее градусная мера равна 45°, а радиус окружности равен 12, поэтому математика для ее длины:
Довольно просто, а?
Об этой статье
Эта статья из книги:
- Геометрия для чайников,
Об авторе книги:
Марк Райан является основателем и владельцем Математического центра в районе Чикаго, где он предоставляет репетиторство по всем математическим предметам, а также подготовка к экзаменам.
Эту статью можно найти в категории:
- Геометрия ,
Дуги и углы окружностей (видео)
TranscriptPractice
Привет и добро пожаловать на это видео об дугах и углах! В этом видео мы рассмотрим различные части кругов и то, как их использовать для решения задач. Давайте узнаем об дугах и углах окружностей!
Когда мы смотрим вокруг себя, после многоугольников круги являются следующей наиболее распространенной формой, которая окружает нас в окружающей среде. Круг создается вращением на 360°.
Круг создается вращением на 360°.
дуга окружности является частью окружности, и мы идентифицируем дуги, используя точки на окружности. Дуга \(RS\) – это изогнутая часть окружности \(A\), отмеченная фиолетовым знаком. Поскольку дуга \(RS\) меньше 180°, мы называем эту дугу малой дугой . Дуга \(RTS\) или \(STR\) является большой дугой , поскольку она больше 180°. Мы можем найти меру дуги, используя тот факт, что окружность равна 360°. Если мы знаем, что мера дуги \(RS\) равна 130°, мы можем найти меру дуги \(RTS\), вычитая меру дуги \(RS\) из 360°, что даст меру дуги дуга \(РТС\) 230°.
Некоторыми важными линиями и сегментами, связанными с окружностями, являются хорды, секущие и касательные.
Хорда — это отрезок, оба конца которого касаются окружности. Отрезок \(LM\) является хордой на окружности \(A\). Секущая линия похожа на хорду, за исключением того, что это линия, которая проходит через две точки на окружности, а не является отрезком. А касательная — это особая линия, которая касается окружности только в одной точке, называемой 9-й.0022 точка касания . Прямая \(PQ\) является касательной, а точка \(Q\) является точкой касания. Знание этих словарных слов, связанных с кругами, важно для понимания теорем о кругах, которые помогут нам решать проблемы.
А касательная — это особая линия, которая касается окружности только в одной точке, называемой 9-й.0022 точка касания . Прямая \(PQ\) является касательной, а точка \(Q\) является точкой касания. Знание этих словарных слов, связанных с кругами, важно для понимания теорем о кругах, которые помогут нам решать проблемы.
Радиус окружности всегда перпендикулярен точке касания.
Когда две хорды имеют общую точку на окружности, образуется вписанный угол
. В окружности \(A\) хорды \(RS\) и \(TS\) образуют вписанный угол \(RST\), вершина которого лежит на окружности. Дуга, образованная катетами угла \(RST\), называется 9-гранной.0022 перехваченная дуга . Угол, вершиной которого является центр окружности, естественно называется центральным углом . В окружности \(C\) угол \(MCN\) является центральным углом, а дуга \(MN\) является его дугой. Если нам дана мера вписанного угла или дуги, на которую опирается, мы сможем найти меру другого, используя теорему о окружности, которая говорит нам, что мера вписанного угла составляет половину меры его перехваченная дуга.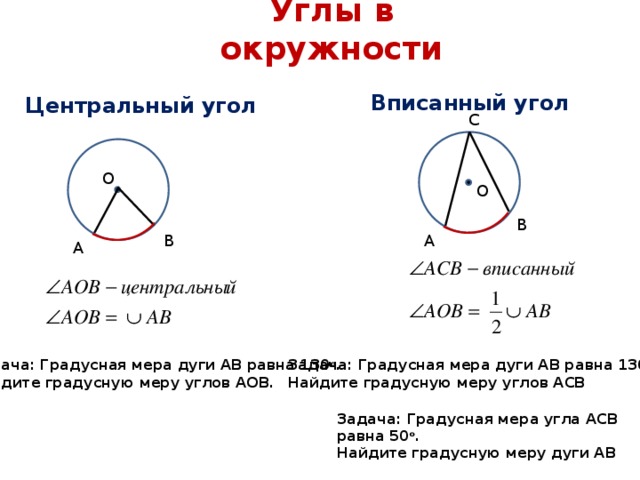 Или мы могли бы сказать, что дуга, на которую она опирается, в два раза длиннее вписанного угла. Например, в окружности \(A\) мера вписанного угла \(RST\) дана нам как 60°. Согласно теорема о вписанном угле , мера дуги \(RT\) равна \(60° \times 2\), что равно 120°.
Или мы могли бы сказать, что дуга, на которую она опирается, в два раза длиннее вписанного угла. Например, в окружности \(A\) мера вписанного угла \(RST\) дана нам как 60°. Согласно теорема о вписанном угле , мера дуги \(RT\) равна \(60° \times 2\), что равно 120°.
Вот частный случай вписанного угла.
В окружности \(A\) вписанный угол \(PQR\) охватывает диаметр окружности, отрезок линии \(PR\) Помните, что диаметр окружности делит окружность на две равные части, называемые полукруги . Круг имеет в общей сложности 360 °, поэтому полукруг имеет 180 ° или половину меры полного круга. Таким образом, это должно означать, что дуга угла \(PQR\), на которую она опирается, равна 180°. Если мы воспользуемся теоремой о вписанном угле, то обнаружим, что угол \(PQR\) равен 90 °, потому что это половина градусной меры дуги, на которую она опирается.
Еще одна важная теорема, которую мы собираемся рассмотреть, — это теорема о центральном угле . Эта теорема говорит, что мера центрального угла равна мере дуги, на которую он опирается. В круге \(C\), так как мера угла \(MCN\), центрального угла, равна 110°, то и дуга \(MN\), образующая его, также равна 110°.
Эта теорема говорит, что мера центрального угла равна мере дуги, на которую он опирается. В круге \(C\), так как мера угла \(MCN\), центрального угла, равна 110°, то и дуга \(MN\), образующая его, также равна 110°.
Давайте рассмотрим пример задачи. Прямая \(LM\) касается окружности \(T\) в точке \(L\). Центральный угол \(T\) равен 35°. Какова мера угла \(LMT\)?
Поскольку мы знаем, что сумма внутренних углов любого треугольника равна 180° и что радиус всегда перпендикулярен точке касания, мы знаем, что угол \(TLM\) равен 90°. Мы можем вычесть \((90°+35°)\) из 180°, чтобы найти меру угла \(LMT\). \(180 – (90+35) = 55\), поэтому мера угла \(LMT\) равна 55°.
Когда секущие пересекаются внутри круга, мы можем найти меру вертикальных углов, образованных с помощью меры дуг, образованных углами. Это также работает и наоборот, если нам нужно найти меру дуг, используя меру углов. Давайте посмотрим на окружность \(K\). Секущие линии \(DE\) и \(FG\) пересекаются в точке \(H\) и образуют дуги \(DF\), \(FE\), \(EG\) и \(GD\) . Найдите меру любого из вертикальных углов (обратите внимание, что их два набора), сложив вместе меры пересекаемых дуг и разделив на 2.
Найдите меру любого из вертикальных углов (обратите внимание, что их два набора), сложив вместе меры пересекаемых дуг и разделив на 2.
Будем использовать формулы \(m\угол DHF=\frac{1}{2}\) (дуга \(DF\) + дуга \(GE\)) и \(m\угол FHE=\frac{ 1}{2}\) (дуга \(КЭ\) + дуга \(ДГ\)). Затем мы воспользуемся теоремой о вертикальном правиле, чтобы найти \(m\угол EHG\) и \(m\угол GHD\).
Давайте потренируемся. Мера дуги \(GE\) равна 170°, дуга \(GD\) равна 80°, дуга \(DF\) равна 60°, а дуга \(FE\) равна 50°. Чтобы найти \(m\угол DHF\), мы добавим пересеченные дуги, \(DF\) и \(GE\), а затем умножим на \(\frac{1}{2}\). Следовательно, \(m\угол DHF=\frac{1}{2}(60° +170°)\). Итак, \(\угол DHF=115°\). Мы будем использовать уравнение \(m\угол FHE=\frac{1}{2}(50° +80°)\), чтобы найти меру \(\угол FHE\), которая равна \(m\угол FHE=65°\).
Когда две секущие пересекаются вне круга, мы используем другой метод для нахождения меры углов. Когда это происходит, вы смотрите на две перехваченные дуги, образованные углом, и вычитаете меру меньшей дуги из меры большей дуги, а затем умножаете на \(\frac{1}{2}\).
Мы хотим найти \(m\угол WYU\), который получается пересечением секущих \(WX\) и \(UV\) на окружности \(Z\). \(\угол WYU\) пересекается дугами \(XV\) и \(WU\). Мера дуги \(XV\) равна 30°; мера дуги \(WU\) равна 80°. Для нахождения меры угла \(WYU\) воспользуемся формулой: \(m\угол WYU= \frac{1}{2}\) (дуга \(WU\) – дуга \(XV\)), следовательно, \(m\угол WYU=\frac{1}{2}(80°-30°) \text{, }m\угол WYU=25°\).
Сектор круга — это участок круга между двумя радиусами. Красная область на диаграмме является примером сектора.
Длину дуги можно найти, зная длину радиуса и величину центрального угла по формуле \(s=\frac{\pi r\theta }{180°}\), где \(s\) — длина дуги, \(r\) — длина радиуса и \(\theta \) — мера центрального угла. В круге A длина радиуса равна 5 см, а угол \(MAN\) равен 70°. Мы хотим найти длину дуги \(MN\). Мы начнем с подстановки того, что у нас есть, в формулу \(s=\frac{\pi (5)(70)}{180°}\). Мы упростим, чтобы получить \(s=6.11\text{cm}\) , что является длиной дуги \(MN\).
Спасибо за просмотр этого видео и удачной учебы!
Вопрос №1:
Если угол \(B\) равен \(21°\), то какова мера дуги \(AC\)?
\(82°\)
\(42°\)
\(165°\)
\(21°\)
Показать Ответ
Ответ:
Согласно теореме о вписанном угле , дуга \(AC\) будет вдвое больше вписанного угла \(B\). Это означает, что дуга \(AC\) будет равна \(2×21°=42°\).
Скрыть ответ
Вопрос №2:
Прямая \(LM\) касается окружности \(J\) в точке \(L\). Если угол \(K\) равен \(27°\), то какова мера угла \(M\)?
\(65°\)
\(83°\)
\(44°\)
\(63°\)
Показать ответ
Ответ:
\900LM\ ) касается окружности \(J\) в точке \(L\), прямая \(KL\) и \(LM\) образуют прямой угол.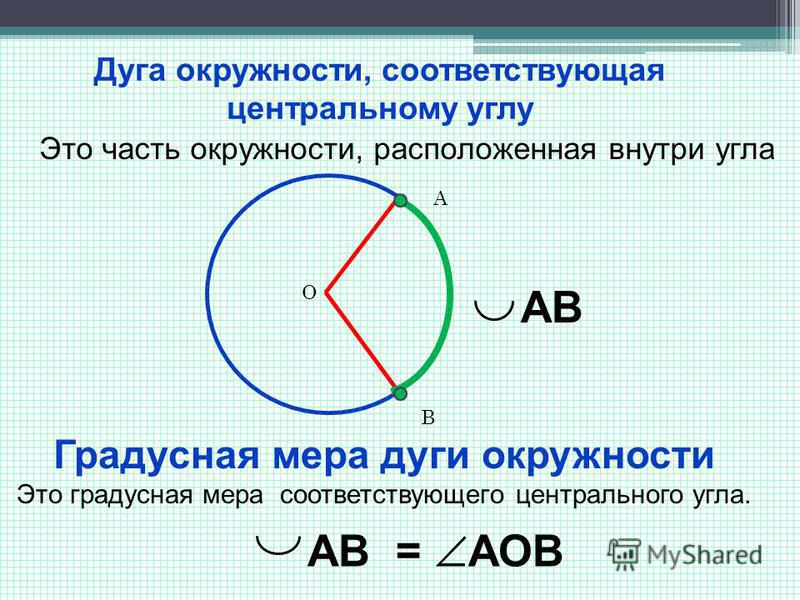 Это означает, что угол \(L\) равен \(90°\). Угол \(K\) равен \(27°\), поэтому складываем угол \(K\) и угол \(L\): \(90+27=117\). Поскольку в треугольнике \(180°\), вычтем \(117\) из \(180\): \(180-117=63\). Мера угла \(M\) равна \(63°\).
Это означает, что угол \(L\) равен \(90°\). Угол \(K\) равен \(27°\), поэтому складываем угол \(K\) и угол \(L\): \(90+27=117\). Поскольку в треугольнике \(180°\), вычтем \(117\) из \(180\): \(180-117=63\). Мера угла \(M\) равна \(63°\).Скрыть ответ
Вопрос №3:
Дуга \(BD\) равна \(15°\). Дуга \(AE\) равна \(48°\). Найдите меру угла \(ACE\).
\(19,5°\)
\(16,5°\)
\(22,5°\)
\(19°\)
Показать ответ
Ответ:
Посмотрите на две перехваченные дуги. Угол \(ACE\) будет равен \(\frac{1}{2}\) разнице между длинами дуг этих пересекаемых дуг. Вычесть меньшую дугу из большей дуги. В этом случае вычитаем дугу \(BD\) из дуги \(AE\): \(48-15=33\). Теперь умножьте это на \(\frac{1}{2}\). \(33×\frac{1}{2}=16,5°\). Угол \(ACE\) равен \(16,5°\).
Скрыть Ответ
Вопрос №4:
Вы идете по круглому пруду от одной звезды к другой.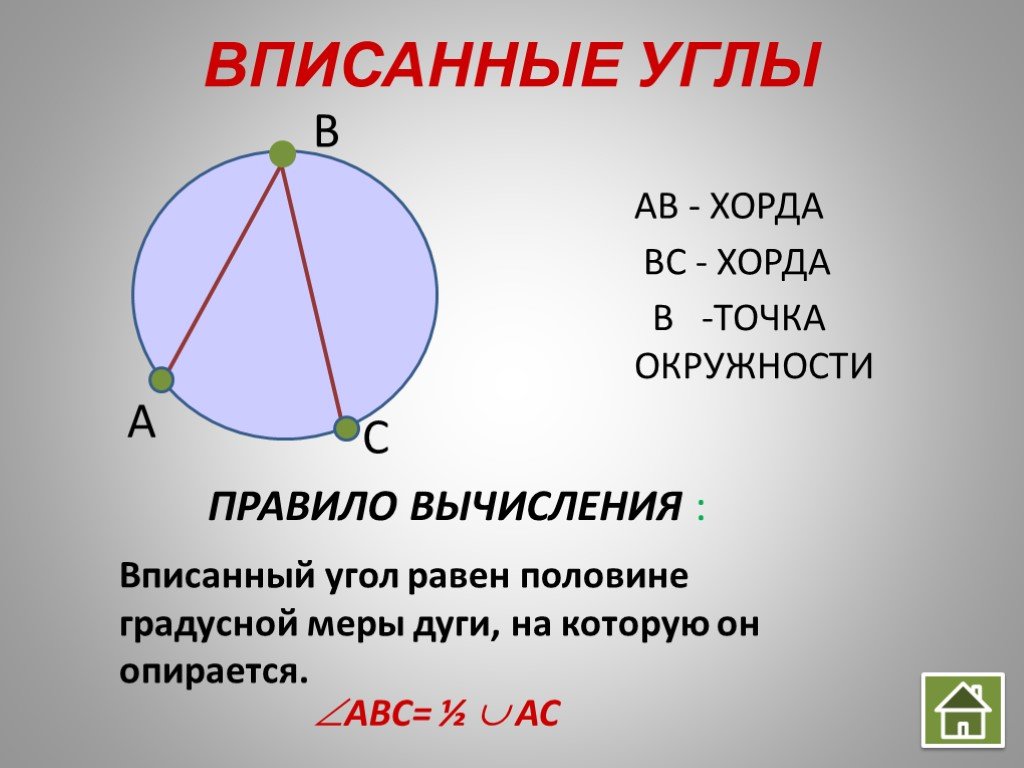 Если радиус пруда равен \(8\text{ футов}\), какое расстояние вы прошли? Используйте \(3.14\) вместо \(π\).
Если радиус пруда равен \(8\text{ футов}\), какое расстояние вы прошли? Используйте \(3.14\) вместо \(π\).
\(22.8\text{ футов}\)
\(19\text{ футов}\)
\(16.78\text{ футов}\)
\(34.5\text{ футов}\)
Показать ответ
Ответ:
Найдите меру дуги по формуле: \(s=\frac{πrϴ}{180°}\)
\(s\) представляет длину дуги.
\(π\) приближается к \(3.14\).
\(r\) — радиус.
\(ϴ\) — мера центрального угла.
\(s=\frac{πrϴ}{180°}\) становится \(s=\frac{(3.14)(8)(120°)}{180°}=16,746\), что упрощается до \( s=16,7\text{ футов}\).
Скрыть ответ
Вопрос № 5:
Фонарик освещает круглое поле. Какова угловая мера пересекаемой дуги, которая будет освещена?
\(104°\)
\(120°\)
\(106°\)
\(130°\)
Показать Ответ
Ответ:
5 Вписанный угол равен( 52°\).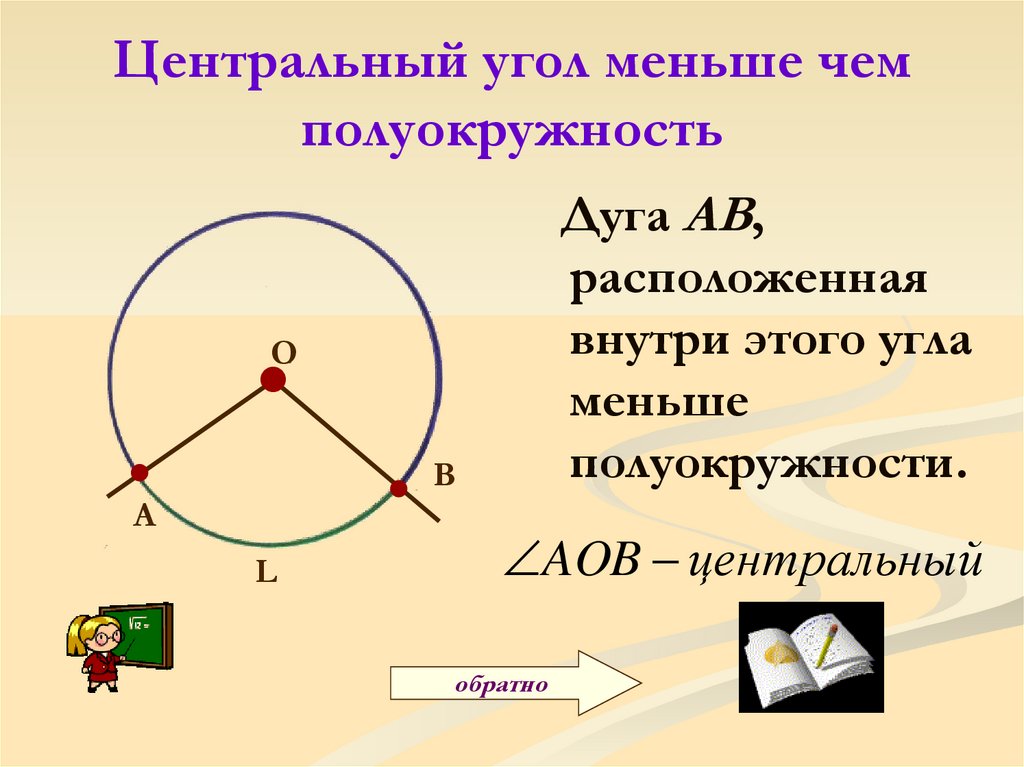

 В этом случае ВО пересекает дугу АС в некоторой точке D. Точка D разделяет дугу АС на две дуги: АD и DC. По доказанному в теореме о вписанном угле ∠ABD=12AD, ∠DBC=12DC. Складывая эти равенства попарно, получаем ∠ABD+∠DBC=12AD+12DC или ∠ABC=12AC.
В этом случае ВО пересекает дугу АС в некоторой точке D. Точка D разделяет дугу АС на две дуги: АD и DC. По доказанному в теореме о вписанном угле ∠ABD=12AD, ∠DBC=12DC. Складывая эти равенства попарно, получаем ∠ABD+∠DBC=12AD+12DC или ∠ABC=12AC.
 Две стороны центрального угла — это радиусы, которые пересекаются с окружностью на противоположных концах дуги, или, как говорят математики, угол пересекает дугу .
Две стороны центрального угла — это радиусы, которые пересекаются с окружностью на противоположных концах дуги, или, как говорят математики, угол пересекает дугу .