Два события называются противоположными: Классификация событий в теории вероятностей

Основные теоремы теории вероятностей. 9 класс

https://mathlesson.ru/node/186

Основные теоремы теории вероятностей

Классическое определение вероятности

Вероятностью события А называется отношение числа исходов m, благоприятствующих его наступлению к числу всех исходов n(несовместных, единственно возможных и равновозможных):  

 P(A) = m/n.

Будем различать достоверные и невозможные события. По определению, их вероятности соответственно равны 1 и 0.

Геометрическое определение вероятности

Если число исходов некоторого опыта бесконечно, то 
классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события A есть отношение меры A (длины, площади, объема) к мере U пространства элементарных событий.

Теоремы о вероятностях событий

Произведением событий A и B называется событие C = A• B, состоящее в том, что в результате испытания произошло и событие A, и событие B, т. е. оба события произошли.

Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.

Теорема. Вероятность произведения двух независимых событий A и Bравна произведению этих вероятностей: P(AB) = P(A) • P(B).

Противоположные события

Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.

Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают 1.

Если событие A может произойти с вероятностью p и опыт повторяют nраз, то вероятность, что оно наступит хотя бы один раз, есть: 1 — qⁿ, где q= 1 — p.

Сложение вероятностей

Суммой событий A и B называется событие C = A + B, состоящее в наступлении, по крайней мере, одного из событий A или B, т. е. в наступлении события A, или события B, или обоих этих событий вместе, если они совместны.

Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P(A+B) = P(A) + P(B).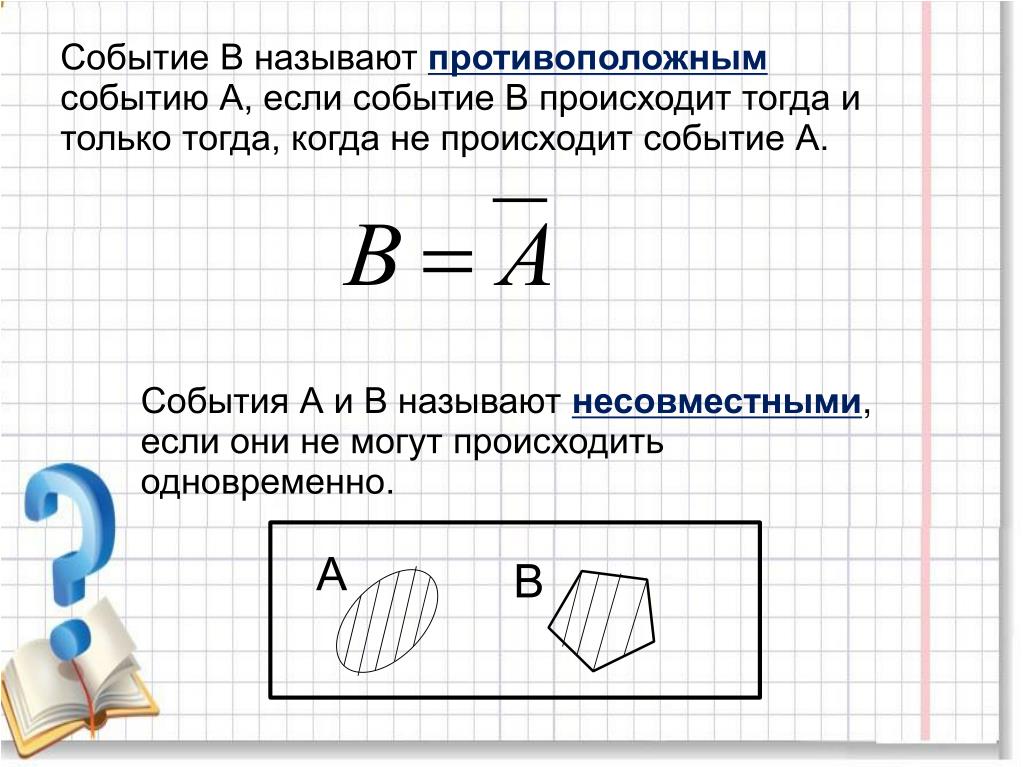

Условная вероятность

Пусть A и B— зависимые события. Условной вероятностью P_A(B)события B называется вероятность события B, найденная в предположении, что событие A уже наступило.

Теорема. Вероятность произведения двух зависимых событий A и Bравна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило: P(AB) = P(A) • P_A(B).

Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения: P(A + B) = P(A) + P(B) – P(AB).

Формула Бернулли

Для многократно повторяемых опытов справедлива формула Бернулли:

P _m, n = C _n^m • p^m •q ^n—m, где m — число удачных исходов среди проводимых n опытов, p — вероятность наступления благоприятного исхода в единичном опыте, q = 1 – p.

Рассмотрим некоторые задачи с решениями. 

Задание 5. № 319353. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение.
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.

Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.

Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019. 

Ответ: 0,019.

Задание 5. № 319355. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. иБ. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение.
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.

Ответ: 0,156.

Задание 5. № 320171. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.

Ответ: 0,35.

Задание 5. № 320172. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение.
Рассмотрим события 

А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате. 

Тогда

A·B = кофе закончится в обоих автоматах,
A + B = кофе закончится хотя бы в одном автомате. 

По условию P(A) = P(B) = 0,3; P(A·B) = 0,12.

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения: 

P(A + B) = P(A) + P(B) − P(A·B) = 0,3 + 0,3 − 0,12 = 0,48. 

Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.

Ответ: 0,52.

Можно привести и другое решение.
Вероятность того, что кофе останется в первом автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется во втором автомате равна 1 − 0,3 = 0,7. Вероятность того, что кофе останется в первом или втором автомате равна 1 − 0,12 = 0,88. ПосколькуP(A + B) = P(A) + P(B) − P(A·B), имеем: 0,88 = 0,7 + 0,7 − х, откуда искомая вероятность х = 0,52.

Примечание.
Важно понимать, что события А и В не являются независимыми. Действительно, вероятность произведения независимых событий была бы равна произведению вероятностей этих событий:P(A·B) = 0,3·0,3 = 0,09, однако по условию эта вероятность равна 0,12.

Задание 5. № 320173. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Решение.
Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. События попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна 

                                              0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02

Ответ: 0,02.

Задание 5. № 320174. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. 

Решение.
Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,05 · 0,05 = 0,0025.

Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0025 = 0,9975.

Ответ: 0,9975.

Есть другое решение.
Вероятность того, что исправен первый автомат (событие А) равна 0,95. Вероятность того, что исправен второй автомат (событие В) равна 0,95. Это совместные независимые события. Вероятность их произведения равна произведению вероятностей этих событий, а вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Имеем: 

P(A + B) = P(A) + P(B) − P(A·B) = P(A) + P(B) − P(A)P(B) = 0,95 + 0,95 − 0,95·0,95 = 0,9975. 

— В чем разница между независимыми и взаимоисключающими событиями?

спросил 8 лет, 6 месяцев назад

Изменено 1 месяц назад

Просмотрено 622к раз

$\begingroup$

Два события являются взаимоисключающими, если они не могут произойти одновременно.

Независимые события — это события, для которых знание вероятности одного не меняет вероятности другого.

Верны ли эти определения? Если возможно, приведите более одного примера и контрпримера.

• вероятность

$\endgroup$

6

$\begingroup$

Да, все в порядке.

События являются взаимоисключающими, если появление одного события исключает появление другого(-их). Взаимоисключающие события не могут происходить одновременно. Например: при подбрасывании монеты результат может быть либо головы или хвосты , но не могут быть оба.

$$\left.\begin{align}P(A\cap B) &= 0 \\ P(A\cup B) &= P(A)+P(B)\\ P(A\mid B )&=0 \\ P(A\mid \neg B) &= \frac{P(A)}{1-P(B)}\end{align}\right\}\text{ взаимоисключающие }A, B$$

События независимы, если появление одного из них не влияет (и не находится под влиянием) возникновения другого(их). Например: при подбрасывании двух монет результат одного броска не влияет на результат другого.

$$\left.\begin{align}P(A\cap B) &= P(A)P(B) \\ P(A\cup B) &= P(A)+P(B)- P(A)P(B)\\ P(A\mid B)&=P(A) \\ P(A\mid\neg B) &= P(A)\end{align}\right\}\ text{ Independent }A,B$$

Это, конечно, означает, что взаимоисключающие события не являются независимыми, а независимые события не могут быть взаимоисключающими. (За исключением событий нулевой меры.)

$\endgroup$

13

$\begingroup$

Прочитав ответы выше, я так и не смог четко понять разницу между взаимоисключающими и независимыми событиями. Я нашел хороший ответ от доктора Пита, размещенный на математическом форуме. Поэтому я прикрепляю его сюда, чтобы ОП и многие другие запутавшиеся ребята вроде меня могли сэкономить немного своего времени.

Если два события A и B независимы , пример из жизни следующий. Рассмотрим честную монету и честную шестигранный кубик. Пусть событие А — получение орла, а событие Б — прокат. a 6. Тогда мы можем разумно предположить, что события A и B независимыми, потому что результат одного не влияет на результат другого другой. Вероятность того, что произойдут и А, и В, равна 9.0005

Р(А и В) = Р(А)Р(В) = (1/2)(1/6) = 1/12.

Ниже приведен пример взаимоисключающего события . Рассмотрим честный шестигранный кубик как и прежде, только в дополнение к цифре 1 через 6 на каждой грани мы имеем свойство, что четные грани окрашены в красный цвет, а грани с нечетными номерами окрашены в зеленый цвет. Пусть в событии A выпадает зеленая грань, а в событии B — 6. Тогда

Р(В) = 1/6

Р(А) = 1/2

, как в нашем предыдущем примере. Но очевидно, что события А и В не может произойти одновременно, так как выпадение 6 означает, что лицо красное, и вращение зеленого лица означает, что число, отображаемое нечетное. Поэтому

Р(А и В) = 0,

Таким образом, мы видим, что взаимоисключающая пара нетривиальных событий также обязательно зависимые события. Это имеет смысл, потому что если A и B исключают друг друга, то если происходит A, то B также не может происходить; и наоборот. Это противоречит тому, чтобы сказать, что результат из A не влияет на результат B, который является независимым от события.

$\endgroup$

0

$\begingroup$

Взаимоисключающее событие :- два события являются взаимоисключающими, если они не могут произойти одновременно. например, если мы подбрасываем монету, она может показать только решку ИЛИ решку, но не то и другое одновременно.

Независимое событие : появление одного события не влияет на появление других например, если мы подбросим монету два раза, в первый раз может выпасть орел, но это не гарантирует, что в следующий раз, когда мы подбросим монету, тоже выпадет орел. Из этого примера видно, что первое событие не влияет на возникновение следующего события.

$\endgroup$

1

$\begingroup$

Если я подброшу монету дважды, результат первого и второго бросков не зависит.

Однако событие, когда выпадает две решки, является взаимоисключающим по отношению к событию, когда выпадает две решки.

Предположим, что вероятность возникновения двух событий не равна нулю.

Тогда, если два события исключают друг друга, они не могут быть независимыми.

Если два события независимы, они не могут быть взаимоисключающими.

$\endgroup$

4

$\begingroup$

На этот вопрос уже есть очень хорошие ответы, я собираюсь добавить визуализацию для независимых событий с помощью некоторых специальных диаграмм. На этих диаграммах доля событий в пространстве выборки представляет их вероятность. Наше тестовое пространство представляет собой прямоугольник из 9x5 = 45 единиц :

У нас есть событие A (3x5) поэтому P(A) = 3x5/9x5 = 15/45 = 1/3 ) SO P (B) = 9x3/9x5 = 27/45 = 3/5 :

Эти два события пересекаются как:

𝐴∩𝐵 ОСКУНТИЯ 3X3 UNITS:

𝑃(𝐴∣𝐵) = 𝑃(𝐴∩𝐵) / 𝑃(𝐵) , значит 𝑃(𝐴∣𝐵) = 9/27 = 1/3 . Но это то же самое, что и Р(А) !

и Но это то же самое, что и P(𝐵) !

Поскольку на двух последних диаграммах возникновение одного события не влияет на вероятность другого события, эти два события называются независимыми . Таким образом, знание о возникновении одного из них не влияет на наше знание о вероятности другого. Но это не потому, что они не имеют ничего общего, наоборот, они как бы гармонируют, стирая (данное событие сводит к себе пространство выборки, т. е. стирает свое дополнение) пространство выборки таким образом, что другое событие к данному событию не изменяется. Я хотел бы запомнить их как перпендикулярные события .

$\endgroup$

$\begingroup$

События независимы, когда появление одного не влияет на появление другого. Извержение вулкана на Земле и орбита Марса не влияют друг на друга, поэтому являются независимыми событиями.

Рост человеческой популяции и сохранение многих других видов взаимно исключают друг друга, поскольку одно может произойти только в том случае, если не произойдет другое.

Строго говоря, взаимоисключающие не означают, что одно из них должно произойти. Если на Землю упадет большой астероид, то ни человеческая популяция не вырастет, ни вымирающие виды не сохранятся.

$\endgroup$

$\begingroup$

Пусть $A$ — событие попадания в яблочко мишени для дартс, а $B$ — событие попадания внутрь его внутреннего кольца.

1. Верны ли эти определения?

   Два события являются взаимоисключающими, если они не могут произойти одновременно.

   Ложь: события $A$ и $B$ являются взаимоисключающими $\Big(P(A\cap B)=P(A)=0\Big),$, но происходят одновременно.

   Определение: два события являются взаимоисключающими , если они почти никогда или никогда и то, и другое не произойдет, то есть если их совместная вероятность нуль.

2. Независимые события — это события, для которых знание вероятности одного не меняет вероятности другого.

   Ложь: события $A$ и $B$ независимы $\Big(P(A\cap B)=P(A)=0=P(A)\,P(B)\Big),$ но знание того, что вероятность $A$ равна $1$ (т.е. что это произойдет) увеличивает $B$' s до $1.$

   Неформальная характеристика: Два события, хотя бы одно из которых имеет положительная вероятность , являются независимыми , если знание того, что происходит, не меняет вероятность другого.

   Определение: События $X$ и $Y$ являются независимыми , если $\,P(X\cap Y)=P(X)\,P(Y).$

3. Есть ли связь между независимыми и взаимоисключающими событиями?

   Пусть $X$ и $Y$ — события с положительной вероятностью. Если $X$ и $Y$ исключают друг друга, то $P(X\cap Y)=0;$, так как $P(X)\,P(Y)>0,$ мы $P(X\cap Y)\ne P(X)\,P(Y),$, то есть $X$ и $Y$ являются зависимый.

   Интуитивно: если $X$ и $Y$ исключают друг друга, то они почти никогда не встречаются одновременно; таким образом, зная, что событие $Y$ происходит, означает знать, что событие $X$ почти не происходит или не происходит случаться; таким образом, зная, что $Y$ произойдет, вероятность $X$ уменьшается до нуль; то есть события $X$ и $Y$ зависимы.

   Однако будьте осторожны: указанные выше события $A$ и $B$ являются взаимоисключающими. но независимы, в то время как события {выпадение $'3'$ при броске кубика} и {выпадение нечетного числа при броске кубика} зависят, хотя не взаимоисключающие.

$\endgroup$

$\begingroup$

Будет проще, если мы будем отличать «взаимоисключаемость» от «независимости», имея в виду выборочное пространство.

• Два события, которые сравниваются на взаимоисключающие, должны быть из одного пространства выборки. Например,

  • Двойное подбрасывание монеты. $A=\{HH\}$ — событие, в котором дважды появляется голова, а $B=\{TT\}$ — событие, в котором дважды появляется хвост. Они используют одно и то же пространство сэмплов $S=\{HH,HT,TH,TT\}$. Поскольку $A\cap B=\{\}$, они исключают друг друга.

• Два события, которые сравниваются на предмет независимости, должны происходить из двух выборочных пространств. Например,

  • Двойное подбрасывание монеты. $A=\{H\}$ — это событие, при котором голова выпадает при первом броске, а $B=\{T\}$ — это событие, при котором хвост появляется при втором броске. Демонстрационное пространство для первого испытания $S_1=\{H,T\}$, а дискретное пространство для второго испытания $S_2=\{H,T\}$. Поскольку $S_1=S_2$, они независимы.

Следующие дополнительные вопросы: "Возможно ли иметь 2 события, которые есть"

Я обновлю этот ответ в будущем, чтобы ответить на дополнительные вопросы выше.

$\endgroup$

1

2.1.3.2.1 - Непересекающиеся и независимые события

Непересекающиеся события и независимые события различны. События считаются непересекающимися, если они никогда не происходят одновременно; они также известны как взаимоисключающих событий . События считаются независимыми, если они не связаны между собой.

Непересекающиеся события  – это события, которые никогда не происходят одновременно. Они также известны как взаимоисключающих событий .

Они часто визуально представлены диаграммой Венна, такой как ниже. На этой диаграмме нет перекрытия между событием A и событием B. Эти два события никогда не происходят вместе, поэтому они являются непересекающимися событиями.