Таинственная математика совершенства / Хабр
Улыбка Моны Лизы, олимпийский прыжок Мэри Лу Реттон, высокая тесситура Мэрайи Кэри — всё это считается совершенным. Так же, как и числа 6 и 28.
Не без участия таланта или атлетизма этих людей, но совершенство находится в глазах смотрящего. Для чисел совершенство же определяется математически. «Совершенные числа» равны сумме своих собственных делителей (делители — положительные целые числа, отличные от рассматриваемого числа, которые делят его без остатка). Например, 6 = 3 + 2 + 1, а 28 = 14 + 7 + 4 + 2 + 1. Хотя эти математические диковины могут так же украшать стены Лувра, как и выполнять сальто назад с поворотом, но тем не менее они действительно являют собой нечто уникальное: совершенную тайну.
Евклид изложил основы совершенных чисел более 2000 лет назад. Он знал, что первыми четырьмя совершенными числами были 6, 28, 496 и 8128. С тех пор было обнаружено гораздо больше совершенных чисел.
Но, как ни странно, все они чётные. Никто не смог найти совершенное нечетное число, и после многих тысяч лет безуспешных поисков может возникнуть соблазн сделать вывод, что нечетных совершенных чисел не существует. Но и математики этого доказать не смогли. Как же так выходит, что мы можем так много знать о четных совершенных числах и в то же время не можем ответить на самый простой вопрос о нечетных? И как современные математики пытаются решить этот древний вопрос?
Наше исследование математического совершенства начинается с делителей. Мы знаем, что 6 является делителем 12, поскольку 12/6 = 2, и мы знаем, что 25 является делителем 100, поскольку 100/25 = 4. Как мы уже говорили, мы знаем, что число является совершенным, когда оно равно сумме своих собственных делителей — тех делителей, которые меньше самого числа. Мы также можем назвать число совершенным, если сумма всех его делителей, собственных и несобственных, вдвое больше числа. Это работает, потому что единственный несобственный делитель числа — это само число.
Мы видим, что число 28 также является совершенным по этому определению: его собственные делители — 1, 2, 4, 7 и 14, его несобственный делитель — 28, а сумма всех его делителей — 1 + 2 + 4 + 7 + 14 + 28, равна 56, что представляет собой 2 × 28. Включение несобственного делителя в сумму удобно для некоторых элементов алгебры, которые мы будем использовать чуть позже с совершенными числами.При работе с совершенными числами мы часто употребляем определение «сумма делителей числа», поэтому математики упростили задачу, превратив это значение в функцию. Мы определим σ(n), или «сигму числа n», как сумму делителей числа n. Мы уже знаем, что σ(28) = 56. Еще несколько примеров: σ(1) = 1, σ(6) = 1 + 2 + 3 + 6 = 12 и σ(10) = 1 + 2 + 5 + 10 = 18. Обратите внимание, что 6 — совершенное число, поскольку σ(6) = 2 × 6, а 1 и 10 — нет. Как мы видим, эта функция σ обладает некоторыми особыми свойствами, которые идеально подходят для изучения совершенных чисел.
Итак, у нас есть базовое определение совершенных чисел и новый математический инструмент, который поможет нам их найти.
С чего начать поиски? Мы начнем с того, с чего математики всегда начинают изучать числа и их закономерности: с простых чисел.
Простое число по определению делится только само на себя и на 1. Это упрощает вычисление σ для простого числа: σ(2) = 1 + 2 = 3, σ(3) = 1 + 3 = 4, σ(5) = 1 + 5 = 6 и σ(7) = 1 + 7 = 8. В общем, для любого простого числа p, σ(p) = 1 + p.
Может ли простое число быть совершенным? Только если σ(p) = 1 + p = 2p. Немного алгебры нам в помощь, и мы видим, что это тождество верно всякий раз, когда p = 1, но поскольку простые числа больше 1 по определению, ни одно простое число не может быть совершенным. Итак, мы знаем, что простые числа не могут быть совершенными. Что дальше?
Степень простых чисел, таких как 24, 53 или 1136, — хороший следующий шаг, так как их делители легко организовать. Рассмотрим степень простого числа, например, 16, или 24. Единственными делителями 24 являются степени от 2 до 24: 20 = 1, 21 = 2, 22 = 4, 23 = 8, 24 = 16.
Таким образом, σ(24) может вычисляться следующим образом:
σ(24) = 1 + 2 + 22 + 23 + 24 = 1 + 2 + 4 + 8 + 16 = 31.
Если обобщить, для любой степени простого числа pn: σ(pn) = 1 + p + p2 + p3 + … + pn.
Станет еще проще, если мы воспользуемся формулой с урока алгебры. Обратите внимание, что каждый из добавляемых членов в σ(p
Подробнее об этой удивительной формуле в упражнениях в конце статьи.
Благодаря формуле ряда геометрической прогрессии, нам не нужно перечислять все делители числа pn для вычисления σ(pn). Мы можем просто использовать формулу:
Например, мы уже видели, что
И мы можем вычислить сумму делителей других простых степеней, просто подставив их в формулу:
и
Обратите внимание, что ни одна из этих степеней простых чисел не удовлетворяет условию совершенности σ(24) ≠ 2 × 24, σ(33) ≠ 2 × 33, and σ(112) ≠ 2 × 112.
Фактически, никакая степень простого числа не может быть совершенной. Чтобы получить совершенное число, нам нужно σ(p n) = 2pn, что будет означать: 1 + p + p2 + p3 + … + pn-1 + pn = 2pn.
Мы можем вычесть pn из обеих частей уравнения и получить: 1 + p + p2 + p3 + … + pn-1 = pn.
Теперь воспользуемся формулой ряда геометрической прогрессии в левой части этого уравнения и получим:
Необходимо, чтобы это было верно, чтобы pn был совершенным. Но обратите внимание, что pn — 1 меньше, чем pn, и деление pn — 1 на p — 1 сделает его еще меньше, поэтому:
Таким образом, никакая простая степень pn не может быть совершенной.
Итак, нет совершенных простых чисел и нет совершенных простых степеней. Что может быть совершенным? Что ж, мы знаем, что 28 — совершенное число, и это произведение двух различных степеней простых чисел: 28 = 2
Любое число, не являющееся простым числом или степенью простого числа, может быть записано как произведение различных степеней простого числа, подобного этому. И эти факторизации вместе с особым свойством функции σ могут помочь нам определить, является ли число совершенным.
Мы уже знаем, что σ(28) = 1 + 2 + 4 + 7 + 14 + 28, но давайте подробнее рассмотрим эту сумму. Обратите внимание, что каждое из последних трех чисел кратно 7:
Мы можем вынести это число 7, чтобы выявить некую скрытую структуру: σ(28) = (1 + 2 + 4) + 7 × (1 + 2 + 4).
И с помощью более умного разложения на множители (факторизации) с распределительным свойством мы можем написать: σ(28) = (1 + 2 + 4)(1 + 7).
Это не говорит нам о том, чего мы раньше не знали: σ(28) = (1 + 2 + 4)(1 + 7) = 7 × 8 = 56, что подтверждает, что 28 является совершенным числом. Но внутри этого умножения скрывается кое-что важное: σ(28)=(1+2+4)(1+7)=(1+21+22)(1+71).
Выражения в скобках кажутся знакомыми: 1 + 21 + 22 = σ(22) и 1 + 71 = σ(7). Это означает, что мы действительно можем написать: σ(28) = σ(22)σ(7).
Чтобы вычислить σ(28) = σ (22 × 7), мы можем фактически вычислить σ(22) и σ(7) и умножить их. Это удивительно, и, в целом, верно: каждый раз, когда вы выполняете разложение числа на простые числа, как это, вы можете использовать эту комбинацию для вычисления σ. Например, поскольку 100 = 22 × 52, мы можем вычислить σ(100) следующим образом:
σ(100) = σ(22)σ(52) = (1 + 2 + 4)(1 + 5 + 25) = 7 × 31 = 217
Почему это работает? Что сказать, делители числа происходят от его простых делителей. Снова рассмотрите число 28, которое является произведением 22 и 7, и подумайте о таблице умножения ниже:
По горизонтали указаны степени числа 2, которые нацело делят 28, а по вертикали — степени 7, которые нацело делят 28.
Обратите внимание, что происходит, когда мы заполняем эту таблицу умножения.
Мы получаем все делители 28. Это потому, что каждый делитель 28 представляет собой комбинацию делителей 22 и 7, степеней простых чисел, которые появляются при факторизации 28.
Теперь сравните таблицу умножения с выражением: (1 + 2 + 4) (1 + 7).
Когда мы умножаем с помощью свойства распределения, это также дает все делители 28, а затем складывает их: (1 + 2 + 4)(1 + 7) = 1 × 1 + 2 × 1 + 4 × 1 + 7 × 1 + 7 × 2 + 7 × 4.
Другими словами, (1 + 2 + 4) (1 + 7) в точности равно σ(28). Но (1 + 2 + 4)(1 + 7) также является σ(22)σ(7). Итак, σ(22)σ(7) = σ(28). Этот пример демонстрирует очень полезный факт о σ: на языке теории чисел эта функция является «мультипликативной». Это означает, что σ (ab) = σ(a)σ(b), если числа a и b «взаимно просты», то есть у них нет общих делителей.
Это особенность σ, которая помогает нам изучать совершенные числа.
Евклид использовал этот факт 2000 лет назад, чтобы создать формулу для нахождения совершенных чисел с помощью особого вида простых чисел и умных аргументов в отношении произведений и делителей. При этом он сделал первый шаг к определению того, как должно выглядеть каждое четное совершенное число. Посмотрим, как он это сделал.
Во-первых, обратите внимание, что для любой степени двойки мы имеем
Это следствие формулы ряда геометрической прогрессии, которую мы обсуждали ранее. Теперь рассмотрим следующий мысленный эксперимент: что, если 2k+1 — 1 простое число?
Итак, поскольку σ(p) = 1 + p для любого простого числа, мы знаем, что σ(2k+1 – 1) = 1 + 2k+1 – 1 = 2k+1. И обратите внимание, что 2k+1 ровно вдвое больше 2k из-за закона экспонент, который гласит, что 2 × 2k = 2k+1. Итак, у нас есть следующие два интересных отношения между числами 2k и 2k+1 — 1:
σ(2k) = 2k+1 – 1 и σ(2k+1 – 1) = 2k+1 = 2 × 2k.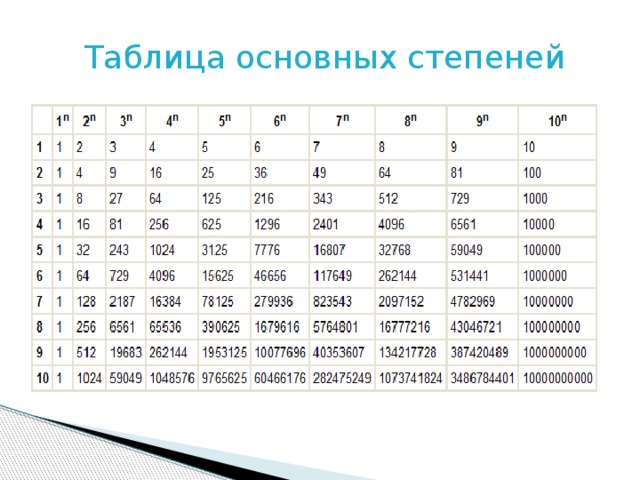
Евклид заметил хитрый способ использовать эти отношения: он перемножил два числа вместе, чтобы получилось число M = 2k × (2k+1 — 1), и пока (2k+1 — 1) — простое число, это число совершенно! Чтобы убедиться в этом, вычислим σ(M) и покажем, что оно равно 2M.
Во-первых, обратите внимание, что 2k+1 — 1 на единицу меньше четного числа, поэтому оно должно быть нечетным. Это означает, что 2k+1 — 1 не делится на 2. Но 2k делится только на степень 2. Таким образом, 2k и 2k+1 — 1 не имеют общих делителей и поэтому взаимно просты. Это позволяет нам использовать мультипликативное свойство σ:
σ(M) = σ (2k ×(2k+1 – 1)) = σ (2k) σ (2k+1 – 1).
Мы уже знаем, что σ(2k) = 2k+1 – 1 и σ(2k+1 – 1) = 2k+1 = 2 × 2k, поэтому мы можем найти σ(M):
Итак, M= 2k ×(2k+1 – 1), как утверждается, совершенно.
Имейте в виду, что это основано на предположении, что число 2k+1 — 1 простое. Эти числа называются простыми числами Мерсенна, и вы, возможно, слышали о них в связи с широкомасштабным проектом добровольных вычислений по поиску простых чисел Мерсенна (GIMPS), совместной онлайн-вычислительной попытки найти огромные простые числа Мерсенна. Каждый раз, когда вы слышите об открытии нового наибольшего простого числа, это, вероятно, результат работы GIMPS. И, благодаря доказательству Евклида, каждый раз, когда открывается новое простое число Мерсенна, также открывается новое совершенное число.
Например, 25 – 1 = 31 это простое число Мерсенна, и, таким образом, 24(25-1) = 16 × 31 = 496 является совершенным числом. Также, 22 – 1 = 3 это простое число Мерсенна, и, таким образом, 21(22 – 1) = 2 × 3 = 6 является совершенным числом. И 23 – 1 = 7 это простое число Мерсенна, и, таким образом 22(23 – 1) = 4 × 7 = 28 является совершенным числом.
Вы могли заметить, что все эти совершенные числа четные. Это имеет смысл, потому что, пока k > 0, число 2k × (2k+1 — 1) будет четным. (И если k = 0, то 2k+1 — 1 равно 1, что не является простым числом).
Возможно, вы также заметили, что все совершенные числа, которые мы обсуждали до сих пор, похоже, связаны с простыми числами Мерсенна. Это не случайно: через 2000 лет после того, как Евклид показал, что эта формула порождает совершенные числа, Леонард Эйлер доказал, что это единственный способ получить четные совершенные числа. Но вопрос о том, какими могут быть нечетные совершенные числа (если они существуют), оставался открытым.
И он остается открытым сегодня. Хотя математики не могут найти такие числа, у них есть много информации о том, как может выглядеть гипотетическое нечетное совершенное число. Оно не может делиться на 105; должно иметь как минимум девять различных простых делителей, второй по величине из которых должен быть больше 10 000.
И оно должно иметь остаток 1 при делении на 12 или остаток 9 при делении на 36.
Может показаться странным доказывать результаты о числах, которых может даже не существовать. Но каждое новое правило еще больше сужает поиск. И если математикам повезет, они могут просто доказать, что нечетные совершенные числа должны удовлетворять двум несовместимым критериям, что раз и навсегда докажет, что нечетных совершенных чисел не существует.
В поисках несовместимых критериев математики даже начали искать не совсем совершенные числа. «Поддельное совершенное число» — это число, которое выглядит как совершенное, если вы притворитесь, что один из его непростых делителей на самом деле является простым. Например, 60, произведение 3, 4 и 5, можно считать «поддельным совершенным числом»: если представить, что 4 в его факторизации — простое число, тогда комбинации, которые мы разработали для σ, дадут нам: (1+3)(1+4)(1+5) = 4 × 5 × 6 = 120.
Если бы σ(60) равнялось 120, то 60 было бы совершенным.
Конечно, σ(60) на самом деле не равно 120, но похоже, что это так, если мы представим, что 4 — простое число. Вот что делает его «поддельным».
Эти «подделки» похожи на обобщения совершенных чисел, и поэтому все, что верно в отношении «подделки», должно быть правдой и в отношении совершенного числа. Понятие нечетных «подделок» было бы особенно полезно, поскольку любое правило, обнаруженное для нечетных «подделок», можно было бы добавить к существующим правилам для нечетных совершенных чисел, увеличивая шансы на обнаружение противоречивых критериев и сужая общее пространство поиска.
Рене Декарт, еще один известный математик, вовлеченный в тайну совершенных чисел, открыл первое «поддельное» нечетное совершенное число и призвал математиков найти другие. Приняв вызов, математики расширили понятие «подделки» и открыли новый класс чисел для изучения. По большей части исследования этих «подделок» совершенных чисел проводятся просто ради удовольствия от математических изысканий. Но, возможно, что-то, что мы узнаем о «подделках», поможет нам доказать, что на самом деле нечетные совершенные числа не могут существовать, или же наоборот.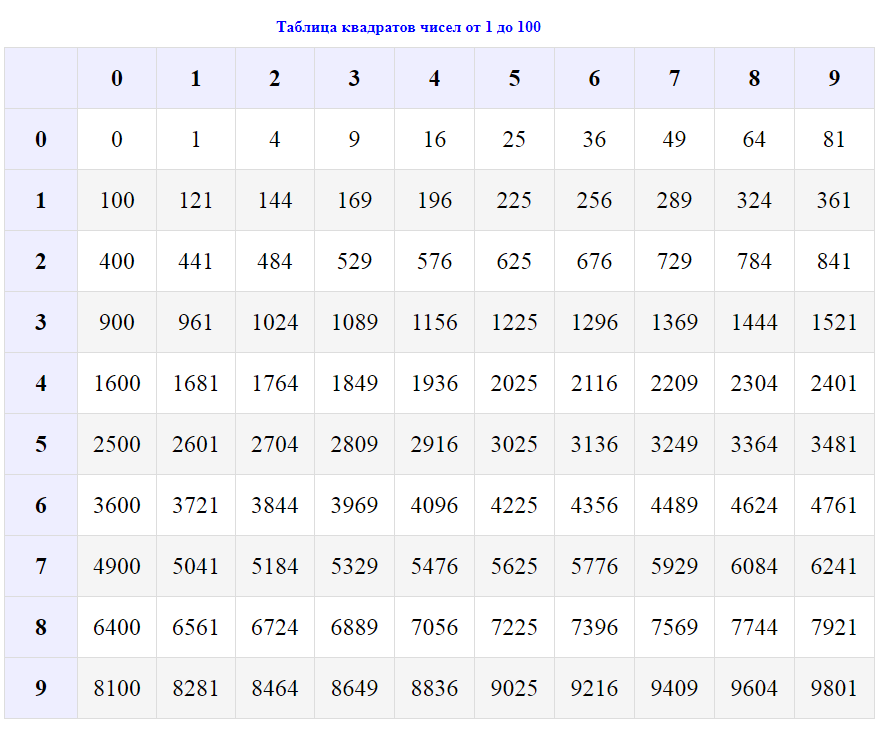
Может показаться странным тратить тысячи лет на поиск чисел с любопытными свойствами, доказывая теоремы об объектах, которые могут даже не существовать, и изобретать новые и даже более странные миры чисел для исследования. Но для математика это имеет совершенный смысл.
Упражнения
- Число называется «избыточным», если оно меньше суммы его собственных делителей. Например, 36 — это избыточное число, поскольку 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 = 55, что больше 36. Назовите наименьшее избыточное число.
- Число считается «недостаточным», если оно больше суммы собственных делителей. Например, 35 является недостаточным, поскольку 1 + 5 + 7 = 13, что меньше 35. Являются ли простые степени недостаточными или избыточными?
- Используйте свойство дистрибутивности, чтобы умножить (p — 1)(1 + p + p2 + p3 +… + pn) и упростить.
- Предположим, что N — нечетное число, и предположим, что M = 2N и является совершенным.
Покажите, что N должно быть равно 3.
Покажите, что N должно быть равно 3.Ответы
Нажмите, чтобы увидеть ответ на задание 1
Наименьшее избыточное число — 12. Наименьшее нечетное избыточное число намного больше! Вы можете доказать, что существует бесконечно много избыточных чисел, доказав, что кратное избыточного числа является избыточным.
Нажмите, чтобы увидеть ответ на задание 2
Выше мы доказали, что:
это приводит к дефициту степеней простых чисел. Конечно, простые числа являются неполноценными, поскольку сумма собственных делителей простого числа всегда равна 1. Обратите внимание, что это доказывает, что существует бесконечно много недостаточных чисел.
Нажмите, чтобы увидеть ответ на задание 3
Используя свойство дистрибутивности, получаем
Обратите внимание, что, поскольку (p – 1) (1 + p + p2 + p3 + … + pn )= pn+1 — 1, мы можем разделить обе части уравнения на p — 1, чтобы получить:
формулу суммы ряда.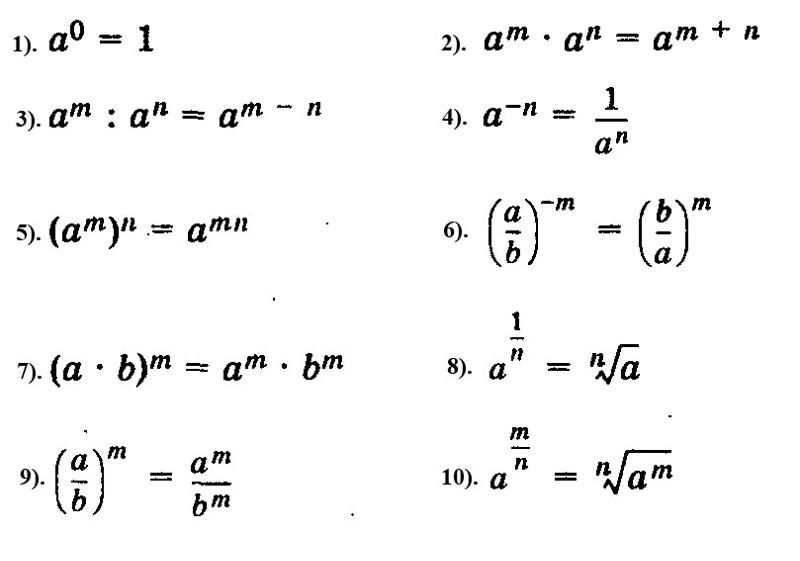
Нажмите, чтобы увидеть ответ на задание 4
Поскольку M = 2N и является совершенным, мы имеем σ(M) = σ(2N) = 4N. Но поскольку N нечетно, N и 2 взаимно просты, поэтому σ(2N) = σ(2)σ(N) = 3σ(N). Итак, 4N = 3σ(N).
Поскольку обе части этого уравнения являются целыми числами и 3 не делит 4, 3 должно делить N. Таким образом, мы можем написать:
Поскольку N/3 должно быть целым числом, оно также является делителем N. N также является делителем N, поэтому мы знаем, что сумма делителей N равна по крайней мере сумме этих двух. То есть,
Но мы уже знаем, что σ(N) = 4/3 * N. Если бы у N было больше делителей, σ(N) было бы больше 4/3 * N, поэтому 3 должно быть его единственным делителем. Таким образом, N = 3, как заявлено.
Это конкретное применение доказательства Эйлера того, что каждое четное совершенное число имеет вид M = 2k × (2k+1 — 1), где 2k+1 — 1 является простым числом Мерсенна.
два в седьмой степени
назовите два равных угла
✌ 1 3 : . ✌1. Это утверждение, состоящее из двух предложений: «если» и «тогда». а. исходное заявление б. гипотеза ста
…
с. условное выражение д. Заключительное утверждение 2. В утверждении, если «p, то q», что вы называете утверждением p? . гипотеза. заключение в. обратный д. обратное 3. «Тогда часть» утверждения «если-то» является выводом, что вы называете «если частью»? а. гипотеза б. заключение в. обратный д. обратный4. Каков вывод утверждения «Если вы влюблены, то вы вдохновлены»? а. Вы не влюблены. б. Вы не вдохновлены. в. Ты влюблен. д. Вы вдохновлены. 5. Каково исходное утверждение «Если две прямые пересекаются под прямым углом, то они перпендикулярны»? а. Перпендикулярные прямые пересекаются под прямым углом. б. Перпендикулярные прямые, когда прямые пересекаются под прямым углом. в. Две прямые, пересекающиеся под прямым углом, перпендикулярны. д. Две прямые пересекаются под прямым углом, если они перпендикулярны. Для позиций с номерами 6–8 см. заявление ниже. «Употребление большего количества овощей делает меня здоровым». 6. Что из следующего является допустимым оператором if-then? а. Если вы не будете есть больше овощей, то не будете здоровы. б. Если вы здоровы, то едите больше овощей. в. Если вы будете есть больше овощей, то будете здоровы. д. Если вы едите больше овощей, значит, вы заботитесь о своем здоровье. 7. Что из следующего является гипотезой? а. Вы не будете есть больше овощей. б. Вы едите больше овощей. в. Вы будете заботиться о своем здоровье. д. Вы будете здоровы. 8. Что из следующего является заключением? а. Вы не будете есть больше овощей. б. Вы едите больше овощей. в. Вы будете заботиться о своем здоровье. д. Вы будете здоровы. Для позиций № 9– 11, см. заявление ниже. «Я сдам предмет по математике, если приду на занятия». 9. Что такое форма «если-то»? а. Если я буду посещать занятия, то я сдам предмет по математике. б. Если я сдам предмет по математике, то я буду посещать занятия.
в. Если я не буду посещать занятия, то я не сдам предмет по математике. д. Если я не сдам предмет «Математика», то я не пойду на занятия. 10. Что такое гипотеза? а. Я не пропущу предмет Математика. б. Я буду присутствовать на уроке. в. Я пропущу предмет Математика. д. Я не буду присутствовать на уроке. 11. Какой вывод? а. Я не пропущу предмет Математика. б. Я буду присутствовать на уроке. в. Я не буду присутствовать на уроке. д. Я пропущу предмет Математика. 12. В утверждении «Все прямые углы ̠c̠̠o̠̠n̠̠̠g̠̠r̠̠u̠̠e̠̠n̠̠t̠» какая часть данного «Если-то утверждение» является подчеркнутым словом? а. гипотеза б. заключение в. конверс д. инверсия 13. В утверждении «A̠ ̠q̠̠u̠a̠̠d̠̠r̠̠i̠̠l̠a̠̠̠l̠a̠̠t̠̠e̠̠r̠a̠̠l̠ ̠i̠̠s̠ a̠ ̠ ̠̠̠o̠̠l̠̠y̠̠̠g̠̠o̠al», какие слова являются частью данного условного выражения под четырьмя сторонами данной условной линии̠n̠al а. гипотеза б. заключение в. конверс д. инверсия 14. «Если вы являетесь лицензированным профессиональным учителем, то». Какая часть данного условного оператора выделена жирным шрифтом? а.
гипотеза б. заключение в. конверс д. инверсия 15. В высказывании «будет повышен в должности» какая часть данного условного высказывания выделена жирным шрифтом? а. гипотеза б. заключение в. конверс д. инверсия
найти следующие три члена каждой геометрической последовательности. 486,162,54,
Решите следующие задачи, применяя основной принцип подсчета. 1. Из цифр 7, 2, 5 и 1 следует составить двузначное число. Хо … w много различных чисел можно составить, если повторение цифр не разрешено? 2. Сколько четырехзначных кодов можно составить из цифр 0, 1, 2, 3, 4 и 5?3. У Маркуса есть шесть возможных маршрутов на работу и четыре маршрута домой. Сколько возможных маршрутов у него есть туда и обратно?
a= 3 , b= 1/2 и c =3 какой ответ??
СЕДЬМОЙ
МОЩНОСТЬ Седьмая сила — s/t (ретроактивная Рекорды) 2006 1. Седьмая сила
— группа, возглавляемая Биллом Менченом, гитаристом Titanic и Final Axe. Вместе с барабанщиком Stryper Робертом Свитом басист Final Axe
Род Риснер из Seventh Power выпустил свой первый одноименный компакт-диск. Музыка
очень похож на другие группы Менхена, упрощенный, прямолинейный, средний темп
тяжелый металл. Тем не менее, Билл добавляет некоторые другие влияния, чтобы все запутать.
добавление влияния пауэр-метала и дума повсюду. Инструментальный
Seven Golden Lampstands и немного более тяжелый и экспериментальный Ocean Of
Emotion Motion также добавляют альбому разнообразия. Седьмая сила — Доминион и сила (обратная сила) 2008 1 «Доминион и
Сила» (4:14) Билл Менхен один занят
музыкант. Что отличает этот компакт-диск
из дебюта группы заключается в том, что Менхен, кажется, преследовал более раздетую
вниз, прямо вперед, музыкальное направление. К сожалению, как и в случае с
дебют, я считаю, что вокал очень отвлекает. Вокал Билла прекрасен
обыденность и отсутствие харизмы. Я думаю, что действительно добавляет к этому отвлечению
тот факт, что весь вокал очень цифровой и обработанный. не я
студийный инженер, но я бы сказал, что слишком много эффекта добавлено к
вокал. |
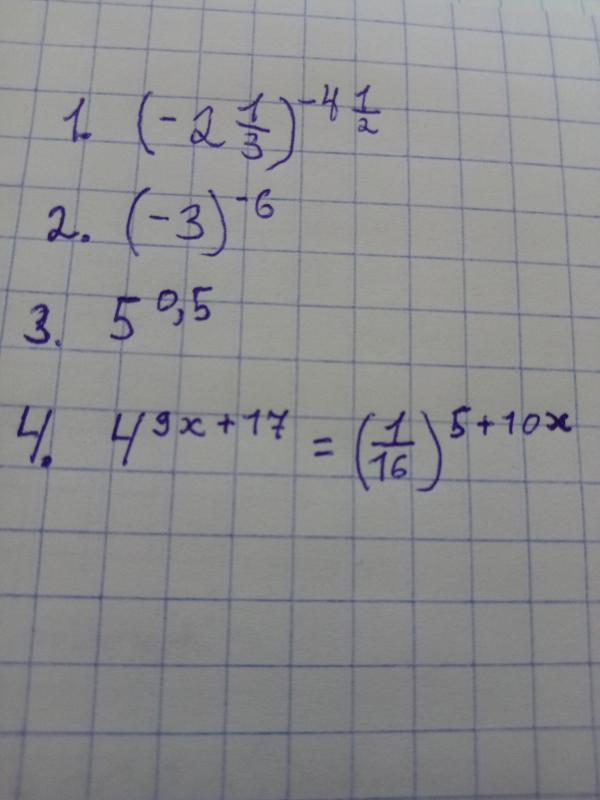«Христос умер»
(3:12) 
«Владетель тебя» добавляет
в некоторых жутко звучащих клавишных, которые также придают песне другой оттенок.
«Eye in the Skies» начинается с приятной смеси фортепианного и гитарного скрипа.
прежде чем перейти к прямолинейному металлическому номеру. «Врата рая» также
предлагает часть этого фортепианно-гитарного микса в середине песни. Это может иметь
было здорово услышать, что группа пошла дальше. Билл становится
вокалист, а также гитарист и автор песен. К сожалению, это самый слабый
часть компакт-диска. Его вокальный стиль довольно прост и обыден, с нотками
Оззи Осборна время от времени. Компенсировать
за отсутствием динамики в вокале Билл использует разные, цифровые, роботизированные
звуковые вокальные эффекты почти в каждой песне. В «Океане эмоций» он играет
вокруг со всеми видами различных и причудливых вокальных эффектов на протяжении всего
песня. Я уверен, что причина этого в том, что эти эффекты помогают отвлечься от
тот факт, что лирика настолько повторяется.
На самом деле вся песня ничего
больше, чем название песни, которое повторяется снова и снова. «Сила» это
также немного повторяется с припевом, «Сила Христа побуждает вас» повторяется в песне не менее двадцати раз. Остальные тексты
все основаны на христианстве, но также хорошо написаны и не кажутся дрянными
или повторяющиеся, как две вышеупомянутые песни. В целом, я нахожу музыку
на Seventh Power быть качественным хэви-металом, просто позор, что
вокал такой монотонный, а вокальные эффекты такие отвлекающие.
Кажется, постоянно что-то выходит с его именем на
это. Титаник, Финал
Топор, Искупитель и Седьмая власть. «Владычество и власть» — это
второй релиз The Seventh Power. Группа остается прежней для записи
номер два и снова включает барабанщика Stryper Роберта Свита, басиста Final Axe.
Род Риснер. Как и большинство проектов Менхена, Dominion & Power понравится
любителям простого, прямолинейного, в основном среднего хэви-метала. Менхен кажется
иметь в своем распоряжении целый арсенал классических металлических риффов. я особенно
понравился пулеметный рифф «Вечного огня». Его игра на гитаре — одна из
основные моменты этого альбома, хотя игра Свита также выделяется. Те
знакомый с работой Свита со Страйпером, знает, чего здесь ожидать. Роберт не слишком броский, но он, безусловно,
стиль его игры, который отличает его от других.
Ключи играют менее важную роль
и многие из прежних штрихов симфонического и пауэр-метала были удалены в
пользу мелодии. Клавишные до сих пор присутствуют в таких песнях, как «Everlasting Fire».
и «King of All Kings», но они, похоже, не являются центром музыки в целом.
Гитары хорошо записаны и имеют плотный хруст, а бас-гитара
заполнение необходимого нижнего конца. Есть несколько хороших гитарных соло-брейков
через. Билл не слишком причудливый соло-игрок, но его соло соответствует ощущению.
песни. На самом деле, мне бы хотелось услышать больше мелодичных соло.
и заливки, разбросанные по песням.