Приложения двойного интеграла. Вычисление объемов тел презентация, доклад
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Приложения двойного интеграла. Вычисление объемов тел, предмет презентации: Математика. Этот материал содержит 10 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Вычисление объемов тел, предмет презентации: Математика. Этот материал содержит 10 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
17.6. ПРИЛОЖЕНИЯ
ДВОЙНОГО ИНТЕГРАЛА
1. Вычисление объемов тел
Из геометрического смысла двойного интеграла следует, что любой двойной интеграл задает объем тела, ограниченного сверху графиком подынтегральной функции, снизу – областью D, с боков – цилиндрической поверхностью с направляющими по границе области D.
Пример.
Вычислить объем тела,
ограниченного поверхностями
Решение.
Поскольку подынтегральная функция должна быть не отрицательна, то область интегрирования ограничена на плоскости ХОУ прямоугольным равнобедренным треугольником с катетами, равными а.
2. Вычисление площадей фигур
Площадь некоторой области D может быть найдена по формуле:
Пример.
Вычислить площадь фигуры,
ограниченной линиями:
Решение.
площадь прямоугольного треугольника,
катеты которого равны 1.
ограничена снизу прямой y=-1 при
сверху кривой y=lnx и справа прямой x=1.
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.
 ru?
ru?Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Объем тела через двойной интеграл : Анализ-I
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| jokesoy |
| ||
29/05/13 |
| ||
| |||
| Legioner93 |
| |||
28/07/09 |
| |||
| ||||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| jokesoy |
| ||
29/05/13 |
| ||
| |||
| Legioner93 |
| |||
28/07/09 |
| |||
| ||||
| svv |
| |||
23/07/08 |
| |||
| ||||
| jokesoy |
| ||
29/05/13 |
| ||
| |||
| Nacuott |
| ||
20/04/12 |
| ||
| |||
| jokesoy |
| ||
29/05/13 |
| ||
| |||
| Nacuott |
| ||
20/04/12 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Интеграция
— Поиск объемов — когда использовать двойные интегралы и тройные интегралы?
спросил
Изменено 6 месяцев назад
Просмотрено 32к раз
$\begingroup$
Это вовсе не технический вопрос, но я совершенно не понимаю, что мне использовать для вычисления объемов в $\mathbb{R}^3$ с интеграцией.
Я где-то читал, что двойной интеграл меняет местами объем по осям $x$ и $y$, а тройной интеграл просто интегрирует все сразу, насколько это точно? Может ли объем, выраженный двойным интегралом, быть выражен тройным интегралом?, И всегда ли тройка может быть выражена двойным? Это не кажется правдой, но у меня нет хорошего ответа, почему.
Я также нашел этот комментарий, когда читал openstudy.com, сделанный кем-то по имени KingGeorge год назад:
Для двойного интеграла нужно интегрировать некоторую функцию, для тройного интеграла нужно интегрировать 1.
Означает ли это, что использование интеграла для получения объема всегда должно выглядеть как $\iiint dxdydz$ без какой-либо функции?
Геометрически есть несколько вещей, на которые вы можете обратить внимание. Во-первых, вы находите 4-томник. То есть четырехмерный эквивалент объема. Во-вторых, если объем в области, в которой вы интегрируете, имеет изменяющуюся плотность, вы можете найти общую массу.
Я не уверен, правильно ли я понял, но это означает, что тройной интеграл вычисляет не точно тот объем, который мне нужен, а его четырехмерный эквивалент?
- интегрирование
- многомерное исчисление
- объем
- многократный интеграл
$\endgroup$
0
$\begingroup$
При расчете объема можно использовать как двойной, так и тройной интеграл. Позвольте мне объяснить вам, используя пример для расчета площади, то же самое относится и к объему. 93$ по своей природе представляет собой -й тройной -й интеграл: $${\rm vol}(B)=\int\nolimits_B 1\ {\rm d}(x,y,z)\ .$$ Теорема Фубини позволяет рекурсивно вычислить этот интеграл в терминах простых, соотв. двойные, интегралы по определенным интервалам или двумерным областям. В зависимости от способа определения $B$ некоторые из возникающих таким образом «внутренних интегралов» могут быть бесплатными, как в следующих примерах:
Когда $B$ является телом, вращающимся вокруг оси $z$ с кривая меридиана $\rho=\rho(z)$ $\>(a\leq z\leq b)$, т.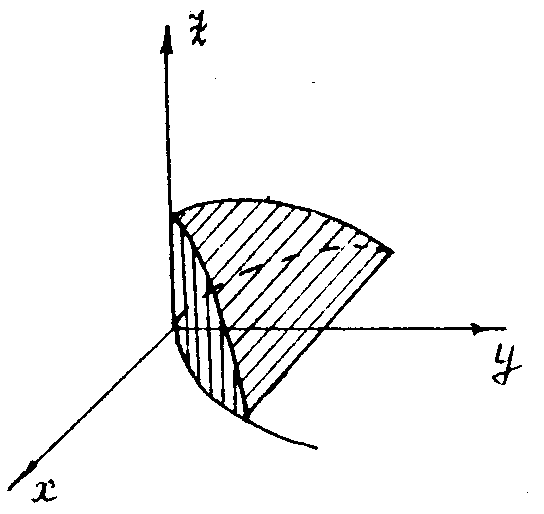 2(z)\ dz\ .$$ 9до н.э $. Та же логика может быть применена к любой другой форме. Объем представляет собой одинарный интеграл площади поперечного сечения или двойной интеграл высоты.
2(z)\ dz\ .$$ 9до н.э $. Та же логика может быть применена к любой другой форме. Объем представляет собой одинарный интеграл площади поперечного сечения или двойной интеграл высоты.
Обратите внимание, что это не единственный способ разделения фигур. Например, вы можете найти объем сферы, проинтегрировав поверхности всех сфер внутри нее с одним и тем же центром.
$\endgroup$
$\begingroup$
Для расчета объемов трехмерных объектов можно использовать как двойной, так и тройной интеграл. Для тройного интегрирования вы можете преобразовать тройной интеграл в двойной, сначала вычислив компонент Z (или любой компонент в зависимости от «типа» объекта), а затем вычислив двойной интеграл по оставшейся двумерной области. Тройное интегрирование используется для функций трех переменных, а двойное — для функций двух переменных. Для функции 1 переменной вы используете методы исчисления 1 для вращения объектов (тел вращения) вокруг осей или линий.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
многомерное исчисление — Объем вычисляется двойным интегралом 92-1)dxdy$, но я не могу понять, что является ортогональным $T$, в котором мы можем интегрировать. Я попытался преобразовать приведенные выше выражения в полярные координаты, но это только ухудшило ситуацию, поэтому вместо этого я попытался рассмотреть систему координат zyx. Я знаю, что результат $\frac{49}{60}$. Любые советы по этой проблеме будут оценены.
- многомерное исчисление
- объем
$\endgroup$
$\begingroup$ 92, 0 \leq y \leq 1$
И $ ~\displaystyle \frac{49}{60}~$ действительно является объемом области.
$\endgroup$
$\begingroup$
Объем интеграции показан на рисунке ниже. Ось $x$ выделена красным цветом, $y$ — зеленым, а $z$ — синим. У вас есть пирамида с вершинами $(0,0,0), (2,0,0), (0,2,0), (0,0,2)$ из первых четырех уравнений. Тогда у вас есть поверхность параболического цилиндра. Вас интересует объем внутри их пересечения. Поэтому, если ваша область интегрирования находится в плоскости $xy$, вам нужно разделить ваш интеграл на две части, где верхний предел $z$ задается пирамидой, а область, где задается верхний предел $z$ по параболе.
У вас есть пирамида с вершинами $(0,0,0), (2,0,0), (0,2,0), (0,0,2)$ из первых четырех уравнений. Тогда у вас есть поверхность параболического цилиндра. Вас интересует объем внутри их пересечения. Поэтому, если ваша область интегрирования находится в плоскости $xy$, вам нужно разделить ваш интеграл на две части, где верхний предел $z$ задается пирамидой, а область, где задается верхний предел $z$ по параболе.
На вашем месте я бы выбрал область интегрирования в плоскости $yz$ ($x=0$), то есть в области, в которой она находится внутри параболы. Тогда «высота» функции — это расстояние от плоскости $x=0$ до плоскости $x+y+z=2$.
$\endgroup$
2
$\begingroup$
Задача значительно упрощается, если выбрать правильный порядок интегрирования координат. В этом случае мы хотим начать с $x$. Это связано с тем, что в плоскости $yz$ высота поверхности всегда равна $2-y-z$, а это означает, что нам не нужно выполнять какое-либо разбиение области.

 Изобразить на чертеже данное тело и область интегрирования.
Изобразить на чертеже данное тело и область интегрирования.
 Только имеет 2 значения, , под интегралом будет их разность, т.е.
Только имеет 2 значения, , под интегралом будет их разность, т.е. 05.2013, 14:55
05.2013, 14:55  Будет тот же самый треугольник, только не , а . А теперь просуммируйте все сечения, умножив их на толщину , получите объём.
Будет тот же самый треугольник, только не , а . А теперь просуммируйте все сечения, умножив их на толщину , получите объём.
 05.2013, 23:28
05.2013, 23:28 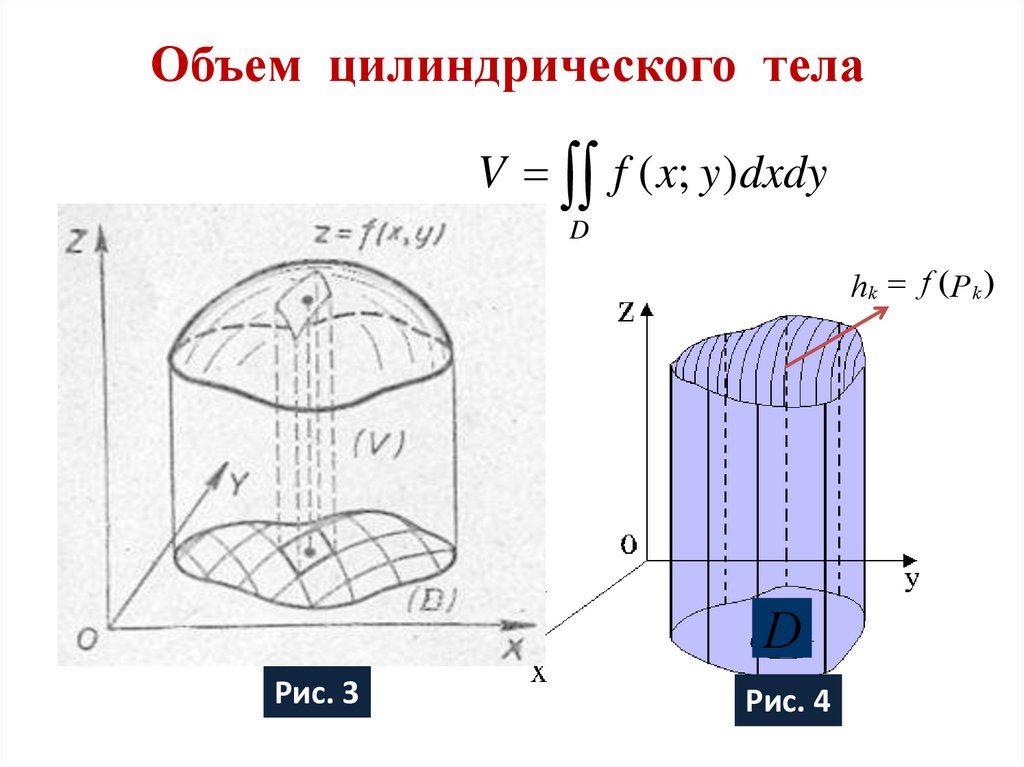 05.2013, 15:17
05.2013, 15:17 