Вычисление двойного интеграла. Двукратный интеграл — Мегаобучалка
При вычислении двойного интеграла элемент площади нам удобно представить в ином виде. Будем разбивать область интегрирования D в плоскости Oxy на частичные области посредством двух систем координатных линий: x=const, y=const. Этими линиями служат прямые, параллельные соответственно оси Oy и оси Ox, а частичными областями — прямоугольники со сторонами, параллельными осям координат. Ясно, что площадь каждой частичной области будет равна произведению соответствующих и . Поэтому элемент площади мы запишем в виде т.е. элемент площади в декартовых координатах является произведением дифференциалов независимых переменных. Мы имеем
. (*)
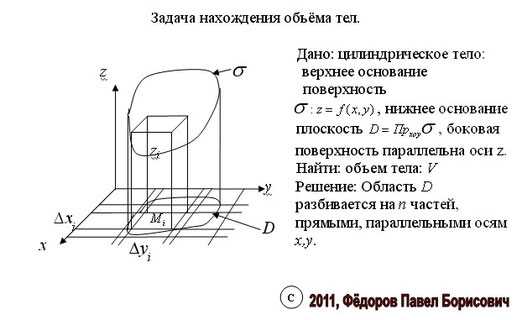
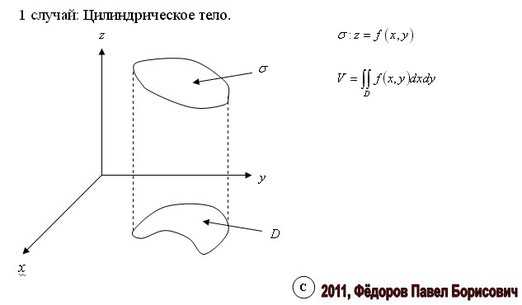
При вычислении двойного интеграла (*) мы будем опираться на тот факт, что он выражает объём V цилиндрического тела с основанием D, ограниченного поверхностью . Напомним, что мы уже занимались задачей об объёме тела, когда рассматривали применения определённого интеграла к задачам геометрии и получили формулу
(**)
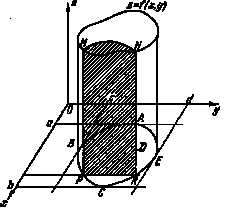
Рис.3
где S(х) — площадь поперечного сечения тела плоскостью, перпендикулярной к оси абсцисс, а и — уравнения плоскостей, ограничивающих тело. Применим теперь эту формулу к вычислению двойного интеграла
Предположим сначала, что область интегрирования D удовлетворяет следующему условию: любая прямая, параллельная оси Ox или Oy, пересекает границу области не более чем в двух точках. Соответствующее цилиндрическое тело изображено на рис.3
Область D заключим внутрь прямоугольника
стороны которого касаются границы области в точках А, В, С, Е. Интервал [а, b] является ортогональной проекцией области D на ось Ох, а интервал [c, d] — ортогональной проекцией области D на ось Oy. На рис.5 область D показана в плоскости Оху.
Точками A и C граница разбивается на две линии: ABC и AEC, каждая из которых пересекается с любой прямой, параллельной оси Oy, в одной точке. Поэтому, их уравнения можно записать в форме, разрешенной относительно y:
(ABC),
(AEC).
Аналогично точками В и Е граница разбивается на линии ВАЕ и ВСЕ, уравнения которых можно записать так:
(BAE),
(BCE).
Двукратный интеграл
Двукратный (повторный) интеграл . Пусть D — область, простая в направлении оси Oy. Рассмотрим выражение . Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная) и подстановки по у в пределах от до получается функция, зависящая только от х, которая интегрируется в пределах от a до b. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:
.
Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:
Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь областиD: ;
теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться — это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область D разбита на две подобласти D1 и D2 прямой, параллельной одной из координатных осей, то двукратный интеграл по области D равен сумме интегралов по D1 и D2: J(D) = J(D1) + J(D2).
Первый случай: прямая x = a1 параллельна оси Oy. Тогда
megaobuchalka.ru
ЛЕКЦИИ по теме: КРАТНЫЕ ИНТЕГРАЛЫ
ПОНЯТИЕ ДВОЙНОГО ИНТЕГРАЛА


ПОНЯТИЕ ДВУКРАТНОГО ИНТЕГРАЛА


СВОЙСТВА ДВУКРАТНОГО ИНТЕГРАЛА




ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА

ЗАМЕНА ПЕРЕМЕННЫХ в ДВОЙНОМ ИНТЕГРАЛЕ



ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА через ДВОЙНОЙ ИНТЕГРАЛ

ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ через ДВОЙНОЙ ИНТЕГРАЛ
ПОНЯТИЕ ТРОЙНОГО ИНТЕГРАЛА



ПОНЯТИЕ ТРЕХКРАТНОГО ИНТЕГРАЛА





ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕГРАЛЕ

ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА В ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ



 СЛАЙДЫ
СЛАЙДЫ30_ЛЕКЦИИ Кратные интегралы.pdf
Adobe Acrobat Document 2.0 MB
ФАЙЛ
11 Лекции по кратным интегралам.pdf
Adobe Acrobat Document 855.1 KB
fedorovkniga.jimdo.com
25. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
Основные свойства двойного интеграла:
Свойство аддитивности:
Свойства линейности:
а)
б)
Модуль интеграла меньше или равен интегралу от модуля:
Теорема о среднем. Так как
то, проинтегрировав это неравенство, получим:
Где
Сведение двойного интеграла к повторному.
Теорема. Если функция f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и если и существует интеграл, тогда существует повторный интеграли он равен двойному:=.
Замечание. Если f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и и существует интегралтогда существует повторный интеграл.
Предположим, что область D произвольного вида. Делаем разбиение и проводим параллельные линии. Заключим область (D) в прямоугольник (D*), , и в нём определим функцию f*(x,y):.
Формула в общем виде: . Так же доказывается, что
Тройной интеграл, сведение его к повторному.
Определение тройного интеграла. Пусть в некоторой области (V) с границей (S) задана в каждой точке функция f(x,y,z). Разобьём тело (V) сеткой поверхностей на частичные области (Vi). В каждой (Vi) возьмём произвольную точку (ξi, ηi, ζi) и составим интегральную сумму:. Устремим максимальный диаметр (макс. расстояние между любой парой точек в области) к нулю:. Тогда, если существует предел интегральных сумм, то он равен тройному интегралу:.
На всякий случай определение интегральной суммы. Пусть на нек-ом отрезке задана. Произведём разбиение отрезка:. Число, называется интегральной суммой функции f(x), соответствующей данному разбиению T(ξi;xi) сегмента [a;b] и данному выбору промежуточных точек ξi на частичных сегментах [xi-1;xi], Δ –хар-тика разбиения:
Сведение к повторному интегралу. Рассмотрим первый простейший случай. Пусть тело V – прямоугольный параллелепипед. Проведём секущую плоскость. Возьмём приращение плоскости (жирные линии). Тогда:.
Рассмотрим второй случай.
Рассмотрим третий случай – область (V) цилиндрического типа.
26. Замена переменных в двойном интеграле. Пример: случай полярных координат.
Вычислим интеграл , используя замену переменных. Рассмотрим интеграл как предел интегральных сумм. Область (D) сеткой кривых разделяется на частичные области Di, внутри каждой частичной области берём произвольные точки (xi, yi). Составляем интегральную сумму:, где Di – площадь i-ой частичной области. Устремим максимальный диаметр к нулю:. По определению,. Совершим замену переменных (*). При замене (*) площадь.
Если , тои, следовательно,
– якобиан преобразования (*).
Пример с полярными координатами.
studfiles.net
3.3. Двойной и тройной интегралы.
Двойной интеграл. Пусть функцияf(x, y)определена в замкнутой ограниченной областиDв плоскостихОу. Разобьем областьDнаnэлементарных областей, имеющих площадиS1, S2,…,Sn
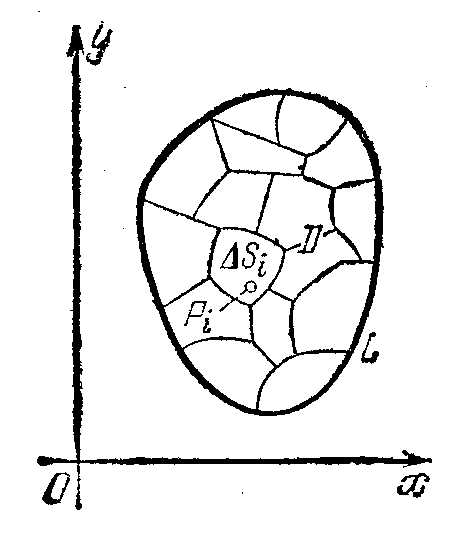
Рис. 7.1
называется сумма вида (7.1).
При f(x, y) 0каждое слагаемое можно рассматривать как объем малого цилиндра с основаниемSiи высотойf (i, i), а сумму – как объем некоторого “ступенчатого” тела (геометрическая интерпретация). Способы разбиения областиDна элементарные могут быть различны, однако, если максимальный диаметр (диаметр наибольшей элементарной области) стремится к нулю (при этомn ), то справедлива следующая теорема:
Если функция f(x, y) непрерывна в замкнутой области D, то предел интегральной суммы (7.1) при max di 0 существует и не зависит ни от способа разбиения области D на элементарные, ни от выбора точек внутри элементарных областей(теорема существования двойного интеграла). Этот предел называется двойным интегралом от функцииf(x, y) по областиD и
обозначается так: (7.2).
Область Dназывается областью интегрирования. Еслиf(x, y) 0в областиD, то двойной интегралчисленно равен объему цилиндрического тела, ограниченного сверху поверхностьюz = f(x, y), сбоку цилиндрической поверхностью с образующими, параллельными осиОz(направляющая- граница областиD), и снизу областьюDплоскостихОу.
Основные свойства двойного интеграла определяются теоремами:
1. Двойной интеграл от суммы функций (х,у) и f(x, y) по области D равен сумме двойных интегралов по области D от каждой из функций, т.е.
(7.3)
2. Постоянный множитель можно вынести за знак двойного интеграла, т.е. если C = const, то (7.4).
3.
Если область D разбита на две области D1 и D2 без общих внутренних 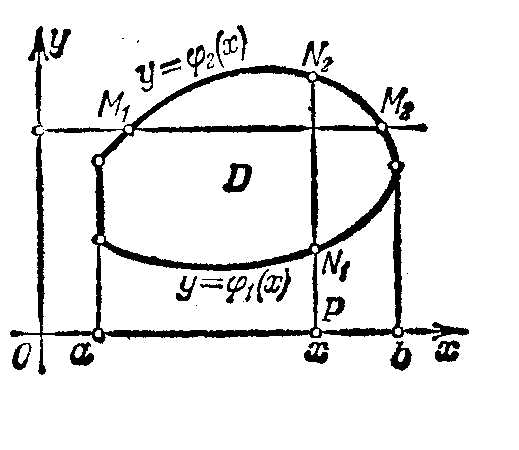
точек, то (7.5).
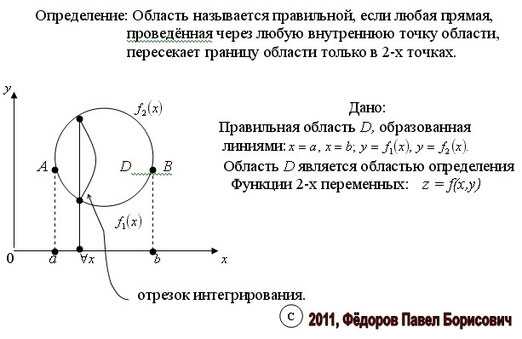
Вычисление двойного интеграла. Пусть областьDтакова, что всякая прямая, проходящая через внутреннюю точку области параллельно одной из осей координат пересекает границу области не более чем в двух точках (рис.7.2.). Если при этом областьDограничена линиямиу = 1(х), у = 2(х), х =а, х = b,причем1(х) 2(х),а < b, а функции1(х)и2(х)непрерывны на отрезке[a, b], то область называютправильной в направлении осиОу. Аналогично определяется область правильная в направлении осиОх. Область, правильную в направлении обеих осей, называют простоправильной.
Рис.7.2
Для вычисления двойного интеграла по правильной области используется разновидность определённого интеграла по плоской области Dназываемаядвукратным интегралом и определяемая выражением:
(7.6)
В этом выражении сначала вычисляется интеграл по dy(«внутренний» интеграл, стоящий в скобках),при этомх считаетсяпостоянной. В результате получится непрерывная (доказательство не приводим) функция отх:. Эта функция интегрируется похв пределах отадоb:.
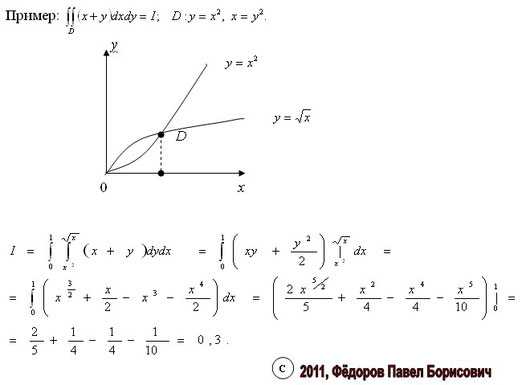
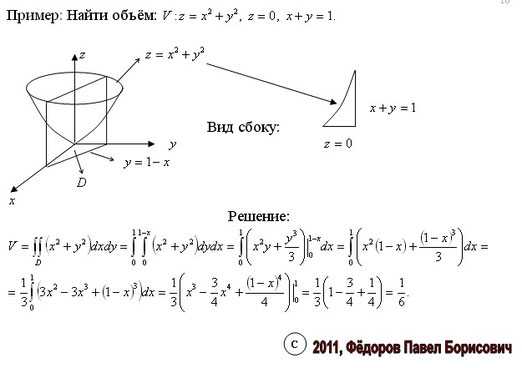
Пример: вычислить (ОбластьDпредставляет собой треугольник: а = 0;b= 1;1(x) = 0 и2(x) = х2). Вычислим
и затем.
Основные свойства двукратного интеграла:
1. Если правильную в направлении оси Оу(Ох) область D разбить на две области D1 и D2 прямой, параллельной оси Оу(Ох) то двукратный интеграл ID по области D будет равен сумме таких же интегралов по областям D1 и D2, т.е. ID = ID1 + ID2.
Следствие: двукратный интеграл по области D равен сумме двукратных интегралов по частичным областям, т.е. ID = I D1 + I D2 + … +I Dn (области Di выбором границ можно сделать правильными в направлении оси Оу(Ох)).
2. (Оценка двукратного интеграла). Если m и М наименьшее и наибольшее значения функции f(x, y) в области D и S – площадь области D, то справедливо неравенство .
3. (Теорема о среднем) Двукратный интеграл от непрерывной функции f(x, y) по области D с площадью S равен произведению полощади S на значение функции в некоторой точке Р области D т.е. .
Свойства двукратного интеграла позволяют доказать теорему, открывающую путь к вычислению двойного интеграла: Двойной интеграл от непрерывной функцииf(x, y)по областиDравен двукратному интегралу от этой функции по областиD т.е. (7.7)
(Полагаем область Dправильная по осиОуи ограничена линиямиу = 1(х), у = 2(х), х =а, х = b).
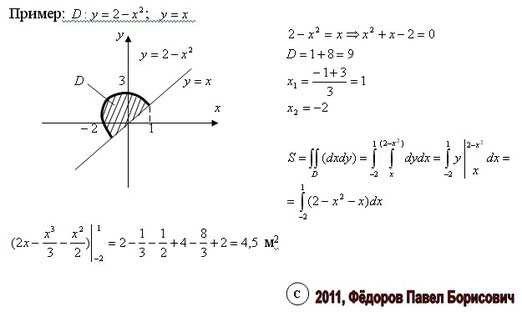
Пример: Вычислить , если областьDограничена линиями у = 1 – х2, у = 2х, х = – 2, х = 0. Построим областьD(рис.7.3). Очевидно, она правильная в направлении оси Оу и искомый интеграл равен двукратному интегралу
Отметим, что если областьDправильная в направлении осиОхи ограничена линиямих = 1(у), х = 2(у), у = с, у = dпричем1(у) 2(у), то
(7.8).
Таким образом, двойной интеграл может быть вычислен по формулам (7.7) или (7.8). Пример: Изменить порядок интегрирования в интеграле . Область интегрирования ограничена прямой у = х и параболой(рис.7.4) и, очевидно, правильная, т.е. интеграл можно вычислить и по формуле (7.8)
полагая у2=1(у), у =2(у), с = 0,d= 1
откуда .
В случае, когда область Dне является правильной ни по одной из осей, двойной интеграл по этой области представить в виде двукратного нельзя. Однако, если областьDразбить на частичные, правильные в направлении той или иной оси, то двойной интеграл по областиDможно представить в виде суммы двойных интегралов по этим областям, а каждое слагаемое – в виде двукратного интеграла по соответствующей частичной области.
Вычисления с помощью двойного интеграла.
1. Объем.Напомним, что объемVтела, ограниченного сверху поверхностьюz = f(x, y)( f(x, y) 0), снизу – плоскостьюz = 0, а сбоку – цилиндрической поверхностью, направляющей для которой служит граница областиD, а образующая параллельна осиOz, определится соотношением
(7.9).
1.1. Если тело ограничено сверху поверхностью z = f1(x, y) 0, снизу – поверхностьюz = f2(x, y) 0, причем проекцией обеих поверхностей на плоскостьхОуявляется областьD, то объемVэтого тела равен разности объемов двух цилиндрических тел: оба имеют нижним основанием областьD, а верхним – поверхностиz = f1(x, y) 0для первого иz = f2(x, y) 0для второго,
(7.10)
Формула (7.10) верна и тогда, когда f1(x, y)иf2(x, y)– любые непрерывные функции, удовлетворяющие неравенствуf1(x, y) f2(x, y).
1.2. Если в области Dфункцияf(x, y)меняет знак, то следует разбить область на две части:D1, гдеf(x, y) 0иD2, гдеf(x, y) 0. Если областиD1иD2таковы, что двойные интегралы по ним существуют, то первый будет равен объему тела, лежащего выше плоскостихОу, а второй – объему тела, лежащего ниже плоскостихОу.
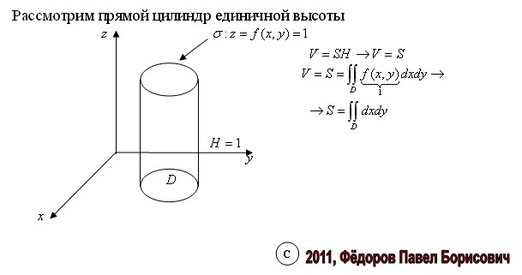
2. Площадь плоской области. Площадь областиDв плоскостихОучисленно равна объему рассмотренного цилиндра, ограниченного сверху в нашем случае поверхностьюz = f(x, y) = 1, т.е.или, если областьDправильная(7.11).
3. Площадь поверхности, заданной уравнениемz = f(x, y)и ограниченной некоторой замкнутой линиейС. Проекцию этой линии на плоскостьхОуобозначим черезL, а область, ограниченную линиейL,обозначим черезD. Если функцияf(x, y)непрерывна и имеет непрерывные частные производные в этой замкнутой области, то искомая площадь поверхности определится выражением(7.12).
С помощью двойного интеграла можно решить и целый ряд “физических” задач: вычисление массы плоских пластин с известной поверхностной плотностью = f(x, y), момента инерции плоской фигуры и т.д.
Тройной интеграл. Пусть в декартовых трехмерных координатах задана «объемная» областьV, ограниченная замкнутой поверхностьюSи пусть в каждой точке этой области, включая границу, определена непрерывная функцияf(x, y, z). Разобьем областьVпроизвольным образом на малые области (объемы)Vi, выберем в каждой произвольную точкуРi(xi, yi, zi)и составиминтегральную сумму вида. Устремляя максимальный диаметрmaxdi(и, соответственно, объемVi) к нулю(maxdi 0)перейдем к пределу интегральной суммы. При условиях, перечисленных выше, этот предел существует и называется тройным интегралом:
(7.13).
где dxdydz = dVэлемент объема в декартовых координатах. Еслиf(x, y, z) 0описывает плотность распределения вещества в объемеV, то (7.13) даст массу этого вещества.
Если: 1. Всякая прямая, параллельная оси Оzи проходящая через внутреннюю точку областиV, пересекает поверхностьSв двух точках;
2. Область Vпроектируется на плоскостьхОув правильную двумерную областьD; 3. всякая часть областиV, отсеченная плоскостью, параллельной одной из координатных обладает свойствами 1. и 2. – областьVназываютправильной.
Введем понятие трехкратного интеграла Ivпо областиVот функцииf(x, y, z)определенной и непрерывной в этой области. Пустьz = 1(x,y)иz = 2(x,y)уравнения поверхностей, ограничивающиxобластьVснизу и сверху (вместе они описывают замкнутую поверхностьS), а областьD– проекцияVна плоскостьxОу– ограничена линиямиу = 1(х), у = 2(х), х = а, x = b.
Трехкратный интегралIvопределяется выражением:
(7.14)
При интегрировании по zпеременныехиусчитаем постоянными. После интегрирования поzи подстановки пределов получаем двукратный интеграл, рассмотренный в предыдущем разделе. Трехкратный интеграл обладает свойствами, аналогичными свойствам двукратного: 1.Если область V разбить на две областии V1 и V2 плоскостью, параллельной одной из координатных, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V1 и V2. (При любом разбиении областиVна конечное числоV1, V2,…,Vnплоскостями, параллельными координатным, справедливо равенство:IV = IV1 + I V2 + … +IVn). 2.Если m и М – наименьшее и наибольшее значения функции f(x, y, z) в области V, то справедливо неравенство mV Iv MV, где V – объем области, Iv – трехкратный интеграл от f(x, y, z) по области V.
3. (теорема о среднем) Трехкратный интеграл Iv от непрерывной функции f(x, y, z) по области V равен произведению ее объема V на значение
функции в некоторой точке Р области V:
Приведенные свойства трехкратного интеграла позволяют доказать теорему о вычислении тройного интеграла:
Тройной интеграл от функции f(x, y, z) по правильной области V равен трехкратному интегралу по этой же области:
(7.15)
(Как и в случае двукратного интеграла, можно изменить порядок интегрирования, если это позволяет сделать форма области V. Можно с этой целью разбить областьVна части).
Если подинтегральная функция f(x, y, z) = 1, то тройной интеграл по областиVдает значение ее объема(7.15`).
Пример: , если областьVопределяется неравенствами: 0х½, ху2х, 0z(т.е. а = 0,b= ½,1(x) =x,2(x) = 2x,1(x,y) = 0,2(x,y) =, областьVпредставляет собой часть сферы единичного радиуса с центром в начале координат, ограниченную снизу плоскостью хОу(z= 0), а «с боков» плоскостями у = х и у = 2х).
Нередко вычисление тройных интегралов значительно упрощается при переходе к цилиндрическимилисферическимпространственным координатам.
В цилиндрических координатахположение точкиРопределяется тремя числами, , z,гдеи– полярные координаты проекции точкиРна плоскостьхОу, аz– аппликата точкиР. Пространственную областьVразбивают на элементарные координатными поверхностями = i, = j, z = zk.Элементарный объемdVпримет вид:dV = dddz, а тройной интеграл:, пределы интегрирования в соответствующем трехкратном интеграле определятся формой областиV. Зная формулы связи:
х = cos, y = sin, z = zнесложно перейти от декартовых координат к цилиндрическим:.
Пример: , если областьVограничена цилиндром х2+ у2= 2х и плоскостями у = 0,z= 0,z=a. Перейдем к цилиндрическим координатам. Уравнение цилиндра примет вид2cos2+2sin2= 2cos=>2(cos2+sin2) = 2cos=>= 2cos. ОбластьVопределяется неравенствами: 02cos, 0/2, 0zа и
В сферических координатахположение точкиРопределяется числами,, , где– расстояние точки от начала координат,– угол междуи осьюОzи– угол между проекциейна плоскостьхОуи осьюОх(отсчитывается, как обычно, от осиОхпротив часовой стрелки). Декартовы координаты связаны со сферическими так:х = sincos, у = sinsin, z = cos (0 , 0 2, 0 ). Элемент объема в сферических координатахdV = 2sinddd. В итоге можем перейти от тройного интеграла в декартовых координатах к тройному интегралу в сферических координатах.
Пример: , если областьV– верхняя половина шараx2+y2+z2r2. Перейдя к сферическим координатам получим: 0r, 02, 0/2,x2+y2=2sin2cos2+2sin2sin2=2sin2и
studfiles.net
16. Кратные, криволинейные, поверхностные интегралы.
16.1. Двойной интеграл.
16.1.1.
Определение двойного интеграла. Теорема
существования двойного интеграла. Пусть
на плоскости Oxy задана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на
области D определена функция 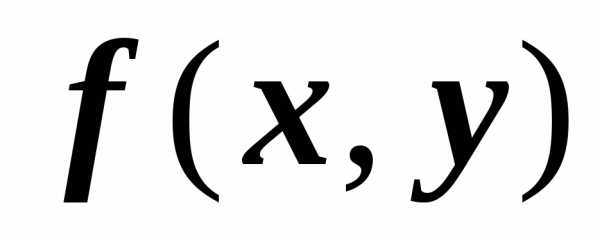 .
.
Разобьём область D произвольным образом на  подобластей
(не имеющих общих внутренних точек).
Символом
подобластей
(не имеющих общих внутренних точек).
Символом 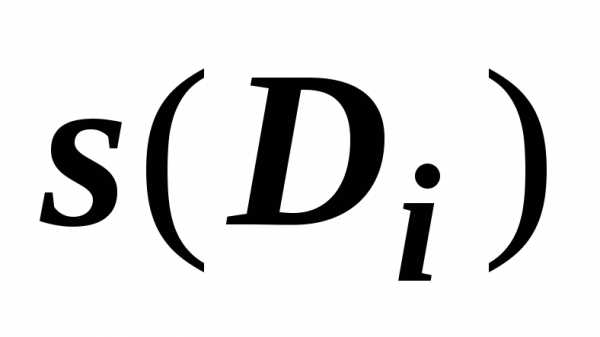 будем обозначать площадь области
будем обозначать площадь области 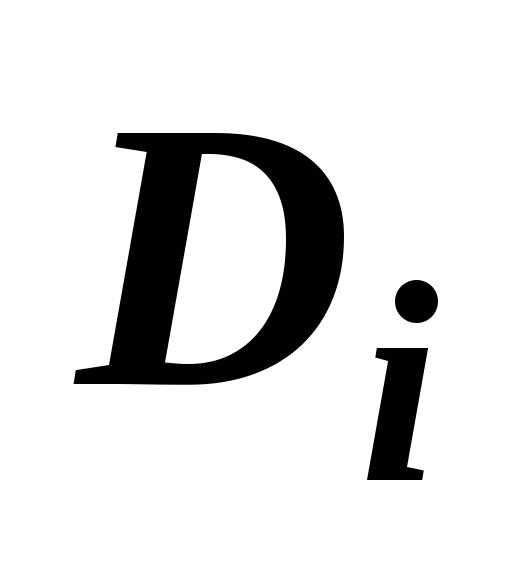 ;
символом
;
символом 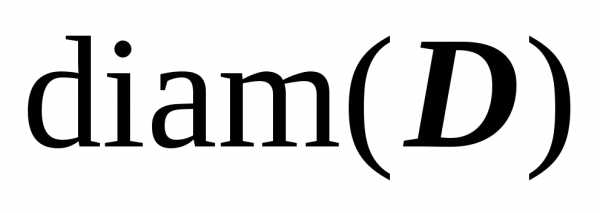 здесь и дальше будет обозначаться
наибольшее расстояние между двумя
точками, принадлежащими области D:
здесь и дальше будет обозначаться
наибольшее расстояние между двумя
точками, принадлежащими области D:
;
символом  обозначим наибольший из диаметров
областей
обозначим наибольший из диаметров
областей 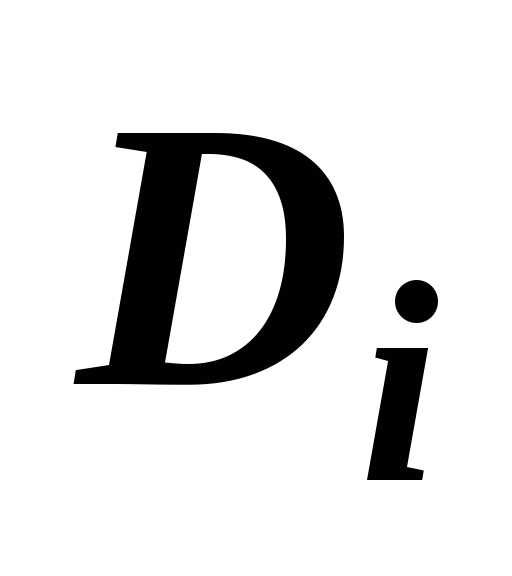 :
.
:
.
В каждой из
подобластей
выберем произвольную точку ,
вычислим в этой точке значение функции
,
и составим интегральную сумму 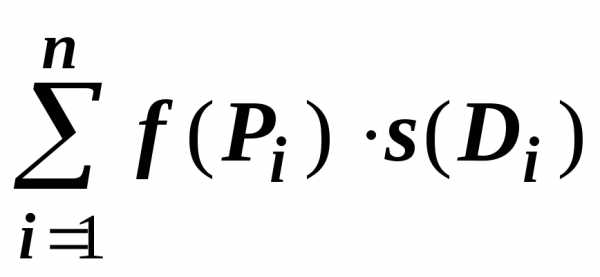 .
.
Если существует
предел последовательности интегральных
сумм при ,
не зависящий ни от способа разбиения
области D на подобласти 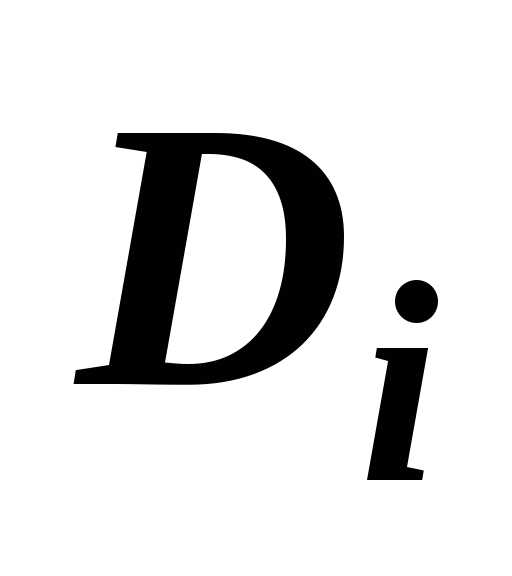 ,
ни от выбора точек
,
ни от выбора точек 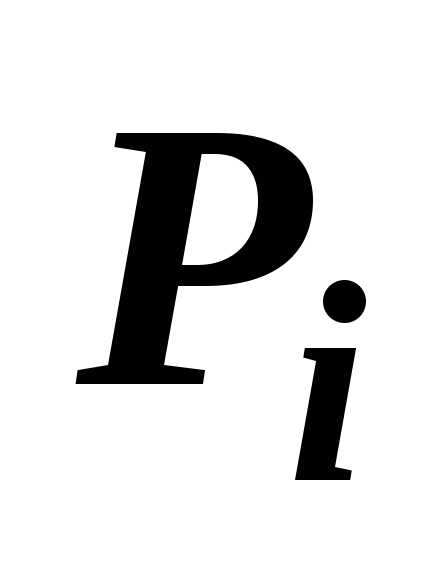 ,
то функция
,
то функция 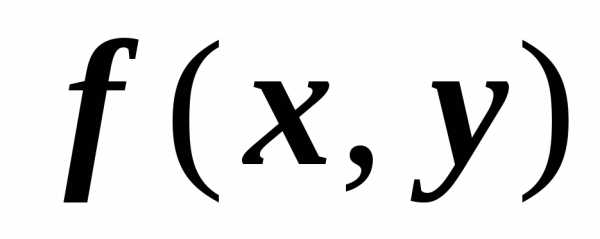 называется интегрируемой по области D,
а значение этого предела называется
двойным интегралом от функции
называется интегрируемой по области D,
а значение этого предела называется
двойным интегралом от функции 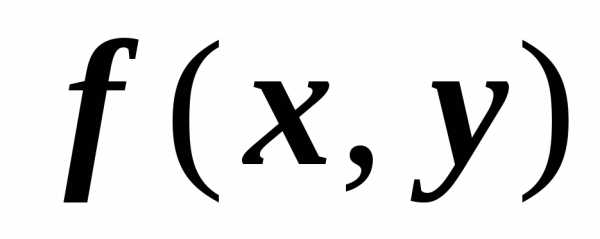 по области D и обозначается
по области D и обозначается 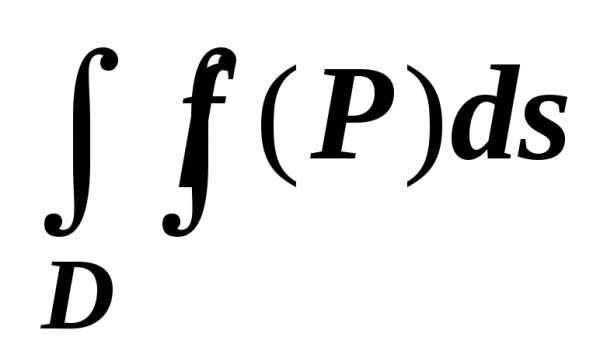 .
.
Если расписать
значение 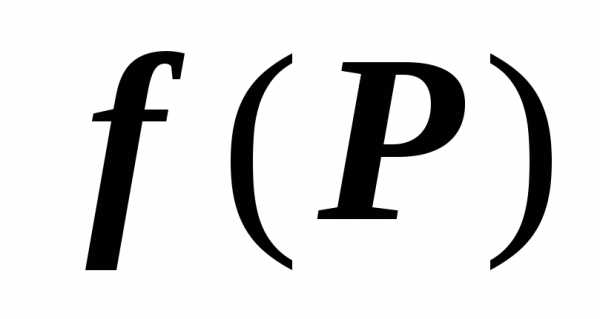 через координаты точки
через координаты точки 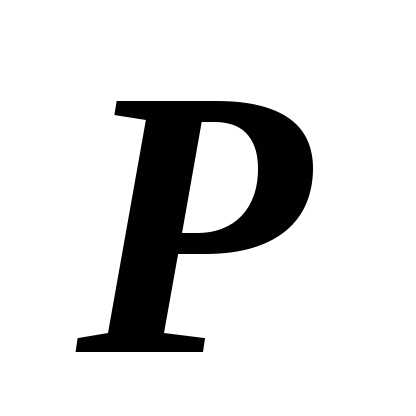 ,
и представить
,
и представить  как ,
получим другое обозначение двойного
интеграла:
как ,
получим другое обозначение двойного
интеграла: 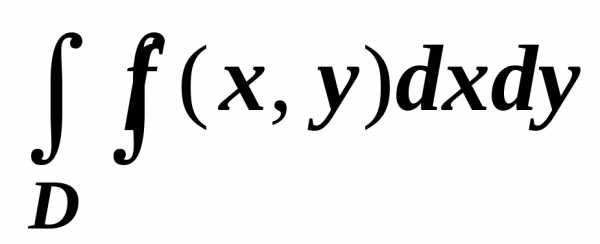 .
Итак, кратко,
.
.
Итак, кратко,
.
Теорема
существования двойного интеграла. Если
подынтегральная функция 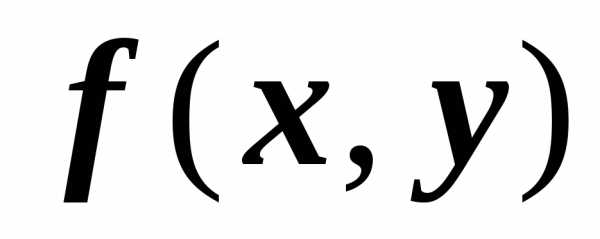 непрерывна на области D,
то она интегрируема по этой области.
непрерывна на области D,
то она интегрируема по этой области.
16.1.2. Геометрический
смысл двойного интеграла. Геометрический
смысл каждого слагаемого интегральной
суммы: если
,
то
— объём прямого цилиндра с основанием 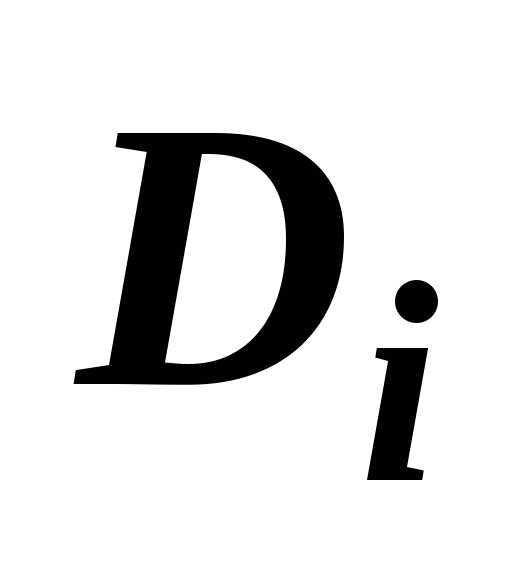 высоты
высоты 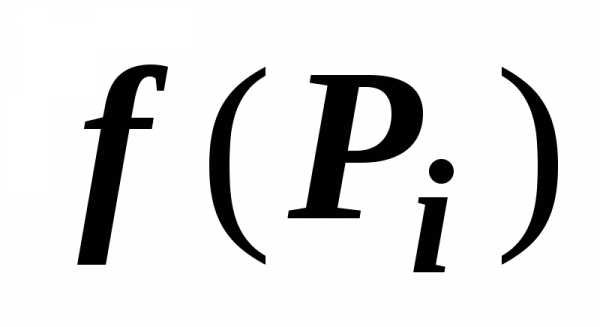 ;
вся интегральная сумма
;
вся интегральная сумма 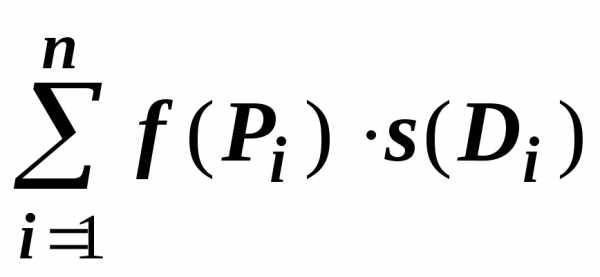 — сумма объёмов таких цилиндров, т.е.
объём некоторого ступенчатого тела
(высота ступеньки, расположенной над
подобластью
— сумма объёмов таких цилиндров, т.е.
объём некоторого ступенчатого тела
(высота ступеньки, расположенной над
подобластью 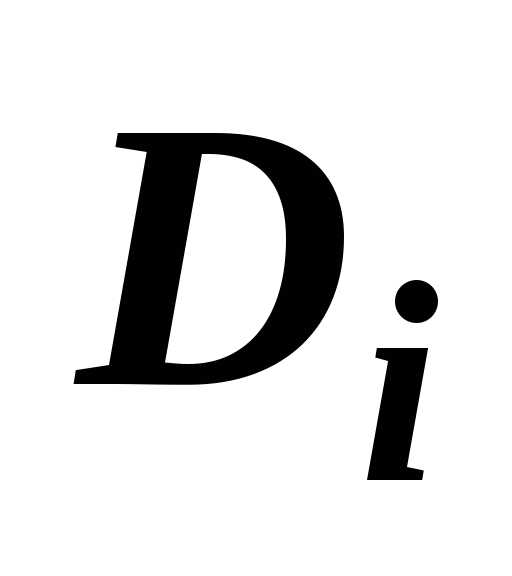 ,
равна
,
равна 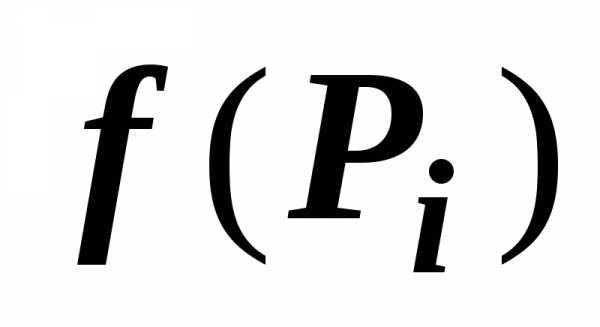 ).
Когда ,
это ступенчатое тело становится всё
ближе к изображенному на рисунке телу,
ограниченному снизу областью
).
Когда ,
это ступенчатое тело становится всё
ближе к изображенному на рисунке телу,
ограниченному снизу областью  ,
сверху — поверхностью ,
с цилиндрической боковой поверхностью,
направляющей которой является граница
области
,
сверху — поверхностью ,
с цилиндрической боковой поверхностью,
направляющей которой является граница
области 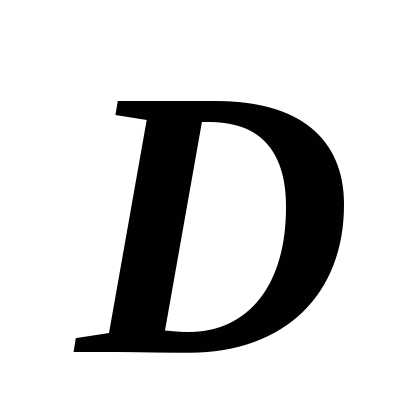 ,
а образующие параллельны оси
,
а образующие параллельны оси  .
Двойной интеграл
.
Двойной интеграл 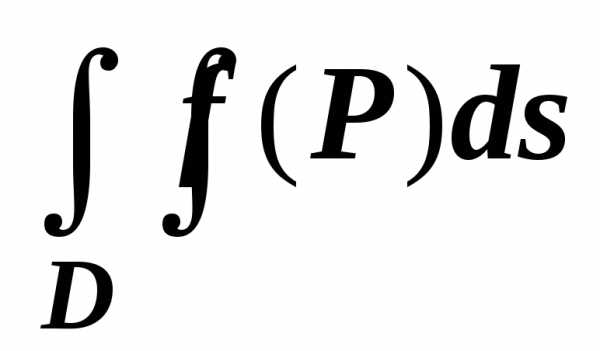 равен объёму этого тела.
равен объёму этого тела.
16.1.3. Свойства двойного интеграла.
16.1.3.1. Линейность. Если функции
 ,
,  интегрируемы по области
интегрируемы по области  ,
то их линейная комбинация
тоже интегрируема по области
,
то их линейная комбинация
тоже интегрируема по области  ,
и
.
,
и
.
Док-во. Для интегральных сумм справедливо равенство . Переходя к пределу при и пользуясь свойствами пределов, рассмотренными в разделе 4.4.6. Арифметические действия с пределами (конкретно, свойствами 4.4.10.1 и 4.4.10.2), получим требуемое равенство.
16.1.3.2. Аддитивность. Если область 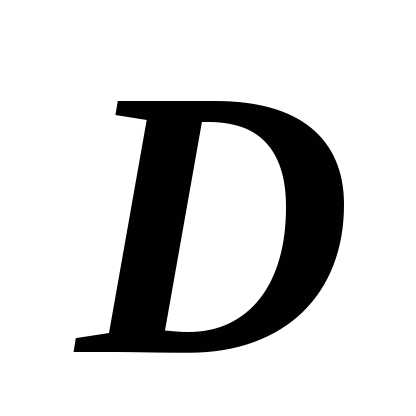 является объединением двух областей
является объединением двух областей 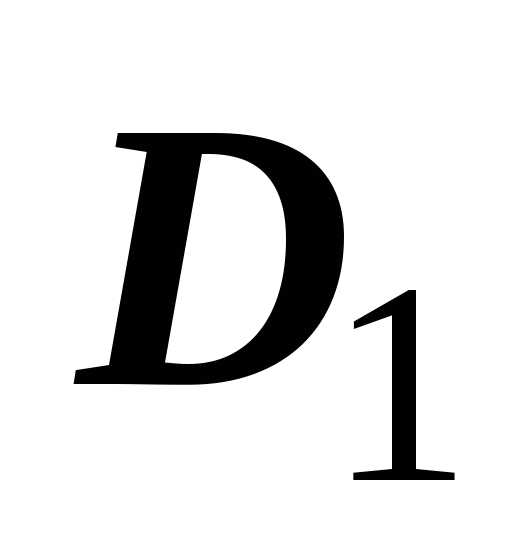 и ,
не имеющих общих внутренних точек, то .
и ,
не имеющих общих внутренних точек, то .
Док-во. Пусть
область 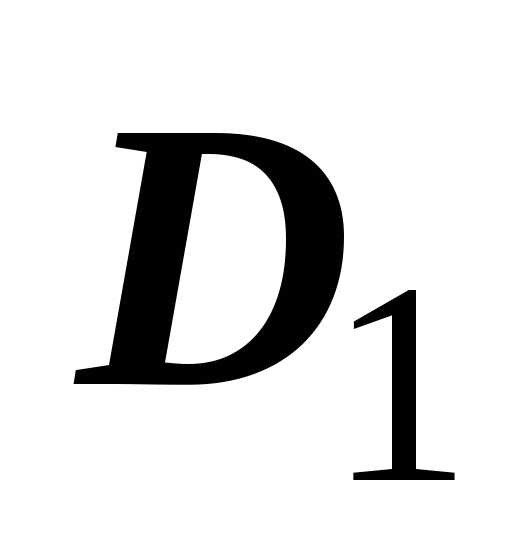 разбита на подобласти ,
область
разбита на подобласти ,
область 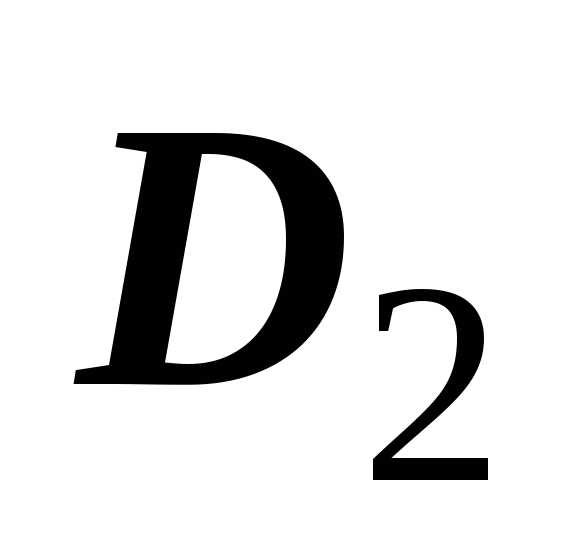 разбита на подобласти .
Тогда объединение этих разбиений даст
разбиение области
разбита на подобласти .
Тогда объединение этих разбиений даст
разбиение области 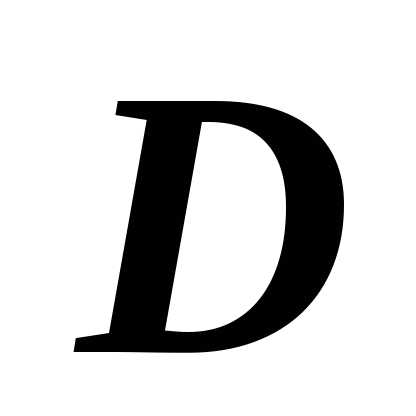 : на
: на 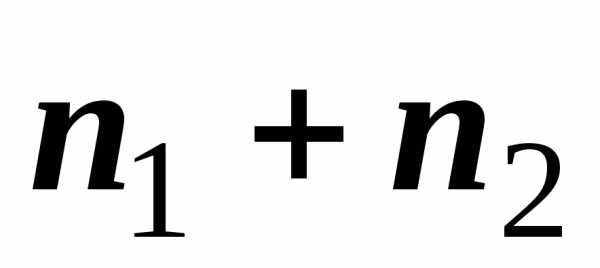 подобластей. Интегральная сумма по
области
подобластей. Интегральная сумма по
области 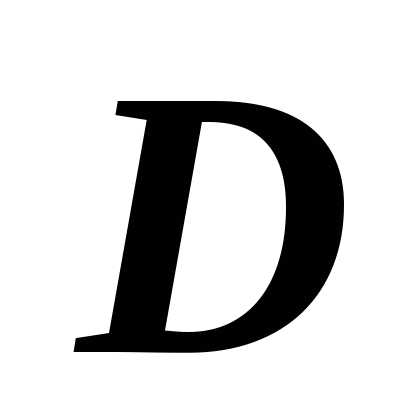 равна сумме сумм по областям
равна сумме сумм по областям 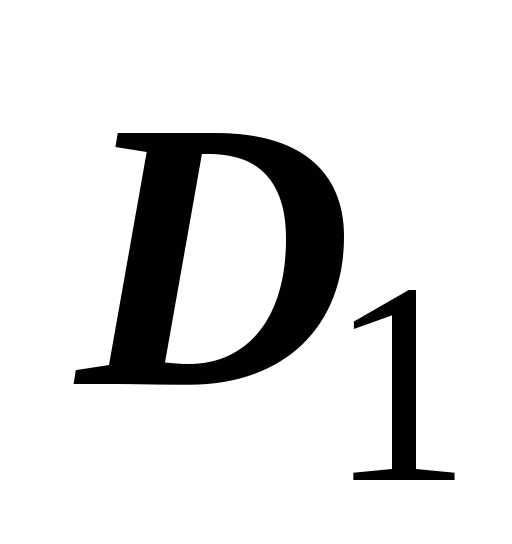 и
и 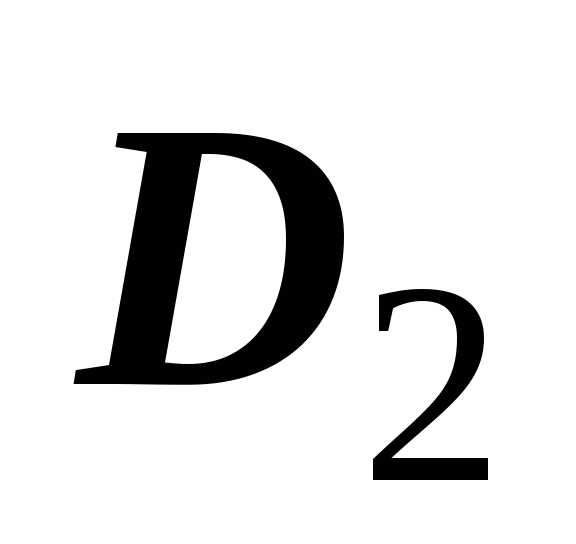 :
.
Как и в предыдущем случае, переходя к
пределу при ,
получим требуемое равенство.
:
.
Как и в предыдущем случае, переходя к
пределу при ,
получим требуемое равенство.
Интеграл от единичной функции по области
 равен
площади этой области:
равен
площади этой области:  .
.
Док-во: Для
любого разбиения 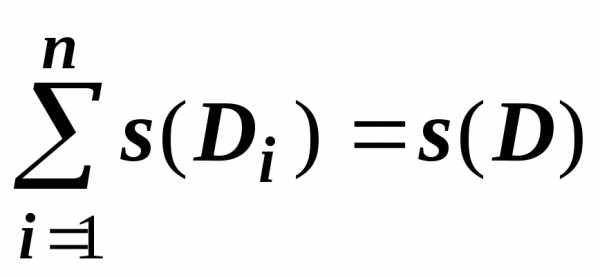 ,
т.е. не зависит ни от разбиения, ни от
выбора точек
,
т.е. не зависит ни от разбиения, ни от
выбора точек 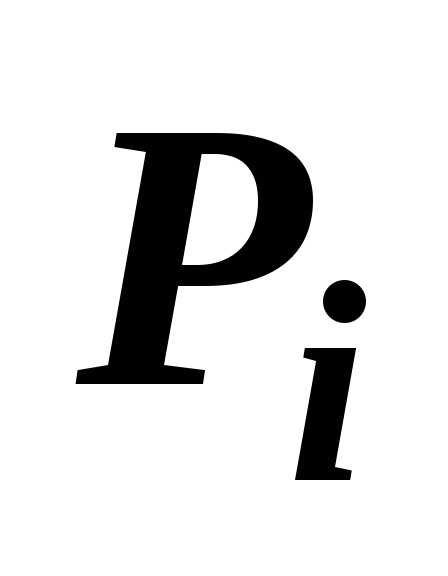 .
Предел постоянной равен этой постоянной,
поэтому
.
.
Предел постоянной равен этой постоянной,
поэтому
.
16.1.3.4. Интегрирование
неравенств. Если в любой точке  выполняется неравенство ,
и функции
интегрируемы по области
выполняется неравенство ,
и функции
интегрируемы по области 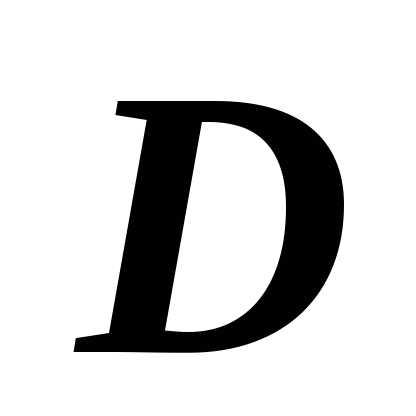 ,
то
.
,
то
.
Док-во. В любой точке 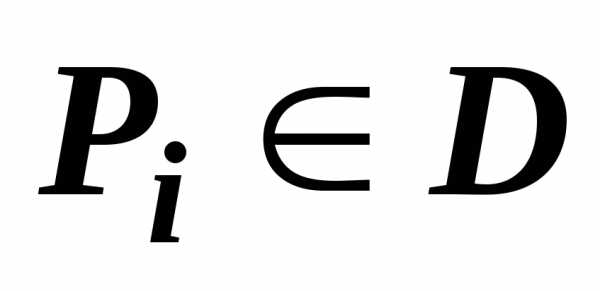 выполняется неравенство ,
поэтому .
По теореме о переходе к пределу в
неравенствах отсюда следует требуемое
утверждение.
выполняется неравенство ,
поэтому .
По теореме о переходе к пределу в
неравенствах отсюда следует требуемое
утверждение.
Теоремы об оценке интеграла.
16.1.3.5.1. Если функция 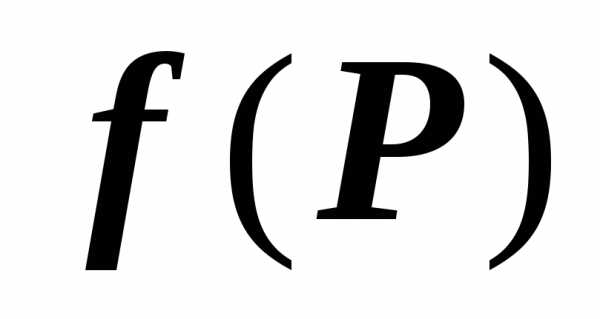 интегрируема по области
интегрируема по области  ,
и для
выполняется ,
то .
,
и для
выполняется ,
то .
Док-во. 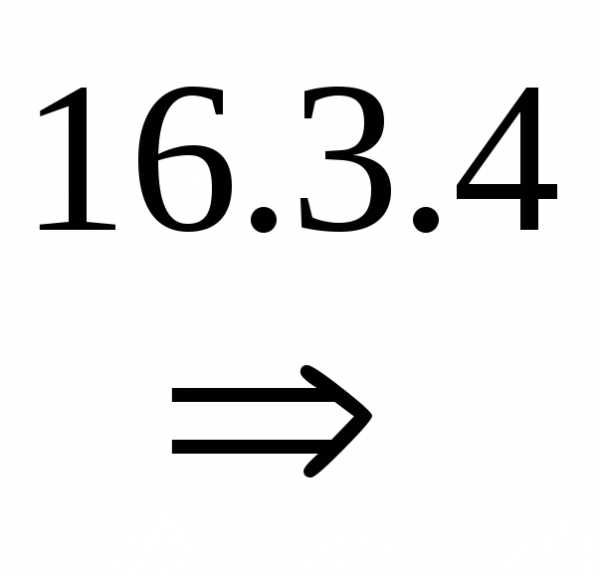
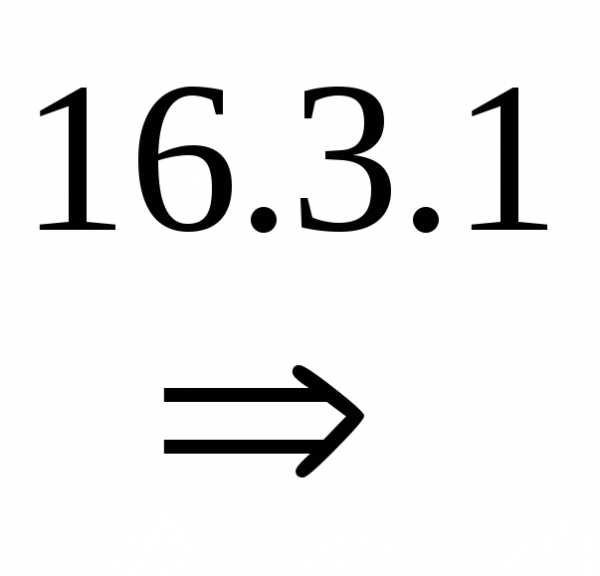
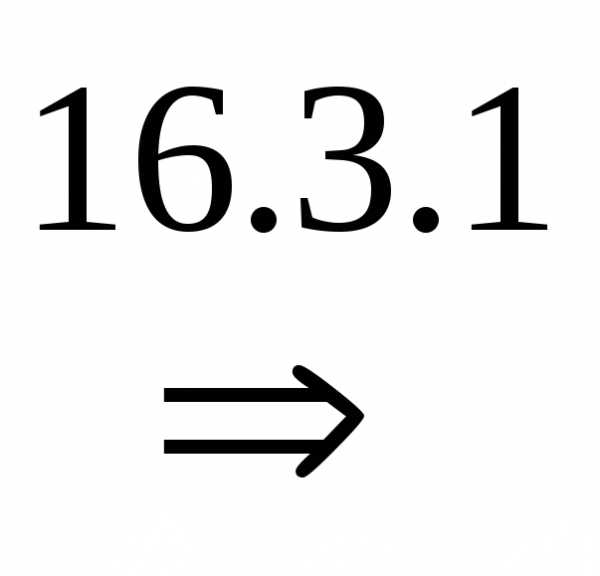
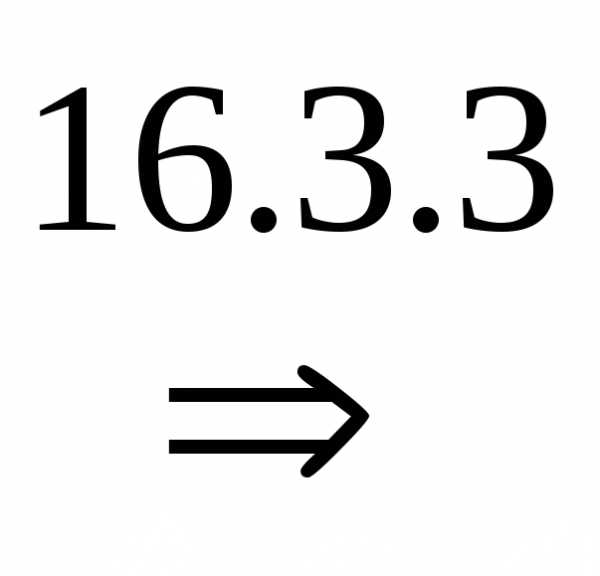 (цифрами над знаками импликации обозначены
номера применяемых ранее доказанных
свойств).
(цифрами над знаками импликации обозначены
номера применяемых ранее доказанных
свойств).
16.1.3.5.2. Если функция 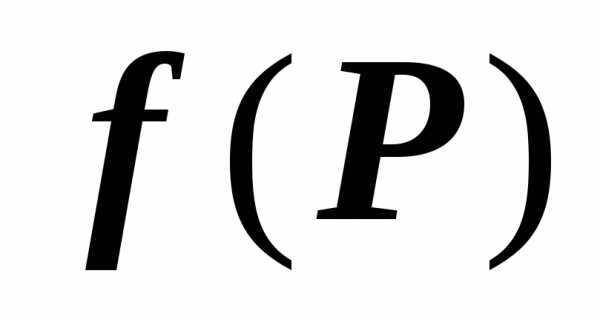 интегрируема по области
интегрируема по области  ,
то .
,
то .
Док-во. Эти неравенства непосредственно следуют из того, что и свойства 16.1.3.4. Интегрирование неравенств.
16.1.3.6. Теорема о
среднем. Если
функция 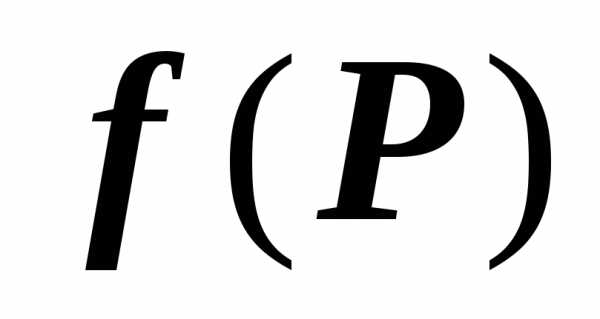 непрерывна на области
непрерывна на области  ,
то существует точка
,
то существует точка 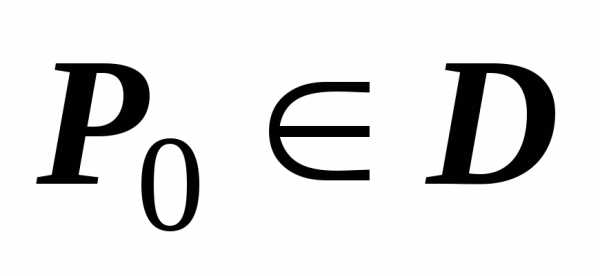 ,
такая что .
,
такая что .
Док-во. Непрерывная на ограниченной замкнутой
области  функция
функция 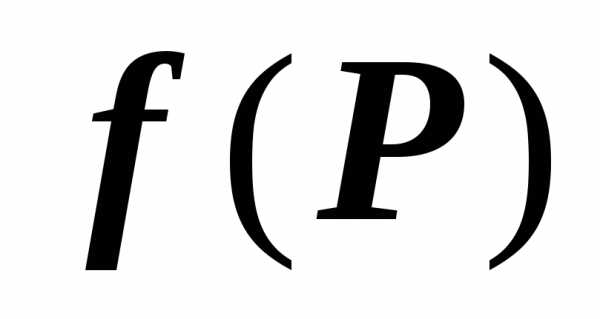 принимает в некоторых точках этой
области своё минимальное
принимает в некоторых точках этой
области своё минимальное  и максимальное
и максимальное  значения. Так как ,
то ,
или .
Непрерывная функция принимает, кроме
того, любое значение, заключённое между
значения. Так как ,
то ,
или .
Непрерывная функция принимает, кроме
того, любое значение, заключённое между 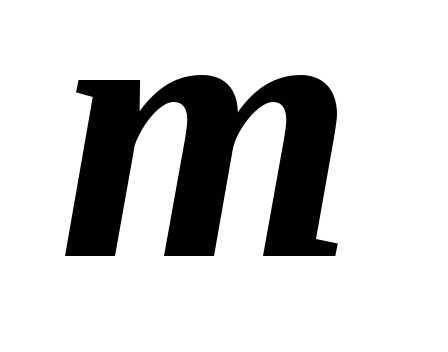 и
и 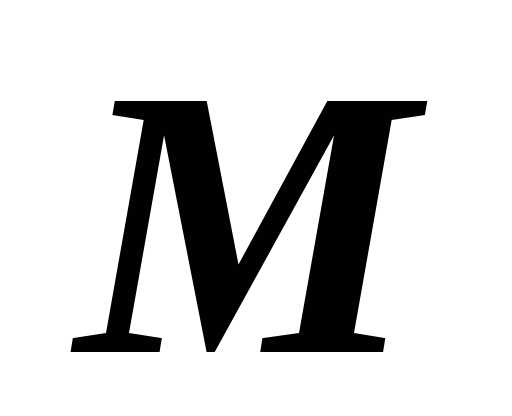 ,
в частности, значение
,
в частности, значение 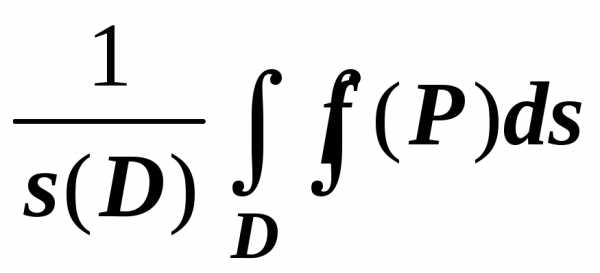 .
Следовательно, ,
откуда и следует доказываемое утверждение.
.
Следовательно, ,
откуда и следует доказываемое утверждение.
Вычисление двойного интеграла. Двукратный (повторный) интеграл.
Определение простой (правильной) области. Область
 на плоскости Oxy будем
называть простой
(правильной) в направлении оси Oy,
если любая прямая, проходящая через
внутреннюю точку области
на плоскости Oxy будем
называть простой
(правильной) в направлении оси Oy,
если любая прямая, проходящая через
внутреннюю точку области  и параллельная оси Oy,
пересекает границу
и параллельная оси Oy,
пересекает границу  в двух точках.
в двух точках.
Аналогично
определяется область, простая
(правильная) в направлении оси Ox:
любая прямая, проходящая через внутреннюю
точку области 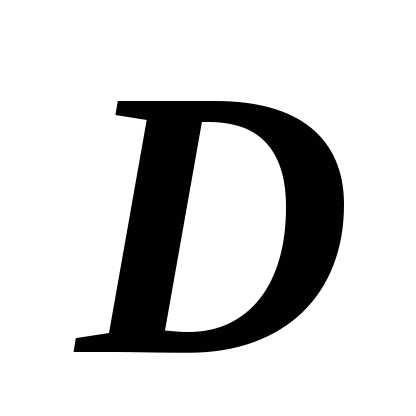 и параллельная оси Oх,
пересекает границу
и параллельная оси Oх,
пересекает границу  в двух точках.
в двух точках.
Область, правильную (простую) в направлении обеих осей, будем называть правильной.
О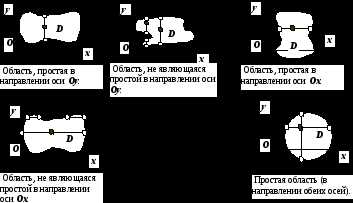 граниченную
замкнутую область
граниченную
замкнутую область ,
правильную в направлении оси Oy,
можно описать неравенствами
.
Числа
,
правильную в направлении оси Oy,
можно описать неравенствами
.
Числа  и
и  существуют вследствие ограниченности
области
существуют вследствие ограниченности
области  ,
функция
,
функция 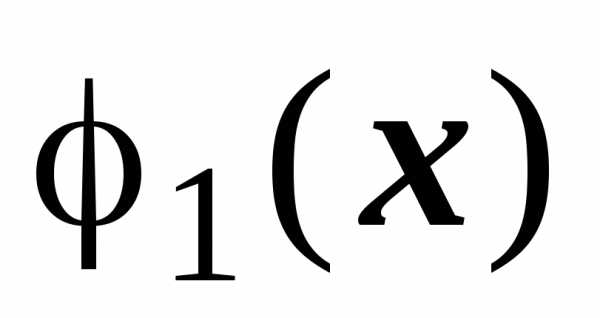 образована нижними точками пересечения
прямой
образована нижними точками пересечения
прямой 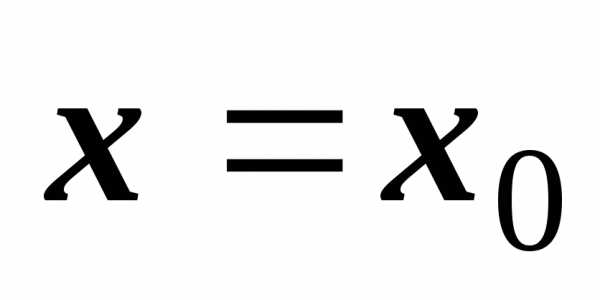 при
с границей области
при
с границей области  ,
функция
,
функция 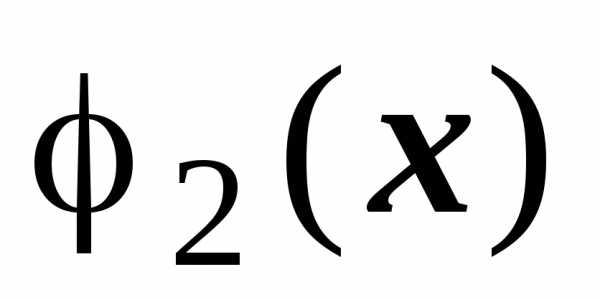 — верхними точками пересечения этой
прямой с границей области
— верхними точками пересечения этой
прямой с границей области  :
:
Аналогичным
образом область 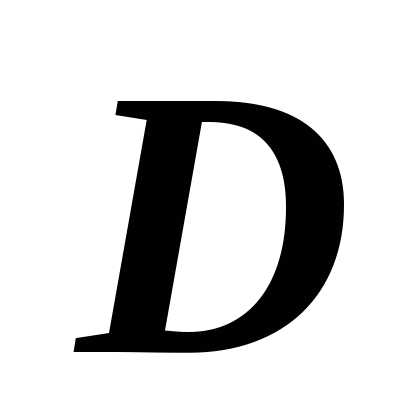 ,
ограниченную, замкнутую и правильную
в направлении оси Oх,
можно описать неравенствами
.
Функция
,
ограниченную, замкнутую и правильную
в направлении оси Oх,
можно описать неравенствами
.
Функция 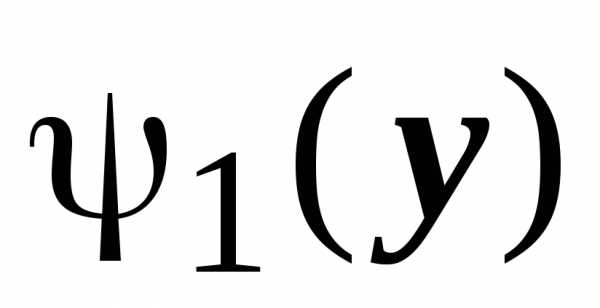 образована левыми точками пересечения
прямой
образована левыми точками пересечения
прямой 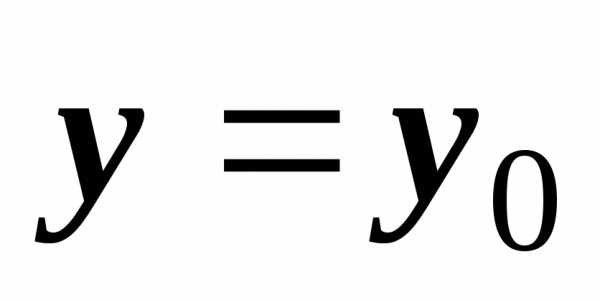 при
с границей области
при
с границей области 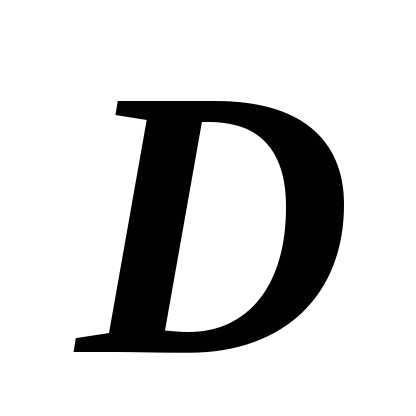 ,
функция
,
функция 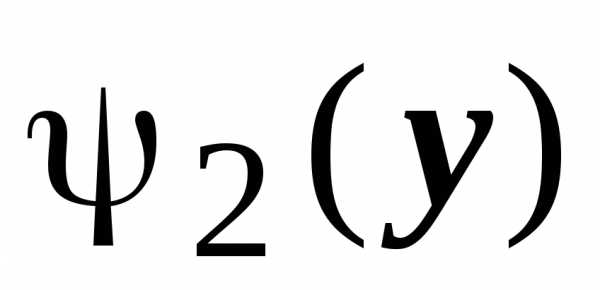 — правыми точками пересечения этой
прямой с границей области
— правыми точками пересечения этой
прямой с границей области  .
.
Для правильной области (т.е. области, правильной в направлении обеих осей) существуют оба способа представления: и , и .
Двукратный (повторный) интеграл. Пусть
 — область, простая в направлении оси Oy.
Рассмотрим выражение
— область, простая в направлении оси Oy.
Рассмотрим выражение  .
Эта конструкция определяется через
два обычных определённых интеграла.
После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная)
и подстановки по у в пределах от
.
Эта конструкция определяется через
два обычных определённых интеграла.
После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная)
и подстановки по у в пределах от  до
до  получается функция, зависящая только
от х,
которая интегрируется в пределах от a до b.
В дальнейшем мы будем обычно записывать
этот объект без внутренних скобок:
получается функция, зависящая только
от х,
которая интегрируется в пределах от a до b.
В дальнейшем мы будем обычно записывать
этот объект без внутренних скобок:
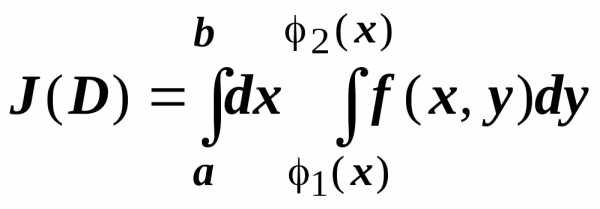 .
.
Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:
Свойства линейности
и интегрирования неравенств следуют
из этих свойств определённого интеграла;
интеграл от единичной функции даёт
площадь области :
;
:
;
теоремы
об оценке и о среднем следуют из
перечисленных свойств. Единственное
свойство, с которым придётся повозиться
— это свойство аддитивности. Мы докажем
его в простой, но достаточной для нас
форме: если область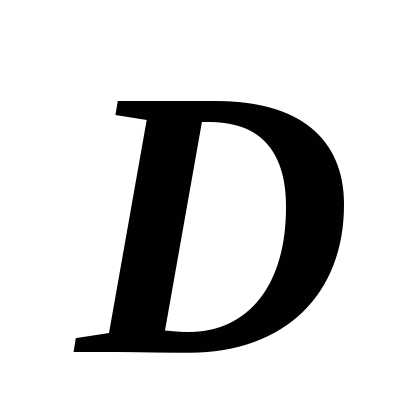 разбита на две подобласти
разбита на две подобласти 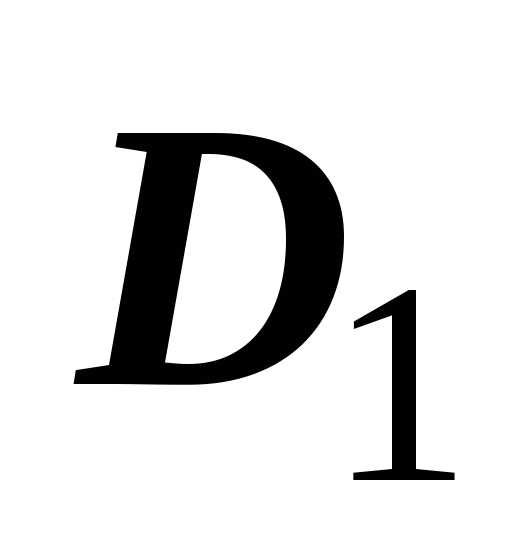 и
и 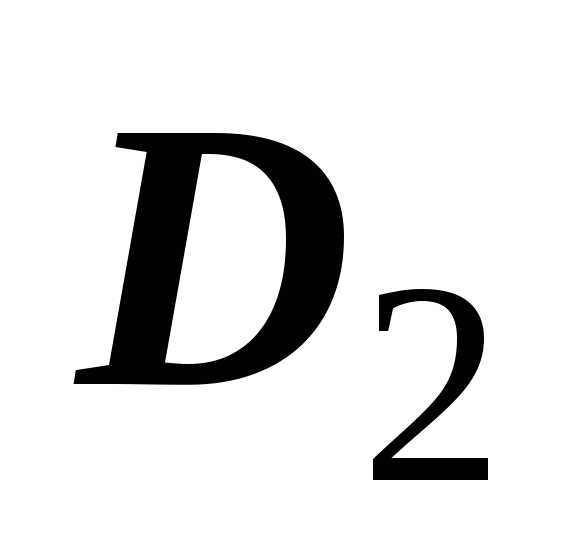 прямой, параллельной одной из координатных
осей, то двукратный интеграл по области
прямой, параллельной одной из координатных
осей, то двукратный интеграл по области  равен сумме интегралов по
равен сумме интегралов по 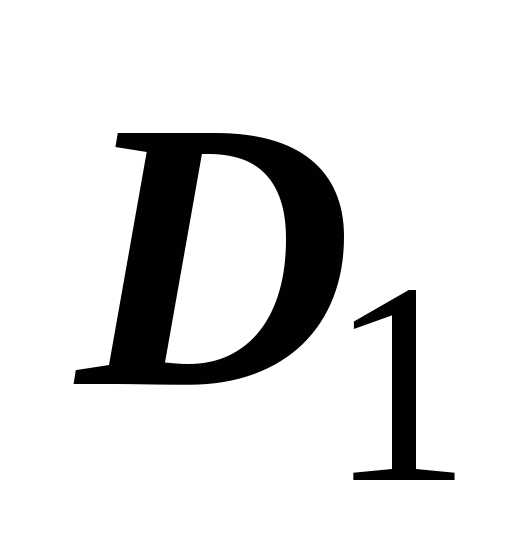 и
и 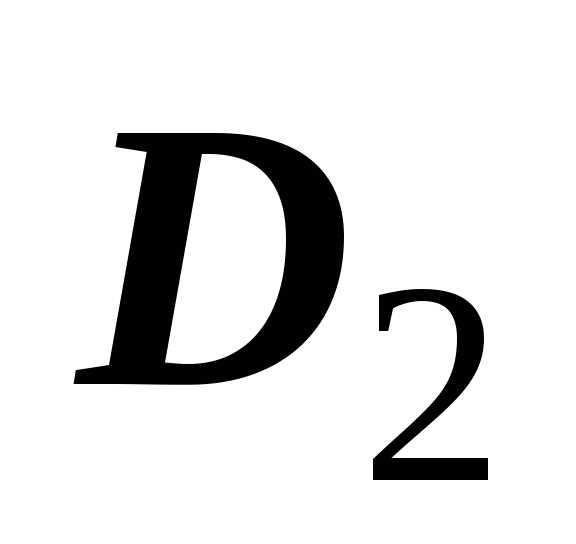 :
.
:
.
Первый
случай: прямая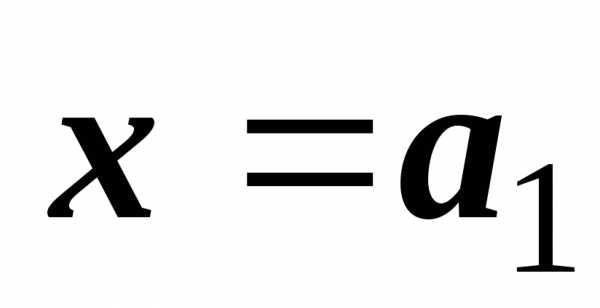 параллельна оси Oy.
Тогда
(аддитивность внешнего интеграла) .
параллельна оси Oy.
Тогда
(аддитивность внешнего интеграла) .
Второй случай:
прямая 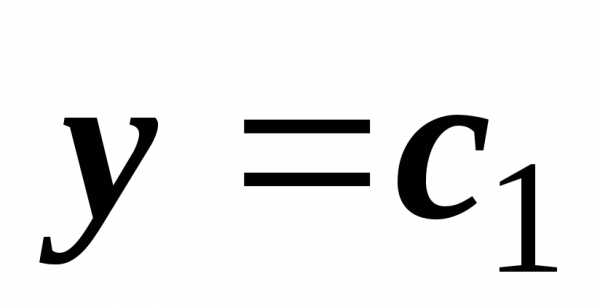 параллельна оси Oх.
Воспользуемся сначала аддитивностью
внешнего интеграла:
параллельна оси Oх.
Воспользуемся сначала аддитивностью
внешнего интеграла:
(первая фигурная
скобка даёт повторный интеграл по 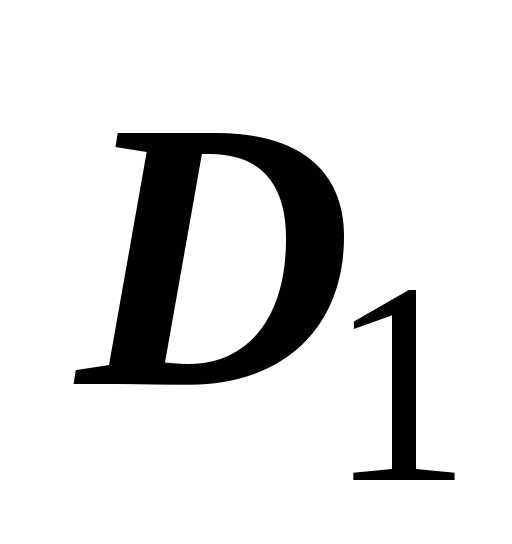 ,
второй — по
,
второй — по 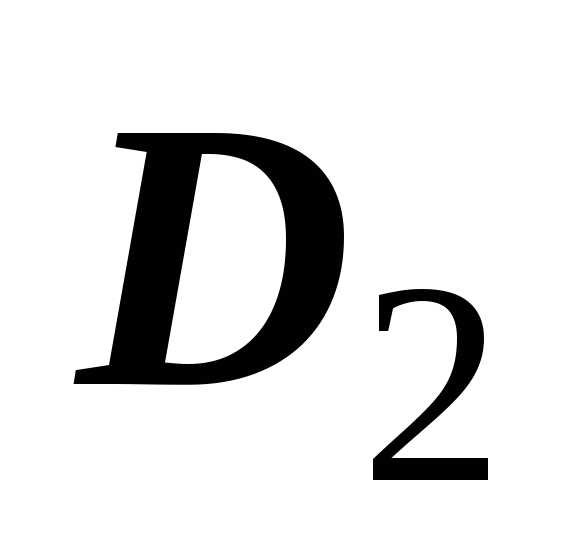 ) .
) .
Понятно,
что воэможны различные случаи взаимного
расположения прямых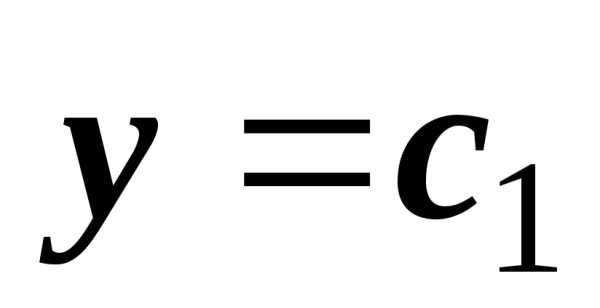 ,
, 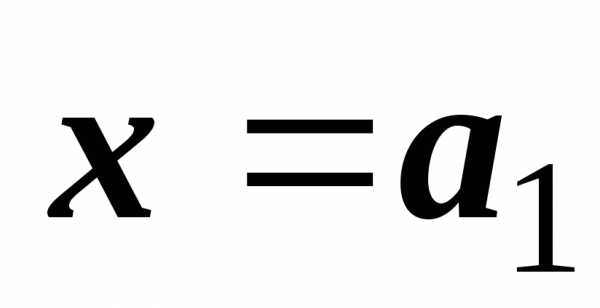 ,
, 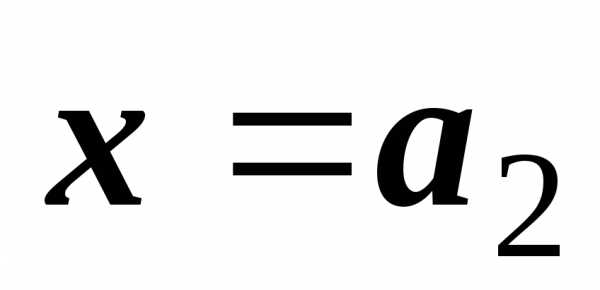 и функций , ,
но логика доказательства во всех случаях
такая же.
и функций , ,
но логика доказательства во всех случаях
такая же.
Обобщим доказанное
свойство. Пусть прямая разбивает область 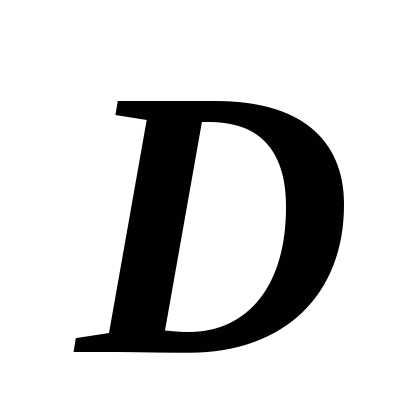 на две подобласти
на две подобласти 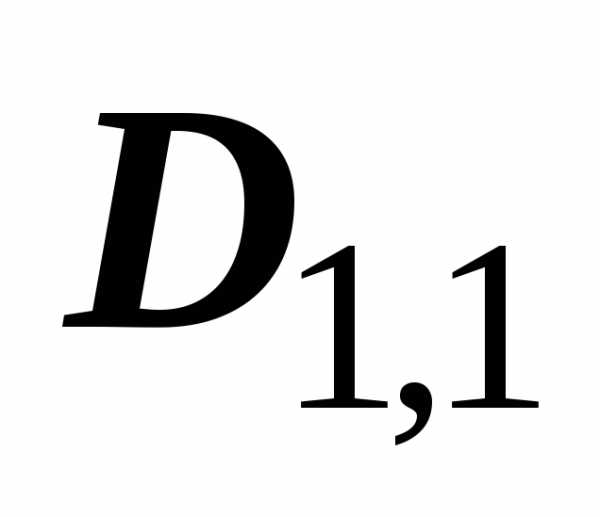 и
и 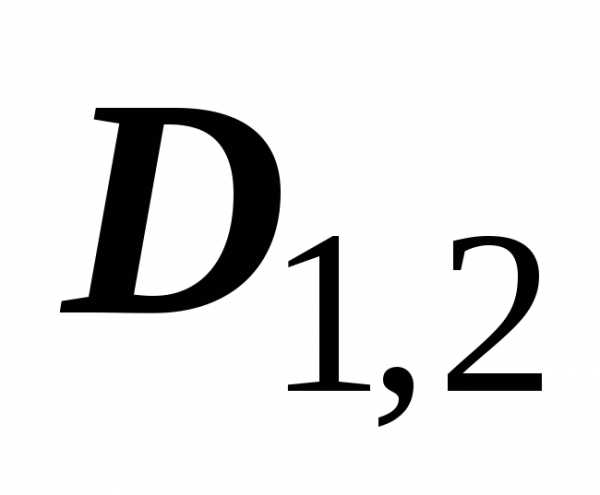 .
Проведём ещё одну прямую, параллельную
какой-либо координатной оси. Пусть эта
прямая разбивает
.
Проведём ещё одну прямую, параллельную
какой-либо координатной оси. Пусть эта
прямая разбивает 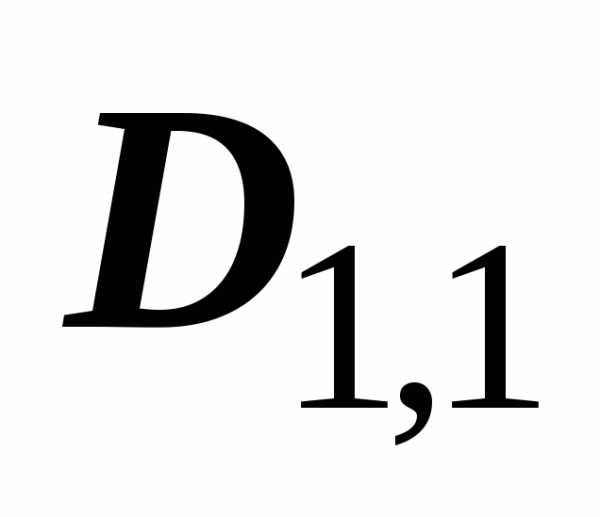 на
на 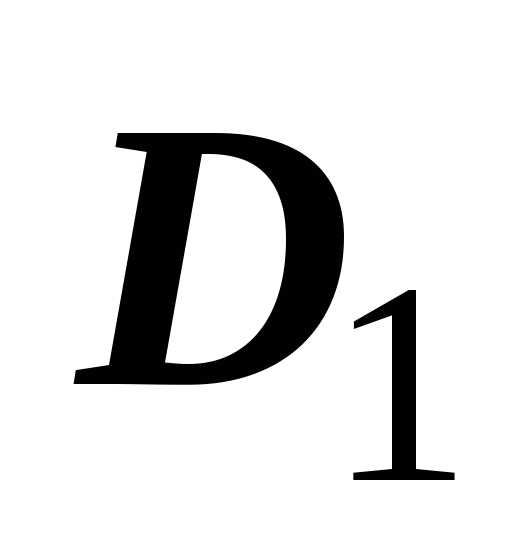 и
и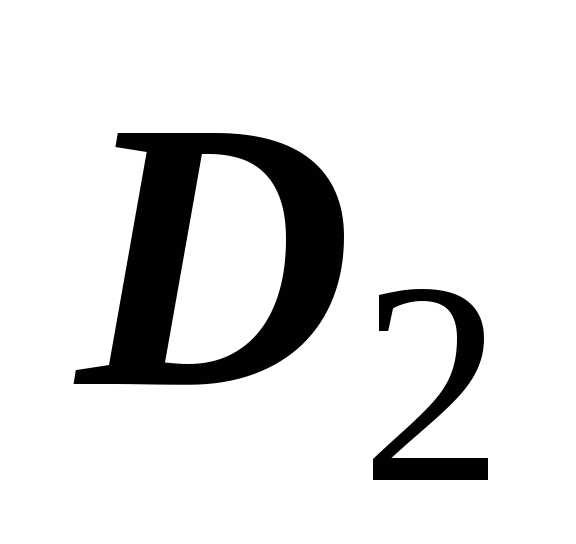 ;
; 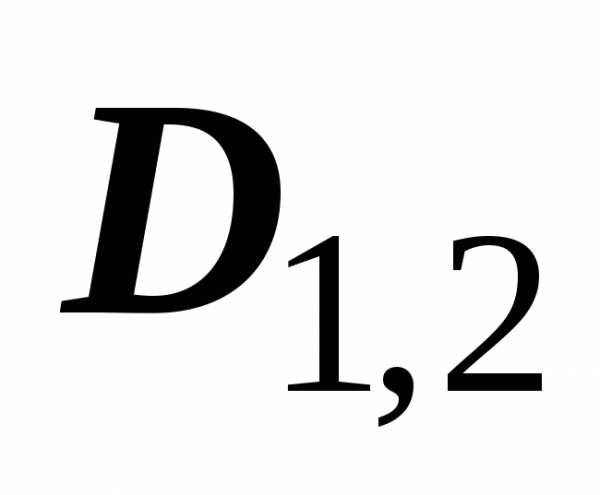 — на
— на 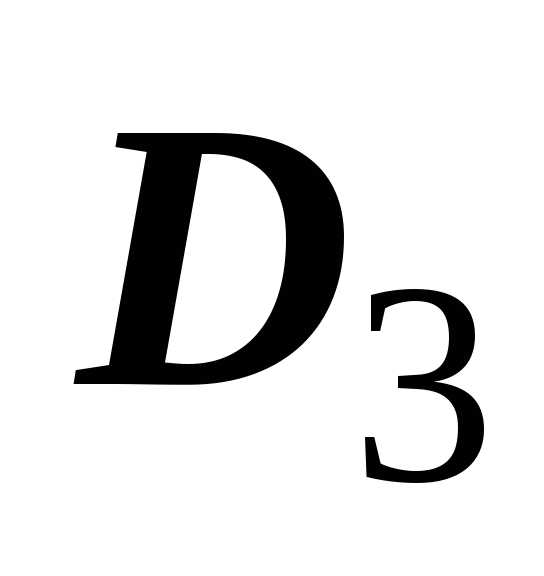 и
и  .
По доказанному, ,
,
поэтому .
Продолжая рассуждать также, убеждаемся
в справедливости следующего утверждения:
если область
.
По доказанному, ,
,
поэтому .
Продолжая рассуждать также, убеждаемся
в справедливости следующего утверждения:
если область 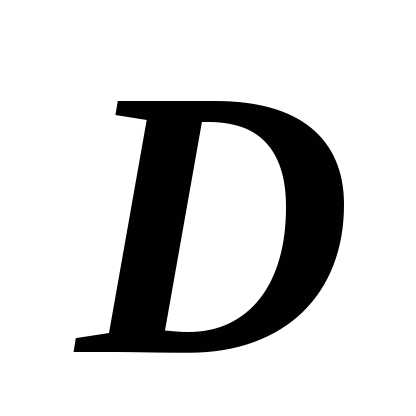 с помощью прямых, параллельных координатным
осям, разбита на подобласти ,
то .
с помощью прямых, параллельных координатным
осям, разбита на подобласти ,
то .
Теорема о переходе от двойного интеграла к повторному. Пусть
 — простая в направлении оси Oy область. Тогда двойной интеграл от
непрерывной функции по области
— простая в направлении оси Oy область. Тогда двойной интеграл от
непрерывной функции по области  равна повторному интегралу от той же
функции по области
равна повторному интегралу от той же
функции по области  :
.
:
.
Док-во. Разобьём область
с помощью прямых, параллельных координатным
осям, на подобласти .
По доказанному выше,
.
К каждому из итегралов 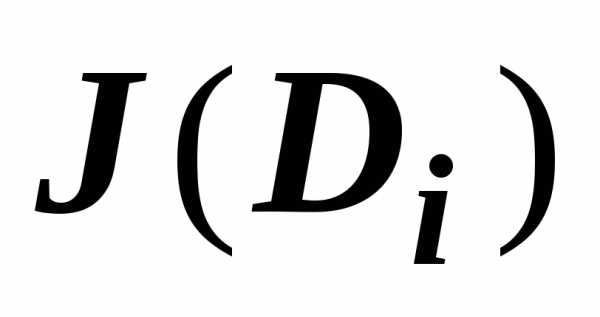 применим теорему о среднем: в любой
области
применим теорему о среднем: в любой
области 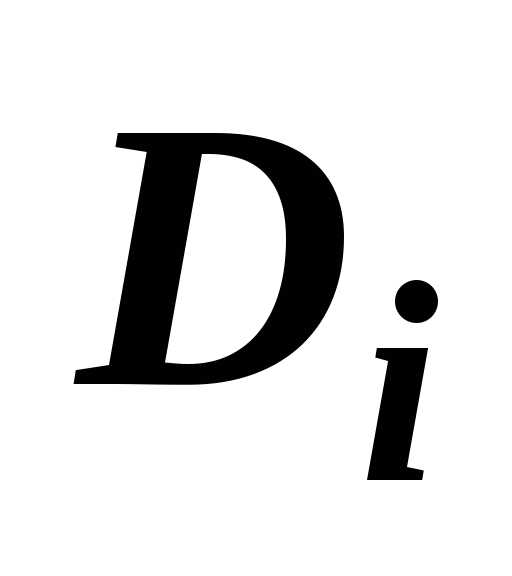 найдётся точка
найдётся точка 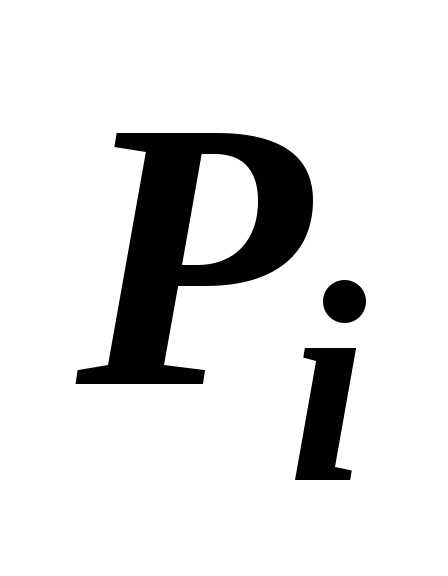 такая, что
.
Следовательно,
.
В последнем равенстве справа стоит
интегральная сумма для двойного интеграла
такая, что
.
Следовательно,
.
В последнем равенстве справа стоит
интегральная сумма для двойного интеграла 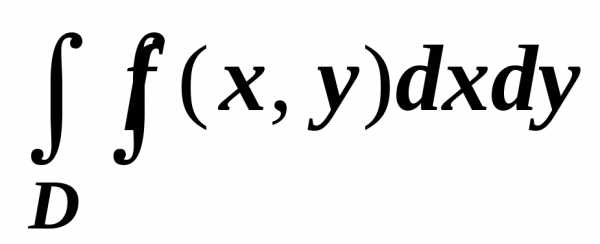 .
Будем мельчить разбиение области так,
чтобы .
Вследствие непрерывности функции
.
Будем мельчить разбиение области так,
чтобы .
Вследствие непрерывности функции 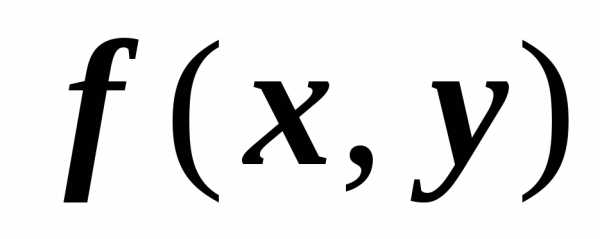 по теореме существования интегральная
сумма при этом стремится к двойному
интегралу
по теореме существования интегральная
сумма при этом стремится к двойному
интегралу  ,
т.е. в пределе получим
,
что и требовалось доказать.
,
т.е. в пределе получим
,
что и требовалось доказать.
Если область 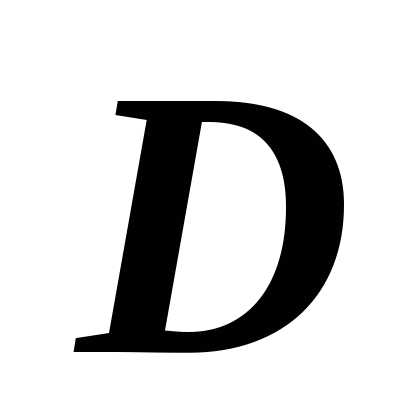 правильная
в направлении оси Oх,
то аналогично доказывается формула
.
Если
правильная
в направлении оси Oх,
то аналогично доказывается формула
.
Если 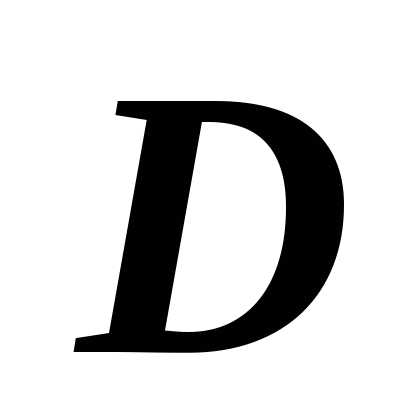 правильна
в направлении обеих осей, то для вычисления
двойного интеграла можно применять
любую из эти формул:
.
правильна
в направлении обеих осей, то для вычисления
двойного интеграла можно применять
любую из эти формул:
.
Если область не является правильной, её разбивают на правильные подобласти.
studfiles.net
Свойства двойного интеграла / Двойной интеграл / 3dstroyproekt.ru
Постоянный множитель может быть вынесен за знак двойного интеграла
(\iint\limits_R { c\left( { x,y }\right)dA } = c\iint\limits_R { f\left( { x,y }\right)dA } ,) где (c) — константа;
Линейность
Если функции $\mathbf { \textit { f } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } )$, $\mathbf { \textit { g } } (\mathbf { \textit { x } } $, $\mathbf { \textit { y } } )$ интегрируемы по области $\mathbf { \textit { D } } $, то их линейная комбинация $\alpha f(x,y)+\beta g(x,y)$ тоже интегрируема по области $\mathbf { \textit { D } } $, и $\iint\limits_D { \left[ { \alpha f(P)+\beta g(P) }\right]ds= } \alpha \iint\limits_D { f(P)ds } +\beta \iint\limits_D { g(P)ds } $.
Док-во:
Для интегральных сумм справедливо равенство
$$\sum\limits_ { i=1 } ^n { \left[ { \alpha f(P_i )+\beta g(P_i ) }\right]s(D_i ) } =\alpha \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } +\beta \sum\limits_ { i=1 } ^n { g(P_i )s(D_i ) } $$
Переходя к пределу при $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(D_i )\to 0$ и пользуясь свойствами пределов, рассмотренными в разделе Арифметические действия с пределами { здесь должна быть ссылка, но пока ее нет } , получим требуемое равенство.
Аддитивность
Если область $\mathbf { \textit { D } } $ является объединением двух областей $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $, не имеющих общих внутренних точек, то $\iint\limits_D { f(P)ds } =\iint\limits_ { D_1 } { f(P)ds } +\iint\limits_ { D_2 } { f(P)ds } $.
Док-во:
Пусть область $\mathbf { \textit { D } } _ { 1 } $ разбита на подобласти $\mathbf { \textit { D } } _ { 1,1 } $, $\mathbf { \textit { D } } _ { 1,2 } , { \ldots } , \mathbf { \textit { D } } _ { 1, n1 } $; область $\mathbf { \textit { D } } _ { 2 } $ разбита на подобласти $\mathbf { \textit { D } } _ { 2,1 } $, $\mathbf { \textit { D } } _ { 2,2 } , { \ldots } , \mathbf { \textit { D } } _ { 2, n2 } $. Тогда объединение этих разбиений даст разбиение области $\mathbf { \textit { D } } $: $D=\left( { \bigcup\limits_ { i_1 =1 } ^ { n_1 } { D_ { 1,i_1 } } }\right)\cup \left( { \bigcup\limits_ { i_2 =1 } ^ { n_2 } { D_ { 2,i_2 } } }\right)$ на $\mathbf { \textit { n } } _ { 1 } +\mathbf { \textit { n } } _ { 2 } $ подобластей. Интегральная сумма по области $\mathbf { \textit { D } } $ равна сумме сумм по областям $\mathbf { \textit { D } } _ { 1 } $ и $\mathbf { \textit { D } } _ { 2 } $: $\sum\limits_ { i=1 } ^ { n_1 +n_2 } { f(P_i )\cdot s(D_i ) } =\sum\limits_ { i_1 =1 } ^ { n_1 } { f(P_ { i_1 } )\cdot s(D_ { i_1 } ) } +\sum\limits_ { i_2 =1 } ^ { n_2 } { f(P_ { i_2 } )\cdot s(D_ { i_2 } ) } $. Как и в предыдущем случае, переходя к пределу при $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n;\;j=1,2 } diam(D_ { i_j } )\to 0$, получим требуемое равенство.
Интеграл от единичной функции по области
$\mathbf { \textit { D } } $ равен площади этой области: $\iint\limits_D { ds } =s(D)\textbf { . } $
Док-во:
Для любого разбиения $\sum\limits_ { i=1 } ^n { s(D_i ) } =s(D)$, т.е. не зависит ни от разбиения, ни от выбора точек $\mathbf { \textit { P } } _ { i } $. Предел постоянной равен этой постоянной, поэтому $\iint\limits_D { ds } =\mathop { \lim } \limits_ { d\to 0 } \sum\limits_ { i=1 } ^n { s(D_i ) } =s(D)$.
Интегрирование неравенств
Если в любой точке $P\in D$ выполняется неравенство $f(P)\leqslant g(P)$, и функции $\mathbf { \textit { f(P } } )$, $\mathbf { \textit { g } } (\mathbf { \textit { P } } )$ интегрируемы по области $\mathbf { \textit { D } } $, то $\iint\limits_D { f(P)ds } \leqslant \iint\limits_D { g(P)ds } $.
Док-во:
В любой точке $P_i \in D$ выполняется неравенство $f(P)\leqslant g(P)$, поэтому $\sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } $. По теореме о переходе к пределу в неравенствах отсюда следует требуемое утверждение.
Теоремы об оценке интеграла
Если функция $\mathbf { \textit { f(P } } )$ интегрируема по области $\mathbf { \textit { D } } $ и для $\forall P\in D$ выполняется $m\leqslant f(P)\leqslant M$, то $m\cdot s(D)\leqslant \iint\limits_D { f(P)ds } \leqslant M\cdot s(D)$.
Док-во:
$m\leqslant f(P)\leqslant M \quad \mathop \Rightarrow \limits^ { ссылки-еще-нет } \quad \sum\limits_ { i=1 } ^n { m\cdot s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { M\cdot s(D_i ) } \mathop \Rightarrow \limits^ { ссылки-еще-нет } \\ \quad \mathop \Rightarrow \limits^ { ссылки-еще-нет } m\sum\limits_ { i=1 } ^n { s(D_i ) } \leqslant \sum\limits_ { i=1 } ^n { f(P_i )s(D_i ) } \leqslant M\sum\limits_ { i=1 } ^n { s(D_i ) } \mathop \Rightarrow \limits^ { ссылки-еще-нет } m\cdot s(D)\leqslant \iint\limits_D { f(P)ds } \leqslant M\cdot s(D)$
Цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств.
Если функция $\mathbf { \textit { f(P } } )$ интегрируема по области $\mathbf { \textit { D } } $, то $\left| { \iint\limits_D { f(P)ds } }\right|\leqslant \iint\limits_D { \vert f(P)\vert ds } $.
Док-во:
Эти неравенства непосредственно следуют из того, что $-\vert f(P)\vert \leqslant f(P)\leqslant \vert f(P)\vert $ и свойства Интегрирование неравенств
Теорема о среднем
Если функция $\mathbf { \textit { f(P } } )$ непрерывна на области $\mathbf { \textit { D } } $, то существует точка $P_0 \in D$, такая что $\iint\limits_D { f(P)ds } =f(P_0 )\cdot s(D)$.
Док-во:
Непрерывная на ограниченной замкнутой области $\mathbf { \textit { D } } $ функция $\mathbf { \textit { f(P } } )$ принимает в некоторых точках этой области своё минимальное $\mathbf { \textit { m } } $ и максимальное $\mathbf { \textit { M } } $ значения. Так как $m\leqslant f(P)\leqslant M$, то $m\cdot s(D)\leqslant \iint\limits_D { f(P)ds } \leqslant M\cdot s(D)$, или $m\leqslant \frac { 1 } { s(D) } \iint\limits_D { f(P)ds } \leqslant M$. Непрерывная функция принимает, кроме того, любое значение, заключённое между $\mathbf { \textit { m } } $ и $\mathbf { \textit { M } } $, в частности, значение
$\frac { 1 } { s(D) } \iint\limits_D { f(P)ds } \leqslant M$. Следовательно, $\exists P_0 \in D\vert \;f(P_0 )=\frac { 1 } { s(D) } \iint\limits_D { f(P)ds } $, откуда и следует доказываемое утверждение.
3dstroyproekt.ru
Лекции кратные интегралы, двойной интеграл
Скачать с Depositfiles
Лекции 5-6
Тема2. Кратные интегралы.
Двойной интеграл.
Контрольные вопросы.
1. Двойной интеграл, его геометрический и физический смысл
2. Свойства двойного интеграла.
3. Вычисление двойного интеграла в декартовых координатах.
4. Замена переменных в двойном интеграле. Вычисление двойного интеграла в полярных координатах.
Замечание. Ниже будем считать все рассматриваемые кривые кусочно-гладкими. Диаметром замкнутой ограниченной области будем называть наибольшее из расстояний между двумя точками границы этой области
Пусть функция z = f(x,y) определена в ограниченной замкнутой области D плоскости. Разобьём область D произвольным образом на n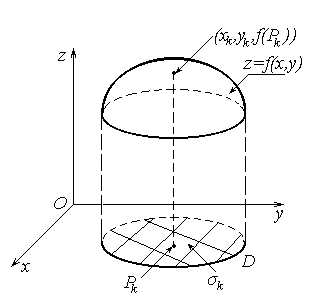 элементарных замкнутых областей 1, … ,n, имеющих площади 1, …, n и диаметры d1 , …, dnсоответственно. Обозначим d наибольший из диаметров областей 1, … ,n . В каждой области k выберем произвольную точку Pk (xk ,yk) и составим интегральную сумму функции f(x,y)
элементарных замкнутых областей 1, … ,n, имеющих площади 1, …, n и диаметры d1 , …, dnсоответственно. Обозначим d наибольший из диаметров областей 1, … ,n . В каждой области k выберем произвольную точку Pk (xk ,yk) и составим интегральную сумму функции f(x,y)
S = 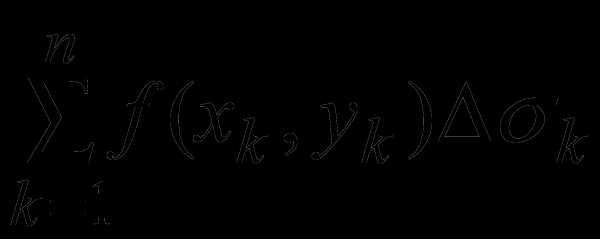 (1)
(1)
Определение. Двойным интегралом функции f(x,y) по области D называется предел интегральной суммы
, (2)
если он существует.
Замечание. Интегральная сумма S зависит от способа разбиения области D и выбора точек Pk (k=1, …, n). Однако, предел 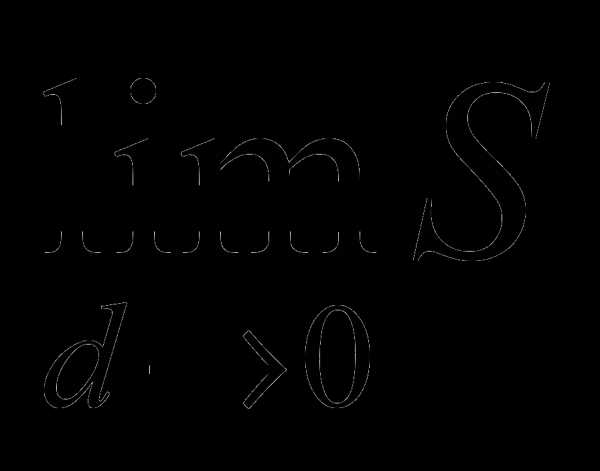 , если он существует, не зависит от способа разбиения области D и выбора точек Pk .
, если он существует, не зависит от способа разбиения области D и выбора точек Pk .
Достаточное условие существования двойного интеграла. Двойной интеграл (1) существует, если функция f(x,y) непрерывна в D за исключением конечного числа кусочно-гладких кривых и ограничена в D. В дальнейшем будем считать, что все рассматриваемые двойные интегралы существуют.
Геометрический смысл двойного интеграла.
Если f(x,y) ≥0 в области D, то двойной интеграл (1) равен объему «цилиндрического” тела, изображенного на рисунке:
V = 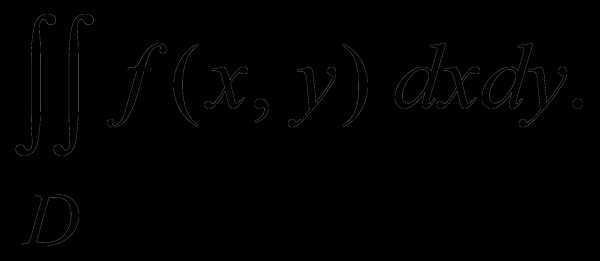 (3)
(3)
Цилиндрическое тело ограничено снизу областью D, сверху частью поверхности z=f(x,y), с боков вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.
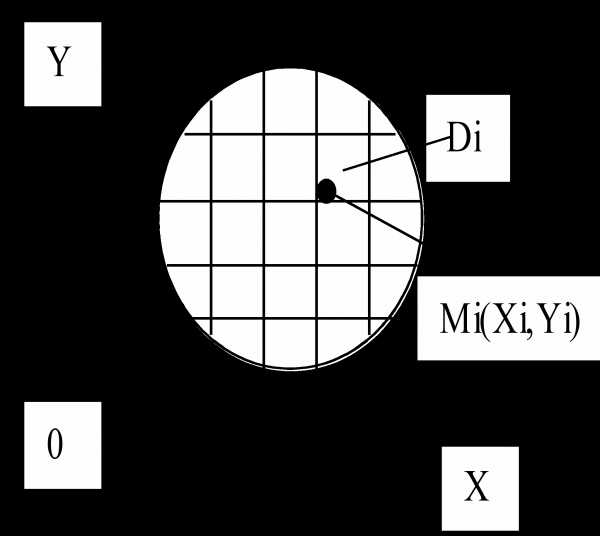
Физический смысл двойного интеграла. Масса плоской пластины.
Пусть задана плоская пластина D с известной функцией плотности γ(х,у), тогда разбивая пластину D на части Di и выбирая произвольные точки , получим для массы пластины 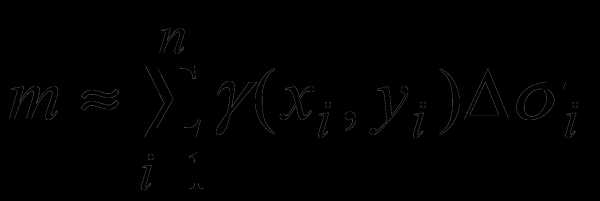 , или, сравнивая с формулой (2):
, или, сравнивая с формулой (2):
(4)
4. Некоторые свойства двойного интеграла.
Линейность. Если С – числовая константа, то
,
Аддитивность. Если область D «разбита” на области D1 и D2, то
.
3) Площадь ограниченной области D равна
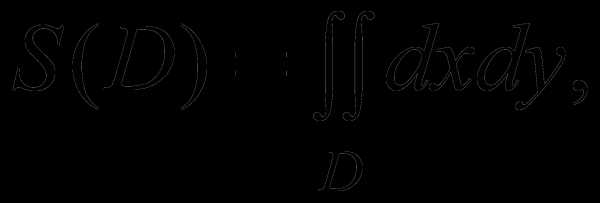 (5)
(5)
Вычисление двойного интеграла в декартовых координатах.
Пусть задана область
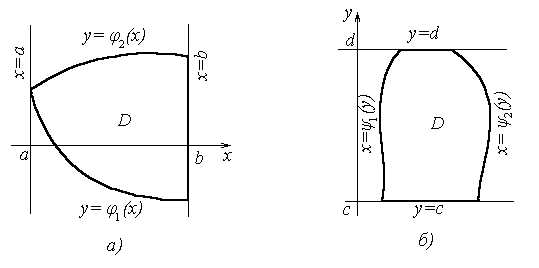
Рисунок 1
D = {(x, y): a ≤ x ≤ b, φ1(x) ≤ y≤ φ2(x)} (6)
Область D заключена в полосе между прямыми x = a, y = b, снизу и сверху ограничена соответственно кривыми y = φ1(x) и y = φ2(x) .
Двойной интеграл (1) по области D (4) вычисляется переходом к повторному интегралу:
(7)
Этот повторный интеграл вычисляется следующим образом. Сначала вычисляется внутренний интеграл
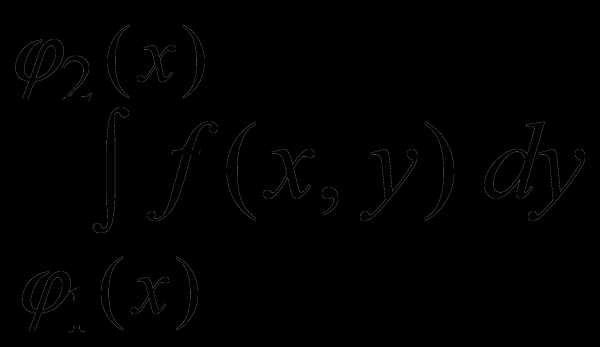
по переменной y, при этом x считается постоянной. В результате получится функция от переменной x, а затем вычисляется «внешний” интеграл от этой функции по переменной x.
Замечание. Процесс перехода к повторному интегралу по формуле (7) часто называют расстановкой пределов интегрирования в двойном интеграле. При расстановке пределов интегрирования нужно помнить два момента. Во-первых, нижний предел интегрирования не должен превышать верхнего, во-вторых, пределы внешнего интеграла должны быть константами, а внутреннего должны в общем случае зависеть от переменной интегрирования внешнего интеграла.
Пусть теперь область D имеет вид
D = { (x, y) : c ≤ y ≤ d, ψ1(y) ≤ x ≤ ψ2(y) } . (8)
Тогда
. (9)
Предположим, что область D можно представить в виде (6) и (8) одновременно. Тогда имеет место равенство
(10)
Переход од одного повторного интеграла к другому в равенстве (10) называется изменением порядка интегрирования в двойном интеграле.
Примеры.
1) Изменить порядок интегрирования в интеграле
Решение. По виду повторного интеграла находим область
D = {(x, y): 0 ≤ x ≤ 1, 2x ≤ y≤ 2} .
Изобразим область D. По рисунку видим, что эта область расположена в горизонтальной полосе между прямыми y=0, y=2 и между линиями x =0и x = y 2. Это значит, что
D = {(x, y): 0 ≤ y ≤ 2, 0 ≤ x≤ y/2} .
Тогда по формуле (10) получаем
2)Вычислить интеграл где D область из примера 1.
Решение. Расставим пределы интегрирования в интеграле подобно примеру 1:
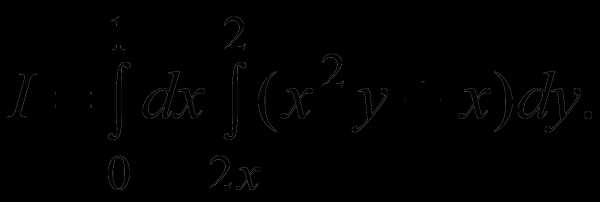
Вычислим внутренний интеграл по переменной y, считая x константой:
Теперь вычислим внешний интеграл по x:
Замена переменных в двойном интеграле.
Иногда для упрощения вычислений делают замену переменных:
, (11)
Если функции (11) непрерывно дифференцируемы и определитель (Якобиан) отличен от нуля в рассматриваемой области:
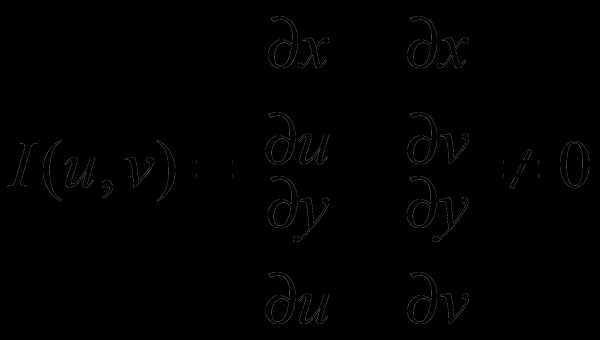 (12)
(12)
то: (13)
greleon.ru

 ,
, 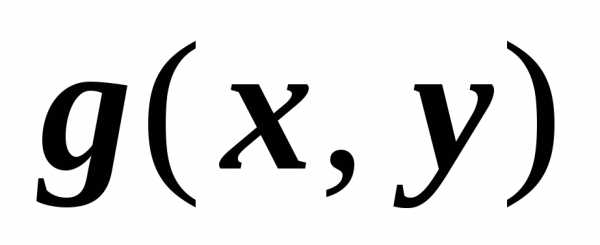 интегрируемы по области
интегрируемы по области  ,
то их линейная комбинация
тоже интегрируема по области
,
то их линейная комбинация
тоже интегрируема по области  ,
и
.
,
и
. равен
площади этой области:
равен
площади этой области: 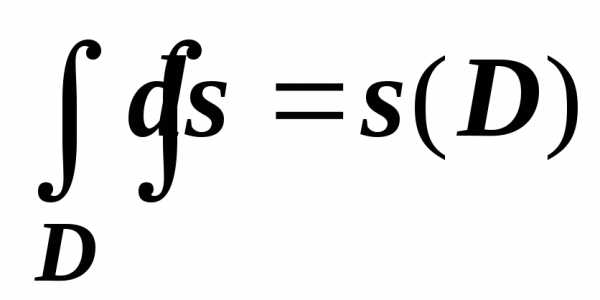 .
.  на плоскости Oxy будем
называть простой
(правильной) в направлении оси Oy,
если любая прямая, проходящая через
внутреннюю точку области
на плоскости Oxy будем
называть простой
(правильной) в направлении оси Oy,
если любая прямая, проходящая через
внутреннюю точку области 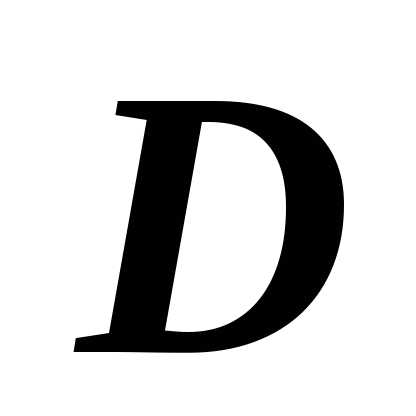 и параллельная оси Oy,
пересекает границу
и параллельная оси Oy,
пересекает границу 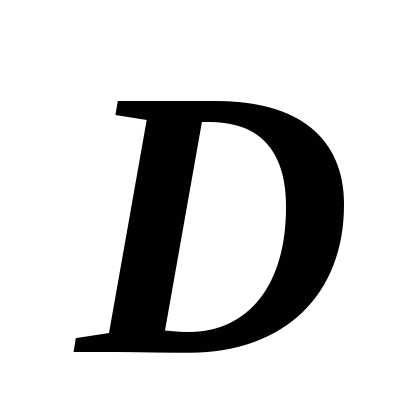 в двух точках.
в двух точках.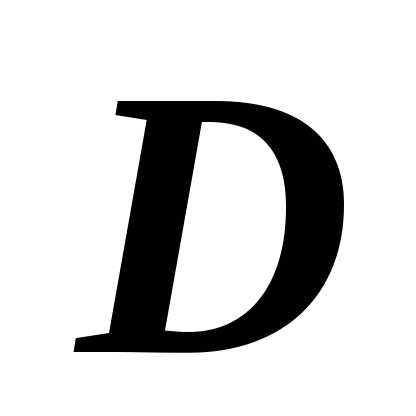 — область, простая в направлении оси Oy.
Рассмотрим выражение
— область, простая в направлении оси Oy.
Рассмотрим выражение  .
Эта конструкция определяется через
два обычных определённых интеграла.
После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная)
и подстановки по у в пределах от
.
Эта конструкция определяется через
два обычных определённых интеграла.
После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная)
и подстановки по у в пределах от 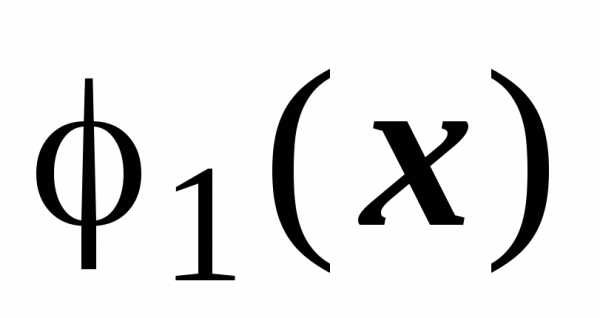 до
до  получается функция, зависящая только
от х,
которая интегрируется в пределах от a до b.
В дальнейшем мы будем обычно записывать
этот объект без внутренних скобок:
получается функция, зависящая только
от х,
которая интегрируется в пределах от a до b.
В дальнейшем мы будем обычно записывать
этот объект без внутренних скобок: — простая в направлении оси Oy область. Тогда двойной интеграл от
непрерывной функции по области
— простая в направлении оси Oy область. Тогда двойной интеграл от
непрерывной функции по области  равна повторному интегралу от той же
функции по области
равна повторному интегралу от той же
функции по области  :
.
:
.