Градус, минута, секунда | это… Что такое Градус, минута, секунда?
Толкование
- Градус, минута, секунда
Градус, минута, секунда — общепринятые единицы измерения плоских углов и земного шара.
Содержание
- 1 Градус
- 2 Минуты и секунды
- 3 Угловая секунда
- 3.1 Использование
- 3.2 Дольные единицы
- 4 Примечания
- 5 Литература
- 6 См. также
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом углу, таким образом, 90°, в развёрнутом — 180°.
Деление окружности на 360° придумали аккады (вавилоняне) — соответственно делению года в вавилонском календаре на 360 дней.
- 1° = радиан ≈ 0,017453293 радиан
- 1° = оборота ≈ 0,002777 оборота
Минуты и секунды
В измерении углов традиционно используется шестидесятеричная система счисления.
 По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″).
По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″).- 1′ = ≈ 2,9088821×10-4 радиан.
- 1″ = ≈ 4,8481368×10-6 радиан.
Угловая секунда
Одна угловая секунда примерно соответствует углу, под которым виден футбольный мяч с расстояния около 45 километров.
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[1]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[2].
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с). Соотношение между этими величинами определяется формулой 1c = 15″.
 [3]
[3]Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[1][4], что является простой транслитерацией с англ. arcsecond.
Дольные единицы
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда)

Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.[6]
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP). [7][8]
Примечания
- ↑ 1 2 Англо-русско-английский астрономический словарь.
 Astronet. Проверено 23 декабря 2007.
Astronet. Проверено 23 декабря 2007. - ↑ 1 2 Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Проверено 23 декабря 2007.
- ↑ Справочник. Некоторые внесистемные единицы. ASTROLAB.
- ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Проверено 23 декабря 2007.
- ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003.
- ↑ Источник: статья Minute of arc в en-wiki.
- ↑ Гурьянов С. Почему звезды называются именно так?.
 проект «Астрогалактика» (29 октября 2005 года). Проверено 26 декабря 2007.
проект «Астрогалактика» (29 октября 2005 года). Проверено 26 декабря 2007. - ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.
Литература
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Малые углы // Тригонометрия. — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
См. также
- Град, минута, секунда
- Оборот
- Радиан
Wikimedia Foundation. 2010.
Нужно решить контрольную?
- Градско (община Градско)
- Градус цельсия
Полезное
Градус, минута, секунда | это… Что такое Градус, минута, секунда?
Толкование
- Градус, минута, секунда
Градус, минута, секунда — общепринятые единицы измерения плоских углов и земного шара.

Содержание
- 1 Градус
- 2 Минуты и секунды
- 3 Угловая секунда
- 3.1 Использование
- 3.2 Дольные единицы
- 4 Примечания
- 5 Литература
- 6 См. также
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом углу, таким образом, 90°, в развёрнутом — 180°.
Деление окружности на 360° придумали аккады (вавилоняне) — соответственно делению года в вавилонском календаре на 360 дней.
- 1° = радиан ≈ 0,017453293 радиан
- 1° = оборота ≈ 0,002777 оборота
- 1° = градов ≈ 1,111111 градов
Минуты и секунды
В измерении углов традиционно используется шестидесятеричная система счисления. По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″).
- 1′ = ≈ 2,9088821×10-4 радиан.

- 1″ = ≈ 4,8481368×10-6 радиан.
Угловая секунда
Одна угловая секунда примерно соответствует углу, под которым виден футбольный мяч с расстояния около 45 километров.
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[1]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[2].
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с). Соотношение между этими величинами определяется формулой 1c = 15″.[3]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[1][4], что является простой транслитерацией с англ.

Дольные единицы
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т.п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд. [6]
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза.
 Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.
Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP).[7][8]
Примечания
- ↑ 1 2 Англо-русско-английский астрономический словарь. Astronet.
- ↑ 1 2 Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Проверено 23 декабря 2007.
- ↑ Справочник.
 Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007.
Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007. - ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Проверено 23 декабря 2007.
- ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003.
- ↑ Источник: статья Minute of arc в en-wiki.
- ↑ Гурьянов С. Почему звезды называются именно так?. проект «Астрогалактика» (29 октября 2005 года). Проверено 26 декабря 2007.
- ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.
Литература
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Малые углы // Тригонометрия.
 — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
— М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
См. также
- Град, минута, секунда
- Оборот
- Радиан
Wikimedia Foundation. 2010.
Нужна курсовая?
- Градско (община Градско)
- Градус цельсия
Полезное
View Преобразование угловых единиц: десятичные градусы и градусы-минуты-секунды
Поиск
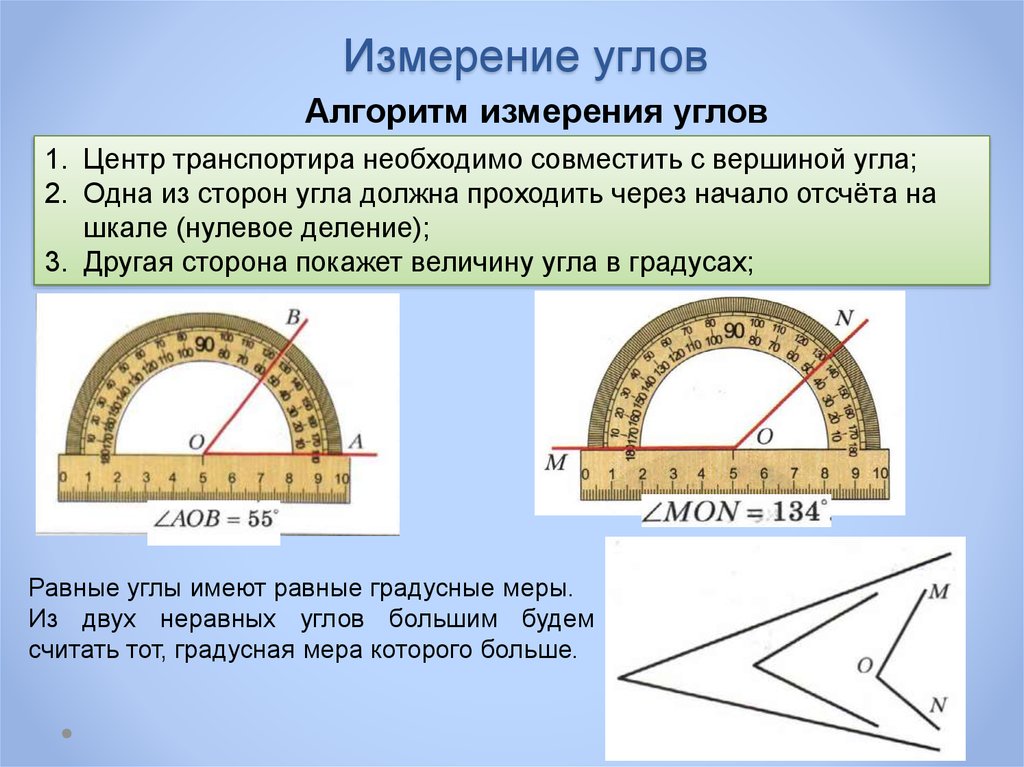
Учащийся будет преобразовывать между десятичными градусами и градусами-минутами-секундами.
Рандомизировать вопросы Рандомизировать ответы
Преобразование 36,25° в градусы, минуты и секунды.
При необходимости округлить до секунды.
- 36°41’40»
- 36°25’00»
- 36°49’15»
- 36°15’00»
Вопрос 1 из 10
Правильно!
Преобразование 36,25° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Правильный ответ
36°15’00»
Следующий вопрос
Вопрос 1 из 10
Неверно
Преобразование 36,25° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Ваш ответ
Правильный ответ
36°15’00»
Следующий вопрос
Вопрос 1 из 10
Преобразование 85,45° в градусы, минуты и секунды.
При необходимости округлить до секунды.
- 85°28’12»
- 85°26’50»
- 85°45’00»
- 85°27’00»
Вопрос 1 из 10
Правильно!
Преобразование 85,45° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Правильный ответ
85°27’00»
Следующий вопрос
Вопрос 1 из 10
Неверно
Преобразование 85,45° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Ваш ответ
Правильный ответ
85°27’00»
Следующий вопрос
Вопрос 1 из 10
Преобразование 17,375° в градусы, минуты и секунды.
При необходимости округлить до секунды.
- 17°23’00»
- 17°22’30»
- 17°22’23»
- 17°22’38»
Вопрос 1 из 10
Правильно!
Преобразование 17,375° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Правильный ответ
17°22’30»
Следующий вопрос
Вопрос 1 из 10
Неверно
Преобразование 17,375° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Ваш ответ
Правильный ответ
17°22’30»
Следующий вопрос
Вопрос 1 из 10
Преобразование 107,219° в градусы, минуты и секунды.
При необходимости округлить до секунды.
- 107°13’23»
- 107°37’05»
- 107°13’00»
- 107°13’08»
Вопрос 1 из 10
Правильно!
Преобразование 107,219° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Правильный ответ
107°13’08»
Следующий вопрос
Вопрос 1 из 10
Неверно
Преобразование 107,219° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Ваш ответ
Правильный ответ
107°13’08»
Следующий вопрос
Вопрос 1 из 10
Преобразование 12,9255° в градусы, минуты и секунды.
При необходимости округлить до секунды.
- 12°55’31»
- 12°55’32»
- 12°01’54»
- 12°55’53»
Вопрос 1 из 10
Правильно!
Преобразование 12,9255° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Правильный ответ
12°55’32»
Следующий вопрос
Вопрос 1 из 10
Неверно
Преобразование 12,9255° в градусы, минуты и секунды.
При необходимости округлить до секунды.
Ваш ответ
Правильный ответ
12°55’32»
Следующий вопрос
Вопрос 1 из 10
Преобразование 80°15′ в десятичные градусы.
Если возможно, укажите точные размеры. В противном случае округлить до двух знаков после запятой.
- 80,15°
- 80,3°
- 80,25°
- 80,5°
Вопрос 1 из 10
Правильно!
Преобразование 80°15′ в десятичные градусы.
Если возможно, укажите точные размеры. В противном случае округлить до двух знаков после запятой.
Правильный ответ
80,25°
Следующий вопрос
Вопрос 1 из 10
Неверно
Преобразуйте 80°15′ в десятичные градусы.
Если возможно, укажите точные размеры. В противном случае округлить до двух знаков после запятой.
Ваш ответ
Правильный ответ
80,25°
Следующий вопрос
Вопрос 1 из 10
Преобразуйте 121°11’45» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
- 121,93°
- 121,1145°
- 121,0652°
- 121,20°
Вопрос 1 из 10
Правильно!
Переведите 121°11’45» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
Правильный ответ
121,20°
Следующий вопрос
Вопрос 1 из 10
Неверно
Переведите 121°11’45» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
Ваш ответ
Правильный ответ
121,20°
Следующий вопрос
Вопрос 1 из 10
Преобразуйте 19°00’21» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
- 19,21°
- 19,35°
- 19,04°
- 19.
 01°
01°
Вопрос 1 из 10
Правильно!
Преобразовать 19°00’21» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
Правильный ответ
19.01°
Следующий вопрос
Вопрос 1 из 10
Неверно
Переведите 19°00’21» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
Ваш ответ
Правильный ответ
19.01°
Следующий вопрос
Вопрос 1 из 10
Преобразуйте 98°34’40» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
- 98,35°
- 98,525°
- 98,344°
- 98,58°
Вопрос 1 из 10
Правильно!
Преобразование 98°34’40» в десятичные градусы.
Если возможно, укажите точные размеры. В противном случае округлить до двух знаков после запятой.
Правильный ответ
98,58°
Следующий вопрос
Вопрос 1 из 10
Неверно
Преобразуйте 98°34’40» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
Ваш ответ
Правильный ответ
98,58°
Следующий вопрос
Вопрос 1 из 10
Преобразуйте 71°03’57» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
- 71,11°
- 71,395°
- 71,07°
- 71,0357°
Вопрос 1 из 10
Правильно!
Преобразовать 71°03’57» в десятичные градусы.
Если возможно, укажите точное значение. В противном случае округлите до двух знаков после запятой.
Правильный ответ
71,07°
Готово
Вопрос 1 из 10
Неверно
Преобразовать 71°03’57» в десятичные градусы.
Если возможно, укажите точные размеры. В противном случае округлить до двух знаков после запятой.
Ваш ответ
Правильный ответ
71,07°
Готово
Вопрос 1 из 10
Вы правильно ответили на 5 из 10 вопросов.
50%
Начать сначала
Смотрите другие карточки и приложения, связанные с:
- угол
- угловая мера
- угловое измерение
- углов
- десятичных градусов
- градусов
- градусов
- градусов-минут-секунд
- измерение
- минут
- минут
- секунд
- секунд
Вопрос 1 из 10
- Автор
- Уэйд Уэллс
- Опубликовано
- 05.
 05.2014
05.2014
- Последнее обновление
- 05.05.2014
- Теги
- угол
- угловая мера
- угловое измерение
- углов
- десятичных градусов
- градусов
- градусов
- градусов-минут-секунд
- измерение
- минут
- минут
- секунд
- секунд
Скачать как документ Word Загрузить пакет SCORM
Комментариев пока нет
Преобразование угловых единиц: десятичные градусы и градусы-минуты-секунды Техническим колледжем Fox Valley распространяется под лицензией Creative Commons Attribution 3.

 По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″).
По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″). [3]
[3]
 Astronet. Проверено 23 декабря 2007.
Astronet. Проверено 23 декабря 2007. проект «Астрогалактика» (29 октября 2005 года). Проверено 26 декабря 2007.
проект «Астрогалактика» (29 октября 2005 года). Проверено 26 декабря 2007.

 Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.
Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника. Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007.
Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007. — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
— М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X 01°
01° 05.2014
05.2014