Экстремумы функции это: Экстремумы функции: признаки существования, примеры решений

Экстремумы функции.

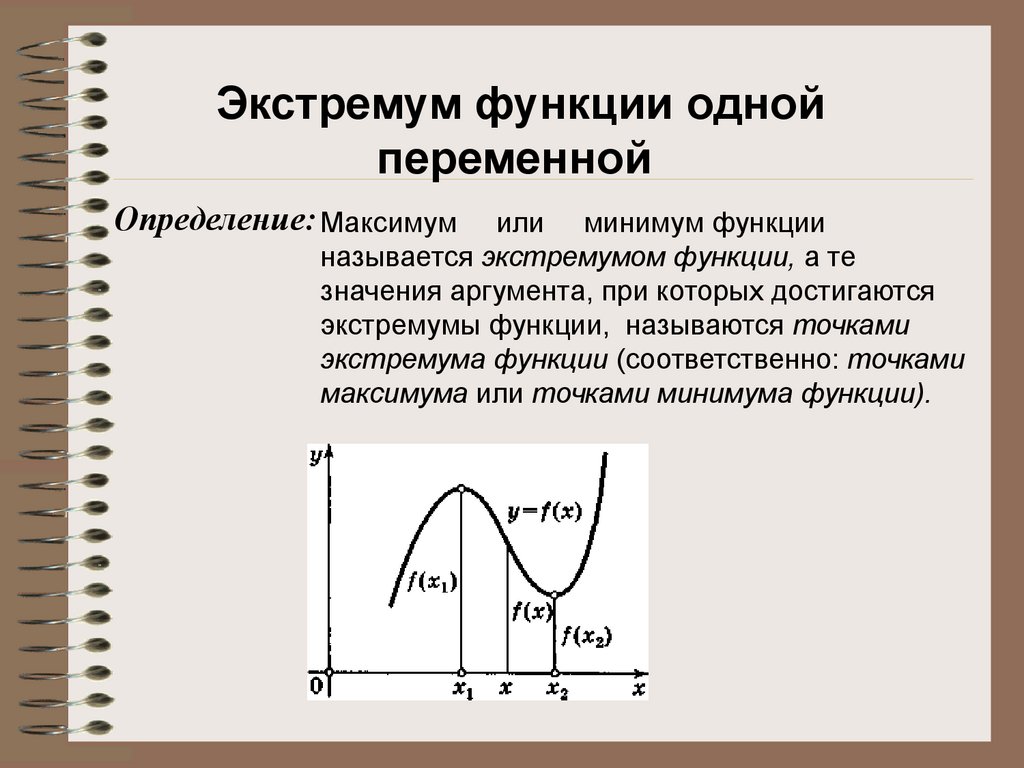
Точка х₀называетсяточкой максимума(минимума) функцииf(х), если в некоторой окрестности точки х₀выполняется неравенствоf(х) ≤f(х₀) (f(х) ≥f(х₀)).

Значение функции в этой точке называется соответственно максимумомилиминимумомфункции. Максимум и минимум функции объединяются общим названиемэкстремумафункции.

Экстремум функции в этом смысле часто называют локальным экстремумом, подчеркивая тот факт, что это понятие связано лишь с достаточно малой окрестностью точки х₀. На одном и том же промежутке функция может иметь несколько локальных максимумов и минимумов, которые не обязательно совпадают сглобальным максимумомилиминимумом(т.е. наибольшим или наименьшим значением функции на всем промежутке).

Необходимое условие экстремума. Для того, чтобы функция имела экстремум в точке, необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала.

Для дифференцируемых функций это условие вытекает из теоремы Ферма. Кроме того, оно предусматривает и случай, когда функция имеет экстремум в точке, в которой она не дифференцируема.

Точки, в которых выполнено необходимое условие экстремума, называются критическими(илистационарнымидля дифференцируемой функции). Эти точки должны входить в область определения функции.

Таким образом, если в какой-либо точке имеется экстремум, то эта точка критическая (необходимость условия). Заметим, что обратное утверждение неверно. Критическая точка вовсе не обязательно является точкой экстремума, т.е. сформулированное условие не является достаточным.

Первое достаточное условие экстремума. Если при переходе через некоторую точку производная дифференцируемой функции меняет свой знак с плюса на минус, то это точка максимума функции, а если с минуса на плюс, — то точка минимума.

Доказательство этого условия вытекает из достаточного условия монотонности (при изменении знака производной происходит переход либо от возрастания функции к убыванию, либо от убывания к возрастанию).

Второе достаточное условие экстремума. Если первая производная дважды дифференцируемой функции в некоторой точке равна нулю, а вторая производная в этой точке положительна, то это точка минимума функции; а если вторая производная отрицательна, то это точка максимума.

Доказательство этого условия также основано на достаточном условии монотонности. В самом деле, если вторая производная положительна, то первая производная является возрастающей функцией. Поскольку в рассматриваемой точке она равна нулю, следовательно, при переходе через нее она меняет знак с минуса на плюс, что возвращает нас к первому достаточному условию локального минимума. Аналогично если вторая производная отрицательна, то первая убывает и меняет знак с плюса на минус, что является достаточным условием локального максимума.

Исследование функции на экстремумв соответствии со сформулированными теоремами включает следующие этапы:

1. Найти первую производную функции f`(x).

2. Проверить выполнение необходимого условия экстремума, т. е. найти критические точки функции f(x), в которых производнаяf`(x) = 0 или не существует.

3. Проверить выполнение достаточного условия экстремума, т.е. либо исследовать знак производной слева и справа от каждой критической точки, либо найти вторую производную f«(x) и определить ее знак в каждой критической точке. Сделать вывод о наличии экстремумов функции.

4. Найти экстремумы (экстремальные значения) функции.

Нахождение глобального максимума и минимума функциина некотором промежутке также имеет большое прикладное значение. Решение этой задачи на отрезке основано на теореме Вейерштрасса, в соответствии с которой непрерывная функция принимает на отрезке свои наибольшее и наименьшее значения. Они могут достигаться как в точках экстремума, так и на концах отрезка. Поэтому решение включает следующие этапы:

1. Найти производную функции f`(x).

2. Найти критические точки функции f(x), в которых производнаяf`(x) = 0 или не существует.

3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.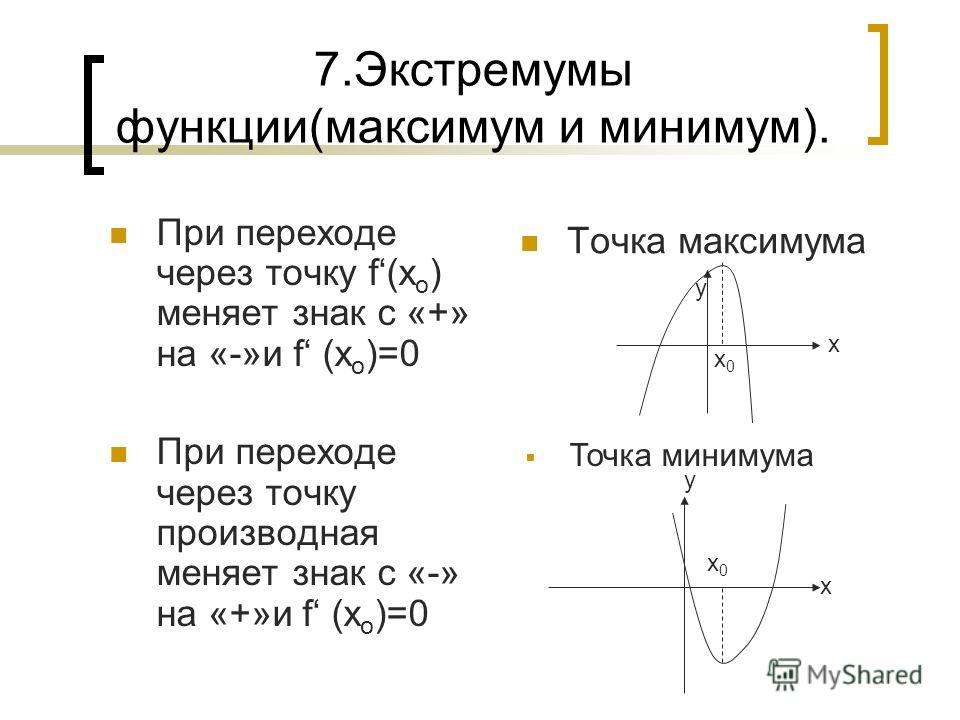

критические точки максимума и минимума

Функции, вовсе необязательно знать о наличии первой и второй производной и понимать их физический смысл. Для начала нужно уяснить следующее:

• экстремумы функции максимизируют или, наоборот, минимизируют значение функции в сколь угодно малой окрестности;
• в точке экстремума не должно быть разрыва функции.

А теперь то же самое, только простым языком. Посмотрите на кончик стержня шариковой ручки. Если ручку расположить вертикально, пишущим концом вверх, то самая середина шарика будет экстремумом — наивысшей точкой. В этом случае говорят о максимуме. Теперь, если повернуть ручку пишущим концом вниз, то на середке шарика уже будет минимум функции. С помощью рисунка, приведенного здесь же, можно представить перечисленные манипуляции для канцелярского карандаша. Итак, экстремумы функции — это всегда критические точки: ее максимумы или минимумы. Прилегающий участок графика может быть сколь угодно острым или плавным, но он должен существовать с обеих сторон, только в этом случае точка является экстремумом. Если график присутствует лишь с одной стороны, точка эта экстремумом являться не будет даже в том случае, если с одной ее стороны условия экстремума выполняются. Теперь изучим экстремумы функции с научной точки зрения. Дабы точка могла считаться экстремумом, необходимо и достаточно, чтобы:

• первая производная равнялась нулю или не существовала в точке;
• первая производная меняла свой знак в этой точке.

Условие трактуется несколько иначе с точки зрения производных более высокого порядка: для функции, дифференцируемой в точке, достаточно, чтобы существовала производная нечетного порядка, неравная нулю, при том, что все производные более низшего порядка должны существовать и быть равными нулю. Это максимально простое толкование теорем из учебников Но для самых обычных людей стоит пояснить этот момент примером. За основу берется обыкновенная парабола. Сразу оговоримся, в нулевой точке у нее имеется минимум. Совсем немного математики:

• первая производная (X 2) | = 2X, для нулевой точки 2Х = 0;
• вторая производная (2Х) | = 2, для нулевой точки 2 = 2.

Таким нехитрым образом проиллюстрированы условия, определяющие экстремумы функции и для производных первого порядка, и для производных высшего порядка. Можно к этому добавить, что вторая производная как раз является той самой производной нечетного порядка, неравной нулю, о которой говорилось чуть выше. Когда речь заходит про экстремумы функции двух переменных, то условия должны выполняться для обоих аргументов. Когда происходит обобщение, то в ход идут частные производные. То есть необходимо для наличия экстремума в точке, чтобы обе производные первого порядка равнялись нулю, либо хотя бы одна из них не существовала. Для достаточности наличия экстремума исследуется выражение, представляющее собой разность произведения производных второго порядка и квадрата смешанной производной второго порядка функции. Если это выражение больше нуля, значит, экстремум имеет место быть, а если присутствует равенство нулю, то вопрос остается открытым, и нужно проводить дополнительные исследования.

Это довольно-таки занятный раздел математики, с которым сталкиваются абсолютно все ученики выпускных классов и студенты. Тем не менее далеко не каждому нравится матан. Некоторые не могут понять даже элементарных вещей наподобие, казалось бы, стандартного исследования функции. Данная статья призвана исправить подобную оплошность. Хотите поподробнее узнать об анализе функции? Желаете узнать, что такое точки экстремума и как их найти? Тогда данная статья для вас.

Исследование графика функции

Для начала стоит понять, зачем вообще необходимо анализировать график. Существуют простые функции, начертить которые не составит труда. Ярким примером подобной функции может служить парабола. Начертить ее график не составит труда. Все что необходимо, так это с помощью простого преобразования найти числа, при которых функция принимает значение 0. И в принципе это все что знать для того, чтобы начертить график параболы.

Но что делать, если функция, график которой нам нужно начертить, намного сложнее? Поскольку свойства сложных функций довольно-таки неочевидны, необходимо проводить целый анализ. Только после этого можно изобразить функцию графически. Как же это сделать? Ответ на этот вопрос вы сможете найти в данной статье.

План анализа функции

Первое, что необходимо сделать, так это провести поверхностное исследование функции, в ходе которого мы найдем область определения. Итак, начнем по порядку. Область определения — это совокупность тех значений, которыми функция задается. Проще говоря, это те числа, которые можно использовать в функции вместо х. Для того чтобы определить область определения, необходимо просто взглянуть на запись. К примеру, очевидно, что у функции у (х) = х 3 + х 2 — х + 43 область определения — множество действительных чисел. Ну а с функцией наподобие (х 2 — 2х)/х все немного иначе. Поскольку число в знаменателе не должно равняться 0, то областью определения данной функции будут все действительные числа, помимо нуля.

Далее необходимо найти так называемые нули функции. Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х 2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х 2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.

Во время исследования графика функции многие сталкиваются с проблемой в виде точек экстремума. И это странно. Ведь экстремумы — это довольно-таки простая тема. Не верите? Убедитесь сами, прочитав данную часть статьи, в которой мы поговорим о точках минимума и максимума.

Для начала стоит разобраться в том, что собой представляет экстремум. Экстремум — это предельное значений, которое достигает функция на графике. Отсюда получается, что существует два крайних значения — максимум и минимум. Для наглядности можно посмотреть на картинку, что расположена выше. На исследованной области точка -1 является максимумом функции у (х) = х 5 — 5х, а точка 1, соответственно, минимумом.

Также не стоит путать между собой понятия. Точки экстремума функции — это те аргументы, при которых заданная функция приобретает крайние значения. В свою очередь, экстремумом называют значение минимумов и максимумов функции. К примеру, вновь рассмотрим рисунок выше. -1 и 1 — это точки экстремума функции, а 4 и -4 — это сами экстремумы.

Нахождение точек экстремума

Но как все-таки найти точки экстремума функции? Все довольно-таки просто. Первое, что необходимо сделать — найти производную уравнения. Допустим, мы получили задание: «Найдите точки экстремума функции y (x), x — аргумент. Для наглядности возьмем функцию у (х) = х 3 + 2х 2 + х + 54. Проведем дифференцирование и получим следующее уравнение: 3х 2 + 4х + 1. В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни.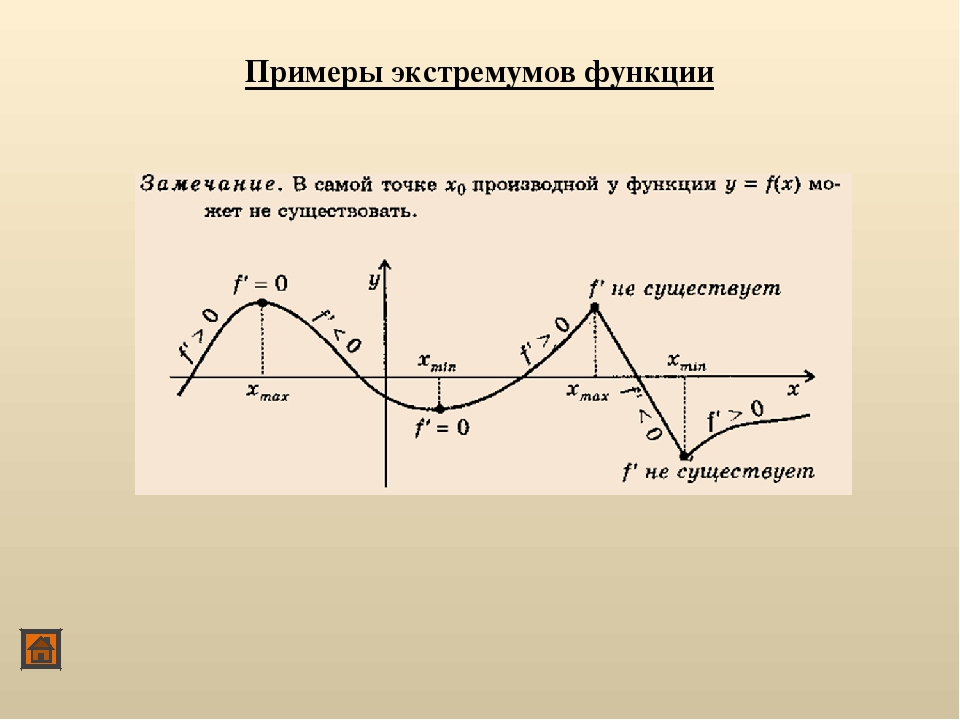

Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.

Также стоит отметить, что на ЕГЭ требуют не просто найти точки экстремума, Но и провести с ними какую-то операцию (прибавить, умножить и т. д.). Именно по этой причине стоит обратить особое внимание на условия задачи. Ведь из-за невнимательности можно потерять баллы.

Как видите, этот признак экстремума функции требует существования производной как минимум до второго порядка в точке .

Пример.

Найти экстремумы функции .

Решение.

Начнем с области определения:

Продифференцируем исходную функцию:

x=1 , то есть, это точка возможного экстремума. Находим вторую производную функции и вычисляем ее значение при x = 1 :

Следовательно, по второму достаточному условию экстремума,

x=1 — точка максимума. Тогда — максимум функции.

Графическая иллюстрация.

Ответ:

Третье достаточное условие экстремума функции.

Пусть функция y=f(x) имеет производные до n -ого порядка в -окрестности точки и производные до n+1 -ого порядка в самой точке . Пусть и .

Пример.

Найти точки экстремума функции .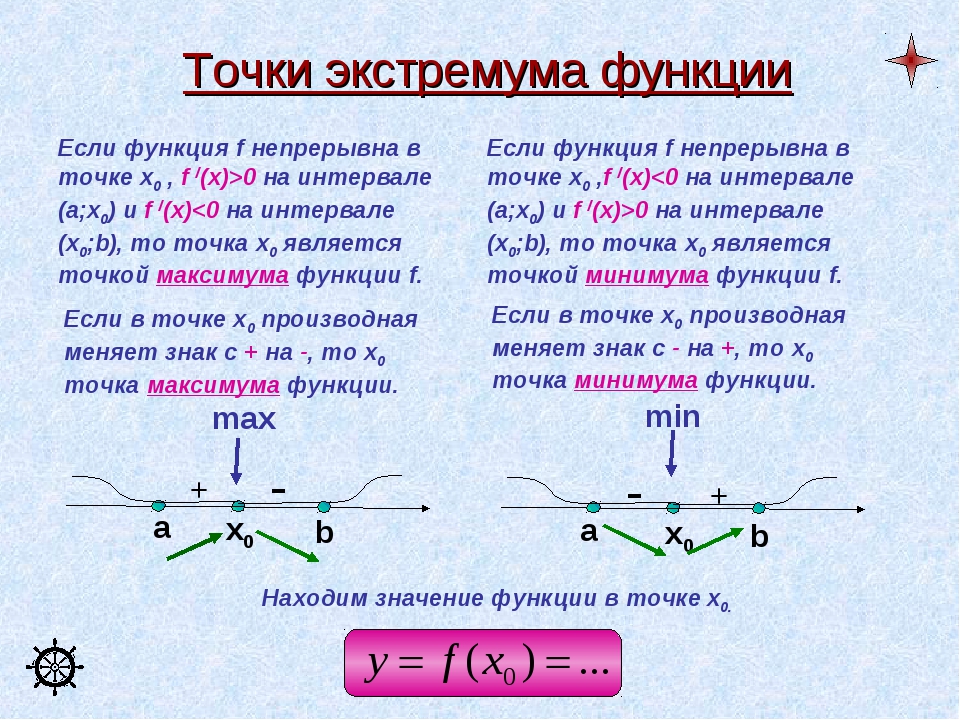

Решение.

Исходная функция является целой рациональной, ее областью определения является все множество действительных чисел.

Продифференцируем функцию:

Производная обращается в ноль при , следовательно, это точки возможного экстремума. Воспользуемся третьим достаточным условием экстремума.

Находим вторую производную и вычисляем ее значение в точках возможного экстремума (промежуточные вычисления опустим):

Следовательно, — точка максимума (для третьего достаточного признака экстремума имеем n=1 и ).

Для выяснения характера точек находим третью производную и вычисляем ее значение в этих точках:

Следовательно, — точка перегиба функции (n=2 и ).

Осталось разобраться с точкой . Находим четвертую производную и вычисляем ее значение в этой точке:

Следовательно, — точка минимума функции.

Графическая иллюстрация.

Ответ:

Точка максимума, — точка минимума функции.

10. Экстремумы функции Определение экстремума

Функция y = f(x) называется возрастающей (убывающей ) в некотором интервале, если при x 1 f(x 2)).

Если дифференцируемая функция y = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке f » (x)  0

(f » (x)  0).

Точка x о называется точкой локального максимума (минимума ) функции f(x), если существует окрестность точки x о , для всех точек которой верно неравенство f(x) ≤ f(x о) (f(x) ≥ f(x о)).

Точки максимума и минимума называются точками экстремума , а значения функции в этих точках — ее экстремумами.

Точки экстремума

Необходимые условия экстремума . Если точка x о является точкой экстремума функции f(x), то либо f » (x о) = 0, либо f (x о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x о — критическая точка. Если f » (x) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную f » (x) в окрестности точки x о и вторую производную в самой точке x о . Если f » (x о) = 0, >0 (x о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .

Пример 3.22. Найти экстремумы функции f(x) = 2x 3 — 15x 2 + 36x — 14.

Решение.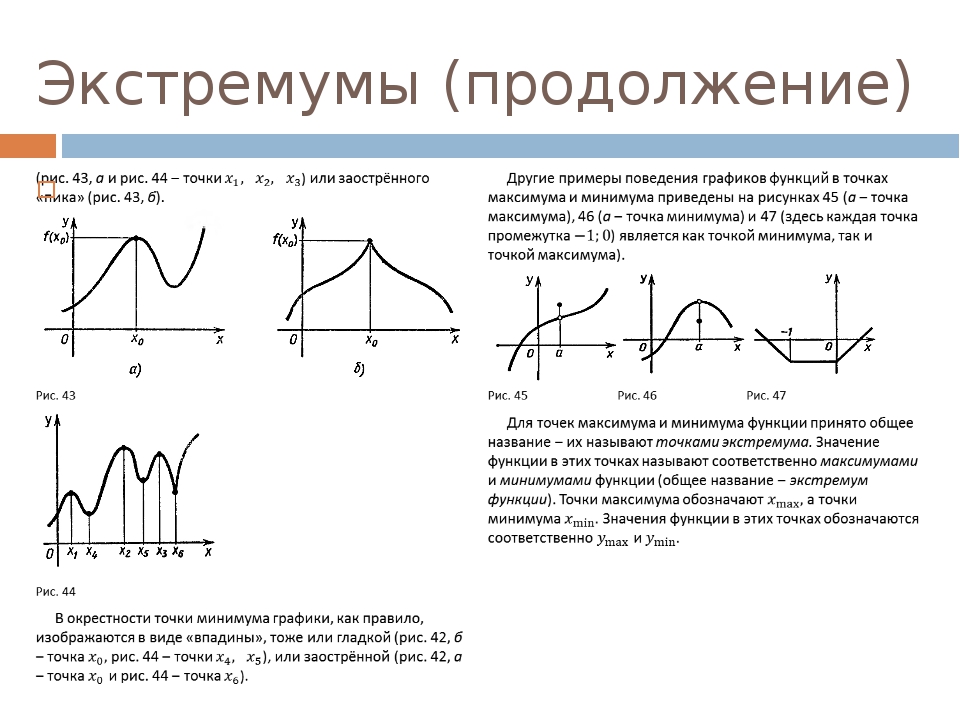 Так как f » (x) = 6x 2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x 1 = 2 и x 2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x 1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x 2 = 3 производная меняет знак минус на плюс, поэтому в точке x 2 = 3 у функции минимум. Вычислив значения функции в точках x 1 = 2 и x 2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.

Определения:

Экстремумом называют максимальное или минимальное значение функции на заданном множестве.

Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.

Точка максимума – это точка, в которой достигается максимальное значение функции.

Точка минимума – это точка, в которой достигается минимальное значение функции.

Пояснение.

На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше).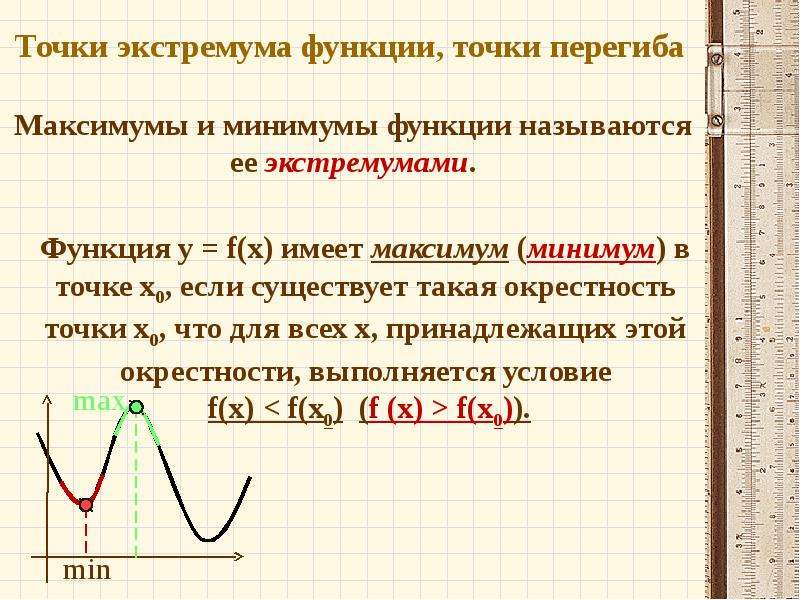 В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:

x max = 3, x max = 8.

В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:

Точки максимума и минимума являются точками экстремума функции , а значения функции в этих точках – ее экстремумами .

Критические и стационарные точки функции:

Необходимое условие экстремума:

Достаточное условие экстремума:

На отрезке функция y = f (x ) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .

Алгоритм исследования непрерывной функции y = f (x ) на монотонность и экстремумы:

Что такое экстремум функции и каково необходимое условие экстремума?

Экстремумом функции называется максимум и минимум функции.

Необходимое условие максимума и минимума (экстремума) функции следующее: если функция f(x) имеет экстремум в точке х = а, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.

Это условие необходимое, но не достаточное. Производная в точке х = а может обращаться в нуль, в бесконечность или не существовать без того, чтобы функция имела экстремум в этой точке.

Каково достаточное условие экстремума функции (максимума или минимума)?

Первое условие:

Если в достаточной близости от точки х = а производная f?(x) положительна слева от а и отрицательна справа от а, то в самой точке х = а функция f(x) имеет максимум

Если в достаточной близости от точки х = а производная f?(x) отрицательна слева от а и положительна справа от а, то в самой точке х = а функция f(x) имеет минимум при условии, что функция f(x) здесь непрерывна.

Вместо этого можно воспользоваться вторым достаточным условием экстремума функции:

Пусть в точке х = а первая производная f?(x) обращается в нуль; если при этом вторая производная f??(а) отрицательна, то функция f(x) имеет в точке x = a максимум, если положительна — то минимум.

Что такое критическая точка функции и как её найти?

Это значение аргумента функции, при котором функция имеет экстремум (т.е. максимум или минимум). Чтобы его найти, нужно найти производную функции f?(x) и, приравняв её к нулю, решить уравнение f?(x) = 0. Корни этого уравнения, а также те точки, в которых не существует производная данной функции, являются критическими точками, т. е. значениями аргумента, при которых может быть экстремум. Их можно легко определить, взглянув на график производной : нас интересуют те значения аргумента, при которых график функции пересекает ось абсцисс (ось Ох) и те, при которых график терпит разрывы.

Для примера найдём экстремум параболы .

Функция y(x) = 3×2 + 2x — 50.

Производная функции: y?(x) = 6x + 2

Решаем уравнение: y?(x) = 0

6х + 2 = 0, 6х = -2, х=-2/6 = -1/3

В данном случае критическая точка — это х0=-1/3. Именно при этом значении аргумента функция имеет экстремум . Чтобы его найти , подставляем в выражение для функции вместо «х» найдённое число:

y0 = 3*(-1/3)2 + 2*(-1/3) — 50 = 3*1/9 — 2/3 — 50 = 1/3 — 2/3 — 50 = -1/3 — 50 = -50,333.

Как определить максимум и минимум функции, т.е. её наибольшее и наименьшее значения?

Если знак производной при переходе через критическую точку х0 меняется с «плюса» на «минус», то х0 есть точка максимума ; если же знак производной меняется с минуса на плюс, то х0 есть точка минимума ; если знак не меняется, то в точке х0 ни максимума, ни минимума нет.

Для рассмотренного примера:

Берём произвольное значение аргумента слева от критической точки: х = -1

При х = -1 значение производной будет у?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (т.е. знак — «минус»).

Теперь берём произвольное значение аргумента справа от критической точки: х = 1

При х = 1 значение производной будет у(1) = 6*1 + 2 = 6 + 2 = 8 (т.е. знак — «плюс»).

Как видим, производная при переходе через критическую точку поменяла знак с минуса на плюс. Значит, при критическом значении х0 мы имеем точку минимума.

Наибольшее и наименьшее значение функции на интервале (на отрезке) находят по такой же процедуре, только с учетом того, что, возможно, не все критические точки будут лежать внутри указанного интервала. Те критические точки, которые находятся за пределом интервала, нужно исключить из рассмотрения. Если внутри интервала находится только одна критическая точка — в ней будет либо максимум, либо минимум. В этом случае для определения наибольшего и наименьшего значений функции учитываем также значения функции на концах интервала.

Например, найдём наибольшее и наименьшее значения функции

y(x) = 3sin(x) — 0,5х

на интервалах:

Итак, производная функции —

y?(x) = 3cos(x) — 0,5

Решаем уравнение 3cos(x) — 0,5 = 0

cos(x) = 0,5/3 = 0,16667

х = ±arccos(0,16667) + 2πk.

Находим критические точки на интервале [-9; 9]:

х = arccos(0,16667) — 2π*2 = -11,163 (не входит в интервал)

х = -arccos(0,16667) — 2π*1 = -7,687

х = arccos(0,16667) — 2π*1 = -4,88

х = -arccos(0,16667) + 2π*0 = -1,403

х = arccos(0,16667) + 2π*0 = 1,403

х = -arccos(0,16667) + 2π*1 = 4,88

х = arccos(0,16667) + 2π*1 = 7,687

х = -arccos(0,16667) + 2π*2 = 11,163 (не входит в интервал)

Находим значения функции при критических значениях аргумента:

y(-7,687) = 3cos(-7,687) — 0,5 = 0,885

y(-4,88) = 3cos(-4,88) — 0,5 = 5,398

y(-1,403) = 3cos(-1,403) — 0,5 = -2,256

y(1,403) = 3cos(1,403) — 0,5 = 2,256

y(4,88) = 3cos(4,88) — 0,5 = -5,398

y(7,687) = 3cos(7,687) — 0,5 = -0,885

Видно, что на интервале [-9; 9] наибольшее значение функция имеет при x = -4,88:

x = -4,88, у = 5,398,

а наименьшее — при х = 4,88:

x = 4,88, у = -5,398.

На интервале [-6; -3] мы имеем только одну критическую точку: х = -4,88. Значение функции при х = -4,88 равно у = 5,398.

Находим значение функции на концах интервала:

y(-6) = 3cos(-6) — 0,5 = 3,838

y(-3) = 3cos(-3) — 0,5 = 1,077

На интервале [-6; -3] имеем наибольшее значение функции

у = 5,398 при x = -4,88

наименьшее значение —

у = 1,077 при x = -3

Как найти точки перегиба графика функции и определить стороны выпуклости и вогнутости?

Чтобы найти все точки перегиба линии y = f(x), надо найти вторую производную, приравнять её к нулю (решить уравнение) и испытать все те значения х, для которых вторая производная равна нулю, бесконечна или не существует. Если при переходе через одно из этих значений вторая производная меняет знак, то график функции имеет в этой точке перегиб. Если же не меняет, то перегиба нет.

Корни уравнения f ? (x) = 0, а также возможные точки разрыва функции и второй производной разбивают область определения функции на ряд интервалов. Выпуклость на каждом их интервалов определяется знаком второй производной. Если вторая производная в точке на исследуемом интервале положительна, то линия y = f(x) обращена здесь вогнутостью кверху, а если отрицательна — то книзу.

Как найти экстремумы функции двух переменных?

Чтобы найти экстремумы функции f(x,y), дифференцируемой в области её задания, нужно:

1) найти критические точки, а для этого — решить систему уравнений

fх? (x,y) = 0, fу? (x,y) = 0

2) для каждой критической точки Р0(a;b) исследовать, остается ли неизменным знак разности

для всех точек (х;у), достаточно близких к Р0. Если разность сохраняет положительный знак, то в точке Р0 имеем минимум, если отрицательный — то максимум. Если разность не сохраняет знака, то в точке Р0 экстремума нет.

Аналогично определяют экстремумы функции при большем числе аргументов.

Когда в ноябре отмечают Всемирный день телевидения
17 декабря 1996 года Генеральная Ассамблея провозгласила 21 ноября «Всемирным днем телевидения» в ознаменование даты проведения первого Всемирного телевизионного форума в Организации Объединенных Наций. Государствам было предложено отмечать этот день, обмениваясь телевизионными программами, посвященными таким проблемам, как мир, безопаснос

Что такое черемуха
Черемуха — вид вишни, семейство розоцветные, произрастает в северной Европе и северной Азии. Это довольно высокий кустарник, который достигает до 16 метров в высоту. Обычно высота черемухи составляет около 9 метров. Характеризуется она своим душистым ароматом цветов. Растет не менее чем 800 метров над уровнем моря. Предпочитает кислые почвы дубовых

Какие две стадии включает период клеточного деления (фаза М)
Клеточный цикл — это период существования клетки от момента её образования путем деления материнской клетки до собственного деления или гибели. Длительность клеточного цикла у разных клеток варьируется. Быстро размножающиеся клетки взрослых организмов, такие как кроветворные или базальные клетки эпидермиса и тонкой кишки, могут входить в клеточный цикл

Почему у браузера Opera («Опера») не отображается главное меню
Для экономии места на экране в браузере Opera, начиная с версии 10. 5, по умолчанию выключено главное меню. Разработчики приняли такое решение в связи с распространением нетбуков, имеющих небольшие дисплеи, и широкоформатных ЖК-мониторов, у которых высота экрана значительно меньше его ширины. Доступ ко всем функциям, которые были в главном меню

Где расположен город Братск
Братск — город в России в Иркутской области. Географическое расположение Братска обусловило его превращение в «ворота» Севера. Город расположен в центре Восточно-Сибирского региона России в центральной части Ангарского кряжа на берегу Братского водохранилища на реке Ангаре. Расстояние до областного центра — города Иркутска:

Что такое аллегория
Аллегория (от греч. allegoria — иносказание) — одна из форм иносказания, условная передача отвлеченного понятия или суждения посредством конкретного образа. Аллегория наиболее распространена в изобразительном искусстве (женщина с повязкой на глазах и весами в руках — правосудие, якорь — надежда и т.д.). В литературе многие аллегорические образы

Как ухаживать за гелихризумом
Гелихризум (Бессмертник, Цмин)Латинское название: Helichrysum. Категории: однолетние растения, растения для альпинария.Семейство: сложноцветные (Compositae). Родина: гелихризум произрастает на территории умеренных районов Европы, Азии, Африки и Австралии. Родина цмина Милфордовой — окрестности Кейптауна.Форма: травянистое растени

Кто написал роман «Белые и черные»
Роман «Белые и черные» — о шахматах и о шахматистах. В качестве центральной фигуры романа выведен великий шахматист, чемпион мира Александр Алёхин. Автор романа «Белые и черные» — выдающийся советский шахматист, международный гроссмейстер, писатель, член Союза писателей

Каково полное название второй книги трилогии Даниеля Дефо о Робинзоне Крузо
Даниель Дефó (англ. Daniel Defoe; родился под именем Daniel Foe; ок. 1660 — 1731) — английский писатель и публицист, известен сегодня главным образом как автор романа «Робинзон Крузо» (таково принятое в научном литературоведении и издательской

Чем питаются горностаи
Горностай (Mustela erminea) — ценный пушной зверёк семейства куньих. Внешний вид. Все представители рода хорьков — зверьки с гибким удлиненным телом, очень изящные и подвижные, от куниц отличаются наличием белого цвета на кончике морды. Уши маленькие, округлые.Длина тела горностая — 16-3

С какими болезнями не берут в армию
Категории годности к военной службе («А», «Б», «В», «Г», «Д») определяются военно-врачебной комиссией при медицинском освидетельствовании призывника. А — годен к военной службе. Б &nd

Экстремум функции

Экстремум (или акут) функции – это степень, при которой достигается максимальное или минимальное значение функции в пределах номера интервала. Экстремум является первым и, следовательно, минимальным значением, необходимым в результате предоставления большого количества данных для выполнения пары и помощи в ответах на вопросы оптимальности.

Что такое экстремум функции?

Экстремумы во множественном числе от слова экстремум представляют собой наибольшее и наименьшее значение функции либо в заданном диапазоне локальных или относительных экстремумов, либо во всей области глобальных или абсолютных экстремумов. Пьер был первым математиком, давшим людям общую методику нахождения максимумов и минимумов функций. Теория экстремумов, наибольшего и наименьшего, применима к практическим задачам оптимизации, таким как определение размеров контейнера, который будет вмещать максимальный объем для заданного количества.

Экстремумы функций двух переменных

Как функции одной переменной, так и функции двух переменных могут иметь локальные и глобальные экстремумы.

 Мы говорим, что f(x, y) имеет глобальный максимум в некоторой степени (a, b) своей области определения Df, если f(x, y) ≤ f(a, b) для всех точек (x, y) в Дф.

Вот почему f (a, b) имеет большее значение, чем значение f в Df. Мы говорим, что f(x, y) охватывает глобальный минимум в некоторой степени (a, b) своей области определения Df, если f(a, b) ⩽ f(x, y) для всех точек (x, y) в Df . мы говорим, что f(x, y) включает локальный максимум в степени (a, b) своей области определения Df, если существует R > 0 таких f(x, y) ⩽ f(a, b) для всех точек ( x, y) в Df, удовлетворяющих условию (x − a) 2 + (y − b) 2 < R2.

Мы говорим, что f(x, y) имеет локальный минимум в степени (a, b) своей области определения Df, если существует R > 0 такое f(a, b) ≤ f(x, y) для всех точек (x, y) в Df, удовлетворяющих (x − a) 2 + (y − b) 2 < R2 . Локальные максимумы и собственные минимумы известны как локальные экстремумы.

Абсолютный экстремум

Абсолютный экстремум или глобальный экстремум функции в заданном интервале — это точка, в которой максимальное или минимальное значение функции достигается очень быстро, заданный интервал является областью определения функции, и поэтому абсолютно экстремумом является та цель, которая соответствует переднему или минимальному значению всей функции. Абсолютный максимум такой переменной во всей области определяется по существу как абсолютный максимум обеих функций, в то время как абсолютный минимум такой функции определяется как абсолютный минимум признака внутри всей области.

Локальные экстремумы

Точка xx является локальным максимумом или минимумом функции, если она является абсолютным максимумом или минимумом значения функции в интервале (x−c,x+c) для некоторого достаточно малого значения cc.

Многие локальные экстремумы также обнаруживаются при определении абсолютного максимума или минимума функции. Те максимумы и минимумы любой переменной, которые происходят в чрезвычайно определенный период, называются локальными максимумами и минимумами. Любое значение такой переменной в области внутри определенного интервала, при котором значение функционала вблизи этого времени всегда кажется меньшим, чем значение обеих функций в конкретной точке, называется максимумом области.

Для заданной функции ff и интервала [a, \, b][a,b] локальные экстремумы также могут быть точками разрыва, точками недифференцируемости или точками, в которых производная имеет значение 00. Однако , ни одна из этих точек не обязательно является локальным экстремумом; поэтому локальное поведение функции необходимо исследовать для каждой точки. То есть для заданной точки xx значения функции в пределах интервала (x – c, \, x + c) (X-C, x+c) должны быть проверены для достаточно малых cc.

Вывод

Экстремум (или экстремальное значение) функции – это степень, при которой достигается максимальное или минимальное значение функции на некотором интервале. экстремумы (множественное число от экстремума) — это наибольшее и наименьшее значение функции либо в заданном диапазоне (локальные или относительные экстремумы), либо во всей области (глобальные или абсолютные экстремумы).

Экстремум

Экстремум

• О
• Статистика
• Теория чисел.

  На одном уровне на этот вопрос можно ответить, установив «границы» на $f$. Другими словами, полезно хотя бы знать, что существует некоторое значение $f(x)$, которое не превышает (или ниже) или что такого значения не существует.

  Однако не все границы созданы одинаковыми — некоторые из них лучше справляются с «ограничением», чем другие. Например, $-100 \le \sin(x) \le 100$, безусловно, верно, но знание того, что $-1 \le \sin(x) \le 1$, вероятно, будет гораздо полезнее!

  Интересно, что мы можем доказать (используя эпсилон-дельта-определение пределов и определение непрерывности), что любая функция, непрерывная на отрезке $[a,b]$, должна быть ограничена (сверху и снизу) на этом отрезке. Это известно как теорема об ограниченности .

  Конечно, мы могли бы дать лучший ответ на поставленный выше вопрос, фактически найдя максимальное (или минимальное) значение $f(x)$, если оно существует.

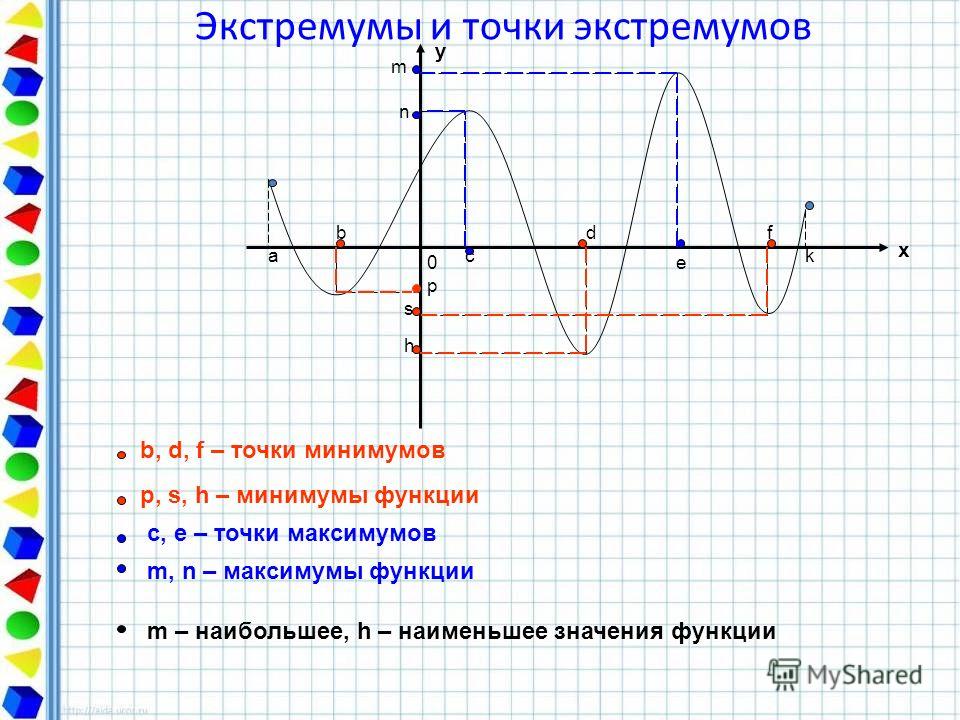
  Обратите внимание, что такое значение не всегда должно существовать, даже если рассматриваемая функция ограничена. Например, следующая функция ограничена сверху, но не достигает своего максимального значения из-за наличия «дыры слева», связанной с разрывом щели при $x=c$; показанная функция также не достигает минимального значения, если предположить, что уменьшение, показанное справа, продолжается линейно.

  Теперь рассмотрим следующий сценарий — предположим, что приведенная ниже функция дает вам вероятную прибыль, связанную с инвестицией $x$ долларов в какой-либо проект. В настоящее время вы инвестируете $\$7{,}129$, и вам интересно, следует ли вам увеличить или уменьшить свои инвестиции. Если вы не можете существенно увеличить свои инвестиции, вам лучше придерживаться ваших текущих инвестиций. Как видите, любое небольшое изменение, будь то увеличение или уменьшение, будет стоить вам денег! Однако предположим, что вы можете инвестировать в этот проект от $\$0$ до $\$40{,}000$. В этом случае вам следует инвестировать $\$36{,}110$ — нет абсолютно никакой другой суммы инвестиций, которая принесла бы вам больше денег.

  Это мотивирует следующие определения:

  • Функция $f$ имеет локальных максимумов в точке $c$ тогда и только тогда, когда существует открытый интервал, содержащий $c$, на котором определена $f$, такой, что $f(c) \ge f(x)$ для всех $x$ в этом интервале.

  • Функция $f$ имеет локальный минимум в точке $c$ тогда и только тогда, когда существует открытый интервал, содержащий $c$, на котором определена $f$, такой, что $f(c) \le f( x)$ для всех $x$ в этом интервале.

  В целом вышеперечисленное называется локальными экстремумами , в отличие от того, что мы теперь определяем ниже:

  • Функция $f$, область определения которой содержит некоторый интервал $I$, имеет абсолютный максимум на интервале I в точке $c$, если и только $c$ находится в этом интервале $I$ и $f(c) \ge f(x)$ для всех $x$ в этом интервале.

  • Функция $f$, область определения которой содержит некоторый интервал $I$, имеет абсолютных минимумов на интервале I в $c$, если и только $c$ находится в этом интервале $I$ и $f(c) \le f(x)$ для всех $x$ в этом интервале.

  Неудивительно, что они, в свою очередь, называются абсолютными экстремумами .

  Если мы хотим знать, возникают ли и где такие экстремумы (как локальные, так и абсолютные), мы должны знать о следующих двух важных результатах. Первый дает нам достаточное (но не необходимое) условие для того, чтобы функция имела абсолютный максимум и минимум. Второй сужает места, которые нам нужно искать, поскольку мы ищем любые присутствующие локальные или абсолютные экстремумы:

  Теорема об экстремальном значении
  Если $f$ непрерывна на $[a,b]$, то $f$ имеет абсолютный максимум и абсолютный минимум в $[a,b]$.

  Теорема Ферма
  Если $f$ дифференцируема в $c$ и $f(c)$ является локальным экстремумом, то $f'(c)=0$.

  Внимательно подумайте, как их можно использовать вместе, чтобы найти все экстремумы. Для заданной функции $f$ скорее всего существует всего несколько мест (если они вообще есть), где $f'(c)=0$. Важно отметить, что теорема Ферма делает , а не , гарантирует, что обнаружение этих мест приведет к искомым экстремумам (как показано на рисунке ниже), но позволяет нам исключить большое количество мест, которые мы могли бы искать в противном случае.

  Конечно, теорема Ферма ничего не говорит об экстремальных значениях, где $f$ не дифференцируема, так что они представляют собой дополнительные критические места, которые нужно искать в нашем поиске экстремумов.

  Имея это в виду, мы делаем следующее определение:

  Пусть $f$ — функция, область определения которой содержит значение $c$. Мы говорим, что $c$ является критическим значением , если либо $f'(c)=0$, либо $f$ не дифференцируема в $c$.

  Итак, чтобы найти экстремумы функции, мы обязательно должны проверить поведение функции при всех ее критических значениях.

  No related posts.