Построение поверхностей
Лабораторная работа №4
Цель работы: изучить основные возможности приложения Microsoft Excel 2010 для построения поверхностей.
4.1. Краткие теоретические сведения
По умолчанию адреса в формулах рассматриваются как относительные. Это означает, что при копировании формулы адреса автоматически изменяются в соответствии с относительным расположением исходной ячейки и создаваемой копии. Например, пусть в ячейке B2 имеется формула с адресом A3. Ячейка A3 относительно ячейки B2 находится на один столбец левее и на одну строку ниже. При копировании формулы в любую ячейку такое относительное расположение адресов сохранится. Например, при копировании формулы в ячейку C4 адрес в формуле автоматически изменится, и будет указывать на ячейку, которая находится на один столбец левее и на одну строку ниже C4,
е. B5.В некоторых случаях такое автоматическое изменение адресов при копировании не требуется. Чтобы запретить автоматическое изменение адреса, используется абсолютный адрес. Перед строкой или столбцом, изменение которых необходимо запретить, ставится символ $. Для изменения способа адресации при редактировании формулы символ $ можно вводить непосредственно с клавиатуры, а можно выделить адрес в формуле и нажать функциональную клавишу F4. При последовательных нажатиях клавиши F4 адрес, например, A1, будет модифицироваться, как показано в таблице 4.1.
Таблица 4.1
Изменение адреса A1 при последовательных нажатиях клавиши F4
Адрес | Способ адресации |
$A$1 | Абсолютный |
A$1 | Относительный по столбцу, абсолютный по строке |
$A1 | Абсолютный по столбцу, относительный по строке |
A1 | Относительный |
4.
2. Примеры4.2.1. Построить поверхность, заданную уравнением
, (1)
которая называется эллиптическим параболоидом, при p = q = 1,
-1 ≤ x ≤ 1, -1 ≤ y ≤ 1.
Методические рекомендации
Запустите приложение Microsoft Excel 2010: Пуск → Все программы →
Сохраните рабочую книгу в своей рабочей папке на диске или на личном внешнем носителе: вкладка Файл – команда Сохранить как. Дайте имя файлу Л.р.№4-пример.
Замените имя текущего рабочего листа. Для этого дважды щелкните левой кнопкой мыши по ярлычку рабочего листа с надписью Лист1 и наберите имя листа Эллиптический параболоид.
Сформируйте массив значений x. Для этого в ячейку с адресом A2 занесите значение -1, а в ячейку с адресом A3 – значение —0,9. Затем выделите диапазон ячеек A2:A3, наведите курсор мыши на маркер заполнения и протяните его вниз с нажатой левой кнопкой мыши до ячейки с адресом A22 включительно.
Сформируйте массив значений y. Для этого в ячейку с адресом B1 занесите значение -1, а в ячейку с адресом C1 значение —0,9. Затем выделите диапазон ячеек B1:C1, наведите курсор мыши на маркер заполнения и протяните его направо с нажатой левой кнопкой мыши до ячейки с адресом V1 включительно.
Пользуясь вкладками Шрифт, Число и Ячейки, добейтесь, чтобы сформированные массивы значений x и y выглядели так, как показано на рисунке 4.
2.
2.Использование абсолютной адресации необходимо чтобы запретить изменение соответствующего адреса при последующем копировании формулы.
Выделите ячейку с адресом B2 и, пользуясь маркером заполнения, заполните формулой диапазон ячеек B2:V2. Для этого наведите курсор мыши на маркер заполнения и протяните его направо с нажатой левой кнопкой мыши до ячейки с адресом V2 включительно. Выделяя последовательно несколько ячеек диапазона B2:V2 проанализируйте как изменяются адреса при использовании абсолютной адресации.
Выделите диапазон ячеек B2:V2 и, пользуясь маркером заполнения, заполните формулой диапазон ячеек B2:V22. Для этого наведите курсор мыши на маркер заполнения и протяните его вниз с нажатой левой кнопкой мыши до ячейки с адресом V22 включительно.
Выделяя последовательно несколько ячеек диапазона B2:V22 проанализируйте как изменяются адреса при использовании абсолютной адресации.Для построения диаграммы выделите диапазон ячеек с данными A1:V22 и перейдите на вкладку Вставка. На вкладке Диаграммы откройте список Гистограмма в котором выберите значение Все типы диаграмм …. Укажите тип диаграммы Поверхность и нажмите кнопку OK.
Отредактируйте построенную диаграмму. Для этого наведите курсор мыши на любую линию сетки и дождитесь всплывающей подсказки Вертикальная ось (значений) – основные линии сетки. Нажмите правую кнопку мыши и в меню укажите пункт Удалить. С правой стороны диаграммы располагается элемент диаграммы Легенда, который при наличии одного графика на диаграмме, не имеет смысла. Для удаления легенды наведите курсор на изображение легенды, дождитесь появления всплывающей подсказки «Легенда», или «Ряд
Yi Элемент легенды», выделите легенду и нажмите клавишу Delete на клавиатуре.Расположите диаграмму на листе так, как показано на рисунке 4.2.
Наведите курсор на любую границу диаграммы, дождитесь появления всплывающей подсказки Область диаграммы и нажмите правую кнопку мыши. В появившемся меню укажите пункт Поворот объемной фигуры …. Выясните, как элементы управления влияют на изображение поверхности.
Поверхности вращения. Основные формулы
Поверхности вращения
Пусть в плоскости yOz дана линия L, имеющая уравнение
. Тогда, чтобы получить уравнение поверхности, образованной вращением линии L, лежащей в плоскости yOz вокруг оси Оу, нужно в уравнении этой линии заменить Z на . Искомое уравнение поверхности вращения будет:
Аналогичные правила будут иметь место и по отношению к поверхностям, полученным вращением плоских линий вокруг других координатных осей.
Поверхности второго порядка и их канонические уравнения.
1. Сфера. Сферой или шаровой поверхностью называется геометрическое место точек пространства, равноудаленных от одной точки, называемой центром сферы.
а) Уравнение сферы имеет вид:
где а, b и с — координаты центра сферы, а r — ее радиус.
б) Уравнение сферы с центром в начале координат имеет вид:
Уравнение второй степени изображает сферу, если коэффициенты при квадратах координат равны между собой, а члены с произведением координат отсутствуют.
Координаты центра и радиус сферы находятся путем приведения уравнения сферы к виду (11).
2. Эллипсоид. Эллипсоидом называется поверхность, каноническое (простейшее) уравнение которой имеет вид
(рис.1). Центр эллипсоида лежит в начале координат.
Рис. 1
Отрезки а, b и с — называются полуосями эллипсоида.
Если
, то уравнение (13) определяет эллипсоид вращения
3.
Гиперболоиды
а) Однополостный гиперболоид.
Однополостным гиперболоидом называется поверхность, каноническое (простейшее) уравнение которой имеет вид:
(рис.2).
При a=b уравнение (14) определяет однополостный гиперболоид вращения.
б) Двухполостный гиперболоид.
Двухполостным гиперболоидом называется поверхность, каноническое (простейшее) уравнение которой имеет вид:
(рис.3). При а=Ь уравнение (15) определяет двухполостный гиперболоид вращения.
Рис. 2 Рис.3
4. Параболоиды
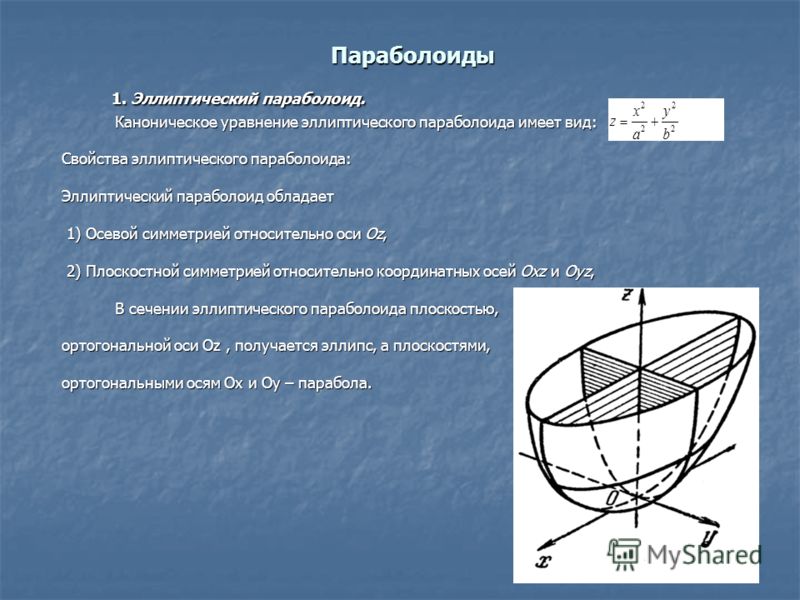
а) Эллиптическим параболоидом называется поверхность, каноническое (простейшее) уравнение которой имеет вид:
(рис.4).
При p = q уравнение (16) определяет параболоид вращения
Рис.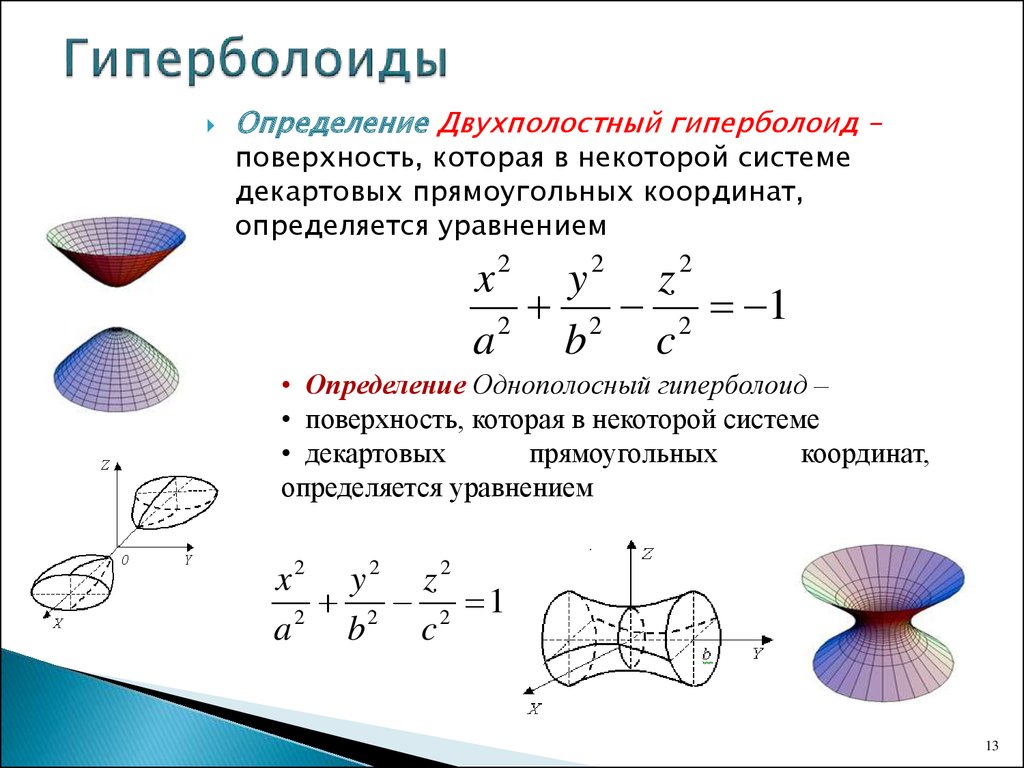
4
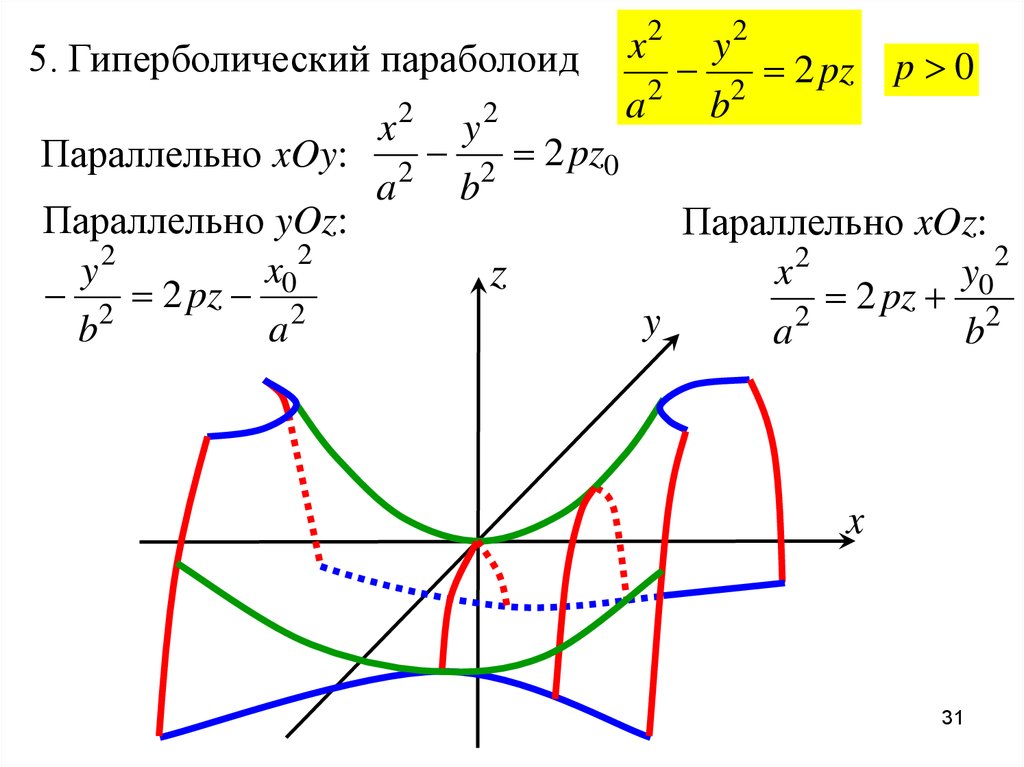
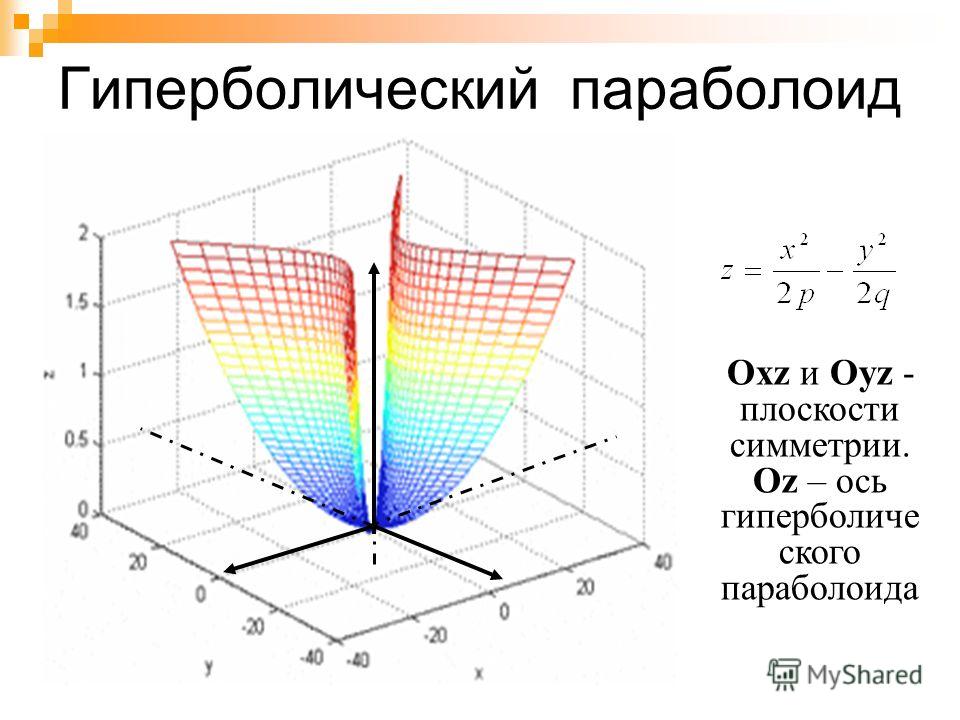
б) Гиперболическим параболоидом называется поверхность, каноническое (простейшее) уравнение которой имеет вид:
(рис.5).
Рис.5
5. Конус второго порядка
(рис.6).
При а = b уравнение (18) определяет круговой конус
Рис.6
6. Цилиндры второго порядка
а) Эллиптическим цилиндром называется поверхность, каноническое уравнение которой имеет вид:
(рис.7).
Рис. 7 Рис.8 Рис.9
При а=b уравнение (19) определяет круговой цилиндр
б) Гиперболическим цилиндром называется поверхность, каноническое уравнение которой имеет вид:
(рис.8).
в) Параболическим цилиндром называется поверхность, каноническое уравнение которой имеет вид:
(рис.
9).
Общий метод исследования поверхностей по их уравнениям заключается в следующем:
1) находят сечения поверхности с каждой из трех координатных плоскостей;
2) находят сечения поверхности с плоскостями, параллельными координатным плоскостям;
3) анализируют кривые, полученные в результате сечений, и делают общее представление об исследуемой поверхности;
4) делают чертеж поверхности.
Выбор материала — Построение эллиптического параболоида
В зависимости от требуемой точности формы, вы можете использовать картон для изготовления отражателя. Если вам не требуется, чтобы это был отражатель, все становится проще!
Учтите, что фигура представляет собой трехмерное вращение двумерной кривой. Придется предположить, что вы можете создать кривую на картоне, используя формулу по вашему выбору.
Вырежьте из картона кривую, затем разрежьте ее пополам по вертикали, удалив немного больше от центральной вертикальной линии разреза.
Имея достаточное количество этих полупарабол, приклейте их вертикально на подходящую основу (картон!) так, чтобы все центральные разрезы были направлены внутрь. Причина, по которой вы удаляете немного на центральной линии разреза, заключается в том, что в противном случае толщина картона помешала бы оптимальному выравниванию каждой изогнутой части.
Если, например, вы решили использовать восемь кусков картона толщиной 6 мм, у вас будет восьмиугольник в центре, причем каждая грань/край восьмиугольника будет иметь длину 6 мм. По мере увеличения количества «плавников» многоугольник в центре становится больше и должен иметь столько же граней.
Вы также можете увеличить количество ребер, обрезав больше от центрального выреза и расширив размещение этого выреза наружу от центра.
Когда у вас есть скелет/основа/структура, вы можете обработать поверхность картона. Это может быть так же просто, как бумажные листы, приклеенные к краям картона. Если вашей целью является отражатель, майларовая пленка, тщательно натянутая на ребра, может обеспечить необходимую поверхность.
Вы можете создать обработку поверхности, вклеив картон между ребрами, оставив его ниже уровня разрезов. Нанесите слой гидроизоляции, такой как краска, эпоксидная смола или что-то подобное, а затем нанесите тонкий слой состава для стеновых панелей. После высыхания вы можете отшлифовать гладкую форму до поверхности, чтобы получить еще лучшие результаты. Я не знаю, как получить оптически отражающую поверхность на стеновой плите, но она обеспечит более гладкую поверхность для майларового покрытия.
Поскольку одно слово стоит одной тысячной картинки, я надеюсь, что прикрепленное изображение будет полезным:
РЕДАКТИРОВАТЬ: Использование более тонкого материала позволит получить больше «плавников» с меньшими зазорами и уменьшит интерполяцию, указанную в разделе комментариев. Возможно, первичная опора из картона с промежуточными сегментами, изготовленными из плотной бумаги с вкраплениями сегментов из обычной бумаги, обеспечит более высокое разрешение, но будет сложнее в изготовлении!
Еще одно решение, возможно, более простое.
Постарайтесь повернуть плоскости картона из положения, параллельного оси вращения, в положение, перпендикулярное ей. Решите уравнение для x и сделайте серию кругов из картона в зависимости от толщины материала y. Более толстый картон означает более низкое разрешение, меньше листов для резки, более тонкий означает более высокое разрешение, вплоть до уровня толщины бумаги.
Простота конструкции играет роль, потому что вам нужно только сложить листы. Вы можете сделать негатив или позитив, используя отверстия или вырезанные части. Выравнивание можно осуществить общим расположением (центр вырезанных кругов) или парой отверстий за пределами вырезанных кругов, просовывая затем в них шканты.
python — Как создать поверхность параболоида и заставить ее реагировать на событие
Я новичок в vispy и компьютерной графике. Я должен сгенерировать параболоид в соответствии с определенным уравнением, центр и параметры которого меняются в зависимости от ввода пользователя. Я просмотрел документацию и примеры Vispy и получил некоторое представление о пакете.
Параболоид, который мне нужно сгенерировать, должен иметь вращательную симметрию, как показано на рисунке ниже:
Тогда как то, что я получил, это
Мой код приведен ниже. Я изменил пример isosurface.py в примерах vispy.
система импорта
импортировать numpy как np
из приложения vispy import, сцена
из matplotlib импортировать pyplot как plt
# Создаем холст с 3D вьюпортом
холст = сцена.SceneCanvas(keys='interactive')
представление = canvas.central_widget.add_view()
## Определяем скалярное поле, из которого мы будем генерировать изоповерхность
def psi3(i, j, k, смещение=(25, 25, 25)):
х = i-смещение [0]
y = j-смещение [1]
z = k-смещение[2]
г = (0,2*х**2 + 0,2*у**2 - 4*z)
вернуть г
# Создать визуализацию изоповерхности
данные = np.fromfunction (psi3, (50, 50, 50))
поверхность = сцена.visuals.Isosurface(данные, уровень=данные.max()/4., цвет=(0,5, 0,6, 1, 1), затенение='гладкий', родитель=вид.сцена)
surface. transform = scene.transforms.STTransform(translate=(-25, -25, -25))
# Добавляем 3D-ось, чтобы ориентироваться
ось = scene.visuals.XYZAxis(parent=view.scene)
# Используйте 3D-камеру
# Ручные границы; Визуальная сетка еще не дает границ
# Обратите внимание, как вы можете установить границы перед назначением камеры в окно просмотра
cam = scene.TurntableCamera (высота = 30, азимут = 30)
cam.set_range((-10, 10), (-10, 10), (-10, 10))
вид.камера = камера
если __name__ == '__main__':
холст.шоу()
если sys.flags.interactive == 0:
app.run()
transform = scene.transforms.STTransform(translate=(-25, -25, -25))
# Добавляем 3D-ось, чтобы ориентироваться
ось = scene.visuals.XYZAxis(parent=view.scene)
# Используйте 3D-камеру
# Ручные границы; Визуальная сетка еще не дает границ
# Обратите внимание, как вы можете установить границы перед назначением камеры в окно просмотра
cam = scene.TurntableCamera (высота = 30, азимут = 30)
cam.set_range((-10, 10), (-10, 10), (-10, 10))
вид.камера = камера
если __name__ == '__main__':
холст.шоу()
если sys.flags.interactive == 0:
app.run()
У меня есть следующие вопросы:
- Как сделать, чтобы параболоид выглядел как на первом изображении (без обрезания краев)
- Есть ли лучший способ нарисовать параболоид, кроме использования изоповерхностей? Коэффициенты параболоида должны варьироваться пользователем.
- Как сделать, чтобы параболоид реагировал на события мыши: наведение, перетаскивание и т.д. Из документации я понял, что мне нужно связать его с классом Node. Я не могу понять, как это сделать, так как я новичок.
Я не могу понять, как это сделать, так как я новичок.Редактировать:
Вот соответствующий код, использующий matplotlib для создания требуемого параболоида. Также я могу создать параболоидную полосу в matplotlib.
импортировать matplotlib.pyplot как plt из matplotlib импорт см импортировать numpy как np # Создаем поверхность радиус = 5 отверстие_радиус = 4 # Генерируем сетку в цилиндрических координатах г = np.linspace (0, радиус, 100) тета = np.linspace (0, 2 * np.pi, 100) R, ТЕТА = np.meshgrid(r, тета) X, Y = R * np.cos(THETA), R * np.sin(THETA) а=0,6;б=0,6;в=0,6 Z1 = (X/a)**2+(Y/b)**2 # Эллиптический параболоид # Не отображать внутреннюю область x = np.where(X**2+Y**2<=hole_radius**2,np.NAN,X) y = np.where(X**2+Y**2<=hole_radius**2,np.NAN,Y) # Построить поверхность рис = plt.figure() топор = fig.gca (проекция = '3d') ax.plot_surface(x, y, Z1, cmap=cm.coolwarm, linewidth=0, antialiased=True, cstride=2, rstride=2) ax.
