|
Хорошо знающий свой предмет, умеющий заинтересовать учеников, понимающий… забудьте эту лирику. Сейчас речь пойдёт не об обучении каких-то одарённых детей Данная статья адресована моим настоящим и будущим коллегам, а также всем тем, кому по роду своей деятельности придётся руководить людьми и заставлять их что-то делать. Это командный состав силовых структур, управляющие, начальники различных коллективов и т.д. Вплоть до будущих президентов 🙂 Первое, и самое важное качество хорошего учителя (командира, руководителя) – это способность поддерживать дисциплину. Наверное, каждый из нас встречал в жизни «монстров», которые ещё ничего-то и не сделали и даже ничего не сказали – а их уже все боятся. Всё верно, без авторитаризма трудно. И чем «труднее» коллектив, тем жёстче С другой стороны, я встречал немало людей, в том числе среди своих учителей, которые ни разу не срываются на крик, но, тем не менее, успешно держали дисциплину. По моим наблюдениям, для них характерна официальность (в одежде, общем облике, манерах) и некоторая отстраненность от класса. Они никогда не переводят общение в личную плоскость, и поэтому на уроках меркнут даже «звёзды» – ну не интересно же – учитель не «ведётся» на различные выходки и никак не даёт себя показать. Нет, такие преподаватели вовсе не «сухари», они вполне дружелюбны и открыты, однако лишь в определённых рамках и в определённой мере. Но и «диктаторов», и «официалов» объединяет второе ключевое качество успешного учителя: Последовательность в своих действиях , а именно незыблемое следование принципу «сказал – сделал». Собственно, это даже не качество, а важнейший инструмент поддержания дисциплины. Если вы сказали, что поставите «двойку» за невыполненное домашнее задание, то вы просто обязаны её за это поставить. Если вы пообещали кого-то «оставить на 2-й год», то вы должны сдержать своё слово. Должны. Никаких поблажек, никакого прощения. В противном случае ваша репутация и статус учителя будут потеряны раз и навсегда.
По той же причине крайне нежелательно менять свои решения (даже ошибочные). Нет, конечно, бывают исключительные случаи, но на то они и исключения, чтобы подтверждать правило. В силовых структурах всё ещё жестче, как метко заметил один мой знакомый из МВД, «у нас приказы сначала выполняют, а затем обсуждают». И конечно, тут ум приходит пресловутая инструкция: 1) вождь племени всегда прав; Разумеется, в любом коллективе найдутся недовольные существующим порядком, и даже бунтари. Дисциплина и последовательность – самое важное, всё остальное вторично. Просто потому, что без этого не будет результата. И если не получается с дисциплиной, то профессия учителя и руководящие должности вам, к сожалению, не подойдут. От чего зависит успех? От характера. Да, для этого нужен определённый склад личности, и он либо есть, либо его нет. Ученики, подчинённые ОЧЕНЬ тонко чувствуют характер и быстро понимают, кто перед ними находится. Может так случиться, что вас назначат на руководящую должность. Тут надо или сразу отказываться (если это совсем не по душе), или постараться выдержать одну из описанных выше стратегий. Но в любом случае проявлять последовательность и выдерживать свою линию. Это аксиома Итак, если рассмотренные выше вопросы РЕШЕНЫ, то разговор заходит о третьем не менее важном качестве успешного наставника. Это простота и последовательность самого обучения. Далее идут все остальные качества, о которых так много говорится в современной гуманистической педагогике. Это умение заинтересовать предметом, использование различных методик обучения, психологических приёмов и так далее. Всё это, конечно, тоже важно, но только в четвертую, пятую и десятую очередь. Часто говорят, что важным является умение заинтересовать. Отчасти да. Однако тут нужно понимать, что значительной, а чаще бОльшей части учеников предмет всё равно будет не интересен. Возможно, некоторые захотят поспорить с построенным приоритетом, но я так подозреваю, они просто не сталкивались с реалиями. Сначала попробуйте использовать гуманные и прогрессивные методики на практике, а затем поспорим 😉 Нет, в этой статьей нет никакой жестокости. У нас начальник премию всем хорошую выписывает, с работы отпускает. Вот и вся благодарность. Весьма типичная. Спасибо за внимание, и успехов вам в начинаниях! Автор: Александр Емелин Знание – сила >>> (к списку статей блога) |
Вспомним того же Макаренко, который «выводил в люди» беспризорников живительным рукоприкладством. Вот и весь гений педагогики.
Всякий «разброд» следует пресекать (с той или иной степенью дипломатии), а последних субъектов просто давить. И один мой знакомый, умудрённый опытом педагог, как-то раз уточнил, что «таких надо не давить – таких надо Удавить». Или по возможности выдавить из коллектива. А иначе никак. Иначе «вынесут из класса», иначе «подсидят» подчиненные – иначе взорвётся склад с боеприпасами. Но это ещё малая беда, история знает примеры, когда мягкость царей и президентов приводила к трагедиям миллионов людей (большая просьба не обсуждать в комментариях конкретные персоналии).
Материал следует излагать просто и коротко – чтобы понял КАЖДЫЙ (в идеале, конечно). Последовательно, от простого к сложному. Следует заметить, что у всех разные способности, и некоторые ученики могут не понимать (действительно не понимать) простых вещей. Тогда нужно объяснить ещё раз, и ещё если потребуется. Задача учителя – научить. То же самое касается директив и приказов. Они должны быть чёткими, простыми и однозначными. А если кто-то не знает где люк танка, тот будет мыть весь танк 🙂
Я вот, например, не особо любил историю. Ни древнюю, ни новую, ни новейшую. Ну не интересна она мне как наука, и всё тут. И с этим ничего не поделать. Таким образом, умение заинтересовать никак не может быть главным качеством педагога.|
чтобы не было мучительно больно за мучительно прожитые годы Этой теме посвящены сотни статей и целые исследования, и сегодня я выскажу своё скромное мнение, исходя из личного опыта (сейчас мне 35+) и опыта знакомых мне людей. Хочу. С моей точки зрения, это базовый круг, фундамент всего остального. Как показала сама жизнь, я сам и многие мои знакомые выбрали дело, исходя из своих интересов, которые начали проявляться ещё в школе и даже раньше. Один мой товарищ с детского сада «фанател» по автомобилям, и сейчас он начальник гаража (несмотря на радиотехническое образование) + ремонт и тюнинг собственных автомобилей в качестве хобби. Другой мечтал стать «крёстным отцом» мафии 🙂 (популярная в 90 годах тема), и, в конце концов, вырос до гендиректора строительной фирмы (50 «рэкетиров» в подчинении). Что касается меня, то моими любимыми игрушками были конструкторы и кубики, и, наверное, я бы стал архитектором или проектировщиком, но в старших классах увлёкся программированием, и решил, что физмат перспективнее. А ещё я всегда любил зарабатывать деньги (не такое, кстати, плохое увлечение 😉 Итак, первое, и самое важное – это интерес. Причём, здесь не обязателен дикий энтузиазм или неземное вдохновение. Важнейшим критерием того, что вы занимаетесь своим делом является удовлетворённость от процесса и/или результатов. Как минимум, дело не должно вызывать отвращения. И если вас уже сейчас тошнит от своей занятости, то обязательно попытайтесь сменить поле деятельности, это можно сделать и в 20, и в 30, и даже в 40-50 лет. Я лично знаю одного человека, который в 50 лет с полного нуля «поднял» тему, которая выросла до масштабов целого региона. Да, конечно, вы можете поспорить с первым пунктом, но поставьте себя в ситуацию: у вас работа. Вы с ней справляетесь и даже получаете хорошие деньги. Очень хорошие. Но… от неё тошнит, болит сердце, голова, постоянные тревоги, напряг…. Или «работа вместо жизни». Хотя, деньги, конечно, могут перевешивать – это личный выбор каждого. 
Таким образом, ориентир «интересно то, что престижно и/или денежно», в общем случае не верный. И я бы не советовал вам выбирать профессию только потому, что она хорошо оплачивается. К тому же, сегодня хорошо, а завтра – плохо или вообще никак (о чём мы ещё поговорим). Круг второй. Могу. Как говорится, хотеть не вредно, нужно ещё и мочь. То есть, справляться с тем делом, которое вам нравится. Все знают, что когда что-то получается, то, конечно же, мы довольны этим фактом, что подкрепляет наш интерес! «Могу» обуславливается нашими задатками, способностями и характером. Существует масса профтестов, которые помогут сориентироваться в выборе конкретной профессии, и я об этом скажу буквально пару слов. Все профессии можно грубо разделить на две категории: 1) работа с людьми, 2) работа с материалами, механизмами, вычислительной техникой. Само собой, если у человека низкие коммуникативные навыки, то он вряд ли сможет эффективно работать с людьми. Темперамент и способности проявляются опять же с раннего возраста. Что касаемо лично меня, то ещё в детстве я отличался недетской усидчивостью. Я мог часами что-нибудь собирать из конструктора или строить из кубиков целые города (у меня их было больше 300 штук). Нет, я вовсе не был каким-то аутистом. Наоборот – вполне общительным и подвижным ребёнком, мог поиграть в футбол (в настоящий – играли всем двором), другие активные игры. Но всё же спокойное «конструирование» мне было больше по душе. В дальнейшем я днями и неделями напролёт занимался программирование, затем решением математических примеров на заказ. И это меня нисколько не напрягало, а наоборот – вызывало чувство глубокой удовлетворенности. В конце концов, я, по сути, создал свою собственную систему обучения, и в фигуральном смысле это тот же самый детский город из кубиков. Довелось поработать и «живым» учителем, но от этой деятельности я сильно уставал (март на дворе – и уже бы никого не видеть и не слышать). Хотя было интересно, тем более, у меня были старшие классы. Для тех, кто планирует стать учителем, тренером, да и вообще любым руководителем, я написал отдельную статью, в которой обрисовал специфику этих профессий. Круг третий. Деньги. Зависит от востребованности того, что вы делаете, и уровня вашей квалификации. Востребованности в свою очередь зависит от политического, экономического строя и развития технического прогресса. Так, например, во времена СССР, совершенно не котировались экономисты и бухгалтеры (более чем скромные зарплаты), однако в 90-00-е годы эти люди оказались «на коне» и стали зарабатывать очень хорошо. Поэтому, чтобы не «остаться у разбитого корыта», я рекомендую вам ознакомиться с Атласом профессий, где перечислены профессии-«пенсионеры» и профессии будущего. Как ни прискорбно, «хочу» и «могу» ещё не гарантируют даже какого-то заработка. Один мой знакомый ещё со школы хотел и мог играть на гитаре и петь песни. Он играл, пел, группу создал, играл, пел, вполне талантливо и профессионально, нравилось ему играть петь, но… его просто никто не слушал. По сути дела, деньги – это следствие вашей востребованности (в условиях капитализма). Ну и понятно, что чем выше квалификация, тем вы больше вы стОите на рынке. Эта закономерность имеет место, как при работе на себя, так и при работе по найму. Кстати, обратите внимание, что организационная форма деятельности не вошла в нашу классификацию, ибо себя можно «найти» и там, и там. И да, чуть не забыл – влияние родителей. Нередко складывается ситуация, когда мама врач и папа юрист (условно говоря) «толкают» вас в престижный экономический ВУЗ, причём без всякого учёта вашего мнения. Тут нужно сразу анализировать предыдущие круги – хочется ли и сможется ли? Выбор родителей может оказаться как правильным, так и неправильным. Чаще, наверное, правильным. Теперь рассмотрим другую характерную ситуацию – когда дети идут «по стопам» родителей. Это не случайность. Надеюсь, эти скромные страницы оказались полезными, и я ещё раз советую вам НЕ ЗАНИМАТЬСЯ нелюбимыми делами, и поменять деятельность, если она вас напрягает. Разумеется, то, что вы прочитали – это не «истина в последней инстанции» и, более того, я даже могу в чём-то заблуждаться, поэтому любой желающий может высказаться в комментариях. Автор: Александр Емелин Знание – сила >>> (к списку статей блога) |
Просматривая в Сети материалы о кругах Эйлера, я наткнулся на один содержательный пример, который захотелось сразу поправить:
Но вот тут его юридическое образование по любому пригодно – удачный выбор 🙂
И, наоборот, для человека общительного будут в тягость профессии плиточника, программиста и др., где требуется сосредоточенность и усидчивость.
Мне нравится строить новые и ремонтировать старые «дома», и мне очень приятно, что это неплохо получается. Кстати, и сейчас – завершу эту статьи, перечитаю, отредактирую и буду очень доволен.
Но уже в ближайшем будущем (если вы не в курсе), некогда престижные профессии уничтожит технический прогресс. Вы можете себе представить, что завтра по всей стране будут ликвидированы все офисы Сбербанка и тысячи работников окажутся «на улице»? А ведь это не фантазии – уже сегодня существует сопоставимый с «гигантами» Тинькофф банк (полностью онлайн банк с единственным офисом в Москве). Если честно, даже не верится, в моём поколении устроиться работать в банк – было просто «мегакруто».
Ну что ж поделать, так и осталось чистым хобби.
Из психологии хорошо известно, что темперамент и задатки передаются по наследству. Поэтому имеет смысл присмотреться к ближайшим родственникам и проанализировать: ДОВОЛЬНЫ ли они (опять это слово!) своей деятельностью, получается ли у них? Если да, то перед вами с высокой вероятностью зажигается «зелёный свет» по той же стезе. Хотя, конечно, может быть по-разному – это всего лишь предпосылка, но никак не готовая инструкция.» Страница не найдена
Опубликовано 8 марта 2023 г.
Автор: Шарон Клифиш
Опубликовано 7 февраля 2023 г. Автор: Шарон Клефиш 2-2023 учебный год, пришло время зарегистрировать вашего ребенка сейчас для подтверждения.
Нажмите на регистрационную форму ниже и верните ее в приходской офис или положите в корзину в церкви до среды, 26 апреля 2023 г.:
Форма подтверждения регистрации 2023
Каждый должен посетить 1 занятие и обязательный ретрит для подтверждения. По любым вопросам обращайтесь в приходской офис по телефону 504-393-2334.
Даты этих занятий и ретрита:
Даты занятий:
Суббота, 29 апреля 2023 г., с 8:00 до 18:00
ИЛИ
Суббота, 10 июня 2023 г., с 8:00 до 18:00
Обязательное отступление :
Суббота, 19 августа 2023 г., с 8:00 до 18:00
Опубликовано 11 ноября 2022 г.
Автор: Шарон Клефиш
Гала-призеры:
1-й приз — 2500 долларов США — Майк Тран
2-й приз — Big Green E gg & Nest — Hermona Berhane
3-я премия — Apple iPad — Blazio
4-й приз — Air Pods Pro True — Скотт Шелли
Большое спасибо за наших УДИВИТЕЛЬНЫХ спонсоров и жертвователей:
Главный спонсор
Gulf Coast Bank & Trust
Специальный гала-спонсор
Healthy Blue
Platinum Plus Спонсор $2000
Quality Pet Care
Аптека Westbank
Platinum Sponsor $1000
Amedee Family
Cada Insurance
Harvey MedCare, Dr. Quang Vu
Robertson Roofing & Siding, Inc.
Золотой спонсор $750
Francesca Albergamo
Серебряный спонсор Plus $500
Анонимный
Серебряный спонсор $350
Анонимный
Бреннан и Калли Бержерон и семья
Виктор и Недра Кальварузо
Сберегательный банк Пятого округа
Памяти Глории Джин Ларусс
Семья Лэндри/Янг
Афина и Райан Лефорт
Ом Электроподрядчики
Доктор и миссис Джейк Роди
Семья Кейн
Бронзовый спонсор $175
Сердце Буфорда
Бриттани Батлер
Семья Кассери
Gucci One Fabrications LLC
Местные рабочие 99
Боб и Джуди Морган
Линда Нгуен
Хай и Куинь Тран
Семья Во
Доноры аукциона
504 Фанк
Академия Богоматери Х.
С.
Academy of Sacred Heart
Ace Hotel New Orleans
Acme Oyster House
A.J. Мальбро
Аннадин
Группа Ансарди
Архиепископ Шоу Х.С.
The Audubon Group at Morgan Stanley
A & W Catering
Beauty Marks Studio-Lauren Flick
Beauty Marks Studio-Megan Marks
Belle Chasse Optical
Big Daddy Wrap
Аквапарк Blue Bayou
BRG Hospitality
Brother Martin H.S.
Café 615/ Home of DaWabbit
Casseri Family
Catalyst Event Solutions
Classique Nails
Cottage Catering
Court of Two Sisters
Crawlins Seafood
Mary Ann & Eddie Dallam
Dental Arts of New Orleans
Di Martino’s
Domenica
Продовольственный центр Dorigacs
Earthsavers Inc.
Eatin’with Izzy
English Turn Golf & Country Club
Рита Фальтерман
Fil-A-Sack
Frames, Inc.
Друзья Кабильдо
Тренер Вилли Фриц
Всемирный центр дикой природы
Greg’s Food Mart #2 Westwood Drive
Семья Гидри
GW Fins
Harrah’s Gulf Coast
Hi-Do Bakery
Hollywood Casino Gulf Coast & 9002 2 Казино Бумтаун Biloxi
Запеченная ветчина с медом
Ресторан Hooters
Houmas House
Island View Casino Resort
Jewell’s Pool Lessons Swim Lessons
Klinger & Marshall Dermatology
Lagniappe Luncheonette
Lakeside Photoworks
Гольф-клуб Лейквуд
Семья Лайтфутов
Кэти Лопес
Волшебные смеси приправ
Ресторан мемов
Бистро Мистера Б.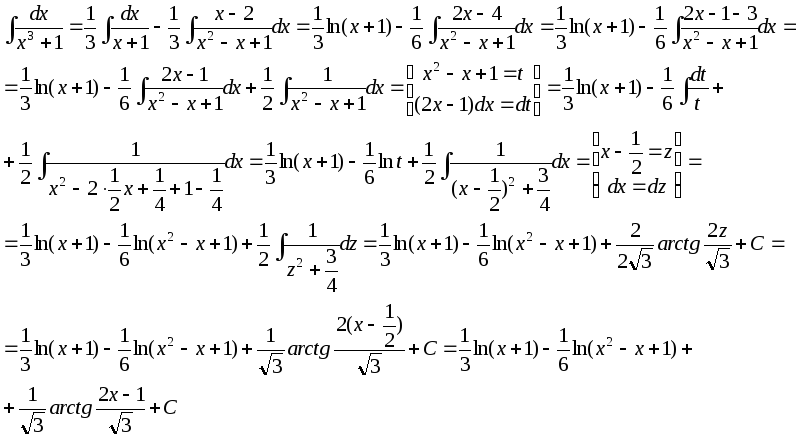
Нгуен Фотография
Карен Никлаус
Нор -Joe Imports – Metairie Road
Музей южного искусства Огдена
Кафе Olive Branch
Терренс Осборн
Park Timbers Swim & Tennis Club
Pastrana & Falcon Families
Perlis Clothing New Orleans
Planet Beach Belle Chasse
Профессиональное семейно-историческое исследование
Pure Life Lawn Care LLC
Rising Canes Chicken Fingers
Romaguera Photography
Студия стекла Rosetree
SAGES
Salon Joe Spa
Salvo’s Seafood
Школьная форма Skobel’s
Sue She phard
Святой Августин Х.С.
John & Linda St. Amant
Специальная школа St. Michael
Гольф-клуб Stonebridge of N.O.
Sun Ray Grill
The Surrency Family
Texas Roadhouse
Ресторан Thanh Thanh
Кулинарная школа Нового Орлеана
The Southern Bell Day Spa
The YMCA Belle Chasse
Модный салон
Steven & Cecile Vu
Walker’s BBQ
Westside Lanes
Wink Design & Events
Пожалуйста, поддержите нашего щедрого спонсора s&
Доноры – спасибо ты!
Опубликовано 29 марта 2022 г.
Автор: Шарон Клефиш
Фр. Джон Таламо будет проводить латинские мессы в церкви:
с понедельника по пятницу в 8:00 латинской мессы
По воскресеньям в 12:15 Латинская месса
Первая суббота месяца в 8:00 Латинская месса
Опубликовано 12 января 2022 г. Автор: Шарон Клифиш
Опубликовано 10 января 2022 г. Автор: Шарон Клефиш le Church начинает новое служение, Войска Святого Георгия, католическую версию Бойскауты. Войска Святого Георгия предназначены для мальчиков с 1-го по последний год обучения в средней школе. Это католическое служение для молодых людей и их отцов, ищущих жизнь, полную приключений и добродетели. Он использует на открытом воздухе как игру с целью. В игре – походы, походы, сплавы на каноэ, рыбалка и другие приключения; научиться готовить, вязать узлы, оказывать первую помощь и другим жизненным навыкам. Цель состоит в том, чтобы взращивать веру, углублять отношения со Христом, развивать отношения отца и сына, воспитывать сильных добродетельных лидеров и учить гражданственности.
Если вы и ваш сын хотели бы присоединиться к нам в различных приключениях, свяжитесь с приходским офисом по телефону 504-393-2334.
Опубликовано 7 сентября 2021 г. Автор: Шарон Клефиш
Нажмите ниже, чтобы увидеть письмо от о. Джон Таламо
Отец Джон 7 сентября Письмо
Опубликовано 2 августа 2021 г. Автор: Шарон Клефиш
FLOCKNOTE ЗДЕСЬ!
Мы призываем каждого прихожанина церкви Св. Андрея (старше 18 лет) подписаться на нашу рассылку текстовых сообщений!
Этот номер будет использоваться для экстренной связи и других важных коммуникаций по мере необходимости.
Простая регистрация (это займет всего 2 минуты)
Текст: standrewnola на номер 84576.
Много благословений!
Опубликовано 16 июля 2021 г.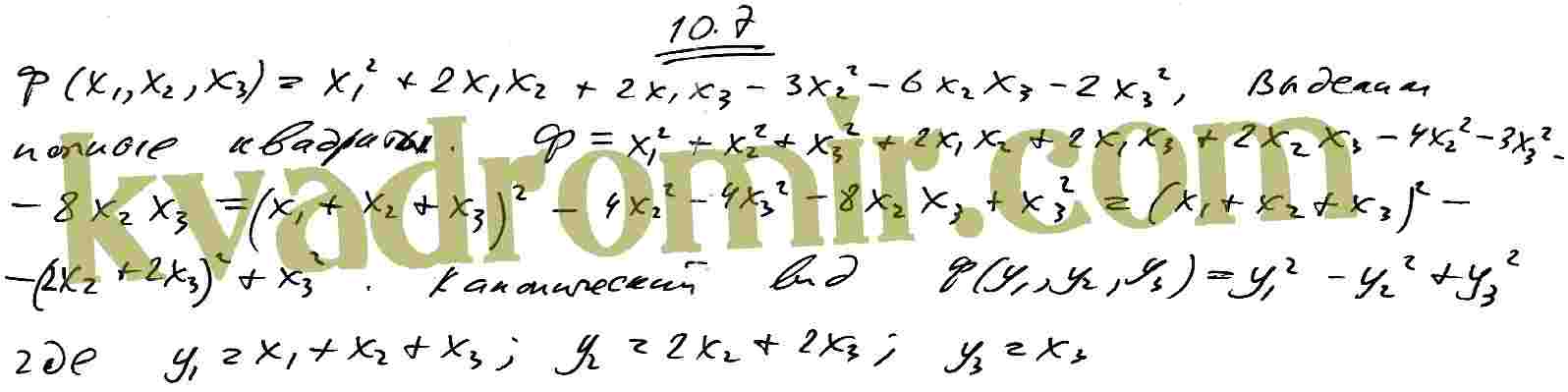
Автор: Sharon Kleefisch
Пожалуйста, поддержите осенний сбор средств на Superfest Bank & Trust в Сент-Эндрю / Побережье Мексиканского залива, став спонсором. Нажмите ниже, чтобы распечатать нашу спонсорскую форму:
Спонсорское письмо 2021
Если вы хотите приобрести футболку Superfest, нажмите на ссылку ниже, чтобы получить форму заказа:
Форма заказа футболки Веб-сайт
Пожалуйста, поддержите наших спонсоров 2021 — Спасибо!
Главный спонсор Superfest $10 000
Gulf Coast Bank & Trust
Платиновый уровень $5 000
Superior Honda
Золотой уровень $3 000
Памяти Марлин Мар
Аптека Westbank
Бронзовый уровень 1500 долларов США
Качественный уход за животными
Адвокатское бюро John W. Redmann, LLC
Archer Level $1000
Страхование CADA
Cafe 615 / Home of DaWabbit
Harvey Medcare, Quang Vu, MD
The Hendrix Family
Lighthouse Lodge & Villas
Nicholson-Uhl Family
NOLA Lubemasters LLC
Lisa Rapier, Realtor, Latter & Blum
River Rental Tools, Inc.
Robertson Roofing & Siding
Russo’s Pharmacy & Gifts
St. д
Van Meter & Associates
Red Plus Level $750
Walker Family
Red Level $500
Acadian Flooring
Arabi Sling & Rigging Co., Inc.
Wayne Breaux Electric LLC. Друг святого Андрея
Макдэниел Family
Monzon Brothers Inc.
Mothe Funeral Homes, LLC
Robert Wolfe Construction, Inc.
TAC Air Conditioning
TCK Property Marketplace
Van’s Transmission
B. Cecile Vu, DDS
Westbank Athletic Club
White Level $300
Abry Brothers, Inc.
Balestra’s Food Center
Семья Боба Будро
Bryans United Air Conditioning
Victor & Nedra Calvaruso
Compass Point Events 9002 2 Семья Доусон
French’s Welding & Marine Services, L.L.C.
Друг святого Андрея
Доктор и миссис Джимми Гобер
Эллисон и Барри Гриффен
Семья Гидри
Рукописный текст Ханны
Билл и Мэри Хеберт
Jefferson Door Company, LLC
Семья Кейн
Жанна и Рик Кин
Кузовной цех Келлера
Местные рабочие #99
Семьи Лэндри/Янг
Катание на лодках на метро
Боб и Джуди Морган
Строительство Дэниела Пастраны
Семья Павлович
Кафе Refueled Nutrition
Рой Суппи Ко.
, Инк.
Ральф и Кэти Сагрера
Скотт и Додди Шелли
Speciality Italian Bistro
Рэндалл и Джен Стейн
Sun Ray Grill
TLC Novelty Co., Inc. / The Hall Family
Джорджи Ле Тран, ООО
Семья Мейсон Тран
Экстремальная физиотерапия
Пожалуйста, поддержите наших щедрых спонсоров
спасибо!
Опубликовано 4 мая 2021 г. Автор: Шарон Клефиш
Высокопреподобный Грегори М. Эймонд формулы и. Самые красивые физические и математические формулы
Математик Анри Пуанкаре писал в своей книге «Наука и метод»: «Если бы природа не была прекрасна, ее не стоило бы знать, не стоило бы переживать жизнь. Я, конечно, не говорю здесь о красоте, которая бросается в глаза… Я имею в виду ту более глубокую красоту, которая открывается в гармонии частей, которая постигается только разумом. Именно она создает почву, создает обрамление для игры видимых красок, ласкающих наши чувства, и без этой опоры красота мимолетных впечатлений была бы несовершенна, как все неотчетливое и преходящее.
Наоборот, интеллектуальная красота приносит удовлетворение сама по себе.
П.А.М. Дирак писал: «Теоретическая физика имеет еще один верный путь развития. Основная особенность в том, что самые основные физические законы описываются математической теорией, аппарат которой обладает необычайной силой и красотой. Чтобы понять эту теорию, нужно иметь необычайно высокую математическую квалификацию. Вы спросите: почему природа такая, какая она есть? На это есть только один ответ: согласно нашим современным знаниям, природа устроена так, а не иначе.
Семь лет назад украинский физик (и художник) Наталья Кондратьева спросила у ряда ведущих математиков мира: «Какие три математические формулы, на ваш взгляд, самые красивые?
Сэр Майкл Атья и Дэвид Эльварси из Великобритании, Яков Синай и Александр Кириллов из США, Фридрих Герцебрух и Юрий Манин из Германии, Давид Руэль из Франции, Анатолий Вершик и Роберт Минлос из России и другие математики из разных стран. От украинцев в дискуссии приняли участие академики НАН Украины Владимир Королюк и Анатолий Скороход.
Часть полученных таким образом материалов легла в основу опубликованной Натальей Кондратьевой научной работы «Три самые красивые математические формулы».
С какой целью вы спросили математиков о красивых формулах?
— Каждое новое столетие приносит обновление научной парадигмы. В самом начале века с ощущением, что мы стоим на пороге новой науки, ее новой роли в жизни человеческого общества, я обратился к математикам с вопросом о красоте идей, стоящих за математическими символами, т.е. о красоте математические формулы.
Некоторые черты новой науки уже можно отметить. Если в науке ХХ века очень важную роль сыграла «дружба» математики с физикой, то сейчас математика эффективно сотрудничает с биологией, генетикой, социологией, экономикой… Следовательно, наука будет исследовать соответствия. Математические структуры будут исследовать соответствия между взаимодействием элементов различных областей и планов. И многое из того, что мы прежде считали само собой разумеющимся философскими утверждениями, будет утверждено наукой как конкретное знание.
Этот процесс начался уже в 20 веке. Итак, Колмогоров математически показал, что случайности нет, а есть очень большая сложность. Фрактальная геометрия подтвердила принцип единства в многообразии и т.д.
— Какие формулы были названы самыми красивыми?
— Сразу скажу, что цели устроить конкурс на формулы не было. В своем письме к математикам я писал: «Люди, которые хотят понять, какие законы управляют миром, встают на путь поиска гармонии мира. Этот путь уходит в бесконечность (ибо движение вечно), но люди все равно идут по нему, т.к. есть особая радость встретить очередную идею или идею. Из ответов на вопрос о красивых формулах можно синтезировать новую грань красоты мира. Кроме того, эта работа может быть полезна будущим ученым как идея великой гармонии мира и математика как способ найти эту красоту.
Тем не менее среди формул были явные фавориты: формула Пифагора и формула Эйлера.
За ними последовали физические, а не математические формулы, которые в ХХ веке изменили наше представление о мире — Максвелл, Шредингер, Эйнштейн.
Также к числу самых красивых относятся формулы, которые до сих пор обсуждаются, например, уравнения физического вакуума. Были упомянуты и другие красивые математические формулы.
— Как вы думаете, почему на рубеже второго и третьего тысячелетий формула Пифагора была названа одной из самых красивых?
— Во времена Пифагора эта формула воспринималась как выражение принципа космической эволюции: два противоположных начала (два квадрата, соприкасающиеся ортогонально) рождают третий, равный их сумме. Можно дать геометрически очень красивые интерпретации.
Возможно, есть какая-то подсознательная, генетическая память о тех временах, когда понятие «математика» означало «науку», а арифметика, живопись, музыка, философия изучались в синтезе.
Рафаэль Хасминский писал в своем письме, что в школе был поражен красотой пифагорейской формулы, во многом определившей его судьбу как математика.
Что вы можете сказать о формуле Эйлера?
— Некоторые математики обратили внимание на то, что в ней «собраны все», т.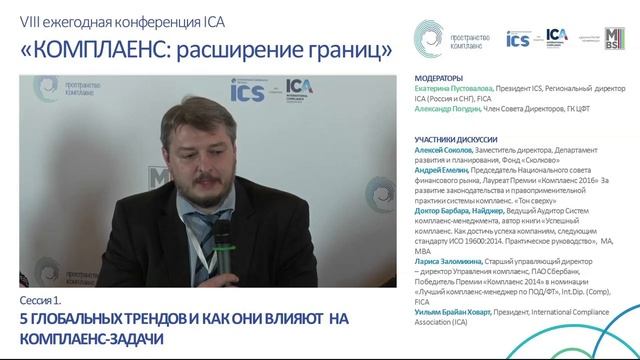
е. все самые замечательные математические числа, а единица таит в себе бесконечность! В этом есть глубокий философский смысл.
Неудивительно, что эту формулу открыл Эйлер. Великий математик много сделал для введения красоты в науку, он даже ввел в математику понятие «степень красоты». Скорее, он ввел это понятие в теорию музыки, которую считал частью математики.
Эйлер считал, что эстетическое чувство можно развить и что это чувство необходимо ученому.
Сошлюсь на авторитеты… Гротендик: «Понимание той или иной вещи в математике настолько совершенно, насколько возможно ощутить ее красоту».
Пуанкаре: «В математике есть чувство». Эстетическое чувство в математике он сравнивал с фильтром, выбирающим из множества решений наиболее гармоничное решение, которое, как правило, и является правильным. Красота и гармония — синонимы, а высшее проявление гармонии — мировой закон равновесия. Математика исследует этот закон на разных планах бытия и в разных аспектах. Неудивительно, что каждая математическая формула содержит знак равенства.
Я думаю, что высшая человеческая гармония – это гармония мысли и чувства. Может быть, поэтому Эйнштейн сказал, что писатель Достоевский дал ему больше, чем математик Гаусс.
Эпиграфом к работе о красоте в математике я взял формулу Достоевского «Красота спасет мир». И это также обсуждалось математиками.
И они согласились с этим утверждением?
— Математики не подтвердили и не опровергли это утверждение. Они уточняли: «Осознание красоты спасет мир». Это сразу напомнило работу Юджина Вигнера о роли сознания в квантовых измерениях, написанную им почти пятьдесят лет назад. В этой работе Вигнер показал, что человеческое сознание воздействует на окружающую среду, т. е. что мы не только получаем информацию извне, но и посылаем в ответ свои мысли и чувства. Эта работа до сих пор актуальна и имеет как своих сторонников, так и противников. Я очень надеюсь, что в 21 веке наука докажет, что осознание прекрасного способствует гармонизации нашего мира.
1. Формула Эйлера.
Многие видели в этой формуле символ единства всей математики, потому что в ней «-1 представляет арифметику, i — алгебру, π — геометрию и e — анализ».
2. Это простое уравнение показывает, что значение 0,999 (и так до бесконечности) эквивалентно единице. Многие не верят, что это может быть правдой, хотя есть несколько доказательств, основанных на теории пределов. Однако равенство показывает принцип бесконечности.
3. Это уравнение было сформулировано Эйнштейном как часть новаторской общей теории относительности в 1919 году.15. Правая часть этого уравнения описывает энергию, содержащуюся в нашей Вселенной (включая «темную энергию»). Левая часть описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна масса и энергия определяют геометрию и в то же время кривизну, являющуюся проявлением гравитации. Эйнштейн говорил, что левая часть уравнений гравитации в общей теории относительности, содержащая гравитационное поле, красива и словно высечена из мрамора, а правая часть уравнений, описывающих материю, по-прежнему безобразна, словно сделана из обычного куска дерева.
4. Другая доминирующая теория физики — Стандартная модель — описывает электромагнитные, слабые и сильные взаимодействия всех элементарных частиц. Некоторые физики считают, что она отражает все процессы, происходящие во Вселенной, кроме темной материи, темной энергии и не включает гравитацию. Бозон Хиггса, неуловимый до прошлого года, тоже вписывается в Стандартную модель, хотя не все специалисты уверены в его существовании.
5. Теорема Пифагора — одна из основных теорем евклидовой геометрии, устанавливающая связь между сторонами прямоугольного треугольника. Мы помним ее со школы и считаем, что автором теоремы является Пифагор. На самом деле эта формула использовалась еще со времен Древнего Египта при строительстве пирамид.
6. Теорема Эйлера. Эта теорема положила начало новому разделу математики — топологии. Уравнение устанавливает связь между количеством вершин, ребер и граней для многогранников, топологически эквивалентных сфере.
7.
специальная теория относительности описывает движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скоростях света в вакууме, в том числе близких к скорости света. Эйнштейн вывел формулу, описывающую, что время и пространство — не абсолютные понятия, а скорее относительные, зависящие от скорости наблюдателя. Уравнение показывает, как время увеличивается или замедляется в зависимости от того, как и где движется человек.
8. Уравнение было получено в 1750-х годах Эйлером и Лагранжем при решении проблемы изохрон. Это задача определения кривой, по которой тяжелая частица достигает фиксированной точки за фиксированное время, независимо от начальной точки. В общем случае, если ваша система обладает симметрией, существует соответствующий закон сохранения симметрии.
9. Уравнение Каллана-Симанзики. Это дифференциальное уравнение, описывающее эволюцию n-корреляционной функции при изменении шкалы энергий, на которой определяется теория, и включает в себя бета-функции теории и аномальные размерности.
Это уравнение помогло лучше понять квантовую физику.
10. Уравнение минимальной поверхности. Это равенство объясняет образование мыльных пузырей.
11. Прямая Эйлера. Теорема Эйлера была доказана в 1765 году. Он обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.
12. В 1928 г. П.А.М. Дирак предложил свой вариант уравнения Шрёдингера — который соответствовал теории А. Эйнштейна. Научный мир был потрясен — свое уравнение для электрона Дирак открыл путем чисто математических манипуляций с высшими математическими объектами, известными как спиноры. И это была сенсация — до сих пор все великие открытия в физике должны стоять на прочной основе экспериментальных данных. Но Дирак считал, что чистая математика, если она достаточно красива, является надежным критерием правильности выводов. «Красота уравнений важнее их соответствия экспериментальным данным. …Кажется, если вы стремитесь к красоте в уравнениях и обладаете здоровой интуицией, то вы на правильном пути».
Именно благодаря его расчетам был открыт позитрон — антиэлектрон, и он предсказал наличие «спина» в электроне — вращение элементарной частицы.
13. Дж. Максвелл получил удивительные уравнения, объединившие все явления электричества, магнетизма и оптики. Замечательный немецкий физик, один из основоположников статистической физики Людвиг Больцман сказал об уравнениях Максвелла: «Разве не Бог писал эти буквы?»
14. Уравнение Шрёдингера. Уравнение, описывающее изменение в пространстве и времени чистого состояния, заданного волновой функцией, в гамильтоновых квантовых системах. Игра в квантовой механике так же важна, как уравнение второго закона Ньютона в классической механике.
Голова идет кругом от множества математических формул, которые нужно знать. Зубрежка и кроватки для слабаков. А для тех, кто хочет стать сильнее в математике, мы дадим несколько советов, как запоминать математические формулы, чтобы они не вылетели из головы перед контрольной, экзаменом или ЦТ.
Понять формулу
Если вы запомните только последовательность переменных, вы рискуете «потерять» всю формулу, когда забудете символ или знак.
Использовать все виды памяти
Прочтите формулы вслух, напишите на листе несколько раз, пока не запомните. Используйте все виды памяти, ориентируясь на ведущую. Зрительная и моторная память вместе дают больший эффект. Конечно, возможности запоминания у всех разные. Есть специальные техники, которые помогают.
Вот еще несколько советов по запоминанию формул
Обязательно сделайте формулы наглядными: обведите формулу в рамке, напишите другим цветом. Так будет легче найти в аннотации и запомнить. А еще лучше запишите формулы в отдельный блокнот, структурировав их по темам. Отметьте, в каких задачах полезна та или иная формула, в чем ее особенность. Возьмите за привычку пополнять список формул. Такой «дневник наблюдения за формулой» поможет освежить в памяти важную информацию перед контрольной, экзаменом или КТ по математике.
Так же поступают и многие школьники: когда раздают штампованные черновики, берешь и сразу пишешь на них важные формулы, которые тебе трудно. За полчаса до КТ вы визуально запоминали эти формулы, а потом быстро их записывали. Это экономит время. Этот лайфхак особенно хорош в тригонометрии. Чем больше формул вы знаете, тем лучше.
Проверь себя
Нужно постоянно возвращаться к изученному материалу, чтобы не забыть его. Попробуйте метод «Две карточки», он подходит для запоминания формул сокращения, сокращенного умножения, тригонометрических формул. Возьмите две стопки карточек разного цвета, на одной напишите левую часть формулы, а на другой – правую. Разделите таким образом все формулы, которые вам нужно запомнить, затем перемешайте обе стопки. Потяните карточку с левой стороной формулы по порядку и выберите ее продолжение среди «правильных» и наоборот.
Карты хороши и в геометрии
Для запоминания формул геометрии заведите себе карточки по темам («Формулы площади», «Формулы треугольника», «Формулы квадрата» и др.
) и запишите в них информацию следующим образом.
Вы можете зафиксировать формулы в отдельной тетради и всегда иметь ее под рукой — как вам удобно
Будьте позитивны
Если чему-то научиться под давлением, мозг сам хочет избавиться от груза знаний. Думайте о запоминании формул как о хорошем упражнении для тренировки памяти. Да и настроение поднимается, когда вспоминаешь нужные формулы решения. Ну и конечно же решаешь, как можно больше тестов и заданий подготовить к зачету, ЕГЭ или КТ!
КТ по математике — это типовые задачи: чем больше тестов вы решите, тем выше шанс встретить что-то похожее на КТ. Невозможно подготовиться к ДТ по одному заданию. Но когда ты решил 100 задач, то 101 задача не вызовет затруднений.
Дмитрий Судник, учитель математики в
Если материал был вам полезен, не забудьте поставить «Мне нравится» в наших социальных сетях
На этой странице вы можете просмотреть или скачать бесплатно 9 самых популярных0004 математические формулы, таблицы , а также справочные материалы по высшей математике.
Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Это было сделано для того, чтобы преодолеть трудности, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на исчерпывающую полноту, но вы найдете ОЧЕНЬ ОБЩЕЕ.
Рассмотрим, например, таблицу тригонометрических формул. Тригонометрических формул много, они давно известны, и нет смысла переписывать справочники. А вот формулы, которые очень часто используются для решения курсовых задач по высшей математике, складываются воедино и могут быть очень полезны при выполнении практических задач. При этом в комментариях я указываю, в каком разделе высшей математики (пределы, производные, интегралы и т. д.) почти всегда фигурирует та или иная формула.
Итак, прямо сейчас у вас есть свободный доступ к ценным справочным материалам, возможен как онлайн просмотр, так и скачивание. Удобнее всего сразу распечатать интересующие вас математические таблицы и справочные материалы.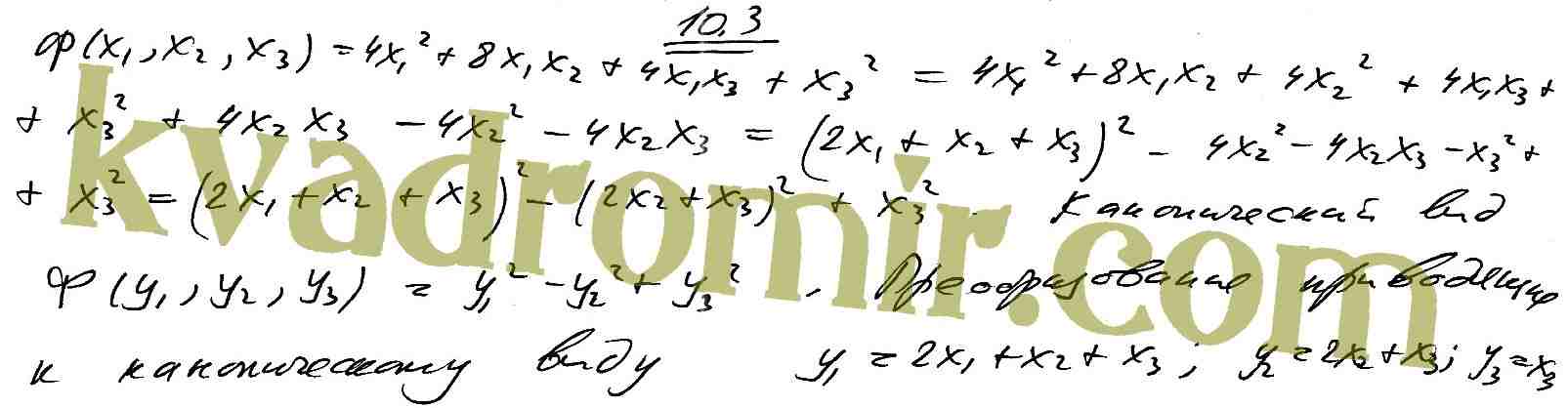
Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, и читать ее с монитора сложнее.
Практически все файлы размещаются непосредственно на сайте, а это значит, что их можно получить в кратчайшие сроки, ограничиваясь только скоростью вашего интернет-соединения.
! В случае некорректного отображения pdf воспользуйтесь следующими рекомендациями
Всем рекомендую к просмотру. Эти формулы встречаются в ходе решения задач по высшей математике буквально на каждом шагу. Без знания этих формул — никуда. С чего начать изучение высшей математики? От повторения этого. Независимо от уровня вашей математической подготовки в этот момент крайне желательно СРАЗУ УВИДЕТЬ возможность выполнения элементарных действий, применения простейших формул в процессе решения пределов, интегралов, дифференциальных уравнений и т. д.
Справочник содержит краткую информацию о модуле, формулах сокращенного умножения, алгоритме решения квадратного уравнения, правилах упрощения многоэтажных дробей, а также наиболее важных свойствах степеней и логарифмов.
Самые «путевые» тригонометрические формулы, которые используются в ходе решения задач по высшей математике. На самом деле таких формул МАЛО, а собирать десятки других из разных математических справочников — пустая трата времени. Здесь есть все (или почти все), что вам может понадобиться.
При выполнении заданий по математике часто возникает необходимость заглянуть в тригонометрические таблицы. В данном справочном материале представлена таблица значений тригонометрических функций (синуса, косинуса, тангенса и котангенса) для значений аргументов от нуля до 360 градусов. Имейте в виду, что эта информация не имеет смысла, но некоторые значения тригонометрических функций полезно знать . Также представлены формулы приведения для приведенных выше тригонометрических функций, иногда (чаще всего при решении лимитов). По просьбам посетителей сайта в файл pdf добавлена таблица значений обратных тригонометрических функций и две формулы: формула перевода градусов в радианы, формула перевода радианов в градусы.
Методический материал представляет собой обзор схем основных элементарных функций и их свойств. Он будет полезен при изучении практически всех разделов высшей математики, к тому же вам очень поможет справочник. лучше и качественнее разбираются в некоторых темах. Также можно узнать, какие значения функции должны быть , чтобы знать наизусть , чтобы не получить «двойку автоматически» при ответе на простейший вопрос экзаменатора. Справка представлена в виде веб-страницы и содержит множество графиков функций, которые также стоит запомнить. По мере развития проекта пособие стало играть роль вводного урока по теме «Функции и графики».
На практике заочникам почти всегда приходится использовать первый и второй замечательные пределы, о которых и идет речь в этой справке. Рассмотрены еще три замечательных предела, которые встречаются гораздо реже. Все замечательные лимиты снабжены дополнительными важными комментариями. Кроме того, файл дополнен информацией о замечательных эквивалентностях.
Справочник содержит правила дифференцирования и таблицу производных основных элементарных функций. Таблица снабжена очень важными примечаниями.
Ваш путеводитель по функциям и графикам. В pdf систематизированы и изложены сведения об основных этапах исследования функции одной переменной. Руководство сопровождается ссылками, а значит экономит много времени. Пособие полезно как чайнику, так и подготовленному читателю.
В целом почти то же, что и в дифференциальном исчислении. Правила интегрирования и таблица интегралов с моими комментариями.
Справочный материал незаменим при изучении степенных рядов. В таблице представлены разложения в степенные ряды следующих функций: экспоненты, синуса, косинуса, логарифма, арктангенса и арксинуса. Также приведены биномиальное разложение и наиболее распространенные частные случаи биномиального разложения. Разложение функции в ряд является самостоятельной задачей, используется для приближенных вычислений, приближенных вычислений определенного интеграла и в некоторых других задачах.
Основной трудностью при решении неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами является правильный выбор частного решения по виду правой части. Данное пособие относится в первую очередь к уроку Как решить неоднородное уравнение второго порядка? и поможет вам легко разобраться в выборе того или иного решения. Справка не претендует на доскональную научную полноту, написана простым и понятным языком, но в 99,99% случаев будет содержать именно то дело, которое вы ищете.
Помощь незаменима при решении прикладных задач комплексного анализа – нахождение частного решения ДУ операционным методом и таким же образом найти частное решение системы DE. Таблица отличается от аналогов тем, что она «заточена» именно под вышеперечисленные задачи, эта особенность позволяет легко освоить алгоритмы решения. Как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае, если информации недостаточно, рекомендую обратиться к солидному математическому справочнику — полная версия содержит более сотни наименований.
Справочный материал содержит формулы факториала, числа перестановок, сочетаний, расстановок (с повторениями и без), а также информативные комментарии к каждой формуле, позволяющие понять их суть. + Правила сложения и умножения комбинаций. Кроме того, pdf содержит краткую информацию о биноме Ньютона и треугольнике Паскаля с примерами их практического использования.
Файл содержит список формул с краткими комментариями по обеим главам тервера — случайных событий и случайных величин , включая формулы и числовые характеристики общих дискретных и непрерывных распределений. Справка систематизирует материал и очень удобна для выполнения практических заданий, заходите и сразу найдете то, что вам нужно!
Специальные программы расчета:В этом разделе вы можете найти программы-помощники для решения широких и узких локальных математических задач. Они помогут вам быстро завершить расчеты и принять решение.
Универсальный калькулятор , реализованный в рабочей книге MS Excel, содержащей три листа.
Программа может заменить обычный калькулятор с множеством функций. Любые степени, корни, логарифмы, тригонометрические функции, арки — без проблем! Кроме того, калькулятор автоматически выполняет основные операции с матрицами, считает определители (до определителя 5 на 5 включительно), мгновенно находит миноры и алгебраические сложения матриц. За считанные секунды можно решить систему линейных уравнений по обратной матрице и по формулам Крамера, посмотреть основные этапы решения. Все это очень удобно для самопроверки. Просто введите свои цифры и получите результат!
Эта полуавтоматическая программа относится к уроку Формула трапеции, формула Симпсона и помогает вычислить приближенное значение определенного интеграла на 2, 4, 8, 10 и 20 отрезках разбиения. В приложении видеоинструкция по работе с калькулятором. Вычислите свой определенный интеграл в течение нескольких минут или даже секунд!
Пока это все.
Раздел постепенно пополняется дополнительными материалами и полезными программами.
Каждый справочник неоднократно редактировался и улучшался, в том числе с учетом ваших пожеланий и замечаний! Если вы считаете, что что-то важное упущено, вы нашли какие-то неточности, а может быть что-то недостаточно понятно объяснили, обязательно пишите!
С уважением, Емелин Александр
Образование — это то, что остается после забвения всего, чему учили в школе.
Новосибирский ученый Игорь Хмелинский, ныне работающий в Португалии, доказывает, что без непосредственного запоминания текстов и формул развитие абстрактной памяти у детей затруднено. Вот выдержки из его статьи «Уроки образовательных реформ в Европе и странах бывшего СССР»
Заучивание наизусть и долговременная память Незнание таблицы умножения имеет более серьезные последствия, чем неспособность обнаружить ошибки в вычислениях на калькуляторе. Наша долговременная память работает по принципу ассоциативной базы данных, то есть одни элементы информации при запоминании связываются с другими на основе ассоциаций, установившихся в момент знакомства с ними.
Поэтому, чтобы сформировать базу знаний в какой-либо предметной области, например, в арифметике, сначала нужно выучить хоть что-то наизусть. Далее вновь поступившая информация будет поступать из кратковременной памяти в долговременную, если в течение короткого промежутка времени (несколько дней) мы сталкиваемся с ней много раз и, желательно, в разных обстоятельствах (что способствует созданию полезные ассоциации). Однако при отсутствии в постоянной памяти знаний по арифметике вновь поступившие элементы информации связываются с элементами, не имеющими к арифметике никакого отношения, — например, личность учителя, погода на улице и т. п. Очевидно, никакой реальной пользы такое заучивание учащемуся не принесет — поскольку ассоциации уводят в сторону от данной предметной области, учащийся не сможет вспомнить никаких знаний, связанных с арифметикой, кроме смутных представлений о том, что он как бы когда-то имел о ней что-то. должен был услышать. Для таких учащихся роль недостающих ассоциаций обычно играют разного рода подсказки — переписать у коллеги, использовать наводящие вопросы в самом контроле, формулы из списка формул, которые разрешено использовать и т.