Если степени одинаковые а основания разные при умножении: Свойства степеней, действия со степенями

alexxlab / / Разное

Что такое процесс умножения показателей?

Изображение предоставлено

В жизни человека есть несколько видов деятельности, например, фондовый рынок, информатика, ядерная физика и другие виды вещей, которые включают умножение показателей. Показатели являются очень важным компонентом алгебры, а также современной математики, и людям очень важно понимать, как все работает. Очень важно, чтобы люди имели четкое представление об экспонентах и ​​некоторых других видах правил, прежде чем решать вопросы.

Показатель степени считается наилучшим способом выражения повторного умножения, и первое число здесь будет называться основанием, потому что оно будет означать, что число должно быть умножено. Второе наименьшее число будет показателем степени, который будет представлять, сколько раз основание должно быть умножено только само на себя. Существуют различные виды правил, которые означают правило произведения степеней, правило отношения степеней, правило мощности, правило мощности, правило нулевой мощности, правило отрицательного показателя и некоторые другие виды вещей.

Содержание

  • 1 Ниже приведены наиболее важные способы умножения показателей степени:
    • 1.1 Умножение показателей степени с одинаковым основанием:
    • 1.2 Умножение показателей степени с разными основаниями:
    • 1.4 Умножение отрицательных степеней:

Всякий раз, когда учащиеся умножают степени с одним и тем же основанием, необходимо применить первое правило, которое обеспечит сложение степеней во время умножения оснований. Это считается самым коротким способом узнать ответ очень точно. Лучше всего то, что этот метод всегда будет работать.

Люди также могут умножать показатели степени с разным основанием, но степени должны быть одинаковыми. Прежде всего, людям нужно умножить основания вместе, а затем добавить показатель степени, вместо того, чтобы складывать два показателя вместе, важно сохранить показатель степени одинаковым. Студентам необходимо распределить мощность по каждому основанию при возведении нескольких переменных в степень, и, кроме того, важно убедиться, что это правило будет выполняться до тех пор, пока показатели степени и переменные одинаковы.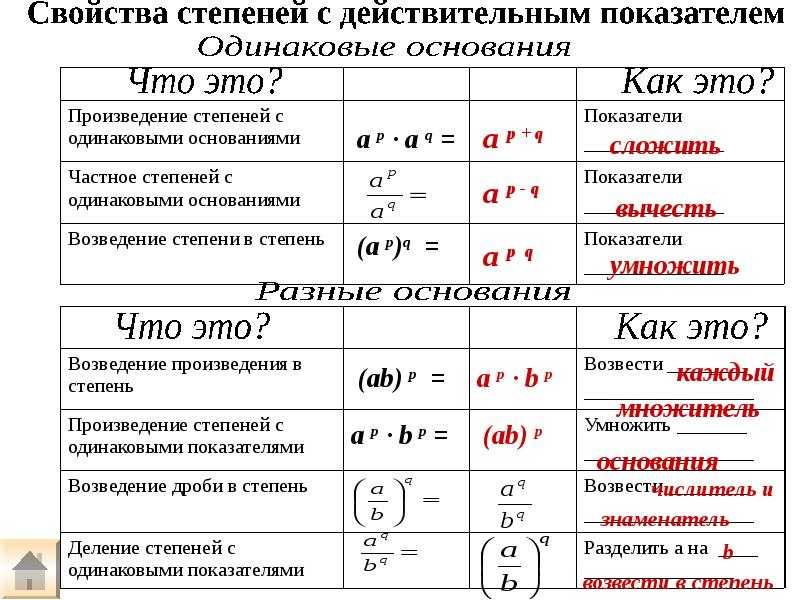

Этот конкретный пункт очень распространен, когда люди хотят умножать разные степени с разными основаниями. В этом случае иногда ответы не могут быть упрощены до одного показателя степени, что является основной причиной того, что он должен быть выражен только как обычное число.

Эта концепция может показаться очень сложной, но обзор свойств отрицательных чисел очень важен, чтобы люди могли очень легко решить этот вопрос. Чтобы изменить отрицательный показатель на положительный, его нужно преобразовать в обратный, чтобы можно было найти ответы, и для дальнейшего решения этого конкретного показателя очень важно, чтобы люди отлично справлялись с вещами. Основание другое, потому что умножение оснований должно выполняться, оставляя показатели одинаковыми. Если показатели не имеют ничего общего, уравнение необходимо решать напрямую.

 Учащиеся должны выполнять различные виды деятельности с точки зрения практики умножения показателей, например чудо, война показателей, охота за мусором, опасность, а также различные другие виды рабочих листов, чтобы они стали мастерами в этой области.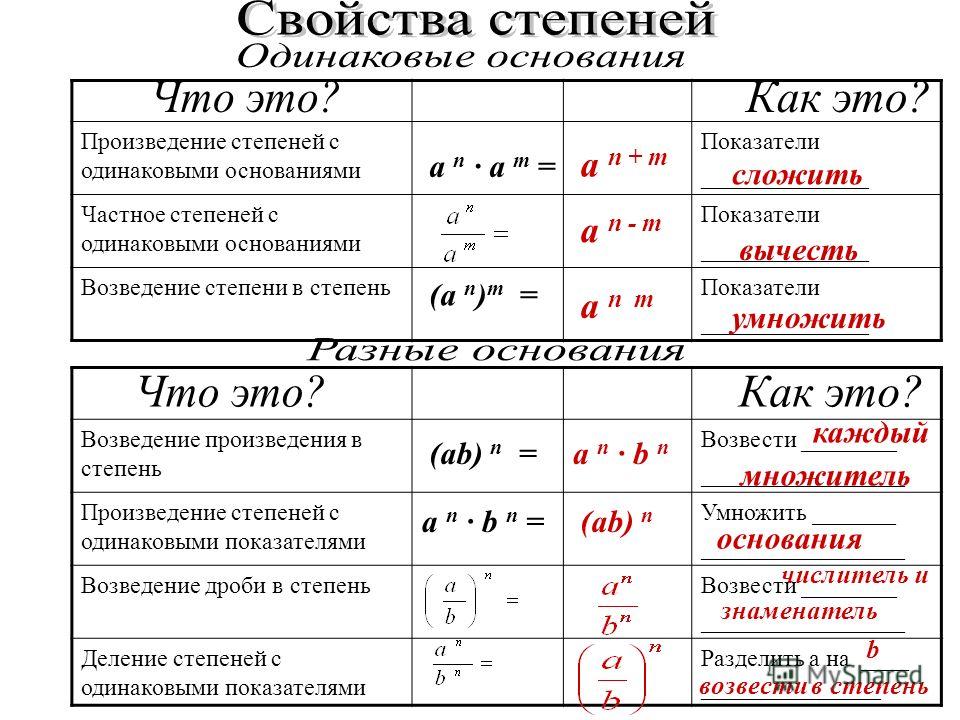 показателей степени и может хорошо разбираться в умножении показателей степени. Кроме того, для учителей очень важно научить студентов правильной процедуре умножения показателей, чтобы они никогда не сталкивались с какими-либо хлопотами во всем процессе. Родители должны регистрировать своих детей на таких платформах, как веб-сайт Cuemath, чтобы они никогда не сталкивались с какими-либо проблемами в течение всего процесса и могли получать удовольствие от математики.

Flashcards — Exponent Rules

Flashcards — Exponent Rules
  1. Дом
  2. Карточки
  3. Предварительный просмотр


Дом


Получить приложение


Создать

Автоматически удаляйте фоновое изображение. Попробуй это сейчас!

https://remove-image-background.com

  1. Правило 1: сложение и вычитание

    • Термины, содержащие экспоненты, могут добавляться или вычитаться, только если
    • они похожи.

    72 х+у + 72 х+у = 2(72 х+у)

  2. Правило II: Умножение

    Термины, содержащие показатели степени, могут умножаться только в том случае, если они имеют одно и то же основание или один и тот же показатель степени.

  3. Правило II: Умножение
    Те же основания

    • Члены с одинаковым основанием можно умножать, добавляя их показатели степени.

    7 x ×7 2x =7 3x

  4. Умножение по правилу II — одинаковые степени

  5. • Члены с одинаковым показателем степени можно умножать путем умножения их оснований.

    7 y5 × 3 y5 = 21 (y2)5

  6. Правило II- Умножение
    Те же основания Те же экспоненты

    • Термины, которые имеют один и тот же показатель степени и один и тот же показатель степени, могут быть умножены либо путем сложения их показателей, либо путем умножения их оснований!

    5 y5 × 5 y5 =25 y10 или 25 (y2)5

  7. Правило III: Деление

    Термины, содержащие показатели степени, могут быть разделены только в том случае, если они имеют одну и ту же основу или один и тот же показатель степени.

  8. Правило III: Деление
    Одинаковые основания

    • • Члены с одним и тем же основанием можно разделить путем вычитания их показателей степени.
    • 5 8 ÷5 2 =5 6

    • основания не должны быть разделены. Обратите внимание, однако, что их коэффициенты
    • должны быть, коэффициенты разнородных оснований должны быть разделены

  9. Правило III: Раздел
    Одинаковые показатели

    Термины, которые имеют один и тот же показатель степени, могут быть разделены путем деления их оснований.

    x 7 ÷y 7 = (x/y)

    7

  10. Правило III: Раздел
    Те же основания и те же показатели степени

    • Члены с одним и тем же показателем и одним и тем же показателем степени всегда равны отношению их коэффициентов, умноженному на 1, поскольку любой член, разделенный сам на себя, равен 1!

    4 5 ÷4 5 = 4 5 / 4 5 =1

  11. Правило IV: Отрицательные показатели степени

    Переверните базу!

    • Любой член с отрицательным показателем можно переписать, перевернув основание и сделав показатель степени положительным.

    Если отрицательный показатель степени содержится в знаменателе, переверните основание в числитель.

    Убедитесь, что коэффициенты не перевернуты!

    2x –2 = 2/x 2

  12. Правило V: Степени единицы и нуля –

    • 1. Любой член, возведенный в первую степень, известен как степень единицы, а любой член, возведенный в нулевую степень, известен как степень нуля. ␣␣␣␣
    • 2. Полномочия единицы• Любой член в первой степени равен самому себе.
    • 3. Любой член в нулевой степени имеет значение единицы, за исключением самого нуля!

  13. Правило VI: Разрешение скобок. Прежде чем разрешать скобки экспоненциального выражения, сначала определите, является ли данный термин простым или сложным.

    • Разрешение простых выражений •
    • Чтобы разрешить круглые скобки простого выражения, распределите показатель степени вне круглых скобок для каждого члена в круглых скобках.

    • Разрешение сложных выражений
    • • Чтобы разрешить круглые скобки сложного выражения, объедините члены с помощью ␣ в круглых скобках, а затем распределите показатель степени.

  14. Правило VII: Последовательные показатели –

    • Умножай! Введение
    • • Любое выражение, содержащее показатели степени внутри и снаружи круглых скобок, можно переписать путем умножения показателей степени. • Например, (x 3)4 =x 12 , так как 3×4=12

  15. Правило VIII: Дробные показатели степени

    • Чтобы упростить выражение с дробным показателем степени:
    • (1) Сначала посмотрите на нижнюю часть дроби. Знаменатель дробного показателя указывает, какой корень брать из исходного основания.
    • (2) Затем посмотрите на верхнюю часть дроби. Числитель дробной степени указывает степень, в которую следует возвести новое основание.

  16. 3 4

    = 81

  18. Разные основания, разные степени. Для решения задач, содержащих экспоненциальные выражения в обеих частях уравнения: