Методические указания и решение типовых задач
5.3. Для изучения влажности пшеницы было проведено обследование 200 одинаковых по массе порций. В результате получено следующее распределение порций по влажности пшеницы:
| Таблица 5.21 | |
|
|
|
Влажность пшеницы, % | Удельный вес порций в общем итоге | |
10-12 | 0,06 |
|
12-14 | 0,06 |
|
14-16 | 0,32 |
|
16-20 | 0,49 |
|
Свыше 20 | 0,07 |
|
Итого | 1,00 |
|
Определите среднюю влажность пшеницы.
5.4. Для изучения качества пряжи было проведено обследование 100 одинаковых по массе образцов пряжи, в результате чего получены следующие результаты:
| Таблица 5.22 | |
| Число проб | |
Группы образцов пряжи по крепости нити, г. | ||
До 160 | 3 |
|
160-180 | 5 |
|
180-200 | 25 |
|
200-220 | 40 |
|
220-240 | 20 |
|
240-260 | 7 |
|
Итого | 100 |
|
Определите среднюю крепость нити.
5.4. Исчисление средней арифметической взвешенной по способу моментов
Расчеты средней арифметической могут быть громоздкими, если варианты и веса имеют большие значения. Однако использование следующих основных математических свойств средней арифметической взвешенной позволяет значительно упростить вычисления. Приведем основные свойства средней арифметической:96
1)если уменьшить все варианты на какое-либо произвольное постоянное число (А), то новая средняя уменьшится на то же число;
2)если уменьшить все варианты в одинаковое число раз (К), то средняя уменьшится во столько же раз;
3)если уменьшить или увеличить веса (частоты) всех вариант на какое-либо постоянное число (А), то средняя арифметическая не изменится;
4)сумма отклонений всех вариант от общей средней равна
нулю.
Рассмотрим методику расчета средней с использованием этих свойств.
Задача 7. Имеются следующие данные о времени горения электроламп:
|
|
| Таблица 5.23 | |
|
|
|
|
|
Группы электроламп | Число электроламп | x |
| x f |
по времени горения, ч. | (f) |
|
|
|
800 -1 000 | 20 | 900 |
| 18 000 |
1 000-1 200 | 80 | 1 100 | 88 000 | |
1 200-1 400 | 160 | 1 300 | 208 000 | |
1 400-1 600 | 90 | 1 500 | 135 000 | |
1 600-1 800 | 40 | 1 700 | 680 00 | |
1 800-2 000 | 10 | 1 900 | 19 000 | |
| 400 | — | 536 000 | |
Для сравнения рассчитаем среднее время горения электроламп обычным, уже известным нам способом, по средней арифметической взвешенной. Результаты расчетов представлены в таблице. Таким образом, среднее время горения электроламп будет равно:
х = ∑∑хff = 536000400 =1340 ч.
Задача 8. Используя данные типовой задачи 7 о времени горения электроламп, произведем расчет арифметической взвешенной по способу моментов:
97
Таблица 5.24
Группы электроламп | Число |
|
|
|
|
|
|
|
|
| х − А |
| f | = |
| ||
| х-А = |
| х − А |
|
| х −1300 |
|
|
| 10 |
| ||||||
по времени горения, | электро- | х |
| = |
|
| i |
|
|
| |||||||
х-1300 |
| i | 200 |
|
| х −1300 |
|
| f |
| |||||||
ч. | ламп |
|
|
|
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
|
| 10 |
| ||||||
|
|
|
|
|
|
|
|
|
|
| 200 |
|
|
| |||
800-1000 | 20 | 900 | -400 |
|
| -2 |
|
| -4 |
|
|
|
| ||||
1000-1200 | 80 | 1100 | -200 |
|
| -1 |
|
| -8 |
|
|
|
| ||||
1200-1400 | 160 | 1300 | 0 |
|
|
| 0 |
|
| 0 |
|
|
|
|
| ||
1400-1600 | 90 | 1500 | 200 |
|
|
| 1 |
|
| 9 |
|
|
|
|
| ||
1600-1800 | 40 | 1700 | 400 |
|
|
| 2 |
|
| 8 |
|
|
|
|
| ||
1800-2000 | 10 | 1900 | 600 |
|
|
| 3 |
|
| 3 |
|
|
|
|
| ||
Итого | 400 |
|
|
|
|
|
|
|
|
| 8 |
|
|
|
|
| |
Рассмотрим методику расчета, результаты которого приведены в таблице.
Воспользуемся первым свойством средней взвешенной, которое позволяет исчислить среднюю не по фактическим значениям вариант, а по отклонениям вариант от постоянной А. В качестве постоянной А принято брать какую-либо серединную варианту ряда с наибольшей частотой. В нашем примере это х = А = 1300.
Найдем отклонения вариант от этой величины и получим значения новых вариант: х-А=х-1300.
Воспользуемся далее вторым свойством и уменьшим варианты в несколько раз. В качестве кратного числа возьмем величину интервала ряда распределения, которая равна 200.
Разделив значения вариант (х — А) на 200, получим новые значения вариант:
х−i А = х−2001300 .
Используя свойство третье, сократим частоты в 10 раз и произведем умножение полученных значений на варианты:
х−i А 10f = х−2001300 10f .
Для получения средней арифметической взвешенной необходимо разделить алгебраическую сумму взвешенных вариант на сумму весов:
98
studfiles.net
ВОПРОС N 18. Продолжите математическое свойство средней арифметической: «Если увеличить или
уменьшить все частоты в одно и то же число раз …»
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. то и средняя арифметическая увеличится или уменьшится во столько же раз
2. то и средняя арифметическая увеличится во столько же раз
3. числовое значение средней арифметической не изменится
4. то средняя арифметическая увеличится или уменьшится на это же число
Верный ответ: 3 Вариантов ответов: 4
ВОПРОС N 19. Дайте определение средних величин:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. показатели, выражающие размер или объем общественного явления
2. показатели, дающие сравнительную характеристику явления
3. показатели, дающие обобщающую количественную характеристику совокупности
4. показатели, характеризующие итоговую величину по той или иной совокупности.
Верный ответ: 3 Вариантов ответов: 4
ВОПРОС N 20. Условием правильного использования средней величины является:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. группировка показателей по любому признаку
2. качественная однородность совокупности
3. использование качественных признаков явлений
4. расчленение совокупности на множество групп
Верный ответ: 2 Вариантов ответов: 4
ВОПРОС N 21. Средние величины исчисляются из:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. абсолютных показателей
2. абсолютных и относительных показателей
3. относительных показателей
4. только из натуральных абсолютных величин
Верный ответ: 2 Вариантов ответов: 4
ВОПРОС N 22. Средняя величина, которую получают путем деления общего размера признака на число
единиц в совокупности, называется:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. гармонической
2. медианой
3. арифметической
4. гармонической простой
Верный ответ: 3 Вариантов ответов: 4
ВОПРОС N 23. В каком случае применяют средние взвешенные величины?
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. если повторяемость каждой варианты одинакова
2. если значения вариант различны
3. если значения вариант встречаются одинаковое число раз
4. если повторяемость каждой варианты различна
Верный ответ: 4 Вариантов ответов: 4
ВОПРОС N 24. Дайте определение темпа прироста:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. отношение последующего уровня к предыдущему
2. разница между последующим уровнем и предыдущим
3. отношение абсолютного прироста к предыдущему уровню
4. разность между абсолютным приростом и 100%.
Верный ответ: 3 Вариантов ответов: 4
ВОПРОС N 25. Как называется данный метод выравнивания динамического ряда: «При расчете
каждого последующего уровня принятый для укрупнения, период сдвигается на одну дату»:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. укрупнение периодов
2. выравнивание способом наименьших квадратов
3. приведение к единому основанию
4. сглаживание методом скользящей средней
Верный ответ: 4 Вариантов ответов: 4
ВОПРОС N 26. Для чего используют методы выравнивания рядов динамики
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. чтобы определить общее направление развития явления
2. чтобы сопоставить несколько рядов динамики
3. чтобы уменьшить число уровней
4. чтобы уровни ряда стали сопоставимы
Верный ответ: 1 Вариантов ответов: 4
ВОПРОС N 27. Назовите приемы преобразования рядов динамики с целью их сопоставления друг с
другом:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. укрупнение периодов; сглаживание методом скользящей средней, выравнивание способом наименьших
квадратов;
2. приведение к единому основанию; выравнивание способом наименьших квадратов
3. смыкание рядов динамики; измерение сезонных колебаний
4. приведение к единому основанию; смыкание рядов динамики
Верный ответ: 4 Вариантов ответов: 4
ВОПРОС N 28. Что такое ряд динамики?
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. ряд чисел, характеризующих распределение единиц исследуемой совокупности в зависимости от величины
признака
2. ряд чисел, характеризующих состояние и изменение явлений во времени
3. ряд чисел, характеризующих изменение явления в вариационном ряду
4. ряд чисел, характеризующих увеличение явления за несколько лет
Верный ответ: 2 Вариантов ответов: 4
ВОПРОС N 29. Из каких показателей состоит ряд динамики?
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. варианты и частоты
2. частоты и моменты времени
3. моменты времени и уровни
4. варианты и уровни
Верный ответ: 3 Вариантов ответов: 4
ВОПРОС N 30. О каком ряде динамики идет речь в этом определении: «Ряд, уровень которого
Характеризует состояние явлений за определенные периоды времени?»
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. о моментном
2. об интервальном
3. в целом и о том, и о другом
4. о ряде динамики средних величин
Верный ответ: 2 Вариантов ответов: 4
ВОПРОС N 31. Как исчисляется средний уровень моментного ряда динамики с равными интервалами
Между датами?
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. как средняя арифметическая простая
2. по формуле средней хронологической
3. как средняя гармоническая
4. по формуле средней арифметической взвешенной
Верный ответ: 2 Вариантов ответов: 4
ВОПРОС N 32. Средний уровень какого ряда динамики исчисляется путем деления суммы уровней на
Их количество?
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. моментного
2. интервального
3. моментного с равными интервалами между датами
4. любого ряда динамики
Верный ответ: 2 Вариантов ответов: 4
ВОПРОС N 33. Статистический индекс – это:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. показатель, характеризующий состояние и изменение явлений во времени
2. показатель, выражающий типичные черты и дающий обобщающую количественную характеристику уровня
по однородным общественным явлениям
3. показатель, характеризующий среднее изменение массовых явлений, состоящих из непосредственно
несоизмеримых элементов
4. показатель, выражающий размер или объем общественного явления в определенное время на
определенной территории.
Верный ответ: 3 Вариантов ответов: 4
ВОПРОС N 34. Величина, позволяющая привести разнородные элементы в сопоставимый вид,
называется:
Тип вопроса: 1. Выбор единственно правильного ответа
Цена вопроса (баллов): 1
Вариантов ответов:
1. коэффициентом роста
2. индексируемой величиной
3. коэффициентом вариации
4. коэффициентом соизмерения
Верный ответ: 4 Вариантов ответов: 4
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
11Порядок расчёта средней арифметической в интервальном ряду
Средняя арифметическая – частное от деления суммы вариант на их число. Она бывает следующих видов: простая или взвешенная.Средняя арифметическая простая, рассматривается в случае, когда известны все значения признаков х1, х2, , хп и рассчитывается по формуле где n – число вариант;х – значение признака. Средняя арифметическая взвешенная, исчисляется, если известны отдельные значения признаков и их частоты, по следующей формуле:
где х – значение признака;f – частота, которая может быть абсолютной (в разах) и относительной (доля, удельный вес частот во всей совокупности) величиной.Средняя арифметическаяимеет следующие свойства: произведение средней арифметической на сумму частот равно сумме произведений вариант на соответствующие им частоты;если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число; если все варианты увеличить или уменьшить в одно и то же число раз, то средняя арифметическая увеличится или уменьшится во
столько же раз; если все частоты одинаково увеличить или уменьшить в одно и то же число раз, то средняя арифметическая не изменится; сумма отклонений вариант от их средней арифметической величины равна нулю.
12Структурные средние: мода и медиана. Порядок расчета моды и медианы в дискретных и интервальных рядах.
В качестве структурных средних чаще всего используют показатели моды и медианы. Мода (Мо) – наиболее часто повторяющееся значение признака. Медиана (Ме) – величина признака, которая делит упорядоченный ряд на две равные по численности части.Если расчет моды и медианы проводится в дискретном ряду, то он опирается на их понятия. В интервальном ряду распределения для расчета моды и медианы применяют следующие формулы.Мода рассчитывается по формуле
,где хМо – нижнее значение модального интервала; iМо – размер модального интервала; fМо– частота модального интервала; fМо–1 – частота, предшествующая модальной частоте; fМо+1 – частота, последующая за модальной частотой.Модальному интервалу соответствует наибольшая (модальная) частота. Медиана рассчитывается по формулегдехМе – нижнее значение медианного интервала;iМе – размер медианного интервала;f – сумма частот;SМе–1 – сумма частот, предшествующих медианной частоте;fМе – медианная частота.Медианному интервалу соответствует медианная частота. Таким интервалом будет интервал, сумма накопленных частот которого равна или превышает половину суммы всех частот.
13Вариация признаков. Методы расчета показателей, её характеризующих
Средние величины дают обобщенную характеристику варьирующего признака, но в них не отражается степень колеблемости отдельных значений признака вокруг среднего уровня. Для измерения колеблемости изучаемого признака в статистике применяются различные показатели.1. Размах вариации (R) определяется по формуле R = хмах – хmin, где хmin – минимальное значение признака; хmах – максимальное значение признака. Этот показатель дает общее, внешнее представление о колеблемости признака, но не характеризует степень его колебаний.2. Среднее линейное отклонение исчисляется по следующим формулам: по несгруппированным данным: ; по сгруппированным данным: .Этот показатель представляет собой среднюю величину из отклонений индивидуальных значений признака от средней арифметической. Как меру вариации признака этот показатель в статистике применяют редко.3. Дисперсия признака (σ2) рассчитывается следующим образом: по несгруппированным данным: , по сгруппированным данным: .Дисперсия является средней арифметической квадратов отклонений каждого значения признака от общей средней, это относительная мера вариации.
4. Среднее квадратическое отклонение – это абсолютная мера вариации, выражается в единицах измерения изучаемого признака и определяется по следующим формулам: по несгруппированным данным: ; по сгруппированным данным: .
5. Коэффициент вариации (V) применяется для сравнения степени вариации различных признаков, выражается в процентах и определяется следующим образом:.
studfiles.net
Средние величины 3
Тема 5. СРЕДНИЕ ВЕЛИЧИНЫ
5.1. Понятие о средней величине
Средняя величина является обобщающей количественной характеристикой изучаемого признака в исследуемой совокупности. В статистике используются различного рода средние величины.
Средняя арифметическая – частное от деления суммы вариант на их число. Она бывает следующих видов: простая или взвешенная.
Средняя арифметическая простая, рассматривается в случае, когда известны все значения признаков х 1 , х 2 , ¼, хп и рассчитывается по формуле
где n – число вариант;
х – значение признака.
Средняя арифметическая взвешенная, исчисляется, если известны отдельные значения признаков и их частоты, по следующей формуле:
где х – значение признака;
f – частота, которая может быть абсолютной (в разах) и относительной (доля, удельный вес частот во всей совокупности) величиной.
Средняя арифметическая имеет следующие свойства:
· произведение средней арифметической на сумму частот равно сумме произведений вариант на соответствующие им частоты;
· если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число;
· если все варианты увеличить или уменьшить в одно и то же число раз, то средняя арифметическая увеличится или уменьшится во столько же раз;
· если все частоты одинаково увеличить или уменьшить в одно и то же число раз, то средняя арифметическая не изменится;
· сумма отклонений вариант от их средней арифметической величины равна нулю.
Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Данный показатель применяется тогда, когда неизвестна численность совокупности и приходится взвешивать варианты по объемам признака. Средняя гармоническая также может быть простой и взвешенной.
Средняя гармоническая простая исчисляется по формуле
Средняя гармоническая взвешенная рассчитывается по следующей формуле:
где W = xf – вес средней гармонической.
Средняя квадратиче ская (и т. д. для любой степени) рассчитывается по следующим формулам:
· простая:
· взвешенная:
Средняя геометрическая определяется по следующим формулам:
· простая:
,где Π – знак перемножения.
· взвешенная:
.Пример 1 . Имеются следующие данные о размере торговой площади магазинов, входящих в районное потребительское общество (табл. 9).
Таблица 9
Необходимо определить среднюю площадь магазина.
Решение
Так как известна площадь каждого магазина, то для вычисления средней площади магазина
следует применить среднюю арифметическую простую: м2 .Средняя площадь магазина составляет 80 м2 .
Пример 2 . Приведенные данные в предыдущем примере могут быть представлены в сгруппированном виде (табл. 10).
Необходимо определить среднюю площадь магазина.
Решение
Если известны отдельные значения признака и соответствующие ему частоты, то применяется средняя арифметическая взвешенная:
м2 .Средняя площадь магазина составляет 80 м2 .
Пример 3 . Имеются следующие данные о распределении магазинов по торговой площади (табл. 11).
Таблица 11
Следует определить среднюю площадь магазина.
Решение
Известны отдельные значения признака и их частоты, следовательно, следует применять среднюю арифметическую взвешенную:
.Так как варианты представлены в виде интервального ряда распределения, то, чтобы воспользоваться указанной формулой, необходимо выразить их одним числом, т. е. следует перейти к дискретному ряду распределения (в этом случае находят середину каждого интервала).
Для первого интервала
м2 и т. д. по остальным интервалам. Расчеты следует производить в табл. 12.Таблица 12
Таким образом,
м2 .Средняя площадь магазина равна 72 м2 .
Пример 4 . Имеются следующие данные о распределении магазинов по площади (табл. 13).
Таблица 13
Необходимо определить среднюю площадь магазина.
Решение
Так как весами является площадь W = xf , то следует применять среднюю гармоническую взвешенную:
м2 .Таким образом, средняя площадь магазина равна 80 м2 .
5.2. Вычисление средней из вариационного ряда
«способом моментов»
«Способ моментов» применяется в рядах с равными интервалами на основе свойств средней арифметической. Средняя арифметическая исчисляется по формуле
,где i – ра
mirznanii.com
Тема 5. Средние величины
5.1. Понятие о средней величине
Средняя величина является обобщающей количественной характеристикой изучаемого признака в исследуемой совокупности. В статистике используются различного рода средние величины.
Средняя арифметическая– частное от деления суммы вариант на их число. Она бывает следующих видов: простая или взвешенная.
Средняя арифметическая простая, рассматривается в случае, когда известны все значения признаков х1, х2, , хп и рассчитывается по формуле
где n – число вариант;
х– значение признака.
Средняя арифметическая взвешенная, исчисляется, если известны отдельные значения признаков и их частоты, по следующей формуле:
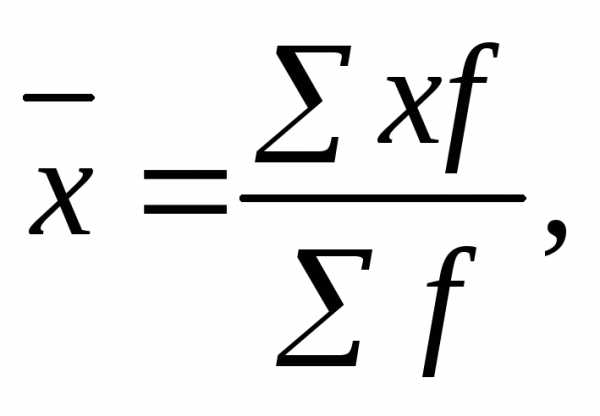
где х – значение признака;
f– частота, которая может быть абсолютной (в разах) и относительной (доля, удельный вес частот во всей совокупности) величиной.
Средняя арифметическая имеет следующие свойства:
произведение средней арифметической на сумму частот равно сумме произведений вариант на соответствующие им частоты;
если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число;
если все варианты увеличить или уменьшить в одно и то же число раз, то средняя арифметическая увеличится или уменьшится во столько же раз;
если все частоты одинаково увеличить или уменьшить в одно и то же число раз, то средняя арифметическая не изменится;
сумма отклонений вариант от их средней арифметической величины равна нулю.
Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Данный показатель применяется тогда, когда неизвестна численность совокупности и приходится взвешивать варианты по объемам признака. Средняя гармоническая также может быть простой и взвешенной.
Средняя гармоническая простая исчисляется по формуле
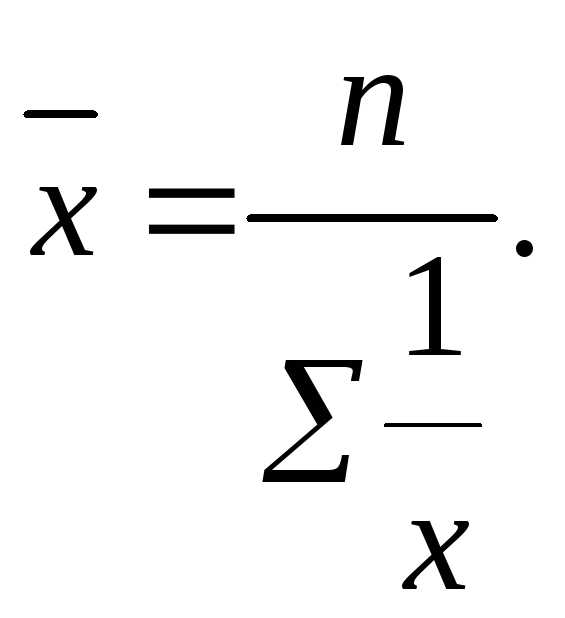
Средняя гармоническая взвешенная рассчитывается по следующей формуле:
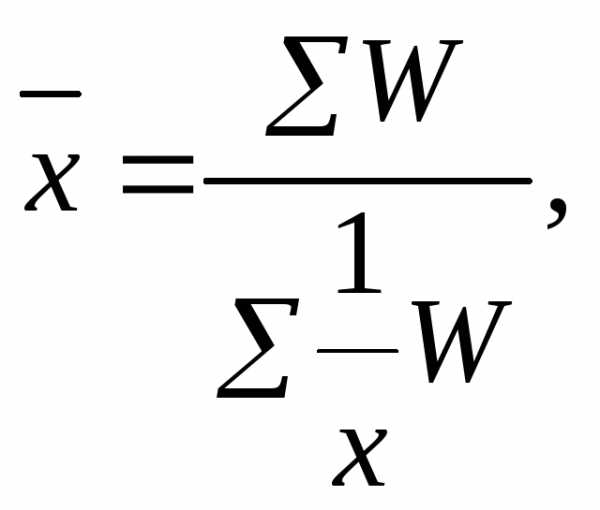
где W = xf – вес средней гармонической.
Средняя квадратическая(и т. д. для любой степени) рассчитывается по следующим формулам:
простая: 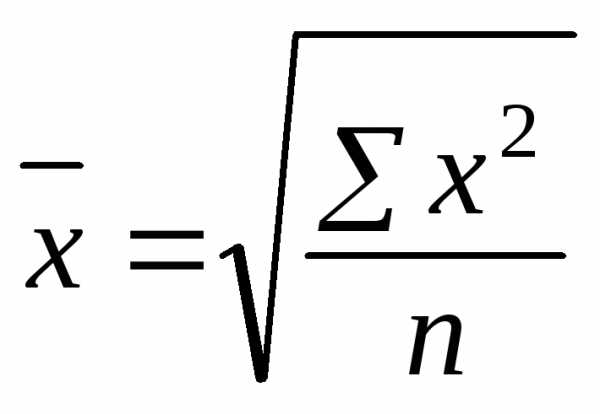
взвешенная: 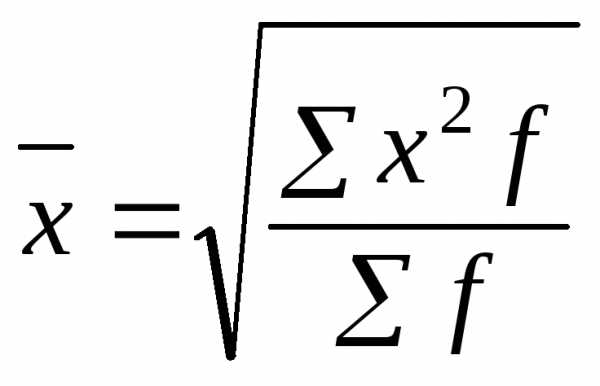
Средняя геометрическая определяется по следующим формулам:
простая: ,
где Π – знак перемножения.
взвешенная: .
В экономической практике чаще всего приходится употреблять среднюю арифметическую (простую и взвешенную) и среднюю гармоническую взвешенную.
Рассмотрим их применение на следующих типовых примерах.
Пример 1. Имеются следующие данные о размере торговой площади магазинов, входящих в районное потребительское общество (табл. 9).
Таблица 9
Магазин | 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | 7-й | 8-й | 9-й | 10-й |
Площадь магазина, м2 | 60 | 100 | 80 | 60 | 60 | 80 | 80 | 80 | 100 | 100 |
Необходимо определить среднюю площадь магазина.
Решение
Так
как известна площадь каждого магазина,
то для вычисления средней площади
магазина 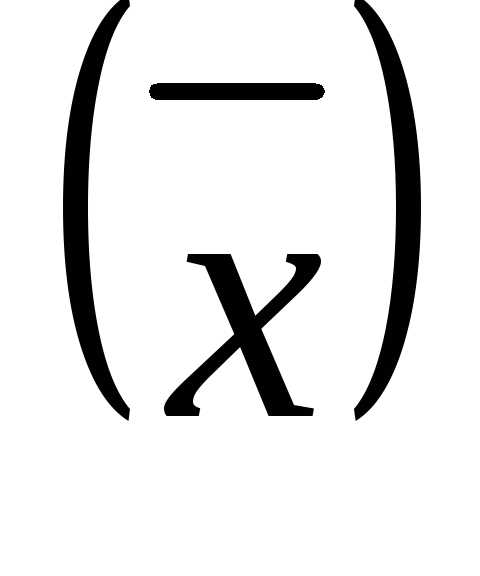 следует применить среднюю арифметическую
простую:
следует применить среднюю арифметическую
простую:
м2.
Средняя площадь магазина составляет 80 м2.
Пример 2. Приведенные данные в предыдущем примере могут быть представлены в сгруппированном виде (табл. 10).
Таблица 10
Площадь магазинов, м2 (признак – х) | 60 | 80 | 100 |
Число магазинов (частота – f ) | 3 | 4 | 3 |
Необходимо определить среднюю площадь магазина.
Решение
Если известны отдельные значения признака и соответствующие ему частоты, то применяется средняя арифметическая взвешенная:
м2.
Средняя площадь магазина составляет 80 м2.
Пример 3. Имеются следующие данные о распределении магазинов по торговой площади (табл. 11).
Таблица 11
Группировка магазинов по торговой площади, м2 (признак – х) | Удельный вес магазинов в общей численности, % (частость – f ) |
40–60 | 20 |
60–80 | 50 |
80–100 | 30 |
Итого | 100 |
Следует определить среднюю площадь магазина.
Решение
Известны отдельные значения признака и их частоты, следовательно, следует применять среднюю арифметическую взвешенную:
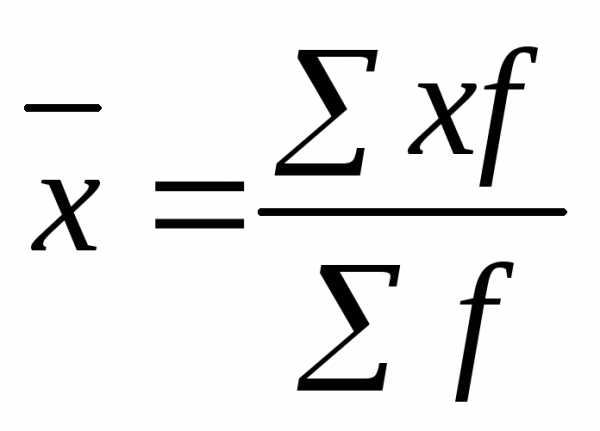 .
.
Так как варианты представлены в виде интервального ряда распределения, то, чтобы воспользоваться указанной формулой, необходимо выразить их одним числом, т. е. следует перейти к дискретному ряду распределения (в этом случае находят середину каждого интервала).
Для
первого интервала 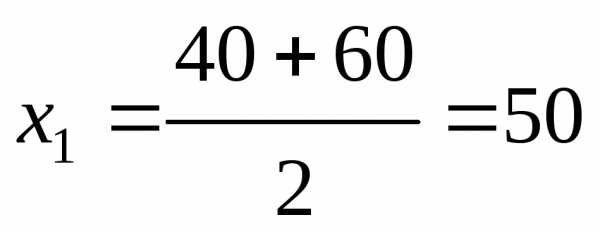 м2 и т. д. по остальным интервалам. Расчеты
следует производить в табл. 12.
м2 и т. д. по остальным интервалам. Расчеты
следует производить в табл. 12.
Таблица 12
Группировка магазинов по торговой площади, м2 (х) | Удельный вес магазинов в общей численности, % ( f ) | Середина интервала (х) | xf |
40–60 | 20 | 50 | 1000 |
60–80 | 50 | 70 | 3500 |
80–100 | 30 | 90 | 2700 |
Итого | 100 | – | 7200 |
Таким образом, м2.
Средняя площадь магазина равна 72 м2.
Пример 4. Имеются следующие данные о распределении магазинов по площади (табл. 13).
Таблица 13
Площадь магазинов, м2 (признак – х) | Общая площадь магазинов, входящих в данную группу, м2 (w = xf ) |
60 | 180 |
80 | 320 |
100 | 300 |
Итого | 800 |
Необходимо определить среднюю площадь магазина.
Решение
Так как весами является площадь W = xf, то следует применять среднюю гармоническую взвешенную:
м2.
Таким образом, средняя площадь магазина равна 80 м2.
studfiles.net
Cредняя арифметическая, Виды средней арифметической
Понятие средней арифметической
Средняя арифметическая — такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий объем импорта за год — это сумма импорта, деленная на 12 месяцев.
Средняя арифметическая может быть вычислена по формуле:
где n — численность совокупности (или число месяцев).
Например, суммарный объем импорта в 2013 году составил 314967 млн. долл. Для нахождения этой величины мы просуммировали данные по месяцам
| Месяц | Импорт |
| Январь | 19806,1 |
| Февраль | 24632,8 |
| Март | 26608,7 |
| Апрель | 28195,9 |
| Май | 24326,4 |
| Июнь | 26097,8 |
| Июль | 28023,7 |
| Август | 25987,2 |
| Сентябрь | 26263,1 |
| Октябрь | 28098,4 |
| Ноябрь | 27193,3 |
| Декабрь | 29733,7 |
| Сумма | 314967,0 |
Средняя арифметическая находится так: 314967 : 12 = 26247,3 млн. долл. (12 — число месяцев)
Смотрите видео по нахождению средней арифметической величины
Виды средней арифметической величины
Средняя арифметическая величина используется в форме простой средней и взвешенной средней. Средняя арифметическая простая равна простой сумме отдельно взятых значений осредняемого признака, разделенная на общее число этих значений. В различных контрольных по статистике она используется тогда, когда имеются несгруппированные индивидуальные значения признака, и может быть вычислена по формуле:
где n — общая численность совокупности значений х.
Средняя арифметическая взвешенная — это средняя из вариантов, которые повторяются разное число раз или имеют различный вес. Она может быть рассчитана по формуле:
Основные свойства средней арифметической
- Если индивидуальные значения признака (варианты), уменьшить (увеличить) в n раз, то среднее значение нового признака соответственно уменьшится или увеличится во столько же.
- Если все варианты осредняемого признака уменьшить (увеличить) на число А, то средняя арифметическая соответственно изменится на это же число.
- Если вес всех осредняемых вариантов уменьшить (увеличить) в k раз, то средняя арифметическая не изменится.
- Сумма отклонений отдельных значений признака от средней арифметической равна нулю.
Часто приходится вычислять среднюю по групповым средним или по средним отдельных частей совокупности. Например, средняя рождаемость в стране представляет собой среднее из средних рождаемости по отдельным регионам страны. Средние из средних определяются так же, как и средние из первоначальных значений признака.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
univer-nn.ru
теория
Вариационными рядами называются:
Ряды распределения единиц совокупности по количественным признакам
Между размером вариации признака в совокупности и типичностью
средней характеристики признака существует зависимость:
Чем больше вариация, тем менее типична средняя
Если все значения вариационного ряда увеличить на произвольное
число m, то дисперсия: Не изменится
Средний квадрат отклонений вариантов признака от некоторой
произвольной величины равен 61. Средняя величина признака больше
произвольной величины на 6 единиц и равна 10. Найдите коэффициент
вариации.
При исчислении показателей вариации применяется:
Средняя квадратическая
Сумма индивидуальных отклонений вариант от средней арифметической:
Равна 0
Если рассчитывать дисперсию для интервального вариационного ряда
при численности совокупности более 1000 единиц по значениям середин
интервалов, то: Оценка дисперсии будет заниженной
Средняя альтернативного признака равна:
Доле единиц совокупности, обладающих альтернативным признаком
Если все значения вариационного ряда уменьшить в m раз, то дисперсия:
Уменьшится в m2раз
Средняя арифметическая представляет собой:
Отношение объёма варьирующего признака к объёму совокупности
Если все значения вариационного ряда увеличить на произвольное число
m, то средняя арифметическая:
Увеличится на m
Внутригрупповую вариацию признака в совокупности, разбитой на
группы, можно оценить с помощью: Остаточной дисперсии
Дисперсия альтернативного признака равна: Произведению долей единиц,
обладающих и единиц, не обладающих альтернативным признаком
Степенная средняя называется средней арифметической, если:
Показатель степени средней m=1
Дисперсия по сравнению со средним квадратом отклонений
индивидуальных значений признака от произвольной величины m
(при условии x≠m): Всегда меньше
Вариацию групповых средних относительно общей средней признака в
совокупности можно оценить с помощью: Факторной дисперсии
Если все частоты признаков в вариационном ряду увеличить в m раз, то
дисперсия: Увеличится в m2 раз
Распределение доходности акций характеризуется левосторонней
асимметрией. Модальное значение равно 14%, а соответствующая ей
частость – 0,345. Будет ли частость, соответствующая ср. арифметической:
Меньше 0,345
Степенная средняя называется средней гармонической, если:
Показатель степени средней m=-1
Средний квадрат отклонений вариантов признака от произвольной
величины равен 300, а сама произвольная величина равна 70 единицам.
Опр-те дисперсию признака, если известно, что ср. вел-на его варианта=80.
300 — (80-70)2
Коэффициент детерминации представляет собой:
Долю факторной дисперсии в общей
Понятия асимметрии и эксцесса распределения возникают:
При сравнении фактических рядов распределения с нормальным распределением
Между размером вариации признака в совокупности и типичностью средней
характеристики признака существует зависимость:
Чем больше вариация, тем менее типична средняя
Вариацию групповых средних относительно общей средней признака в
совокупности можно оценить с помощью: Факторной дисперсии
Степенная средняя называется средней геометрической, если:
Показатель степени средней m=0
Структурные средние явл-ся: Конкретными знач-ми ряда распределения
Дисперсия постоянной величины равна: Нулю
Если все частоты признаков в вариационном ряду увеличить в m раз,
то средняя арифметическая: Увеличится в m раз
Эмпирическое корреляционное отношение стремится к 1, когда:
Остаточная дисперсия стремится к 0
Сумма индивидуальных отклонений вариант от средней арифметической:
Равна 0
Если рассчитывать дисперсию для интервального вариационного ряда при
численности совокупности более 1000 ед. по знач-ям середин интервалов, то:
Оценка дисперсии будет заниженной
Средняя альтернативная признака равна:
Доле единиц совокупности, обладающих альтернативным признаком
1)На моментные и интервальные делятся ряды динамики:
— абсолютных величин
2)Средний уровень моментного динамического ряда с одинаковыми
промежутками времени между моментами фиксации явления во времени
определяется по формуле: — средней хронологической
3) Величина корреляционного отношения близка к 1,когда:
— остаточная дисперсия близка к 0
4) Для изменения тесноты связи в случае множественной корреляции
применяются: — парные коэффициенты корреляции
5) Мерой тесноты связи атрибутивных признаков является:
коэффициент конкордации
6) Различают цепную и базисную систему расчета индексов динамики
7) Субъиндексы охватывают сравнением
— некоторую часть элементов совокупности
8) Выборочная совокупность при применении выборочного метода
формируется — в случайном порядке
9) Размер случайных ошибок с увеличением численности выборки
— уменьшается
10)Тенденциозные ошибки выборки возникают
— при нарушении принципа случайности отбора ед-ц из ген.совокупности
11) Произведение цепных коэффициентов роста равняется
— базисному коэффициенту роста последнего периода
12) Средний абсолютный прирост может быть рассчитан на основе
— как цепных, так и базисных абсолютных приростов
13)Абсолютное значение 1го процента прироста равняется
— отношению абсолютного приросту к темпу прироста за тот же период
14)Сезонные колебания представляют собой
— устойчивые внутригодичные колебания уровней ряда
15) Линейный коэффициент корреляции варьирует
— от -1 до +1
16) Агрегатный индекс количественно величины можно представить
в виде индекса среднего арифметического
17) Объектом факторного анализа с помощью системы взаимосвязанных
агрегатных индексов является абсолютное изменение сложного явления
18) при типическом отборе в формулах для определения необходимой
численности выборки применяется внутригрупповая дисперсия
19) Независимо от характера распределения генеральной совокупности
при увеличении объёма выборки распр-ие вероятностей появления того
или иного знач-ия выборочной средней приближается к норм. распр-нию
20) малой называется выборка объемом
— менее 30 единиц
21) интервальный ряд динамики показывает
— данные, характеризующие размеры явлений за определенный промежуток
времени
22) при помощи теории корреляции изучаются связи факторные
23) При построении параллельных рядов в порядке возрастания располагают
— значения признака X
24) Корреляционной называется таблица, в которой
— приведено комбинированное распределение единиц совокупности по двум
количественным признакам
25) Величина корреляционного отношения близка к 1, когда
— остаточная дисперсия близка к 0
26) При серийной выборке в формулах для определения необходимой
численности выборки применяется
— межгрупповая дисперсия
27) Агрегатный индекс качественной величины можно представить в виде
индекса среднего гармонического
28)Если отбирается каждая 20ая единица генеральной совокупности, то это
— 5-ти процентная выборка
29) При формировании выборочной совокупности методом случайного
спора возникает случайные ошибки выборки
30) Индекс цен переменного состава отражает влияние на средних цен
— для изменения цен на отдельные виды продукции…
31) Аналитическое выравнивание производится
— методом наименьших квадратов
32) Коэфициент Фехнера основан
— на знаках отклонений значений признака от своих средних величин
33) Мерой тесноты связи атрибутивных признаков является
— коэффициент конкордации
34) Сводную числовую характеристику основной тенденции динам.
ряда можно получить
— с помощью аналитического выравнивания динамического ряда
35) Средний уровень моментного динамического ряда с одинаковыми
промежутками времени между моментами фиксации явления
опр. по формуле средней хронолической
36) Бесповторным называется отбор, при котором
— одна и та же единица генеральной совокупности не может быть отобрана
более одного раза
37) Сомножитель индексируемой величины наз-ся весом-соизмерителем
38) В сис-ме взаимосвязанных агрегатных индексов при индексации
качественных величин веса фиксируется на уровне отчетного периода
39) Если отбирается каждая 20-я единица генеральной совокупности, то это
— 5-ти процентная выборка
40)При собственно-случайном отборе в формулах ошибок выборки
применяется общая дисперсия
studfiles.net
