Интерполировать в Excel — voxt.ru
Интерполяция в Excel
Интерполяция в Excel помогает нам найти значение между двумя точками на линии графика или линии кривой. Простыми словами «Интер» предлагает заглянуть внутрь тех данных, которые у нас уже есть. Не только в статистике, но и в области науки, торговли, бизнеса он используется для поиска или прогнозирования будущей стоимости, которая находится между двумя существующими точками данных.
Пример интерполяции данных в Excel
Чтобы понять концепцию интерполяции данных в Excel, давайте посмотрим на приведенный ниже пример. На ферме фермер выращивает рис, и он следит за его ростом.
Вы можете скачать этот шаблон Интерполяции в Excel здесь — Шаблон Интерполяции в Excel
Фермер зарегистрировал рост рисовых полей ниже тенденции за 20 дней, причем он отмечал рост один раз в 4 дня.
Из приведенной выше таблицы фермер хочет знать, какой высоты был падди на 5-м участке. th
th
Посмотрев на данные, мы можем легко оценить, что на 5-й день рост риса составил 2,5 дюйма. Причина, по которой мы можем легко определить рост рисовых культур, потому что они росли по линейному закону, т. Е. Существовала взаимосвязь между количеством записанных дней и размером рисового поля в дюймах. Ниже приведен график, показывающий линейный рост рисового поля.
На приведенном выше графике легко показана линейная модель роста рисового риса. Но если рисовые поля росли линейно, то сложно предсказать рост на 5-й день.
Основываясь на этой кривой, фермеры не могут оценить рост на 5-й день. Итак, именно здесь наша концепция интерполяции помогает нам найти рост на 5th день.
Для интерполяции у нас есть формула ниже.
Здесь у нас есть две переменные, то есть X1 и Y1. «X» — это первый набор значений, а «Y» — второй набор значений.
В нашем примере роста рисовых полей первый набор значений — (4,2). Здесь «4» — это день, а «2» — это дюймы роста рисового поля.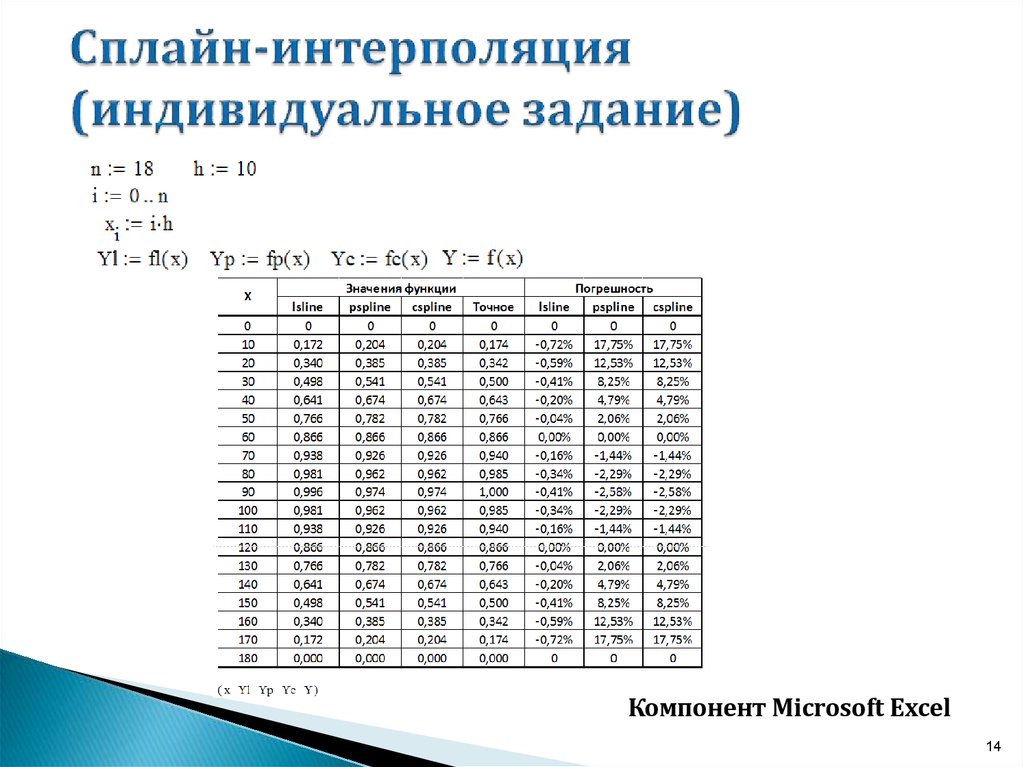
Второй набор значений — (8,4). Здесь «8» — это день, а «4» — это дюйм роста рисового поля.
Поскольку нам нужно найти рост по переменной 5-го дня, «x» становится 5 для переменной роста в дюймах «y».
Итак, давайте применим значения к приведенной выше формуле.
Теперь сделайте первый шаг расчета.
Примечание «x» равно
Таким образом, на 5-й день рост риса составит 2,5 дюйма.
Линейная интерполяция в Excel
Та же линейная интерполяция в Excel также переносит те же данные в Excel.
Теперь нам нужно найти рост в дюймах для 5th день, так х = 5.
Набор 1 (x1, y1)
Набор 2 (x2, y2)
Так x1 = 4, y1 = 2, x2 = 8 и y2 = 4.
Введите эти значения в ячейки листа Excel.
Я упомянул вопросительные знаки для x1, y1, x2 и y2. Потому что с этими простыми данными мы можем легко найти их глазами. Но всегда полезно находить эти значения с помощью формулы. Чтобы найти значение «x1», примените следующую формулу.
Но всегда полезно находить эти значения с помощью формулы. Чтобы найти значение «x1», примените следующую формулу.
Теперь, чтобы найти значение «y1», примените следующую формулу.
Чтобы найти значение «x2», примените формулу ниже.
Чтобы найти значение «y2», примените формулу ниже.
Таким образом, используя эти формулы, мы можем найти значения для всех параметров формулы Интерполяции в Excel.
Затем, чтобы найти дюймы для роста рисового риса на 5-й день, примените следующую формулу.
Итак, поскольку мы вычислили вручную по формуле, мы также получили 2,5 в качестве ответа. При необходимости мы можем вставить линейный график для данных.
Что нужно помнить здесь
- Интерполяция — это процесс нахождения среднего значения существующих данных.
- В Excel нет встроенной формулы для расчета значения интерполяции Excel.
- В функции ПОИСКПОЗ нам нужно использовать «1» для параметра «тип соответствия», который помогает пользователям найти значение, превышающее значение подстановки.

УЗНАТЬ БОЛЬШЕ >>
Post Views: 1 295
Похожие записи
Прокрутить вверхPers.narod.ru. Обучение. Интерполяционный полином Ньютона
Pers.narod.ru. Обучение. Интерполяционный полином НьютонаЭтот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье
|
Pers.narod.ru. Обучение. Интерполяционный полином Ньютона |
Дана таблица значений функции y = f(x)
|
x |
x0 |
x1 |
… |
xn |
|
y |
y0 |
y1 |
. |
yn |
и два значения аргумента x= a и x = b, отличные от данных в таблице. Требуется с помощью полиномов Ньютона третьей степени вычислить приближенные значения функции y = f(x) в точках x = a и x = b, т.е.
Пример решения
|
x |
1.6 |
1.7 |
1.8 |
1.9 |
2.0 |
a = 1. |
|
y |
1.6416 |
2.3961 |
3.3536 |
4.5441 |
6.0000 |
b = 1.68 |
Построим таблицу конечных разностей:
|
i |
xi |
yi |
Δyi |
Δ2yi |
Δ3yi |
|
0 |
1. |
1.6416 |
0.7545 |
0.2030 |
0.0300 |
|
1 |
1.7 |
2.3961 |
0.9575 |
0.2330 |
0.0324 |
|
2 |
1.8 |
3.3536 |
1. |
0.2654 |
|
|
3 |
1.9 |
4.5441 |
1.4559 |
|
|
|
4 |
2.0 |
6.0000 |
|
|
|
Поскольку точка b =
1.68 находится ближе к началу таблицы, а точка a = 1. 92 – ближе к концу таблицы,
то для нахождения значения f(b) будем использовать первый полином
Ньютона, а для нахождения f(a) – второй. Ближайшее меньшее к точке
b значение узла таблицы = 1.6, а ближайшее большее к точке a = 2.
92 – ближе к концу таблицы,
то для нахождения значения f(b) будем использовать первый полином
Ньютона, а для нахождения f(a) – второй. Ближайшее меньшее к точке
b значение узла таблицы = 1.6, а ближайшее большее к точке a = 2.
Выпишем первый и второй полиномы третьей степени:
Скриншот реализации задачи в Excel показан ниже. Значения полинома вычисляются в точках a и b,
а также строятся значения полинома в пределах изменения x с шагом, равным 0.05 и автоматическим выбором первой или второй формулы.
Интерполяционный полином Ньютона — скачать пример в Excel XP/2003 (28 Кб)
Следует учесть, что в документе расчёт делается всегда по первым конечным разностям (от точек y0, y1), если точка a или b лежит ближе к началу интервала, и по последним (от точек y3, y4), если она ближе к концу. Есть и другие способы расчёта, берущие ближайший слева или справа узел.
Есть и другие способы расчёта, берущие ближайший слева или справа узел.
Как интерполировать в Excel
Если вы увлекаетесь математикой и вам нужно обнаружить неизвестные точки данных из выборки известных точек данных, интерполяция с помощью Excel — это простой выбор.
Excel — надежный калькулятор с визуализацией данных. Таким образом, для различных математических и статистических анализов он вам всегда пригодится. Хотя прямой функции для интерполяции не существует, вы можете использовать различные функции для оценки новых точек данных из заданной таблицы данных значений X и Y.
Читайте дальше, чтобы узнать о популярных и простых методах интерполяции данных в Excel.
1. Использование математического уравнения
Одним из основных подходов интерполяции данных в Microsoft Excel является применение математической формулы линейной интерполяции. Вы можете использовать этот метод, если получаете линейную линию тренда для графика.
Y= Y1 + (X-X1)⨯(Y2-Y1)/(X2-X1)
Например, вы хотите узнать значение Y, когда X равно 15 из этой таблицы. Вот как:
- Создайте таблицу значений X1, X2, Y1 и Y2, проанализировав таблицу.
- Вы должны выбрать точки данных на один шаг выше и ниже нового значения X, которое вы ищете.
- Теперь примените следующую формулу в любой ячейке, чтобы найти интерполированное значение Y, соответствующее значению X 15.
=G5+(K4-E5)*(H5-G5)/(F5-E5)
Процесс довольно простой и выполняется вручную. Для больших наборов данных вам придется потратить много времени на интерполяцию точек данных.
Загрузка: Интерполяция в электронной таблице Excel (бесплатно)
Связано: Как сделать точечную диаграмму в Excel и представить свои данные
2. Использование метода подбора кривой
Подгонка кривой — еще один быстрый, но ручной метод интерполяции в Excel. Просто создайте точечную диаграмму и сгенерируйте уравнение графика. Excel использует линейную регрессию для заполнения уравнения. Вам нужно применить это уравнение подгонки кривой, чтобы найти значение Y:
Excel использует линейную регрессию для заполнения уравнения. Вам нужно применить это уравнение подгонки кривой, чтобы найти значение Y:
Y= Наклон * X + точка пересечения Y
Чтобы узнать значение Y по заданному значению X, равному 15, вы можете попробовать выполнить следующие действия:
- Выберите таблицу и вставьте точечную диаграмму.
- Щелкните правой кнопкой мыши линию тренда и выберите Формат линии тренда .
- Установите флажки рядом с Показать значение R-квадрата на графике и Показать уравнение на графике .
- Также выберите линию тренда Linear .
- Как только на точечной диаграмме появится уравнение, подставьте в него значение X, чтобы найти значение Y.
- Следующая формула показывает значение Y.
=0,9889*K4+3,5333
Метод подбора кривой подходит только для небольших наборов данных. Для этого процесса нет простой автоматизации, и вы можете полагаться только на макросы Microsoft Excel для автоматизации на основе горячих клавиш.
3. Использование функций Excel: наклон и точка пересечения
Вы можете использовать функции НАКЛОН и ОТРЕЗОК в Excel для линейной интерполяции значения Y. Вы можете легко применить эти функции, поскольку они требуют только известных значений X и Y. Ниже приведены синтаксисы, которые вам необходимо использовать:
= НАКЛОН (известные_y, известные_x)
=ПЕРЕХОД (известные_y, известные_x)
Вот как вы можете интерполировать точки данных с помощью этого метода:
- Переименуйте две ячейки с помощью Наклон и Точка пересечения .
- Примените функцию SLOPE под заголовком Slope и выберите соответствующие данные из таблицы.
- Аналогичным образом примените функцию INTERCEPT и заполните значение intercept.
- Теперь примените формулу Y = Slope * X + Y-intercept , чтобы узнать значение Y.
- Вы можете создать формулу Excel для приведенного выше уравнения, где вы можете просто изменить значение X, чтобы узнать другие неизвестные точки данных.

Вы можете выполнять интерполяцию быстрее, если создадите ячейки для значения X, наклона и точки пересечения. Однако этот процесс может не дать точных данных для нелинейной интерполяции.
4. Использование функции Excel: ПРОГНОЗ
Это популярная функция Excel для прогнозирования производительности путем анализа набора реальных точек данных. Вы найдете FORECAST и FORECAST.LINEAR в Excel 2016 и более поздних версиях. Для получения надежных результатов полезно использовать FORECAST.LINEAR.
Функция использует три аргумента для создания прогнозируемой точки данных. Эти аргументы представляют собой заданное значение X, известные значения Y и значения X из таблицы. Проверьте синтаксис ниже:
=ПРОГНОЗ.ЛИНЕЙНЫЙ(x, известные_y, известные_x)
Вы можете быстро определить значение Y, выполнив следующие действия:
- Ячейка, в которую вы хотите ввести значение Y, должна иметь знак равенства ( = ).
- Сейчас введите Прогноз и выберите функцию FORECAST.
 LINEAR из раскрывающегося меню формулы.
LINEAR из раскрывающегося меню формулы. - Нажмите на значение X и поставьте запятую.
- Затем выберите диапазон ячеек с известным значением Ys и поставьте запятую.
- Выберите известный диапазон ячеек X и закройте формулу скобками.
- Нажмите Введите , чтобы получить интерполированное значение Y.
- Вы можете продолжать изменять значение X в диапазоне заданной таблицы, чтобы получить значения Y.
- Формула ПРОГНОЗА в этом руководстве выглядит следующим образом:
=ПРОГНОЗ.ЛИНЕЙНЫЙ(K4,C2:C10,B2:B10)
Функции FORECAST.LINEAR предлагают высокоточный прогноз данных для линейных и слегка нелинейных точек данных. Он использует первое и последнее значения для заданного значения X и учитывает весь набор данных.
Таким образом, вы увидите использование этой функции для анализа критически важных данных, таких как прогнозирование веб-трафика, моделирование финансовых данных и расчет эффективности бизнеса.
5. Функция РОСТА для нелинейной интерполяции
Когда у вас есть таблица реальных данных в экспоненциальной форме, FORECAST.LINEAR не даст точных интерполированных точек данных. В Excel есть еще одна отличная функция для прогнозирования данных, и это РОСТ. Как и другие функции, упомянутые выше, эта формула также проста в применении.
Помимо знакомых аргументов, таких как известный диапазон ячеек X, известные значения Y и заданное значение X, РОСТ использует дополнительное логическое значение. Обычно вам нужно ввести единицу для этой логической константы. Вот как выглядит синтаксис:
= РОСТ (известные_y,[известные_x],[новые_x],[постоянные])
Чтобы интерполировать данные в Excel с помощью функции РОСТ, вы можете выполнить следующие шаги:
- Вставьте функцию РОСТ в любую ячейку, где вы хотите получить интерполированное значение для Y.
- Введите диапазон ячеек для известных значений Y, после чего поставьте запятую.

- Повторите описанный выше шаг, чтобы ввести диапазон ячеек для известных значений X.
- Теперь введите значение заданного X и поставьте запятую.
- Введите 1 в качестве последнего аргумента и закройте формулу.
- Нажмите Введите , чтобы сгенерировать интерполированное значение Y.
- Вы можете использовать ссылки на ячейки вместо фактических значений, чтобы найти больше значений, просто изменив заданные данные.
- Окончательная формула будет выглядеть так:
=РОСТ(B2:B12,A2:A12,E2,1)
По сравнению с функцией ПРОГНОЗ функция РОСТ создает более надежные и точные интерполированные точки данных для экспоненциальных наборов данных, которые в основном являются нелинейными. Подобно ПРОГНОЗУ, вы также можете автоматизировать функцию РОСТ, не прилагая особых усилий.
Интерполяция данных и прогнозирование стали проще
Теперь вы можете эффективно интерполировать данные для предстоящих задач на работе или в школе.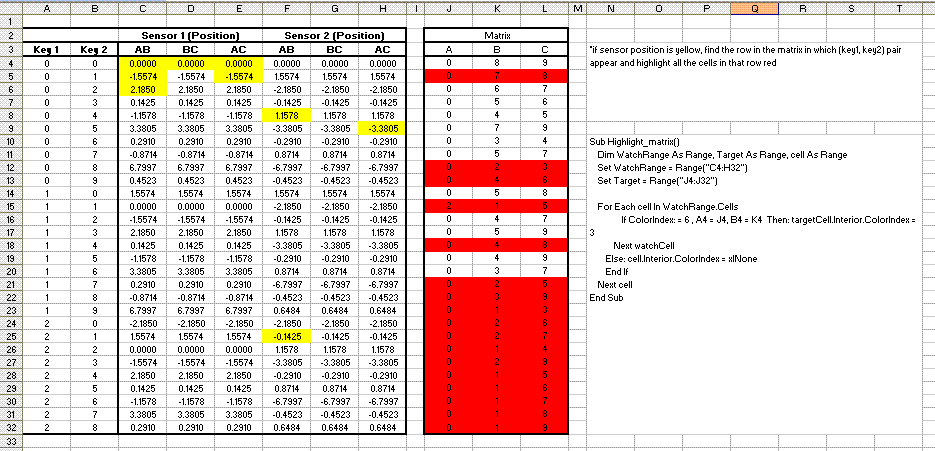
Такая быстрая аналитика данных помогает вам по-разному, например, сократить несколько повторяющихся шагов исследования данных или оценить нагрузку на задачи, прежде чем приступать к новым проектам.
Как выполнять интерполяцию в Excel: 4 простых способа
Интерполяция — это процесс оценки точек данных в существующем наборе данных. Поскольку это блог Excel, то, очевидно, мы хотим ответить на вопрос: можем ли мы интерполировать с помощью Excel. Это распространенный вопрос. На самом деле именно следующий вопрос читателя заставил меня заглянуть в эту тему:
«У меня вопрос по Excel — есть ли способ интерполировать значение из таблицы? У меня есть X и Y, которых нет в таблице, но есть коррелированные данные, поэтому я хочу рассчитать интерполированное значение».
В качестве простого примера, если для того, чтобы пройти 1 милю в понедельник, требуется 15 минут, а для того, чтобы пройти 4 мили во вторник, требуется 1 час, мы можем обоснованно оценить, что для того, чтобы пройти 2 мили, потребуется 30 минут.
Не следует путать с экстраполяцией, которая оценивает значения вне набора данных. Оценка того, что для прохождения 8 миль потребуется 2 часа, будет экстраполяцией, поскольку оценка выходит за пределы известных значений.
Excel — отличный инструмент для интерполяции, так как, в конечном счете, это большой визуальный калькулятор.
Скачать файл примера
Я рекомендую вам скачать файл примера для этого поста. Затем вы сможете работать с примерами и увидеть решение в действии, а файл будет полезен для дальнейшего использования.
Скачать файл: 0020 Interpolate with Excel.xlsx
Посмотреть видео
Содержание
Варианты интерполяции с Excel
Что касается ответа на вопрос, существует несколько сценариев, которые могут привести к различным решениям.
Во-первых, мы могли бы использовать простую математику. Это сработало бы, если бы результаты были совершенно линейными (т. е. значения X и Y перемещались бы непосредственно синхронно друг с другом). Но если это не так, мы можем получить слегка искаженный результат.
В качестве альтернативы мы могли бы использовать функцию ПРОГНОЗ Excel (или ПРОГНОЗ.ЛИНЕЙНЫЙ в Excel 2016 и более поздних версиях). Судя по названию, функция ПРОГНОЗ кажется странным выбором. Казалось бы, это функция специально для экстраполяции; однако это также один из лучших вариантов линейной интерполяции в Excel. ПРОГНОЗ использует все значения в наборе данных для оценки результата; поэтому он отлично подходит для линейных отношений, даже если они не полностью коррелированы.
Затем еще одна мысль, а что, если отношения X и Y вовсе не линейны? Как мы можем интерполировать значение, когда данные экспоненциальны?
Давайте рассмотрим все эти сценарии.
Интерполяция с использованием простой математики
Простая математика хорошо работает, когда есть только две пары чисел или когда отношение между X и Y абсолютно линейно.
Вот базовый пример (см. вкладку Example 1 в файле загрузки):
Формула в ячейке E4:
=B2+(E2-A2)*(B3-B2)/(A3-A2)
Некоторым это может показаться немного сложным, поэтому вот краткий обзор формула.
=B2+(E2-A2)* (B3-B2)/(A3-A2)
В последнем разделе (выделено зеленым выше) вычисляется, насколько значение Y изменяется при изменении значения X на 1. В В нашем примере Y сдвигается на 1,67 за каждую единицу числа X.
=B2+ (E2-A2)* (B3-B2)/(A3-A2)
интерполированный X отличается от первого X, а затем умножается на значение, рассчитанное выше. В нашем примере результат вычисляется как 17,5 (ячейка E2) минус 10 (ячейка A2), результат которого затем умножается на 1,67. Все это равно 12,5.
= B2+ (E2-A2)*(B3-B2)/(A3-A2)
Наконец, мы подходим к первому разделу формулы (выделено зеленым выше), который складывает первое значение Y.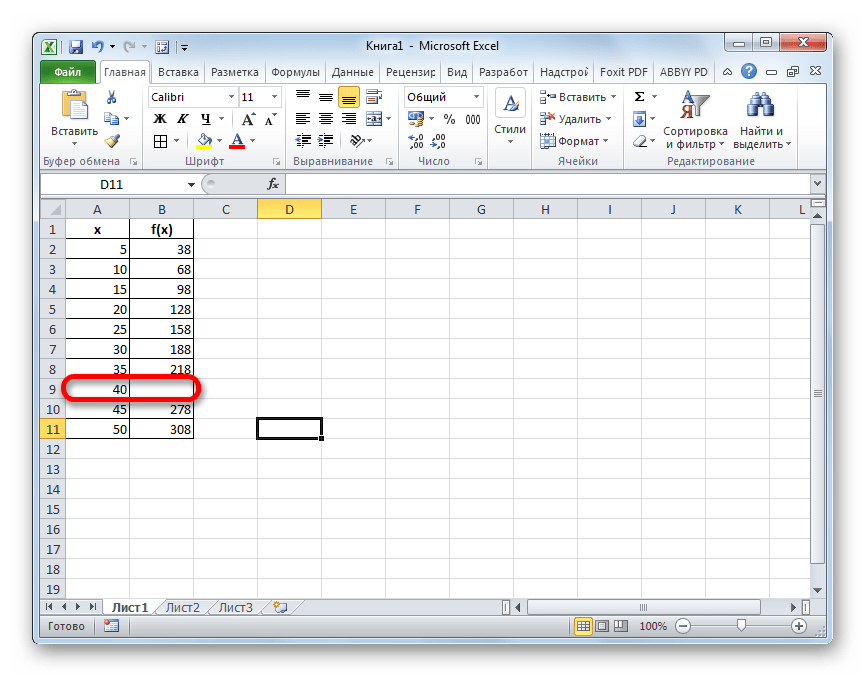 В нашем примере это дает окончательный результат 77,5 (65 + 12,5). Для тех, кто помнит школьную математику, формула выглядит следующим образом:
В нашем примере это дает окончательный результат 77,5 (65 + 12,5). Для тех, кто помнит школьную математику, формула выглядит следующим образом:
Вот результат, наложенный на диаграмму.
Даже если вы не помните линейную интерполяцию из школы, хорошая новость заключается в том, что Excel предоставил нам более простой вариант — функцию ПРОГНОЗ.
Интерполяция с использованием функции ПРОГНОЗ
В версии Excel 2016 года было добавлено множество новых статистических функций. Чтобы освободить место для этих новых функций, ПРОГНОЗ был заменен функцией ПРОГНОЗ.ЛИНЕЙНЫЙ. Хотя ПРОГНОЗ по-прежнему остается на данный момент с целью обратной совместимости с Excel 2013 и более ранними версиями.
Поскольку ПРОГНОЗ и ПРОГНОЗ.ЛИНЕЙНЫЙ фактически одно и то же, мы будем использовать эти термины как синонимы.
Интерполяция при идеальной линейности
Теперь воспользуемся ПРОГНОЗОМ для интерполяции результата.
Используя те же числа из примера выше, формула в ячейке E6 будет следующей:
=ПРОГНОЗ(E2,B2:B3,A2:A3)
Функция ПРОГНОЗ имеет следующий синтаксис: ПРОГНОЗ(x,известные_y,известные_x)
Три аргумента функции:
- x – точка данных, для которой мы хотим предсказать значение
- known_y’s — диапазон ячеек или массив значений, содержащих известные значения Y
- known_x’s — диапазон ячеек или массив значений, содержащих известные значения X
При использовании функции ПРОГНОЗ результат ячейки E6 также равен 77,5 (так же, как и в математическом подходе).
Для полноты примера файл также содержит использование функции FORECAST.LINEAR. Как и следовало ожидать, результат идентичен устаревшей функции ПРОГНОЗ.
Интерполяция при приближении к линейной
Но… что, если наши данные не идеально линейны? Посмотрите на график ниже, данные явно имеют линейную зависимость, но она не идеальна. Посмотрите на Пример 2 вкладка в вспомогательном файле.
В этих обстоятельствах функция ПРОГНОЗ даже более полезна, так как она не просто интерполирует между первым и последним значениями. Вот данные, используемые в диаграмме.
Функция ПРОГНОЗ в ячейке E4 интерполирует значение Y на основе значения X, равного 17,5.
=ПРОГНОЗ(E2,B2:B11,A2:A11)
В этом сценарии ПРОГНОЗ оценивает значение на основе всех доступных точек данных, а не только начала и конца. Результат функции ПРОГНОЗ в ячейке E4 равен 77,3 (округлено до 1 знака после запятой), что в большинстве случаев будет более точным, чем простая линейная интерполяция, применяемая в математическом подходе.
Помните, интерполяция используется для оценки значений. 77,3 может быть неточным результатом, но это разумная оценка, основанная на имеющейся у нас информации.
И снова FORECAST.LINEAR вычисляет тот же результат.
Краткое описание функции ПРОГНОЗ
Изображение ниже содержит краткое описание функции ПРОГНОЗ.
Узнайте больше о функциях ПРОГНОЗ и ПРОГНОЗ.ЛИНЕЙНЫЙ в этой статье: ПРОГНОЗ и ПРОГНОЗ.ЛИНЕЙНАЯ функция (support.office.com)
Интерполяция, когда данные нелинейны
Но вот более сложный вопрос, что если данные вообще нелинейны? Тогда что?
Посмотрите на вкладку Example 3 в вспомогательном файле. Вот наш новый сценарий графика:
Если бы мы использовали простой линейный подход, это дало бы нам значение 77,5, что, как вы можете видеть ниже, довольно далеко от кривой. Использование функции ПРОГНОЗ даст результат 70,8, что лучше, но также далеко от кривой.
Есть еще два варианта получения более точной оценки (1) интерполяция экспоненциальных данных с использованием функции РОСТ (2) расчет внутренней линейной интерполяции к данным с экспоненциальным ростом.
Результат функции РОСТ в ячейке E10 равен 70,4. Еще раз, это ближе к линии, но все еще немного далеко.
Формула в ячейке E10:
=РОСТ(B2:B11,A2:A11,E2)
Функция РОСТ имеет следующий синтаксис:
=РОСТ(известные_y,[известные_x],[новые_x],[ const])
Четыре аргумента в функции РОСТ (только имейте в виду, что аргументы не в том же порядке, что и в функции ПРОГНОЗ).
- known_y’s – диапазон ячеек или массив значений, содержащих известные значения Y
- [known_x’s] – диапазон ячеек или массив значений, содержащих известные значения X
- [new_x’s] – точка данных, для которой мы хотим предсказать значение .
- [Const] — истина/ложь, указывающая, как формула должна вычислять.
 Для нашего сценария мы можем опустить этот последний аргумент.
Для нашего сценария мы можем опустить этот последний аргумент.
Квадратные скобки указывают, какие аргументы являются необязательными для функции при вычислении результата. Нам нужны known_y , known_x , и new_x , но мы проигнорировали const аргумент.
Хотя результат 70.4 является более близким приближением, мы не должны слепо полагаться на функцию РОСТА. Проверьте свои интерполяции, чтобы убедиться, что они разумны.
Краткое описание функции РОСТ
Изображение ниже содержит краткое описание функции РОСТ.
Узнайте больше о функции РОСТ в этой статье: Функция РОСТ (support.office.com)
Внутренняя линейная интерполяция
Разумным вариантом может быть найти результат выше и ниже нового значения X, а затем применить линейная интерполяция между этими двумя точками. Это было бы довольно близко.
В нашем примере значения по обе стороны X от 17,5:
- X:16 и 18
- Д: 66,3 и 68
Используя эти значения, теперь мы можем выполнить стандартную линейную интерполяцию.
Быстрый одноразовый метод
Если бы это было одноразовое действие, мы могли бы сделать это быстро, включив в формулу только основные ячейки.
=ПРОГНОЗ(E2,B6:B7,A6:A7)
Однако, как только мы изменим интерполированное значение, ПРОГНОЗ может вычислить неточный результат. Итак, давайте перейдем к рассмотрению гибкого метода.
Гибкий подход
Чтобы создать гибкий подход, мы будем использовать функции ИНДЕКС, ПОИСКПОЗ и ПРОГНОЗ вместе. Это может показаться сложным, но не волнуйтесь, мы пройдем через это медленно. В конечном итоге мы пытаемся достичь того же результата, что и вышеописанный одноразовый метод, но автоматически настраивая диапазоны в зависимости от интерполируемого значения.
ПРИМЕЧАНИЕ. Чтобы этот метод работал, требуется, чтобы диапазон известных X был указан в порядке возрастания.
Функция ПОИСКПОЗ
Во-первых, мы используем функцию ПОИСКПОЗ для получения позиции значения ниже 17,5.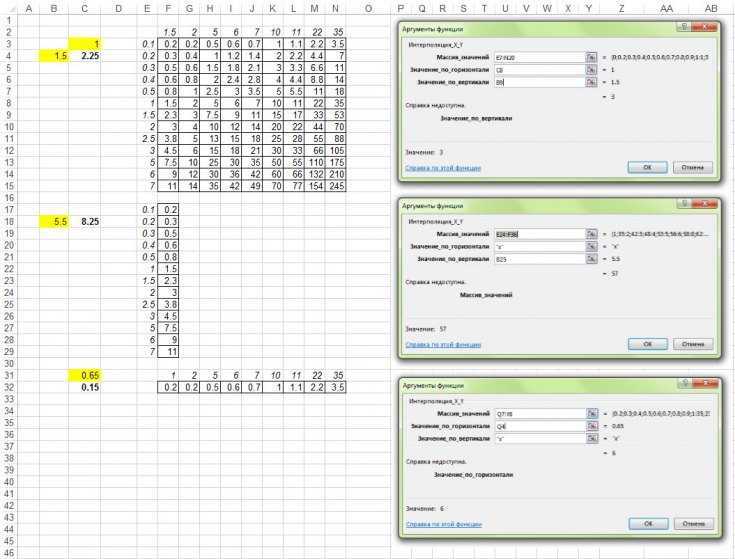
=ПОИСКПОЗ(E2,A2:A11,1)
Эта формула говорит найти значение в ячейке E2 из диапазона ячеек A2-A11. 1 в конце формулы сообщает функции ПОИСКПОЗ, что мы хотим использовать приблизительное совпадение (т. е. ближайшее значение ниже искомого значения). 16 — ближайшее значение ниже 17,5. Поскольку 16 — это пятый элемент в ячейках A2–A11, ПОИСКПОЗ возвращает значение 5.
Функция ИНДЕКС
Определив на предыдущем этапе, что 5-я позиция содержит значение ниже, мы можем использовать функцию ИНДЕКС, чтобы определить ссылку на ячейку для этого значения.
ИНДЕКС(A2:A11,ПОИСКПОЗ(E2,A2:A11,1))
Будет возвращена ссылка на ячейку A6.
Чтобы найти указанное выше значение, мы можем использовать ту же функцию, но добавить 1 к функции ПОИСКПОЗ.
ИНДЕКС(A2:A11,ПОИСКПОЗ(E2,A2:A11,1) +1 )
Приведенная выше формула возвращает ссылку на ячейку A7.
Динамический диапазон
Теперь все становится интереснее.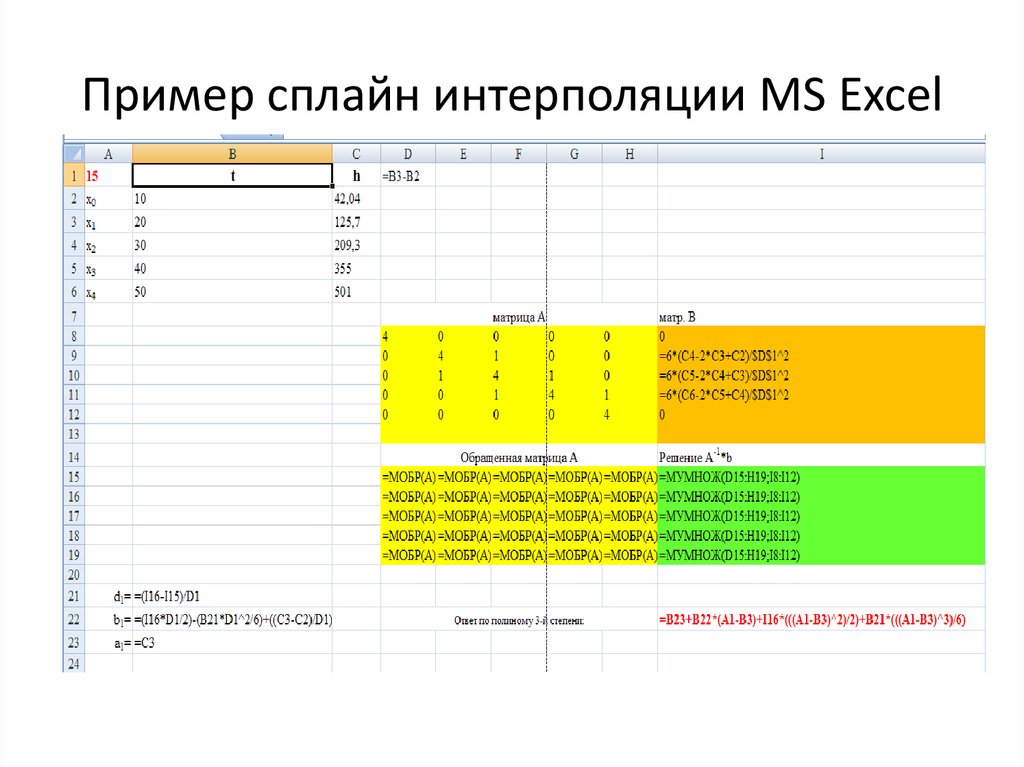 Мы можем объединить эти функции с двоеточием ( : ) посередине, чтобы создать диапазон для двух значений X.
Мы можем объединить эти функции с двоеточием ( : ) посередине, чтобы создать диапазон для двух значений X.
ИНДЕКС(A2:A11,ПОИСКПОЗ(E2,A2:A11,1)) : ИНДЕКС(A2:A11,ПОИСКПОЗ(E2,A2:A11,1)+1)
Первая функция ИНДЕКС возвращает ссылку в ячейку A6 (результат выделенного зеленым цветом раздела). Вторая функция ИНДЕКС возвращает ссылку на ячейку A7 (результат раздела, выделенного фиолетовым цветом). Они разделены двоеточием ( : ) (выделены красным) для создания диапазона – A6:A7
Мы можем сделать то же самое, чтобы создать диапазон для двух значений Y. Единственное отличие состоит в том, что функции ИНДЕКС будут смотреть на ячейки B2-B11.
ИНДЕКС(B2:B11,ПОИСКПОЗ(E2,A2:A11,1)) : ИНДЕКС(B2:B11,ПОИСКПОЗ(E2,A2:A11,1)+1)
Используя ячейки B2-B11 в ИНДЕКС функция, она рассчитает диапазон B6:B7.
ИНДЕКС СОВПАДЕНИЕ И ПРОГНОЗ
Теперь у нас есть два диапазона; значения X A6:A7 и значения Y B6:B7. Давайте объединим все это в функции ПРОГНОЗ.
=ПРОГНОЗ(E2, ИНДЕКС(B2:B11,ПОИСКПОЗ(E2,A2:A11,1)):ИНДЕКС(B2:B11,ПОИСКПОЗ(E2,A2:A11,1)+1), ИНДЕКС(A2:A11,ПОИСКПОЗ(E2,A2:A11,1)):ИНДЕКС(A2:A11,ПОИСКПОЗ(E2,A2:A11,1)+1))
Довольно большая формула, верно. Но, надеюсь, мне удалось объяснить это так, чтобы это не было слишком страшно.
Результат внутренней линейной интерполяции с использованием функции ПРОГНОЗ равен 67,6 (с точностью до 1 знака после запятой, показан в ячейке E14). Взгляните на график еще раз; вы увидите, что 67,6 является разумной оценкой, основанной на доступных данных.
ПРЕДУПРЕЖДЕНИЕ. В конечном счете, это по-прежнему расчет линейной интерполяции, основанный на двух значениях по обе стороны от значения X. Расстояние между значениями выше и ниже будет иметь прямое влияние на точность интерполяции.
Заключение
Сначала казалось, что простой вопрос привел нас к множеству потенциальных решений для трех различных сценариев. Суть в том, что вам нужно знать свои данные, чтобы выбрать метод, который дает наиболее точные результаты.
В процессе мы рассмотрели функции ПРОГНОЗ и ПРОГНОЗ.ЛИНЕЙНЫЙ и увидели, что они полезны как для интерполяции, так и для экстраполяции.
Кроме того, в этом посте мы использовали ИНДЕКС и ПОИСКПОЗ для создания динамических диапазонов, что является очень мощным методом для сложных формул в Excel.
Если вам нужна дополнительная информация о методах прогнозирования в Excel, посетите Engineer Excel (https://engineerexcel.com/blog). Хотя вы можете не работать в инженерном контексте, методы применимы во многих других обстоятельствах.
Об авторе
Привет, меня зовут Марк, и я запускаю Excel Off The Grid.
Мои родители рассказали мне, что в возрасте 7 лет я объявил, что стану квалифицированным бухгалтером. Либо я был экстрасенсом, либо у меня не было воображения, как это и произошло. Однако мое путешествие по-настоящему началось только в 35 лет.
В 2015 году я устроился на новую работу, на которой регулярно работал после 22:00. В результате я редко видел своих детей в течение недели. Итак, я начал искать секреты автоматизации Excel. Я обнаружил, что, создав небольшое количество простых инструментов, я могу комбинировать их по-разному, чтобы автоматизировать почти все свои обычные задачи. Это означало, что я мог работать меньше часов (и мне повысили зарплату!). Сегодня я обучаю этим техникам других специалистов в рамках нашей программы обучения, чтобы они тоже могли проводить меньше времени на работе (и больше времени со своими детьми и любимым делом).
В результате я редко видел своих детей в течение недели. Итак, я начал искать секреты автоматизации Excel. Я обнаружил, что, создав небольшое количество простых инструментов, я могу комбинировать их по-разному, чтобы автоматизировать почти все свои обычные задачи. Это означало, что я мог работать меньше часов (и мне повысили зарплату!). Сегодня я обучаю этим техникам других специалистов в рамках нашей программы обучения, чтобы они тоже могли проводить меньше времени на работе (и больше времени со своими детьми и любимым делом).
Вам нужна помощь в адаптации этого поста к вашим потребностям?
Я предполагаю, что примеры в этом посте не совсем соответствуют вашей ситуации. Мы все используем Excel по-разному, поэтому невозможно написать пост, который удовлетворит все потребности. Потратив время на то, чтобы понять методы и принципы, изложенные в этом посте (и в других местах на этом сайте), вы сможете адаптировать его к своим потребностям.
Но если вы все еще испытываете трудности, вам следует:
- Почитайте другие блоги или посмотрите видео на YouTube по той же теме.


 ..
..  92
92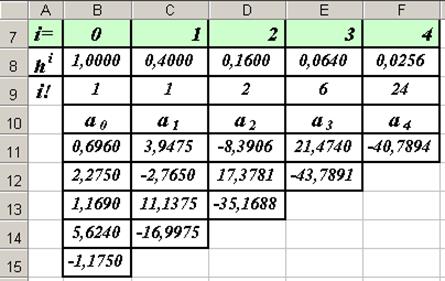 6
6 1905
1905
 LINEAR из раскрывающегося меню формулы.
LINEAR из раскрывающегося меню формулы.
 Для нашего сценария мы можем опустить этот последний аргумент.
Для нашего сценария мы можем опустить этот последний аргумент.