exp, exp2, exp10, expm1 (включая half_ и native_)
Экспоненциальные функции.
гентип exp(гентип х) гентип exp2(гентип) гентип exp10(гентип) гентип expm1 (гентип х) gentype half_exp(gentype x) gentype half_exp2 (gentype x) гентип half_exp10(гентип х) gentype native_exp(gentype x) gentype native_exp2 (гентип x) gentype native_exp10(gentype x)
Описание
exp вычисляет базовую экспоненту e x .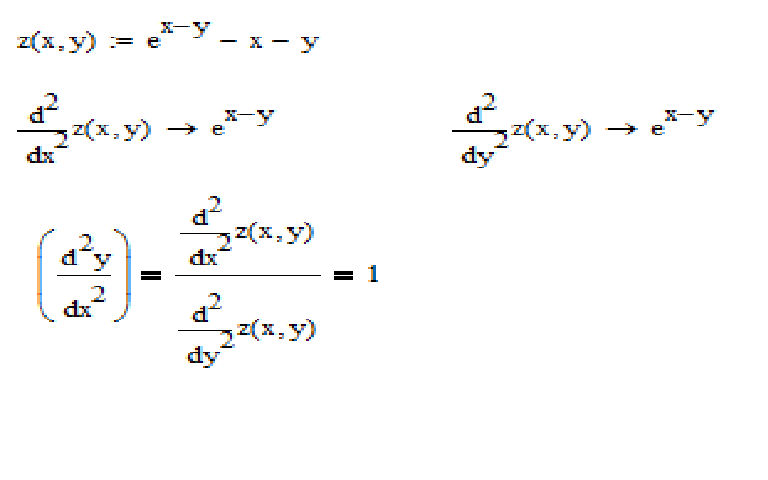
exp2 — экспоненциальная функция с основанием 2.
exp10 — экспоненциальная функция с основанием 10.
expm1 вычисляет e x — 1.0.
half_exp вычисляет базовую экспоненту e x .
half_exp2 вычисляет экспоненту по основанию 2 от x
half_exp10 вычисляет экспоненту с основанием 10 для x .
родное_выражение вычисляет базовую экспоненту e от x в диапазоне, определяемом реализацией.
Максимальная ошибка определяется реализацией.
native_exp2 вычисляет экспоненту по основанию 2 от x в диапазоне, определяемом реализацией.
Максимальная ошибка определяется реализацией.
native_exp10 вычисляет экспоненту с основанием 10 от x в диапазоне, определяемом реализацией.
Максимальная ошибка определяется реализацией.
Примечания
Общая информация о встроенных математических функциях: Встроенные математические функции подразделяются на следующие категории:
Список встроенных функций, которые имеют скалярные или векторные версии аргументов, и,
Список встроенных функций, которые принимают только скалярные аргументы с плавающей запятой.
Векторные версии математических функций работают покомпонентно. Описание для каждого компонента.
На встроенные математические функции не влияет преобладающий режим округления в вызывающей среде, и они всегда возвращают то же значение, что и при вызове с округлением до ближайшего четного режима округления.
Встроенные математические функции принимают скалярные или векторные аргументы. Для любого конкретного использования этих функций фактический тип должен быть одинаковым для всех аргументов и возвращаемого типа, если не указано иное.
Имя универсального типа gentype используется для указания того, что функция может принимать float , float2 , float3 , float4 , float8 , 90 009 поплавок16 , двойной , двойной2 , double3 , double8 или double16 в качестве типа аргументов.
При расширении с помощью cl_khr_fp16 имя универсального типа gentype может указывать half и half{2|3|4|8|16} в качестве аргументов и возвращаемых значений.
Имя универсального типа gentypef используется для указания того, что функция может принимать float , float2 , float3 , float4 , float8 или float16 в качестве типа аргументов.
Имя универсального типа gentyped используется для указания того, что функция может принимать double , double2 , double3 , double4 , double8 , или double16 как тип аргументов.
Формы Half и Native
Подмножество математических функций (таблица 6.8) определяется префиксом half_ .
Эти функции реализованы с точностью не менее 10 бит, т.е.
значение ULP ≤ 8192 мкл.
Подмножество математических функций (таблица 6.8) определяется с префиксом native_ .
Эти функции могут сопоставляться с одной или несколькими собственными инструкциями устройства и обычно имеют более высокую производительность по сравнению с соответствующими функциями (без префикса native__ ).
Точность (и, в некоторых случаях, входной диапазон(ы)) этих функций определяется реализацией.
Для половинной и собственной форм мы используем имя общего типа gentype, чтобы указать, что функции (таблица 6.9) может принимать float , float2 , float3 , float4 , float8 или float16 в качестве типа аргументов.
Поддержка денормализованных значений необязательна для функций Выпуск45917 ➜ Это средство отслеживания проблем было перенесено на GitHub ,
и в настоящее время доступен только для чтения . Создан 28.11.2021 17:47 автор Гидеон , последнее изменение 11.04.2022 14:59 автор admin . Эта проблема закрыта . этап: проверка исправления -> разрешено pull_requests:
+ pull_request28060 half_ .
Функции half_ могут возвращать любой результат, разрешенный разделом 7.5.3, даже если -cl-denorms-are-zero (см. раздел 5.8.4.2) не действует. Поддержка денормальных значений определяется реализацией для
Поддержка денормальных значений определяется реализацией для native_ 9х
Для получения дополнительной информации,
см. часто задаваемые вопросы GitHub в Руководстве разработчика Python. URL-адрес Статус Связано Править PR 29829 объединены python-dev,
2021-11-29 04:48 msg407214 - (просмотреть) Автор: Гидеон (Gideon) * Дата: 28.  11.2021 17:47
11.2021 17:47 Уважаемая команда поддержки Python,
Я просматривал список поддерживаемых методов Python в математическом модуле и заметил, что C99-й метод exp2 не был реализован. Этот метод возводит 2 в степень переданного аргумента. Я понимаю, что это довольно тривиально в Python, используя 2**x или math.pow(x, 2), но я думаю, что есть несколько причин, по которым мы могли бы захотеть это включить:
Единообразие: этот метод существует в большинстве других языков программирования и библиотек, включая numpy.
Согласованность: все математические методы из C99, кроме exp2, находятся в модуле math или cmath Python (math.cbrt будет добавлен в Python 3.11).
Тривиальность: этот метод является частью C99, а также поддерживается Visual Studio, поэтому его очень легко реализовать.
Точность (?): libm exp2 предположительно более точен, чем pow (2.0, x), хотя я действительно не понимаю, как это может быть (см. https://bugs.python.org/issue31980)
Тем не менее, этот метод немного избыточен, поэтому я полностью понимаю, если этот запрос будет отклонен.

msg407230 - (просмотреть) Автор: Марк Дикинсон (mark.dickinson) * Дата: 2021-11-28 20:56 Звучит хорошо для меня, при условии, что все распространенные платформы, которые нам интересны, имеют реализацию приемлемого качества. Это должна быть прямая оболочка функции C99, и при наличии достаточного количества тестов билдботы должны сообщить нам, есть ли какие-либо проблемы на распространенных платформах.
 @Gideon: вы заинтересованы в работе над запросом на вытягивание? С удовольствием пересмотрю.
(В идеале хотелось бы и ехр10, но этого нет в С99, поэтому поддержка платформы, скорее всего, будет неравномерной. Если кто-то заинтересован в этом, мы должны сделать это отдельной темой.)
>
@Gideon: вы заинтересованы в работе над запросом на вытягивание? С удовольствием пересмотрю.
(В идеале хотелось бы и ехр10, но этого нет в С99, поэтому поддержка платформы, скорее всего, будет неравномерной. Если кто-то заинтересован в этом, мы должны сделать это отдельной темой.)
> msg407231 - (просмотреть) Автор: Марк Дикинсон (mark.  dickinson) *
dickinson) * Дата: 28.11.2021 21:00 См. также предыдущее обсуждение в конце https://bugs.python.org/issue3366.
FWIW, я не думаю, что добавление exp2 в модуль cmath также имеет смысл: нам придется написать собственную реализацию, а это просто не та функция, которая часто встречается в сложном мире.
msg407233 - (просмотреть) Автор: Марк Дикинсон (mark.dickinson) * Дата: 28.11.2021 21:33 Что касается точности, то на моем ноутбуке Mac этого не так много, и похоже, что pow(2.0, x) дает правильно округленные результаты так же часто (если не чаще, как) exp2( Икс).
Вот журнал сеанса терминала после перекомпиляции Python для добавления exp2. Он показывает ошибку ulps (проверенную на высокоточном десятичном вычислении, которое мы рассматриваем как представляющее «точный» результат) как для exp2(x), так и для pow(2.

 49803564f5b8ap+8 -329.50081473349621319 0.49736, -0.50264
-0x1.534cf08081f4bp+8 -339.300544762627 -0.50180, 0.49820
-0x1.b430821fb4ad2p+8 -436,18948553238908517 -0,49883, 0,50117
0x1.2c87a8431bd8fp+8 300,52991122655743084 -0,50376, 0,49624
0x1.3e476f9a09c8cp+7 159,13952332848964488 0,50062, -0,49938
0x1.cb8b9c61e7e89p+9 919.09070991347937252 0.49743, -0.50257
0x1.ab86ed0e6c7f6p+9 855,05410938546879152 0,49742, -0,50258
0x1.97bc9af3cbf85p+9 815,47347876986952997 -0,50076, 0,49924
-0x1.b5434441ba11bp+8 -437,26276026528074681 -0,50062, 0,49938
-0x1.0ead35218910ep+9 -541.35318392937347198 0.50192, -0.49808
-0x1.dbae0b861b89ср+9 -951,35972668022759535 0,50601, -0,49399
0x1.522f005d2dcc4p+6 84.54589982597377684 -0.50704, 0.49296
0x1.398ff48d53ee1p+9 627.12465063665524667 -0.50102, 0.49898
-0x1,381307fbd89f5p+5 -39,00929257159069863 -0,50526, 0,49474
0x1.9dc4c85f7c53ap+9 827,53736489840161994 -0,50444, 0,49556
0x1.b357f6012d3c2p+9 870,68719496449216422 -0,50403, 0,49597
-0x1.
49803564f5b8ap+8 -329.50081473349621319 0.49736, -0.50264
-0x1.534cf08081f4bp+8 -339.300544762627 -0.50180, 0.49820
-0x1.b430821fb4ad2p+8 -436,18948553238908517 -0,49883, 0,50117
0x1.2c87a8431bd8fp+8 300,52991122655743084 -0,50376, 0,49624
0x1.3e476f9a09c8cp+7 159,13952332848964488 0,50062, -0,49938
0x1.cb8b9c61e7e89p+9 919.09070991347937252 0.49743, -0.50257
0x1.ab86ed0e6c7f6p+9 855,05410938546879152 0,49742, -0,50258
0x1.97bc9af3cbf85p+9 815,47347876986952997 -0,50076, 0,49924
-0x1.b5434441ba11bp+8 -437,26276026528074681 -0,50062, 0,49938
-0x1.0ead35218910ep+9 -541.35318392937347198 0.50192, -0.49808
-0x1.dbae0b861b89ср+9 -951,35972668022759535 0,50601, -0,49399
0x1.522f005d2dcc4p+6 84.54589982597377684 -0.50704, 0.49296
0x1.398ff48d53ee1p+9 627.12465063665524667 -0.50102, 0.49898
-0x1,381307fbd89f5p+5 -39,00929257159069863 -0,50526, 0,49474
0x1.9dc4c85f7c53ap+9 827,53736489840161994 -0,50444, 0,49556
0x1.b357f6012d3c2p+9 870,68719496449216422 -0,50403, 0,49597
-0x1. a6446703677bbp+9 -844,53439371636284250 0,50072, -0,49928
0x1.e3dd54b28998bp+7 241.93228681497234334 0,49897, -0,50103
0x1.b4f77f18a233ep+8 436,96678308448815642 0,49593, -0,50407
-0x1,578c4ce7a7c1bp+3 -10,73587651486564276 -0,50505, 0,49495
0x1.25a9540e1ee65p+5 36.70767985374258302 0.49867, -0.50133
-0x1.6e220f7db7668p+8 -366.13304887511776542 -0.49904, 0.50096
-0x1,94214ed3e5264p+9 -808,26021813095985635 0,50420, -0,49580
0x1.9dcc3d281da18p+5 51,72472602215219695 -0,50423, 0,49577
-0x1.3ba66909e6a40p+7 -157,82502013149678532 -0,50077, 0,49923
-0x1.9eac2c52a1b47p+9 -829,34510262389892432 -0,50540, 0,49460
a6446703677bbp+9 -844,53439371636284250 0,50072, -0,49928
0x1.e3dd54b28998bp+7 241.93228681497234334 0,49897, -0,50103
0x1.b4f77f18a233ep+8 436,96678308448815642 0,49593, -0,50407
-0x1,578c4ce7a7c1bp+3 -10,73587651486564276 -0,50505, 0,49495
0x1.25a9540e1ee65p+5 36.70767985374258302 0.49867, -0.50133
-0x1.6e220f7db7668p+8 -366.13304887511776542 -0.49904, 0.50096
-0x1,94214ed3e5264p+9 -808,26021813095985635 0,50420, -0,49580
0x1.9dcc3d281da18p+5 51,72472602215219695 -0,50423, 0,49577
-0x1.3ba66909e6a40p+7 -157,82502013149678532 -0,50077, 0,49923
-0x1.9eac2c52a1b47p+9 -829,34510262389892432 -0,50540, 0,49460 msg407235 - (просмотреть) Автор: Гидеон (Gideon) * Дата: 28.11.2021 22:09 Звучит хорошо. Я уже внес необходимые изменения в код своей сборки, так что просто закончу писать тесты + документацию и отправлю PR.
msg407245 - (просмотреть) Автор: Гидеон (Gideon) * Дата: 29.  11.2021 05:05
11.2021 05:05 Я отправил PR на https://github.com/python/cpython/pull/29829.
Я просто хотел бы добавить, что вся команда Python потрясающая. Спасибо за то, что вы делаете!
msg407317 - (просмотр) Автор: Марк Дикинсон (mark.dickinson) * Дата: 29.11.2021 18:55
Новый набор изменений 6266e4af873a27c9d352115f2f7a1ad0885fc031 от Гидеона в ветке 'main':
bpo-45917: Добавлен метод math.exp2() — возвращает 2, возведенное в степень x (GH-29829)
https://github.com/python/cpython/commit/6266e4af873a27c9d352115f2f7a1ad0885fc031
msg407318 - (просмотр) Автор: Марк Дикинсон (mark.dickinson) * Дата: 29.11.2021 19:04 Готово. Большое спасибо, Гидеон!
msg407321 - (просмотреть) Автор: Тим Питерс (tim.  peters) *
peters) * Дата: 29.11.2021 19:50 Плохая новость: в Windows exp2(x) намного хуже, чем pow(2, x). Здесь я изменил цикл маленького драйвера Марка следующим образом:
отличается = действительно_плохо = 0
худшее = 0,0
для n в диапазоне (100_000):
x = случайный.равномерный(-1000.0, 999.0) + случайный.случайный()
если exp2(x) != pow(2.0, x):
отличается += 1
exp2err = exp2_error_ulps(x)
pow2err = pow2_error_ulps(x)
утверждать абс (pow2err) < 0,52
если abs(exp2err) >= 1.0:
если abs(exp2err) > abs(худший):
худшее = exp2err
действительно_плохо += 1
если действительно_плохо < 25:
print(f"{x.hex():21} {x:22.17f} {exp2err:.5f}, {pow2err:.5f}")
печать (f "{отличается =:,}")
распечатать (f"{действительно_плохо=:,}")
print(f"худшая ошибка exp2 ulp {худшая:. 5f}")
Затем вывод из одного прогона:
0x1.0946680d45f28p+9 530,55005041041749791 -1,04399, -0,04399
0x1.de4f9662d84f8p+9 956,62177691995657369 -1,00976, -0,00976
-0x1.60f9152be0a09p+4 -22.06081120624188330 1.02472, 0.02472
-0x1.687b056d7a81ap+8 -360.48055156937482479 1.48743, 0.48743
0x1.8e97e9d405622p+9 797.18682337057930454 1.05224, 0.05224
-0x1.2d1e3a03eda7fp+9 -602.23614548782632028 -1.21876, -0.21876
0x1.3af55e79cd45dp+8 314.95847283612766887 -1.10044, -0.10044
0x1.0e7fba610cde6p+9 540,99787533882476964 -1,39782, -0,39782
0x1.9c7d0258e460dp+9 824.97663413192060489 1.19690, 0.19690
0x1.3de5064eb1598p+9 635.78925498637818237 1.75376, -0.24624
-0x1.d5189d23da3d0p+9 -938,19229553371587826 1,07734, 0,07734
0x1.967d0857aa500p+9 812.97681709114112891 1.23630, 0.23630
-0x1.30ee89e018914p+6 -76.23294782781550794 -1.10275, -0.10275
-0x1.e35eb8936dddbp+9 -966.74000780930089149 -1.02686, -0.02686
-0x1.28d40d7693088p+6 -74.20708260795993283 1.00352, 0.00352
-0x1.e965d067d1084p+7 -244,69885563303625986 1,21136, 0,21136
-0x1.
5f}")
Затем вывод из одного прогона:
0x1.0946680d45f28p+9 530,55005041041749791 -1,04399, -0,04399
0x1.de4f9662d84f8p+9 956,62177691995657369 -1,00976, -0,00976
-0x1.60f9152be0a09p+4 -22.06081120624188330 1.02472, 0.02472
-0x1.687b056d7a81ap+8 -360.48055156937482479 1.48743, 0.48743
0x1.8e97e9d405622p+9 797.18682337057930454 1.05224, 0.05224
-0x1.2d1e3a03eda7fp+9 -602.23614548782632028 -1.21876, -0.21876
0x1.3af55e79cd45dp+8 314.95847283612766887 -1.10044, -0.10044
0x1.0e7fba610cde6p+9 540,99787533882476964 -1,39782, -0,39782
0x1.9c7d0258e460dp+9 824.97663413192060489 1.19690, 0.19690
0x1.3de5064eb1598p+9 635.78925498637818237 1.75376, -0.24624
-0x1.d5189d23da3d0p+9 -938,19229553371587826 1,07734, 0,07734
0x1.967d0857aa500p+9 812.97681709114112891 1.23630, 0.23630
-0x1.30ee89e018914p+6 -76.23294782781550794 -1.10275, -0.10275
-0x1.e35eb8936dddbp+9 -966.74000780930089149 -1.02686, -0.02686
-0x1.28d40d7693088p+6 -74.20708260795993283 1.00352, 0.00352
-0x1.e965d067d1084p+7 -244,69885563303625986 1,21136, 0,21136
-0x1. b1fbeec1c1ba3p+7 -216,99205594529948371 -1,05536, -0,05536
-0x1.543d715a5824cp+9 -680.48002175620922571 1.24955, 0.24955
0x1.526829d46c034p+9 676.81377654336984051 -1.17826, -0.17826
-0x1.bdaf1d7850c74p+6 -111.42101085656196346 1.08670, 0.08670
-0x1.48218d1605dd0p+9 -656.26211810385029821 1.06103, 0.06103
-0x1.16298bcdb9103p+9 -556.32457896744051595 -1.23732, -0.23732
0x1.39ff24b1a7573p+8 313,9966536553
b1fbeec1c1ba3p+7 -216,99205594529948371 -1,05536, -0,05536
-0x1.543d715a5824cp+9 -680.48002175620922571 1.24955, 0.24955
0x1.526829d46c034p+9 676.81377654336984051 -1.17826, -0.17826
-0x1.bdaf1d7850c74p+6 -111.42101085656196346 1.08670, 0.08670
-0x1.48218d1605dd0p+9 -656.26211810385029821 1.06103, 0.06103
-0x1.16298bcdb9103p+9 -556.32457896744051595 -1.23732, -0.23732
0x1.39ff24b1a7573p+8 313,9966536553 msg407352 - (просмотреть) Автор: Тим Питерс (tim.peters) * Дата: 2021-11-30 05:11 После миллионов попыток одно и то же: Windows exp2 отключается как минимум на 1 ulp в течение трети времени и более чем на 2 ulp примерно в 3 случаях на миллион.
 До сих пор не наблюдалось снижения pow(2, x) на целых 0,52 ulp.
Судя по его поведению, Windows реализует exp2(x) следующим образом:
я = этаж (х)
x -= i # теперь 0 <= x < 1
вернуть ldexp(exp2(x), я)
Таким образом, он, по-видимому, использует какое-то несовершенное приближение к 2 ** x в области [0, 1].
Но следствием этого является то, что он делает это абсолютно правильно, когда x является целым числом, поэтому вряд ли кто-то заметит, что это небрежно ;-)
Я ожидаю, что мы должны просто жить с этим.
До сих пор не наблюдалось снижения pow(2, x) на целых 0,52 ulp.
Судя по его поведению, Windows реализует exp2(x) следующим образом:
я = этаж (х)
x -= i # теперь 0 <= x < 1
вернуть ldexp(exp2(x), я)
Таким образом, он, по-видимому, использует какое-то несовершенное приближение к 2 ** x в области [0, 1].
Но следствием этого является то, что он делает это абсолютно правильно, когда x является целым числом, поэтому вряд ли кто-то заметит, что это небрежно ;-)
Я ожидаю, что мы должны просто жить с этим. msg407380 - (просмотреть) Автор: Марк Дикинсон (mark.dickinson) * Дата: 2021-11-30 15:30 [Тим]
> в Windows exp2(x) намного хуже, чем pow(2, x)
Штопать.
> Я полагаю, что мы должны просто жить с этим.
Согласованный.
Дата Пользователь Действие Аргументы 2022-04-11 14:59:52 администратор набор github: 2021-11-30 15:30:49 mark.  dickinson
dickinson set сообщения:
+ msg407380 2021-11-30 05:11:01 tim.peters set сообщения:
+ msg407352 2021-11-29 19:50:53 tim.peters set сообщения:
+ сообщение 407321 2021-11-29 19:04:35 mark.dickinson set статус: открыто -> закрыто
разрешение: исправлено
сообщений:
+ msg407318 2021-11-29 18:55:54 mark.dickinson set сообщения:
+ msg407317 2021-11-29 05:05:35 Гидеон набор сообщения:
+ сообщение 407245 29.11.202104:48:30 python-dev set ключевые слова:
+ патч
любопытный:
+ python-dev
этап: обзор исправления 2021-11-28 22:09:09 Гидеон набор сообщения:
+ msg407235 2021-11-28 21:33:10 mark. 

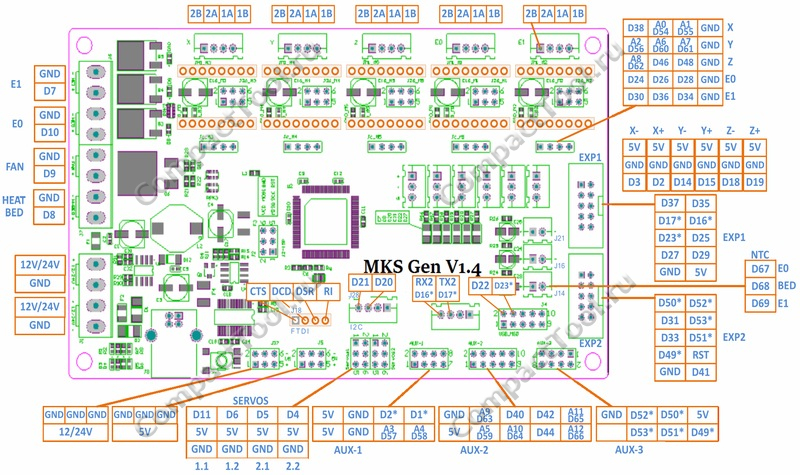
 Оборудование отличается высокой надежностью, производительностью и комфортностью в эксплуатации.
Оборудование отличается высокой надежностью, производительностью и комфортностью в эксплуатации.
 .. Купить
.. Купить