Формула бинома Ньютона 11 класс онлайн-подготовка на Ростелеком Лицей
Рассмотрение некоторых формул сокращенного умножения
Вспомним некоторые формулы сокращенного умножения.
– формула квадрата суммы. Рассмотрим, как вывести эту формулу.
раскрываем скобки, перемножая почленно:
Аналогично, для куба суммы:
Раскрываем скобки, почленно перемножая, получаем:
Когда необходимо будет возвести сумму в более высокую степень, умножать почленно скобку на скобку будет проблематично. В этом нам поможет формула бинома Ньютона. По определению, бином – это двучлен, то есть сумма двух слагаемых.
Доказательство формулы бинома Ньютона
Формула бинома Ньютона позволяет возводить сумму двух слагаемых в любую степень.
Попробуем раскрыть скобки. Выберем из каждой скобки . Получим . Предположим, что из скобки выбрать , а из одной скобки выбрать , получим . Но получится такое произведение не один раз, как и в случае с формулами квадрата суммы и куба суммы.
Ведь можно выбрать из 1-й скобки, из 2-й скобки и так далее. Количество вариантов выбрать. получим
Предположим, что из скобок выберем число , а из оставшихся скобок выберем число . Получим .
Сколько способов из скобок выбрать число ? То есть из скобок выбрать скобок, из которых выбрать число . Это в точности сочетание: выбрать объектов из без учёта порядка, а это . Получаем
Подставляя все возможные k от 0 до n, получим формулу бинома Ньютона:
Перепишем формулу. Заметим, что в формуле есть и .
– это количество способов выбрать из объектов один. Таких способов . Поэтому в формуле можно заменить на , а можно заменить на так как количество способов выбрать из объектов один равно количеству способов выбрать из объектов . Ведь выбрать – то же самое, что не выбрать .
Получим:
Формула бинома Ньютона: =.
Пример использования формулы бинома Ньютона для суммы 4-й степени
Пример.
. В данном решение был изменен порядок следования: начали не с , а с . Разницы нет, так как или же:
Чтоб дописать формулу четвертой степени суммы, нужно знать значение (по треугольнику Паскаля (Источник).
=.
Пример использования формулы бинома Ньютона для квадрата суммы
Пример.
Найдем квадрат суммы по формуле бинома Ньютона: =.
Формула бинома Ньютона для разности
Пример. Получение формулы бинома Ньютона для разности
Подставим вместо в формулу бинома Ньютона :
Получим степень для суммы и Когда в соответствующем примере из формулы бинома Ньютона число в четной степени – знак «-» уйдет, когда в нечетной степени – останется.
Формула бинома Ньютона для разности:
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.
: Мнемозина. - Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
: Мнемозина.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Cleverstudents.ru (Источник).
- www-formula.ru (Источник).
- Edu.sernam.ru (Источник).
- Oldskola1.narod.ru (Источник).
Домашнее задание
- Разложить выражение по формуле бинома Ньютона.
- Разложить выражение по формуле бинома Ньютона.
- Разложить выражение по формуле бинома Ньютона.
- Вычислить число сочетаний .
- Вычислить число сочетаний .
Общий Член Разложения Бинома – Telegraph
⚡ 👉🏻👉🏻👉🏻 ИНФОРМАЦИЯ ДОСТУПНА ЗДЕСЬ ЖМИТЕ 👈🏻👈🏻👈🏻
Общий Член Разложения Бинома
Бинома Ньютона.
Формула общего члена бинома Ньютона. Алгебра 11 класс. Теория вероятностей. Примеры с решением.
0:35 — Пример 1: Найдите 13-й член разложения бинома Ньютона.
1:42 — Пример 2: Найдите средний член разложения бинома Ньютона.
3:23 — Пример 3: Найдите номер члена в разложении бинома Ньютона, не зависящий от х.
4:55 — Пример 4: В разложении бинома Ньютона коэффициент третьего члена на 44 больше коэффициента второго. Найдите член не зависящий от х.
Математика. Решение заданий с объяснением. Видеоуроки по математике. Устранение пробелов в знаниях по математике. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
Автор Сизоненко Ольга.
Дистанционное обучение. Теория вероятностей. Базовый Онлайн курс
http://math.xfresh.info/index.php/vys…
Поддержка проекта http://xfresh.info/pomoshch-proektu
#БиномНьютона #Бином #ФормулаNгоЧлена #БиномиальныеКоэффициенты #ОбщийЧленБинома #ВысшаяМатематика #Математика #ФормулаОбщегоЧлена #Алгебра11Класс #ТеорияВероятностей #ТреугольникПаскаля #ПодготовкаКЕгэ #ВидеоурокиПоМатематике
математика, треугольник паскаля, егэ, образование, биноминальный коэффициент, комбинаторика, подготовка к егэ, бином, биномиальные коэффициенты, видеоуроки по математике, ньютон, школа, подготовка в ниш, подготовка к ент, биномиальный коэффициент ньютона, рфмш, тесты по математике, егэ математика, ент математика, math, огэ, факториал, ньютон биномы, алгебра 9 кл, разложение двучлена, высшая математика, онлайн, сочетание, математический анализ, вероятности, формула бинома ньютона, бином ньютона и треугольник паскаля, видео урок, университет, вуз, 11 класс, перестановка, сочетания, класс презентация, сдать, успешно, ньютон биномы 3, класс, рабочий тетрадь, контрольная работа, сочетание без повторений, алгебра 11 класс, экзамены, домашнее задание, задания, онлайн школа, вычисление биномиальных коэффициентов, школьный, ньютона, школьный класс, уроки, видео уроки, доказательство формулы, математика 2016, егэ 2016, онлайн помощь, сдать матан, формула, подготовка к экзамену, репетитор, экзамен, экзамен по математике, школьное образование, бином ньютона примеры, просто математика, формула бинома, бином ньютона для чайников, математика для всех, перестановки, видео, степень суммы, бином ньютона комбинаторика, математика видео, видеоурок алгебры, математика это просто, готовимся к егэ по математике, алгебра 11 класс видео, математика с нуля, видео уроки по алгебре 10 класс, алгебра 10 класс видео, алгебра 10 класс видео уроки, видео математики, видео уроки математика, огэ по математике, зно, примеры с решением, подготовка к зно, вно по математике, объем, олимпиады, разложение, паскаль,
861 тыс.
просмотров
11 месяцев назад
Бином Ньютона, биноминальное разложение с использованием треугольника…
Урок 11. Бинома Ньютона. Формула общего члена. Алгебра 11 класс. — YouTube
Бином Ньютона
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра…)
Бином Ньютона — Википедия
Внимание! Zaochnik не продает дипломы, аттестаты об образовании и иные документы об образовании. Все услуги на сайте предоставляются исключительно в рамках законодательства РФ.
Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:
Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.
Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:
Для этого необходимо применить метод математической индукции.
Для доказательства необходимо выполнить несколько пунктов:
Произведем подстановку в полученное равенство. Получим, что
Не парься, мы поможем разобраться и подарим скидку 10% на любую работу
Для полного понятия использования формулы рассмотрим примеры.
Ниже приведен пример, где используется бином для доказательства делимости выражения с заданным числом.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Основное свойство алгебраической дроби
Не получается написать работу самому?
Я даю согласие на обработку своих персональных данных в соответствии с политикой конфиденциальности и принимаю условия договора публичной оферты
Специалисты сайта Zaochnik осуществляют работу по сбору, обработке и структурированию информации по предложенной Клиентом теме. Результат подобной работы не является готовым научным трудом, однако может служить основным источником для его написания.
© 2000 — 2021, Zaochnik.com Все права защищены.
Порно Фільми Целки
Секс С Сальмой Хайк Видео
Откровенные Фото Сиара
Порно Актриса С Самой Большая Грудью
Ассы Акиры Лубокий Миньет
Биномиальная теорема — MathCracker.com
Алгебра Учебники
Биномиальная теорема — одна из самых известных теорем алгебры, и она имеет множество приложений в области алгебры, теории вероятностей и статистики. В нем содержится красивая и краткая формула для n 9н\)
Впервые меня неофициально представил сэр Исаак Ньютон в 1665 году.
n \]
где термин \({n \выбрать i}\) читается как «n выбрать i» или также как «комбинаторный коэффициент», и он определяется как
\[\large \displaystyle {n \choose i}= \frac{n!}{i! \раз (n-i)!}\]Например,
\[\large \displaystyle {5 \выберите 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]Общая биномиальная теорема с использованием суммирования 9{n-i}\) (умножить на константу).
6\)? Почему?
9н\). Почему ты такой жестокий». Подожди. Я не разыгрываю тебя. Всегда есть хитрость (не забывайте эту строчку, она часто встречается в математике).Заметьте, что \(a — b\) совпадает с \(a + (-b)\). 93 \]
Подробнее о биномиальном расширении
Биномиальная теорема настолько важна, что она рассматривается практически во всех курсах, включая алгебру, исчисление, теорию вероятностей и статистику.
Есть некоторые обобщения, такие как отрицательное биномиальное разложение, которое выходит за рамки этого руководства.
Треугольник Паскаля
Иногда учащиеся застревают, когда им нужно вычислить константы (комбинаторные коэффициенты), которые входят в биномиальное разложение. Один действительно простой способ сделать это — использовать треугольник Паскаля.
Треугольник Паскаля показывает, как последовательные биномиальные коэффициенты могут быть вычислены на основе коэффициентов предыдущего значения \(n\), путем сложения двух коэффициентов, которые находятся непосредственно выше.
Приложения
Биномиальное разложение имеет множество приложений в алгебре и теории вероятностей. Например, в теории вероятности биномиальное распределение основано на биномиальной теореме.
Действительно, рассмотрим число \(0 \le p \le 1\). Тогда \(p + (1-p) = 1\) и мы можем использовать биномиальную теорему: 9{n-i} = 1 \]
где \(X\) — число успехов после \(n\) испытаний, когда вероятность успеха каждого испытания равна \(p\). Переменная \(X\) известна как биномиальная случайная величина.
Связанные калькуляторы
Вы также можете
вычислить вероятности для биномиального распределения с помощью этого калькулятора
. Кроме того, вы можете захотеть вычислить
коэффициенты перестановки
, которые связаны с комбинаторными коэффициентами.
Учебник по алгебре Биномиальный коэффициент Биномиальная теорема Формула биномиального расширения Треугольник Паскаля
KryssTal : Треугольник Паскаля
KryssTal : Треугольник Паскаля [Домашняя страница] [Введение в числа] [Отзывы читателей (математика)] [Язык] |
Математика – это язык науки. Что-то, что может быть трудно представить может быть легко понять математически. математический Уравнение может занимать одну строку, тогда как то же самое, написанное словами, может занимать большой абзац.
В этом эссе я хотел бы представить несколько умных способов алгебры и вычислений с помощью простого калькулятора. Под простым калькулятором я подразумеваю тот, который выполняет только основные операции (плюс, минус, умножение и деление). В конце вы должны быть в состоянии вычислить довольно сложные корни с помощью этого калькулятора.
Блез Паскаль (1623—1662) — французский математик. Его фамилия используется как единица измерения давления. Одно из его высказываний заключалось в том, что «если бы нос Клеопатры был другой формы, история мира была бы другой». Он наиболее известен треугольником, названным в его честь, Треугольник Паскаля .
На самом деле треугольник был известен как китайцам, так и арабам за несколько сотен лет до этого.
Это не геометрический треугольник, а треугольник чисел. Вот ниже:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
Каждое число в треугольнике является суммой двух указанных выше. Например, 6 в строке 5 — это сумма пары троек выше. Итак, следующая строка
Сейчас я, по-видимому, меняю тему и обращаюсь к алгебре.
Представьте, что вам нужно расширить выражение вроде
.
Под «расширением» я имею в виду удаление скобок.
Напоминаю, выражение расширяется следующим образом:
В средней паре скобок каждый член в левой скобке умножается на каждый член в правой скобке. Мы можем сделать то же самое с кубом, то есть (1 + x) 3 .
= 1 + 3х + 3х 2 + х 3
Если вы посмотрите на коэффициенты (числа сами по себе и перед иксами) результатов, вы увидите, что для первого они равны 1, 2, 1, а для второго они равны 1, 3, 3, 1. Это, конечно, строки из треугольника Паскаля. И да, это работает для всех положительных целых чисел индекса. Докажите себе с помощью алгебры, что
На самом деле существует общее правило, что
+ B 4
.
Как видите, индексы начинаются с 4 и уменьшаются для a, в то время как они возрастают до 4 для b. Коэффициенты 1, 4, 6, 4, 1 из треугольника Паскаля. Итак, давайте попробуем пример.
Расширить (2 + 3x) 5 .
Применяя общее правило возрастания и убывания индексов и коэффициенты из Паскаля, мы можем немедленно расширить приведенное выше уравнение (если мы установим a равным 2 и b равным 3):
Это упрощает до
Настало время снова сменить тему…
Представьте, что у вас есть пять книг. Давайте представим, что вы хотели прочитать один. Сколько существует способов выбрать одну книгу? Ну, это легко, есть 5 способов.
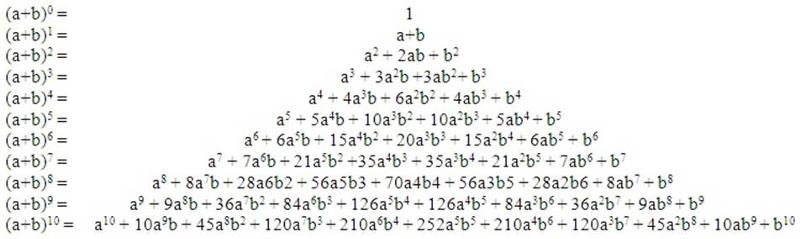Если мы обозначим книги A, B, C, D, E, мы можем выбрать любую из пяти; пять различных вариантов.Сколько существует вариантов выбора, если мы хотим выбрать две книги? Ну давайте перечислим все комбинации:
А если бы мы хотели из трех из пяти? Ну, это легко. Выбрать три из пяти — это то же самое, что отбрасывая два из пяти, так что есть десять способов сделать это. Комплектация четыре из пяти — это то же самое, что отбросить один из пяти, пяти способов. Конечно, если вы хотите выбрать все пять книг, это можно сделать только одним способом. Существует также только один способ не выбирать книги! Итак, в таблице имеем:
| Количество вариантов от 5 | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество способов выбора | 1 | 5 | 10 | 10 | 5 | 1 |
Удивительный аспект математики состоит в том, что два, казалось бы, не связанных между собой предмета на самом деле связаны. В этом
случае мы имеем связь между алгебраическими расширениями и выборками. Количество способов выбора r объектов из общего числа n записывается как
Таким образом, приведенные выше выборы могут быть записаны математически следующим образом:
| Есть один способ не выбирать книги из 5 | 5 C 0 = 1 |
| Есть 5 способов выбрать 1 книгу из 5 | 5 C 1 = 5 |
| Есть 10 способов выбрать 2 книги из 5 | 5 C 2 = 10 |
| Есть 10 способов выбрать 3 книги из 5 | 5 С 3 = 10 |
| Есть 5 способов выбрать 4 книги из 5 | 5 C 4 = 5 |
| Есть один способ выбрать 5 книг из 5 | 5 С 5 = 1 |
Математически ответ равен 8 C 6 . В треугольнике Паскаля всего восемь объектов, поэтому вы смотрите на строку, начинающуюся с 1, 8 и т. д. Вы хотите выбрать шесть, поэтому вы считаете от нуля до шести. Номер есть 28 , так что есть 28 вариантов.Математически мы можем написать 8 C 6 = 28.
Вместо того, чтобы запоминать треугольник Паскаля, было бы полезно, если бы существовала формула для вычисления n C r . Его можно было использовать как для выборок, так и для расширения алгебраических выражений. Помните, что
= 1 + 2x + x 2 .
Формула для n C r :
Срок н! (произносится как n factorial ) означает перемножить все целые числа от 1 до n. Итак,
| 1! = 1 |
| 2! = 1 x 2 = 2 |
| 3! = 1 х 2 х 3 = 6 |
| 4! = 1 х 2 х 3 х 4 = 24 |
| 5! = 1 х 2 х 3 х 4 х 5 = 120 |
Кроме того, 0! определяется как 1.
Настало время вернуться к выбору. Сколькими способами можно выбрать 8 книг из 11? Ответ конечно 11 C 8 который определяется как: 1 х 2 х 3 х 4 х 5 х 6 х 7 х 8 х 9 х 10 х 11 / 1 х 2 х 3 х 1 х 2 х 3 х 4 х 5 х 6 х 7 х 8 = 9 х 10 х 11 / 1 х 2 х 3
Теперь это случай сокращения до 165.
Таким образом, есть 165 способов выбрать 8 книг из 11.
Используя приведенную выше формулу вместо Треугольник Паскаля мы можем посмотреть на одно из наших расширений и сказать, что
и покажите, что
3 С 1 = 3! / 2! 1! = 1 х 2 х 3 / 1 х 2 х 1 = 3
3 С 2 = 3! / 1! 2! = 1 х 2 х 3 / 1 х 1 х 2 = 3
3 С 3 = 3! / 0! 3! = 1 х 2 х 3 / 1 х 1 х 2 х 3 = 1.
- для формирования основы вероятностей выбора (они называются Комбинации , отсюда буква C в n C r выше).
- для определения коэффициентов разложений (1 + x) n , где n — целое положительное число.
Напомню, что когда n — целое положительное число, разложение содержит x + 1 членов.
Расширение для (1 + x) 3 содержит 4 члена.
В течение 10 века различные арабские математики разработали математический ряд для вычисления коэффициентов для (1 + x) n , когда n было положительным целым числом.
Английский математик Исаак Ньютон распространил его на нецелочисленные индексы в
17 век.Он решил, что есть расширение для (1 + x) n , который мог быть получен из формулы для n C r , которая работала для все значения n (дробные, отрицательные и т.д.). Прежде чем мы посмотрим, что на самом деле означают дробные и отрицательные индексы Я запишу формулу Ньютона.
Когда n — целое положительное число, ряд имеет n + 1 терминов и дает те же результаты, что и раньше. Однако, когда n равно , а не , положительному целому числу, тогда ряд продолжается вечно. Это называется бесконечным рядом .
Существует два типа бесконечных рядов. Представьте себе бесконечный ряд, который выглядит так:.
Подобный ряд становится больше, чем больше терминов вы добавляете. Если дойти до бесконечности, то сумма ряда будет бесконечное . Это называется расходящийся ряд . Такой сериал ни на что не годится.
А теперь посмотрите на этот бесконечный ряд:.
Этот ряд также бесконечен, он тоже продолжается вечно. Однако, чем больше терминов вы берете, тем меньше получает каждый из них. Эта серия никогда не превышает 2 . По мере того, как вы берете все больше и больше терминов, сумма приближается к 2. Говорят, что такой ряд является сходится .
Полезная вещь в сходящихся рядах заключается в том, что их можно использовать для вычислений. Вы берете столько терминов, сколько необходимо, чтобы расчет был настолько точным, насколько вам нужно .
В приведенном выше примере использование первых пяти членов дает точность в 2 знака после запятой.
В биномиальном ряду Ньютон обнаружил, что для значений n, не являющихся целыми положительными числами (т. е. для дробных и отрицательных индексов), ряд сходится, только если значение x равно 1 или меньше и больше -1 . В символах ряд сходится за
Я скоро объясню, что означает индекс 1/2.
Немного упрощая алгебру, мы получаем:
..
Таким образом, приведенная выше формула, разложение (1 + x) 1/2 , может быть использована для вычисления приблизительных значений для квадратных корней при условии, что x меньше или равно 1 .
Если мы допустим x = 1, то эта формула даст нам значение квадратного корня из 2, поскольку
2 1/2 = (1 + 1) 1/2 , и это можно разложить в приведенный выше ряд. Если мы произведем расчет до членов с x 9 включительно0006 3 тогда получаем
Это равно 1,4375. Ответ калькулятора: 1,4142. Чем больше терминов вы используете, тем ближе приближение к реальному ответу. Обратите также внимание на то, что каждый член меньше предыдущего.
Найдите приближение квадратного корня из 1,77.
Начните с выражения 1,77 1/2 = (1 + 0,77) 1/2 , которое можно расширить с помощью биномиальной теоремы, чтобы получить:
= 1 + 0,385 — 0,0741 + 0,0285 — …
что дает 1,3394 (калькулятор 1,3304). Вы видите, что это с точностью до двух знаков после запятой.
Это все хорошо, но что, если нужен квадратный корень из большего числа (например, 30)?
Вы не можете написать 30 1/2 = (1 + 29) 1/2 , потому что Биномиальный ряд не сходится, если x > 1.
Есть способ обойти это.
Сначала вы представляете 30 в виде, включающем самый большой полный квадрат.
Вместо того, чтобы говорить 30 1/2 = (1 + 29) 1/2 , что не работает, мы пишем:
25 — это самый большой полный квадрат меньше 30.
Мы можем вынуть 25 (не забывая индекс) и разделить все, что внутри скобки, на 25.
Это дает нам следующее:
Поскольку 25 1/2 равно 5 (квадратный корень из 25), мы можем переписать это выражение как:
Член в скобках теперь имеет форму (1 + x), где x < 1, поэтому мы можем использовать биномиальное расширение Ньютона, чтобы получить значение квадратного корня из 1,2. Затем мы умножаем это значение на 5 (число вне скобок). Это даст нам квадратный корень из 30. Выполнив вычисления, мы получим:
..) = 5 (1,0955) = 5,4775
Калькулятор показывает 5,4772 (то есть мы с точностью до трех знаков!). Попробуй сам. Помните, что хитрость заключается в том, чтобы записать число в виде идеального квадрата плюс или минус другое число.
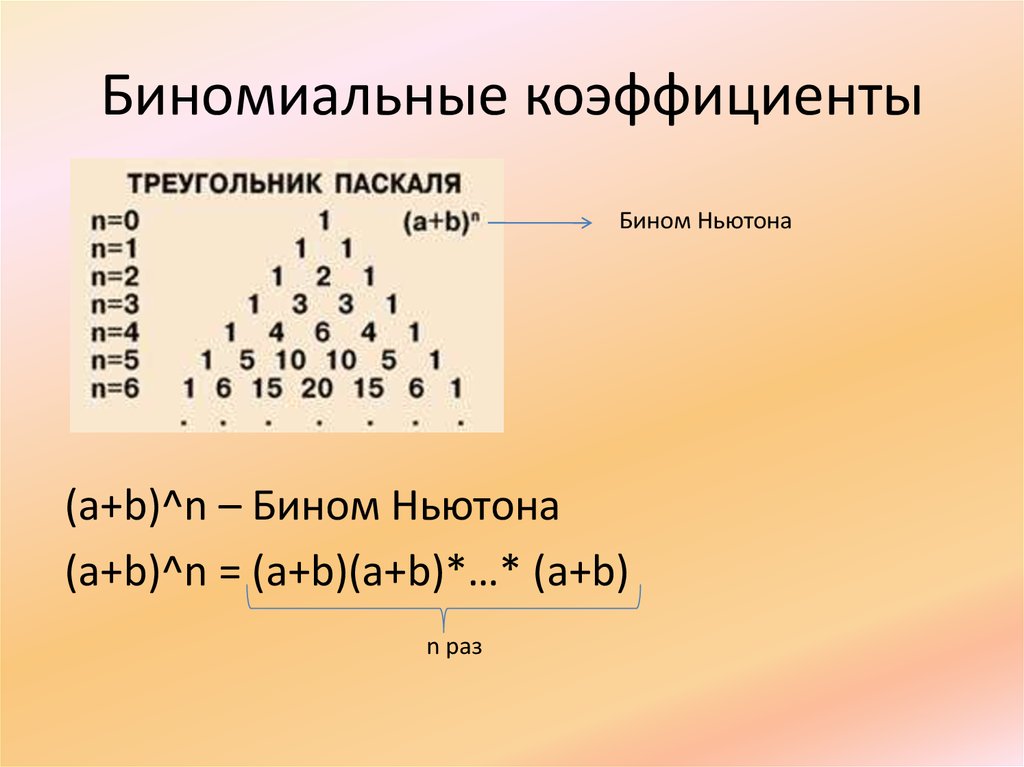
Чтобы найти квадратный корень из 45, запишем его как
.
Это дает
..
что упрощается до:
Это можно использовать для нахождения кубических корней. Найдем кубический корень из 30. Как и ранее, нам нужно записать его в виде суммы двух чисел. На этот раз одно из чисел должно быть идеальным кубом.
Мы можем сказать 30 1/3 = (27 + 3) 1/3 , потому что 27 — это совершенный куб (3 х 3 х 3 = 27). Вычитая 27 1/3 и используя формулу Ньютона, мы можем написать:
Теперь это расширяется (используя приведенную выше формулу) до:
Калькулятор показывает 3,10723, значит, мы снова ошиблись с точностью до двух знаков после запятой.
Я закончу здесь кое-чем, чтобы читатель узнал.
что означают 2 1,5 , 2 0 (неочевидный ответ) и 2 -1 ?
Вот ответы и еще о свойствах индексы (множественное число индекс) в сочинении о логарифмах.
© 1998, 2009 КрысТалПодробнее о сериале. Знакомство с различными типами чисел: действительными, мнимыми, рациональными, иррациональными, трансцендентными. Введение в алгебру и как решать простые, одновременные и квадратные уравнения. Прямоугольные треугольники, синусы, косинусы, тангенсы. Использование тригонометрических функций, рядов и формул. Подробнее об индексах и рядах. Вычисления умножения, деления, корней и степеней с использованием логарифмов.
