Формула биссектрисы прямоугольного треугольника: Все формулы биссектрисы прямоугольного треугольника

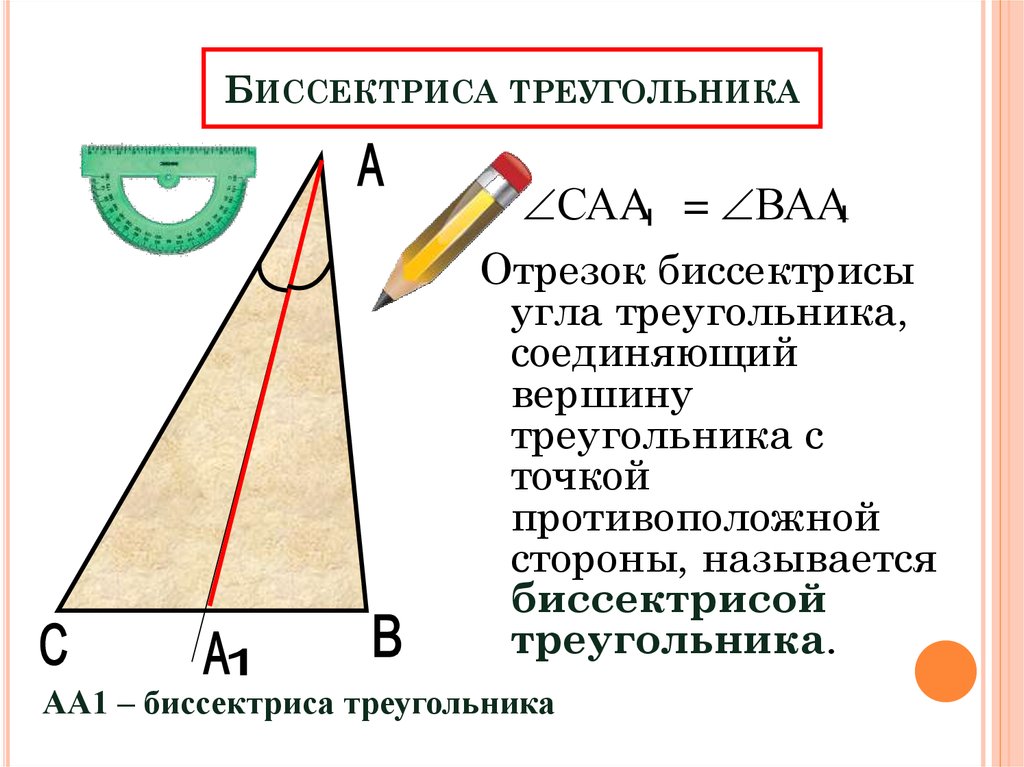
Свойства биссектрисы угла прямоугольного треугольника: прямого, острого

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Свойства биссектрисы прямоугольного треугольника

В данной публикации мы рассмотрим основные свойства биссектрисы прямоугольного треугольника, проведенной из прямого и острого углов, а также разберем примеры решения задач по данной теме.

Примечание: напомним, что прямоугольным называется треугольник, в котором один из углов прямой (т.е. равен 90°), а два остальных – острые (<90°).

• Свойства биссектрисы прямоугольного треугольника
  • Свойство 1
  • Свойство 2
• Примеры задач

Свойства биссектрисы прямоугольного треугольника

Свойство 1

Если в прямоугольном треугольнике известны катеты, то длину биссектрисы, проведенной из прямого угла к гипотенузе, можно вычислить по формуле:

• a и b – катеты;
• c – гипотенуза;
• l_c – биссектриса к гипотенузе.

Свойство 2

Длину биссектрисы в прямоугольном треугольнике, проведенную из острого угла к противолежащему катету, можно вычислить по формуле:

• l_a – биссектриса к катету;
• α – острый угол, из которого проведена биссектриса.

Также можно использовать другую формулу, если известны все три стороны треугольника:

Примечания:

• Прямоугольный треугольник может быть равнобедренным, и в этом случае к нему, в т.ч., применимы свойства биссектрисы равнобедренного треугольника.
• Общие свойства биссектрисы в любом треугольнике представлены в нашей публикации – “Определение и свойства биссектрисы угла треугольника”.

Примеры задач

Задача 1
Найдите длину биссектрисы, которая проведена к гипотенузе прямоугольного треугольника, если известно, что его катеты равны 21 и 28 см.

Решение
Воспользуемся формулой, приведенной в Свойстве 1, подставив в нее известные значения:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Вычислите длину биссектрисы, проведенной к катету с наименьшей длиной.

Решение
Пример катеты за “a” (9 см) и “b” (12 см).

Для начала найдем гипотенузу треугольника (c), воспользовавшись теоремой Пифагора, согласно которой квадрат гипотенузы равняется сумме квадратов катетов:
c² = a² + b² = 9² + 12² = 225.
Следовательно, c = 15 см.

Теперь мы можем применить формулу, рассмотренную в Свойстве 2 для нахождения длины биссектрисы:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Биссектриса прямоугольного треугольника — Мегаобучалка

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

 

L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b — катеты прямоугольного треугольника

с — гипотенуза

α — угол прилежащий к гипотенузе

 

Формула длины биссектрисы через катеты, ( L):

 

Формула длины биссектрисы через гипотенузу и угол, ( L):

 

 

2. Найти по формулам длину биссектрисы из острого угла на катет:

 

L — биссектриса, отрезок ME , исходящий из острого угла

a, b — катеты прямоугольного треугольника

с — гипотенуза

α , β — углы прилежащие к гипотенузе

 

Формулы длины биссектрисы через катет и угол, (L):

 

Формула длины биссектрисы через катет и гипотенузу, (L):

 

 

Длина биссектрисы равнобедренного треугольника

L — высота = биссектриса = медиана

a — одинаковые стороны треугольника

b — основание

α — равные углы при основании

β — угол образованный равными сторонами

 

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

 

 

 

Формула высоты, биссектрисы и медианы, через стороны, (L):

 

 

Найти медиану биссектрису высоту равностороннего треугольника

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

 

L — высота=биссектриса=медиана

a — сторона треугольника

 

 

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):

 

 

Найти длину медианы треугольника по формулам

Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

 

 

M — медиана, отрезок |AO|

c — сторона на которую ложится медиана

a, b — стороны треугольника

γ — угол CAB

 

Формула длины медианы через три стороны, (M):

 

Формула длины медианы через две стороны и угол между ними, (M):

 

 

Длина медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.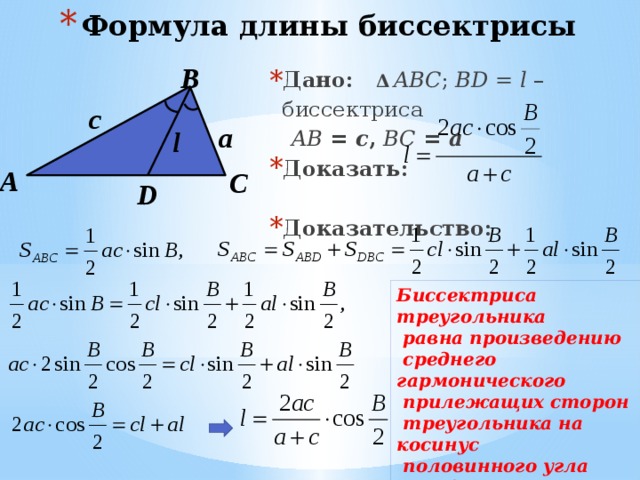

Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

 

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

 

Медиана равна радиусу и половине гипотенузы, (M):

 

Формула длины через катеты, (M):

 

Формула длины через катет и острый угол, (M):

 

 

Формула длины высоты через сторону и площадь, (H):

 

Формула длины высоты через стороны и радиус, (H):

 

 

тригонометрия — Биссектриса угла в прямоугольном треугольнике

спросил

5 лет, 8 месяцев назад

Изменено 3 года назад

Просмотрено 24к раз

$\begingroup$

В прямоугольном треугольнике катеты, примыкающие к прямому углу, равны $a$ и $b$. Докажите, что длина биссектрисы (прямого угла) равна $$\frac{a\cdot b\cdot \sqrt{2}}{a+b}.$$

Подходя к этому вопросу, я был очень озадачен тем, как я получу это выражение.

Кроме того, я не мог понять, откуда берется $\sqrt{2}$, кроме как от синуса или косинуса $45$ градусов (от биссектрисы).

• тригонометрия
• треугольники

$\endgroup$

1

$\begingroup$

Элементарное решение: На следующем рисунке $|BC|=a,|CA|=b,|AB|=c$ и $[CD]$ биссектриса угла. Нарисуем квадрат $CEDF$ и $|CE|=x$. Итак, $|BE|=a-x$ и $|CD|=x\sqrt2$. Теперь $\triangle ABC \sim \triangle DBE$ и $$\dfrac{b}{a}=\dfrac{x}{a-x} $$ 9\circ})}=\frac{ab}{c(\frac{a}{c} \cdot \frac{1}{\sqrt{2}}+\frac{b}{c}\cdot\frac{ 1}{\sqrt{2}})}=\frac{\sqrt{2}ab}{a+b}.$$

$\endgroup$

$\begingroup$

Просто используйте тот факт, что площадь треугольника PQR равна PQsinx, где x — угол между P и Q. И здесь сумма площадей двух треугольников (образованных биссектрисой угла) равна 1/2*AB*BC (т.е. площадь ABC). sin45 даст 1/root2

$\endgroup$

Теорема о биссектрисе угла — Доказательство, Обратное, Формула, Примеры

Теорема о биссектрисе угла утверждает, что биссектриса угла треугольника делит противоположную сторону на два отрезка, которые пропорциональны двум другим сторонам треугольника. Биссектриса угла — это луч, который делит данный угол на два угла равной величины. Давайте узнаем больше о теореме биссектрисы угла в этой статье.

о биссектрисах угла

1.	Что такое теорема о биссектрисе угла?
2.	Доказательство теоремы о биссектрисе
3.	Теорема, обратная теореме о биссектрисе угла
4.	Формула теоремы о биссектрисе угла
5.	Часто задаваемые вопросы по теореме

Что такое теорема о биссектрисе угла?

Теорема о биссектрисе угла треугольника утверждает, что в треугольнике биссектриса любого угла будет делить противоположную сторону в отношении сторон, содержащих этот угол.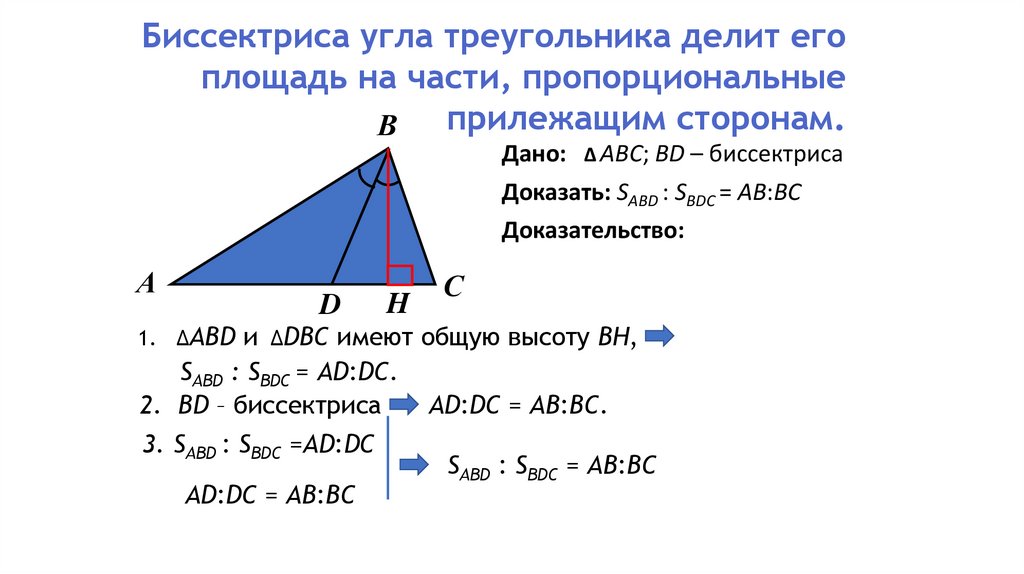

Рассмотрим рисунок ниже:

Здесь PS — биссектриса ∠P. Согласно теореме о биссектрисе угла , PQ/PR = QS/RS или a/b = x/y.

Биссектриса угла — это прямая или луч, который делит угол в треугольнике на две равные части. Основные свойства биссектрисы угла заключаются в том, что любая точка биссектрисы угла равноудалена от сторон угла, а биссектриса угла делит противоположную сторону треугольника в отношении прилежащих сторон, что известно как угол свойство биссектрисы треугольника.

Доказательство теоремы о биссектрисе угла

Утверждение: В треугольнике биссектриса любого угла будет делить противолежащую сторону в отношении сторон, содержащих этот угол. Давайте посмотрим на доказательство этого.

Нарисуйте луч CX, параллельный AD, и продолжите BA, чтобы пересечь этот луч в точке E. стороны в разных точках, две другие стороны делятся в таком же отношении.

В ΔCBE DA параллелен CE.

BD/DC = BA/AE ⋯ (1)

Теперь нам осталось доказать, что AE = AC.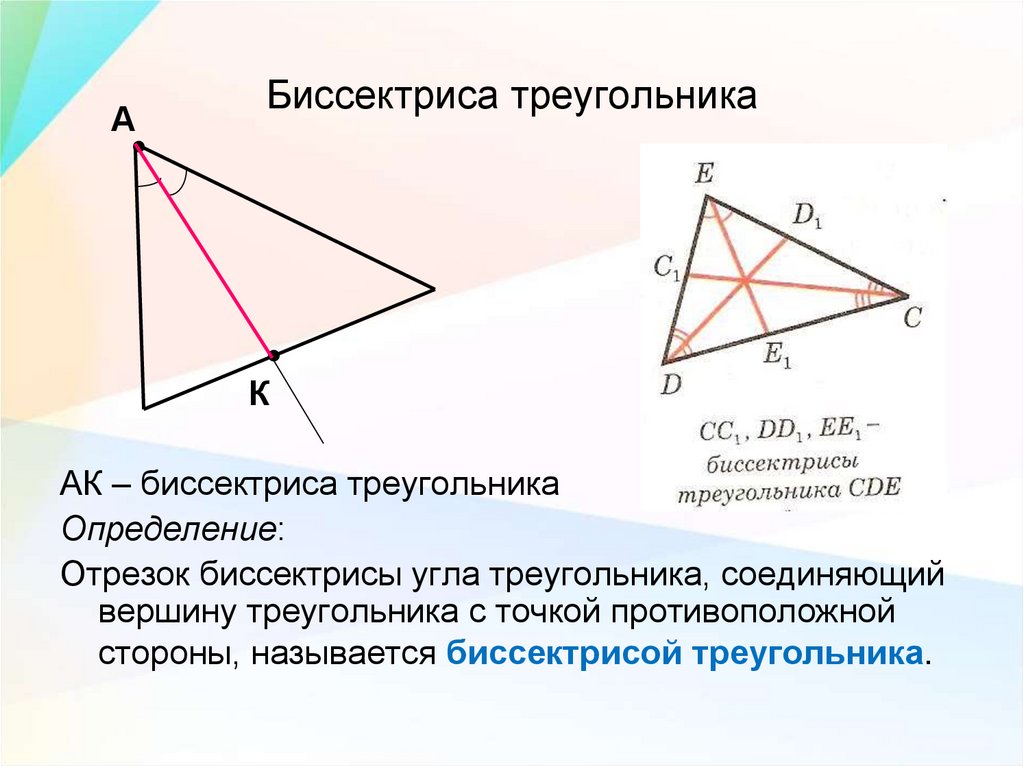

Отметим углы на рисунке выше.

Поскольку DA параллелен СЕ, имеем

∠DAB = ∠CEA (соответствующие углы) —— (2)

∠DAC = ∠ACE (чередующиеся внутренние углы) —— (3)

Так как AD является биссектрисой ∠BAC, мы имеем ∠DAB = ∠DAC —- (4).

Из (2), (3) и (4) мы можем сказать, что ∠CEA = ∠ACE. Это делает ΔACE равнобедренным треугольником. Так как стороны, противоположные равным углам, равны, то AC = AE.

Замените AC на AE в уравнении (1).

BD/DC = BA/AC

Отсюда доказано.

Теорема, обратная теореме о биссектрисе угла

Теорема, обратная биссектрисе угла, утверждает, что если стороны треугольника удовлетворяют следующему условию: «Если линия, проведенная из вершины треугольника, делит противоположную сторону на две части так, что они пропорциональны двум другим сторонам треугольника, треугольник», это означает, что точка на противоположной стороне этого угла лежит на его биссектрисе угла. Здесь нам известно, что стороны пропорциональны, и отсюда мы пришли к выводу, что прямая/луч/отрезок является биссектрисой соответствующего угла.

Это известно как обратная теорема о биссектрисе угла в геометрии.

Посмотрите на изображение ниже, чтобы понять его визуально.

Формула теоремы о биссектрисе угла

Теорема о биссектрисе угла треугольника гласит, что «в треугольнике биссектриса любого угла будет делить противоположную сторону в отношении сторон, содержащих этот угол». Отсюда мы можем записать формулу теоремы о биссектрисе угла треугольника как

\(\dfrac{\text{BD}}{\text{DC}} = \dfrac{\text{AB}}{\text{AC} }\)

► Похожие темы

Ниже перечислены несколько интересных тем, связанных с теоремой о биссектрисе угла треугольника.

• Теорема о биссектрисе перпендикуляра
• Построение биссектрисы угла
• Теорема о сходстве треугольников
• Теорема о внешнем угле

Часто задаваемые вопросы по теореме о биссектрисах угла

Что такое теорема о биссектрисах треугольника?

Теорема о биссектрисе угла треугольника гласит, что «Биссектриса любого угла внутри треугольника делит противоположную сторону на две части, пропорциональные двум другим сторонам треугольника, которые содержат этот угол».

Какая формула теоремы о биссектрисе угла?

Пусть AD — биссектриса ∠A в ΔABC. Согласно формуле теоремы о биссектрисе угла, BD/DC = AB/AC.

Чем похожи теорема о делителях сторон и теорема о биссектрисе угла?

Единственное сходство между теоремой о делителях сторон и теоремой о биссектрисе угла заключается в том, что обе теоремы связаны с пропорциями длин сторон треугольника.

Как использовать теорему о биссектрисе угла?

Теорема о биссектрисе угла треугольника может быть использована для нахождения недостающих длин сторон треугольника. Он устанавливает отношения между сторонами.

Что является обратной теоремой о биссектрисе угла?

Если линия или луч AD проведены в ΔABC так, что BD/DC = AB/AC, то AD делит ∠A пополам. Это утверждение обратной теоремы о биссектрисе угла.

Как доказать теорему о биссектрисе угла?

Чтобы доказать теорему о биссектрисе угла, нам нужно продолжить стороны треугольника и построить рядом с ним еще один треугольник.