«Что такое дискриминант? Откуда взята его формула? Есть ли некое его «доказательство»?» — Яндекс Кью
Популярное
Сообщества
Образование
Александр Киселёв
·
23,8 K
ОтветитьУточнитьПервый
альберт т.
13
28 дек 2019
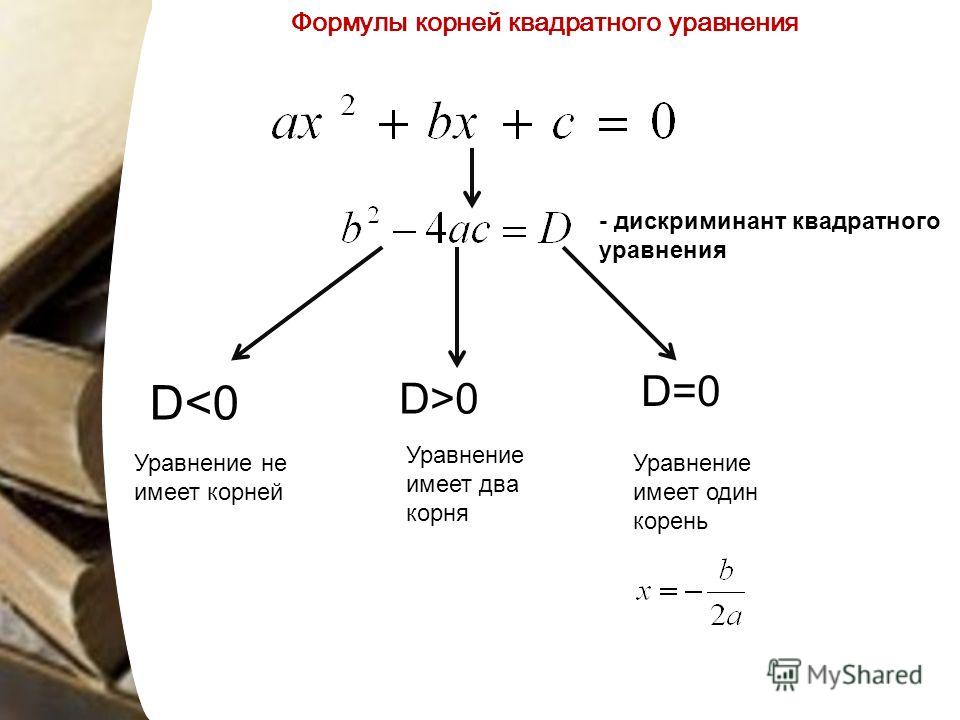
ax²+bx+c=0
Неизвестное — это x; Известное: a, b, c
Чтобы понять есть ли решения или найти эти решения надо перенести известное в одну сторону, неизвестное в другую.
Вынесем a за скобки:
a(x²+(b/a) *x) +c=0
Теперь хорошо бы сделать из суммы в скобках сумму, которая собирается как (a+b)². Для этого умножаем b/a на 2 и делим на 2 (для удобства) :
a(x²+2(b/2a)*x)+c=0
Помним как должна выглядеть искомая сумма (n²+2mn+m²).
Нам не хватает «m²», найдем m:
2mn=2(b/2a)*x, где n =x;
2mx=2(b/2a)*x
2m=2(b/2a)
m=b/2a
m²=b²/4a²
Получаем:
a(x²+2(b/2a)+b²/4a²)+c = нет не 0, так как мы просто так добавили b²/4a², да и ещё и умножили это на a. А значит увеличили на (b²/4a²)*a= b²/4a. А значит:
a(x²+2(b/2a)+b²/4a²)+c = b²/4a
Теперь переносим x и собираем по формуле (m+n) ²:
a(x+b/2a)²=(b²/4a)-c
находим общий знаменатель для правой части уравнения:
a(x+b/2a)²=(b²-4ac)/4a
ну и финал, переносим 4a:
4a²(x+b/2a)²=b²-4ac
Итог:
1) мы вынесли вправо и a, и b, и c;
2) уравнение квадратное, а значит в зависимости от известных значений может:
не быть
два разных
вроде два одинаковых(может ошибаюсь)
3)левая часть уравнения всегда больше нуля, а значит если b²-4ac <0 ответов нет
ну остальное это уже другой вопрос, если понадобится напишу, как влияет D на корень уравнения.
Евгений Иванов
8 ноября 2020
Может я невнимательно прочитал, тогда уж меня простите, но почему в самом начале вы и «с» на «а» не поделили?
Комментировать ответ…Комментировать…
Artyom B.
590
Программист, Deutsche Bank · 4 нояб 2015
В математике нет «доказательств», есть доказательства. В случае с дискриминантом и формулой корней квадратного уравнения доказательство достаточно простое. Нужно подставить предлагаемые формулой корни в уравнение и убедиться, что уравнение превращается в тождество. Если вы вдруг забудете эту формулу, её всегда можно вывести самостоятельно, например так, как сделано в… Читать далее
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Проект Карла III Ребане и хорошей компании | Раздел недели: Водные растворы и смеси для обработки металлов — мытья, обезжиривания, нанесения покрытий, очистки и т. | |||||||||||
| Техническая информация тут Поиск на сайте DPVA Полезные ссылки О проекте Обратная связь Оглавление | Адрес этой страницы (вложенность) в справочнике DPVA.xyz: главная страница / / Техническая информация/ / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы. / / Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.
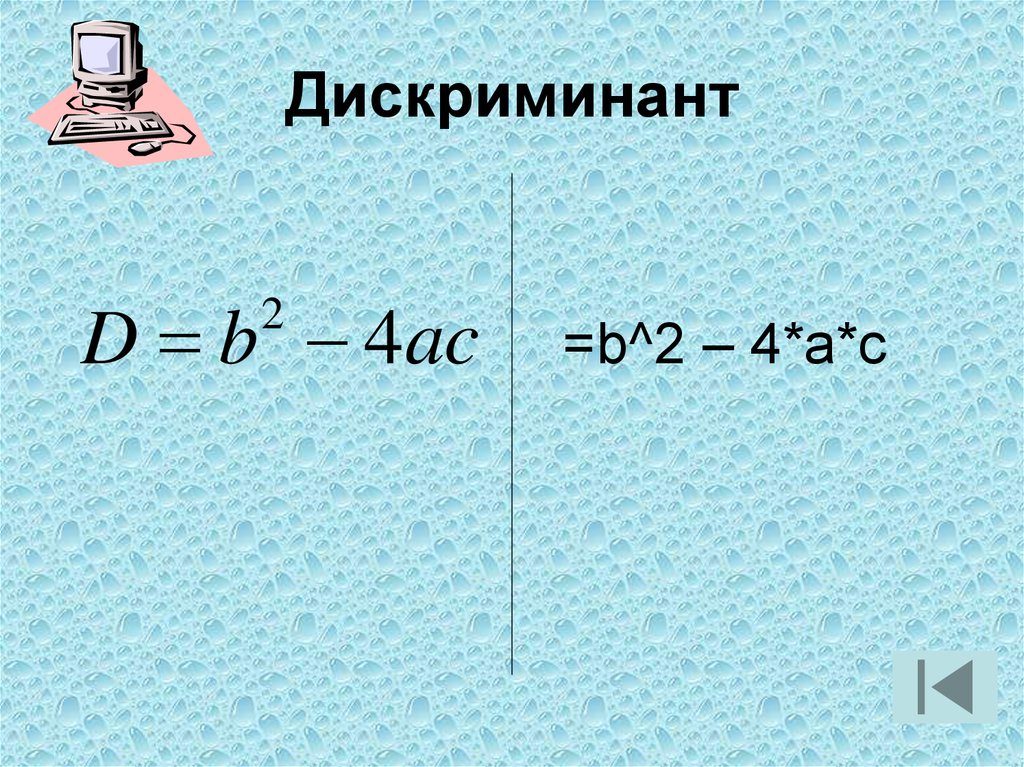 Введите свой запрос: | |||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||
Коды баннеров проекта DPVA.xyz Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.DPVA.xyz не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. | |||||||||||
п. Составы для очистки и обезжиривания поверхности и нанесения покрытий.
Приведенным квадратным уравнением называется уравнение вида
Дискриминант | Определение, примеры и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
- Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю. - Britannica Beyond
Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Связанный контент
Понимание дискриминанта в квадратной формуле
Квадратное уравнение в алгебре — это уравнение, в котором наибольшая степень неизвестной переменной равна 2.
Вы пишете квадратные уравнения, используя следующую формулу: ax² + bx + c = 0 примеры квадратных уравнений включают:
-
2x² + 5x – 8 = 0 -
7x² + 9 = 0 -
xx² – 26 = 3x
В этой конкретной статье я покажу вам, как дискриминант влияет на решения квадратных уравнений. Дискриминант квадратной формулы — часть квадратной формулы, определяющая тип корня в квадратном уравнении (мнимый, вещественный, сингулярный).
Решения квадратного уравнения
Решения квадратного уравнения — это значения неизвестной переменной, которые делают уравнение верным. Существует четыре стандартных способа нахождения корней квадратного уравнения.
Метод факторизации
Этот метод применим, если вы можете разложить на множители коэффициенты квадратного уравнения как av + bx + c = a( rx + n )(px + m ) = 0 . Где n и m — корни квадратного уравнения.
Квадратный метод
Этот метод полезен, когда вы не можете разложить на множители коэффициенты квадратного уравнения, как показано выше.
При завершении метода квадратов квадратное уравнение выражается в виде
-
ax² + bx + c = x2 + (b/a)x + (c/a) = 0, -
x² + (b/a)x + (c/a) = (x +½b)2 + (c/a) – (b²/4) = 0 -
( х +½b )2 = ( b² / 4 ) – ( с / а )
Решение x дает корни квадратного уравнения.
Квадратичная формула
Квадратную формулу можно получить, выполнив метод квадрата. Если квадратное уравнение задано как ax² + bx + c , то корни квадратного уравнения задаются как x = (-b+-(b²–4ac )1/2 )/2a .
Графический метод
В этом методе вы строите квадратное уравнение, а точки, в которых график пересекает ось X, являются корнями уравнения.
Однако в рамках этой темы мы сосредоточимся на квадратичной формуле.
Дискриминант квадратной формулы
Вы можете решить все квадратные уравнения, используя метод квадратной формулы. Из-за его универсальности мы называем его всемогущей формулой.
Вы можете найти корни квадратного уравнения, используя х = (-b +- (b² – 4ас)1/2)/2а .
Член b² – 4ac под квадратным корнем определяет корни квадратного уравнения и является дискриминантом квадратного уравнения. Дискриминант может иметь три возможных исхода.
b² - 4ac > 0
Это происходит, когда b ² больше 4ac. Если это так, вы получите два действительных корня квадратного уравнения. Это верно, потому что квадратный корень из любого положительного числа является положительным числом. Если вы построите график квадратного уравнения, он будет пересекать ось x в двух точках.
b² – 4ac = 0
Это происходит, когда b² равно 4ac. Когда это ваш результат, у квадратного уравнения есть только один действительный корень. Квадратный корень из нуля равен нулю. Если вы построите график квадратного уравнения, он будет касаться оси x только в одной точке.
(b² - 4ac) = 0
Это происходит, когда b ² меньше 4ac.
Это работа для мнимых корней. Корни мнимые, так как квадратный корень из отрицательного числа является мнимым числом. График такого квадратного уравнения не будет касаться оси x.
Проиллюстрируем различные случаи, когда дискриминант определяет корни квадратных уравнений.
Пример 1
Найдите корни следующих квадратных уравнений:
-
x² + 7x + 3 = 0 -
3x² – 13x – 12 = 0 -
6y² + 10y = 0
Так как мы хотим продемонстрировать, как дискриминант влияет на корни квадратного уравнения, мы будем использовать метод формул для решения вышеуказанных задач.
Квадратная формула x = (-b + -(b² - 4ac)1 / 2) / 2a
Уравнение 1
x² + 7x + 3 = 0
a = 1, b 7 и c = 3
Подставьте значения коэффициентов a, b и c в квадратную формулу.
-
(-7 +- (72 – 4*1*3)1/2)/(2*1)
Дискриминант здесь равен ( 72 – 4 * 1 * 3 ) и достигает 37.
Поскольку 37 больше 0, это означает, что у нас есть два действительных корня. Давайте решим и получим корни!
-
(-7 +- (72 – 4*1*3)1/2)/(2*1) -
(-7 +- 371/2)/(2*1) -
(-7 +- 6,08)/(2*1)
Корни
-
(-7 + 6,08)/(2*1) и (-7 – 6,08)/(2*1) -
-0,46 и -6,54
Корни x² + 7x + 3 = 0 равны -0,46 и -6,54
Уравнение 2
3x² – 13x – 12 = 0
a = 3 , b = -13 и c = -12
+- (-132 – 4*3*-12)1/2)/(2*3)
(13 +- (313)1/2)/(2*3) (13+-17,69)/(2*3) Корни
-
(13 + 17,69)/(2*3) и (13 – 17,69)/(2*3) - 5,11 и -0,78
Корни 3x2 -13x -12 = 0 -5,11 и -0,78
Уравнение 3
6y² + 10y = 0
A = 6 9y = 0
a = 6 9y = 0
A = 6 9y33,
A = 6 9y, 0
A = 6 9y = 0
A = 6 9y = 0
, ,
.
Коэффициент c равен нулю, поэтому он не фигурировал в вопросе.
После подстановки значений a, b и c в квадратичную формулу получаем:
-
(-10 +- (102 – 4 * 6 * 0)1/2) / (2 * 6) -
(-10 +- (102)1/2)/(2 * 6)
Корни следующие:
-
(-10 + 10)/12 и (-10 – 10)/12 -
0 и -1,67
Во всех вопросах дискриминант был больше 0. Все корни вещественные и парные.
Пример 2
Ваше квадратное уравнение 2x2 + 4x + 2 = 0 .
а = 2 , б = 4 и c = 2
Подставьте значения коэффициентов для a, b и c в квадратное уравнение.
-
( -4 +- ( 42 – 4 * 2 * 2 )1/2 ) / 2 * 2 -
(-4 +- 0) / 4
Корни
-
(-4 + 0)/4 или (-4 – 0)/4 - -1 и -1
Корень квадратного уравнения равен -1.
В этом примере дискриминант равен 0, и мы получили только один корень.
Пример 3
Найдите корни числа 3x2 + 2x + 7 = 0 .
a = 3 , b = 2 и c = 7
Введите значения a, b и c в квадратичную формулу.
-
( -2 +- ( 22 – 4 * 3 * 7 )1/2 ) / 2 * 2 -
(-2 +- (-80)1/2)/4 -
(-2 +- 8,9j) / 4
Корни
-
(-2 + 8,9j)/4 и (-2 – 8,9j)/4 - Дальнейшее упрощение корней невозможно.
Корни здесь мнимые. Они содержат мнимую переменную j, которую мы определяем как (-1)1/2 или квадратный корень из -1. Мы пришли к мнимым корням, потому что дискриминант был меньше нуля.
Подведение итогов
Понять, как дискриминант влияет на результат решения квадратного уравнения, так же просто, как запомнить формулу. Если вы когда-либо сталкивались с этой математической задачей, всегда выбирайте квадратную формулу.