Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность — окружность, радиус которой равна единице.
Определение. Круг — часть плоскости, ограничена окружностью.
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:L = πD
2. Формула длины окружности через радиус:L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:S = πr2
2. Формула площади круга через диаметр:S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:r2 = (x — a)2 + (y — b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
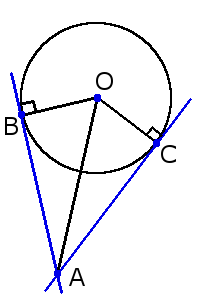 3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:Секущая окружности и ее свойства
Определение. Секущая окружности — прямая, которая проходит через две точки окружности.
Основные свойства секущих
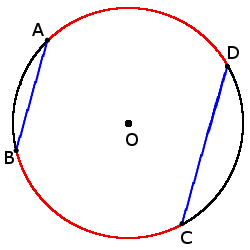
 1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:AQ ∙ BQ = CQ ∙ DQ
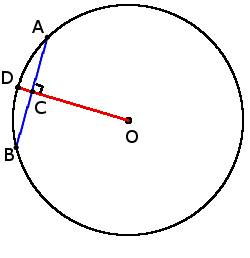
 2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности — отрезок, который соединяет две точки окружности.
Длина хорды
 1. Длина хорды через центральный угол и радиус:
1. Длина хорды через центральный угол и радиус:AB = 2r sin α2
 2. Длина хорды через вписанный угол и радиус:
2. Длина хорды через вписанный угол и радиус:AB = 2r sin α
Основные свойства хорд
 1. Две одинаковые хорды стягивают две одинаковые дуги:
1. Две одинаковые хорды стягивают две одинаковые дуги:если хорды AB = CD, то
дуги ◡ AB = ◡ CD
 2. Если хорды параллельные, то дуги между ними будут одинаковые:
2. Если хорды параллельные, то дуги между ними будут одинаковые:если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
 3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:если OD ┴ AB, то
AC = BC
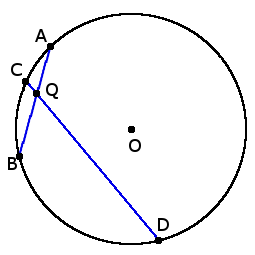 4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:AQ ∙ BQ = DQ ∙ QC
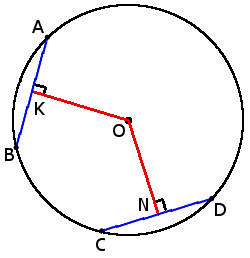 5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.если хорды AB = CD, то
ON = OK
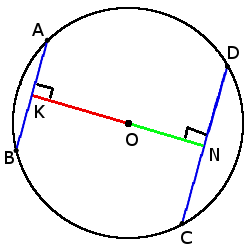 6. Чем больше хорда тем ближе она к центру.
6. Чем больше хорда тем ближе она к центру.если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
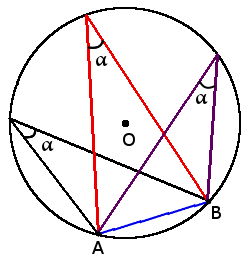 1. Все вписанные углы, которые опираются на одну дугу — равны.
1. Все вписанные углы, которые опираются на одну дугу — равны. 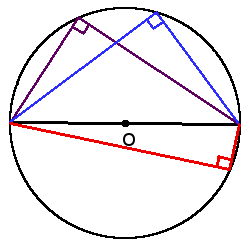 2. Вписанний угол, который опирается на диаметр будет прямым (90°).
2. Вписанний угол, который опирается на диаметр будет прямым (90°).  3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
3. Вписанный угол равен половине центрального угла, что опирается на ту же дугуβ = α2
 4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.α + β = 180°
Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
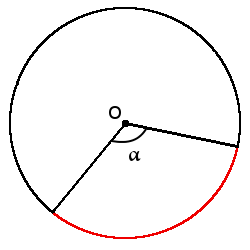 Формула длины дуги через центральный угол (в градусах):
Формула длины дуги через центральный угол (в градусах):l = πr180°∙ α
Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
 Формула. Формула площади сектор через центральный угол (в градусах)
Формула. Формула площади сектор через центральный угол (в градусах)S = πr2360°∙ α
Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность |  | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |  | Часть окружности, расположенная между двумя точками окружности |
| Круг |  | Конечная часть плоскости, ограниченная окружностью |
| Сектор |  | Часть круга, ограниченная двумя радиусами |
| Сегмент |  | Часть круга, ограниченная хордой |
| Правильный многоугольник |  | Выпуклый многоугольник, у которого все стороны равны и все углы равны |
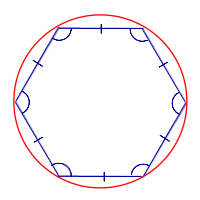 | Около любого правильного многоугольника можно описать окружность |
| Окружность |
 Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |
 Часть окружности, расположенная между двумя точками окружности |
| Круг |
 Конечная часть плоскости, ограниченная окружностью |
| Сектор |
 Часть круга, ограниченная двумя радиусами |
| Сегмент |
 Часть круга, ограниченная хордой |
| Правильный многоугольник |
 Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
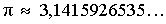
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
Формулы для длины окружности и её дуг
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
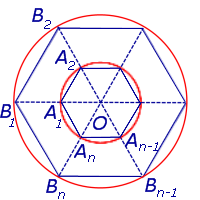
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
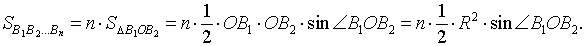
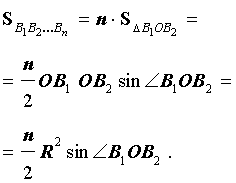
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
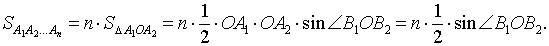
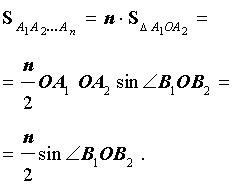
Следовательно,
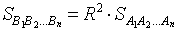
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
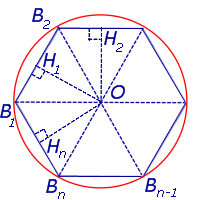
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна
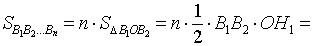
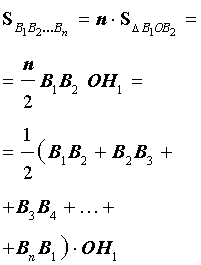
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
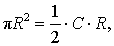
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
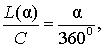
из которой вытекает равенство:
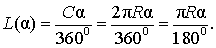
В случае, когда величина α выражена в радианах, справедлива пропорция
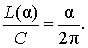
из которой вытекает равенство:
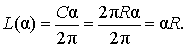
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
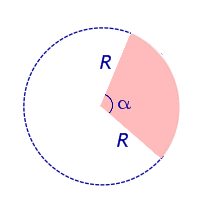
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
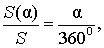
из которой вытекает равенство:
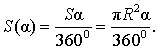
В случае, когда величина α выражена в радианах, справедлива пропорция
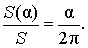
из которой вытекает равенство:
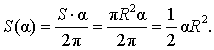
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
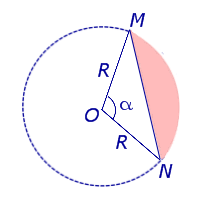
Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
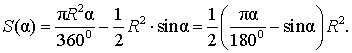
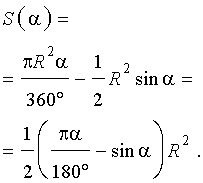
Следовательно,
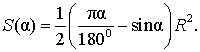
В случае, когда величина α выражена в в радианах, получаем
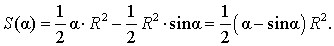
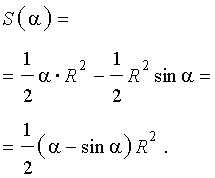
Следовательно,

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как найти длину окружности — Лайфхакер
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
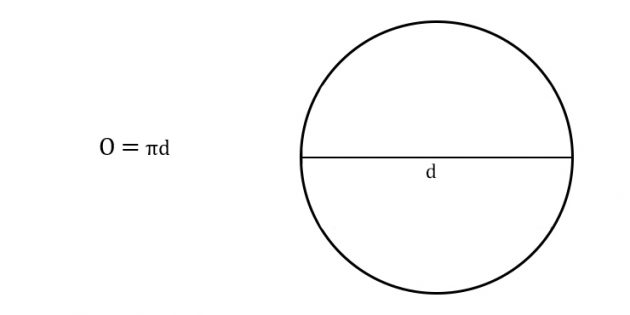 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
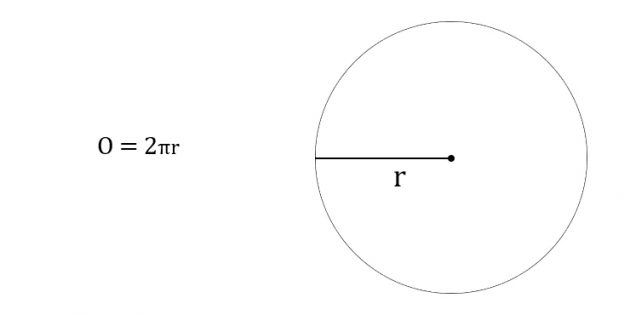 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
Сейчас читают 🔥
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
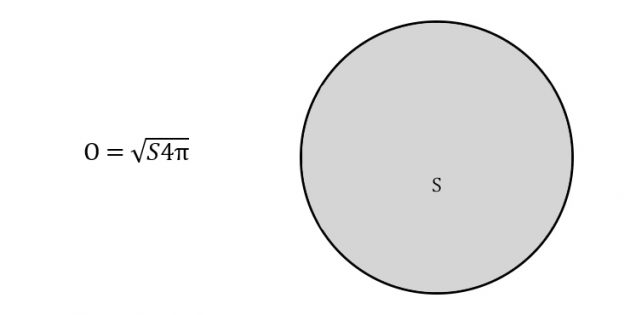 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
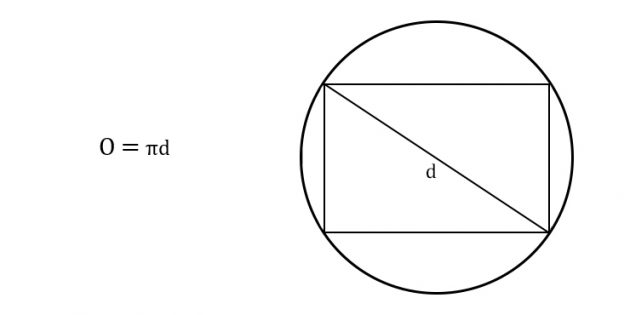 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
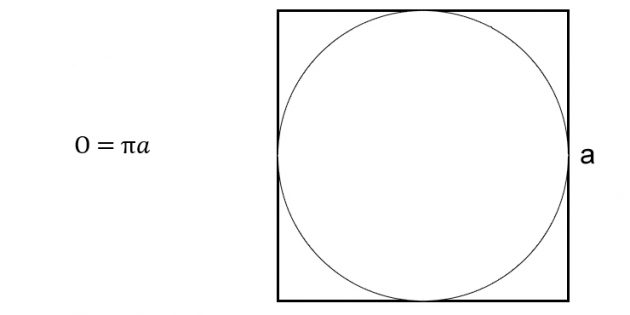 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
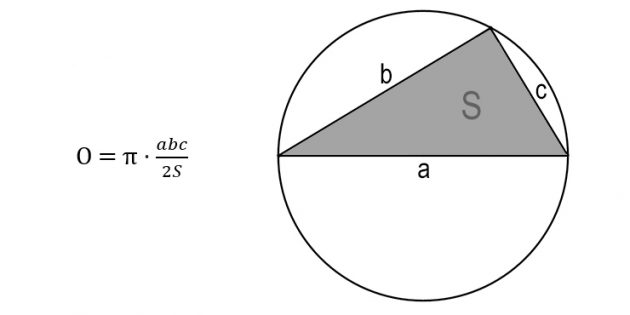 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
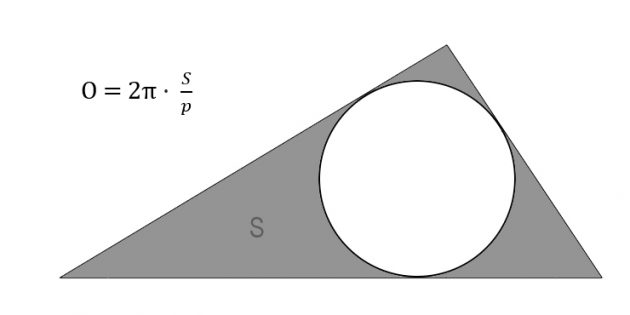 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
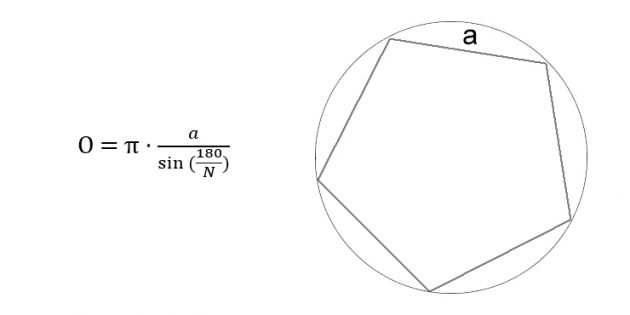 Иллюстрация: Лайфхакер
Иллюстрация: Лайфхакер- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).

R — радиус окружности (круга)
D — диаметр, D = 2R
O — центр круга
π ≈ 3.14
Формула для определения длины радиуса, если известна площадь круга :

Формула для определения длины радиуса, если известна длина окружности :


R — радиус окружности (круга)
h — высота сегмента
L — длина хорды
O — центр круга
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :

Сегмент — часть круга ABC, отсеченная хордой AC
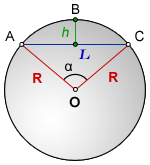
h — высота сегмента ABC
L — хорда AC
R — радиус кружности
O — центр окружности
α — центральный угол AOC
Формула высоты через радиус и центральный угол, (h):

Формула высоты через хорду и центральный угол, (h):
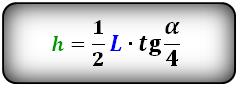
Формула высоты через радиус и хорду, (h):
Дополнительные формулы для окружности:
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.

L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
Формула длины хорды, (L):

Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
В данной публикации мы рассмотрим, каким образом можно посчитать длину/периметр окружности (круга) и разберем примеры решения задач.
Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π:
C = 2 * π * r

Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π:
C = π * d

Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Примеры задач
Задание 1
Найдите длину окружности, если ее радиус равен 12 см.
Решение:
Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2
Найдите периметр круга, если ее диаметр составляет 15 см.
Решение:
Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
Формула расчета длины окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
L = πD = 2πr
r – радиус окружности
D – диаметр окружности
L – длина окружности
π – 3.14
Пример нахождения длинны окружности
Задача:
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
L = πD = 2πr
где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Формулы круга и окружности
Понятие окружности и круга
Перед тем, как ввести основные формулы для окружности и круга, введем, непосредственно понятия окружности и круга, и связанные с ними определения.
Определение 1
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Определение 2
Центром окружности будем называть точку, которая задается в рамках определения 1.
Определение 3
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
Определение 4
Кругом будем называть часть плоскости, которая имеет своей границей окружность.
Длина окружности
Будем выводить длину произвольной окружности $C$ с помощью её радиуса, равного $τ$.
Будем рассматривать две произвольные окружности. Обозначим их длины через $C$ и $C’$, у которых радиусы равняются $τ$ и $τ’$. Будем вписывать в эти окружности правильные $n$-угольники, периметры которых равняются $ρ$ и $ρ’$, длины сторон которых равняются $α$ и $α’$, соответственно. Как мы знаем, сторона вписанного в окружность правильного $n$ – угольника равняется
Готовые работы на аналогичную тему
$α=2τsin \frac{180^0}{n}$
Тогда, будем получать, что
$ρ=nα=2nτsin \frac{180^0}{n}$
$ρ’=nα’=2nτ’sin \frac{180^0}{n}$
Значит
$\frac{ρ}{ρ’}=\frac{2nτsin \frac{180^0}{n}}{2nτ’sin \frac{180^0}{n}}=\frac{2τ}{2τ’}$
Получаем, что отношение $\frac{ρ}{ρ’}=\frac{2τ}{2τ’}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
$\lim_{n→∞}(\frac{ρ}{ρ’})=\frac{2τ}{2τ’}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$\lim_{n→∞}(\frac{ρ}{ρ’})=\frac{C}{C’}$
Из последних двух равенств получим, что
$\frac{C}{C’}=\frac{2τ}{2τ’}$
То есть
$\frac{C}{2τ}=\frac{C’}{2τ’}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$\frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$\frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
$C=2πτ$
Площадь круга
Будем выводить площадь $S$ произвольного круга с помощью радиуса окружности, ограничивающей его, равного $τ$.
Впишем в такую окружность правильный $n$-угольник, площадь которого равняется $S_n$. В такой многоугольник впишем окружность, площадь которого равняется $S’_n$ (рис. 2).
Будет очевидна верность неравенства
$S >S_n >S’_n$
Используем формулу, которая связывает радиусы вписанной и описанной окружностей для правильного многоугольника:
$τ=Rcos \frac{180^0}{n}$
Если неограниченно увеличивать число сторон в таком правильном многоугольнике (то есть взять $n→∞$), то получим, что
$cos \frac{180^0}{n}→1$, $τ→R$
Тогда будет выполняться
$S→S’_n$, $S→S_n$
Также
$P_n→2πτ$
По формуле, площадь такого многоугольника равняется $S_n=\frac{1}{2} P_n τ$, следовательно
$S=S_n=\frac{1}{2}\cdot 2πτ\cdot τ=πτ^2$
То есть, для нахождения площади круга, нужно пользоваться формулой
$S=πτ^2$
Пример задачи
Пример 1
Найти длину окружности и площадь круга, который вписан в квадрат со стороной, равной $α$.
Решение.
Пусть нам дан квадрат $ABCD$, в который вписана окружность с центром $O$. Изобразим рисунок по условию задачи (рис. 3).
Очевидно, что центр окружности будет совпадать с центром квадрата, в которой она вписана. Так как квадрат описан вокруг окружности, то его стороны будут касательными к ней, то есть радиус, проведенный, к примеру, к стороне $AB$ будет перпендикулярен к ней. Значит, диаметр окружности равняется стороне квадрата. То есть
$τ=\frac{α}{2}$
По формуле длины окружности, получим, что
$C=2π\cdot \frac{α}{2}=πα$
По формуле площади круга, получим, что
$S=π(\frac{α}{2})^2=\frac{πα}{4}$
Ответ: $C=πα$, $S=\frac{πα}{4}$.
Уравнения окружности
Круг легко сделать:
Нарисуйте кривую, которая находится в радиусе
от центральной точки.
И так:
Все точки находятся на одинаковом расстоянии
от центра.
На самом деле определение круга
Круг на графике
Поместим круг радиуса 5 на график:
Теперь давайте отработаем , точно , где все точки.
Делаем прямоугольный треугольник:
А затем использовать Пифагор:
x 2 + y 2 = 5 2
Таких точек бесконечное множество, вот несколько примеров:
| x | и | x 2 + y 2 |
|---|---|---|
| 5 | 0 | 5 2 + 0 2 = 25 + 0 = 25 |
| 3 | 4 | 3 2 + 4 2 = 9 + 16 = 25 |
| 0 | 5 | 0 2 + 5 2 = 0 + 25 = 25 |
| −4 | −3 | (−4) 2 + (−3) 2 = 16 + 9 = 25 |
| 0 | −5 | 0 2 + (−5) 2 = 0 + 25 = 25 |
Во всех случаях точка на окружности следует правилу x 2 + y 2 = радиус 2
Мы можем использовать эту идею, чтобы найти пропущенное значение
Пример: x значение 2 и радиус 5
Начать с: x 2 + y 2 = r 2
Известные нам значения: 2 2 + y 2 = 5 2
Перегруппировать: y 2 = 5 2 — 2 2
Квадратный корень с обеих сторон: y = ± √ (5 2 — 2 2 )
Решить: у = ± √21
г. ≈ ± 4.58 …
( ± означает, что есть два возможных значения: одно с + , другое с — )
И вот две точки:
Более общий случай
Теперь давайте поместим центр в (а, б)
Таким образом, круг равен , все точки (x, y) , которые находятся на расстоянии «r» от центра (a, b) .
Теперь давайте выясним, где находятся точки (используя прямоугольный треугольник и Пифагора):
Это та же идея, что и раньше, но нам нужно вычесть а и б :
И это «Стандартная форма» для уравнения круга!
Показывает всю важную информацию с одного взгляда: центр (a, b) и радиус r .
Пример: круг с центром в (3,4) и радиусом 6:
Начать с:
(x-a) 2 + (y-b) 2 = r 2
положить в (a, b) и r:
(x − 3) 2 + (y − 4) 2 = 6 2
Затем мы можем использовать наши навыки алгебры, чтобы упростить и перестроить это уравнение в зависимости от того, для чего оно нам нужно.
Попробуй сам
«Общая форма»
Но вы можете увидеть уравнение окружности, а — не знать !
Потому что это может быть не в аккуратной «Стандартной форме» выше.
В качестве примера, давайте поместим некоторые значения в a, b и r, а затем расширим их
Начать с: (x-a) 2 + (y-b) 2 = r 2
Пример: a = 1, b = 2, r = 3: (x − 1) 2 + (y − 2) 2 = 3 2
Расширить: x 2 — 2x + 1 + y 2 — 4y + 4 = 9
Соберите одинаковые термины: x 2 + y 2 — 2x — 4y + 1 + 4 — 9 = 0И мы в конечном итоге с этим:
x 2 + y 2 — 2x — 4y — 4 = 0
Это круговое уравнение, но «замаскированное»!
Итак, когда вы видите что-то подобное, подумайте «хмм…. что может быть кругом! «
Фактически мы можем записать это в «Общая форма» , поместив константы вместо чисел:
x 2 + y 2 + Axe + By + C = 0
Примечание. Общая форма всегда имеет x 2 + y 2 для первых двух слагаемых .
Переход от общей формы к стандартной форме
Теперь представьте, что у нас есть уравнение в Общая форма :
x 2 + y 2 + Axe + By + C = 0
Как мы можем получить это в Стандартной Форме , как это?
(x-a) 2 + (y-b) 2 = r 2
Ответ состоит в том, чтобы завершить квадрат (читайте об этом) дважды… один раз за x и один раз за y :
Пример: x 2 + y 2 — 2x — 4y — 4 = 0
Начать с: x 2 + y 2 — 2x — 4y — 4 = 0
Соедините x с и y с: (x 2 — 2x) + (y 2 — 4y) — 4 = 0
Константа справа: (x 2 — 2x) + (y 2 — 4y) = 4
Теперь завершите квадрат для x (возьмите половину -2, возведите в квадрат и добавьте к обеим сторонам):
(x 2 — 2x + (-1) 2 ) + (y 2 — 4y) = 4 + (-1) 2
И завершите квадрат для y (возьмите половину −4, возведите в квадрат и добавьте к обеим сторонам):
(x 2 — 2x + (-1) 2 ) + (y 2 — 4y + (-2) 2 ) = 4 + (-1) 2 + (-2) 2
Убирать:
Упростить: (x 2 — 2x + 1) + (y 2 — 4y + 4) = 9
Наконец: (x — 1) 2 + (y — 2) 2 = 3 2
И у нас это есть в стандартной форме!
(Примечание: здесь использовался пример a = 1, b = 2, r = 3, поэтому мы правильно поняли!)
Unit Circle
Если мы поместим центр круга в (0,0) и установим радиус в 1, мы получим:
(x-a) 2 + (y-b) 2 = r 2 (x − 0) 2 + (y − 0) 2 = 1 2 x 2 + y 2 = 1 Что является уравнением единичного круга |
Как построить круг вручную
1.Участок центр (а, б)
2. Нанесите 4 точки «радиуса» от центра в направлении вверх, вниз, влево и вправо
3. Сделайте набросок!
Пример: участок (x − 4) 2 + (y − 2) 2 = 25
Формула для круга: (x-a) 2 + (y-b) 2 = r 2
Таким образом, центр находится в (4,2)
А р 2 составляет 25 , поэтому радиус составляет √25 = 5
Таким образом, мы можем построить:
- Центр: (4,2)
- Up: (4,2 + 5) = (4,7)
- Вниз: (4,2−5) = (4, −3)
- Слева: (4-5,2) = (-1,2)
- Справа: (4 + 5,2) = (9,2)
Теперь просто нарисуйте в круге как можно лучше!
Как построить круг на компьютере
Нам нужно изменить формулу, чтобы мы получили «у =».
Мы должны получить два уравнения (верх и низ круга), которые затем можно построить.
Пример: участок (x − 4) 2 + (y − 2) 2 = 25
Таким образом, центр находится в (4,2), а радиус √25 = 5
Переставь, чтобы получить «y =»:
Начните с: (x − 4) 2 + (y − 2) 2 = 25
Переместить (x − 4) 2 вправо: (y − 2) 2 = 25 — (x − 4) 2
Возьмем квадратный корень: (y − 2) = ± √ [25 — (x − 4) 2 ]
(обратите внимание на ± «плюс / минус»…
может быть два квадратных корня!)
Переместите «−2» вправо: y = 2 ± √ [25 — (x − 4) 2 ]
Итак, когда мы строим эти два уравнения, у нас должен быть круг:
- y = 2 + √ [25 — (x − 4) 2 ]
- y = 2 — √ [25 — (x − 4) 2 ]
Попробуйте нанести эти функции на график функций.
Также возможно использовать уравнение уравнений, чтобы сделать все это за один раз.
,2 $$ где r — радиус круга.Диаграмма 1
Площадь Круг Концепции
Площадь круга — это все пространство внутри окружности круга. На диаграмме 1 площадь круга обозначена синим цветом.
Область на самом деле не является частью круга. Помните, что круг — это просто локус точек. Область заключена внутри этого локуса точек.
Интересный факт об окружности и площади
Исследуйте и откройте для себя связь между формулой площади, радиусом круга и его графиком с помощью нашего интерактивного апплета.
Задача 1
Какая площадь круга на картинке?
Округлите свой ответ до десятых.
Покажи ответПомните формулу:
$$ Площадь = \ pi \ cdot r ^ 2 \\ A = \ pi \ cdot (22 ‘) ^ 2 \\ A = \ pi \ cdot 484 \\ A = \ pi \ cdot 1520.2 \\ \ sqrt {114.59155902616465} = r \\ r = 10.704744696916627 \ text {дюймов} \\ $$
Теперь, когда мы нашли радиус, как нам найти диаметр?
Ответ$$ диаметр = 2 \ радиус cdot \\ = 2 \ cdot 10.704744696916627 \\ = +21,409489393833255 \\ \ boxed {диаметр = 21,41} \\ \ text {дюймов, округлено до ближайшей сотой} $$
Задачи Проблемы
Круг имеет диаметр 12 дюймов. Какова его площадь с точки зрения $$ \ pi $$.2 \\ A = 36 \ pi $$
Задача 7
Если радиус круга удвоится, то насколько увеличилась его площадь?
Покажи ответПоскольку формула для площади круга возводит в квадрат радиус , площадь большего круга всегда в 4 (или 2 2 ) раз меньше круга. Подумайте об этом: вы удваиваете число (что означает × 2) и затем возводите его в квадрат (то есть возводите в квадрат 2), что приводит к новой области, которая в четыре раза меньше.
Вы можете увидеть, что это соотношение верно, если вы выберете некоторые фактические значения для радиуса круга.2 $$
$$ A_ {больше} = \ color {красный} {4} \ cdot A_ {меньше}
Определение. Круг — это набор всех точек на плоскости, которые находятся на равном расстоянии от заданной точки 9 , называемой центром круга .
Определение. Единица окружности — это окружность, радиус которой равен единице.
Определение. Диск является частью плоскости, ограниченной кругом.
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки на окружности.
Определение. Диаметр окружности D — это отрезок, который соединяет две точки на окружности и проходит через его центр.
Свойства круга
1. Диаметр круга равен двум радиусам.D = 2r
2. Кратчайшее расстояние от центрального круга до секущего (хорды) всегда меньше радиуса.
3. Три точки, которые не расположены на прямой линии, могут содержать только один круг.
4. Из всех замкнутых кривых одинаковой длины круг имеет наибольшую площадь.
5. Если два круга касаются одной точки, эта точка помещается на линию, проходящую через центры окружностей.
Площадь и окружность круга
Длина окружности
1. Формула длины окружности в пересчете на диаметр:C = πD
2.Формула длины окружности в единицах радиуса:C = 2πr
Формула площади круга
1. Формула площади круга по радиусу:A = № 2
2. Формула площади круга в пересчете на диаметр:A = πD 2 4
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой координаты:r 2 = x 2 + y 2
2.Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой координате:r 2 = (x — a) 2 + (y — b) 2
3. Параметрические уравнения окружности с радиусом r и центром в точке с координатами (a, b) в декартовой координате:| { | x = a + r cos t |
| y = b + r sin t |
Касательный круг и его свойства
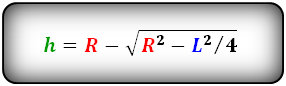
Определение. Касательная — это копланарная прямая, которая касается круга в одной точке.
Касательные свойства
1. Касательная всегда перпендикулярна радиусу окружности, нарисованной в точке контакта.
2. Кратчайшее расстояние от центра окружности до касательной — это радиус окружности.
 3. Если две касательные из точек касания B и C на одной и той же окружности не параллельны, они пересекаются в точке A, а точка соприкосновения между сегментом и точкой пересечения касательной является одним и тем же отрезком на другой касательной:
3. Если две касательные из точек касания B и C на одной и той же окружности не параллельны, они пересекаются в точке A, а точка соприкосновения между сегментом и точкой пересечения касательной является одним и тем же отрезком на другой касательной:AB = AC
Кроме того, если вы проведете линию через центр О и точку пересечения этих касательных, углы между этой линией и касательными будут равны:∠ОAС = ∠OAB
Секант круга и его свойства
Определение. Секущий круг — это прямая линия, соединяющая две точки круга.
Свойства секущих секций
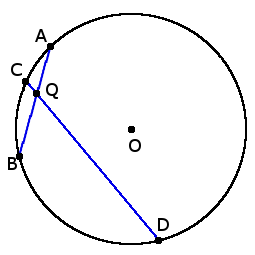
 1. Если точка за пределами круга (Q) получила два секущих, пересекая круг в двух точках A и B для первого секущего и C и D для другого секущего, произведения двух пересекающихся сегментов равны:
1. Если точка за пределами круга (Q) получила два секущих, пересекая круг в двух точках A и B для первого секущего и C и D для другого секущего, произведения двух пересекающихся сегментов равны:AQ ∙ BQ = CQ ∙ DQ
 2. Если точка выходит из секущей окружности Q, пересекая окружность в двух точках A и B и касательную точку контакта C, то произведение сегментирует длины секущих, равные квадрату касательной:
2. Если точка выходит из секущей окружности Q, пересекая окружность в двух точках A и B и касательную точку контакта C, то произведение сегментирует длины секущих, равные квадрату касательной:AQ ∙ BQ = CQ 2
Аккорд круга и его свойства
Определение. Аккорд круга — это отрезок, соединяющий две точки круга. Аккорд является отрезком касательной.
Длина хорды
 1. Формула длины хорды в терминах радиуса и центрального угла:
1. Формула длины хорды в терминах радиуса и центрального угла:AB = 2r sin α2
 2. Формула длины хорды по радиусу и вписанному углу:
2. Формула длины хорды по радиусу и вписанному углу:AB = 2r sin α
Свойства аккордов
 1. Два равных аккорда, затягивающие две одинаковые дуги:
1. Два равных аккорда, затягивающие две одинаковые дуги:если аккорды AB = CD, то
дуги ◡ AB = ◡ CD
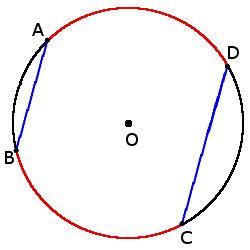 2.Если хорды параллельны, дуги между ними будут одинаковыми:
2.Если хорды параллельны, дуги между ними будут одинаковыми:если аккорды AB ∣∣ CD, то
◡ AD = ◡ BC
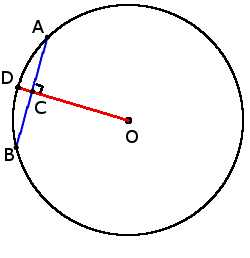 3. Если радиус круга перпендикулярен хорде, он делит хорду пополам в точке пересечения:
3. Если радиус круга перпендикулярен хорде, он делит хорду пополам в точке пересечения:, если OD ┴ AB, то
AC = BC
 4. Если в точке Q пересекаются два аккорда AB и DE, то на сегментах продукта, образованных на пересечении, один аккорд является произведением разных сечений аккордов:
4. Если в точке Q пересекаются два аккорда AB и DE, то на сегментах продукта, образованных на пересечении, один аккорд является произведением разных сечений аккордов:AQ ∙ BQ = DQ ∙ QC
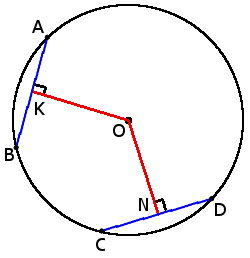 5.Аккорды равной длины равноудалены от центра круга.
5.Аккорды равной длины равноудалены от центра круга.если аккорды AB = CD, то
ВКЛ = ОК
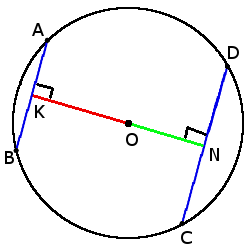 6. Чем больше аккорд, тем ближе он к центру.
6. Чем больше аккорд, тем ближе он к центру., если CD> AB, то
ВКЛ. <ОК
Центральный угол и вписанный угол окружности и его свойства
Определение. Центральный угловой круг — это угол, вершина которого является центром круга.
Определение. Вписанный угол — это угол внутри круга, вершина которого лежит на круге.
Угловые свойства
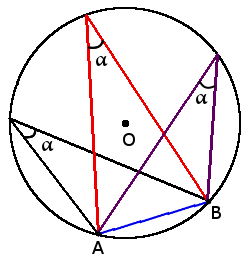 1. Все вписанные углы, основанные на одной дуге, равны (один конец хорды).
1. Все вписанные углы, основанные на одной дуге, равны (один конец хорды). 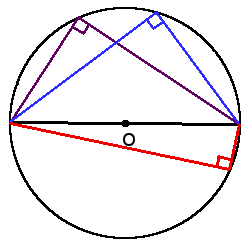 2. Вписанный угол будет прямым (90 °), если он основан на диаметре круга.
2. Вписанный угол будет прямым (90 °), если он основан на диаметре круга.  3. Любой вписанный угол всегда равен половине центрального угла, основанного на одной и той же дуге.
3. Любой вписанный угол всегда равен половине центрального угла, основанного на одной и той же дуге.β = α2
 4. Если два вписанных угла основаны на хорде и расположены по обе стороны от нее, сумма углов составляет 180 °.
4. Если два вписанных угла основаны на хорде и расположены по обе стороны от нее, сумма углов составляет 180 °.α + β = 180 °
Определение. Дуга круга (◡) является частью круга, соединяющего две точки на круге.
Определение. Угол отклонения дуги — это угол между двумя радиусами, которые ограничивают эту дугу. Угол наклона вспомогательной дуги всегда равен центральному углу между радиусами, что ограничивает конечные точки этой дуги.
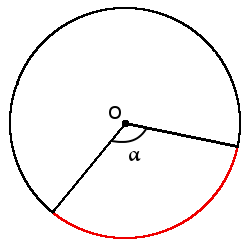 Формула длины дуги в терминах центральных углов (в градусах) и радиуса:
Формула длины дуги в терминах центральных углов (в градусах) и радиуса:л = πr180 ° ∙ α
Определение. Полукруг — дуга, концы которой связаны диаметром круга.
Определение. Полудиск (◓) является частью диска, который ограничен полукругом и диаметром.
Определение. Сектор (◔) является частью диска, который ограничен двумя радиусами и дугой между радиусами.
 Формула. Формула площади сектора в терминах радиуса и центральных углов (в градусах)
Формула. Формула площади сектора в терминах радиуса и центральных углов (в градусах)A = πr 2 360 ° ∙ α
Определение. Сегмент является частью диска, который ограничен дугой и хордой, соединяющей концы этой дуги.
Определение. Концентрический круг — это круг с разными радиусами, имеющий общий центр.
Определение. Кольцевое пространство является частью плоскости, ограниченной двумя концентрическими окружностями.
,формул и теорем кругов | GMAT GRE Geometry Tutorial
Вот краткий обзор хорошо округленного члена геометрического семейства — круга. В этом уроке мы рассмотрим основные понятия, свойства, формулы и теоремы, необходимые для решения вступительных экзаменов MBA и MS.
Определение: Круг — это простая замкнутая фигура, в которой все лежащие на ней точки равноудалены от точки, называемой центром.
Вот круг с центром О.
Вот некоторые основы относительно круга и его свойств:
Радиус : отрезок, соединяющий центр круга с любой точкой на круге, называется радиусом. OB, OA, OX, OY — это различные радиусы окружности на рисунке выше. Для любого круга можно нарисовать бесконечное количество радиусов.
Диаметр : отрезок, проходящий через центр и соединяющий две точки на окружности, называется диаметром. AB — диаметр круга.Как и радиус, бесконечное количество диаметров может быть нарисовано по кругу.
диаметр = 2 * радиус или
Радиус = Диаметр / 2
Аккорд : отрезок, соединяющий любые две точки на окружности, является хордой. Бесконечное количество аккордов можно нарисовать по кругу. XY — аккорд круга.
Видимо, диаметр — самый длинный аккорд круга.
Окружность:
Мера расстояния по краю круга — это длина окружности.
Окружность круга задается формулой
C = 2пр
Где C — окружность, а r — радиус.
Так как 2 * radius = диаметр, Окружность также дается
C = pd
Значение p составляет примерно 22/7 или 3,14159.
Площадь:
Площадь круга определяется по формуле
A = pr 2
Где r — радиус круга.
Так как r = d / 2, Площадь также задается
A = pd 2 /4
Дуги и секторы :
Дуга является частью окружности круга.XY — дуга на рисунке выше.
Сектор — это область, покрытая двумя радиусами и дугой, соединяющей их. XLY и XOY — два сектора на рисунке выше.
Длина дуги определяется по формуле (х / 360) * 2пр
Площадь сектора определяется по формуле (х / 360) * пр 2
Где x — угол, образованный дугой, а r — радиус.
Центральный угол: Угол, одна вершина которого лежит в центре круга, является центральным углом.OYXOY — центральный угол на рисунке выше.
Вписанный угол: Угол, одна вершина которого лежит на одной части окружности, а две другие конечные точки лежат в другом месте на окружности, называется вписанным углом. LYXLY, ∠OXY, ∠OYX — некоторые из вписанных углов на рисунке выше.
Вписанные углы, образованные одной и той же дугой, равны.
Центральный угол в два раза больше соответствующего вписанного угла.
На рисунке выше,
∠XOY = 2 ∠XLY
Касательная: Касательная окружности — это линия, которая просто касается окружности в одной точке, не пересекая ее.MN является касательной на рисунке выше.
Описанный круг : Если многоугольник находится внутри круга таким образом, что все его вершины лежат на круге или просто касаются круга, то круг называется описанным кругом.
Примечание: Если треугольник вписан в круг и если одна из сторон треугольника является диаметром круга, то диаметр действует как гипотенуза, и треугольник является правильным. Это называется теорема Фалеса.
Вписанный круг : Если круг присутствует внутри многоугольника таким образом, что стороны многоугольника просто касаются окружности круга, то этот круг называется вписанным кругом.
Полукруг: Полукруг — это полукруг.
Площадь полукруга = пр 2 /2
Окружность полукруга = половина периметра круга + длина диаметра
→ (2пр / 2) + 2р
→ пр + 2р
→ r (2 + p)
Решенные примеры с участием кругов
Задача 1: Площадь круга выше 81p.ABDAB = 55 °. Найти центральный угол, представленный дугой DB, а также площадь и окружность сектора DOB.
Решение:
Площадь круга = пр 2 = 81р
→ r 2 = 81 и r = 9.
ABDAB — вписанный угол, представленный дугой DB. Вписанный угол составляет половину центрального угла.
∠DAB = 55 ° → ∠DOB = 110 °.
Площадь сектора DOB = (110/360) * 81p = 24,75 p
Окружность сектора — это длина двух радиусов + длина дуги DB
Длина дуги DB = (110/360) * 2 * p * 9 = 5.5 р
Окружность сектора DOB = 9 + 9 + 5,5p = 18 + 5,5p
Задача 2: Если QS — это диаметр, а QR = 6 и радиус = 5, найдите площадь заштрихованной области.
Решение:
Площадь заштрихованной области = Площадь круга — (Площадь треугольника QRS + Площадь полукруга)
Площадь круга = 25р
Площадь полукруга = 12.5p
Нахождение площади треугольника:
Согласно теореме Фалеса, если диаметр — это сторона треугольника, то он становится гипотенузой, и треугольник прав.
Следовательно, RSQRS = 90 °.
Радиус = 5 → Диаметр, QS = 10
QR = 6 (дано)
Согласно теореме Пифагора, QS 2 = QR 2 + RS 2
100 = 36 + RS 2 → RS = 8. Мы также можем видеть, что этот триплет кратен известному пифагорейскому триплету 3, 4, 5.
Площадь треугольника = основание * высота / 2 = 48/2 = 24
Площадь заштрихованной области = 25p — (24 + 12,5p) = (12,5p — 24) кв.единицы.
Узнайте о многих других математических понятиях.
,