Формулировка теоремы Фалеса по геометрии 8 класса: обобщенная, обратная
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Теорема Фалеса: формулировка и пример решения задачи
В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.
- Формулировка теоремы
- Обобщенная формулировка
- Обратная теорема Фалеса
- Пример задачи
Формулировка теоремы
Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.
- A1A2 = A2A3 …
- B1B2 = B2B3 …
Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.
Обобщенная формулировка
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.
В соответствии с этим для нашего чертежа выше справедливо следующее равенство:
* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.
Обратная теорема Фалеса
1. Для пересекающихся секущих
Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.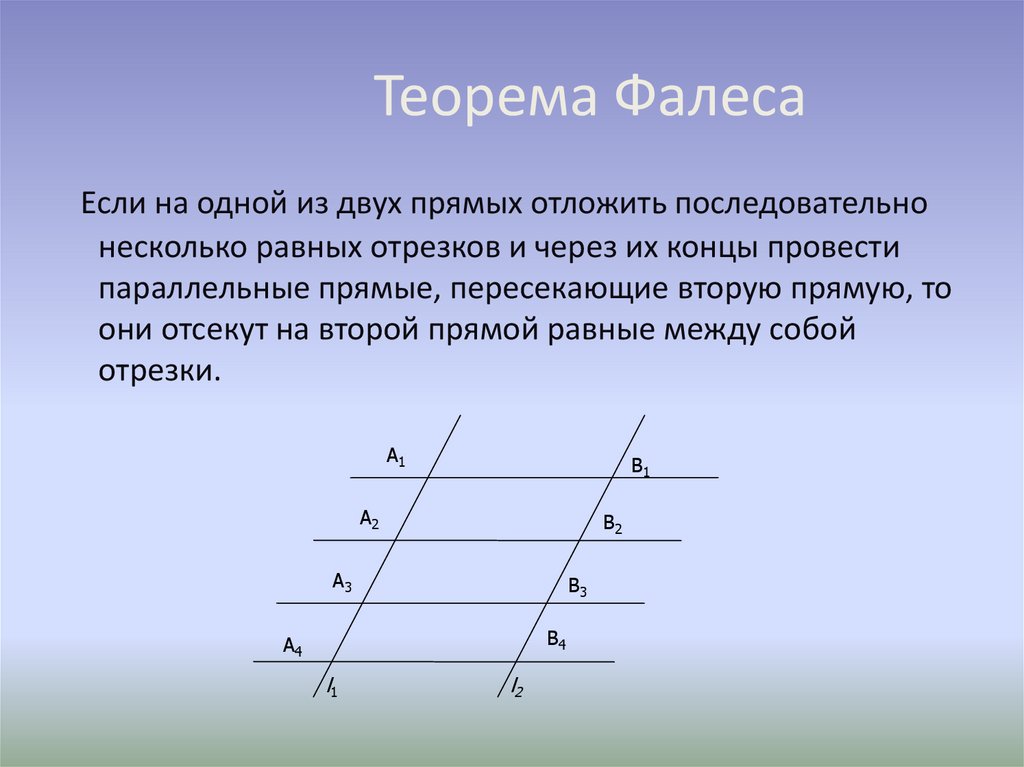
Из обратной теоремы следует:
Обязательное условие: равные отрезки должны начинаться от вершины.
2. Для параллельных секущих
Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.
- a || b
- A1A2 = B1B2 = A2A3 = B2B3 …
Пример задачи
Дан отрезок AB на плоскости. Разделите его на 3 равные части.
Решение
Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.
Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.
Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Теорема Фалеса
Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на другой прямой тоже одинаковые по длине отрезки.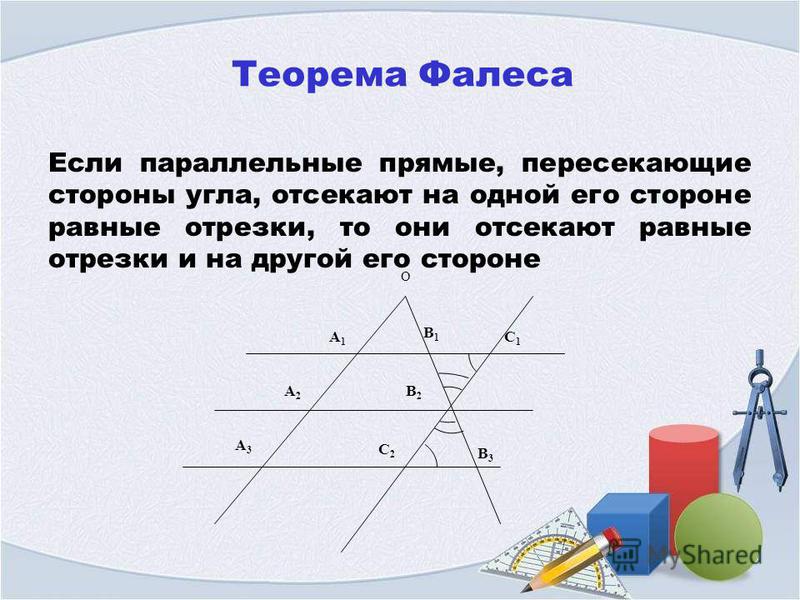
Причем происходит это независимо от угла между прямыми. Это достаточно произвольная формулировка теоремы Фалеса, но достаточно емко описывающая ее суть. Разные учебники приводят разные формулировки, но суть остается неизменной.
Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.
Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать в такой редакции:
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
А можно и в такой:
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Рис 2.
Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.
Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А1В1 могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.
A1A2/B1B2=A2A3/B2B3=A1A3/B1B3
Для иллюстрации можно воспользоваться рисунком 1.
Содержание
- Как пользоваться теоремой Фалеса на практике
- Обратная теорема Фалеса
- Доказательство теоремы Фалеса
- Кто впервые доказал теорему о пропорциональных отрезках
Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур.
Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.
Для решения задачи нарисуем отрезок ВС, образующий с данным ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:
BD=DE=EF=FG=GH=HJ=JC.
Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.
С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.
Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых.
Формулируется обратная теорема Фалеса так:
Если две или более прямых (a, b, c) отсекают от двух других прямых (d, f) равные или пропорциональные отрезки, то они параллельные.
Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.
Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.
Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.
Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:
Выберем точку В2 и проведем прямую, параллельную стороне угла ОС.
При этом отмечаем, что А1А3 || EF. Рассматривая четырехугольник
А1FЕА3 замечаем, что А1F и ЕА3 параллельны по определению, а А1А3 и FВ3 параллельны по построению. Отсюда вытекает, что А1 FЕА 3 — параллелограм и А1А3 = EF.
Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B1B2F=∠B3B2E и ∠B2FB1=∠B2EB3 треугольники B2B1F и B2B3E равны, откуда вытекает, что B1B2=B2B3.
Именно это и требовалось доказать.
По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью. Для сравнения длины отрезков использовалась воткнутая рядом палка.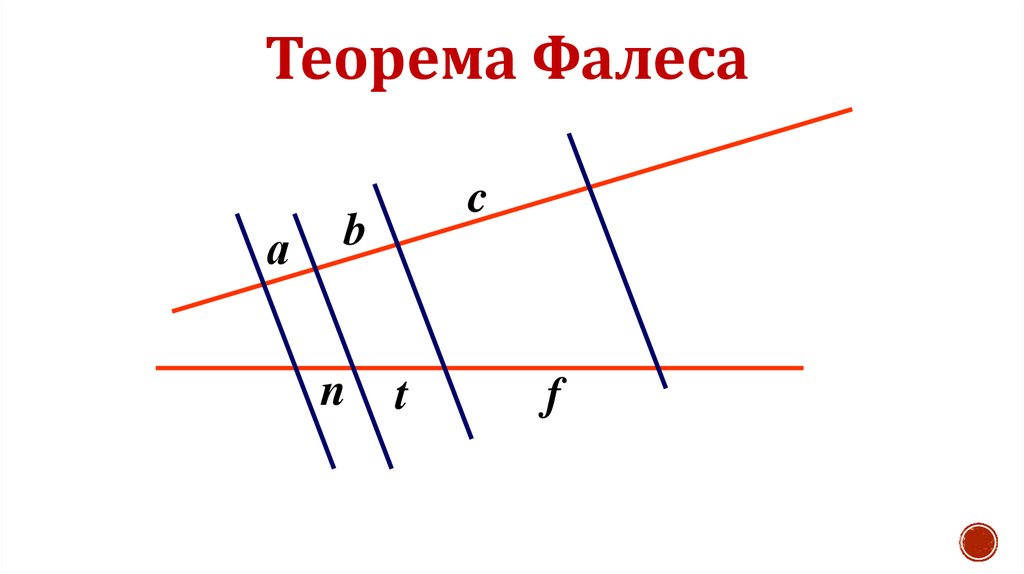
Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.
Основная теорема о пропорциональности | Теорема Фалеса | Утверждение и доказательство
Основная теорема пропорциональности была предложена известным греческим математиком Фалесом, поэтому ее также называют теоремой Фалеса
Понятие теоремы Фалеса было введено в подобных треугольниках. Если данные два треугольника подобны друг другу, то
- Соответствующие углы обоих треугольников равны
- Соответствующие стороны обоих треугольников пропорциональны друг другу
Таким образом, эта теорема также помогает нам лучше понять концепцию подобных треугольников.
Теперь давайте попробуем понять основную теорему пропорциональности.
| 1. | Формулировка основной теоремы пропорциональности |
| 2. | Доказательство основной теоремы о пропорциональности |
| 3. | Обратное из основной теоремы пропорциональности |
| 4. | Часто задаваемые вопросы |
Доказательство основной теоремы о пропорциональности
Теперь попробуем доказать основное утверждение теоремы о пропорциональности (BPT).
Утверждение: Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равных пропорциях.
Дано: Рассмотрим треугольник ΔABC, как показано на данном рисунке. В этом треугольнике мы проводим линию DE, параллельную стороне BC треугольника ΔABC и пересекающую стороны AB и AC в точках D и E соответственно.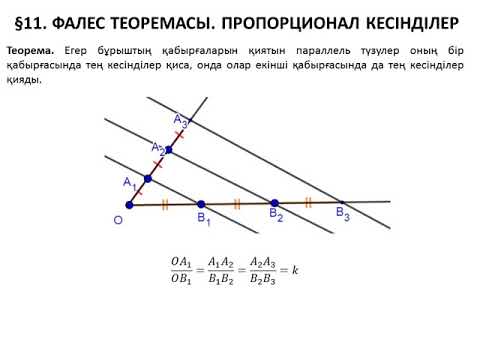
Конструкция: На приведенной выше диаграмме создайте воображаемые линии, где вы можете соединить C с D и B с E. Нарисуйте перпендикуляр DP перпендикулярно AE и EQ перпендикулярно AD.
Доказательство:
Рассмотрим треугольники ADE и BDE. Оба эти треугольника находятся на одном основании AB и имеют одинаковую высоту EQ.
(Площадь ADE)/(Площадь BDE) = (1/2 × AD × EQ)/(1/2 × BD × EQ)
(Площадь ADE)/(Площадь BDE) = AD/BD
Теперь рассмотрим треугольники CDE и ADE. Оба эти треугольника лежат на одном основании AC и имеют одинаковую высоту DP.
(Площадь ADE)/(Площадь CDE) = (1/2 × AE × DP)/(1/2 × CE × DP)
(Площадь ADE)/(Площадь CDE) = AE/CE
Оба треугольника BDE и CDE находятся между одним и тем же набором параллельных прямых.
Площадь треугольника BDE = Площадь треугольника CDE
Применяя это, мы имеем (Площадь треугольника ADE)/(Площадь треугольника BDE) = (Площадь треугольника ADE)/(Площадь треугольника CDE)
AD/BD = AE/CE
Следствие:
Приведенное выше доказательство также помогает доказать другую важную теорему, называемую теоремой о средней точке.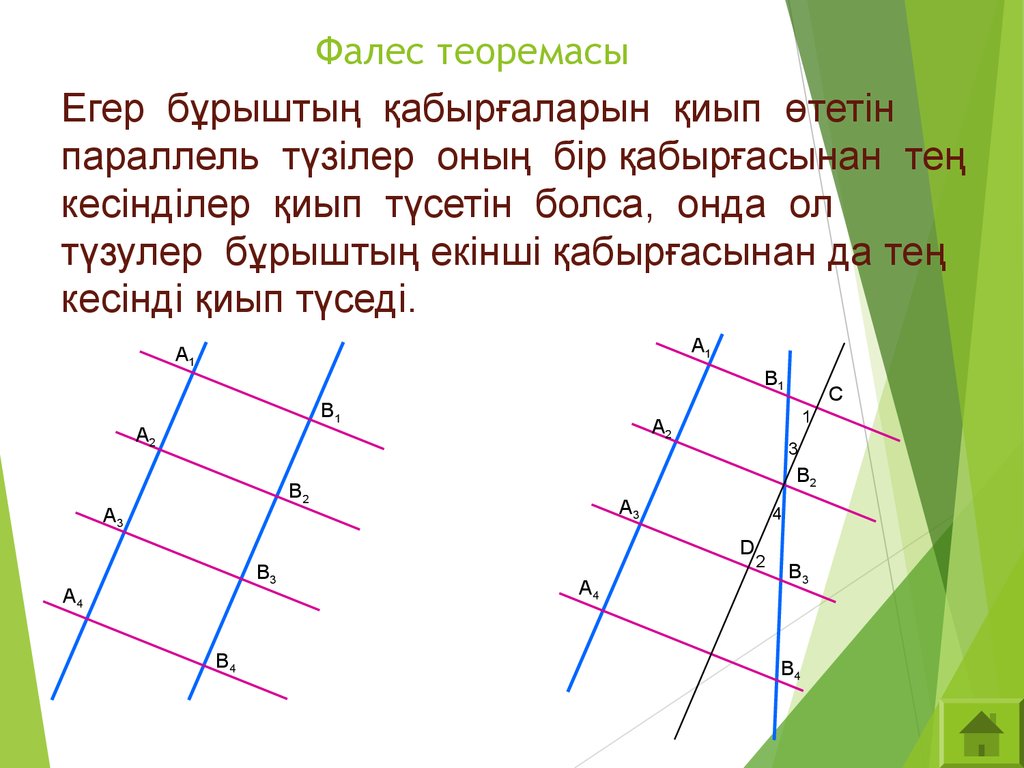
Вывод:
Таким образом, мы доказываем основную теорему о пропорциональности. Следовательно, прямая DE, проведенная параллельно стороне BC треугольника ABC, делит две другие стороны AB, AC в равной пропорции. Кроме того, обратная теорема BPT о средней точке также остается верной. В нем говорится, что линия, проведенная через середину стороны треугольника и параллельная другой стороне, делит пополам третью сторону треугольника.
Обращение к основной теореме пропорциональности
В соответствии с обратной теоремой о пропорциональности: «Если отрезок нарисован так, чтобы разделить две стороны треугольника в равных пропорциях, то он параллелен третьей стороне».
Дано:
ABC — треугольник, и прямая DE пересекает стороны AB и AC в равных пропорциях.
AD/BD = AE/CE
Доказательство:
Предположим, что DE не параллелен BC. Поэтому проведем еще одну прямую DF, параллельную ВС. Применяя основную теорему пропорциональности, мы имеем: AD/BD = AF/CF. Но уже дано, что: AD/BD = AE/CE. Соблюдая равенство левых частей двух приведенных выше утверждений, мы заключаем следующее утверждение: AE/CE = AF/CF. Добавьте 1 с обеих сторон этого утверждения.
(AE/CE) + 1= (AF/CF) + 1
(AE + CE)/CE = (AF + CF)/CF
AC/CE = AC/CF
∴ CE = CF
Для приведенного выше утверждения точки E и F являются одними и теми же точками, и они совпадают. Следовательно, прямая DE параллельна BC, что доказывает обратное утверждение основной теоремы о пропорциональности.
Важные примечания
- Основная теорема пропорциональности. Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции.
- Обратное из основной теоремы о пропорциональности: линия, проведенная для разрезания двух сторон треугольника в равных пропорциях, параллельна третьей стороне.
- Теорема о средней точке. Линия, проведенная параллельно одной стороне треугольника и половине этой стороны, делит две другие стороны в своей середине.
Контрольные вопросы
- Диагонали четырехугольника PQRS пересекаются в точке O, так что PO/QO = RO/SO. Докажите, что PQRS — трапеция.
Часто задаваемые вопросы по основной теореме пропорциональности
Что такое Теорема Фалеса?
Теорема Фалеса, которую также называют основной теоремой пропорциональности, утверждает, что линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит эти две стороны в равной пропорции.
Каковы применения основной теоремы пропорциональности?
Основная теорема о пропорциональности помогает найти длины, на которые две стороны треугольника делятся линией, проведенной параллельно третьей стороне. Кроме того, у него есть приложения, чтобы найти взаимосвязь между двумя равноугольными треугольниками.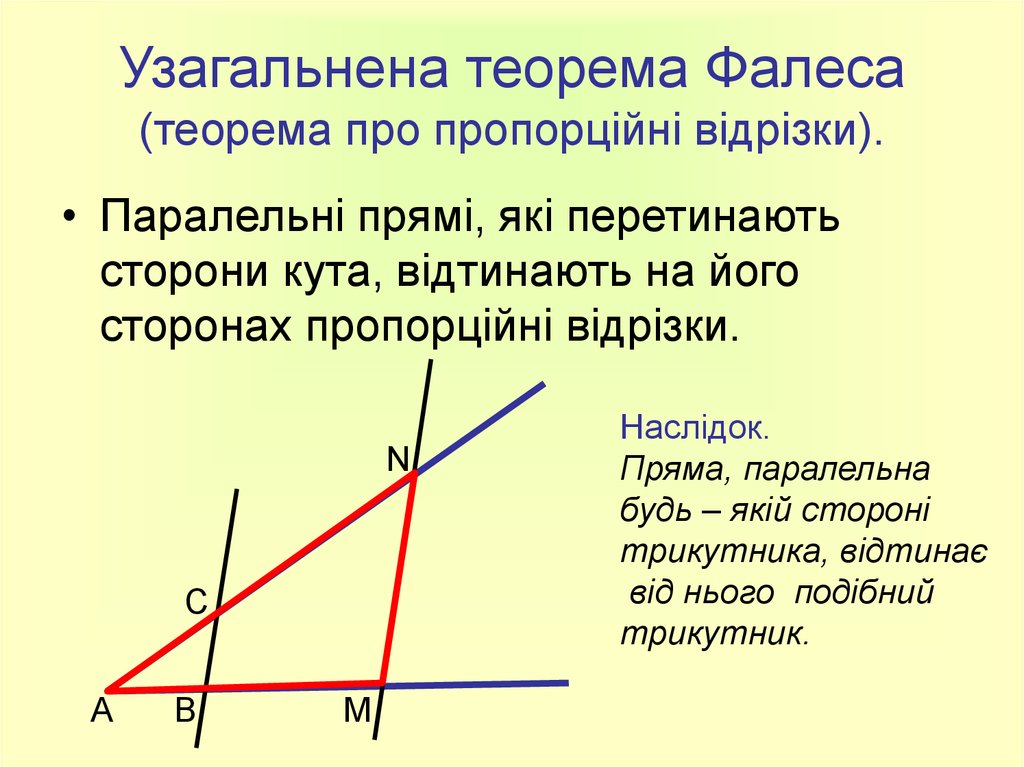
Что такое История Теоремы Фалеса?
Теорема Фалеса была предложена Фалесом, греческим математиком и философом около 625 г. до н.э. Сейчас ее называют основной теоремой пропорциональности, и она помогает найти соотношение между сторонами двух равноугольных треугольников.
Что такое формула основной теоремы пропорциональности?
Базовая формула теоремы пропорциональности для треугольника ABC с точкой D на AB, точкой E на AC и DE // BC выглядит следующим образом,
AD/DB = AE/EC
Что вы подразумеваете под основной теоремой пропорциональности?
Основная теорема о пропорциональности гласит, что если прямая проведена параллельно одной стороне треугольника и пересекает две другие стороны, то две другие стороны она делит в равной пропорции.
Как доказать основную теорему о пропорциональности, вырезая бумагу?
Чтобы показать основную теорему о пропорциональности, вырежьте из цветной бумаги треугольник и обозначьте его вершины как ABC.
Поместите его на разлинованную бумагу так, чтобы одна сторона BC совпадала с линией на разлинованной бумаге. Теперь отметьте точки D на АВ и Е на АС так, чтобы DE была параллельна стороне ВС. Теперь измерьте длины AD, BD, AE и CE и проверьте, пропорциональны ли они.
AD/DB = AE/EC
Как решить теорему Фалеса?
Теорема Фалеса аналогична основной теореме о пропорциональности. Чтобы решить ее, нам нужно доказать, что прямая, проведенная параллельно одной стороне треугольника, делит две другие стороны в равной пропорции.
Является ли последняя динамика акций Thales S.A. (EPA:HO) отражением ее финансового состояния?
Большинство читателей уже знают, что акции Thales (EPA:HO) значительно выросли на 6,2% за последний месяц. Учитывая впечатляющие результаты компании, мы решили более внимательно изучить ее финансовые показатели, поскольку финансовое состояние компании в долгосрочной перспективе обычно определяет рыночные результаты. В частности, сегодня мы уделим внимание ROE от Thales.
ROE или рентабельность собственного капитала — полезный инструмент для оценки того, насколько эффективно компания может получать доход от инвестиций, полученных от своих акционеров. Короче говоря, ROE показывает прибыль, которую приносит каждый доллар по отношению к инвестициям акционеров.
Посмотрите наш последний анализ Thales
Как рассчитать рентабельность капитала?
ROE можно рассчитать по формуле:
Рентабельность собственного капитала = Чистая прибыль (от продолжающихся операций) ÷ Акционерный капитал
Итак, исходя из приведенной выше формулы, ROE для Thales составляет:
15% = 1,1 млрд евро ÷ 7,8 млрд евро (на основе последних двенадцати месяцев до июня 2022 года).
«Доход» — это доход, полученный предприятием за последний год. Другой способ представить это так: на каждый €1 собственного капитала компания могла получить €0,15 прибыли.
Почему ROE важен для роста прибыли?
Мы уже установили, что ROE служит эффективным показателем будущих доходов компании.
Основываясь на том, какую часть своей прибыли компания решает реинвестировать или «сохранить», мы можем оценить будущую способность компании получать прибыль. Предполагая, что все остальное остается неизменным, чем выше ROE и удержание прибыли, тем выше темпы роста компании по сравнению с компаниями, которые не обязательно обладают этими характеристиками.
Сравнение роста прибыли Thales и 15% ROE
Начнем с того, что ROE Thales выглядит приемлемо. Особенно по сравнению со средним показателем по отрасли в 12% ROE компании выглядит довольно впечатляюще. Однако нам любопытно, как высокая доходность по-прежнему приводила к неизменному росту Thales за последние пять лет. Мы полагаем, что здесь могут действовать и другие факторы, ограничивающие рост компании. К ним относятся низкое удержание прибыли или плохое распределение капитала.
Затем, сравнив рост чистой прибыли в отрасли, мы обнаружили, что рост Thales довольно высок по сравнению со средним ростом в отрасли на 0,04% за тот же период, что приятно видеть.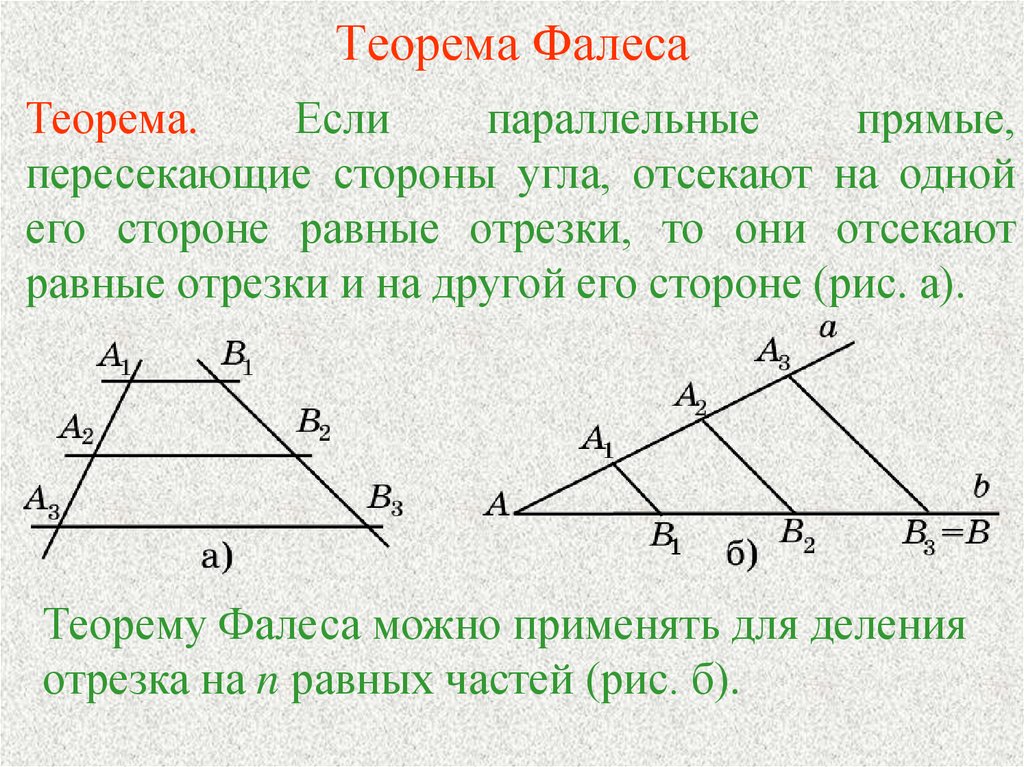
Рост прибыли является важным фактором в оценке акций. Инвестору важно знать, учел ли рынок ожидаемый рост (или снижение) прибыли компании. Таким образом, они будут иметь представление о том, направляется ли стадо в чистые голубые воды или их ждут болотистые воды. Учел ли рынок будущие перспективы HO? Вы можете узнать об этом в нашем последнем инфографическом отчете о внутренней стоимости.
Эффективно ли Thales использует нераспределенную прибыль?
Несмотря на нормальный трехлетний средний коэффициент выплат в размере 42% (подразумевается, что компания оставляет себе 58% своего дохода) за последние три года, Thales продемонстрировала незначительный рост прибыли, как мы видели выше. Таким образом, здесь могут быть другие факторы, которые потенциально могут препятствовать росту. Например, бизнес столкнулся с некоторыми встречными ветрами.
Кроме того, Thales выплачивает дивиденды в течение как минимум десяти лет, что свидетельствует о том, что поддержание выплаты дивидендов гораздо важнее для руководства, даже если это происходит за счет роста бизнеса.
Наши последние аналитические данные показывают, что будущий коэффициент выплат компании в течение следующих трех лет, как ожидается, составит примерно 40%. Несмотря на это, прогнозируется, что в будущем ROE для Thales вырастет до 21%, несмотря на то, что не ожидается больших изменений в коэффициенте выплат.
Резюме
В целом, мы очень довольны работой Thales. В частности, нам нравится, что компания активно реинвестирует в свой бизнес и получает высокую норму прибыли. Неудивительно, что это привело к впечатляющему росту доходов. При этом, глядя на текущие оценки аналитиков, мы обнаружили, что доходы компании, как ожидается, будут расти. Чтобы узнать больше о прогнозах роста прибыли компании в будущем, взгляните на этот бесплатный 9Отчет 0004 о прогнозах аналитиков для компании, чтобы узнать больше.
Оценка — это сложно, но мы помогаем упростить ее.
Узнайте, потенциально ли Thales переоценена или недооценена, изучив наш всесторонний анализ, который включает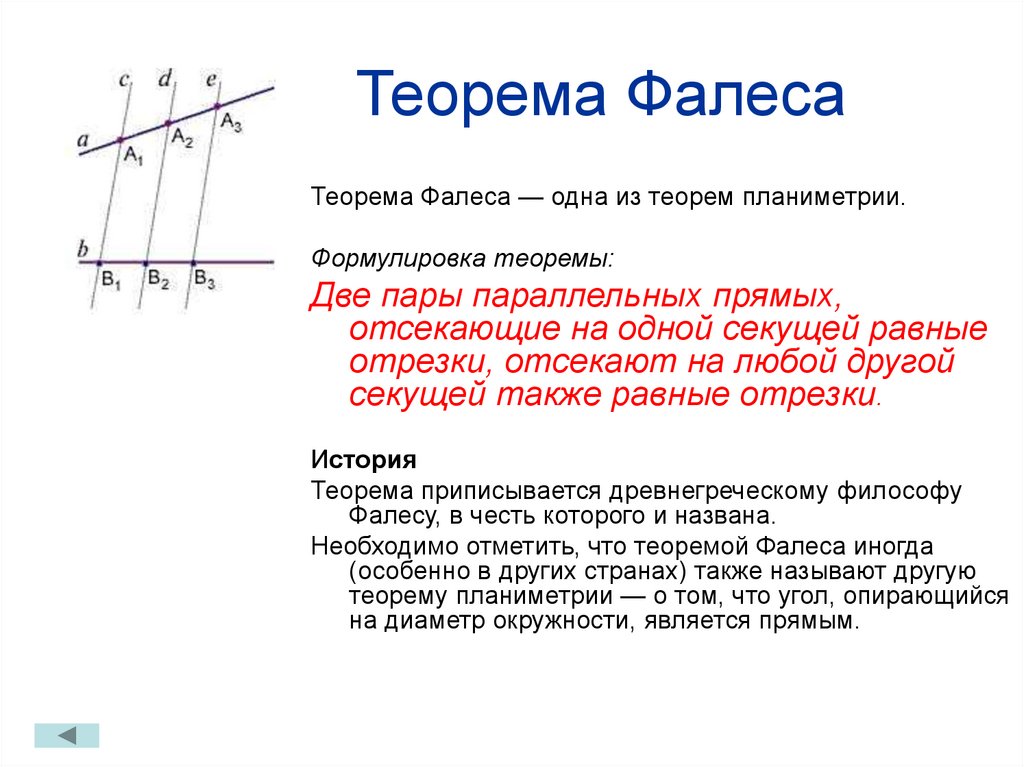 
Посмотреть бесплатный анализ
Есть отзывы об этой статье? Беспокоитесь о содержании? Свяжитесь с нами напрямую по телефону . В качестве альтернативы отправьте электронное письмо в редакцию (at) Simplywallst.com.
Эта статья от Simply Wall St носит общий характер. Мы предоставляем комментарии, основанные на исторических данных и прогнозах аналитиков, используя только беспристрастную методологию, и наши статьи не предназначены для предоставления финансовых рекомендаций. Это не является рекомендацией покупать или продавать какие-либо акции и не принимает во внимание ваши цели или ваше финансовое положение. Мы стремимся предоставить вам долгосрочный целенаправленный анализ, основанный на фундаментальных данных. Обратите внимание, что наш анализ может не учитывать последние объявления компаний, чувствительные к ценам, или качественные материалы.