Критерий Фишера | matematicus.ru
Критерий Фишера используют в качестве проверке равенства (однородности) дисперсий двух выборок, в том числе проверки значимости модели регрессии.
Критерий Фишера находится по формуле:
при σ1>σ2
σ1 – большая дисперсия выборки;
σ2 – меньшая дисперсия выборки.
Формула критерий Фишера для оценки значимости уравнения регрессии:
При Fнабл<Fкр нулевая гипотеза принимается.
Число степеней свободы исправленных дисперсий находятся по формулам:
для первой выборки
f1=n1−1
для второй выборки
f2=n2−1
Fкр (α, f1, f2) определяется по таблице
Пример
Дана выборка успеваемости по двум группам.
| № п/п | X | Y |
| 1 | 34 | 45 |
| 2 | 44 | 68 |
| 3 | 97 | 76 |
| 4 | 62 | 56 |
| 5 | 39 | 78 |
| 6 | 73 | 64 |
| 7 | 42 | 84 |
| 8 | 95 | 54 |
| 9 | 35 | 81 |
| 10 | 37 | 79 |
| 11 | 45 | 41 |
| 12 | 43 | 47 |
| 13 | 73 | 79 |
| 14 | 53 | 32 |
| 15 | 32 | 44 |
Требуется определить различия в оценках между двумя группами при α = 0.05.
Решение
Вычислим дисперсию по X и по Y
| № п/п | X | Y | D(X) | D(Y) |
| 1 | 34 | 45 | 42,684 | 31,609 |
| 2 | 44 | 68 | 10,24 | 4,1798 |
| 3 | 97 | 76 | 209,28 | 22,195 |
| 4 | 62 | 56 | 7,84 | 3,8242 |
| 5 | 39 | 78 | 23,684 | 28,92 |
| 6 | 73 | 64 | 41,818 | 0,5057 |
| 7 | 42 | 84 | 14,951 | 54,432 |
| 8 | 95 | 54 | 190,44 | 6,876 |
| 9 | 35 | 81 | 38,44 | 40,676 |
| 10 | 37 | 79 | 30,618 | 32,617 |
| 11 | 45 | 41 | 8,2178 | 48,38 |
| 12 | 43 | 47 | 12,484 | 24,558 |
| 13 | 73 | 79 | 41,818 | 32,617 |
| 14 | 53 | 32 | 0,04 | 99,113 |
| 15 | 32 | 44 | 51,84 | 35,469 |
| Сумма | 804 | 928 | 724,4 | 465,97 |
| Среднее | 53,6 | 61,867 |
По критерию Фишера находим Fэмп.
k1=15 — 1 = 14,
k2=15 — 1 = 14
По таблице критерия Фишера находим критическое значение
Fкрит=2.49, следовательно, 2.49>1.55, Fкрит>Fэмп
Отсюда, различия в оценках между двумя выборками групп присутствует, принимаем гипотезу.
Методы статистики
Критерии и методы
Рональд Фишер
Точный критерий Фишера – это критерий, который используется для сравнения двух и более относительных показателей, характеризующих частоту определенного признака, имеющего два значения. Исходные данные для расчета точного критерия Фишера обычно группируются в виде четырехпольной таблицы, но могут быть представлены и многопольной таблицей.
1. История разработки критерия
Впервые критерий был предложен Рональдом Фишером в его книге «Проектирование экспериментов». Это произошло в 1935 году. Сам Фишер утверждал, что на эту мысль его натолкнула Муриэль Бристоль. В начале 1920-х годов Рональд, Муриэль и Уильям Роуч находились в Англии на опытной сельскохозяйственной станции. Муриэль утверждала, что может определить, в какой последовательности наливали в ее чашку чай и молоко. На тот момент проверить правильность ее высказывания не представлялось возможным.
Это произошло в 1935 году. Сам Фишер утверждал, что на эту мысль его натолкнула Муриэль Бристоль. В начале 1920-х годов Рональд, Муриэль и Уильям Роуч находились в Англии на опытной сельскохозяйственной станции. Муриэль утверждала, что может определить, в какой последовательности наливали в ее чашку чай и молоко. На тот момент проверить правильность ее высказывания не представлялось возможным.
Это дало толчок идее Фишера о «нуль гипотезе». Целью стала не попытка доказать, что Муриэль может определить разницу между по-разному приготовленными чашками чая. Решено было опровергнуть гипотезу, что выбор женщина делает наугад. Было определено, что нуль-гипотезу нельзя ни доказать, ни обосновать. Зато ее можно опровергнуть во время экспериментов.
Было приготовлено 8 чашек. В первые четыре налито молоко сначала, в другие четыре – чай. Чашки были помешаны. Бристоль предложили опробовать чай на вкус и разделить чашки по методу приготовления чая. В результате должно было получиться две группы. История говорит, что эксперимент прошел удачно.
История говорит, что эксперимент прошел удачно.
Благодаря тесту Фишера вероятность того, что Бристоль действует интуитивно, была уменьшена до 0.01428. То есть, верно определить чашку можно было в одном случае из 70. Но все же нет возможности свести к нулю шансы того, что мадам определяет случайно. Даже если увеличивать число чашек.
Эта история дала толчок развитию «нуль гипотезы». Тогда же был предложен точный критерий Фишера, суть которого в переборе всех возможных комбинаций зависимой и независимой переменных.
2. Для чего используется точный критерий Фишера?
Точный критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен (что нашло отражение даже в его названии), что позволяет его использовать в исследованиях с небольшим числом наблюдений.
Особое место отводится точному критерию Фишера в медицине. Это важный метод обработки медицинских данных, нашедший свое применение во многих научных исследованиях. Благодаря ему можно исследовать взаимосвязь определенных фактора и исхода, сравнивать частоту патологических состояний между разными группами пациентов и т.д.
3. В каких случаях можно использовать точный критерий Фишера?
- Сравниваемые переменные должны быть измерены в номинальной шкале и иметь только два значения, например, артериальное давление в норме или повышено, исход благоприятный или неблагоприятный, послеоперационные осложнения есть или нет.
- Критерий подходит для сравнения очень малых выборок: точный критерий Фишера может применяться для анализа четырехпольных таблиц в случае значений ожидаемого явления менее 10, что является ограничением для применения критерия хи-квадрат Пирсона.
- Точный критерий Фишера бывает односторонним и двусторонним.
 При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет.
При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет.
Двусторонний тест является предпочтительным, так как оценивает различия частот по двум направлениям. То есть оценивается верятность как большей, так и меньшей частоты явления в экспериментальной группе по сравнению с контрольной группой.
Аналогом точного критерия Фишера является Критерий хи-квадрат Пирсона, при этом точный критерий Фишера обладает более высокой мощностью, особенно при сравнении малых выборок, в связи с чем в этом случае обладает преимуществом.
4. Как рассчитать точный критерий Фишера?
Допустим, изучается зависимость частоты рождения детей с врожденными пороками развития (ВПР) от курения матери во время беременности.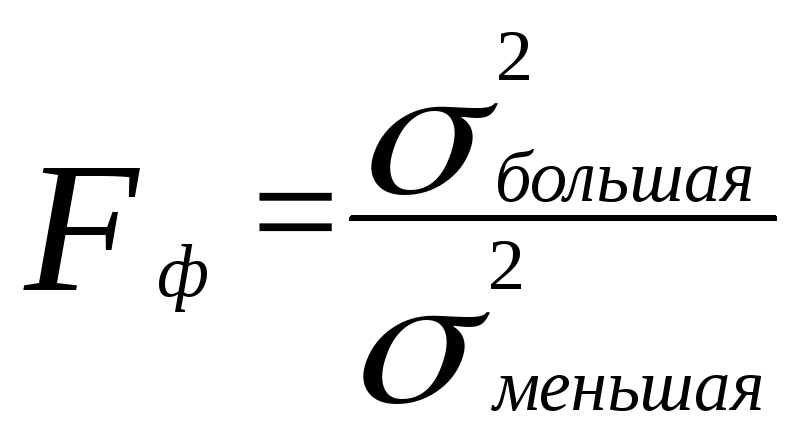 Для этого выбраны две группы беременных женщин, одна из которых — экспериментальная, состоящая из 80 женщин, куривших в первом триместре беременности, а вторая — группа сравнения, включающая 90 женщин, ведущих здоровый образ жизни на протяжении всей беременности. Число случаев ВПР плода в экспериментальной группе составило 10, в группе сравнения — 2.
Для этого выбраны две группы беременных женщин, одна из которых — экспериментальная, состоящая из 80 женщин, куривших в первом триместре беременности, а вторая — группа сравнения, включающая 90 женщин, ведущих здоровый образ жизни на протяжении всей беременности. Число случаев ВПР плода в экспериментальной группе составило 10, в группе сравнения — 2.
Вначале составляем четырехпольную таблицу сопряженности:
| Исход есть (Наличие ВПР) | Исхода нет (Отсутствие ВПР) | Всего | |
| Фактор риска есть (Курящие) | A = 10 | B = 70 | (A + B) = 80 |
| Фактор риска отсутствует (Некурящие) | C = 2 | D = 88 | (C + D) = 90 |
| Всего | (A + C) = 12 | (B + D) = 158 | (A + B + C + D) = 170 |
Точный критерий Фишера рассчитывается по следующей формуле:
где N — общее число исследуемых в двух группах; ! — факториал, представляющий собой произведение числа на последовательность чисел, каждое из которых меньше предыдущего на 1 (например, 4! = 4 · 3 · 2 · 1)
В результате вычислений находим, что P = 0,0137.
5. Как интерпретировать значение точного критерия Фишера?
Достоинством метода является соответствие полученного критерия точному значению уровня значимости p. То есть, полученное в нашем примере значение 0,0137 и есть уровень значимости различий сравниваемых групп по частоте развития ВПР плода. Необходимо лишь сопоставить данное число с критическим уровнем значимости, обычно принимаемым в медицинских исследованиях за 0,05.
- Если значение точного критерия Фишера больше критического, принимается нулевая гипотеза и делается вывод об отсутствии статистически значимых различий частоты исхода в зависимости от наличия фактора риска.
- Если значение точного критерия Фишера меньше критического, принимается альтернативная гипотеза и делается вывод о наличии статистически значимых различий частоты исхода в зависимости от воздействия фактора риска.
В нашем примере P < 0,05, в связи с чем делаем вывод о наличии прямой взаимосвязи курения и вероятности развития ВПР плода. 2}\]
2}\]
На практике в числитель приведенной формулы обычно помещают бóльшую дисперсию, а в знаменатель — меньшую.
F-критерий можно использовать для сравнения и более, чем двух совокупностей (как, например, в дисперсионном анализе). В таких случаях критерий рассчитывается как отношение межгрупповой дисперсии к внутригрупповой дисперсии. Кроме того, F-критерий широко используется при оценке значимости линейной регрессии (подробне см. здесь).
Очевидно, что чем ближе рассчитанное значение F к 1, тем больше у нас оснований сделать заключение о справедливости приведенной выше нулевой гипотезы. И наоборот — чем больше это значение, тем больше имеется оснований отклонить нулевую гипотезу о равенстве дисперсий. Критическое значение F, начиная с которого нулевую гипотезу отклоняют, определятся уровнем значимости (например, α = 0.05) и количеством степеней свободы для каждой из сравниваемых дисперсий. Кроме того, нулевую гипотезу можно проверить при помощи Р-значения для F-критерия, т. е. вероятности того, что случайная величина с соответствующим распределением Фишера окажется равной или превысит рассчитанное по выборочным данным значение F.
е. вероятности того, что случайная величина с соответствующим распределением Фишера окажется равной или превысит рассчитанное по выборочным данным значение F.
Для выполнения теста Фишера в R имеется функция var.test() (от variance — дисперсия, и test — тест). Используем рассмотренный ранее пример о суточном потреблении энергиии у ходощавых женщин (lean) и женщин с избыточным весом (obese):
library(ISwR) data(energy) attach(energy) energy expend stature 1 9.21 obese 2 7.53 lean 3 7.48 lean 4 8.08 lean 5 8.09 lean 6 10.15 lean 7 8.40 lean 8 10.88 lean 9 6.13 lean 10 7.90 lean 11 11.51 obese 12 12.79 obese 13 7.05 lean 14 11.85 obese 15 9.97 obese 16 7.48 lean 17 8.79 obese 18 9.69 obese 19 9.68 obese
Дисперсии в этих двух весовых группах женщин можно легко сравнить следующим образом:
var.test(expend ~ stature)
F test to compare two variances
data: expend by stature
F = 0. 7844, num df = 12, denom df = 8, p-value = 0.6797
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.1867876 2.7547991
sample estimates:
ratio of variances
0.784446
7844, num df = 12, denom df = 8, p-value = 0.6797
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.1867876 2.7547991
sample estimates:
ratio of variances
0.784446Как видим, полученное P-значение значительно превышает 5%-ный уровень значимости, на основании чего мы не можем отклонить нулевую гипотезу о равенстве дисперсий в исследованных совокупностях. Истинное отношение сравниваемых дисперсий с вероятностью 95% находится в интервале от 0.19 до 2.75 (см. 95 percent confidence interval). Исходя из данного результата, мы, например, вправе были бы использовать вариант t-критерия Стьюдента для совокупностей с одинаковыми дисперсиями при сравнении среднего потребления энергии у женщин из рассматриваемых весовых групп (подробнее см. здесь).
При выполнении F-теста и интерпретации получаемых с его помощью результатов важно помнить о следущих ограничениях (Zar 2010):
Функция FРАСПОБР — Служба поддержки Office
Возвращает значение, обратное (правостороннему) F-распределению вероятностей. Если p = FРАСП(x;…), то FРАСПОБР(p;…) = x.
Если p = FРАСП(x;…), то FРАСПОБР(p;…) = x.
F-распределение может использоваться в F-тесте, который сравнивает степени разброса двух множеств данных. Например, можно проанализировать распределение доходов в США и Канаде, чтобы определить, похожи ли эти две страны по степени плотности доходов.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Чтобы узнать больше о новых функциях, см. статьи Функция F.ОБР и Функция F.ОБР.ПХ.
статьи Функция F.ОБР и Функция F.ОБР.ПХ.
Синтаксис
FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)
Аргументы функции FРАСПОБР описаны ниже.
-
Вероятность — обязательный аргумент. Вероятность, связанная с интегральным F-распределением.
-
Степени_свободы1 — обязательный аргумент. Числитель степеней свободы.
-
Степени_свободы2 — обязательный аргумент.
 10, то #NUM! значение ошибки #ЗНАЧ!.
10, то #NUM! значение ошибки #ЗНАЧ!.
Функцию FРАСПОБР можно использовать для определения критических значений F-распределения. Например, результаты дисперсионного анализа обычно включают данные для F-статистики, F-вероятности и критическое значение F-распределения с уровнем значимости 0,05. Чтобы определить критическое значение F, нужно использовать уровень значимости как аргумент «вероятность» функции FРАСПОБР.
По заданному значению вероятности функция FРАСПОБР ищет значение x, для которого FРАСП(x;степени_свободы1;степени_свободы2) = вероятность. Таким образом, точность функции FРАСПОБР зависит от точности FРАСП. Для поиска функция FРАСПОБР использует метод итераций. Если поиск не закончился после 100 итераций, возвращается значение ошибки #Н/Д.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Данные | Описание | |
|---|---|---|
|
0,01 |
Вероятность, связанная с интегральным F-распределением |
|
|
6 |
Числитель степеней свободы |
|
|
4 |
Знаменатель степеней свободы |
|
|
Формула |
Описание |
Результат |
|
=FРАСПОБР(A2;A3;A4) |
Значение, обратное F-распределению вероятностей для приведенных выше данных |
15,206865 |
Изучение свойств ранговых аналогов F-критерия Фишера при отклонениях от гауссовской модели дисперсионного анализа Текст научной статьи по специальности «Математика»
ВЕСТНИК ТОМСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
2008 Управление, вычислительная техника и информатика № 1(2)
УДК 519. 24
24
В.П. Шуленин, В.В. Табольжин
ИЗУЧЕНИЕ СВОЙСТВ РАНГОВЫХ АНАЛОГОВ Р-КРИТЕРИЯ ФИШЕРА ПРИ ОТКЛОНЕНИЯХ ОТ ГАУССОВСКОЙ МОДЕЛИ ДИСПЕРСИОННОГО АНАЛИЗА
Проводится сравнение характеристик F-критерия Фишера, Н-критерия Краскела — Уоллиса и L-критерия Пейджа в рамках различных супермоделей, описывающих отклонения от классической гауссовской модели дисперсионного анализа. Сравнение проводится как при конечных объемах выборки методом статистического моделирования, так и в асимптотике путем вычисления относительной эффективности Питмена.
Ключевые слова: ранговые критерии, дисперсионный анализ, непараметрические модели.
Пусть объекты изучаемой совокупности (или популяции) Ж характеризуются некоторым результирующим показателем X. В соответствии с факторным признаком А, который может принимать к значений Аь. к из совокупностей Жь…,Жк с непрерыв-
к из совокупностей Жь…,Жк с непрерыв-
ными распределениями изучаемого показателя X. Исходные данные кратко записываются в виде [Ху],у = 1,__,к, г = 1,…,Иу , они получены в результате пу на-
блюдений за результирующим показателем X при каждом фиксированном у-м уровне Ау, у = 1,…,к, фактора А. Рассмотрим различные модели наблюдений.
1. Гауссовская модель
Предполагается, что исходные данные [Ху], г = 1,-■■,«/, У = 1,—,к, представляют собой выборку, полученную в результате п независимых наблюдений над показателем X из к нормальных совокупностей Ж,…,Жк со средними значениями
2 2 2 2
ццк и с равными, но неизвестными дисперсиями С) = а2 = ••• = ак = а . Эту модель наблюдений называют нормальной (или гауссовской) моделью 1 однофакторного дисперсионного анализа с фиксированными эффектами. Для удобства дальнейших ссылок выделим в явном виде и пронумеруем все предположения этой модели наблюдений:
Для удобства дальнейших ссылок выделим в явном виде и пронумеруем все предположения этой модели наблюдений:
X/ = Н/ + £/•, г = 1,-,П] , у = 1,…,к , п = (щ + ••• + пк), (1)
где
а) ц7- = М(X | А = Aj), у = 1,…, к , постоянные величины,
б) Егу — независимые случайные величины,
в) Еу — нормальные случайные величины, т.е. Ь(&у) = N(0; а2),
г) дисперсии совокупностей Жь…,Жк равны неизвестному параметру о2, то
2 2 2 2 есть С) = а2 = • • • = ак = а .
В рамках этой модели требуется убедиться в том, что изменение фактора А не влияет на итоговый показатель X. при гипотезе Я0 имеет F-распределение Фишера с числами степеней свободы (к -1) и (п — к), то есть справедливо выражение
при гипотезе Я0 имеет F-распределение Фишера с числами степеней свободы (к -1) и (п — к), то есть справедливо выражение
1{Р = Б2В / БІ | Н0} = Г(к -1, п — к). (3)
Критическая область размера а находится справа от квантиля Г-а (к -1, п — к) уровня (1 -а) для F-рaспределения с числами степеней свободы (к — 1) и (п — к).
2. Непараметрическая модель с произвольными альтернативами
На практике предположения нормальности наблюдений не всегда могут быть обоснованы. В таких случаях рассматривают более общие модели наблюдений и предполагают, что {Ху}, і = 1,—,Пу , 7 = 1,—,к, являются независимыми случайными величинами, которые одинаково распределены лишь при фиксированном у-м уровне Ау , у = 1,…,к, фактора А, то есть ХуXу является выборкой из
условной функции распределения Гу (х) = Р{Хгу < х | А = Ау}, у = 1,. .., к, V/ е (1,…,Пу). Отметим, что Гу (х) является произвольным непрерывным распределением, функциональный характер которого не конкретизируется и изучение влияния фактора А на итоговый показатель X в условиях этой непараметрической модели сводится к проверке гипотез
.., к, V/ е (1,…,Пу). Отметим, что Гу (х) является произвольным непрерывным распределением, функциональный характер которого не конкретизируется и изучение влияния фактора А на итоговый показатель X в условиях этой непараметрической модели сводится к проверке гипотез
Нд : Г= Г2 =… = Гк , И* : не все Гу равны, у = 1,…, к . (4)
Эти гипотезы проверяются с помощью Н-критерия Краскела — Уоллиса (см., например, [2, 3]), статистика которого вычисляется не по исходным наблюдениям {Ху}, а по их рангам {Лу} , і = 1,…,Пу, у = 1,…,к, по формуле
12 к _
н =-—т Е «у{Я.у -(« +1)/2}2 , (5)
п(п +1) у=1 7 7
где Я,у — средний ранг наблюденийу-й группы, у = 1,…,к . При больших объемах выборки Н-критерий определяется асимптотической критической областью раз-
мера а в виде неравенства Н > %1_а (к -1), где х2-а (к -1) обозначает квантиль уровня (1 — а) для хи-квадрат распределения с числом степеней свободы к — 1.
3. Непараметрическая модель с упорядоченными альтернативами сдвига
Часто на практике уровни Аь…,Ак фактора А отражают эффективность воздействия на показатель X в определенном направлении, например по мере увеличения интенсивности воздействия. В таких случаях рассматривают упорядоченные альтернативы. Предполагается, что XуХп,у — н.о.р. случайные величины
с произвольной непрерывной функцией распределения ¥(х-0у), у = 1,…,к, V/ ё (1,…, пу). Для изучения влияния фактора А на итоговый показатель X в условиях этой непараметрической модели проверяются гипотезы
Я0“ : 0! =02 =… = 0* , К : 01 — 02 *… — 0*, (6)
где хотя бы одно из неравенств строгое. Эти гипотезы также непараметрические, так как ¥(х -0у) — произвольная непрерывная функция распределения, и они
проверяются с помощью Ь-критерия Пейджа (см. , например, [2, 3]), статистика которого вычисляется также не по исходным наблюдениям {Ху}, а по их рангам
, например, [2, 3]), статистика которого вычисляется также не по исходным наблюдениям {Ху}, а по их рангам
{Щ}, * = 1, п] , У = 1,…, к, по формуле
1 к -Ь =— X {У — (к +1) / 2}{ Я.у — (пк +1)/2}. (7)
пк у=1
При больших объемах выборки Ь-критерий Пейджа определяется асимптотической критической областью размера а в виде неравенства
Ь > Х-а {(к2 — 1)(пк +1)/144п}172,
где А,1-а = Ф-1 (1 — а) и Ф-1 обозначает квантильную функцию стандартного нормального распределения Ф(х).
4. Рассматриваемые типы супермоделей
Понятие «супермодель» (см., например, [4]) используют при изучении свойств робастности статистических процедур. (х) = (1 -є)Ф(х) + єФ(х/т)}, 0 <є< 1/2 , т> 1. (9)
(х) = (1 -є)Ф(х) + єФ(х/т)}, 0 <є< 1/2 , т> 1. (9)
Отметим, что при є = 0, или при т = 1, имеем нормальное распределение Ф(х), х є Я1.
5. Сравнение критериев при конечных объемах выборки
В рамках описанных типов супермоделей приведем результаты сравнения характеристик F-критерия Фишера, Н-критерия Краскела — Уоллиса и Ь-критерия Пейджа. В качестве сравниваемых характеристик критериев используются их вероятности ошибок первого и второго рода. Изучение робастности F-критерия Фишера по уровню значимости при конечных объемах выборки проводится методом статистического моделирования, при этом исходные наблюдения {X/} вычисляются по формуле
Ху =\ + [и/3 — (1 — и )»3 ]/Х2, і = 1,…, П] , у = 1,…, к , (10)
где и у случайные величины с равномерным распределением в интервале [0,1]. = 0,0148 у2 = 5 Х2 = -0,0870 Х3 = -0,0443 Ъ = 9 Х2 = -0,3203 Х3 = -0,1359 у2=1,75 Х2 = 0,5943 Хз = 1,4501
= 0,0148 у2 = 5 Х2 = -0,0870 Х3 = -0,0443 Ъ = 9 Х2 = -0,3203 Х3 = -0,1359 у2=1,75 Х2 = 0,5943 Хз = 1,4501
А 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60
Р 0,051 0,093 0,283 0,601 0,872 0,051 0,107 0,300 0,622 0,870 0,046 0,102 0,300 0,622 0,871 0,045 0,103 0,323 0,642 0,862 0,051 0,093 0,273 0,585 0,879
п = 5 Н 0,038 0,069 0,221 0,517 0,813 0,038 0,081 0,257 0,564 0,828 0,036 0,083 0,269 0,587 0,847 0,036 0,091 0,317 0,651 0,864 0,033 0,068 0,194 0,459 0,771
Ь 0,053 0,265 0,644 0,912 0,991 0,051 0,288 0,680 0,930 0,993 0,053 0,302 0,708 0,935 0,992 0,051 0,328 0,757 0,955 0,995 0,052 0,256 0,610 0,889 0,989
Р 0,051 0,169 0,614 0,949 0,998 0,049 0,179 0,613 0,943 0,998 0,051 0,177 0,621 0,943 0,996 0,048 0,184 0,639 0,941 0,992 0,053 0,165 0,603 0,950 0,999
п= 10 н 0,045 0,152 0,569 0,930 0,997 0,041 0,170 0,608 0,942 0,999 0,045 0,179 0,649 0,955 0,998 0,046 0,209 0,720 0,973 0,999 0,044 0,144 0,517 0,897 0,996
ь 0,053 0,424 0,895 0,996 1,000 0,052 0,457 0,922 0,998 1,000 0,051 0,479 0,935 0,999 1,000 0,050 0,544 0,954 0,999 1,000 0,053 0,410 0,871 0,995 1,000
р 0,046 0,350 0,928 1,000 1,000 0,055 0,357 0,929 1,000 1,000 0,047 0,350 0,925 1,000 1,000 0,050 0,356 0,926 0,998 1,000 0,049 0,333 0,935 1,000 1,000
и = 20 н 0,045 0,324 0,914 0,999 1,000 0,051 0,366 0,941 1,000 1,000 0,044 0,386 0,954 1,000 1,000 0,048 0,443 0,977 1,000 1,000 0,045 0,306 0,892 0,999 1,000
ь 0,053 0,658 0,993 1,000 1,000 0,054 0,701 0,996 1,000 1,000 0,047 0,734 0,998 1,000 1,000 0,050 0,788 0,999 1,000 1,000 0,049 0,650 0,990 1,000 1,000
Таблица 2. Оценки уровня значимости и мощности Р-, Н- и Ь-критериев в условиях модели Тьюки — — семейство распределений Стьюдента
Оценки уровня значимости и мощности Р-, Н- и Ь-критериев в условиях модели Тьюки — — семейство распределений Стьюдента
Объем выбор- ки Парам. г = 1 Х2 = -3,0674 Х3 = -1,000 г = 5 Х2 = -0,2480 Х3 = -0,1358 г = 9 Х2 = -0,0003 Х3 = -0,0002 г = 25 Х2= 0,1342 Х3 = 0,0892 г = да Х2 = 0,1975 Х3 = 0,1350
А 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60
Р 0,016 0,017 0,027 0,051 0,078 0,042 0,075 0,200 0,436 0,675 0,050 0,089 0,215 0,453 0,714 0,049 0,097 0,271 0,563 0,838 0,051 0,102 0,296 0,609 0,868
п = 5 Н 0,034 0,050 0,102 0,188 0,285 0,036 0,066 0,191 0,418 0,478 0,039 0,072 0,184 0,404 0,669 0,035 0,071 0,216 0,487 0,782 0,036 0,076 0,233 0,521 0,808
Ь 0,056 0,162 0,347 0,523 0,679 0,056 0,247 0,583 0,840 0,962 0,053 0,230 0,550 0,836 0,961 0,054 0,262 0,633 0,898 0,987 0,053 0,269 0,651 0,910 0,992
Р 0,015 0,024 0,032 0,048 0,082 0,044 0,126 0,412 0,767 0,845 0,049 0,130 0,450 0,818 0,975 0,054 0,168 0,564 0,922 0,996 0,053 0,175 0,615 0,946 0,999
п= 10 н 0,046 0,090 0,225 0,417 0,620 0,041 0,137 0,479 0,842 0,978 0,045 0,124 0,447 0,829 0,975 0,047 0,154 0,533 0,906 0,994 0,047 0,157 0,567 0,929 0,998
ь 0,051 0,242 0,539 0,787 0,914 0,052 0,377 0,842 0,984 1,000 0,052 0,366 0,807 0,980 1,000 0,054 0,417 0,886 0,993 1,000 0,052 0,427 0,898 0,996 1,000
р 0,015 0,018 0,032 0,052 0,087 0,049 0,219 0,736 0,976 0,999 0,050 0,242 0,792 0,990 1,000 0,055 0,316 0,905 0,999 1,000 0,052 0,342 0,935 1,000 1,000
и = 20 н 0,046 0,137 0,476 0,784 0,937 0,046 0,272 0,847 0,997 1,000 0,047 0,255 0,815 0,993 1,000 0,051 0,302 0,895 0,999 1,000 0,047 0,318 0,916 1,000 1,000
ь 0,049 0,368 0,790 0,962 0,995 0,05 0,604 0,982 1,000 1,000 0,051 0,569 0,976 1,000 1,000 0,052 0,645 0,991 1,000 1,000 0,048 0,659 0,993 1,000 1,000
Изучение свойств ранговых аналогов Р-нритерия Фишера
Таблица 3
Оценки уровня значимости и мощности Е- и И-критериев для ¥ е Зе т (Ф) , число групп к = 5 , число опытов М = 10000
Объем выборки А 8 = 0 , Т = 1 3 = Т 0, = 8
0,00 0,15 0,30 0,45 0,60 0,00 0,15 0,30 0,45 0,60
п = 20 Б 0,046 0,220 0,803 0,995 1,000 0,048 0,135 0,495 0,892 0,992
Н 0,045 0,203 0,775 0,993 1,000 0,047 0,169 0,639 0,971 1,000
Анализируя данные этих таблиц, можно сделать следующие выводы.
1. Эмпирический уровень значимости F-критерия обладает стабильностью при
отклонениях от гауссовской модели по эксцессу в рамках супермодели (у 2)
(см. табл.1). Однако F-критерий не обладает свойством робастности по уровню значимости в рамках супермодели (г). В частности, для распределений с «тяжелыми хвостами» (см. табл.2 при г = 1), вместо заданного уровня а = 0,005, эмпирический уровень значимости равен « 0,016 . При увеличении числа степеней свободы г «затянутость хвостов» распределений начинает приближаться к гауссовской и эмпирические уровни начинают проявлять стабильность в окрестности заданного уровня.
2. Асимптотическая аппроксимация точного распределения ранговой статистики Н-критерия Краскела — Уоллиса при нулевой гипотезе с помощью выражения Ь(Н | Н0) = %2 (к -1), является неудовлетворительной при малых объемах выборки. ж. Вместо заданного уровня значимости а=0,005, эмпирический уровень значимости равен « 0,03 . При увеличении объемов выборки качество аппроксимации улучшается, и при п > 10 она уже является удовлетворительной для целей практики. Этот вывод сохраняется и для супермодели, описывающей отклонения от гауссовской модели по эксцессу, то есть для ¥ е (у2).
ж. Вместо заданного уровня значимости а=0,005, эмпирический уровень значимости равен « 0,03 . При увеличении объемов выборки качество аппроксимации улучшается, и при п > 10 она уже является удовлетворительной для целей практики. Этот вывод сохраняется и для супермодели, описывающей отклонения от гауссовской модели по эксцессу, то есть для ¥ е (у2).
3. Для рассмотренных в эксперименте альтернатив и для гауссовской модели
наблюдений вида (1), F-критерий имеет незначительное преимущество в мощности перед Н-критерием. Однако при отклонениях от гауссовской модели, то есть в рамках супермоделей (Х2), (г) и 3ЁТ (Ф), ситуация меняется. Н-критерий
имеет преимущество в мощности по сравнению с F-критерием, причем оно проявляется в большей степени при «утяжелении хвостов распределений» и при увеличении объемов выборки. Для рассмотренных в эксперименте упорядоченных альтернатив, Ь-критерий Пейджа, как и ожидалось, имеет существенно большую мощность по сравнению с F и Н-критериями. Причем качество нормальной аппроксимации распределения ранговой статистики Ь при нулевой гипотезе вполне удовлетворительное и для малых объемов выборки, начиная с п = 5.
Причем качество нормальной аппроксимации распределения ранговой статистики Ь при нулевой гипотезе вполне удовлетворительное и для малых объемов выборки, начиная с п = 5.
4. Проведенные эксперименты при числе групп к = 10, качественно не меняют эти выводы.
Отметим, что рассмотренные в предыдущих экспериментах супермодели
(X 2), (г) и 3Ё,Т (Ф), были использованы, в частности, для изучения робаст-
ности по распределению уровня значимости F-критерия. Эти супермодели описывают различные варианты отклонения от предположения нормальности (1в) гаус-
совской модели (1). Изучим теперь робастность уровня значимости F-критерия при отклонениях от предположения (1г) о равенстве дисперсий в группах ЖЬ…,ЖЬ оставив все остальные предположения гауссовской модели (1) верными. }, j = 1,■■■,k, равны. Приведенные данные для Н-критерия превышают заданный уровень значимости а = 0,05, что является проявлением свойства «несмещенности» Н-критерия, так как эти данные характеризуют его мощность при рассмотренных альтернативах.
}, j = 1,■■■,k, равны. Приведенные данные для Н-критерия превышают заданный уровень значимости а = 0,05, что является проявлением свойства «несмещенности» Н-критерия, так как эти данные характеризуют его мощность при рассмотренных альтернативах.
6. Асимптотическое сравнение критериев
В литературе разработаны различные подходы к асимптотическому сравнению критериев. Наиболее часто используют асимптотическую относительную эффективность Питмена (см. [2, 5]), которая вычисляется не для фиксированной альтернативы, а для последовательности контигуальных альтернатив, сходящихся к нулевой гипотезе при неограниченном увеличении объема выборки. Для многих непараметрических критериев получены общие выражения для эффективности Питмена по отношению к их «конкурентам» из нормальной теории. В частности, в [2] показано, что эффективность Питмена для Н-критерия Краскела — Уоллиса относительно F-критерия Фишера вычисляется по формуле
АКЕр (Н: Г) = 12а
= 12а у
| / (г -1 («)^«)
1_0
(12)
где а2 = П(X) и /(х) — плотность функции распределения Г(х) наблюдений
над показателем X. 2 2[1 /(2Х3 +1) — Б( Х3 +1, Х3 +1)]2
2 2[1 /(2Х3 +1) — Б( Х3 +1, Х3 +1)]2
+ ЪБ(2Хъ +1,2X3 +1) (14)
2[1 /(2Х3 +1) — Б(Х3 +1, Х3 +1)]2 ’
где В(х, у) обозначает бета-функцию. Кроме того, выражение для дисперсии имеет вид
о} = 2[1/(2Х3 +1) — Б(Х3 +1,Х3 +1)]/X2 . (15)
С учетом формул (13) и (15), выражение (12) для Г еЗ1 запишется в виде АЯЕр (Н : Г) = 24 [1 /(2Х3 +1) — Б(Х3 +1, Х3 +1)] х
х(|[Х3{ы%3-1 + (1 -м)Хзйы )2 . (16)
о
Численные расчеты показывают, что для Г е (X2) асимптотическая относительная эффективность Питмена Н-критерия относительно F-критерия при значениях эксцесса у2: 3, 4, 5, 9, 1,75 соответственно равна 0,954, 1,067, 1,167, 1,379, 1,066, а для семейства распределений Стьюдента Г е (г) при числе степеней свободы г: 5, 7, 25 и г она соответственно равна 1,382, 1,162, 0,993, 0,954. 2 6(1 -б)/л/ т2 +1 +б2 / т}2 . (17)
2 6(1 -б)/л/ т2 +1 +б2 / т}2 . (17)
Численные значения асимптотической относительной эффективности Питмена Н-критерия относительно F-критерия для гауссовской модели с масштабным засорением приведены в табл. 5.
Таблица 5
Эффективность Питмена ЛЯЕР (Н : Р) для Г еЗЁ1 (Ф)
т 8
0,00 0,01 0,03 0,05 0,08 0,10 0,15 0,20
3 0,955 1,009 1,108 1,196 1,309 1,373 1,497 1,575
5 0,955 1,150 1,505 1,814 2,201 2,412 2,795 3,006
7 0,955 1,369 2,115 2,759 3,553 3,977 4,724 5,099
Из приведенной таблицы следует, что Н-критерий Краскела — Уоллиса, проигрывая лишь 5% в эффективности оптимальному при гауссовском распределении F-критерию Фишера, обладает существенными преимуществами даже при небольших, трудно обнаруживаемых, отклонениях от гауссовской модели. Или, другими словами, можно сказать, что F-критерий Фишера теряет оптимальность очень быстро при переходе от нормальной модели к модели из ее окрестности, содержащей распределения с «более тяжелыми хвостами».
Или, другими словами, можно сказать, что F-критерий Фишера теряет оптимальность очень быстро при переходе от нормальной модели к модели из ее окрестности, содержащей распределения с «более тяжелыми хвостами».
Таким образом, подводя итог, можно сказать, что при возможных отклонениях от предположений гауссовской модели наблюдений вида (1) в условиях реального эксперимента, предпочтение в выборе критерия следует отдать ранговому критерию Краскела — Уоллиса (или критерию Пейджа при упорядоченных альтернативах), а не классическому F-критерию Фишера.
ЛИТЕРАТУРА
1. Афифи А., Эйзен С. Статистический анализ: Подход с использованием ЭВМ: Пер. с англ. М.: Мир, 1982.
2. Хеттсманспергер Т. Статистические выводы, основанные на рангах. М.: Финансы и статистика, 1987.
3. Холлендер М., Вулф Д. Непараметрические методы статистики. М.: Финансы и статистика, 1983.
Холлендер М., Вулф Д. Непараметрические методы статистики. М.: Финансы и статистика, 1983.
4. Шуленин В.П. Введение в робастную статистику. Томск: Изд-во Том. ун-та, 1993.
5. Кендэлл М., Стьюарт А. Статистические выводы и связи. М.: Наука, 1973.
6. Randles R.H., Wolf P.H. Introduction to the Theory of Nonparametric Statistics. N.Y.: Wiley, 1979.
7. Ramberg J.S. An approximation method for generation symmetric random variables // Com-mun. ACM. 1972. V. 15. P. 987 — 990.
Статья представлена кафедрой теоретической кибернетики факультета прикладной математики и кибернетики Томского государственного университета, поступила в научную редакцию 17 сентября 2007 г.
Фишера критерий критерий — Справочник химика 21
Для решения этого вопроса привлекают / -критерий (критерий Фишера).
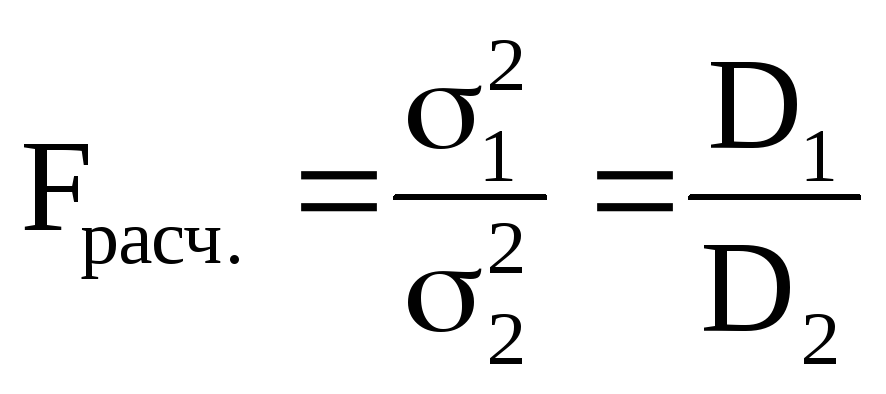 Вычисляют отношение двух дисперсий [c.66]
Вычисляют отношение двух дисперсий [c.66]Точность получаемых оценок устанавливают с помощью статистич. критериев Стьюдента (/-критерий), Фишера (Р-критерий) и т. д. При этом количеств, мерами служат т. наз. доверит, вероятность Р и уровень значимости статистич. критерия р = 1 — р. При заданных требованиях на точность результатов измерений доверит, вероятность (уровень значимости) определяет надежность полученной оценки. [c.323]
Предварительным условием применения t — критерия является проверка на нормальность каждой из выборок хц , хл и проверка равенства дисперсии (т , нормальность распределения проверялась по показателям асимметрии и эксцесса, равенство дисперсии — по критерию Фишера (F — критерий) [2] [c.190]
Необходимо установить, обусловлено ли это несовпадение случайной погрешностью или разница результатов статистически значима. С этой целью сначала выясняется, нет ли значимой разницы между дисперсиями обеих серий. Сравнение ведется при помощи F-распределения (F-критерия, критерия Фишера). [c.70]
Сравнение ведется при помощи F-распределения (F-критерия, критерия Фишера). [c.70]
Надежность и объективность полученных результатов анализа — одни из основных условий, позволяющие делать выводы при решении производственных и научных проблем. Определения того или иного компонента в пробах при этом могут быть выполнены в разное время, на различных приборах, разными аналитиками, в различных лабораториях, наконец, различными методами анализа, в том числе и вновь разработанными, и т. д. Поэтому тождественность полученных значений X при различных условиях должна быть строго оценена. Статистическая оценка результатов анализа является относительной и заключается в сравнении в первую очередь стандартных погрешностей двух выборок, одна из которых является как бы эталонной, и затем — в сравнении средних арифметических значений. Однородность выборок, т. е. их принадлежность к одной генеральной совокупности, проверяют с помощью f-критерия (критерий Фишера). Если выборки однородны, то сравнивают их средние арифметические при помощи i-критерия. Вывод об однородности или неоднородности двух сравниваемых при помощи f-критерия выборок, или ответ иа вопрос, одинакова или неодинакова их стандартная погрешность, имеют большое практическое значение и позволяют решить задачи, требующие оценки точности сравниваемых вариантов. В качестве примеров приведем следующие. [c.97]
Вывод об однородности или неоднородности двух сравниваемых при помощи f-критерия выборок, или ответ иа вопрос, одинакова или неодинакова их стандартная погрешность, имеют большое практическое значение и позволяют решить задачи, требующие оценки точности сравниваемых вариантов. В качестве примеров приведем следующие. [c.97]
Сравнение дисперсий двух выборок при помощи / -критерия (критерия Фишера) проводят следующим образом. Получают расчетное значение критерия Рр по формуле [c.98]
Поскольку дисперсия ау. известна лишь в редких случаях, необходимо определить ее несмещенную оценку — выборочную дисперсию — на основании повторных измерений, использовав адекватную модель. Прежде чем как-либо анализировать модель, следует проверить, подходит ли она, с помощью соответствующего критерия, например критерия Фишера. Р-критерий сопоставляет сумму квадратов отклонений величин, рассчитанных по модели, от полученных экспериментально, деленную на число степеней свободы, с суммой квадратов отклонений экспериментальных величин от их средних значений, деленной на экспериментальное число степеней свободы (см. [39]). [c.148]
[39]). [c.148]
Табличные значения критерия Фишера зависят от числа степеней свободы при постановке опытов с варьируемыми параметрами п — р) и от числа параллельных опытов на воспроизводимость (т — 1), а также от так называемого уровня значимости. Под ним понимают вероятность несоответствия данной модели истинному виду, причем в химико-технологических исследованиях считается достаточным уровень значимости 0,05, а в некоторых других случаях даже 0,01 (5%- и 1 % чый уровни значимости). Табличные значения критерия Фишера для уровня значимости 0,05 приве-ленч в табл. 13. [c.261]
Проверка однородности дисперсий производилась по критерию Фишера (Р-критерию), представляющему собой отношение большей дисперсии к меньшей с последующим сравнением с табличным значением [1, с.204]. [c.11]
Проверка адекватности проводится по критерию Фишера [c.146]
Хорошее перемешивание реагирующих фаз при высоте рабочей зоны колонны около 15 м делает малоэффективной установку в колонне устройств, предназначенных для дополнительного перераспределения внутренней циркуляции потоков газа и жидкости. Были проведены сопоставительные испытания двух промышленных колонн диаметром 2,2 м и высотой рабочей зоны 14—15 м одна из колонн была пустотелая, другая — снабжена рассекателями, представляющими собой смонтированные под углом 45° к горизонтальной плоскости и расходящиеся из центра стальные пластины. Сравнение сделано для битумов с температурой размягчения по КиШ, равной 53 4 °С, при температуре окисления 280 5°С и расходе воздуха 3400 100 м /ч. В результате установлено отсутствие значимой разницы между средними квадратичными ошибками и средними значениями измерений содержания кислорода в испытуемых колоннах (оценка по критериям Фишера и Стьюдента). Следовательно, эффективность обеих колонн одинакова [82]. [c.59]
Были проведены сопоставительные испытания двух промышленных колонн диаметром 2,2 м и высотой рабочей зоны 14—15 м одна из колонн была пустотелая, другая — снабжена рассекателями, представляющими собой смонтированные под углом 45° к горизонтальной плоскости и расходящиеся из центра стальные пластины. Сравнение сделано для битумов с температурой размягчения по КиШ, равной 53 4 °С, при температуре окисления 280 5°С и расходе воздуха 3400 100 м /ч. В результате установлено отсутствие значимой разницы между средними квадратичными ошибками и средними значениями измерений содержания кислорода в испытуемых колоннах (оценка по критериям Фишера и Стьюдента). Следовательно, эффективность обеих колонн одинакова [82]. [c.59]
При проведении эксперимента, когда меняется несколько факторов, прежде всего возникает вопрос об оценке их влияния на функцию отклика. Изучение влияния различных факторов на статистические характеристики объекта является задачей дисперсионного анализа, который позволяет специальной обработкой результатов наблюдений разложить их общую вариацию на систематическую и случайную, оценить достоверность систематической вариации по отношению к случайной, вызванной неучтенными факторами. За количественную меру вариации принимают дисперсию, полученную статистической обработкой экспериментальных данных. Сравнение дисперсий выполняют обычно по критерию Фишера. [c.16]
Адекватность уравнения, т. е. возможность описания процесса линейной моделью, проверяют ио критерию Фишера Е, величина которого должна быть меньше табличной. Критерий рассчитывают [c.19]
Проверка по критерию Фишера показывает, что при полученных коэффициентах уравнения регрессии являются адекватными. Статистически незначимые коэффициенты заменяют в уравнениях регрессии нулями. Так, /1 не зависит от произведений х х , х х , х Хз, а также от х и х . [c.49]
Найденную величину Р сравнивают с критическим значением критерия (Фишера) для выбранного уровня значимости (табл. П-2). При Рк > Р уравнение регрессии можно считать адекватным. В противном случае следует проверить уравнение с большим числом коэффициентов. [c.45]
Проверка гипотезы об адекватности Гфоводится с использованием Р-критерия Фишера. Критерий Фишера позволяет проверить нуль-гипотезу о равенстве двух генеральных дисперсий Одд и а (у). Если выборочные дисперсии у), то / -критерий формируется как отношение [c.482]
Одно из наиболее частых применений распределения и, соответственно, критерия Фишера — проверка качества аппроксимации экспериментальных данных математическими формулами. Если проведены аппроксимации двумя различными формулами, например полиномами двух различных степеней, то предпочтительна, как более точная, аппроксимация, дающая значимо меньшую дисперсию, что и проверяется по критерию Фишера. Если различие незначимо, предпочтение не может быть отдано той или другой формуле. В частности, степень аппроксимирующего полинома целесообразно повышать только до тех пор, пока дисперсия значимо убывает. Следует иметь в виду, что наилучший аппроксимирующий полином может не содержать некоторых сте -пеней, поэтому необходимо продолжить анализ еще на несколько шагов после достижения ситуации, когда повышение степени полинома не приводит к зна -чимому уменьшению дисперсии. Необходимо помнить, что по мере повышения степени полинома, чисто степеней свободы убывает для вычисления коэффициента полинома нулевой степени, т.е. среднего значения, использовано одно уравнение, и число степеней свободы уменьшилось на единицу. После вычисления коэффициентов полинома первой степени число степеней свободы уменьшается на два и т.д. [c.235]
Критерий значимости — случайная величина, распределение которой представляет собой специально подобранную функцию, зависящую только от числа опытов (числа степеней свободы) применяется для установления значимости некоторых статистик. Обычно критерий значимости называют именем автора, предложившего соответствующий вид распределения, и обозначают буквой этого распределения, например, критерий Стьюдента ( pa пpeдeлeниe), критерий Фишера ( -распределение), критерий Кохрена (О-распределение). [c.263]
Оценка адекватности однооткликовых моделей с помощью критерия Фишера. В случае однооткликовых моделей адекватность может быть проверена с помощью критерия Фишера ( -критерия). Для этого находят отношение [c.45]
В табл. 2П20-4П20 Приложения П20 приведены значения квантилей критических статистик т-критерия, критериев Стьюдента и Фишера, которые широко применяются при анализе контрольных карт процессов (20.2.4). [c.705]
Оценку гипотезы линейности формулы (2) проводят ирн поиощи критержя Фишера (Г-критерия) по формуле [c.274]
Парафины иного происхождения (например, из углей или получаемые в различных процессах по реакции Фишера — Тропша) могут содержать 15—20% углеводородов изостроения, а неочищенные парафинистые фракции (гач, петролатум) с пониженной точкой плавления — также циклические углеводороды. Состав жидких фракций (керосин, газойль) зависит от природы исходной нефти и процессов ее переработки. Содержание масла в твердых парафинах — важный критерий выбора сырья для окисления. [c.148]
Для того чтобы отвергнуть 0-гипотезу, нужно доказать значимость различий между а и при выбранном уровне значимости р. Это удобно сделать при помощи критерия Фишера. Р-распределением Фишера называется распределение случайной величины Р = (в /ог)- Сравнивать дисперсии необходимо именно по критерию Фишера, а не по критерию, например, Стьюдента, поскольку, как легко видеть, распределение 5 не есть распределение Гаусса, хотя и очень медленно приближается к нему при Уа ->оо. Распределение положительно асимметрично, т. е. значения 5 большие значения допустимы. Если5 2> ( 11 р ), то с вероятностью ро дисперсия 5 больше дисперсии [c.142]
Если модель линейна относительно подбираемых коэффициентов и рассчитывается только одна величина х, эффективность модё Ли можно строго оценить по критерию Фишера Когда найденная указанным в главе I образом величина Р = 8р/ э меньше критического значения критерия Фишера для выбранного уровня значимости (обычно 5%), модель можно считать адекватной. При Г, модель следует изменить. Поскольку величина используется достаточно часто, в табл. П-1 приведены ее значения. [c.55]
Если же модель нелинейна относительно подбираемых коэффициентов, применение критерия Фишера становится неоправданным. В этом случае можно строго проверить адекватность модели, перейдя к линеаризованному относительно коэффициентов описанию. Последнее можно получить по линейной части разложения в ряд Тейлора, а для химических процессов и более простыми методами [2]. Прй таком подходе дискриминация моделей заключается в отбрасывании тех из них, для которых Р-Отдать же предпочтение какой-либо -модели с Р нельзя. Этот подход был использован для анализа моделей паровой конверсии метана было найдено, что из двенадцати предложенных в литературе моделей лишь четыре можно считать адекватными 13]. [c.55]
Экспериментальная дисперсия величины у, найденная повторением приблизительно 20 опытов в одинаковых режимах, = 0,9. Следовательно, величина Р = 2,23/0,9 2,48. Табличная величина критерия Г (Фишера) составляет для нашпх условий при 5% уровне значимости 3,55, и уравнение регрессии можно считать адекватным. [c.49]
При разработке оптимальной технологической схемы ТС в качестве основных элементов, так же как и в исходном проектном варианте ТС, использовались кожухотрубчатые теплообменники типов ТН и ТЛ, которые, как известно из опыта эксплуатации и проектирования, наиболее эффективны на нефтеперерабатывающих производствах. Значения коэффициентов» стоимостной функции Ц приведены в табл. VI-1S. Величины коэффициентов а и 6 определялись отдельно для трех диапазонов поверхностей теплообменников, для различного числа ходов и коиструкционных материалов. В табл. VI-15 показаны также значения относительных погрешностей расчета и критерия Фишера. Полученные значений коэффициентов стоимостной функции Ц, позволяющей определить стоимость основных элементов ТС в зависимости от величины поверхности теплообмена, могут быть рекомендованы для использования в проектных расчетах, так как ошибка в определении стоимости элементов ТС не превышает допустимой в практи- [c.277]
Фишера критерий — Энциклопедия по машиностроению XXL
Разновидностью энергетических критериев прочности анизотропных материалов является предложенный Л. Фишером критерий, включающий в себя различные упругие (модули упругости Е и коэ( фициенты Пуассона (х) и прочностные (пределы прочности [c.151]Фишера критерий 40 Форсунка 98 [c.317]
Проверка гипотезы об адекватности проводится с использованием / -критерия Фишера. Критерий Фишера позволяет проверить нуль-гипотезу о равенстве двух генеральных дисперсий и [c.506]
Критерий Фишера (Е-критерий) применяется для решения задач от однородности генеральных дисперсий путем сравнения выборочных дисперсий 1 и (проверка однородности [c.105]
Рассмотрим однофакторный дисперсионный анализ. В самом простом случае дисперсия наблюдений о2 известна заранее и исследуется один переменный фактор х. Пусть в этом случае при изменении фактора х получились результаты наблюдений рь у2,… …, уп- Найдем выборочную дисперсию 52. Сравним эту дисперсию с генеральной дисперсией сг2 Если 52 от о2 отличается незначимо, то и влияние фактора х нужно признать незначимым. Если же 52 отличается значимо от сг2 то это может быть вызвано только влиянием фактора х, которое следует признать значимым. Факт значимости устанавливается по критерию Фишера Р=5 1а . Задавшись уровнем значимости а, найдем табличное значение Рг-а-Если Рр1-а, то 52 и сг2 неоднородны и X влияет на у на фоне помех. [c.106]
Далее, используя критерий Фишера [c.107]
Проверить адекватность уравнения — это значит убедиться в том, что оно достаточно верно описывает качественно и количественно реальный процесс. Адекватность уравнения проверяется 10 критерию Фишера [c.109]
Проверка адекватности состоит в выяснении соотношения между дисперсией адекватности 5ад и дисперсией воспроизводимости 5 у и проводится с использованием критерия Фишера Е, который в данном случае формируется как отношение Если вычисленное значение критерия меньше критического Е, р Для соответствующих степеней свободы /ад= — г и 1Е=к т— 1) при заданном уровне значимости а (см. 5.4), то описание признается адекватным объекту. [c.122]
Проверка его адекватности с использованием критерия Фишера показала, что в диапазонах изменения Ке,= (0,8364-1,533) 10 Я=0,2345-=-1,2 и 2= = 0,1586- 0,8414 оно достаточно точно описывает опытные данные. [c.123]
Критерием такой оценки является критерий Фишера, определяемый как отношение дисперсий [c.82]
Экспериментальные исследования титановых сплавов [127], показывают, что в интервале 0,4 титановых сплавов величина Kis = 30 МПа-м / . Статистическая проверка нулевых гипотез о равенстве средних значений величин Kis и дисперсии по критериям Стьюдента и Фишера при уровне значимости 5 % показала, что нулевые гипотезы принимаются. [c.253]
Проверка адекватности построенной полиномиальной модели приводится по критерию Фишера Р. [c.28]
Проверка соответствия критерия Фишера [c.183]
Варьирование температуры в цикле сжатия значительно влияет на долговечность. Проверка по критерию Фишера [c.347]
Л. Фишером был предложен критерий прочности для плоского напряженного состояния, который имеет следующий вид [47] [c.30]
Для оценки несущей способности по данному критерию необходимо определить три показателя прочности при линейном напряженном состоянии по стандартной методике и четыре упругих характеристики. Анализ критерия Фишера показал, что все упругие характеристики, а также значения степени анизотропии прочностных и упругих характеристик могут быть определены при помощи неразрушающего метода, например, по параметрам распространения упругих волн в композиционной среде. Ниже будет показана возможность преобразования критерия Фишера для неразрушающего контроля прочностных характеристик некоторых изделий из композиционных материалов. [c.30]
Далее определим значимость коэффициентов по /-Крите-рмю и адекватность выбранной модели по критерию Фишера. Дисперсия воспроизводимости [c.118]
Проверка гипотезы равенства математических ожиданий является традиционной задачей дисперсионного анализа, для решения которой применим критерий Фишера [б]. Например, при неизменной величине выборки L [c.55]
Приведена методика проверки стационарных и эргодических свойств виброакустических сигналов машин с использованием критериев серий Фишера. Коч-рена. Дается пример оценки стационарности и эргодичности случайного процесса — виброскорости абсолютных смещений корпуса шпинделя токарного станка. [c.117]
Осуществим проверку адекватности полученной модели по критерию Фишера, согласно которому уравнение адекватно, если FR FT [c.238]
Как уже упоминалось, при расчете вариантов становятся известными нагрузки внутри механизма, его точность, быстродействие, неравномерность движения звеньев при разных значениях V . Тем самым получается область допустимых значений варьируемых параметров No СГ N, а также области дефектных состояний Nj, N2,. . ., С N. Для построения алгоритма диагностирования (определения Nj., А = О, 1, 2,. . . ) нужно установить чувствительность выходных параметров к изменению отдельных vj, В качестве функций цели при этом используются те же критерии, что и при идентификации, либо любые другие функции, рассчитываемые по результатам натурных измерений и моделирования. Оценка чувствительности может производиться, например, по критерию Фишера. В этом случае для каждой из выбранных функций цели Ф (т. е. предполагаемых диагностических параметров) рассчитываются [c.60]
Затем определяется критерий Фишера Рф Рф = dA/ R при d% или Рф = rI a при dl) и сравнивается с табличным значением табл при заданном уровне значимости -го параметра. В качестве контрольных параметров выбираются те из функций цели Ф, изменение которых наиболее значимо при выходе v из N, в качестве диагностических — те, изменение которых значимо-при переходе v из N в Nj, i= j, г, / = О, 1, 2,. .. [c.61]
Для количественной оценки выдвигаемой нулевой гипотезы в математической статистике применяются разные статические критерии значимости. В методе ПЛП-поиск в качестве такого был выбран простейший в вычислительном аспекте критерий Фишера F [6, 71, равный отношению двух оценок дисперсии и s [c.5]
Таким образом, следует продолжать оценку величины s x» при возрастании п лишь постольку, поскольку статистические критерии указывают на значимость величины s . Для этой цели используется критерий Фишера. Так как величина F = Л /а имеет распределение , т-п-и то каждое значение s» может быть испытано на его значимость. В результате может быть выбран оптимальный аппроксимирующий полином. [c.161]
Фишера критерий 173, 174 Фотогидролиз 61, 117, 118 Фотоокислительная деструкция покрытий закономерности процесса [c.188]
X, у, г,. .. — числовые значения признаков, варианты или даты (по терминологии Р. Фишера) г — преобразованный коэффициент корреляции (по Фишеру) критерий знаков а (альфа) —уровень значимости оценок Р (бета) — критерий достоверности Блекмана [c.5]
Адекватность модели оценивали по критерию Фишера, для расчета дисперсии и доверительного интервала выполняли дублирующие опыты на основном уровне. Математическую обработку результатов экспериментов осуществляли с доверительной вероятностью не менее 95% (см. табл. 101). Расчет коэффициентов модели проводили с помощью компьютеров. При реализации вспомогательной матрицы для переплава использовали отходы проката стали 4Х5МФС. [c.386]
Прежде чем производить объединение дисперсий, надо убедиться в их однородности. Проверка производится с помощью критериев Фишера и Кохрэна (см. гл. 5). Гипотеза об однородности дисперсий принимается, если экспериментальное значение критерия Кохрэна или Фишера не превышает табличного значения. [c.121]
Распределение Фишера (f-кpитepий) используется для проверки однородности (сравнения) двух выборочных дисперсий а1 и (причем а1 >а ), найденных соответственно со степенями свободы у=П1—] и f2=/l2—1. Проверка гипотезы об однородности двух выборочных дисперсий нормалью распределенной величины состоит в том, что по данным опытов вычисляется / -критерий значение которого [c.105]
Подобный критический анализ можно было бы провести и для других квадратичных критериев — Норриса [33], Фишера [15], Франклина [17] и Чамиса [9]. Однако при помощи довольно утомительных алгебраических выкладок можно прийти к выводу о том, что все эти критерии также представляют собой частные случаи общей тензорно-полиномиальной формулировки. После этих замечаний мы можем перейти к общему исследованию тензорно-полиномиальной формулировки критерия, представленной уравнением (5). [c.449]
Необходимо отметить, что перечисленные этапы имеют много общих процедур определение средних, дисперсий, решение системы нормальных уравнений, построение графиков, определение значений критерия Стьюдента и Фишера. Поэтому целесообразно не разрабатывать отдельные вычислительные программы для ЭВМ, а построить на базе ЭВМ автоматизированную систему обработки статистических данных (АСОСД), основанную на модульном принципе. [c.184]
Анализ рассмотренных критериев прочности показал, что для неразрушающего контроля, по-видимому, наиболее целесообразно использовать критерии Мизеса—Хилла (2.8), Фишера (2.9), Прагера (2.15), Веррена (2.17), Ашкенази (2.18). При неразрушающем Контроле прочности изделий с использованием критериев (2.8), (2.15), (2.17), (2.18) необходимо определить степень анизотропии скорости продольных волн в изделии и одну характеристику прочности материала. Для критерия Фишера, кроме перечисленных параметров, необходимо знать также упругие характеристики. Данные характеристики можно также определить непосредственно в изделии неразрушающим методом по значениям скоростей упругих волн [c.43]
Для проверки гипотезы равенства математических ожиданий использовался критерий Фишера, табличные значения которого (0,05 7 133)=2,1 (0,05 133 7)=3,24 больше полученных значений /»=1,18, i =3,23, что позволяет считать средние значения в каждой выборке равными. Аналогично критерий Кочрена g (0,05 8 19)—0,23 (0,05 8 511) =0,15) позволяет принять гипотезу равенства дисперсий Df. Из анализа табл. 3 следует, что численные значения М. D , полученные осреднением по множеству и по времени, близки друг к другу сравнение графиков корреляционных функций с осреднением по мнон еству и по времени (рис. 2) также показывает практически тождественность полученных коррелограмм, отличие которых состоит в различной степени сглаживания ( шероховатости ), вызванной разным числом осреднений по ансамблю и по времени. Интервал корреляции корреляционных функций примерно одинаков и составляет 0,04 с. [c.59]
Оценка параметров уравнения линии регрессии дала в нашем случае а = 4,87 Ь = — 6,22, X = 1,68. Уравнение эмпирической линии регрессии имеет вид / = 15,14 — 6,23 X, а соответствующее ему семейство усталостных кривых показано на рис. 13. Линейность кривой регрессии проверяли путем вычисления критерия Фишера, при этом дисперсия внутри системы S, =0,9999 и дисперсия вокруг эмпирической линии регресии S] = 0,4095. Дисперсионное отношение их f = 0,9999/0,4095 = 2,44 [c.37]
На основе анализа конструкции и технологии изготовления и сборки механизмов на заводе-изготовителе, а также опыта их исследования в условиях эксплуатации установлены восемь» параметров, величины которых претерпевают наиболее сильные изменения из-за нестабильности качества изготовления, сборки и процессов разрегулирования, разгерметизации, происходящих при эксплуатации. Это параметры С , С , Сд, т , К , а, р , тр (я 5). Для анализа модели предварительно экспериментально определялись жесткости С , g, g и возможные диапазоны их изменения. Далее требовалось выделение тех параметров, изменение которых приводит к заклиниванию червячного зацепления [14]. В процессе заклинивания момент трения в червячном зацеплении, возникающий при остановке механизма на жестком упоре, становится больше, чем момент, развиваемый гидромотором. ВЬгделение доминирующих факторов проводилось на основе дисперсионного анализа, и значимость параметров оценивалась по критерию Фишера. Организация машинного эксперимента состояла в вариации всех восьми разыгрываемых параметров, значения которых рассчитывались по формуле [66 [c.137]
По табл. XVril [5] при =— 7V — 1 =15 и Va = JV — iVi = 80 находим, что при Р = 0,05 (5%-ный уровень значимости) критерий Фишера F равен 1,84. Сопоставление этого значения с данными табл. 2 показывает, что в гиперпараллелепипеде G , определяемом системой неравенств (8), параметры и 4 оказывают в среднем существенное влияние на значения Ф, а аз, а , ав и а не оказывают такого влияния. Очевидно, что и параметры а, и связанные с 1 и 014 формулами (6), следует отнести к существенным. Таким образом, если в заданной области организовать поиск оптимальной модели, то параметры мз, 5, в и з можно зафиксировать. [c.30]
Мощным методом решения этой задачи является использование критерия Фишера f, с номош,ью которого проверяется значимость коэффициента я . [c.160]
Наглядное введение в линейный дискриминант Фишера
Введение
Для решения проблем классификации с 2 или более классами большинство алгоритмов машинного обучения (ML) работают одинаково.
Обычно они применяют к входным данным какое-то преобразование с эффектом уменьшения исходных входных размеров до новых (меньших). Цель состоит в том, чтобы спроецировать данные в новое пространство. Затем, после проецирования, они пытаются классифицировать точки данных, находя линейное разделение.
Для задач с небольшими входными размерами задача несколько проще. В качестве примера возьмем следующий набор данных.
Предположим, мы хотим правильно классифицировать красные и синие круги. Понятно, что с простой линейной моделью хорошего результата мы не получим. Не существует линейной комбинации входных данных и весов, которая сопоставляет входные данные с их правильными классами. Но что, если бы мы могли преобразовать данные так, чтобы нарисовать линию, разделяющую 2 класса?
Вот что произойдет, если возвести в квадрат два входных вектора признаков.Теперь линейная модель легко классифицирует синие и красные точки.
Однако иногда мы не знаем, какое преобразование следует использовать. На самом деле найти лучшее представление — нетривиальная задача. Мы можем применить к нашим данным множество преобразований. Точно так же каждый из них может привести к другому классификатору (с точки зрения производительности).
Одно из решений этой проблемы — научиться правильному преобразованию. Это известно как репрезентативное обучение , и это именно то, о чем вы думаете — глубокое обучение.Магия в том, что нам не нужно «угадывать», какое преобразование приведет к наилучшему представлению данных. Алгоритм разберется.
Однако имейте в виду, что независимо от обучения представлению или функций, созданных вручную, шаблон остается одним и тем же. Нам нужно как-то изменить данные, чтобы их можно было легко разделить.
Давайте сделаем несколько шагов назад и рассмотрим более простую задачу.
В этой статье мы собираемся изучить, как линейный дискриминант Фишера (FLD) позволяет классифицировать многомерные данные.Но прежде чем мы начнем, откройте блокнот Colab и следуйте за ним.
Линейный дискриминант Фишера
Мы можем рассматривать модели линейной классификации с точки зрения уменьшения размерности.
Для начала рассмотрим случай двухклассовой задачи классификации (K = 2) . Синие и красные точки в R². В общем, мы можем взять любой входной вектор размерности D и спроецировать его до размеров D. Здесь D представляет исходные входные размеры, а D ’ — проектируемые размеры пространства.На протяжении всей статьи считайте, что D ’ меньше, чем D .
В случае проецирования в одно измерение (числовая линия), то есть D ’= 1 , мы можем выбрать порог t для разделения классов в новом пространстве. Учитывая входной вектор x :
- , если прогнозируемое значение y> = t , то x принадлежит классу C1 (класс 1) — где.
- в противном случае классифицируется как C2 (класс 2).
В качестве игрушечного примера возьмем набор данных ниже.Мы хотим уменьшить исходные размеры данных с D = 2 до D ’= 1. Другими словами, нам нужно преобразование T, которое отображает векторы из 2D в 1D — T (v) = ℝ² → ℝ¹.
Во-первых, давайте вычислим средние векторы m1 и m2 для двух классов.
Обратите внимание, что N1 и N2 обозначают количество баллов в классах C1 и C2 соответственно. Теперь рассмотрим использование средних классов в качестве меры разделения. Другими словами, мы хотим спроецировать данные на вектор W , объединяющий средства 2 классов.
Важно отметить, что любой вид проекции на меньшее измерение может повлечь за собой некоторую потерю информации. В этом сценарии обратите внимание, что два класса четко разделяются (линией) в их исходном пространстве.
Однако после повторного проецирования данные демонстрируют своего рода перекрытие классов, что показано желтым эллипсом на графике и гистограмме ниже.
Вот где вступает в игру линейный дискриминант Фишера.
Идея, предложенная Фишером, состоит в том, чтобы максимизировать функцию, которая даст большое разделение между прогнозируемыми средними классами, а также даст небольшую дисперсию внутри каждого класса, тем самым минимизируя перекрытие классов.
Другими словами, FLD выбирает проекцию, которая максимизирует разделение классов. Для этого он максимизирует соотношение между межклассовой дисперсией и внутриклассовой дисперсией.
Короче говоря, для проецирования данных в меньшее измерение и во избежание перекрытия классов FLD поддерживает 2 свойства.
- Большой разброс между классами набора данных.
- Небольшая разница в каждом из классов набора данных.
Обратите внимание, что большая разница между классами означает, что прогнозируемые средние значения классов должны быть как можно дальше друг от друга.Напротив, небольшая дисперсия внутри класса приводит к тому, что прогнозируемые точки данных остаются ближе друг к другу.
Чтобы найти проекцию со следующими свойствами, FLD изучает вектор весов W со следующим критерием.
Если мы подставим средние векторы m1 и m2 , а также дисперсию s , заданную уравнениями (1) и (2), мы придем к уравнению (3). Если мы возьмем производную от (3) по W (после некоторых упрощений), мы получим уравнение обучения для W (уравнение 4). То есть W (желаемое преобразование) прямо пропорционально обратной величине ковариационной матрицы внутри класса, умноженной на разность средних значений класса.
Как и ожидалось, результат обеспечивает идеальное разделение классов с простой установкой пороговых значений.
Линейный дискриминант Фишера для множественных классов
Мы можем обобщить FLD на случай более чем K> 2 классов. Здесь нам нужны формы обобщения для ковариационных матриц внутри классов и между классами.
Для ковариационной матрицы внутри класса SW для каждого класса возьмите сумму умножения матрицы между централизованными входными значениями и их транспонированием. Уравнения 5 и 6.
Для оценки ковариации между классами SB для каждого класса k = 1,2,3,…, K возьмите внешнее произведение среднего локального класса mk и глобального среднего m . Затем масштабируйте его по количеству записей в классе k — уравнение 7.
Максимизация критерия FLD решается посредством собственного разложения матричного умножения между инверсией SW и SB . Таким образом, чтобы найти вектор весов ** W **, мы берем собственные векторы ** D ’**, которые соответствуют их наибольшим собственным значениям (уравнение 8).
Другими словами, если мы хотим уменьшить нашу входную размерность с D = 784 до D ‘= 2 , весовой вектор W состоит из 2 собственных векторов, которые соответствуют наибольшему значению D’ = 2 . собственные значения.Это дает окончательную форму W = (N, D ’) , где N — количество входных записей, а D’ — уменьшенные размеры элемента.
Построение линейного дискриминанта
До этого момента мы использовали линейный дискриминант Фишера только как метод уменьшения размерности. Чтобы действительно создать дискриминант, мы можем смоделировать многомерное распределение Гаусса по D-мерному входному вектору x для каждого класса K как:
Здесь μ (среднее) — D-мерный вектор. Σ (сигма) — матрица DxD — ковариационная матрица. И | Σ | — определитель ковариации. В питоне это выглядит так.
Параметры распределения Гаусса: μ и Σ вычисляются для каждого класса k = 1,2,3,…, K с использованием прогнозируемых входных данных. Мы можем вывести априорные вероятности классов P (Ck) , используя доли точек данных обучающего набора в каждом из классов (строка 11).
Когда у нас есть гауссовы параметры и априорные значения, мы можем вычислить условные плотности классов P (x | Ck) для каждого класса k = 1,2,3,…, K индивидуально. Для этого мы сначала проецируем D-мерный входной вектор x на новое пространство D ’ . Имейте в виду, что D P (Ck | x) для каждого класса k = 1,2,3,…, K , используя уравнение 10.
Уравнение 10 оценивается в строке 8 функции оценки ниже.
Затем мы можем присвоить входной вектор x классу k ∈ K с наибольшим апостериорным значением.
Тестирование по MNIST
Использование MNIST в качестве набора данных для тестирования игрушек. Если мы решим уменьшить исходные исходные размеры с D = 784 до D ’= 2 , мы получим точность 56% на тестовых данных. Однако если мы увеличим проектируемые размеры пространства до D ’= 3, мы достигнем точности почти 74% .Эти 2 проекции также упрощают визуализацию пространства функций.
Некоторые ключевые выводы из этой статьи.
Линейный дискриминант Фишера, по сути, является методом уменьшения размерности, а не дискриминантом. Для двоичной классификации мы можем найти оптимальный порог t и соответствующим образом классифицировать данные. Для мультиклассовых данных мы можем (1) смоделировать условное распределение классов с помощью гауссиана. (2) Найдите апостериорные вероятности класса P (Ck) и (3) используйте байесовский метод для нахождения апостериорных вероятностей класса
p (Ck | x).Чтобы найти оптимальное направление для проецирования входных данных, Fisher нужны контролируемые данные.
Учитывая набор данных с размерами D , мы можем спроецировать его максимум до D ’ равно D-1 измерений.
Эта статья основана на главе 4.1.6 Распознавания образов и машинного обучения. Книга Кристофера Бишопа
Спасибо за чтение!
Укажите как:
@article {
silva2019fisherdiscriminant,
title = {Наглядное введение в линейный дискриминант Фишера},
author = {Сильва, Таллес Сантос},
журнал = {https: // sthalles.github.io},
год = {2019}
url = {https://sthalles.github.io/fisher-linear-discriminant/}
}
(PDF) Мультиклассовая классификация на основе критериев Фишера с взвешенным расстоянием
Мультиклассовая классификация на основе критериев Фишера
Со взвешенным расстоянием
1
1 ВВЕДЕНИЕ
Линейный дискриминантный анализ (LDA) как эффективный
Алгоритм уменьшения размерностишироко используется в обществе распознавания образов и машинного обучения
.Основная цель
LDA — минимизировать уплотнение образцов внутри класса
при одновременном максимальном разделении образцов класса
. И критерий Фишера (FC) [1-5] —
— лишь одно из нескольких практических воплощений этой идеи.
Однако FC не всегда является золотым критерием для мультиклассовой классификации
[6], как показано на рисунке 1. Проекция
направленияна фиг.1. (а) показывает, что образцы разделимы.
На основе тех же выборок направление w на рис.1. (b)
нельзя разделить на классы 2 и 3 в соответствии с ФК.
Class3
Class2
Class1
w
w
Class3
Class2
Class1
(a) (b)
Рис.1. Проекция одного и того же набора образцов на две разные линии
в направлениях, отмеченных буквой w.На левом рисунке показано направление
, разделимое для всех классов. В то время как на рисунке справа показано, что
направлениестановится большей суммой расстояний между выборками между
классами.
Эта проблема возникает из объяснения основной идеи
LDA, которая заключается в минимизации уплотнения
образцов внутри класса при максимальном разделении
образцов между классами. И основная сложность состоит в том, как
сформулировать и рассчитать уплотнение и расслоение.В
FC матрица разброса внутри класса вводится для описания
уплотнения и матрица разброса между классами для разделения
[7]. Однако в таких математических описаниях
могут отсутствовать некоторые аспекты для классификации. В задаче
классификации наиболее важным вопросом является то, превышает ли расстояние
межклассовых выборок
внутриклассовых выборок, в то время как насколько велико из
такое расстояние, все еще неважно вопрос [6].
FC по-разному относится к разным классам. Что касается распределения данных
, то класс с большим удалением от центра
всех выборок имеет больший вес, чем близкие. Обычно
такого класса легко отделить от других. Но для
классов вокруг центра выборки сложно разделить их
в соответствии с FC. Это означает, что результирующая проекция
сохраняет расстояния уже хорошо разделенных классов
и имеет большое перекрытие между соседними классами
.Хорошо известно, что сложные образцы
важны в SVM [8]. Как расширение этой точки зрения,
трудным классам в многоклассовой задаче должно быть
присвоено более высокий вес, чем другим.
Существует несколько алгоритмов для улучшения LDA, например
PCA + LDA [2], Direct LDA (DLDA) [9], Regularized
Discriminant Analysis (RDA) [10] и Null space LDA
(NLDA) [11]. Тем не менее, они сосредоточены на решении проблемы небольшой выборки
размером(S3) в LDA.Объектная функция из них —
еще FC. Приблизительный критерий парной точности
(aPAC) взвешивает вклад отдельных пар классов на
, приближая коэффициент ошибок Байеса к общему критерию в
, чтобы улучшить LDA [6]. Однако эта приблизительная частота ошибок Байеса
также зависит от расстояния классов в
исходном пространстве, и такая весовая функция делает aPAC
субоптимальным решением.
В этой статье мы предлагаем новый критерий Фишера с взвешенным расстоянием
(FCWWD), в котором мы заменяем классическую линейную функцию
нелинейной весовой функцией для описания
расстояний между выборками в критериях Фишера. Используя
из нового определения внутриклассового уплотнения и
межклассового разделения, FCWWD достигает лучшего результата
за счет приближения оптимизации ROC, которая может
преодолеть субоптимальную проблему.Кроме того, мы также предлагаем
решение, основанное на этом критерии под названием WD-LDA
Meng Ao, Stan Z.Li1
1. Институт автоматики Китайской академии наук, Пекин 100190, Китай
Электронная почта : [email protected] [email protected]
Аннотация: Линейный дискриминантный анализ (LDA) — это эффективный алгоритм уменьшения размерности. В этой статье мы предлагаем
новых критериев Фишера с взвешенным расстоянием (FCWWD), чтобы найти оптимальную проекцию для задач мультиклассовой классификации.Мы
заменяем классическую линейную функцию нелинейной весовой функцией для описания расстояний между выборками в критериях Фишера.
Более того, мы даем новый алгоритм, основанный на этих критериях, вместе с теоретическим объяснением того, что наш алгоритм выигрывает от
— приближения оптимизации ROC. Экспериментальные результаты демонстрируют эффективность нашего метода в улучшении характеристик мультиклассовой классификации
.
Линейный, квадратичный и регуляризованный дискриминантный анализ
LDA как метод визуализации
Мы можем преобразовать обучающие данные в канонические координаты, применив матрицу преобразования к масштабированным данным.Чтобы получить те же результаты, что и возвращаемые функцией pred.lda , нам нужно сначала центрировать данные вокруг взвешенных средних:
# 1. Ручное преобразование
# центрировать данные вокруг взвешенных средних и преобразовывать
означает <- colSums (lda.model $ Prior * lda.model $ означает)
train.mod <- scale (train.set, center = means, scale = FALSE)% *%
lda.model $ масштабирование
# 2. Используйте функцию прогнозирования для преобразования:
lda.prediction.train <- предсказать (lda.model, train.set)
все.равно (lda.prediction.train $ x, train.mod) ## [1] ИСТИНА Мы можем использовать первые две дискриминантные переменные для визуализации данных:
# визуализировать функции в двух измерениях LDA
plot.df <- data.frame (train.mod, "Outcome" = train.responses)
библиотека (ggplot2)
ggplot (plot.df, aes (x = LD1, y = LD2, color = Outcome)) + geom_point () Построение данных в двух измерениях LDA показывает три кластера:
- Кластер 1 (слева) состоит из а.о. и а.о. фонем
- Кластер 2 (внизу справа) состоит из dcl и iy фонем
- Кластер 3 (вверху справа) состоит из sh фонем
Это означает, что двух измерений недостаточно для различения всех 5 классов.Однако кластеризация указывает на то, что фонемы, которые достаточно отличаются друг от друга, можно очень хорошо различать.
Мы также можем построить отображение обучающих данных на все пары дискриминантных переменных, используя функцию plot.lda , где параметр dimen может использоваться для указания количества рассматриваемых измерений:
Библиотека (RColorBrewer)
цвета <- brewer.pal (8, "Акцент")
my.cols <- colors [match (lda.prediction.train $ class, levels (df $ g))]
сюжет (lda.модель, размер = 4, col = my.cols) Построение графика обучающих данных для всех пар измерений показывает, что по построению улавливается большая часть дисперсии. Используя график, мы можем получить интуитивное представление о количестве измерений, которые мы должны выбрать для LDA с пониженным рангом. Помните, что LD1 и LD2 перепутали aa с ao и dcl с iy . Таким образом, нам нужны дополнительные измерения для дифференциации этих групп. Глядя на графики, кажется, что нам действительно нужны все четыре измерения, потому что dcl и iy хорошо разделены только в LD1 и LD3, в то время как aa и ao хорошо разделены только когда LD4 в сочетании с любым другим размером.
Чтобы визуализировать центроиды групп, мы можем создать собственный график:
plot_lda_centroids <- function (lda.model, train.set, response) {
центроиды <- предсказать (lda.model, lda.model $ means) $ x
библиотека (RColorBrewer)
цвета <- brewer.pal (8, "Акцент")
my.cols <- colors [match (lda.prediction.train $ class, levels (df $ g))]
my.points <- предсказать (lda.model, train.set) $ x
кол-во классов <- длина (уникальный (ответ))
par (mfrow = c (кол-во классов -1, нет.классы -1), mar = c (1,1,1,1), oma = c (1,1,1,10))
for (i in 1: (кол-во классов - 1)) {
for (j in 1: (кол-во классов - 1)) {
y <- my.points [, i]
x <- my.points [, j]
cen <- cbind (центроиды [, j], центроиды [, i])
if (i == j) {
сюжет (x, y, type = "n")
max.y <- max (my.points [, i])
max.x <- max (my.points [, j])
min.y <- min (my.points [, i])
min.x <- min (my.points [, j])
Максимум.оба <- max (c (max.x, max.y))
мин. оба <- макс (c (мин. x, мин. y))
центр <- мин. оба + ((макс. оба - мин. оба) / 2)
текст (center, center, colnames (my.points) [i], cex = 3)}
еще {
plot (x, y, col = my.cols, pch = as.character (response), xlab = "", ylab = "")
точки (cen [, 1], cen [, 2], pch = 21, col = "black", bg = colors, cex = 3)
}
}
}
номинал (xpd = NA)
легенда (x = par ("usr") [2] + 1, y = mean (par ("usr") [3: 4]) + 20,
легенда = rownames (центроиды), col = цвета, pch = rep (20, длина (цвета)), cex = 3)
}
plot_lda_centroids (lda.модель, поезд.набор, поезд.ответы) Интерпретация апостериорных вероятностей
Помимо преобразования данных в дискриминантные переменные, которое обеспечивается компонентом x , функция прогнозирования также дает апостериорные вероятности, которые можно использовать для дальнейшей интерпретации классификатора. Например:
posteriors <- lda.prediction.train $ posterior # N x K матрица
# Классификация MAP для образца 1:
пред.class <- names (which.max (posteriors [1,])) # <=> lda.prediction.train $ class [1]
print (paste0 ("Апостол предсказанного класса '", pred.class,
"'is:", круглый (posteriors [1, pred.class], 2))) ## [1] "Апостериор предсказанного класса 'sh': 1" # каковы средние значения апостериоров для отдельных групп?
классы <- colnames (апостериорные)
res <- do.call (rbind, (lapply (классы, функция (x) apply (posteriors [train.responses == x,], 2, mean))))
rownames (res) <- классы
печать (круглый (res, 3)) ## aa ao dcl iy sh
## аа 0.797 0,203 0,000 0,000 0,000
## ао 0,123 0,877 0,000 0,000 0,000
## dcl 0,000 0,000 0,985 0,014 0,002
## iy 0,000 0,000 0,001 0,999 0,000
## ш 0,000 0,000 0,000 0,000 1.000 Таблица апостериоров для отдельных классов демонстрирует, что модель наиболее неуверенна в отношении фонем aa и ao , что согласуется с нашими ожиданиями от визуализаций.
LDA как классификатор
Как упоминалось ранее, LDA имеет то преимущество, что мы можем выбирать количество канонических переменных, которые используются для классификации.Здесь мы по-прежнему продемонстрируем использование LDA с пониженным рангом, выполнив классификацию с использованием до четырех канонических переменных.
dims <- 1: 4 # количество канонических переменных для использования
точность <- rep (NA, длина (тускл.))
for (i in seq_along (dims)) {
lda.pred <- предсказать (lda.model, test.set, dim = dims [i])
acc <- длина (которая (lda.pred $ class == test.responses)) / длина (test.responses)
точность [i] <- acc
}
уменьшенный.df <- data.frame ("Ранг" = затемнение, "Точность" = округление (точность, 2))
печать (уменьшено.df) ## Точность ранга
## 1 1 0,51
## 2 2 0,71
## 3 3 0,86
## 4 4 0,92 Как и ожидалось при визуальном исследовании преобразованного пространства, точность теста увеличивается с каждым дополнительным измерением. Поскольку LDA с четырьмя измерениями обеспечивает максимальную точность, мы бы решили использовать все дискриминантные координаты для классификации.
Чтобы интерпретировать модель, мы можем визуализировать работу классификатора полного ранга:
lda.pred <- предсказать (lda.model, test.set)
plot.df <- data.frame (lda.pred $ x [, 1: 2], "Outcome" = test.responses,
"Прогноз" = lda.pred $ class)
ggplot (plot.df, aes (x = LD1, y = LD2, color = Outcome, shape = Prediction)) +
geom_point () На графике ожидаемые фонемы показаны разными цветами, а прогнозы модели показаны разными символами. Модель со 100% точностью присвоит каждому цвету по одному символу.Таким образом, неверные прогнозы обнаруживаются, когда один цвет показывает разные символы. Используя график, мы быстро видим, что большая часть путаницы возникает, когда наблюдения, помеченные как aa , неправильно классифицируются как ao и наоборот.
Использование линейного дискриминантного анализа (LDA) для данных Исследуйте: шаг за шагом.
Введение
В предыдущем посте (Использование анализа главных компонентов (PCA) для исследования данных: шаг за шагом) мы представили технику PCA как метод матричной факторизации.В этой публикации мы указали, что при работе с машинным обучением для анализа данных мы часто сталкиваемся с огромными наборами данных, которые обладают сотнями или тысячами различных функций или переменных. Как следствие, размер пространства переменных значительно увеличивается, что затрудняет анализ данных для получения выводов. Для решения этой проблемы матричная факторизация - это простой способ уменьшить размерность пространства переменных при рассмотрении многомерных данных.
В этом посте мы представляем еще один метод уменьшения размерности для анализа многомерных наборов данных. В частности, мы объясним, как использовать технику линейного дискриминантного анализа (LDA) для уменьшения размерности пространства переменных и сравнить ее с техникой PCA, чтобы у нас были некоторые критерии, которые следует использовать в данной ситуации. дело.
Что такое линейный дискриминантный анализ (LDA)?
Линейный дискриминантный анализ (LDA) - это обобщение линейного дискриминанта Фишера, метода, используемого в статистике, распознавании образов и машинном обучении для поиска линейной комбинации функций, которая характеризует или разделяет два или более классов объектов или событий.Этот метод проецирует набор данных на пространство меньшей размерности с хорошей возможностью разделения классов, чтобы избежать переобучения («проклятие размерности») и снизить вычислительные затраты. Полученная комбинация может использоваться в качестве линейного классификатора или, чаще, для уменьшения размерности перед последующей классификацией.
Первоначальный линейный дискриминант был описан для задачи с двумя классами, а затем он был обобщен как «многоклассовый линейный дискриминантный анализ» или «множественный дискриминантный анализ» К.Р. Рао в 1948 г. (Использование множественных измерений в задачах биологической классификации)
Вкратце, цель LDA часто состоит в том, чтобы проецировать пространство признаков (набор данных $ n $ -мерных выборок) в меньшее подпространство $ k $ (где $ k \ leq n − 1 $), сохраняя при этом класс -дискриминационная информация. В общем, уменьшение размерности не только помогает снизить вычислительные затраты для данной задачи классификации, но также может помочь избежать переобучения за счет минимизации ошибки в оценке параметров.
Сравнение LDA с (PCA).
Как линейный дискриминантный анализ (LDA), так и анализ главных компонентов (PCA) - это методы линейного преобразования, которые обычно используются для уменьшения размерности (оба являются методами матричной факторизации данных). Наиболее важным различием между обоими методами является то, что PCA можно описать как «неконтролируемый» алгоритм, поскольку он «игнорирует» метки классов и его цель - найти направления (так называемые главные компоненты), которые максимизируют дисперсию в наборе данных. , в то время как LDA является «контролируемым» алгоритмом, который вычисляет направления («линейные дискриминанты»), представляющие оси, которые максимизируют разделение между несколькими классами.
Интуитивно мы могли бы подумать, что LDA превосходит PCA для задачи классификации нескольких классов, когда метки классов известны. Однако это может быть не всегда. Например, сравнение точности классификации для распознавания изображений после использования PCA или LDA показывает, что PCA имеет тенденцию превосходить LDA, если количество образцов в классе относительно невелико (PCA против LDA, A.M. Martinez et al., 2001). На практике нередки случаи, когда LDA и PCA используются в комбинации: e.g., PCA для уменьшения размерности с последующим LDA.
Вкратце, мы можем сказать, что PCA - это неконтролируемый алгоритм, который пытается найти оси ортогональных компонентов с максимальной дисперсией в наборе данных ([см. Наш предыдущий пост по его теме]), в то время как цель LDA как контролируемого алгоритма - чтобы найти подпространство функций, которое оптимизирует разделимость классов.
На следующем рисунке мы можем увидеть концептуальную схему, которая помогает нам иметь геометрическое представление об обоих методах
Как показано на оси x (новый компонент LD 1 с уменьшенной размерностью) и оси y (новый компонент LD 2 с уменьшенной размерностью) в правой части предыдущего рисунка, LDA обычно разделяет два компонента. хорошо распределены классы.
Следующий вопрос: Что такое «хорошее» подпространство функций, которое максимизирует оси компонентов для разделения классов?
Чтобы ответить на этот вопрос, предположим, что наша цель - уменьшить размерность d-мерного набора данных, проецируя его на (k) -мерное подпространство (где k Для этого мы вычислим собственные векторы (компоненты) из нашего набора данных и соберем их в так называемые матрицы рассеяния (т.е., матрица разброса между классами и матрица разброса внутри класса). Каждый из этих собственных векторов связан с собственным значением, которое говорит нам о «длине» или «величине» собственных векторов. Если мы заметим, что все собственные значения имеют одинаковую величину, то это может быть хорошим индикатором того, что наши данные уже спроецированы на «хорошее» пространство признаков. И в другом сценарии, если некоторые из собственных значений намного больше, чем другие, мы могли бы быть заинтересованы в сохранении только тех собственных векторов с наивысшими собственными значениями, поскольку они содержат больше информации о нашем распределении данных.Другой способ, если собственные значения, близкие к 0, менее информативны, и мы могли бы рассмотреть возможность их удаления для построения нового подпространства признаков (та же процедура, что и в случае PCA). Мы перечислили 5 общих шагов для выполнения линейного дискриминантного анализа; мы рассмотрим их более подробно в следующих разделах. Вычислить $ d-мерные векторы $ средних для различных классов из набора данных. Вычислить матрицы разброса (матрицу разброса между классами и внутри класса). Вычислить собственные векторы ($ e_1, e_2, ..., e_d $) и соответствующие собственные значения ($ \ lambda_1, \ lambda_2, ... \ lambda_d $) для матриц рассеяния. Отсортируйте собственные векторы по убыванию собственных значений и выберите k собственных векторов с наибольшими собственными значениями, чтобы сформировать $ d \ times k $ размерную матрицу $ W $ (где каждый столбец представляет собственный вектор). Используйте эту матрицу собственных векторов $ d \ times k $ для преобразования выборок в новое подпространство.Это можно резюмировать умножением матриц: $ Y = X \ times W $, где $ X $ - $ n \ times d-мерная $ матрица, представляющая $ n $ выборок, а $ y $ - преобразованные $ n \ умножить на k-мерных $ выборок в новом подпространстве. Чтобы зафиксировать концепции, мы применяем эти 5 шагов в наборе данных радужной оболочки для классификации цветов. В следующем руководстве мы будем работать со знаменитым набором данных Iris, который был размещен в репозитории машинного обучения UCI (https: // archive.ics.uci.edu/ml/datasets/Iris). Набор данных ириса содержит измерения для 150 цветков ириса трех разных видов. Три класса в наборе данных Iris: Четыре характеристики набора данных Iris: Чтение набора данных В матричной форме $
\ mathbf {X} = \ begin {bmatrix} x_ {1 _ {\ text {sepal length}}} & x_ {1 _ {\ text {sepal width}}} & x_ {1 _ {\ text {длина лепестка}}} & x_ {1 _ {\ text {ширина лепестка}}} \ новая строка
... \новая линия
x_ {2 _ {\ text {длина чашелистника}}} & x_ {2 _ {\ text {ширина чашелистика}}} & x_ {2 _ {\ text {длина лепестка}}} & x_ {2 _ {\ text {ширина лепестка}} } \новая линия
\ end {bmatrix}, y = \ begin {bmatrix} \ omega _ {\ text {iris-setosa}} \ newline
... \новая линия
\ omega _ {\ text {iris-virginica}} \ newline \ end {bmatrix} Поскольку с числовыми значениями работать удобнее, мы будем использовать LabelEncode из библиотеки scikit-learn для преобразования меток классов в числа: 1, 2 и 3. Получаем $ y = \ begin {bmatrix} {\ text {setosa}} \ newline
{\ текст {сетоса}} \ новая строка
... \новая линия
{\ text {virginica}} \ end {bmatrix} \ quad \ Rightarrow
\ begin {bmatrix} {\ text {1}} \
{\ текст {1}} \ новая строка
... \новая линия
{\ text {3}} \ end {bmatrix} Чтобы получить приблизительное представление о том, как распределены выборки наших трех классов $ \ omega_1, \ omega_2 $ и $ \ omega_3 $, давайте визуализируем распределения четырех различных функций на одномерных гистограммах. Просто взглянув на эти простые графические представления признаков, мы уже можем сказать, что длина и ширина лепестков, вероятно, лучше подходят как потенциальные признаки, разделенные между тремя классами цветов. На практике, вместо уменьшения размерности с помощью проекции (здесь: LDA), хорошей альтернативой будет метод выбора признаков.Для низкоразмерных наборов данных, таких как Iris, взгляд на эти гистограммы уже был бы очень информативным. Другой простой, но очень полезный метод - использование алгоритмов выбора функций (см. Rasbt.github.io/mlxtend/user_guide/feature_selection/SequentialFeatureSelector и scikit-learn). Важное примечание о допущениях нормальности: Следует отметить, что LDA предполагает нормальные распределенные данные, статистически независимые функции и идентичные ковариационные матрицы для каждого класса.Однако это относится только к LDA в качестве классификатора, а LDA для уменьшения размерности также может работать достаточно хорошо, если эти предположения нарушаются. И даже для задач классификации LDA может быть довольно устойчивым к распределению данных. После того, как мы прошли несколько подготовительных этапов, наши данные наконец готовы для фактического LDA. На практике LDA для уменьшения размерности будет просто еще одним этапом предварительной обработки для типичной задачи машинного обучения или классификации шаблонов. На этом первом этапе мы начнем с простого вычисления средних векторов $ m_i $, $ (i = 1,2,3) $ трех различных классов цветов: $ m_i = \ begin {bmatrix}
\ mu _ {\ omega_i (\ text {длина чашелистика)}} \ новая строка
\ mu _ {\ omega_i (\ text {ширина чашелистика})} \ новая строка
\ mu _ {\ omega_i (\ text {длина лепестка)}} \ newline
\ mu _ {\ omega_i (\ text {ширина лепестка})} \ newline
\ end {bmatrix} \; , \ quad \ text {with} \ quad i = 1,2,3 $ получаем: Теперь мы вычислим две матрицы размерности 4x4: матрицу разброса внутри класса и матрицу разброса между классами.п \; \ pmb x_k $ получаем: Подготовка образца набора данных
О наборе данных Iris
feature_dict = {i: метка для i, метка в zip (
диапазон (4),
('длина чашелистика в см',
'ширина чашелистика в см',
'длина лепестка в см',
'ширина лепестка в см',))}
импортировать панд как pd
df = pd.io.parsers.read_csv (
filepath_or_buffer = 'https: //archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
заголовок = Нет,
sep = ',',
)
df.columns = [l для i, l в отсортированном (feature_dict.items ())] + ['метка класса']
df.dropna (how = "all", inplace = True) # чтобы удалить пустую строку в конце файла
df.tail ()
% встроенная библиотека matplotlib
из склеарна.предварительная обработка импорта LabelEncoder
X = df [[0,1,2,3]]. Значения
y = df ['метка класса']. значения
enc = LabelEncoder ()
label_encoder = enc.fit (y)
y = label_encoder.transform (y) + 1
label_dict = {1: 'Setosa', 2: 'Versicolor', 3: 'Virginica'} Гистограммы и выбор функций
% встроенная библиотека matplotlib
из matplotlib импортировать pyplot как plt
импортировать numpy как np
импортная математика
fig, axes = plt.subplots (nrows = 2, ncols = 2, figsize = (12,6))
для ax, cnt в zip (axes.ravel (), range (4)):
# установить размеры корзины
min_b = math.floor (np.min (X [:, cnt]))
max_b = math.ceil (np.max (X [:, cnt]))
bins = np.linspace (min_b, max_b, 25)
# построение гистограмм
для лаборатории, col in zip (range (1,4), ('blue', 'red', 'green')):
ax.hist (X [y == lab, cnt],
цвет = col,
label = 'class% s'% label_dict [lab],
бункеры = бункеры,
альфа = 0.5,)
ylims = ax.get_ylim ()
# аннотация сюжета
leg = ax.legend (loc = 'верхний правый', fancybox = True, fontsize = 8)
leg.get_frame (). set_alpha (0,5)
ax.set_ylim ([0, макс (ylims) +2])
ax.set_xlabel (feature_dict [cnt])
ax.set_title ('Гистограмма радужки #% s'% str (cnt + 1))
# скрыть отметки оси
ax.tick_params (axis = "both", which = "both", bottom = "off", top = "off",
labelbottom = "on", left = "off", right = "off", labelleft = "on")
# удалить шипы оси
ax.spines ["вверху"]. set_visible (Ложь)
топор.шипы ["вправо"]. set_visible (Ложь)
ax.spines ["снизу"]. set_visible (Ложь)
ax.spines ["влево"]. set_visible (Ложь)
оси [0] [0] .set_ylabel ('количество')
оси [1] [0] .set_ylabel ('количество')
fig.tight_layout ()
plt.show () LDA за 5 шагов
Шаг 1. Вычисление d-мерных средних векторов
нп.set_printoptions (точность = 4)
mean_vectors = []
для cl в диапазоне (1,4):
mean_vectors.append (np.mean (X [y == cl], ось = 0))
print ('Класс среднего вектора% s:% s \ n'% (cl, mean_vectors [cl-1]))
Среднее значение класса вектора 1: [5,006 3,418 1,464 0,244]
Среднее значение класса вектора 2: [5,936 2,77 4,26 1,326]
Среднее значение вектора класса 3: [6,588 2,974 5,552 2,026] Шаг 2: Вычисление матриц рассеяния
S_W = np.zeros ((4,4))
для cl, mv в zip (диапазон (1,4), mean_vectors):
class_sc_mat = np.zeros ((4,4)) # матрица разброса для каждого класса
для строки в X [y == cl]:
row, mv = row.reshape (4,1), mv.reshape (4,1) # создаем векторы-столбцы
class_sc_mat + = (строка-МВ). точка ((строка-МВ) .Т)
S_W + = class_sc_mat # сумма матриц разброса классов
print ('Матрица разброса внутри класса: \ n', S_W)
Матрица разброса внутри класса:
[[38. T $
, где $ m $ - общее среднее, а mmi и $ N_i $ - выборочное среднее и размеры соответствующих классов.
total_mean = np.mean (X, ось = 0)
S_B = np. нули ((4,4))
для i, mean_vec в перечислении (mean_vectors):
n = X [y == i + 1,:]. shape [0]
mean_vec = mean_vec.reshape (4,1) # создаёт вектор-столбец
total_mean = total_mean.reshape (4,1) # создать вектор-столбец
S_B + = n * (среднее_век - общее_среднее) .dot ((среднее_век - общее_среднее) .T)
print ('Матрица разброса между классами: \ n', S_B) Получаем
Матрица разброса между классами:
[[63,2121 -19,534 165.{-1} S_ {B} $ для получения линейных дискриминантов.
eig_val, eig_vecs = np.linalg.eig (np.linalg.inv (S_W) .dot (S_B))
для i в диапазоне (len (eig_val)):
eigvec_sc = eig_vecs [:, i] .reshape (4,1)
print ('\ nEigenvector {}: \ n {}'. format (i + 1, eigvec_sc.real))
print ('Собственное значение {:}: {: .2e}'. format (i + 1, eig_val [i] .real))
получаем
Собственный вектор 1:
[[-0.2049]
[-0,3871]
[0,5465]
[0,7138]]
Собственное значение 1: 3.23e + 01
Собственный вектор 2:
[[-0,009]
[-0.589]
[0,2543]
[-0,767]]
Собственное значение 2: 2.78e-01
Собственный вектор 3:
[[0.179]
[-0,3178]
[-0,3658]
[0.6011]]
Собственное значение 3: -4.02e-17
Собственный вектор 4:
[[0.179]
[-0,3178]
[-0,3658]
[0.6011]]
Собственное значение 4: -4.02e-17
После этого разложения нашей квадратной матрицы на собственные векторы и собственные значения, давайте кратко резюмируем, как мы можем интерпретировать эти результаты. И собственные векторы, и собственные значения предоставляют нам информацию об искажении линейного преобразования: собственные векторы в основном являются направлением этого искажения, а собственные значения являются коэффициентом масштабирования для собственных векторов, которые описывают величину искажения.{-1} S_B $, $ \ pmb {v} = \ text {Eigenvector} $ и $ \ lambda = \ text {Eigenvalue} $
для i в диапазоне (len (eig_val)):
eigv = eig_vecs [:, i] .reshape (4,1)
np.testing.assert_array_almost_equal (np.linalg.inv (S_W) .dot (S_B) .dot (eigv),
eig_val [i] * eigv,
decimal = 6, err_msg = '', verbose = True)
print ('ок')
получаем
нормально
Шаг 4: Выбор линейных дискриминантов для подпространства новых функций
4.1. Сортировка собственных векторов по убыванию собственных значений
Помните из введения, что мы не только заинтересованы в простом проецировании данных в подпространство, которое улучшает разделимость классов, но также снижает размерность нашего пространства признаков (где собственные векторы будут формировать оси этого нового подпространства признаков).
Однако собственные векторы определяют только направления новой оси, поскольку все они имеют одинаковую единицу длины 1.
Итак, чтобы решить, какие собственные векторы мы хотим отбросить для нашего подпространства меньшей размерности, мы должны взглянуть на соответствующие собственные значения собственных векторов.Грубо говоря, собственные векторы с наименьшими собственными значениями несут наименьшее количество информации о распределении данных, и это те, которые мы хотим отбросить.
Обычный подход заключается в ранжировании собственных векторов от самого высокого до самого низкого соответствующего собственного значения и выборе верхних собственных векторов $ k $.
# Составить список кортежей (собственное значение, собственный вектор)
eig_pairs = [(np.abs (eig_val [i]), eig_vecs [:, i]) для i в диапазоне (len (eig_val))]
# Сортировать кортежи (собственное значение, собственный вектор) от большего к меньшему
eig_pairs = sorted (eig_pairs, key = lambda k: k [0], reverse = True)
# Визуально подтверждаем, что список правильно отсортирован, уменьшая собственные значения
print ('Собственные значения в порядке убывания: \ n')
для i в eig_pairs:
print (i [0])
получаем
Собственные значения в порядке убывания:
32.2719577997
0,27756686384
5.71450476746e-15
5.71450476746e-15
Если мы посмотрим на собственные значения, мы уже увидим, что 2 собственных значения близки к 0. Причина, по которой они близки к 0, не в том, что они неинформативны, а в неточности чисел с плавающей запятой. Фактически, эти два последних собственных значения должны быть точно равны нулю: в LDA количество линейных дискриминантов не превышает $ c − 1 $, где $ c $ - количество меток классов, поскольку промежуточная матрица рассеяния $ S_B $ равна сумма $ c $ матриц ранга 1 или меньше.Обратите внимание, что в редком случае идеальной коллинеарности (все выровненные точки выборки попадают на прямую линию) ковариационная матрица будет иметь ранг один, что приведет только к одному собственному вектору с ненулевым собственным значением.
Теперь давайте выразим «объясненную дисперсию» в процентах:
print ('Разница объяснена: \ n')
eigv_sum = сумма (eig_val)
для i, j в перечислении (eig_pairs):
print ('собственное значение {0:}: {1: .2%}'. format (i + 1, (j [0] / eigv_sum) .real))
получаем
Расхождение объяснено:
собственное значение 1:99.15%
собственное значение 2: 0,85%
собственное значение 3: 0,00%
собственное значение 4: 0,00%
Первая собственная пара на сегодняшний день является наиболее информативной, и мы не потеряем много информации, если сформируем одномерный признак, разнесенный на основе этой собственной пары.
4.2. Выбор k собственных векторов с наибольшими собственными значениями
После сортировки собственных пар путем уменьшения собственных значений пришло время построить нашу $ k \ times d-мерную матрицу $ W $ собственных векторов (здесь 4 × 2: на основе 2 наиболее информативных собственных пар) и тем самым уменьшить начальные 4- пространство пространственных признаков в 2-мерное подпространство признаков.
W = np.hstack ((eig_pairs [0] [1] .reshape (4,1), eig_pairs [1] [1] .reshape (4,1)))
print ('Матрица W: \ n', W.real)
Получаем
Матрица W:
[[0,2049 -0,009]
[0,3871 -0,589]
[-0,5465 0,2543]
[-0,7138 -0,767]]
Шаг 5: Преобразование образцов в новое подпространство
На последнем этапе мы используем $ 4 \ times 2-мерную матрицу $ W $, которую мы только что вычислили, для преобразования наших выборок в новое подпространство с помощью уравнения $ Y = X \ times W $.',' s ',' o '), (' синий ',' красный ',' зеленый ')): plt.scatter (x = X_lda [:, 0] .real [y == label],
y = X_lda [:, 1] .real [y == label],
marker = маркер,
color = цвет,
альфа = 0,5,
label = label_dict [метка]
) plt.xlabel ('LD1')
plt.ylabel ('LD2') leg = plt.legend (loc = 'верхний правый', fancybox = True)
leg.get_frame (). set_alpha (0,5)
plt.title ('LDA: проекция радужки на первые 2 линейных дискриминанта') # скрыть отметки оси
plt.tick_params (axis = "both", which = "both", bottom = "off", top = "off",
labelbottom = "on", left = "off", right = "off", labelleft = "on") # удалить шипы оси
ax.spines ["вверху"]. set_visible (Ложь)
ax.spines ["право"]. set_visible (Ложь)
ax.spines ["снизу"]. set_visible (Ложь)
ax.spines ["влево"]. set_visible (Ложь) plt.grid ()
plt.tight_layout
plt.show () plot_step_lda ()
Диаграмма рассеяния выше представляет наше новое подпространство функций, которое мы создали с помощью LDA.Мы видим, что первый линейный дискриминант «LD1» довольно хорошо разделяет классы. Однако второй дискриминант, LD2, не добавляет много ценной информации, что мы уже пришли к выводу, когда рассматривали ранжированные собственные значения, это шаг 4.
Ярлык - LDA в scikit-learn
Теперь, после того как мы увидели, как работает линейный дискриминантный анализ с использованием пошагового подхода, есть также более удобный способ добиться того же с помощью класса LDA, реализованного в библиотеке машинного обучения scikit-learn.
# import library
импортировать панд как pd
из sklearn.preprocessing import LabelEncoder
из sklearn.discriminant_analysis import LinearDiscriminantAnalysis как LDA
из matplotlib импортировать pyplot как plt
feature_dict = {i: метка для i, метка в zip (
диапазон (4),
('длина чашелистика в см',
'ширина чашелистика в см',
'длина лепестка в см',
'ширина лепестка в см',))}
# Чтение набора данных
df = pd.io.parsers.read_csv (
filepath_or_buffer = 'https: //archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
заголовок = Нет,
sep = ',',
)
df.columns = [l для i, l в отсортированном (feature_dict.items ())] + ['метка класса']
df.dropna (how = "all", inplace = True) # чтобы удалить пустую строку в конце файла
# используйте LabelEncode из библиотеки scikit-learn, чтобы преобразовать метки классов в числа: 1, 2 и 3
X = df [[0,1,2,3]]. Значения
y = df ['метка класса']. значения
enc = LabelEncoder ()
label_encoder = enc.fit (y)
y = label_encoder.',' s ',' o '), (' синий ',' красный ',' зеленый ')):
plt.scatter (x = X [:, 0] [y == label],
y = X [:, 1] [y == label] * -1, # перевернуть фигуру
marker = маркер,
color = цвет,
альфа = 0,5,
label = label_dict [метка])
plt.xlabel ('LD1')
plt.ylabel ('LD2')
leg = plt.legend (loc = 'верхний правый', fancybox = True)
leg.get_frame (). set_alpha (0,5)
plt.title (заголовок)
# скрыть отметки оси
plt.tick_params (axis = "both", which = "both", bottom = "off", top = "off",
labelbottom = "on", left = "off", right = "off", labelleft = "on")
# удалить шипы оси
топор.шипы ["верх"]. set_visible (Ложь)
ax.spines ["право"]. set_visible (Ложь)
ax.spines ["снизу"]. set_visible (Ложь)
ax.spines ["влево"]. set_visible (Ложь)
plt.grid ()
plt.tight_layout
plt.show ()
plot_scikit_lda (X_lda_sklearn, title = 'LDA по умолчанию через scikit-learn') получаем
Резюме:
В этой статье мы продолжили знакомство с методами матричной факторизации для уменьшения размерности многомерных наборов данных.В частности, в этом посте мы описали основные шаги и основные концепции анализа данных с помощью линейного дискриминантного анализа (LDA). Мы показали универсальность этого метода на одном примере и описали, как можно интерпретировать результаты применения этого метода.
Линейный дискриминантный анализ Фишера в Python с нуля | by Vrutik Halani
Линейный дискриминантный анализ Фишера (LDA) - это алгоритм уменьшения размерности, который также можно использовать для классификации.В этом сообщении блога мы узнаем больше о LDA Fisher и реализуем его с нуля на Python.
LDA?
Линейный дискриминантный анализ (LDA) - это метод уменьшения размерности. Как следует из названия, методы уменьшения размерности уменьшают количество измерений (то есть переменных) в наборе данных, сохраняя при этом как можно больше информации. Например, предположим, что мы построили связь между двумя переменными, где каждый цвет представляет другой класс.
ПОЧЕМУ?
Основная идея состоит в том, чтобы изучить набор параметров w ∈ R (d × d ′), которые используются для проецирования данных x ∈ R (d) в меньшее измерение d ′. На рисунке ниже (Bishop, 2006) показана иллюстрация. Исходные данные имеют 2 измерения, d = 2, и мы хотим спроецировать их на 1 измерение, d = 1.
Если мы проецируем двумерные точки данных на линию (1-D) из всех таких линий, наша цель - найти ту, которая максимизирует расстояние между средними значениями двух классов после проецирования.Если бы мы могли это сделать, мы могли бы добиться хорошего разделения между классами в 1-D. Это проиллюстрировано на рисунке слева и может быть отражено в идее максимизации «ковариации между классами ». Однако, как мы видим, это вызывает много совпадений между проектируемыми классами. Мы также хотим минимизировать это перекрытие. Чтобы справиться с этим, Fisher's LDA пытается минимизировать « внутриклассовую ковариацию » для каждого класса. Минимизация этой ковариации приводит нас к проекции на рисунке справа, которая имеет минимальное перекрытие.Формализуя это, мы можем представить цель следующим образом.
Минимизировать это выражение = Цель Fischer LDA, где Sb ∈ R (d × d) и Sw ∈ R (d × d) - ковариационные матрицы между классами и внутри классов соответственно. Они рассчитываются как
Calculation of Sb и Sw, где Xnk - n-й пример данных в k-м классе, Nk - количество примеров в классе k, m - общее среднее всех данных, а mk - среднее значение k-го класс. Теперь, используя двойственные лагранжианы и условия KKT, проблема максимизации J может быть преобразована в решение:
, которое является проблемой собственных значений для матрицы inv (Sw).Сб. Таким образом, нашим окончательным решением для w будут собственные векторы приведенного выше уравнения, соответствующие наибольшим собственным значениям. Для сокращения до размеров d ′ мы берем наибольшие собственные значения d ′, поскольку они будут содержать наибольшее количество информации. Также обратите внимание, что если у нас есть K классов, максимальное значение d ′ может быть K − 1. То есть мы не можем проецировать данные класса K в размерность больше K − 1. (Конечно, d 'не может быть больше, чем исходное измерение данных d). Это происходит по следующей причине. Обратите внимание, что матрица разброса между классами, Sb, была суммой K матриц, каждая из которых имеет ранг 1 и является внешним произведением двух векторов.Кроме того, поскольку общее среднее и среднее значение отдельного класса связаны, только (K − 1) из этих K матриц являются независимыми. Таким образом, Sb имеет максимальный ранг K − 1 и, следовательно, имеется только K − 1 ненулевых собственных значений. Таким образом, мы не можем проецировать данные более чем на K − 1 измерения.
Линейный дискриминантный анализ в Python
импортировать numpy как np
импортировать matplotlib.pyplot как plt
из стиля импорта matplotlib
style.use ('пятьсот тридцать восемь')
np.random.seed (семя = 42)
# Создать данные
прямоугольники = np.массив ([[1,1.5,1.7,1.45,1.1,1.6,1.8], [1.8,1.55,1.45,1.6,1.65,1.7,1.75]])
треугольники = np.array ([[0.1,0.5,0.25,0.4,0.3,0.6,0.35,0.15,0.4,0.5,0.48], [1.1,1.5,1.3,1.2,1.15,1.0,1.4,1.2,1.3, 1.5,1.0]])
круги = np.array ([[1.5,1.55,1.52,1.4,1.3,1.6,1.35,1.45,1.4,1.5,1.48,1.51,1.52,1.49,1.41,1.39,1.6,1.35,1.55,1.47,1.57, 1,48,
1.55,1.555,1.525,1.45,1.35,1.65,1.355,1.455,1.45,1.55,1.485,1.515,1.525,1.495,1.415,1.395,1.65,1.355,1.555,1.475,1.575,1.485]
, [1.3,1.35,1.33,1.', c =' желтый ', edgecolor =' черный ')
ax0.scatter (круги [0], круги [1], marker = 'o', c = 'blue', edgecolor = 'black')
# Вычислить средние векторы для каждого класса
mean_rectangles = np.mean (rectangles, axis = 1) .reshape (2,1) # Создает вектор 2x1, состоящий из средних значений размеров
mean_triangles = np.mean (треугольники, ось = 1) .reshape (2,1)
mean_circles = np.mean (круги, ось = 1) .reshape (2,1)
# Вычислить матрицы разброса для SW (разброс внутри) и просуммировать элементы
scatter_rectangles = np.dot ((средние_прямоугольники), (средние_прямоугольники).Т)
# Помните, что мы не вычисляем ковариационную матрицу здесь, потому что тогда нам нужно разделить на n или n-1, как показано ниже
#print ((1/7) * np.dot ((прямоугольные-средние_ прямоугольные), (прямоугольные-средние_ прямоугольные) .T))
#print (np.var (прямоугольники [0], ddof = 0))
scatter_triangles = np.dot ((треугольники-средние_треугольники), (треугольники-средние_треугольники) .T)
scatter_circles = np.dot ((круги-средние_круги), (круги-средние_круги) .T)
# Вычислить SW, добавив скаттеры внутри классов
SW = scatter_triangles + scatter_circles + scatter_rectangles
печать (SW)
plt.показывать()
Алгоритм оценки Фишера для метода взвешенной регрессии для картирования QTL
Модель
Модель следует за Xu (1998b) и Feenstra et al. (2006), что составляет
, где y j - фенотипическое значение индивидуума j ( j = 1, ⋯, n ), U j - ожидание переменных, указывающих генотип QTL с учетом информации маркера, β - вектор эффектов QTL (включая среднее значение по популяции) и e j - остаточная ошибка.Остаточная ошибка имеет нулевое среднее значение и дисперсию
, где - матрица условной дисперсии-ковариации индикаторных переменных QTL с учетом маркерной информации (это не знак суммирования). Обратите внимание, что если наблюдается генотип QTL (то есть QTL перекрывается с полностью информативным маркером), он будет равен нулю, и, таким образом, дисперсия остаточной ошибки будет идентична дисперсии ошибки окружающей среды σ 2 . Определения и формулировки U j и даны Xu (1998b), а также описаны позже в этом исследовании для популяции F 2 .Вектор параметров равен y j , U j и. Пусть
и
Функция правдоподобия основана на предположении о независимости для j = 1, ⋯, n . Следовательно, логарифм функции правдоподобия равен
, где
алгоритм оценки Фишера
Частные производные правдоподобия для индивидуума j по параметрам равны
где.Дальнейшие манипуляции с уравнением (7) приводят к
Позвольте быть вектором оценок и быть матрицей Гессе. Информационная матрица есть. Используя следующее тождество (Wedderburn, 1974)
, мы получили
Вектор оценок равен
Вывод уравнений (10) и (11) представлен в Приложении A для опытных читателей. Информационная матрица и вектор оценок требуются для выполнения следующего алгоритма оценки Фишера для оценки ML
, где - значение параметра в t- -й итерации.Начиная с начального значения, мы повторяем уравнение (12) до тех пор, пока не будет достигнут определенный критерий сходимости, т.е. Решение ML для t удовлетворяет критерию сходимости. Матрица дисперсии-ковариации оцениваемых параметров задается
W-test statistic
Когда известна матрица дисперсии-ковариации оцениваемых параметров, тесты отношения правдоподобия не нужны. Вместо этого можно использовать статистику W-критерия (Wald, 1941). Теперь мы используем схему сопряжения F 2 в качестве примера, чтобы показать, как построить статистику W-критерия.Пусть
- индикаторные переменные для генотипа QTL, линейная модель фенотипической ценности особи j равна
, где β 0 = μ - среднее значение популяции (отрезок), β 1 = a - это аддитивный эффект, а β 2 = d - эффект доминирования и ошибка среды. Используя информацию о маркере, мы вычисляем
где. Матрица представляет собой
, где
и
Вероятности генотипов QTL, обусловленные маркерной информацией, составляют и, соответственно, для трех генотипов.Они рассчитываются на основе многоточечного метода Jiang and Zeng (1997).
Вектор параметров равен. Следовательно, var ( θ ) является матрицей 4 × 4. Пусть и
будет подмножеством матрицы. Статистика W-критерия для гипотезы составляет
. В соответствии с H 0 , эта статистика теста приблизительно соответствует распределению χ 2 с двумя степенями свободы. Следовательно, статистика W-критерия сравнима со статистикой теста отношения правдоподобия. Статистика W-критерия имеет простую взаимосвязь со статистикой F-критерия, то есть W = 2 F, где статистика F-критерия следует F-распределению со степенями свободы числителя 2 и степенями свободы знаменателя n −3 под H 0 .
Информационная матрица алгоритма EM
Метод машинного обучения на основе смешанной модели, реализованный с помощью алгоритма максимизации ожидания (EM) (Lander and Botstein, 1989), не имеет простого метода для вычисления ковариационно-дисперсионной матрицы оцениваемых параметров. . Метод Као и Цзэна (1997) для вычисления дисперсионно-ковариационной матрицы довольно сложен. Если положение QTL фиксировано в определенном месте генома, то есть положение QTL не является параметром, их формулы могут быть упрощены.Упрощенную версию ковариационно-дисперсионной матрицы относительно легко запрограммировать. Чтобы сравнить алгоритм подсчета очков Фишера с методом ML на основе смешанной модели для матрицы дисперсии-ковариации оцениваемых параметров, мы ввели здесь матрицу дисперсии-ковариации в рамках алгоритма EM. Алгоритм EM получен на основе следующей модели QTL с полными данными (при условии, что генотипы QTL наблюдаемы)
Функция оценки при полном соблюдении X j равна
Матрица Гессе (вторые частные производные)
Информационная матрица Луи (1982):
Ожидания взяты в отношении пропущенного значения X с использованием апостериорных вероятностей генотипов QTL.Вычислить первый член несложно, но второй член вычислить сложно.

 При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет.
При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет. 7844, num df = 12, denom df = 8, p-value = 0.6797
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.1867876 2.7547991
sample estimates:
ratio of variances
0.784446
7844, num df = 12, denom df = 8, p-value = 0.6797
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.1867876 2.7547991
sample estimates:
ratio of variances
0.784446 10, то #NUM! значение ошибки #ЗНАЧ!.
10, то #NUM! значение ошибки #ЗНАЧ!.