формулы вычисления. Формула нахождения корней квадратного уравнения
Некоторые задачи в математике требуют умения вычислять значение корня квадратного. К таким задачам относится решение уравнений второго порядка. В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
Что такое квадратный корень?
В математике этому понятию соответствует символ √. Исторические данные говорят, что он начал использоваться впервые приблизительно в первой половине XVI века в Германии (первый немецкий труд по алгебре Кристофа Рудольфа). Ученые полагают, что указанный символ является трансформированной латинской буквой r (radix означает «корень» на латыни).

Корень из какого-либо числа равен такому значению, квадрат которого соответствует подкоренному выражению. На языке математики это определение будет выглядеть так: √x = y, если y2 = x.
Корень из положительного числа (x > 0) является также числом положительным (y > 0), однако если берут корень из отрицательного числа (x < 0), то его результатом уже будет комплексное число, включающее мнимую единицу i.
Приведем два простых примера:
√9 = 3, поскольку 32 = 9; √(-9) = 3i, поскольку i2 = -1.
Итерационная формула Герона для нахождения значений корней квадратных
Приведенные выше примеры являются очень простыми, и вычисление корней в них не представляет никакого труда. Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.
Во всех вышеназванных случаях следует применять специальный метод вычисления корня квадратного. В настоящее время таких методов известно несколько: например разложение в ряд Тейлора, деление столбиком и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский способ определения квадратных корней (существуют свидетельства, что древние вавилоняне применяли ее в своих практических вычислениях).
Пусть необходимо определить значение √x. Формула нахождения квадратного корня имеет следующий вид:
an+1 = 1/2(an+x/an), где limn->∞(an) => x.
Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a0 (оно может быть произвольным, однако для быстрого получения результата следует выбирать его таким, чтобы (a0)2 было максимально близко к x. Затем подставить его в указанную формулу вычисления квадратного корня и получить новое число a1, которое уже будет ближе к искомому значению. После этого необходимо уже a1 подставить в выражение и получить a2. Эту процедуру следует повторять до получения необходимой точности.
Пример применения итерационной формулы Герона
Описанный выше алгоритм получения корня квадратного из некоторого заданного числа для многих может звучать достаточно сложно и запутанно, на деле же оказывается все гораздо проще, поскольку эта формула сходится очень быстро (особенно если выбрано удачное число a0).
Приведем простой пример: необходимо вычислить √11. Выберем a0 = 3, так как 32 = 9, что ближе к 11, чем 42 = 16. Подставляя в формулу, получим:
a1 = 1/2(3 + 11/3) = 3,333333;
a2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
a3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Дальше нет смысла продолжать вычисления, поскольку мы получили, что a2 и a3 начинают отличаться лишь в 5-м знаке после запятой. Таким образом, достаточно было применить всего 2 раза формулу, чтобы вычислить √11 с точностью до 0,0001.
В настоящее время широко используются калькуляторы и компьютеры для вычисления корней, тем не менее отмеченную формулу полезно запомнить, чтобы иметь возможность вручную вычислять их точное значение.
Уравнения второго порядка
Понимание того, что такое корень квадратный, и умение его вычислять используется при решении квадратных уравнений. Этими уравнениями называют равенства с одной неизвестной, общий вид которых приведен на рисунке ниже.
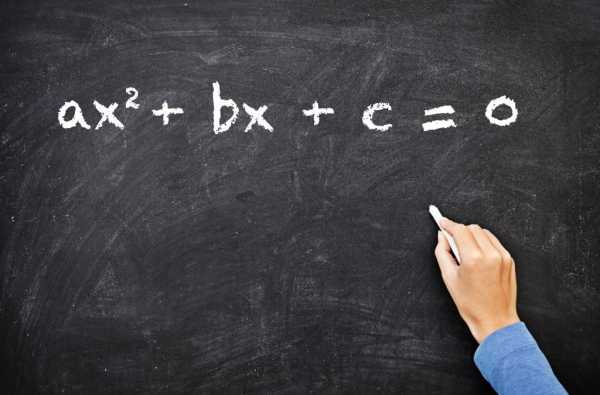
Здесь c, b и a представляют собой некоторые числа, причем a не должно равняться нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.
Любые значения икса, удовлетворяющие указанному на рисунке равенству, называются его корнями (следует не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x2), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.
Нахождения корней квадратного уравнения (формула)
Этот способ решения рассматриваемого типа равенств также называется универсальным, или методом через дискриминант. Его можно применять для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:

Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление x1 отличается от расчета x2 только знаком перед корнем квадратным. Подкоренное выражение, которое равно b2 — 4ac, является не чем иным, как дискриминантом рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, поскольку он определяет число и тип решений. Так, если он равен нулю, то решение будет всего одно, если он положительный, то уравнение обладает двумя действительными корнями, наконец, отрицательный дискриминант приводит к двум комплексным корням x1 и x2.
Теорема Виета или некоторые свойства корней уравнений второго порядка
В конце XVI века один из основоположников современной алгебры француз Франсуа Виет, изучая уравнения второго порядка, смог получить свойства его корней. Математически их можно записать так:
x1 + x2 = -b / a и x1 * x2 = c / a.
Оба равенства легко может получить каждый, для этого необходимо лишь выполнить соответствующие математические операции с корнями, полученными через формулу с дискриминантом.

Совокупность этих двух выражений можно по праву назвать второй формулой корней квадратного уравнения, которая предоставляет возможность угадывать его решения, не используя при этом дискриминант. Здесь следует оговориться, что хотя оба выражения справедливы всегда, применять их для решения уравнения удобно только в том случае, если оно может быть разложено на множители.
Задача на закрепление полученных знаний
Решим математическую задачу, в которой продемонстрируем все приемы, обсуждаемые в статье. Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.

Это условие сразу напоминает о теореме Виета, применяя формулы суммы квадратных корней и их произведения, записываем:
x1 + x2 = -b / a = 4;
x1 * x2 = c / a = -13.
Если предположить, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:
x2 — 4x — 13 = 0.
Воспользуемся формулой с дискриминантом, получим следующие корни:
x1,2 = (4 ± √D)/2, D = 16 — 4 * 1 * (-13) = 68.
То есть задача свелась к нахождению числа √68. Заметим, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получим: √68 = 2√17.
Теперь воспользуемся рассмотренной формулой квадратного корня: a0 = 4, тогда:
a1 = 1/2(4 + 17/4) = 4,125;
a2 = 1/2(4,125 + 17/4,125) = 4,1231.
В вычислении a3 нет необходимости, поскольку найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставляя его в формулу для x1,2, получим:
x1 = (4 + 8,246)/2 = 6,123 и x2 = (4 — 8,246)/2 = -2,123.
Как видим, сумма найденных чисел действительно равна 4, если же найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.
fb.ru
формулы вычисления. Формула нахождения корней квадратного уравнения — OneKu
Содержание статьи:Некоторые задачи в математике требуют умения вычислять значение корня квадратного. К таким задачам относится решение уравнений второго порядка. В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
Что такое квадратный корень?
В математике этому понятию соответствует символ √. Исторические данные говорят, что он начал использоваться впервые приблизительно в первой половине XVI века в Германии (первый немецкий труд по алгебре Кристофа Рудольфа). Ученые полагают, что указанный символ является трансформированной латинской буквой r (radix означает «корень» на латыни).
Вам будет интересно:Гимназия при Русском музее, Санкт-Петербург: отзывы

Корень из какого-либо числа равен такому значению, квадрат которого соответствует подкоренному выражению. На языке математики это определение будет выглядеть так: √x = y, если y2 = x.
Корень из положительного числа (x > 0) является также числом положительным (y > 0), однако если берут корень из отрицательного числа (x
Приведем два простых примера:
√9 = 3, поскольку 32 = 9; √(-9) = 3i, поскольку i2 = -1.
Итерационная формула Герона для нахождения значений корней квадратных
Приведенные выше примеры являются очень простыми, и вычисление корней в них не представляет никакого труда. Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.
Во всех вышеназванных случаях следует применять специальный метод вычисления корня квадратного. В настоящее время таких методов известно несколько: например разложение в ряд Тейлора, деление столбиком и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский способ определения квадратных корней (существуют свидетельства, что древние вавилоняне применяли ее в своих практических вычислениях).
Пусть необходимо определить значение √x. Формула нахождения квадратного корня имеет следующий вид:
an+1 = 1/2(an+x/an), где limn->∞(an) => x.
Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a0 (оно может быть произвольным, однако для быстрого получения результата следует выбирать его таким, чтобы (a0)2 было максимально близко к x. Затем подставить его в указанную формулу вычисления квадратного корня и получить новое число a1, которое уже будет ближе к искомому значению. После этого необходимо уже a1 подставить в выражение и получить a2. Эту процедуру следует повторять до получения необходимой точности.
Пример применения итерационной формулы Герона
Вам будет интересно:Психология и философия: связь наук, общие понятия, отличия
Описанный выше алгоритм получения корня квадратного из некоторого заданного числа для многих может звучать достаточно сложно и запутанно, на деле же оказывается все гораздо проще, поскольку эта формула сходится очень быстро (особенно если выбрано удачное число a0).
Приведем простой пример: необходимо вычислить √11. Выберем a0 = 3, так как 32 = 9, что ближе к 11, чем 42 = 16. Подставляя в формулу, получим:
a1 = 1/2(3 + 11/3) = 3,333333;
a2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
a3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Дальше нет смысла продолжать вычисления, поскольку мы получили, что a2 и a3 начинают отличаться лишь в 5-м знаке после запятой. Таким образом, достаточно было применить всего 2 раза формулу, чтобы вычислить √11 с точностью до 0,0001.
В настоящее время широко используются калькуляторы и компьютеры для вычисления корней, тем не менее отмеченную формулу полезно запомнить, чтобы иметь возможность вручную вычислять их точное значение.
Уравнения второго порядка
Понимание того, что такое корень квадратный, и умение его вычислять используется при решении квадратных уравнений. Этими уравнениями называют равенства с одной неизвестной, общий вид которых приведен на рисунке ниже.
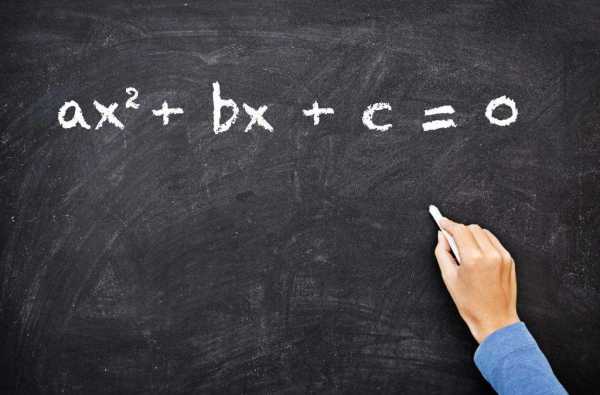
Здесь c, b и a представляют собой некоторые числа, причем a не должно равняться нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.
Любые значения икса, удовлетворяющие указанному на рисунке равенству, называются его корнями (следует не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x2), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.
Нахождения корней квадратного уравнения (формула)
Этот способ решения рассматриваемого типа равенств также называется универсальным, или методом через дискриминант. Его можно применять для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:
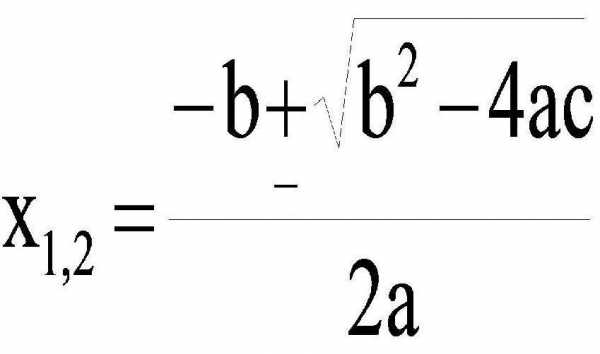
Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление x1 отличается от расчета x2 только знаком перед корнем квадратным. Подкоренное выражение, которое равно b2 — 4ac, является не чем иным, как дискриминантом рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, поскольку он определяет число и тип решений. Так, если он равен нулю, то решение будет всего одно, если он положительный, то уравнение обладает двумя действительными корнями, наконец, отрицательный дискриминант приводит к двум комплексным корням x1 и x2.
Теорема Виета или некоторые свойства корней уравнений второго порядка
В конце XVI века один из основоположников современной алгебры француз Франсуа Виет, изучая уравнения второго порядка, смог получить свойства его корней. Математически их можно записать так:
x1 + x2 = -b / a и x1 * x2 = c / a.
Оба равенства легко может получить каждый, для этого необходимо лишь выполнить соответствующие математические операции с корнями, полученными через формулу с дискриминантом.

Совокупность этих двух выражений можно по праву назвать второй формулой корней квадратного уравнения, которая предоставляет возможность угадывать его решения, не используя при этом дискриминант. Здесь следует оговориться, что хотя оба выражения справедливы всегда, применять их для решения уравнения удобно только в том случае, если оно может быть разложено на множители.
Задача на закрепление полученных знаний
Решим математическую задачу, в которой продемонстрируем все приемы, обсуждаемые в статье. Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.

Это условие сразу напоминает о теореме Виета, применяя формулы суммы квадратных корней и их произведения, записываем:
x1 + x2 = -b / a = 4;
x1 * x2 = c / a = -13.
Если предположить, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:
x2 — 4x — 13 = 0.
Воспользуемся формулой с дискриминантом, получим следующие корни:
x1,2 = (4 ± √D)/2, D = 16 — 4 * 1 * (-13) = 68.
То есть задача свелась к нахождению числа √68. Заметим, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получим: √68 = 2√17.
Теперь воспользуемся рассмотренной формулой квадратного корня: a0 = 4, тогда:
a1 = 1/2(4 + 17/4) = 4,125;
a2 = 1/2(4,125 + 17/4,125) = 4,1231.
В вычислении a3 нет необходимости, поскольку найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставляя его в формулу для x1,2, получим:
x1 = (4 + 8,246)/2 = 6,123 и x2 = (4 — 8,246)/2 = -2,123.
Как видим, сумма найденных чисел действительно равна 4, если же найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.
Источник
1ku.ru
Формула корней квадратного уравнения. Теорема Виета. Формула корней квадратного уравнения.
О.Уравнение вида,
где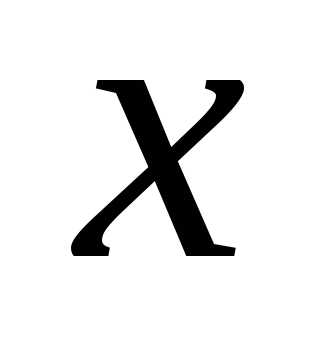 – переменная,
– переменная, называетсяквадратным.
называетсяквадратным.
О.Если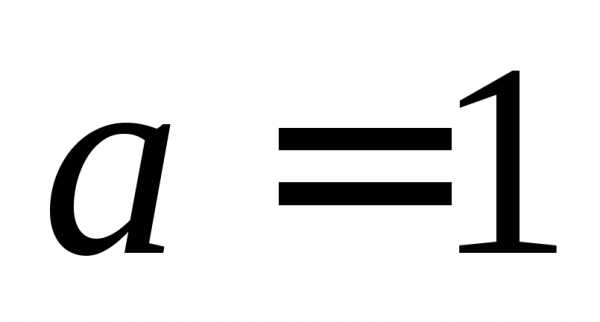 ,
то уравнение называется
,
то уравнение называется
О.Квадратное уравнение, в котором хотя
бы один из коэффициентов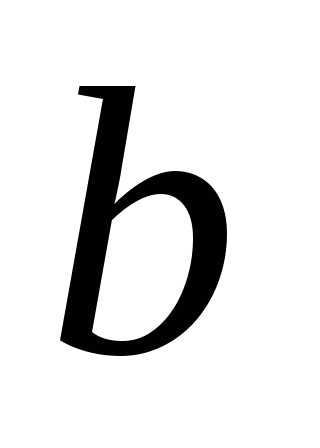 или
или равен
равен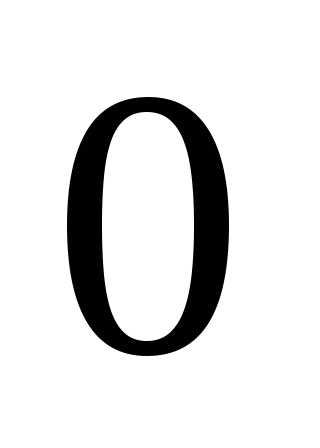 ,
называетсянеполным квадратным
уравнением
,
называетсянеполным квадратным
уравнением
Выведем формулу корней квадратного уравнения в общем случае:
, 
Поделим
обе части уравнения на  .
При этом корни уравнения не изменятся(почему?).
.
При этом корни уравнения не изменятся(почему?).
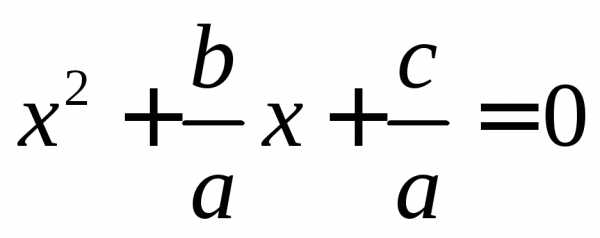
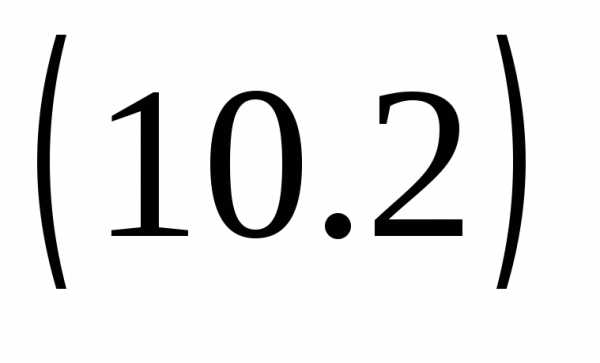
Выделим полный квадрат:
О.Выражение: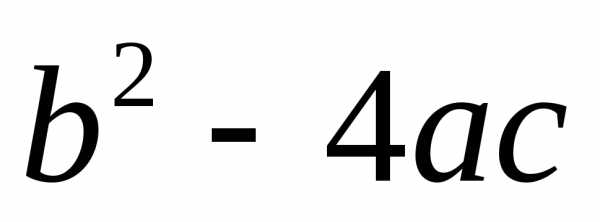 называетсядискриминантом
квадратного уравнения, и
обозначается через
называетсядискриминантом
квадратного уравнения, и
обозначается через  ,
тогда уравнение можно записать так:
,
тогда уравнение можно записать так:
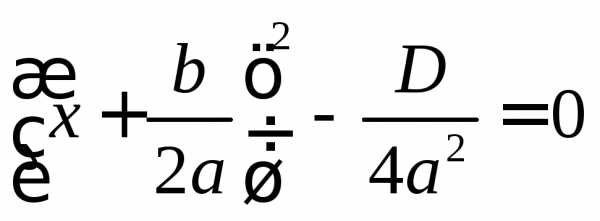
Возможны следующие 3 случая:
Если
 ,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения:
,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения:

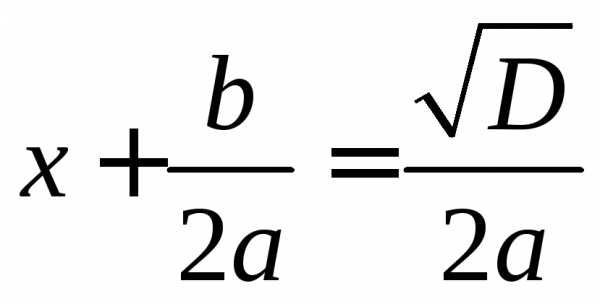 или
или 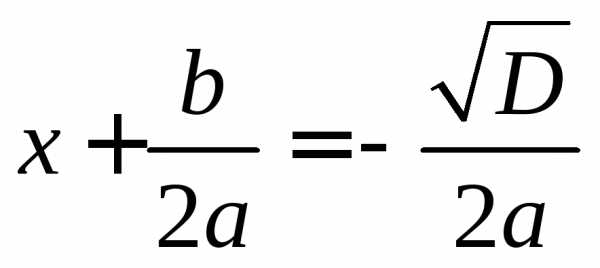
То есть

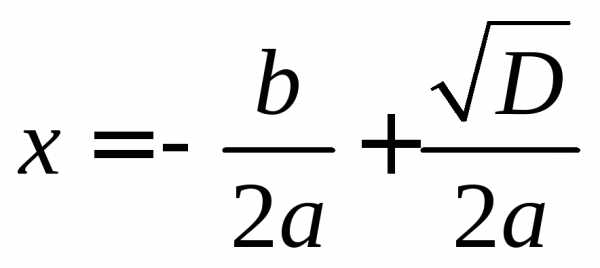 или
или 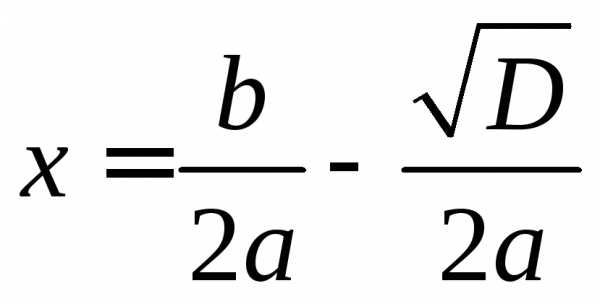

 или
или 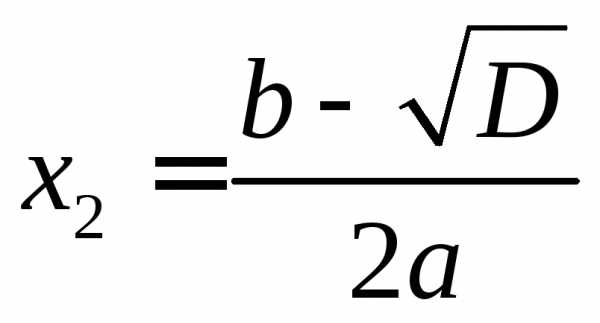
Эти две формулы можно объединить в следующую:
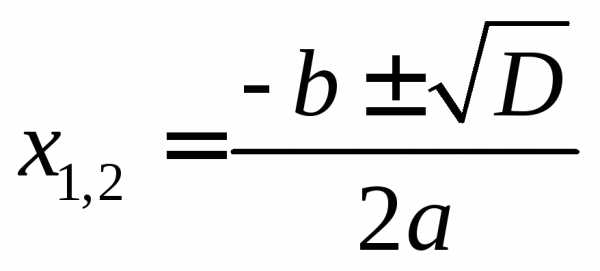 —
эта формула
называется формулой
корней квадратного уравнения
—
эта формула
называется формулой
корней квадратного уравнения
Если
 ,
то уравнение
,
то уравнение  примет вид:
примет вид:
В этом случае уравнение имеет один корень.
Замечание: можно также сказать, что в этом случае квадратное уравнение имеет два совпадающих корня.
Если
 ,
то значение дроби
,
то значение дроби ,
поэтому уравнение
,
поэтому уравнение  ,
а значит и уравнение
,
а значит и уравнение  не
имеет корней (почему?).
не
имеет корней (почему?).
Таким образом,
Если  ,
то уравнение
,
то уравнение  имеет 2 различных корня:
имеет 2 различных корня: 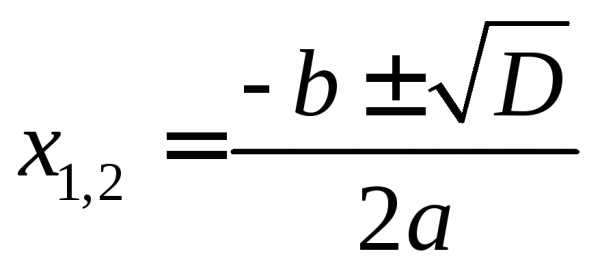
Если 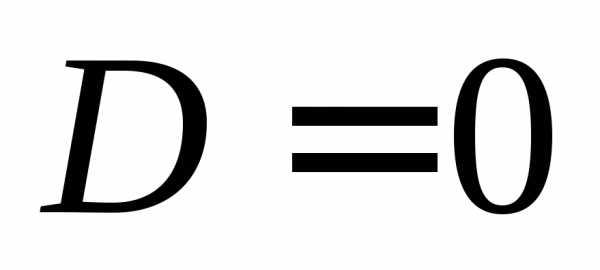 ,
то уравнение
,
то уравнение 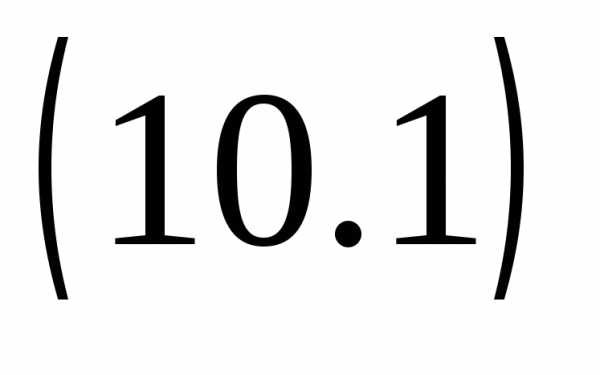 имеет 2 совпадающих корня:
имеет 2 совпадающих корня: 
Если 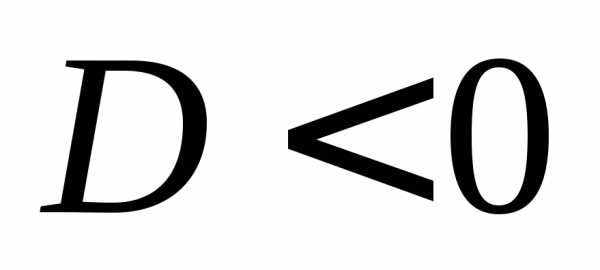 ,
то уравнение
,
то уравнение 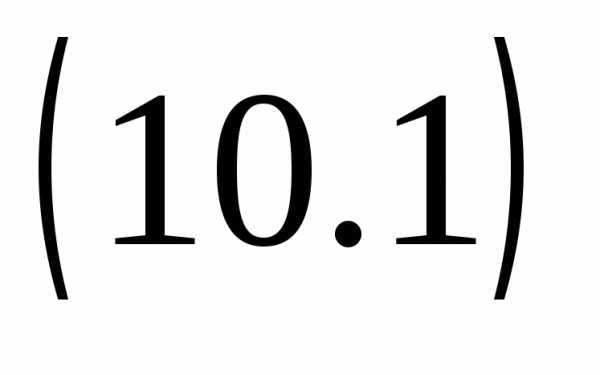 корней не имеет.
корней не имеет.
Теорема Виета.
Пусть
дано уравнение
, 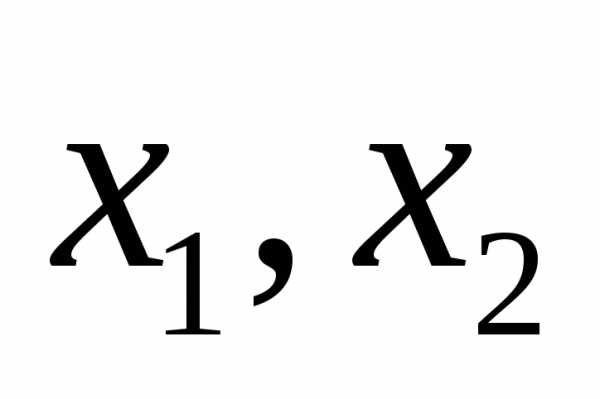 – корни уравнения, тогда
– корни уравнения, тогда

Доказательство:
Пусть
уравнение
имеет 2 различных корня ( ):
):
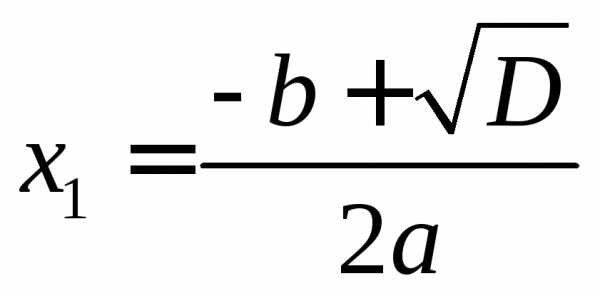
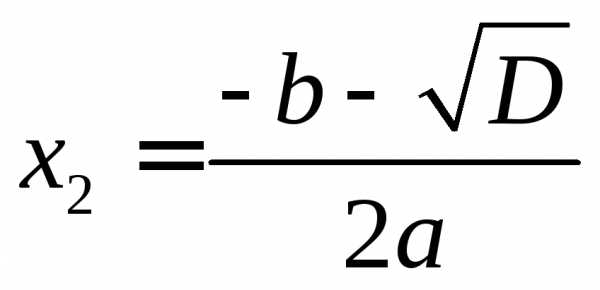
Итак,
действительно 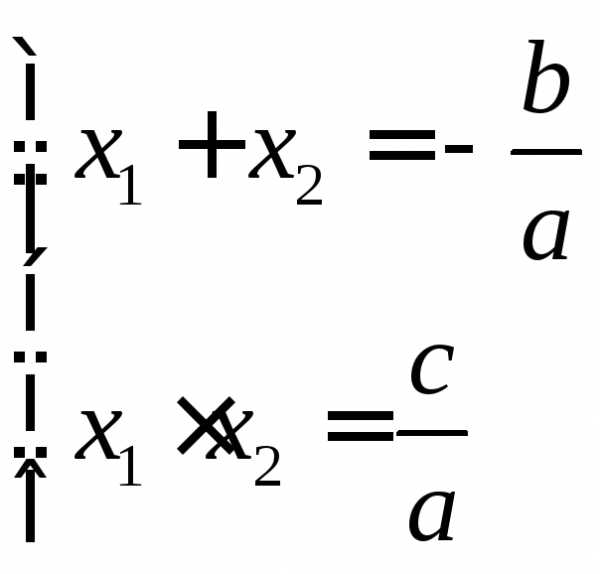
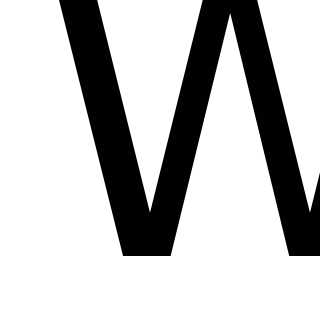
Замечание:
Если рассмотреть приведенное квадратное
уравнение
,
то формулы Виета будут выглядеть так:  .
.
В школьном курсе математики чаще всего формулы Виета применяются именно для приведенного квадратного уравнения.
Имеет место теорема, обратная теореме Виета:
Если
числа 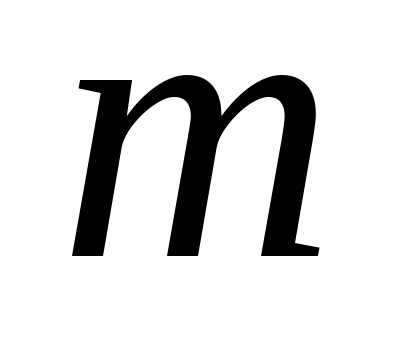 и
и таковы, что
таковы, что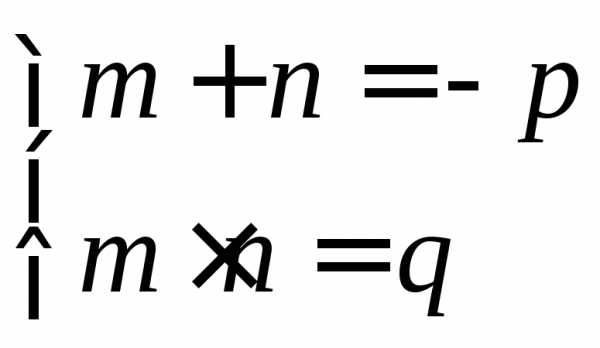
То эти числа являются корнями уравнения
Доказательство:
Значит,
числа 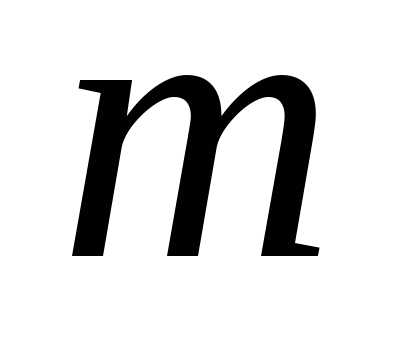 и
и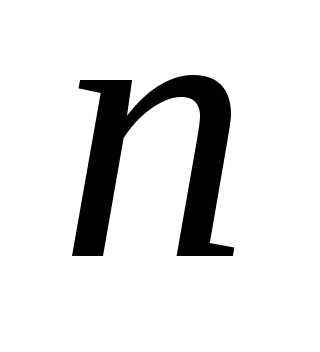 действительно являются корнями уравнения
.
действительно являются корнями уравнения
. 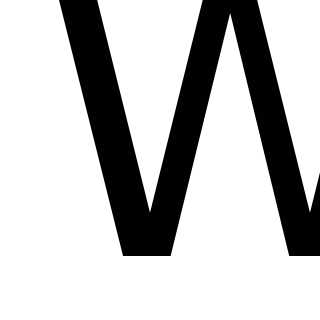
Замечание: теорема, обратная теореме Виета, позволяет составлять квадратные уравнения по его корням.
Например, если , то, тогда эти числа являются корнями уравнения
Разложение квадратного трехчлена на линейные множители
О.Многочлен вида:,
где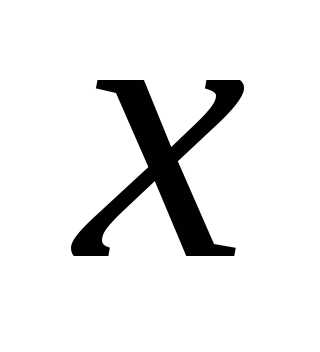 – переменная,
– переменная, называетсяквадратным трехчленом.
называетсяквадратным трехчленом.
О.Корнемквадратного трехчлена называется значение переменной, при которой значение этого трехчлена равно нулю.
Теорема.
Если 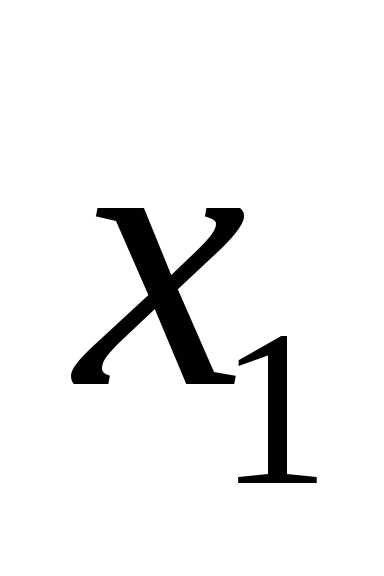 и
и – корни квадратного трёхчлена ,
то
– корни квадратного трёхчлена ,
то
Доказательство:
Вынесем за скобки
в многочлене множительа. Получим:.
Так как корни квадратного трёхчленаявляются корнями квадратного уравнения,
то, по теореме Виета,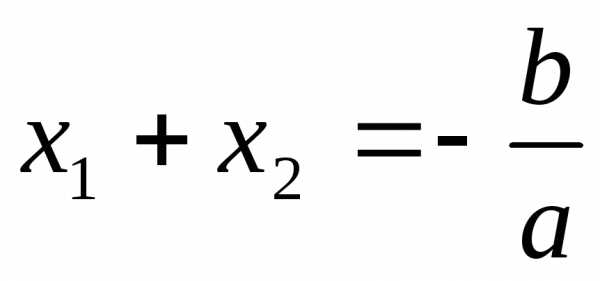 ,
,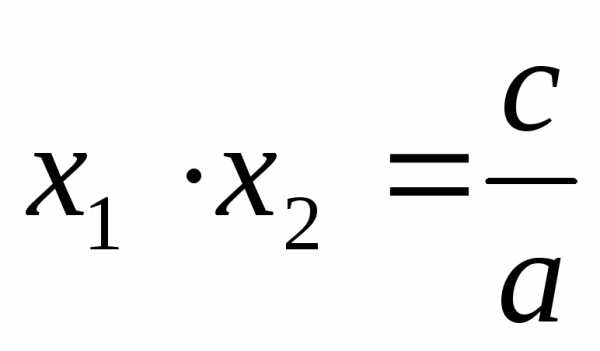 .
.
Поэтому
Итак, 
Если квадратный
трёхчлен имеет один корень (два
совпадающих корня), то формула 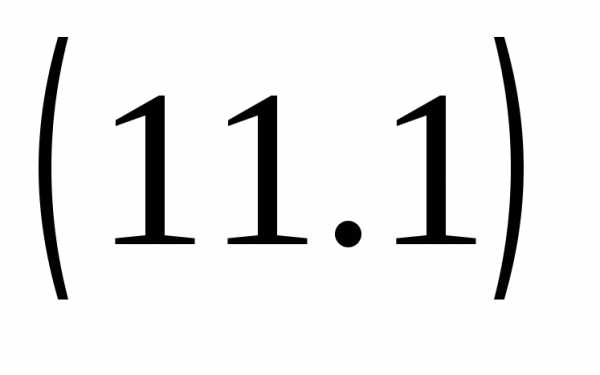 примет вид,
где
примет вид,
где — корень квадратного трёхчлена.
— корень квадратного трёхчлена.
Заметим, что если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
studfiles.net
Урок «Формула корней квадратного уравнения»
Муниципальное бюджетное общеобразовательное учреждение
«Кожаевская основная общеобразовательная школа»
Урок математики в 8 классе
Тема: « Формула корней квадратного уравнения»

Составитель: учитель математики и физики
МБОУ «Кожаевская ООШ»
Парфенова Лия Алексеевна
Д.Кожаево
2016г.
Урок математики в 8 классе.
Тема: «Формула корней квадратного уравнения».
Парфенова Лия Алексеевна.
МБОУ «Кожаевская ООШ».
Учитель математики и физики.
Математики.
8 класс.
Тема урока и номер урока: «Формула корней квадратного уравнения». Первый урок в данной теме.
Базовый учебник: Ю.Н. Макарычев, Н.Г. Миндюг, К.И. Нешков, С.Б. Суворова «Алгебра», М.: Просвещение, 2010г.
Цели урока: вывести общую формулу нахождения корней квадратного уравнения, формировать умение ее использовать.
Задачи: Образовательные: — обобщить и систематизировать знания, полученные по данной теме; — проверка навыков решения. Развивающие: — развивать память, внимание, логическое мышление; — развивать познавательную и творческую активность; — совершенствовать культуру коллективного умственного труда; — развивать умение выполнять инструкции учителя. Воспитательные: — воспитывать ответственность, трудолюбие, умение работать на доверии, взаимопомощи; — продолжать формировать интерес к математической науке.
Тип урока: изучение нового материала.
Формы работы учащихся: фронтальная работа, практическая работа, индивидуальная.
Планируемый (конечный) результат: научиться применять формулу для решения квадратного уравнения.
Методы работы: поисковый, работа с учебником, рефлексия.
Структура и ход урока: — Организационный момент (1 мин.) — Постановка целей урока(1 мин.) — Проверка домашнего задания (5 мин.) — Практическая работа (10 мин.) — Объяснение нового материала (13 мин.) — Первичное закрепление изученного материала (10 мин.) — Итог урока. Домашнее задание (3 мин.) — Рефлексия (2 мин.)
Ход урока.
1). Организационный момент. Приветствие, проверка отсутствующих и готовности учащихся (отчет дежурных по классу). 2).Объявление темы и целей урока (запись темы на доске и в тетрадях). 3). Проверка домашнего задания. Работа в парах: дети меняются тетрадями и проверяют друг у друга домашнее задание, сверяясь с решением на слайде. Выставляют оценку. Разбираем непонятные задания. 4).Практическая работа: проверочная работа. 1. Выпишите коэффициенты а,б,с квадратного уравнения: Вариант 1 Вариант 2 а) х2 – 3х +17 = 0 а) 7х2 + 6х – 4 = 0 б) 3х2 = 2 б) – х2 = 5х в) – 7х + 16х2 = 0 в) 18 – х2 = 0 г) х2 = 0 г) х2 – 4 = 0
2.Найдите корни уравнения: Вариант 1 Вариант 2 а) 2х2 – 18 =0 а) х2 = 7 б) 4 у2 + 7у = 0 б) 8у2 – 5у = 0 в) х2 + 16 = 0 в) х2 + 9 =0 г) (х – 3)2 — 9 =0 г) (х + 3) – 4 = 0
3. Решите уравнение приемом выделением квадратного двучлена: Вариант 1 Вариант 2 2х2 – 24х + 54 = 0 3х2 + 24х – 27 = 0
5). Объяснение нового материала.
Для мотивации изучения общей формулы корней квадратного уравнения достаточно обратить внимание учащимся на два момента: 1) решение квадратного уравнения выделением квадрата двучлена часто приводит к громоздким преобразованиям; 2) каждый раз, решая квадратное уравнение данным приемом, мы повторяем одни и те же шаги (алгоритм). Указанные пункты позволяют предположить, что можно провести рассуждения о решении квадратного уравнения приёмом выделения квадрата двучлена для уравнения общего вида. Для наглядности и осознанности восприятия процесс вывода формулы корней квадратного уравнения разобьём на несколько шагов, записывая при этом на доске и в тетрадях решение конкретного уравнения и уравнения общего вида.
Шаг 1. Преобразуем уравнение в приведенное. Шаг 2. Представим второе слагаемое в виде удвоенного произведения, в котором один из множителей есть х. Шаг 3. Прибавим к левой части уравнения выражение ()2 и вычтем его. Шаг 4. Выделим квадрат двучлена. Шаг 5. Решим полученное уравнение. Заметим, что в левой части уравнения находится квадрат выражения (двучлен). Количество корней уравнения зависит от знака правой части уравнения. Более того, 4а2 0 для любого а0,значит для решения важен только знак выражения б2 – 4ас. Так появилось понятие дискриминанта. Его обозначим буквой D. «Дискриминант» в переводе с латинского – различитель. D = б2 – 4ас— дискриминант квадратного уравнения
Найдем чему равны корни квадратного уравнения в общем виде:
(х + )2 =
(х + )2 =
Х1 = и Х2 =
Принята следующая краткая запись:
- Х1,2 = , где D = б2 – 4ас
— формула корней квадратного уравнения
Рассмотрим теперь различные всевозможные случаи в зависимости от значения D.
1). Если D0, то уравнение ах2 + бх + с =0 имеет два корня Х1,2 =
2). Если D = 0, то уравнение ах2 + бх + с =0 имеет один корень Х =
3). Если D0, то уравнение ах2 + бх + с =0 не имеет корней.
Запишем алгоритм решения квадратного уравнения вида ах2 + бх + с =0:
1) Выпишем коэффициенты квадратного уравнения.
2). Вычислим дискриминант и сравним его с нулём.
3). Если дискриминант положителен или равен 0, то воспользуемся формулой корней, если дискриминант отрицателен, то записать, что корней нет.
Найдем его в учебнике и прочитаем.
6). Первичное закрепление изученного материала.
Пример 1. Решим квадратное уравнение 12+ 7х + 1 = 0 Выпишем коэффициенты: а = 12, б = 7, с = 1 Найдём дискриминант: D = в2 – 4ас = 72 – 4 121 = 49 – 48 = 10, значит уравнение имеет два корня.
Х1 = = = = — или Х2 = = = —
Ответ: Х1 = , Х2 = — Пример 2. Решим квадратное уравнение – 12х + 36 = 0 Выпишем коэффициенты: а = 1,б = — 12,с = 36. Найдём дискриминант: D = в2 – 4ас = (-12)2 — 41 36 = 144 – 144 = 0, значит уравнение имеет одно решение.
Х = = = = 6
Ответ: х = 6.
Пример 3. Решим уравнение 7- 25х + 23 = 0 Выпишем коэффициенты: а = 7, б = — 25, с = 23. Найдём дискриминант: D = в2 – 4ас = (-25)2 — 4 7 23 = 625 – 644 = — 19 0,значит корней уравнение не имеет.
Ответ: корней нет.
Выполните упражнение по учебнику № 533(а,б)
Докажите, что уравнение имеет единственный корень – 5х +9 = 0
Убедитесь, что уравнение имеет единственный корень, найдите этот корень – 8х + 16 = 0
Выполните упражнение по учебнику №534(а,в), 535(а,в,г),536(в,д), 538(а).
7) Итог урока.
— На чём основан вывод формулы корней квадратного уравнения?
— Как вычислить дискриминант квадратного уравнения?
— Сколько корней может иметь квадратное уравнение?
— Как определить количество корней квадратного уравнения?
— Если квадратное уравнение имеет единственный корень, то что можно сказать о трёхчлене, стоящем в левой части уравнения?.
Домашнее задание: п. 22, №534(а,б,в,г),535(а,б,в),536(а,б,в)
8)Рефлексия.
— Что нового вы узнали на уроке?
— Что вам понравилось?
-Что вызвало затруднение?
— Оцените свою работу с помощью смайлика.
Спасибо всем за работу!
infourok.ru
Формулы корней квадратных уравнений
Урок. Алгебра 8 класс
Тема: Формулы корней квадратных уравнений
Цели:
Показать способ решения полных квадратных уравнений с использованием формулы корней квадратного уравнения.
Сформировать умение решать квадратные уравнения.
У каждого ученика на парте лежит рабочая карта урока (приложение №1) и карточки – задания (приложение №2).
Ход урока
1. Организационный момент.
2. Самостоятельная работа. ( Карточки на партах)
Вариант 1
1. Решить уравнения:
а)
б)
2. Решить уравнение способом разложения на множители:
3. Решить уравнение, выделив в левой части полный квадрат (способом извлечения квадратного корня)
Вариант 2
1. Решить уравнения:
а)
б)
2. Решить уравнение способом извлечения квадратного корня:
3. Решить уравнение, выделив в левой части полный квадрат (способом разложения на множители)
Ответы заготовлены на доске
Самопроверка.
Критерии оценки:
“5” – если все задания выполнены верно.
“4” – если допущена одна ошибка.
“3” – если допущены две ошибки.
“ — ” – если допущено более трёх ошибок.
Учитель:
Поставьте “минус” возле того задания, в правильности которого вы не уверены или же не знаете, как его выполнить.
Затем разбирается задания, в которых ученики допустили больше всего ошибок или не справились с его выполнением.
Оценки своей деятельности ученики заносят в рабочую карту урока.
Учитель записывает тему урока и формулирует цели урока ( слайд)
Учитель проводит беседу с учениками и обсуждает, всегда ли удобно решать уравнение выделением в левой части полного квадрата. Ученики делают соответствующие выводы. После этого учитель предлагает выделить полный квадрат в левой части уравнения
( слайд)
Учитель и учащиеся работают с карточками – заданиями.
Ученики записывают алгоритм решения квадратного уравнения.
1) Выделить в квадратном уравнении коэффициенты: а = , в = , с =
2) Вычислить дискриминант по формуле
3) Если D < 0, уравнение не имеет действительных корней
4). Если D = 0, уравнение имеет один действительный корень
5) Если D > 0, уравнение имеет два различных действительных корня
“Различителем” числа корней квадратного уравнения является выражение Ему дано специальное имя — дискриминант (от “discriminantis ” — по латыни “различающий”, “разделяющий”. Дискриминант обозначается буквой D: .
Попробуйте установить аналогию между понятием “светофор” и “дискриминант”.
Вернемся к самостоятельной работе и решим по алгоритму задание №3
Работа в парах. Каждая пара проговаривает вслух алгоритм решения квадратного уравнения.
Оценка своей деятельности на данном этапе заносится в рабочую карту урока.
Критерии оценки:
“5” – если можете воспроизвести алгоритм, как мы его записали.
“4” – если в целом поняли материал, частично можете воспроизвести алгоритм, ответить на вопросы.
“3” – поняли лишь часть материала.
“ — ” – ничего не поняли.
Учитель еще раз воспроизводит алгоритм, возвращается к решению задания №3.
4. Закрепление нового материала.
( слайд)
Внимательно посмотрите на уравнения и устно проговорите алгоритм решения. ( В стандартном ли виде записаны уравнения?)
1) — 5х+14=0;
2) 0,6+0,8х-7,8=0;
3) -11х+-42=0;
4) =2х+48;
5) 4=-4х-;
6) х(х-5)+6=0
7) х(3х+1)+7=0
Первые три уравнения решим у доски и в тетрадях
Четвертое и пятое уравнение работа в группах . Учитель распределяет уравнения по группам. (первая группа выполнившая задание оформляет решение у доски одним представителем)
Шестое и седьмое уравнение работа по вариантное. 1 вариант – 6 уравнение, 2 вариант -7 уравнение ( Взаимопроверка, ученики обмениваются тетрадями и обсуждают решение с учителем)
Оценки ученики выставляют в рабочую карту урока.
Критерии оценки:
“5” – если все задания выполнены верно.
“4” – если допущено две ошибки.
“3” – если допущены три ошибки.
“ — ” – если допущено более трёх ошибок.
5. Домашнее задание;
1) № 25.11(в), 25.18(в), 25.24, 25.37(б)
2) № 25.11(в), 25.18(в), 25.24, 25.19(в)
3) № 25.11(в), 25.18(в), 25.24
Итоги урока. Учащиеся ставят себе отметку за урок в зависимости от промежуточных результатов и общего понимания изученного материала.
6. Рефлексия.
— Что нового мы узнали?
— Какие затруднения встретились?
— Что помогло выйти из затруднения?
— Каковы ваши собственные результаты?
Задание: закончите предложения…
Самым интересным для меня на занятии было…
Я научился…
Теперь бы я хотел еще узнать…
Самым скучным на занятии было…
infourok.ru
Формулы корней. Свойства квадратных корней. — МегаЛекции
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…» )
В предыдущем уроке мы разобрались, что такое квадратный корень. Пришла пора разобраться, какие существуют формулы для корней, каковы свойства корней, и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Напоминаю (из предыдущего урока): а и b — неотрицательные числа! Иначе формула смысла не имеет…
Это свойство корней, как видите простое, короткое и безобидное. Но с помощью этой формулы корней можно делать массу полезных вещей! Разберём на примерах все эти полезные вещи.
Полезная вещь первая. Эта формула позволяет нам умножать корни.
Как умножать корни?
Да очень просто. Прямо по формуле. Например:
Казалось бы, умножили, и что? Много ли радости?! Согласен, немного… А вот как вам такой пример?
Из множителей корни ровно не извлекаются. А из результата — отлично! Уже лучше, правда? На всякий случай сообщу, что множителей может быть сколько угодно. Формула умножения корней всё равно работает. Например:
Так, с умножением всё ясно, зачем нужно это свойство корней — тоже понятно.
Полезная вещь вторая. Внесение числа под знак корня.
Как внести число под корень?
Предположим, что у нас есть вот такое выражение:
Можно ли спрятать двойку внутрь корня? Легко! Если из двойки сделать корень, сработает формула умножения корней. А как из двойки корень сделать? Да тоже не вопрос! Двойка — это корень квадратный из четырёх!
Вот и пишем:
Корень, между прочим, можно сделать из любого неотрицательного числа! Это будет корень квадратный из квадрата этого числа. 3 — корень из 9. 8 — корень из 64. 11 — корень из 121. Ну, и так далее.
Конечно, расписывать так подробно нужды нет. Разве что, для начала… Достаточно сообразить, что любое неотрицательное число, умноженное на корень, можно внести под корень. Но — не забывайте! — под корнем это число станет квадратом самого себя. Это действие — внесение числа под корень — можно ещё назвать умножением числа на корень. В общем виде можно записать:
Процедура простая, как видите. А зачем она нужна?
Как и любое преобразование, эта процедура расширяет наши возможности. Возможности превратить жестокое и неудобное выражение в мягкое и пушистое). Вот вам простенький пример:
Как видите, свойство корней, позволяющее вносить множитель под знак корня, вполне годится для упрощения.
Кроме того, внесение множителя под корень позволяет легко и просто сравнивать значения различных корней. Безо всякого их вычисления и калькулятора! Третья полезная вещь.
Как сравнивать корни?
Это умение очень важно в солидных заданиях, при раскрытии модулей и прочих крутых вещах.
Сравните вот эти выражения. Какое из них больше? Без калькулятора! С калькулятором каждый… э-э-э… короче, каждый справится!)
Так сразу и не скажешь… А если внести числа под знак корня?
и
Запомним (вдруг, не знали?): если число под знаком корня больше, то и сам корень — больше! Отсюда сразу правильный ответ, безо всяких сложных вычислений и расчётов:
и, следовательно:
Здорово, да? Но и это ещё не всё! Вспомним, что все формулы работают как слева направо, так и справа налево. Мы пока формулу умножения корней слева направо употребляли. Давайте запустим это свойство корней наоборот, справа налево. Вот так:
И какая разница? Разве это что-то даёт!? Конечно! Сейчас сами увидите.
Предположим, нам нужно извлечь (без калькулятора!) корень квадратный из числа 6561. Кое-кто на этом этапе и падёт в неравной борьбе с задачей… Но мы упорные, мы не сдаёмся! Полезная вещь четвёртая.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Формула корней квадратного уравнения. — КиберПедия
О. Уравнение вида , где – переменная , называется квадратным.
О. Если , то уравнение называется приведенным квадратным уравнением.
О. Квадратное уравнение, в котором хотя бы один из коэффициентов или равен , называется неполным квадратным уравнением
Выведем формулу корней квадратного уравнения в общем случае:
,
Поделим обе части уравнения на . При этом корни уравнения не изменятся (почему?).
Выделим полный квадрат:
О. Выражение: называется дискриминантом квадратного уравнения, и обозначается через , тогда уравнение можно записать так:
Возможны следующие 3 случая:
1.Если , то из дискриминанта можно извлечь корень (почему?), тогда получаем решения уравнения:
или
То есть
или
или
Эти две формулы можно объединить в следующую:
— эта формула называется формулой корней квадратного уравнения
2.Если , то уравнение примет вид:
В этом случае уравнение имеет один корень.
Замечание: можно также сказать, что в этом случае квадратное уравнение имеет два совпадающих корня.
3.Если , то значение дроби , поэтому уравнение , а значит и уравнение не имеет корней (почему?).
Таким образом,
Если , то уравнение имеет 2 различных корня:
Если , то уравнение имеет 2 совпадающих корня:
Если , то уравнение корней не имеет.
Теорема Виета.
Пусть дано уравнение , – корни уравнения, тогда
Доказательство:
Пусть уравнение имеет 2 различных корня ( ):
Итак, действительно
Замечание: Если рассмотреть приведенное квадратное уравнение , то формулы Виета будут выглядеть так: .
В школьном курсе математики чаще всего формулы Виета применяются именно для приведенного квадратного уравнения.
Имеет место теорема, обратная теореме Виета:
Если числа и таковы, что
То эти числа являются корнями уравнения
Доказательство:
Значит, числа и действительно являются корнями уравнения .
Замечание: теорема, обратная теореме Виета, позволяет составлять квадратные уравнения по его корням.
Например, если , то , тогда эти числа являются корнями уравнения
16. Разложение квадратного трехчлена на линейные множители
О. Многочлен вида: , где – переменная , называется квадратным трехчленом.
О.Корнем квадратного трехчлена называется значение переменной, при которой значение этого трехчлена равно нулю.
Теорема.
Если и – корни квадратного трёхчлена , то
Доказательство:
Вынесем за скобки в многочлене множитель а.Получим: . Так как корни квадратного трёхчлена являются корнями квадратного уравнения , то, по теореме Виета, , .
Поэтому
Итак,
Если квадратный трёхчлен имеет один корень (два совпадающих корня), то формула примет вид , где — корень квадратного трёхчлена.
Заметим, что если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
17. Формулы сокращенного умножения.
Доказательство:
( ,т.к. по определению произведения многочленов, операции над многочленами обладают свойствами коммутативности, ассоциативности и дистрибутивности.)
Доказательство:
.
Доказательство:
.
Доказательство:
.
Доказательство:
Пусть , рассмотрим произведение
Доказательство:
18. Свойства числовых неравенств.
О. Число больше числа , если разность – положительное число; число меньше числа , если разность – отрицательное число.
Теорема 1.
Если , то ; если , то .
Доказательство.
Если , то по определению разность – положительное число, тогда разность — отрицательное число, а это значит, по определению, что . И наоборот.
Теорема 2.
Если и , то .
Доказательство.
По условию и , значит, по определению разность – отрицательное число и разность – отрицательное число. Сумма отрицательных чисел – число отрицательное, поэтому сумма – отрицательна. Преобразуем эту сумму . Следовательно, разность – отрицательна и, по определению, .
Теорема 3.
Если и – любое число, то .
Доказательство.
Преобразуем разность . По условию, , поэтому – отрицательное число. Значит, и разность — отрицательна. Следовательно, .
Теорема 4.
Если и – положительное число, то ,
Если и – отрицательное число, то ,
Доказательство.
Преобразуем разность . Так как , то разность – отрицательное число. Если , то произведение – отрицательно, и, следовательно, . Если , то произведение – положительно, и, следовательно, .
Следствие.
Если и – положительные числа и , то .
Доказательство.
Разделим обе части неравенства на положительное число : .
Сократив дробь, получим, что , т.е. .
Теорема 5.
Если и , то
Доказательство.
Прибавим к обеим частям неравенства число , получим .
Прибавим к обеим частям неравенства число , получим .
Из неравенств и ,и теоремы 2 следует, что
Теорема 6.
Если и , где – положительные числа, то .
Доказательство.
Умножим обе части неравенства на положительное число , получим неравенство .
Умножим обе части неравенства на положительное число , получим неравенство
Из неравенств и и теоремы 2 следует, что .
19. Свойства числовых равенств.
Числовым равенством называется числовое выражение, содержащее знак
Свойство 1.
(если к обеим частям верного числового равенства прибавить одно и то же число, то получится также верное числовое равенство)
Свойство 2.
(если из одной части верного числового равенства перенести в другую часть слагаемое с противоположным знаком, то получится также верное числовое равенство)
Свойство 3.
(если обе части верного числового равенства умножить на одно и то же число, то получится также верное числовое равенство)
Свойство 4.
(если обе части верного числового равенства возвести в одну и ту же натуральную степень, то получится также верное числовое равенство)
20. Метод интервалов
О.Метод интервалов – метод решения рациональных неравенств.
Этот метод основан на следующей теореме математического анализа
(теореме Больцано-Коши), которую мы рассмотрим без доказательства:
Пусть функция на отрезке и на концах его принимает разные по знаку значения,
cyberpedia.su

 ,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения:
,
то из дискриминанта можно извлечь
корень (почему?),
тогда получаем решения уравнения: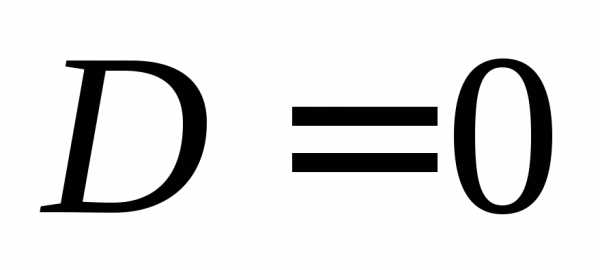 ,
то уравнение
,
то уравнение 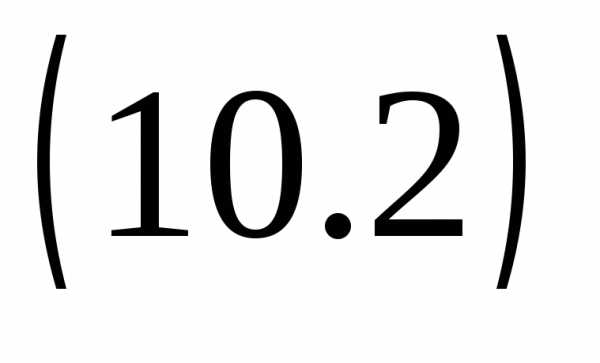 примет вид:
примет вид: ,
то значение дроби
,
то значение дроби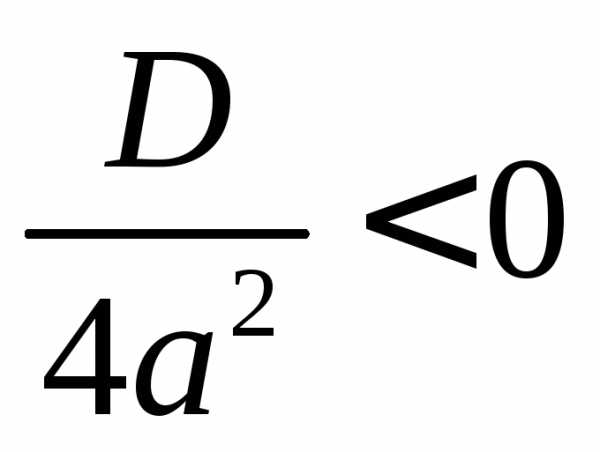 ,
поэтому уравнение
,
поэтому уравнение 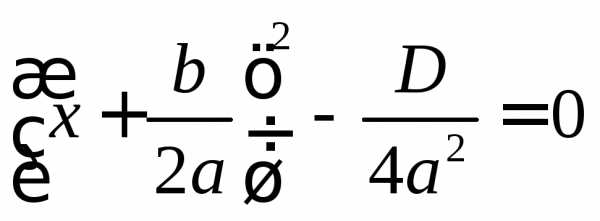 ,
а значит и уравнение
,
а значит и уравнение 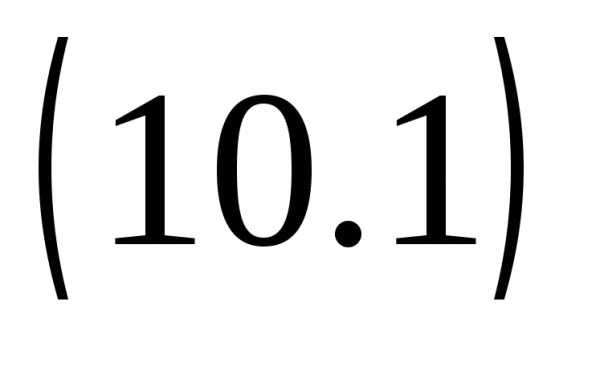 не
имеет корней (почему?).
не
имеет корней (почему?).