Внеклассный урок — Формулы двойного аргумента
Формулы двойного аргумента (двойного угла)Выражения sin 2x, cos 2x, tg 2x можно выразить через sin x, cos x, tg x. Эти преобразующие формулы называются формулами двойного аргумента (или двойного угла).
Логику преобразования можно понять на примере выражения sin 2x.
Представим это выражение в виде sin (x + x).
Тогда мы легко можем применить формулу синуса суммы аргументов:
sin (x + x) = sin x cos x + cos x sin x = 2 sin x cos x.
Мы получили первую из формул двойного аргумента. А вот все формулы:
sin 2x = 2 sin x cos x cos 2x = cos2x – sin2x cos 2x = 1 – 2 sin2x 2 tg x |
В первых строках мы показали, как была получена первая формула из таблицы. Вычислим остальные три.
Вычислим остальные три.
2) cos 2x = cos2x – sin2x.
Здесь так же представляем 2х в виде х + х и применяем формулу косинуса сложения аргументов:
cos 2x = cos (x + x) = cos x cos x – sin x sin x = cos2x – sin2x.
3) cos 2x = 1 – 2 sin2x.
Здесь мы просто продолжим преобразовывать предыдущую формулу.
Используем для этого основное тригонометрическое тождество cos2x + sin2x = 1.
Из этого тождества следует, что cos2x = 1 – sin2x. Итак, выпишем предыдущую формулу, вставим значение cos2x, сведем подобные члены и получим результат:
cos 2x = cos2x – sin2x = 1 – sin2x – sin2x = 1 – 2sin2x.
2 tg x
4) tg 2x = ————
1 – tg2x
Способов, как прийти к такому тождеству, два.
Первый способ. Здесь нам поможет формула тангенса сложения аргументов. Для этого представим tg 2x в виде tg (x + х). Итак:
tg х + tg х 2 tg х
tg 2x = tg (x + х) = —————— = —————
1 – tg х tg х 1 – tg2х
Второй способ. Он сложнее. Сначала применяем формулы синуса и косинуса сложения аргументов:
sin (x + х) sin x cos х + cos x sin х
tg 2x = tg (x + х) = —————— = ———————————
cos (x + х) cos x cos х – sin x sin х
Теперь, чтобы упростить выражение, делим все его части на cos x cos х, сокращаем подобные члены и приходим к решению:
sin x cos х cos x sin х 2 sin х
————— + ————— —————
cos x cos х cos x cos х 2 cos х 2 tg x
———————————— = ——————— = —————
cos x cos x sin x sin х sin2x 1 – tg2x
————— – ————— 1 – ————
cos x cos x cos x cos х cos2x
ПРИМЕЧАНИЕ:
При решении конкретных задач важно помнить, что задача имеет смысл лишь в том случае, если в процессе решения знаменатели нигде не оказываются равны нулю.
Теперь для наглядности решим несколько примеров по теме.
Пример 1. Упростить выражение:
sin 2α
———
sin α
Решение:
sin 2α 2 sin α cos α
——— = —————— = 2 cos α
sin α sin α
Пример 2. Пусть tg α = 3/4 и 180º < α < 270º.
Найти sin 2α.
Решение.
В первую очередь, отмечаем, что угол находится в третьей четверти. Значит, синус будет со знаком минус.
1
1) Значение синуса мы могли бы найти через формулу 1 + ctg2 α = ———.
sin2 α
Значит, нам надо сначала вычислить значение котангенса. Мы знаем, что tg α · ctg α = 1. Следовательно:
1 1 4
ctg α = —— = —— = ——
tg α 3/4 3
2) Теперь находим значение синуса:
1 1 1 1 9
sin2 α = ————— = ————— = ———— = —— = ——
1 + ctg2 α 1 + (4/3)2 1 + 16/9 25/9 25
3
sin α = – ——
5
3) Мы знаем, что sin 2α = 2 sin α cos α. Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:
Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:
9 16
cos2 α = 1 – sin2 α = 1 – —— = ——
25 25
4
cos α = – ——
5
4) Осталось применить формулу двойного угла:
3 4 2 · 3 · 4 24
sin 2α = 2 · (– ——) · (– ——) = ———— = —— = 0,96.
5 5 5 · 5 25
Пример решен.
Пример 3: Вычислить
π π
cos2 — – sin2 —
8 8
Решение.
Это выражение соответствует правой части формулы косинуса двойного
аргумента (cos 2x = cos2x – sin2x). Значит, просто приравняем его к левой части. Для этого замечаем, что
Значит, просто приравняем его к левой части. Для этого замечаем, что
π
х = —
8
Остается ввести в формулу это значение х и решить уравнение:
π π π 2π π √2
cos2 —— – sin2 —— = cos 2 ∙ —— = cos —— = cos —— = —— .
8 8 8 8 4 2
Пример решен.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) ) |
|
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | ||
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) |
|
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) |
|
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | sin(theta)^2+cos(theta)^2 | ||
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.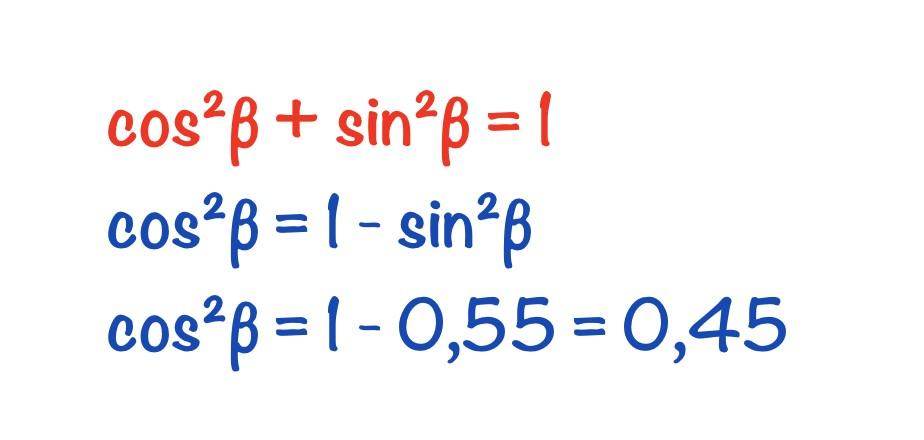 ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Все формулы по тригонометрии
Все формулы по тригонометрии
Основные тригонометрические тождества
sin2x + cos2x = 1
tgx ctgx = 1
tg2x + 1 | = | 1 |
cos2x |
ctg2x + 1 | = | 1 |
sin2x |
Формулы двойного аргумента
sin2x = 2sinx cosx
sin2x | = | 2tgx | = | 2ctgx | = | 2 |
1 + tg2x | 1 + ctg2x | tgx + ctgx |
cos2x = cos2 — sin2x = 2cos2x — 1 = 1 — 2sin2x
cos2x | = | 1 — tg2x | = | ctg2x — 1 | = | ctgx — tgx |
1 + tg2x | ctg2x + 1 | ctgx + tgx |
tg2x | = | 2tgx | = | 2ctgx | = | 2 |
1 — tg2x | ctg2x — 1 | ctgx — tgx |
ctg2x | = | ctg2x — 1 | = | ctgx — tgx |
2ctgx | 2 |
Формулы тройного аргумента
sin3x = 3sinx — 4sin3x cos3x = 4cos3x — 3cosx
tg3x | = | 3tgx — tg3x |
1 — 3tg2x |
ctg3x | = | ctg3x — 3ctgx |
3ctg2x — 1 |
Формулы половинного аргумента
sin2 | x | = | 1 — cosx |
2 | 2 |
cos2 | x | = | 1 + cosx |
2 | 2 |
tg2 | x | = | 1 — cosx |
2 | 1 + cosx |
ctg2 | x | = | 1 + cosx |
2 | 1 — cosx |
tg | x | = | 1 — cosx | = | sinx |
2 | sinx | 1 + cosx |
ctg | x | = | 1 + cosx | = | sinx |
2 | sinx | 1 — cosx |
Формулы квадратов тригонометрических функций
sin2x | = | 1 — cos2x |
2 |
cos2x | = | 1 + cos2x |
2 |
tg2x | = | 1 — cos2x |
1 + cos2x |
ctg2x | = | 1 + cos2x |
1 — cos2x |
sin2 | x | = | 1 — cosx |
2 | 2 |
cos2 | x | = | 1 + cosx |
2 | 2 |
tg2 | x | = | 1 — cosx |
2 | 1 + cosx |
ctg2 | x | = | 1 + cosx |
2 | 1 — cosx |
Формулы кубов тригонометрических функций
sin3x | = | 3sinx — sin3x |
4 |
cos3x | = | 3cosx + cos3x |
4 |
tg3x | = | 3sinx — sin3x |
3cosx + cos3x |
ctg3x | = | 3cosx + cos3x |
3sinx — sin3x |
Формулы тригонометрических функций в четвертой степени
sin4x | = | 3 — 4cos2x + cos4x |
8 |
cos4x | = | 3 + 4cos2x + cos4x |
8 |
Формулы сложения аргументов
sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ — sinα sinβ
tg(α + β) | = | tgα + tgβ |
1 — tgα tgβ |
ctg(α + β) | = | ctgα ctgβ — 1 |
ctgα + ctgβ |
sin(α — β) = sinα cosβ — cosα sinβ cos(α — β) = cosα cosβ + sinα sinβ
tg(α — β) | = | tgα — tgβ |
1 + tgα tgβ |
ctg(α — β) | = | ctgα ctgβ + 1 |
ctgα — ctgβ |
Формулы суммы тригонометрических функций
sinα + sinβ | = 2sin | α + β | ∙ cos | α — β |
2 | 2 |
cosα + cosβ | = 2cos | α + β | ∙ cos | α — β |
2 | 2 |
(sinα + cosα)2 = 1 + sin2α
tgα + tgβ | = | sin(α + β) |
cosα cosβ |
ctgα + ctgβ | = | sin(α + β) |
sinα sinβ |
Формулы разности тригонометрических функций
sinα — sinβ | = 2sin | α — β | ∙ cos | α + β |
2 | 2 |
cosα — cosβ | = -2sin | α + β | ∙ sin | α — β |
2 | 2 |
(sinα — cosα)2 = 1 — sin2α
tgα — tgβ | = | sin(α — β) |
cosα cosβ |
ctgα — ctgβ | = – | sin(α — β) |
sinα sinβ |
Формулы произведения тригонометрических функций
sinα ∙ sinβ | = | cos(α — β) — cos(α + β) |
2 |
sinα ∙ cosβ | = | sin(α — β) + sin(α + β) |
2 |
cosα ∙ cosβ | = | cos(α — β) + cos(α + β) |
2 |
tgα ∙ tgβ | = | cos(α — β) — cos(α + β) | = | tgα + tgβ |
cos(α — β) + cos(α + β) | ctgα + ctgβ |
ctgα ∙ ctgβ | = | cos(α — β) + cos(α + β) | = | ctgα + ctgβ |
cos(α — β) — cos(α + β) | tgα + tgβ |
tgα ∙ ctgβ | = | sin(α — β) + sin(α + β) |
sin(α + β) — sin(α — β) |
Косинус двойного угла
В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.
Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.
Итак, нам нужны косинус двойного угла и тригонометрическая единица:
Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:
и подставить его в косинус двойного угла, то получим:
Это — еще одна формула косинуса двойного угла:
Эта формула — ключ к получению формулы понижения степени:
Итак, формула понижения степени синуса:
Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:
Теперь из тригонометрической единицы выразим синус:
Подставим это выражение в формулу косинуса двойного угла:
Получили еще одну формулу косинуса двойного угла:
Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.
Таким образом, формула понижения степени косинуса:
Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:
Так как тангенс — отношение синуса к косинусу то формула для тангенса:
Котангенс — отношение косинуса к синусу. Поэтому формула для котангенса:
Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.
Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.
Решить уравнение косинус 2х. Тригонометрические уравнения — формулы, решения, примеры
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов (или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота
, которые соответствуют точкам окружности, ордината которых равна
.
Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату . Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где
,
. (2)
(2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем (то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем (то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение :
ОСОБЫЕ РЕШЕНИЯ:
Отметим на окружности точки, ордината которых равна 0:
Отметим на окружности единственную точку, ордината которой равна 1:
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать .
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда. При любом а.
При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается. ) Собственно, для этого и разбираемся. Что, как и откуда.
) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно. ) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т. п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Геометрическое определение синуса и косинуса
|BD| — длина дуги окружности с центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin
x
и y = cos
x
периодичны с периодом 2
π
.
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 \circ }=5\)
\circ }=5\)Ответ: \( \displaystyle 5\).
2. \( \displaystyle \frac{8}{\sin \left( -\frac{27\pi }{4} \right)\text{cos}\left( \frac{31\pi }{4} \right)}\)
\( \displaystyle \frac{8}{\sin \left( -\frac{27\pi }{4} \right)\text{cos}\left( \frac{31\pi }{4} \right)}\)
Опять задача целиком на формулы приведения. Вначале….
\( \displaystyle \frac{8}{\sin \left( -\frac{27\pi }{4} \right)\text{cos}\left( \frac{31\pi }{4} \right)}=\frac{8}{-\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{2}}{2}}=\frac{8}{-\frac{2}{4}}=-8:\left( \frac{2}{4} \right)=-16\)
…избавимся от минуса, вынеся его перед синусом (поскольку синус – функция нечетная!!!). Затем рассмотрим углы:
\( \displaystyle \frac{27\pi }{4}=\frac{26\pi }{4}+\frac{\pi }{4}=6\pi +\frac{\pi }{4}\)
Отбрасываем целое количество кругов – то есть три круга (\( \displaystyle 6\pi \)). Остается вычислить: \( \displaystyle sin\frac{\pi }{4}=\frac{\sqrt{2}}{2}\)
Так же поступаем и со вторым углом:
\( \displaystyle \frac{31\pi }{4}=7\frac{3}{4}\pi =7\pi +\frac{3}{4}\pi \)
Удаляем целое число кругов –3 круга (\( \displaystyle 6\pi \)) тогда:
\( \displaystyle \text{cos}\left( \frac{31\pi }{4} \right)=\cos \left( 7\pi +\frac{3}{4}\pi \right)=\cos \left( \pi +\frac{3}{4}\pi \right)\)
Теперь думаем: в какой четверти лежит оставшийся угол? Он «не дотягивает» до \( \displaystyle 2\pi \) всего \( \displaystyle \frac{\pi }{4}\).
 {2}}\frac{5\pi }{12} \right)=\sqrt{3}\cdot \left( -\frac{\sqrt{3}}{2} \right)=-\frac{3}{2}=-1,5\)
{2}}\frac{5\pi }{12} \right)=\sqrt{3}\cdot \left( -\frac{\sqrt{3}}{2} \right)=-\frac{3}{2}=-1,5\)Ответ: \( \displaystyle -1,5\).
9. Найдите значение выражения \( \displaystyle 5tg\left( 5\pi -\gamma \right)-tg\left( -\gamma \right)\), если \( \displaystyle tg\gamma =7\).
У тангенса период – \( \displaystyle \pi \), так что не задумываясь отбрасываем его:
\( \displaystyle 5tg\left( 5\pi -\gamma \right)=5tg\left( -\gamma \right)\ =-5tg\gamma \)
Здесь мы использовали еще и тот факт, что тангенс – функция нечетная.
\( \displaystyle 5tg\left( 5\pi -\gamma \right)-tg\left( -\gamma \right)=-5tg\gamma -\left( -tg\gamma \right)=-5tg\gamma +tg\gamma =-4tg\gamma =\)
\( \displaystyle=-4\cdot 7=-28\)\( \displaystyle=-4\cdot 7=-28\)
Ответ: \( \displaystyle -28\).
10. Найдите \( \displaystyle \sin \left( \frac{7\pi }{2}-\alpha \right)\), если \( \displaystyle sin\alpha =0,8\) и \( \displaystyle \alpha \in \left( \frac{\pi }{2};\pi \right)\)
Вначале упростим выражение, используя формулы приведения (вначале отбросим целые круги и уберем минус):
\( \displaystyle \sin \left( \frac{7\pi }{2}-\alpha \right)=\sin \left( 2\pi -\frac{\pi }{2}-\alpha \right)=\sin \left( -\frac{\pi }{2}-\alpha \right)=-\text{sin}\left( \frac{\pi }{2}+\alpha \right)\)
Наш оставшийся угол – во третьей четверти (посмотри на условия для угла в условии задачи!!!).
 {2}}}=\pm \sqrt{0,36}=\pm 0,6\)
{2}}}=\pm \sqrt{0,36}=\pm 0,6\)Так как сам угол лежит во второй четверти, а косинус второй четверти отрицательный, то выбираем знак «минус». Окончательно получим:
\( \displaystyle \sin \left( \frac{7\pi }{2}-\alpha \right)=-0,6\).
Ответ: \( \displaystyle -0,6\).
Ну вот, справился со всем без проблем? Очень на это надеюсь!
Интеграл косинуса
Неопределенный интеграл от косинуса cos (x) равен синусу. Для первоначальной косинуса к правой стороне добавляем постоянную Постоянную определяют с дополнительного условия на первоначальную.
График косинуса имеет вид
Само по себе определение интеграла косинуса достаточно простое. Но как только задают вычислить интеграл косинуса двойного угла, тройного или половины угла, сразу возникают трудности в половины студентов. Выведем формулу интегрирования для функции cos (k*x). Для применения табличной формулы интегрирования надо внести коэффициент под дифференциал, что может привести к изменению самого интеграл. Поэтому одновременно необходимо разделить на этот коэффициент.
Поэтому одновременно необходимо разделить на этот коэффициент.
.
Зная приведенную формулу, проинтегрировать косинус двойного угла сможет каждый школьник 10, 11 класса. Все что необходимо это подставить 2 или 3 в интеграл
и по индукции следующие интегралы
int(sin(k*x)=-1/k*cos(k*x).
Приведенная формула позволяет вычислить интеграл от косинуса половины угла
и интеграл от косинуса одной трети угла
В этих случаях коэффициент, стоящий при переменной в косинусе при интегрировании становится обратным значением перед синусом.Распространенные примеры интегрирования косинуса
Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинусПример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрированиеПример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интегралПример 4. Найти интеграл функции y= cos (x/5).

Решение: Записываем неопределенный интегралПример 5. Найти интеграл функции y= cos (x/6).
Решение: Проинтегрируем по приведенной выше формуле
Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинусаПример 7. Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрированияПример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1.
Решение: Находим первоначальную
С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
Подставляем полученную постоянную в уравнение
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
Находим определенный интеграл в указанных пределах
Он равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
Таким образом площадь необходимо искать на трех промежутках
Ось абсцисс можем записать функцией y = 0. Таким образом на первом промежутке площадь равна интегралу от косинуса,
Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = — cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy). Вычисляем площадь интегрированием в указаных пределах
Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
На этом знакомство с интегрированием косинуса завершается. Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса. Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории «Интегрирование функций».Cos 2x Formula — Объяснение, решаемые примеры и часто задаваемые вопросы
Что такое формула Cos 2x?
В прямоугольном треугольнике тригонометрические отношения угла объясняют нам связь, существующую между углом и длиной его сторон.
 Но тогда что такое cos 2x? Формула Cosine 2x или Cos 2x также является одной из таких тригонометрических формул, которая также известна как формула двойного угла. Это называется формулой двойного угла, потому что в ней есть двойной угол.Это причина, по которой он основан на выражениях для тригонометрических функций суммы и разности двух чисел (углов) и связанных выражениях. Теперь, когда мы знаем, что такое формула cos 2x, мы можем двигаться дальше и узнать некоторые более важные вещи о тригонометрии, а также узнать, что такое формула cos2x.
Но тогда что такое cos 2x? Формула Cosine 2x или Cos 2x также является одной из таких тригонометрических формул, которая также известна как формула двойного угла. Это называется формулой двойного угла, потому что в ней есть двойной угол.Это причина, по которой он основан на выражениях для тригонометрических функций суммы и разности двух чисел (углов) и связанных выражениях. Теперь, когда мы знаем, что такое формула cos 2x, мы можем двигаться дальше и узнать некоторые более важные вещи о тригонометрии, а также узнать, что такое формула cos2x.Тригонометрия и прямоугольный треугольник
В прямоугольном треугольнике гипотенуза, основание (смежное) и перпендикуляр (противоположный), т. Е. Три стороны прямоугольного треугольника определяют тригонометрические соотношения. получены.В математике существует три основных тригонометрических соотношения, которые также известны как тригонометрические тождества. Мы можем найти недостающие углы и недостающие стороны прямоугольного треугольника с помощью тригонометрических соотношений.
 В прямоугольном треугольнике один угол равен 90 градусам, а остальные два угла — по 45 градусов каждый. Три стороны прямоугольного треугольника:
В прямоугольном треугольнике один угол равен 90 градусам, а остальные два угла — по 45 градусов каждый. Три стороны прямоугольного треугольника:Гипотенуза: Гипотенуза противоположна 90 градусам и является самой длинной стороной треугольника.
Перпендикуляр (напротив): это сторона, которая противоположна неизвестному углу, представленному как θ, и перпендикулярна основанию (то есть угол между основанием и перпендикуляром составляет 90 градусов).
Основание (рядом): это основание, на котором опирается треугольник, и оно также содержит оба угла, то есть 90 градусов, а также неизвестный угол θ.
[Изображение будет загружено в ближайшее время]
Теорема Пифагора
Согласно теореме Пифагора,
В прямоугольном треугольнике
(напротив) 2+ (рядом) 2 = (Гипотенуза) 2
Что такое функция косинуса?
Отношение стороны, прилегающей к углу (θ), к гипотенузе (самой длинной стороне) в треугольнике определяется как косинус угла.
 {2} x} \]
{2} x} \] Тригонометрические функции острых углов
грех X = opp / hyp = a / c, csc X = hyp / opp = c / a
загар X = opp / adj = a / b, детская кроватка X = adj / opp = b / a
cos X = adj / hyp = b / c, сек X = hyp / adj = c / b,Тригонометрические функции произвольных углов
грех X = b / r, csc X = r / b
загар X = b / a, детская кроватка X = a / b
cos X = a / r, сек X = r / aОсобые треугольники
С помощью специальных треугольников можно найти тригонометрические функции специальных углов: 30, 45 и 60 градусов.
Законы синуса и косинуса в треугольниках
В любом треугольнике мы имеем:
1 — Синусоидальный закон
грех A / a = грех B / b = грех C / c
2 — Законы косинусов
a 2 = b 2 + c 2 -2 b c cos A
b 2 = a 2 + c 2 — 2 a c cos B
c 2 = a 2 + b 2 — 2 a b cos CОтношения между тригонометрическими функциями
cscX = 1 / sinX
sinX = 1 / cscX
сек X = 1 / cos X
cosX = 1 / секX
tanX = 1 / cotX
cotX = 1 / tanX
tanX = sinX / cosX
cotX = cosX / sinXПифагорейские тождества
sin 2 X + cos 2 X = 1
1 + загар 2 X = сек 2 X
1 + детская кроватка 2 X = csc 2 XИдентификаторы с отрицательным углом
sin (-X) = — sinX, нечетная функция
csc (-X) = — cscX, нечетная функция
cos (-X) = cosX, четная функция
сек (-X) = секX, четная функция
tan (-X) = — tanX, нечетная функция
кроватка (-X) = — cotX, нечетная функцияCofunctions Identities
sin (π / 2 — X) = cosX
cos (π / 2 — X) = sinX
загар (π / 2 — X) = cotX
детская кроватка (π / 2 — X) = tanX
сек (π / 2 — X) = cscX
csc (π / 2 — X) = secXФормулы сложения
cos (X + Y) = cosX cosy — sinX sinY
cos (X — Y) = cosX cosy + sinX sinY
sin (X + Y) = sinX cosy + cosX sinY
sin (X — Y) = sinX cosy — cosX sinY
tan (X + Y) = [tanX + tanY] / [1 — tanX tanY]
tan (X — Y) = [tanX — tanY] / [1 + tanX tanY]
детская кроватка (X + Y) = [cotX cotY — 1] / [cotX + cotY]
детская кроватка (X — Y) = [cotX cotY + 1] / [cotY — cotX]Сумма к формулам произведения
cosX + cosy = 2cos [(X + Y) / 2] cos [(X — Y) / 2]
sinX + sinY = 2sin [(X + Y) / 2] cos [(X — Y) / 2]Отличие от формул продукта
cosX — cosy = — 2sin [(X + Y) / 2] sin [(X — Y) / 2]
sinX — sinY = 2cos [(X + Y) / 2] sin [(X — Y) / 2]Формулы произведения суммы / разности
cosX cosy = (1/2) [cos (X — Y) + cos (X + Y)]
sinX cosy = (1/2) [sin (X + Y) + sin (X — Y)]
cosX sinY = (1/2) [sin (X + Y) — sin [(X — Y)]
sinX sinY = (1/2) [cos (X — Y) — cos (X + Y)]Формула разности квадратов
sin 2 X — грех 2 Y = sin (X + Y) sin (X — Y)
cos 2 X — cos 2 Y = — sin (X + Y) sin (X — Y)
cos 2 X — sin 2 Y = cos (X + Y) cos (X — Y)Формулы двойных углов
грех (2X) = 2 sinX cosX
cos (2X) = 1-2sin 2 X = 2cos 2 X — 1
загар (2X) = 2tanX / [1 — загар 2 X]Формулы множественных углов
sin (3X) = 3sinX — 4sin 3 X
cos (3X) = 4cos 3 X — 3cosX
sin (4X) = 4sinXcosX — 8sin 3 XcosX
cos (4X) = 8cos 4 X — 8cos 2 X + 1Формулы полууглов
sin (X / 2) = + или — √ ((1 — cosX) / 2)
cos (X / 2) = + или — √ ((1 + cosX) / 2)
tan (X / 2) = + или — √ ((1 — cosX) / (1 + cosX))
= sinX / (1 + cosX) = (1 — cosX) / sinXФормулы для снижения мощности
sin 2 X = 1/2 — (1/2) cos (2X))
cos 2 X = 1/2 + (1/2) cos (2X))
грех 3 X = (3/4) sinX — (1/4) sin (3X)
cos 3 X = (3/4) cosX + (1/4) cos (3X)
sin 4 X = (3/8) — (1/2) cos (2X) + (1/8) cos (4X)
cos 4 X = (3/8) + (1/2) cos (2X) + (1/8) cos (4X)
грех 5 X = (5/8) sinX — (5/16) sin (3X) + (1/16) sin (5X)
cos 5 X = (5/8) cosX + (5/16) cos (3X) + (1/16) cos (5X)
sin 6 X = 5/16 — (15/32) cos (2X) + (6/32) cos (4X) — (1/32) cos (6X)
cos 6 X = 5/16 + (15/32) cos (2X) + (6/32) cos (4X) + (1/32) cos (6X)Периодичность тригонометрических функций
sin (X + 2π) = sin X, период 2π
cos (X + 2π) = cos X, период 2π
сек (X + 2π) = сек X, период 2π
csc (X + 2π) = csc X, период 2π
tan (X + π) = tan X, период π
детская кроватка (X + π) = детская кроватка X, период π- Тригонометрические таблицы.
 2 {\ theta}} $
2 {\ theta}} $Упрощенная форма
Он также используется для упрощения частного вычитания тангенса в квадрате угла из единицы на сумму единицы и тангенса в квадрате угла как косинуса двойного угла.2 {A}}
долл. СШАПроба
Узнайте, как доказать правило косинуса двойного угла в терминах квадрата функции загара в тригонометрии.
Доказательство формулы cos (2x) | cos (2A) Идентификационный номер
Тождество двойного угла cos — это математическая формула в тригонометрии, которая используется для раскрытия функций cos, содержащих двойной угол. Например, если theta ($ \ theta $) — угол прямоугольного треугольника, то cos двойного угла записывается как $ \ cos {(2θ)} $. Математически он расширяется следующим образом.2 {\ theta}
долл. СШАПришло время узнать, как cos формулы двойного угла выводится в математической форме в тригонометрии по геометрии.
Строительство
Cos тождества двойного угла можно вывести в тригонометрии, построив прямоугольный треугольник с двойным углом.
 Выполните следующие шаги, чтобы получить требуемый треугольник.
Выполните следующие шаги, чтобы получить требуемый треугольник.- Угол $ \ small \ Delta FDE $ делится пополам прямой линией, проведенной от точки $ \ small D $ к стороне $ \ small \ overline {EF} $, и пересекает сторону $ \ small \ overline {EF}. $ в точке $ \ small G $.Два угла равны, и каждый угол обозначается символом $ x $.
- Проведите перпендикулярную линию к стороне $ \ small \ overline {DG} $ от точки $ \ small G $ по направлению к стороне $ \ small \ overline {DE} $, и она пересекает сторону $ \ small \ overline {DE} $ в точке $ \ small H $.
- Теперь проведите перпендикулярную линию к стороне $ \ small \ overline {DF} $ от точки $ \ small H $. Он пересекает сторону $ \ small \ overline {DG} $ в точке $ \ small I $, а также перпендикулярно пересекает сторону $ \ small \ overline {DF} $ в точке $ \ small J $.
- Проведите перпендикулярную линию к стороне $ \ small \ overline {HJ} $ от точки $ \ small G $, которая разделяет сторону $ \ small \ overline {HJ} $ в точке $ \ small K $.

Проба
Прямоугольный треугольник построен геометрически с двойным углом и используется для математического вычисления разложения функции двойного угла cos в тригонометрической форме.
Выразительный косинус двойного угла
Угол $ \ Delta FDE $ равен $ 2x $, и это двойной угол. Геометрически $ \ Delta FDE $ и $ \ Delta JDH $ — подобные треугольники.Таким образом, угол $ \ Delta JDH $ также равен $ 2x $.
Согласно $ \ Delta JDH $, запишите cos двойного угла в форме отношения. $ \ overline {DJ} $ — смежная сторона (основание), а $ \ overline {DH} $ — гипотенуза в этом треугольнике.
$ \ cos {2x} = \ dfrac {DJ} {DH}
долл. СШАНа самом деле сторона $ \ overline {HJ} $ делит сторону $ \ overline {DF} $ на две стороны $ \ overline {DJ} $ и $ \ overline {JF} $.
$ DF \, = \, DJ + JF $
$ \ подразумевает DJ = DF \, — \, JF $
Следовательно, длину стороны $ \ overline {DJ} $ можно записать как вычитание длин стороны $ \ overline {DF} $ из стороны $ \ overline {JF} $.

$ \ implies \ cos {2x} $ $ \, = \, $ $ \ dfrac {DF-JF} {DH} $
$ \ implies \ cos {2x} $ $ \, = \, $ $ \ dfrac {DF} {DH} — \ dfrac {JF} {DH} $
Сторона $ \ overline {KG} $ параллельна стороне $ \ overline {JF} $. Точно так же стороны $ \ overline {HJ} $ и $ \ overline {EF} $ также являются параллельными прямыми. Следовательно, длины сторон $ \ overline {KG} $ и $ \ overline {JF} $ геометрически равны.
$ JF =
KG $Следовательно, длину стороны $ \ overline {JF} $ можно заменить длиной стороны $ \ overline {KG} $ в разложении функции $ \ cos {(2x)} $.
$ \ implies \ cos {2x} $ $ \, = \, $ $ \ dfrac {DF} {DH} — \ dfrac {KG} {DH} $
Преобразование сторон в тригонометрические функции
Функция двойного угла cos расширена по сторонам. Итак, пора преобразовать их в тригонометрические функции.
$ \ overline {DF} $ — это сторона, прилегающая к $ \ Delta FDG $, и ее угол равен $ x $. Связь между ними можно записать следующим образом.

$ \ cos {x} \, = \, \ dfrac {DF} {DG} $
$ \ подразумевает DF = {DG} \ cos {x} $
Замените длину стороны $ \ overline {DF} $ равным ей значением в разложении $ \ cos {2x} $.
$ \ implies \ cos {2x} $ $ \, = \, $ $ \ dfrac {{DG} \ cos {x}} {DH} — \ dfrac {KG} {DH} $
$ \ implies \ cos {2x} $ $ \, = \, $ $ \ dfrac {DG} {DH} \ times \ cos {x} $ $ — $ $ \ dfrac {KG} {DH} $
$ \ overline {DG} $ и $ \ overline {DH} $ — смежная сторона и гипотенуза $ \ Delta GDH $. Их соотношение можно представить функцией косинуса.
$ \ cos {x} \, = \, \ dfrac {DG} {DH}
долл. СШАТеперь заменим соотношение между длинами сторон $ \ overline {DG} $ и $ \ overline {DH} $ в разложении на двойной угол cos.2 {x} — \ dfrac {KG} {DH}
долл. СШАТаким же образом попробуем преобразовать оставшееся соотношение в тригонометрическую форму.
$ \ overline {KG} $ — это сторона $ \ Delta KHG $, но угол этого прямоугольного треугольника неизвестен.
 Таким образом, невозможно продолжить вывод разложения $ \ cos {(2x)} $ до тех пор, пока это препятствие не будет преодолено.
Таким образом, невозможно продолжить вывод разложения $ \ cos {(2x)} $ до тех пор, пока это препятствие не будет преодолено.Найти неизвестный угол треугольника
$ \ overline {KG} $ и $ \ overline {DF} $ — две параллельные прямые, а $ \ overline {DG} $ — их трансверсаль. $ \ Angle FDG $ и $ \ angle KGD $ — это чередующиеся внутренние углы, и они геометрически равны, но $ \ angle GDF $ равен $ x $.° + x $ 9 0003
$ \, \, \, \ следовательно \, \, \, \, \, \, $ $ \ angle KHG \, = \, x $
Следовательно, получается, что угол $ \ Delta KHG $ также равен $ x $, потому что это аналогичный треугольник. Теперь вывод тождества $ \ cos {(2x)} $ можно продолжить.
Продолжить преобразование коэффициента в тригонометрической форме
$ \ overline {KG} $ находится на противоположной стороне от $ \ Delta KHG $, и было определено, что угол этого треугольника равен $ x $. Теперь выразите отношение между ними в тригонометрической форме.2 {x} — \ dfrac {{HG}} {DH} \ times \ sin {x}
долл. 2x равна 2.2 и 1 / x.
2x равна 2.2 и 1 / x.Что такое секанс в квадрате 0?
Секанс — это величина, обратная косинусу. Косинус 0 четко определен и равен 1. Следовательно, секанс 0 также равен 1. А квадрат секанса 0 равен 1² = 1.
Какой угол tan1?
Важные углы: 30 °, 45 ° и 60 °
Уголок Загар = Sin / Cos 30 ° 1 √3 = √3 3 45 ° 1 60 ° √3 Обратный загар Атана?
Функция Excel ATAN возвращает арктангенс числа.Функция противоположна TAN.
Tan 1 — это то же самое, что и детская кроватка?
Использование соглашения tan-1x может привести к путанице относительно разницы между арктангенсом и котангенсом. Оказывается, что arctan и cot на самом деле разные вещи: cot (x) = 1 / tan (x), поэтому котангенс в основном является обратной величиной касательной, или, другими словами, мультипликативной обратной величиной.

Как найти обратный синус?
Пример: найти угол «а»
- Начинаем с: sin a ° = противоположно / гипотенуза.
- sin a ° =
- Вычислить sin a ° = 0,6293…
- Обратный синус: a ° = sin − 1 (0,6293…)
- Воспользуйтесь калькулятором, чтобы найти sin − 1 (0,6293…): a ° = 39,0 ° (с точностью до 1 знака после запятой)
Как найти обратный синус?
Обратный синус
- Функция, обратная синусу (также называемая арксинусом), является функцией, обратной синусу.
- sin θ = (сторона, противоположная θ / гипотенуза)
- Или θ = Sin-1 (сторона, противоположная θ / гипотенузе)
- Таким же образом можно определить обратный косинус и обратный загар.
Как найти журналы и антилогарифмические таблицы?
Ниже приведены шаги, чтобы найти файл Antilog. Первый шаг — разделить характеристику и мантиссу числа. Используйте таблицу антилогарифма, чтобы найти соответствующее значение для мантиссы.
 Первые две цифры мантиссы работают как номер строки, а третья цифра равна номеру столбца.
Первые две цифры мантиссы работают как номер строки, а третья цифра равна номеру столбца.KryssTal: тригонометрические уравнения
KryssTal: тригонометрические уравнения
В алгебре мы рассматривали решение простых уравнений, таких как 5X — 2 = 0 и квадратные уравнения типа Х 2 — 3X + 1 = 0 .В тригонометрии мы ввели тригонометрические функции (синусы, косинусы и касательные).В этом эссе мы объединим тригонометрическую функцию в уравнения, которые можно решить.
Начнем с напоминания о тригонометрических отношениях: Sin X / Cos X = Желто-коричневый X Sin 2 X + Cos 2 X = 1 Кроме того, существуют отношения, называемые двойными углами : Sin 2X = 2 Sin X Cos X Cos 2X = Cos 2 X — Sin 2 X Поскольку Sin 2 X + Cos 2 X = 1, это последнее соотношение также можно записать как: Cos 2X = 1-2 Sin 2 X Cos 2X = 2 Cos 2 X — 1
Прежде чем мы сможем решить сложные тригонометрические уравнения, мы должны посмотреть, как изменяются синусы и косинусы. Ниже приведен график Y = Sin X. X измеряется в радианах. Синусы периодические. Они колеблются между 1 и -1 на 360 o (2 π радиан), начиная с 0 и заканчивая 0.
Ниже приведен график Y = Sin X. X измеряется в радианах. Синусы периодические. Они колеблются между 1 и -1 на 360 o (2 π радиан), начиная с 0 и заканчивая 0.Ниже представлен график Y = Cos X. Это похоже, но в другой фазе.
Косинусы также колеблются между 1 и -1 на протяжении 360 o (2 π радианов), начиная с 1 и заканчивая 1.В таблице ниже обобщена информация как для синусов, так и для косинусов между 0 o и 360 o (от 0 до 2 π радианов).Эта информация будет использоваться при решении тригонометрических уравнений.
Угол
( o )Угол
(рад)Синус Косинус 0 0 0 1 30 π / 6 1/2 √3 / 2 45 π / 4 1 / √2 1 / √2 60 π / 3 √3 / 2 1/2 90 π / 2 1 0 120 2π / 3 √3 / 2 -1 / 2 135 3π / 4 1 / √2 -1 / √2 150 5π / 6 1/2 -√3 / 2 180 π 0 -1 210 7π / 6 -1 / 2 -√3 / 2 225 5π / 4 -1 / √2 -1 / √2 240 4π / 3 -√3 / 2 -1 / 2 270 3π / 2 -1 0 300 5π / 3 -√3 / 2 1/2 315 7π / 4 -1 / √2 1 / √2 330 11π / 6 -1 / 2 √3 / 2 360 2π 0 1
Используя таблицу или графики выше и некоторую алгебру, решите следующие уравнения для значений от 0 o до 360 o . Sin X = 1/2
Sin X = 1/2 Используя таблицу, легко увидеть, что X имеет два значения в требуемом диапазоне. Это:
X = 30 o и X = 150 o .
Cos X + 1/2 = 0Изменив уравнение (чтобы получить Cos X с одной стороны и числа с другой стороны) дает:
Cos X = -1 / 2
Используя таблицу, мы видим, что X имеет два значения в требуемом диапазоне.Это:
X = 120 o и X = 240 o .
Cos X Tan X = 1 / √2Использование идентичности для замены Tan X дает:
Cos X (Sin X / Cos X) = 1 / √2
Косинусы сокращаются, чтобы дать:
Sin X = 1 / √2
Это дает два значения X:
X = 45 o и X = 135 o .
2 Cos 2X + 1 = 0Переставьте уравнение:
Cos 2X = — 1/2
Следовательно, 2X = 120 o и 240 o , что дает:
X = 60 o и X = 120 o .
Sin X — Cos 2X = 0
Используя тождество двойного угла, замените Cos 2X на (1-2 Sin 2 X):
Грех X — (1-2 Sin 2 X) = 0
Sin X — 1 + 2 Sin 2 X = 0
который преобразуется в квадратное уравнение в Sin 2 X:
2 Sin 2 X + Sin X — 1 = 0
Это можно решить путем факторизации:
(2 Sin X — 1) (Sin X + 1) = 0
Это уравнение дает 0, если либо 2 Sin X — 1 = 0, либо Sin X + 1 = 0.Другими словами:
Sin X = 1/2 или Sin X = -1
Первое уравнение дает два значения (X = 30 o , X = 150 o ), второе уравнение дает одно значение (270 o ). Таким образом, решение исходного уравнения:
X = 30 o , X = 150 o и X = 270 o .
2 Cos 2 X + Sin 2X = 0
Используя идентичность двойного угла, Sin 2X можно заменить на 2 Sin X Cos X:
2 Cos 2 X + 2 Sin X Cos X = 0
2 Cos X является общим для обоих терминов, поэтому его можно переписать:
2 Cos X (Cos X + Sin X) = 0
Это уравнение дает 0, если либо 2 Cos X = 0, либо Cos X + Sin X = 0.Другими словами:
Cos X = 0 или Sin X = -Cos X
Первое уравнение дает два значения (X = 90 o , X = 270 o ). Второе уравнение также дает два значения (135 o и 315 o — проверьте эти цифры в таблице). Таким образом, решение исходного уравнения:
X = 90 o , X = 135 o , X = 270 o и 315 o .
© 2000, 2009 KryssTal
Введение в алгебру и способы решения простых, одновременных и квадратных уравнений. Прямоугольные треугольники, синусы, косинусы, касательные. Использование тригонометрических функций, рядов и формул.
Графы — это способ визуализации алгебраических функций. Декартова система координат вводится вместе с описанием построения графика из первых принципов.Есть примеры разных типов графиков.
Индекс и база. Определены логарифмы. База 10 и база e. Использование логарифмов в расчетах. Ряды для логарифмов.
Сферическая тригонометрия — это тригонометрия треугольников, нарисованных на сфере.
Прямоугольные треугольники, синусы, косинусы, касательные. Использование тригонометрических функций, рядов и формул.
Графы — это способ визуализации алгебраических функций. Декартова система координат вводится вместе с описанием построения графика из первых принципов.Есть примеры разных типов графиков.
Индекс и база. Определены логарифмы. База 10 и база e. Использование логарифмов в расчетах. Ряды для логарифмов.
Сферическая тригонометрия — это тригонометрия треугольников, нарисованных на сфере.Чему равен cos 2X?
Чему равно cos 2X?
cos (2x) = 2cos2 (x) — 1 = 2 (0,4) 2-1 = −0,68. В следующем упражнении вам дадут информацию об угле и попросят применить формулы двойного угла, чтобы найти синус двойного угла и косинус двойного угла.2 (х) = 1.
Какова формула cos a B?
= sinA cosB — cosA sinB cos (A + B) = cosA cosB — sinA sinB cos (A — B) = cosA cosB + sinA sinB sin2 A + cos2 A = 1, sin 2A = 2 sinA cosA cos 2A = 2 cos2 A — 1 = 1-2 sin2 A 2 sinA cosB = sin (A + B) + sin (A — B) 2 cosA sinB = sin (A + B) — sin (A — B)
Какая производная от cos 3x?
Это означает, что цепное правило позволит нам дифференцировать выражение cos (3x)… .
 Используя цепное правило, найти производную cos (3x)
Используя цепное правило, найти производную cos (3x)cos3x ► Производная cos3x = -3sin (3x) cos 3 x ► Производная cos 3 x = -3sin (3x) cos 3x ► Производная cos 3x = -3sin (3x) cos (3x) ► Производная cos (3x) = -3sin (3x) Как отличить cos 3?
Вот наш пост о том, как различать cos (3x)….3 = -3cos2 (x) sin (x)
Как сложить sin и cos?
Формулы сложения и вычитания для синуса и косинуса
- Формула сложения для косинуса: cos (a + b) = cosa cosb − sina sinb (a + b) = cos
- Формула вычитания для косинуса: cos (a − b) = cosa cosb + sina sinb (a — b) = cos
- Формула сложения для синуса: sin (a + b) = sina cosb + cosa sinb (a + b) = sin
Что такое Cos Alpha Beta?
Мы шаг за шагом изучим доказательство формулы составного угла cos (α — β).

Решенные примеры
Пример 1) Докажите Cos3x = 4 Cos³x — 3 Cos x
Решение 1) У нас есть Cos3x = Cos (2x + x)
Cos 3x = Cos2x Cosx — Sin 2x Sin x
Cos 3x = (2Cos²x — 1) Cos x — 2Sinx Cosx Sinx
Cos3x = (2Cos²x — 1) Cosx — 2Cosx (1-Cos²x )
Cos3x = 2Cos³x — Cosx — 2Cosx + Cos³x
Cos3x = 4 Cos³x — 3Cosx
Следовательно, это доказано.
Пример 2) Решить cos 2a = sin a, для — ≤ a <Π
Решение 2) Мы можем использовать формулу двойного угла cos 2a = 1-2 sin2 a
Следовательно, получается 1-2 sin2 a = sin a
2 sin2 a + sin a — 1 = 0,
факторизация этого квадратного уравнения с переменной sin x
(2 sin a — 1) (sin a + 1) = 0
2 sin a — 1 = 0 или sin a + 1 = 0
sin a = 1/2 или sin a = −1
Тригонометрические тождества и формулы
Ниже приведены некоторые из наиболее важных определений, тождеств и формул в тригонометрии.

 \circ }=5\)
\circ }=5\)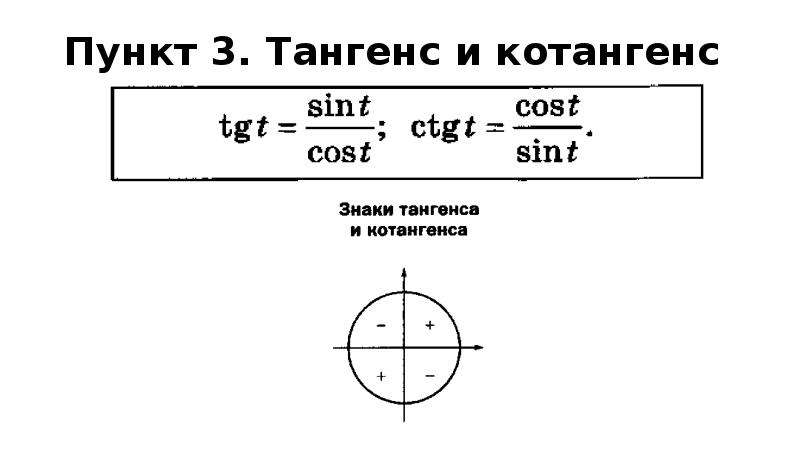 {2}}\frac{5\pi }{12} \right)=\sqrt{3}\cdot \left( -\frac{\sqrt{3}}{2} \right)=-\frac{3}{2}=-1,5\)
{2}}\frac{5\pi }{12} \right)=\sqrt{3}\cdot \left( -\frac{\sqrt{3}}{2} \right)=-\frac{3}{2}=-1,5\) {2}}}=\pm \sqrt{0,36}=\pm 0,6\)
{2}}}=\pm \sqrt{0,36}=\pm 0,6\)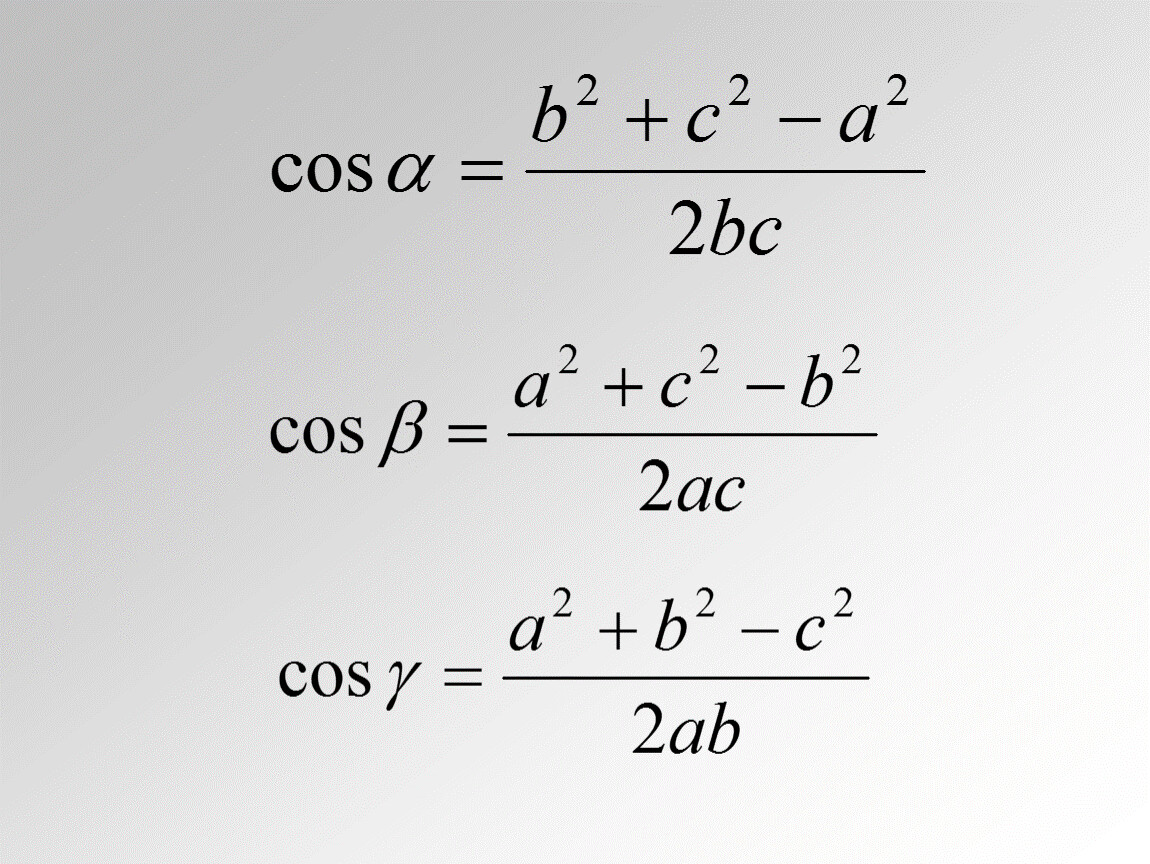 Поэтому одновременно необходимо разделить на этот коэффициент.
Поэтому одновременно необходимо разделить на этот коэффициент.
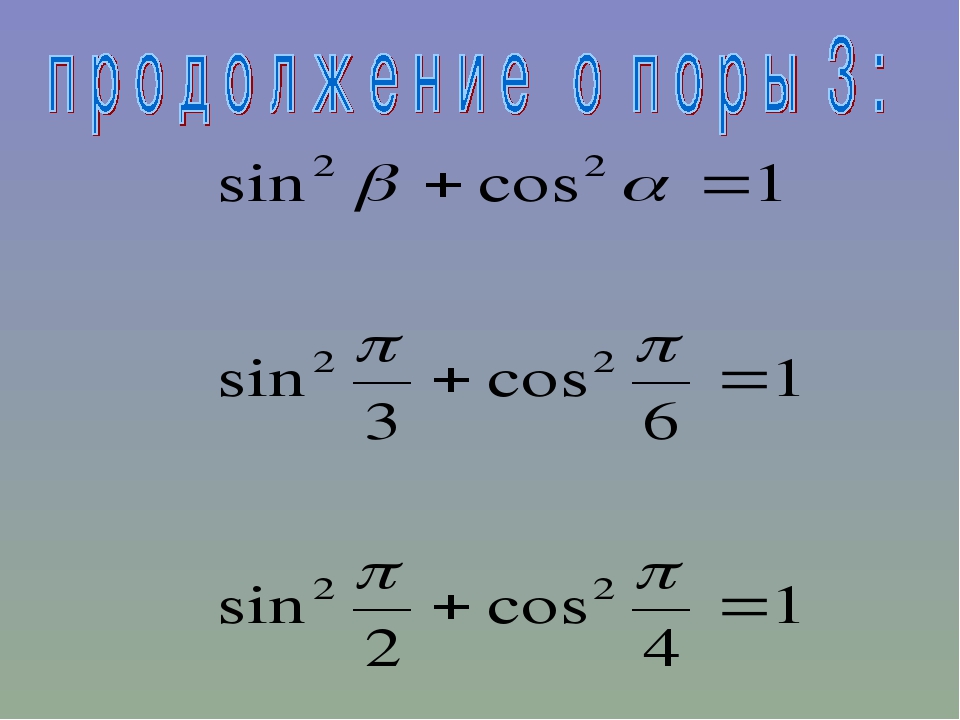
 Таким образом на первом промежутке площадь равна интегралу от косинуса,
Таким образом на первом промежутке площадь равна интегралу от косинуса, Но тогда что такое cos 2x? Формула Cosine 2x или Cos 2x также является одной из таких тригонометрических формул, которая также известна как формула двойного угла. Это называется формулой двойного угла, потому что в ней есть двойной угол.Это причина, по которой он основан на выражениях для тригонометрических функций суммы и разности двух чисел (углов) и связанных выражениях. Теперь, когда мы знаем, что такое формула cos 2x, мы можем двигаться дальше и узнать некоторые более важные вещи о тригонометрии, а также узнать, что такое формула cos2x.
Но тогда что такое cos 2x? Формула Cosine 2x или Cos 2x также является одной из таких тригонометрических формул, которая также известна как формула двойного угла. Это называется формулой двойного угла, потому что в ней есть двойной угол.Это причина, по которой он основан на выражениях для тригонометрических функций суммы и разности двух чисел (углов) и связанных выражениях. Теперь, когда мы знаем, что такое формула cos 2x, мы можем двигаться дальше и узнать некоторые более важные вещи о тригонометрии, а также узнать, что такое формула cos2x. В прямоугольном треугольнике один угол равен 90 градусам, а остальные два угла — по 45 градусов каждый. Три стороны прямоугольного треугольника:
В прямоугольном треугольнике один угол равен 90 градусам, а остальные два угла — по 45 градусов каждый. Три стороны прямоугольного треугольника: {2} x} \]
{2} x} \]
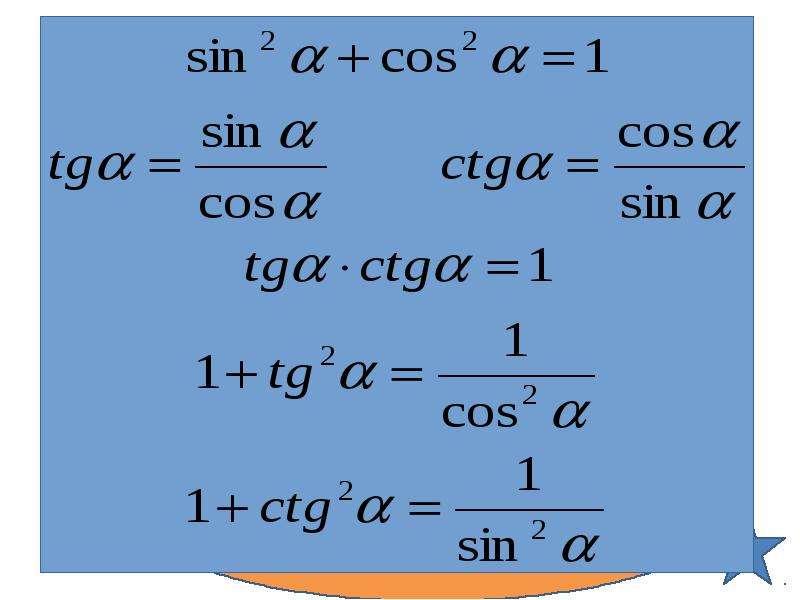 2 {\ theta}} $
2 {\ theta}} $ Выполните следующие шаги, чтобы получить требуемый треугольник.
Выполните следующие шаги, чтобы получить требуемый треугольник.

 Таким образом, невозможно продолжить вывод разложения $ \ cos {(2x)} $ до тех пор, пока это препятствие не будет преодолено.
Таким образом, невозможно продолжить вывод разложения $ \ cos {(2x)} $ до тех пор, пока это препятствие не будет преодолено. 2x равна 2.2 и 1 / x.
2x равна 2.2 и 1 / x.
 Первые две цифры мантиссы работают как номер строки, а третья цифра равна номеру столбца.
Первые две цифры мантиссы работают как номер строки, а третья цифра равна номеру столбца. Ниже приведен график Y = Sin X. X измеряется в радианах. Синусы периодические. Они колеблются между 1 и -1 на 360 o (2 π радиан), начиная с 0 и заканчивая 0.
Ниже приведен график Y = Sin X. X измеряется в радианах. Синусы периодические. Они колеблются между 1 и -1 на 360 o (2 π радиан), начиная с 0 и заканчивая 0. Sin X = 1/2
Sin X = 1/2 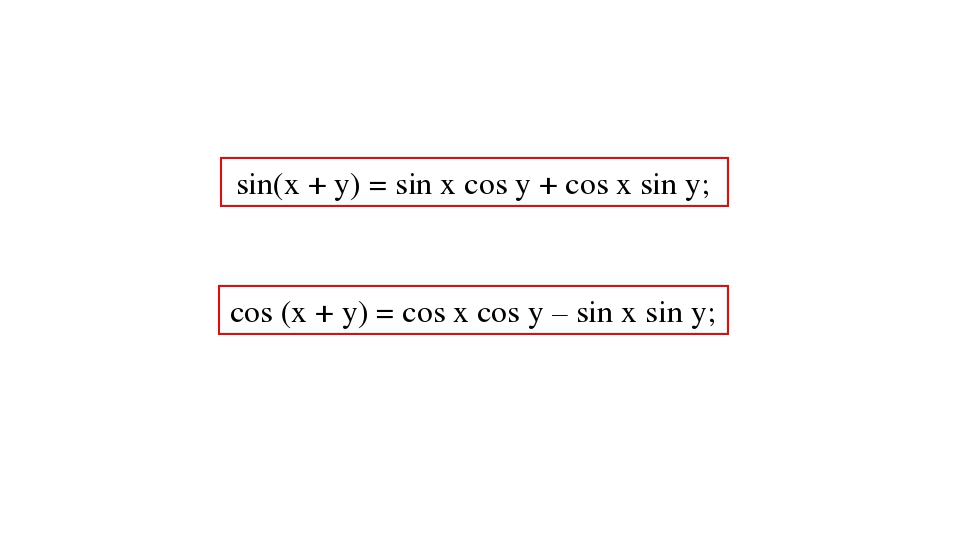

 Прямоугольные треугольники, синусы, косинусы, касательные. Использование тригонометрических функций, рядов и формул.
Графы — это способ визуализации алгебраических функций. Декартова система координат вводится вместе с описанием построения графика из первых принципов.Есть примеры разных типов графиков.
Индекс и база. Определены логарифмы. База 10 и база e. Использование логарифмов в расчетах. Ряды для логарифмов.
Сферическая тригонометрия — это тригонометрия треугольников, нарисованных на сфере.
Прямоугольные треугольники, синусы, косинусы, касательные. Использование тригонометрических функций, рядов и формул.
Графы — это способ визуализации алгебраических функций. Декартова система координат вводится вместе с описанием построения графика из первых принципов.Есть примеры разных типов графиков.
Индекс и база. Определены логарифмы. База 10 и база e. Использование логарифмов в расчетах. Ряды для логарифмов.
Сферическая тригонометрия — это тригонометрия треугольников, нарисованных на сфере. Используя цепное правило, найти производную cos (3x)
Используя цепное правило, найти производную cos (3x)