Длина окружности, формула как найти длину окружности
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Как найти длину окружности через диаметр
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
l=πd, где
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
l=2πr , где
π — число пи, равное 3,14
r — радиус окружности
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
l=πd, где
π — число пи, равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
l=πa, где
π — математическая константа, равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
l=πd
Подставляем туда известные переменные и получается, что длина окружности равна
l=πd=3,14·5=15,7(см)
Ответ: 15,7 (см)
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Так и сделаем:
l=2πr=2·π·4≈2·3,14·4=25,12(дм)
Ответ: l=25,12(дм)
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и захватывающие математические игры и головоломки. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом.
Геометрия. Урок 5. Окружность — ЁП
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности.
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Часть окружности, заключенная между двумя точками, называется дугой окружности.
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается. ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
M N – диаметр.
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
∪ A B = ∪ C D = α
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
l = 2 π R
Длина дуги окружности, на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Модуль геометрия: задания, связанные с окружностями.
Круг и окружность | Формулы и расчеты онлайн
Геометрическим местом точек называется совокупность всех точек, удовлетворяющих заданным условиям. Окружность есть геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). Равные отрезки, соединяющие центр с точками окружности, называются радиусами и обозначаются буквами r или R. Дуга — это часть окружности. Секущая — это прямая проходящая через две точки окружности. Хорда — это отрезок секущей, лежащий внутри окружности. С приближением к центру хорда увеличивается.
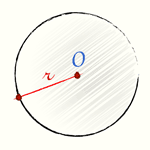 Окружность и радиус | 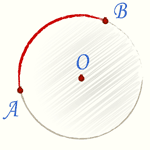 Окружность и дуга окружности | 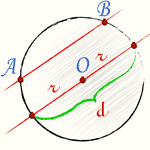 Окружность и секущая |
Диаметр — это хорда проходящая через центр окружности (обозначается d или D). Диаметр равен двум радиусам:
\[d=2r\]
Круг есть часть плоскости, лежащая внутри окружности. Касательная — это прямая пересекающаяся окружность только в одной точке. Касательная это выродившаяся секущая. Касательная к окружности перпендикулярна радиусу проведенному в точку касания. Из одной точки вне круга можно провести к окружности две касательные. Их длины будут равны.
 Окружность и касательная | 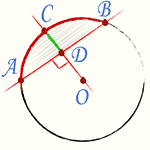 Сегмент окружности | 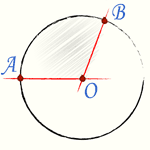 Сектор окружности |
Сегмент — это часть круга, ограниченная дугой и стягивающей ее хордой. Стрелка дуги — это перпендикуляр восстановленный из середины хорды до пересечения с дугой. Высота сегмента — это длина стрелки дуги. Сектор — это часть круга, ограниченная дугой и двумя радиусами, проведенными к концам дуги. Квадрант — это сектор, отсекаемый радиусами, образующими угол 90°.
В помощь студенту
Круг и окружность |
стр. 240 |
|---|
формула через длину окружности, площадь
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса круга
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2πR
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
S – это площадь круга; равна числу π, умноженному на квадрат его радиуса:
S = πR2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см2.
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Найти длину радиуса окружности (круга), все основные формулы.
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2R
O — центр круга
π ≈ 3.14
Формула для определения длины радиуса, если известна площадь круга :
Формула для определения длины радиуса, если известна длина окружности :
R — радиус окружности (круга)
h — высота сегмента
L — длина хорды
O — центр круга
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
- Подробности
- Автор: Сергей Кондратов
Формулы окружности для диаметра, площади и окружности с примерами
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образцы документов CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9 Решения NCERT
- для математики класса 10 Глава 10 Решения
- NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава 13
- NCERT Sol Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10 Глава 1
- Решения NCERT для науки класса 10 Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки 10 класса, глава 8
- Решения NCERT для науки класса 10 Глава 9
- Решения NCERT для науки класса 10 Глава 10
- Решения NCERT для науки класса 10 Глава 11
- Решения NCERT для науки класса 10 Глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки 10 класса Глава 15
- Решения NCERT для науки 10 класса Глава 16
- Class 11 Commerce Syllabus
- ancy Account
- Учебная программа по бизнесу, класс 11
- Учебная программа по экономике, класс 11
- Учебная программа по коммерции, класс 12
Объектов Круга | Формулы Круга
Круг — это замкнутая форма, образованная путем отслеживания точки, которая движется в плоскости таким образом, что расстояние до нее от данной точки постоянно. Слово «круг» происходит от греческого слова «киркос», что означает обруч или кольцо. В этой статье мы рассмотрим важные термины, связанные с кругами, их свойствами и различными формулами кругов.
Ниже приводится краткое описание тем, которые мы рассмотрим в этой статье:
Определение круга
Когда набор всех точек , которые находятся на фиксированном расстоянии от фиксированной точки , соединены, полученная геометрическая фигура называется окружностью.
Давайте теперь немного узнаем о терминологии, используемой в кругах.
1) Термины, относящиеся к Кругам
1.1) Центр
Неподвижная точка в окружности называется центром.
- Итак, набор точек находится на фиксированном расстоянии от центра круга.
1,2) Радиус
Радиус — это фиксированное расстояние между центром и набором точек. Обозначается цифрой «R» .
1,3) Диаметр
Диаметр — это отрезок прямой, имеющий граничные точки в виде окружностей на концах и проходящий через центр.
- Итак, логически диаметр можно разбить на две части:
- Одна часть от одной граничной точки окружности до центра
- А, другая часть от центра до другой граничной точки.
- Следовательно, Диаметр = Двойная длина радиуса или «D = 2R»
1.4) Окружность
Это мера внешней границы круга.
Итак, длина круга или периметр круга называется Окружностью.
1,5) Дуга окружности
Дуга круга — это часть окружности.
Из любых двух точек, лежащих на границе круга, можно создать две дуги: Малую и Большую дугу.
- Малая дуга: Более короткая дуга, образованная двумя точками.
- Major Arc: Более длинная дуга, образованная двумя точками.
1.6) Сектор круга:
Сектор образуется путем соединения концов дуги с центром.
- При соединении конечных точек с центром будут получены два сектора: Minor и Major.
- По умолчанию мы учитываем только второстепенный сектор, если не указано иное.
1,7) Полукруг
Полукруг — это половина круга или,
- Полукруг получается, когда круг делится на две равные части.
Теперь, когда мы знаем всю терминологию, связанную с кругами, давайте узнаем о свойствах круга.
Геометрия — важная тема для асов, если вы планируете набрать 700+ на GMAT. Позвольте нам помочь вам достичь совершенства в GMAT Geometry. Начните с подписки на бесплатную пробную версию и учитесь у лучших в отрасли. В конце концов, о нас больше всего отзывают на gmatclub.
Кэрри Лоу, Гильермо, Сириш и Рагхав — это лишь некоторые из учеников, получивших оценку Q50 + в разделе GMAT Quant с помощью электронного GMAT.
2) Важные свойства круга — линии
Объекты собственности, относящиеся к линиям в окружности
2.1) Хорда
Хорда — это отрезок прямой, концы которого лежат на границе круга.
Свойства хорды
- Перпендикуляр, опущенный из центра, делит хорду на две равные части.
2.2) Касательная
Касательная — это линия, на которой касается окружности в любой точке.
Свойства касательной
- Радиус всегда перпендикулярен касательной в точке, где он касается окружности.
3) Важные свойства круга, связанные с углами
Свойства, относящиеся к углам в окружности
3.1) Угол вписанный
Вписанный угол — это угол между двумя хордами, когда они встречаются на границе круга.
Свойства вписанных углов
1.Углы, образованные одной и той же дугой на окружности круга, всегда равны.
2. Угол в полукруге всегда равен 90 °. 3.2) Центральный угол
Центральный угол — это угол, образующийся, когда две линейные сегменты встречаются, так что одна из конечных точек обоих линейных сегментов находится в центре, а другая — на границе круга.
Свойство центральных углов
- Угол, образованный дугой в центре, вдвое больше угла вписанного , образованного той же дугой.
4) Важные формулы круга: площадь и периметр
Ниже приведены некоторые математические формулы, которые помогут вам вычислить площадь и периметр / длину окружности.
Периметр:
- Периметр или окружность круга = 2 × π × R.
- Длина дуги = (Центральный угол дуги / 360 °) × 2 × π × R.
Площадь:
- Площадь круга = π × R²
- Площадь сектора = (Центральный угол, образованный сектором / 360 °) × π × R².
Обзор всех свойств круга
Вот обобщенный список всех свойств, которые мы изучили в статье до этого момента.
[two_third]
| Важные свойства | ||
| Линии по кругу | Хорда | Перпендикуляр, опущенный из центра, делит хорду на две равные части. |
| Касательная | Радиус всегда перпендикулярен касательной в точке, где он касается окружности. | |
| Углы по окружности | Угол вписанный | 1. Углы, образованные одной и той же дугой на окружности круга, всегда равны. 2. Угол в полукруге всегда равен 90. |
| Центральный угол | Угол, образованный дугой в центре, в два раза больше вписанного угла, образованного той же дугой. | |
| Важные формулы | Окружность круга | 2 × π × R. |
| Длина дуги |
| |
| Площадь круга | π × R² | |
| Площадь сектора |
| |
[/ two_third]
[two_third_last] [/ two_third_last]
Применение свойств в вопросах
Вопрос 1
Длины двух сторон прямоугольного треугольника, кроме гипотенузы, составляют 6 см и 8 см.Если этот прямоугольный треугольник вписан в круг, то какова площадь круга?
- 5 π
- 10 π
- 15 π
- 20 π
- 25 π
Решение
Шаг 1: Дано
- Длины двух сторон прямоугольного треугольника, кроме гипотенузы, равны 6 см и 8 см.
- Этот треугольник вписан в круг.
Шаг 2: найти
Шаг 3: подход и разработка
Нарисуем схематическое изображение.
Применяя свойство, что угол в полукруге равен 90º, мы можем сказать, что AB — это диаметр окружности.
- И, как только мы найдем длину диаметра, мы сможем найти радиус, а затем мы также сможем найти площадь круга.
Применение теоремы Пифагора в △ ABC,
- AB² = AC² + BC²
- AB² = 6² + 8² = 36 +64 = 100
- AB = 10 см
Поскольку AB — диаметр, AB = 2R = 10
Площадь круга = π × R² = π × 5² = 25 π.
Следовательно, правильный ответ — вариант E.
Вопрос 2
На приведенной выше диаграмме О — центр круга. Если OB = 5 см и ∠ABC = 30 0 , то какова длина дуги AC?
- 5π / 6
- 5π / 3
- 5π / 2
- 5π
- 10π
Решение
Шаг 1: Дано
Шаг 2: найти
Шаг 3: подход и разработка
- Длина дуги = (Центральный угол дуги / 360 °) × 2 × π × R.
Чтобы найти длину дуги, нам нужно значение двух переменных: центрального угла дуги и радиуса.
- Нам уже дан радиус как OB = 5см
- Нам нужно найти ∠AOC
При визуализации диаграммы угол, вписанный дугой AC, равен ∠ABC, а центральный угол дугой AC равен AOC.
- Следовательно, мы можем применить свойство, согласно которому угол, образованный дугой в центре, вдвое превышает вписанный угол, образованный той же дугой.
- Таким образом, AOC = 2 × ∠ABC = 2 × 30 ° = 60 °
Теперь мы знаем и центральный угол, образованный дугой.
- Следовательно, длина дуги AC = (Центральный угол дуги / 360 °) × 2 × π × R.
- = (60 ° / 360 °) × 2 × π × 5.
- = (1/6) × 2 × π × 5.
- = (5π / 3) см
Таким образом, правильный ответ — вариант Б.
Если вам понравилась эта статья, вот еще несколько статей, связанных с геометрией:
.Формулы круга в математике | Площадь, окружность, сектор, хорда, круговая дуга
Свойства круга в математике | Дуга, Периметр, Отрезок окружности
Круг можно определить как геометрическое место всех точек, равноудаленных от центральной точки. Здесь мы обсуждаем около свойств круга , формул круга , таких как площадь , периметр , длина дуги, длина сегмента, площадь сегмента .. . пр.
Терминология, связанная с кругами в математике:
Начало координат: Это центральная (равноудаленная) точка круга.Здесь «O» — начало круга.
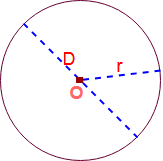
Радиус: Расстояние от центра круга до любой точки вокруг него окружности называется Радиус окружности. Обычно обозначается буквой «r».
Диаметр: Наибольшее расстояние от одного конца круга до другого конца круга называется диаметром круга. Обычно обозначается буквой «D». Диаметр круга = 2 x Радиус круга.я. е D = 2r.
Дуга круга: Это часть окружности круга. Большая дуга называется большой, а меньшая — вспомогательной.
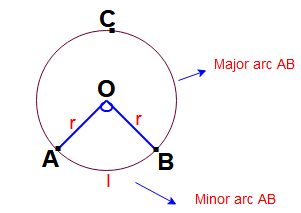Сектор круга: Это часть площади круга между двумя радиусами (клин круга).
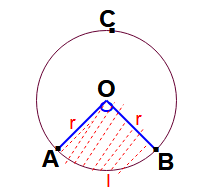
Хорда: Линия , отрезок внутри круга, который касается двух точек на окружности, называется хордой окружности.
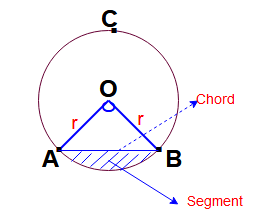
Окружность: Расстояние по окружности называется окружностью или периметром окружности.
Пи (π ): Это число, равное 3,141592… или 22/7.
пи (π ) = (окружность) / (диаметр) любого круга.
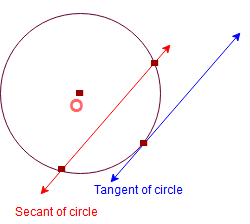
Касательная окружности: линия, перпендикулярная радиусу, которая касается ТОЛЬКО одной точки на окружности.
Секанс окружности : Линия, пересекающая окружность в двух точках, называется Секанс окружности .
Свойства круга:
- Конгруэнтность : две окружности могут быть конгруэнтными тогда и только тогда, когда они имеют равных радиусов.
- Перпендикуляр от центра окружности к хорде делит хорду пополам. Обратное также верно.
- Серединные перпендикуляры двух хорд окружности пересекаются в центре.
- Может быть одна и только одна окружность, проходящая через три или более неколлинеарных точек.
- Если две окружности пересекаются в двух точках, то прямая, проходящая через центры, является серединным перпендикуляром к общей хорде.
- Если две хорды окружности равны, то центр окружности лежит на биссектрисе двух хорд.
- Равные хорды окружности или равные окружности равноудалены от центра.
- Равноудаленные хорды от центра окружности равны друг другу по длине.
- Градус дуги окружности равен удвоенному углу, образуемому ею в любой точке альтернативного сегмента окружности.
- Равные хорды окружности (или конгруэнтных окружностей) проходят равные углы в центре (в соответствующих центрах). Верно и обратное.
- Если сумма противоположных углов четырехугольника равна 180 °, то четырехугольник является вписанным.
- Секущая означает прямую, пересекающую окружность в двух точках. Касательная означает, что это линия, которая касается круга ровно в одной точке.
- В двух концентрических окружностях хорда большего круга, касательная к меньшему, делится пополам в точке контакта.
Круговых формул в математике:
Площадь и длина окружности:
Здесь Начало круга = O, Диаметр = D и Радиус = r
Площадь круга (A) = π r 2 = (π / 4) D 2 = 0,7854 D 2
Окружность круга (C) = 2 π r = π Д.
Площадь круга = (1/2) x окружность x радиус
A = (1/2) x C x r
Диаметр окружности (D) = √ (A / 0.7854).
Дуга и сектор круга:
Здесь угол между двумя радиусами равен ”θ” в градусах. . И сектор круга AOB.
Длина дуги окружности (l) (второстепенная) = (θ / 360) x 2 π r = θ π r / 180
Площадь сектора (второстепенная) = (θ / 360) x π r 2
Если угол θ выражен в радианах, то
Площадь сектора = (θ / 2) r 2
Секторный угол окружности θ = (180 x l) / (π r).
Отрезок круга и периметр отрезка:
Здесь радиус окружности = r, угол между двумя радиусами равен ”θ” в градусах.
Площадь сегмента круга = Площадь сектора — Площадь ΔOAB.
Площадь сегмента = (θ / 360) x π r 2 — (1/2) x sinθ x r 2
Периметр отрезка = (θ π r / 180) + 2r sin (θ / 2).
Длина хорды окружности = 2 √ [h (2r — h)] = 2r sin (θ / 2).
Дуга Длина сегмента круга = l = 0,01745 x r x θ
Онлайн калькулятор для расчета площади отрезка круга
Площадь кругового кольца:
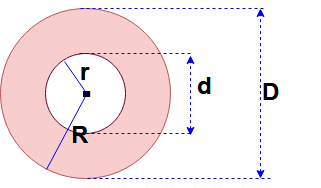
Здесь радиус большого круга = R и Dia = D,
Радиус малого круга = r и диаметр = d,
Площадь кругового кольца = 0,7854 (D 2 — d 2 ) = (π / 4) (D 2 — d 2 )
Площадь кругового кольца = π (R 2 — r 2 ).
Формула пересечения хорд в окружности:
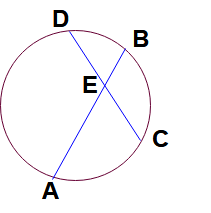
Здесь AB и CD — две окружные хорды, пересекающиеся каждая в точке E.
Тогда AE: EB = DE: EC.
Формула длины касательных окружностей:
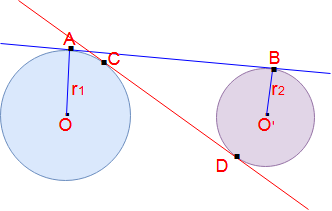
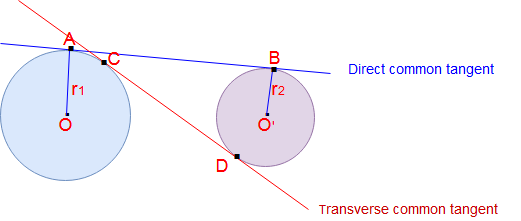
Здесь Две окружности, начало O и O ’и радиус равны r1 и r2 соответственно.
Общий прямой тангенс AB и поперечный общий тангенс = CD
Длина прямой общей касательной AB = √ [(Расстояние между двумя исходными точками) 2 — (r1 -r2) 2 ]
= √ [(OO ’) 2 — (r1 -r2) 2 ]
Длина общей поперечной касательной AB = √ [(Расстояние между двумя исходными точками) 2 — (r1 + r2) 2 ]
= √ [(OO ’) 2 — (r1 + r2) 2 ]
Геометрия по математике
Формулы двухмерных фигур.
Четырехугольник Недвижимости | Трапеция, параллелограмм, Ромб
Типы треугольников с примерами | Свойства треугольника
Система счисления.
Категории номеров
Правила делимости чисел
Формулы суммы n последовательных чисел
Методы поиска HCF и LCM
Проблемы и решения GCD и LCM
Привет, друзья Спасибо за чтение. Надеюсь, вам понравилось. Оставляйте отзывы, комментарии и, пожалуйста, не забудьте поделиться ими.
.Калькулятор кругов
Форма круга
r = радиус
d = диаметр
C = окружность
A = площадь
π = пи = 3,1415926535898
√ = квадратный корень
Использование калькулятора
Используйте этот калькулятор окружности, чтобы найти площадь, длину окружности, радиус или диаметр окружности.Учитывая любую одну переменную A, C, r или d круга, вы можете вычислить три других неизвестных.
Единицы: Обратите внимание, что единицы длины показаны для удобства. На расчеты они не влияют. Единицы измерения указывают на порядок результатов, например футы, футы 2 или футы 3 . Можно заменить любой другой базовый блок.
Формулы окружности через Pi π, радиус r и диаметр d
Радиус и диаметр:
г = д / 2
д = 2рПлощадь круга:
A = πr 2 = πd 2 /4
Окружность круга:
С = 2πr = πd
Вычисления круга:
Используя приведенные выше формулы и дополнительные формулы, вы можете вычислить свойства данного круга для любой данной переменной.2 \]
\ [C = 2 \ pi r \]
\ [d = 2r \]
Вычислить r, C и d | Учитывая A
Зная площадь круга, вычислите радиус, длину окружности и диаметр. Положив r, C и d через A, получим следующие уравнения:
\ [r = \ sqrt {\ frac {A} {\ pi}} \]
\ [C = 2 \ pi r = 2 \ pi \ sqrt {\ frac {A} {\ pi}} \]
\ [d = 2r = 2 \ sqrt {\ frac {A} {\ pi}} \]
Вычислить A, r и d | Учитывая C
По длине окружности вычислите радиус, площадь и диаметр.2} {4} \]
\ [C = 2 \ pi r = 2 \ pi \ frac {d} {2} = \ pi d \]
.